信号与系统实验(MATLAB 西电版)实验19 离散系统状态方程的求解
信号与系统matlab实验报告

信号与系统MATLAB实验报告实验目的本实验旨在通过MATLAB软件进行信号与系统的相关实验,探究信号与系统的特性与应用。
实验步骤1. 准备工作在正式进行实验之前,我们需要做一些准备工作。
首先,确保已经安装好MATLAB软件,并且熟悉基本的操作方法。
其次,准备好实验所需的信号与系统数据,可以是已知的标准信号,也可以是自己采集的实际信号。
2. 信号的生成与显示使用MATLAB编写代码,生成不同类型的信号。
例如,可以生成正弦信号、方波信号、三角波信号等。
通过绘制信号波形图,观察不同信号的特点和变化。
t = 0:0.1:10; % 时间范围f = 1; % 信号频率s = sin(2*pi*f*t); % 正弦信号plot(t, s); % 绘制信号波形图3. 系统的建模与分析根据实验需求,建立相应的系统模型。
可以是线性时不变系统,也可以是非线性时变系统。
通过MATLAB进行模型的建立和分析,包括系统的时域特性、频域特性、稳定性等。
sys = tf([1, 2], [1, 3, 2]); % 系统传递函数模型step(sys); % 绘制系统的阶跃响应图4. 信号与系统的运算对于给定的信号和系统,进行信号与系统的运算。
例如,进行信号的卷积运算、系统的响应计算等。
通过MATLAB实现运算,并分析结果的意义与应用。
x = [1, 2, 3]; % 输入信号h = [4, 5, 6]; % 系统响应y = conv(x, h); % 信号的卷积运算plot(y); % 绘制卷积结果的波形图5. 实验结果分析根据实验数据和分析结果,对实验进行结果总结与分析。
可以从信号的特性、系统的特性、运算结果等方面进行综合性的讨论和分析。
实验总结通过本次实验,我们学习了如何在MATLAB中进行信号与系统的实验。
通过生成信号、建立系统模型、进行运算分析等步骤,我们深入理解了信号与系统的基本原理和应用方法。
通过实验数据和结果分析,我们对信号与系统有了更深刻的认识,并掌握了MATLAB在信号与系统实验中的应用技巧。
matlab信号与系统实验报告
实验一 基本信号的产生与运算一、 实验目的学习使用MATLAB 产生基本信号、绘制信号波形、实现信号的基本运算。
二、 实验原理MATLAB 提供了许多函数用于产生常用的基本信号:如阶跃信号、脉冲信号、指数信号、正弦信号和周期方波等等。
这些信号是信号处理的基础。
1、 利用MATLAB 产生下列连续信号并作图。
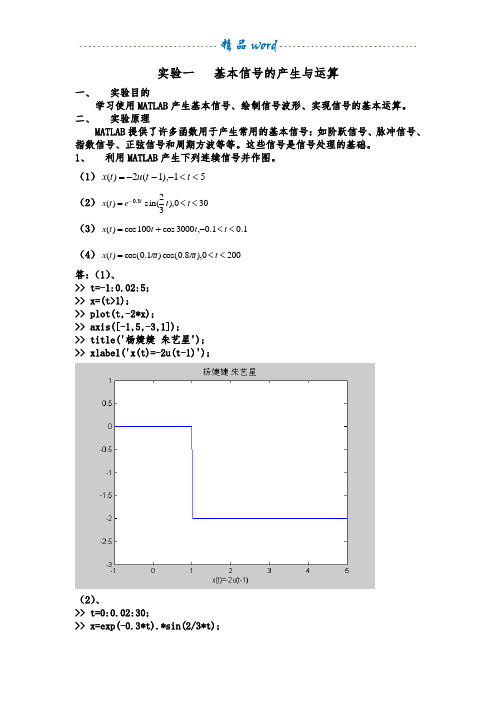
(1)51),1(2)(<<---=t t u t x (2)300),32sin()(3.0<<=-t t e t x t (3)1.01.0,3000cos 100cos )(<<-+=t t t t x (4)2000),8.0cos()1.0cos()(<<=t t t t x ππ 答:(1)、>> t=-1:0.02:5; >> x=(t>1);>> plot(t,-2*x);>> axis([-1,5,-3,1]);>> title('杨婕婕 朱艺星'); >> xlabel('x(t)=-2u(t-1)');(2)、>> t=0:0.02:30;>> x=exp(-0.3*t).*sin(2/3*t);>> plot(t,x);>> title('杨婕婕朱艺星');>> xlabel('x(t)=exp(-0.3*t).*sin(2/3*t)');因为原函数在t=15后x(t)取值接近于零,所以将横坐标改成0到15,看得更清晰axis([0,15,-0.2,0.6]);(3)>> t=-0.1:0.01:0.1;x=cos(100*t)+cos(3000*t);plot(t,x);>> title('杨婕婕朱艺星');>>xlabel('x=cos(100*t)+cos(3000*t)');因为t的间隔取太大,以至于函数不够准确,缩小t的间隔:t=-0.1:0.002:0.2;x=cos(100*t)+cos(3000*t);plot(t,x);title('杨婕婕')>> t=-0.1:0.0001:0.1;x=cos(100*t)+cos(3000*t);>> plot(t,x);title('杨婕婕朱艺星');>> xlabel('x=cos(100*t)+cos(3000*t)');(4)、t=0:0.01:200;>> x=cos(0.1*pi*t).*cos(0.8*pi*t);>> plot(t,x);>> title('杨婕婕朱艺星');>> xlabel('x=cos(0.1*pi*t).*cos(0.8*pi*t)');因为为周期函数,可以将横坐标t间隔扩大以便于观察图像>> axis([0,30,-1,1]);2、利用MATLAB 产生下列离散序列并作图。
信号与系统实验(MATLAB 西电版)实验17 离散系统的Z域分析

实验17 离散系统的Z域分析
离散系统的分析方法可分为时域解法和变换域解法两大 类。其中离散系统变换域解法只有一种,即Z变换域解法。Z 变换域没有物理性质,它只是一种数学手段,之所以在离散 系统的分析中引入Z变换的概念,就是要像在连续系统分析 时引入拉氏变换一样,简化分析方法和过程,为系统的分析 研究提供一条新的途径。
F=ztrans(f): 实现函数f(n)的Z变换,默认返回函数F是 关于z
F=ztrans(f,w):实现函数f(n)的Z变换,返回函数F是关 于w
F=ztrans(f,k,w):实现函数f(k)的Z变换,返回函数F是 关于w的函数。
实验17 离散系统的Z域分析
2. 单边逆Z变换函数iztrans 功能:iztrans可以实现信号F(z)的逆Z
实验17 离散系统的Z域分析
3) 一个离散LTI系统,差分方程为y(k)-0.81y(k-2)=f(k)-f(k-2),
(1) 系统函数H(z); (2) 单位序列响应h(k)的数学表达式,并画出波形; (3) 单位阶跃响应的波形g(k); (4) 绘出频率响应函数H(ejθ)
实验17 离散系统的Z域分析
实验17 离散系统的Z域分析
MATLAB %确定信号的Z syms n z% f1=3^n f1_z=ztrans(f1) f2=cos(2*n) f2_z=ztrans(f2);
实验17 离散系统的Z域分析
f1 = 3^n f1_z = 1/3*z/(1/3*z-1) f2 = cos(2*n) f2_z = (z+1-2*cos(1)^2)*z/(1+2*z+z^2-4*z*cos(1)^2)
极点图见图17.3
实验17 离散系统的Z域分析
信号与系统实验(MATLAB 西电版)实验8 离散LTI系

实验8 离散LTI系统的时域分析
MATLAB 程序:
y0=0;
%初值y(0)=0
y(1)=1; y(2)=5/6*y(1)-1/6*y0+cos(2*pi/4)/6;
实验8 离散LTI系统的时域分析
(1) 在计算机中输入程序,验证实验结果,并将实验结 (2) 对于程序设计实验,要求通过对验证性实验的练习, 自行编制完整的实验程序,实现对信号的模拟,并得出实验 (3) 在实验报告中写出完整的自编程序,并给出实验结
实验8 离散LTI系统的时域分析
(1) 试用卷积求离散时间系统y(k)-5y(k-1)+6y(k-1)= f(k),y(-1)=0,y(-2)=1
实验8 离散LTI系统的时域分析
一、实验目的 二、实验原理 三、涉及的MATLAB函数 四、实验内容与方法 五、实验要求 六、思考题
实验8 离散LTI系统的时域分析
(1) 熟悉离散时间序列卷积和、离散系统单位序 列响应的MATLAB实现方法;
(2) 掌握函数conv、impz的调用格式及功能; (3) 熟悉差分方程迭代解法的MATLAB实现方 法; (4) 通过该实验,掌握离散LTI系统的时域根本
离散系统的全响应如图8.2
实验8 离散LTI系统的时域分析 图 8.2 离散系统的全响应
实验8 离散LTI系统的时域分析
(3) 采用函数impz编程,求离散时间系统的单位序列响
某离散LTI系统的差分方程为y(k)-y(k-1)+0.9y(k-2)f(k), 那么对应的向量为 a=[1,-1,0.9],b=[1]。试画出该 系统的单位序列响应h(k)
求解系统的状态方程

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载求解系统的状态方程地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容求解系统的状态方程一、实验设备PC计算机,MATLAB软件,控制理论实验台二、实验目的(1)掌握状态转移矩阵的概念。
学会用MATLAB求解状态转移矩阵(2)学习系统齐次、非齐次状态方程求解的方法,计算矩阵指数,求状态响应;(3)通过编程、上机调试,掌握求解系统状态方程的方法,学会绘制输出响应和状态响应曲线;(4)掌握利用MATLAB导出连续状态空间模型的离散化模型的方法。
三、实验原理及相关基础(1)参考教材P99~101“3.8利用MATLAB求解系统的状态方程”(2)MATLAB现代控制理论仿真实验基础(3)控制理论实验台使用指导实验内容(1)求下列系统矩阵A对应的状态转移矩阵(a)(b)代码:syms lambdaA=[lambda 0 0;0 lambda 0;0 0 lambda];syms t;f=expm(A*t)(c)代码:syms t;syms lambda;A=[lambda 0 0 0;0 lambda 1 0;0 0 lambda 1;0 0 0 lambda];f=expm(A*t)(2) 已知系统a) 用MATLAB求状态方程的解析解。
选择时间向量t,绘制系统的状态响应曲线。
观察并记录这些曲线。
(1)代码:A=[0 1; -2 -3];B=[3;0];C=[1 1];D=[0];u=1;syms t;f=expm(A*t);%状态转移矩阵x0=0;s1=f*B*u;s2=int(s1,t,0,t)%状态方程解析解状态曲线:(2)A=[0 1;-2 -3];syms t;f=expm(A*t);X0=[1;0];t=[0:0.5:10];for i=1:length(t);g(i)=double(subs(f(1),t(i)));endplot(t,g)状态转移矩阵syms lambdaA=[lambda 0 0;0 lambda 0;0 0 lambda];syms tf=expm(A*t)b) 计算系统在初始状态作用下状态响应和输出响应的数值解(用函数initial( )), 绘制系统的状态响应曲线和输出响应曲线。
离散信号及离散系统的MATLAB编程实现

数字信号处理课程实验报告实验名称离散信号及离散系统的MATLAB编程实现系别教师姓名实验地点实验日期一、实验内容1、用MATLAB仿真(编写)离散序列2、常见序列运算3、差分方程的求解4、系统零极点的求解。
(红色部分为必做项目)二、实验目的1. 复习离散时间的信号和系统,复习离散时间重要类型的信号和它们的运算的实现。
2. 熟悉MATLAB软件的集成开发环境,学会利用MATLAB编程及获得帮助的方法。
3. 学会利用MATLAB的绘图功能。
三、涉及实验的相关情况介绍(包含使用软件或实验设备等情况)matlab软件,计算机四、实验试做记录(含程序、数据记录及分析)1、 Matlab表示序列MATLAB中,可采用向量表示序列,由于MATLAB中对序列下标默认为从1开始递增,因此要表示离散信号,一般应采用两个向量分别对信号的自变量和因变量进行描述。
如, n= -3~4,在MATLAB中表示为>> n = [-3, -2, -1, 0, 1, 2, 3, 4]; %自变量取值>> x = [ 2, 1, -1, 0, 1, 4, 3, 7]; %因变量取值说明:(1)向量可用方括号[ ]表示。
(2)当向量取值连续变化时可用冒号运算符“:”简化赋值过程,如的n值,可简化为n=[-3:4]或n= -3:4 。
(3)分号“;”表示不回显表达式的值。
(4)“%”表示其后内容为注释对象。
(5)符号“>>”是MATLAB命令窗口的输入提示符,此外,为便于多次调用,也可在m文件中输入相应的命令语句。
利用MATLAB,还可对信号的波形进行描述,常采用的绘图语句有stem,plot,subplot, axis,title,xlabel,ylabel,gtext, hold on, hold off, grid 等。
其中stem 绘制离散图形;plot 绘制连续图形;subplot 用于绘制子图,应在stem 或plot 语句前调用;axis 指定x 和y轴的取值范围,用在stem或plot语句后;title 标注图形名称,xlabel, ylabel 分别标注x轴和y轴名称;gtext可将标注内容放置在鼠标点击处;hold on和 hold off 用于控制对象绘制方式,是在原图上还是在新图上绘制;grid用于绘制网格。
信号与系统实验(MATLAB 西电版)实验19 离散系统状态方程的求解
(2) 描述离散时间系统的信号流图如图所示,确定该系 统的系统函数(离散系统信号流图的形式与连续系统相同,只 不过是变量s换为z,在此不再详述。请参照上一节)
实验19 离散系统状态方程的求解 图 19.3 系统的信号流图
实验19 离散系统状态方程的求解
(1) 对于程序设计实验,要求通过对验证性实验的练习, 自行编制完整的实验程序,实现对信号的模拟,并得出实验
(2) 在计算机中输入程序,验证实验结果,并将实验结 (3) 在实验报告中写出完整的自编程序,并给出实验结
离散系统状态变量分析方法的特点。
实验19 离散系统状态方程的求解 图 19.1 离散系统状态方程的求解
实验19 离散系统状态方程的求解
(2) MATLAB A=[0 1; -2 3]; B=[0; 1]; % C=[1 1; 2 -1]; D=zeros(2,1); x0=[1; -1]; % N=10; f=ones(1,N);
实验19 离散系统状态方程的求解
%f=input(′输入信号f=′) %要求长度为n clear all A=[0.5 0; 0.25 0.25]; B=[1; 0]; x0=[-1; 0.5]; n=10; f=[0 0.5*ones(1,n-1)]; x(:,1)=x0; for i=1:n
x(:,i+1)=A*x(:,i)+B*f(i); end subplot(2,1,1); stem([0:n],x(1,:)); subplot(2,1,2); stem([0:n],x(2,:)); 离散系统状态方程的求解结果如图19.1所示。
实验19 离散系统状态方程的求解
sys=ss(A,B,C,D,[]); y=lsim(sys,f,[],x0); k=0:N-1; subplot(2,1,1); stem(k,y(:,1),′b′); subplot(2,1,2); stem(k,y(:,2),′b′); 离散系统状态方程的求解结果如图19.2
信号与系统利用MATLAB进行信号与系统分析与方程讲解
0.2
0.1
0
-3
-2
-1
0
1
2
3
1
0.9
0.8
0.7
ft=tripuls(t,4,1);
0.6
0.5
0.4
0.3
0.2
信号与系统利用MATLA0.B1 进行信号与系
统分析和方程0讲解
-3
-2
-1
0
1
2
3
一、基本信号的MATLAB表示
% unit impuls sequence
1 0.9
k=-50:50;
0.8
0.7
uk=[zeros(1,50), ones(1,51Fra bibliotek];0.6
0.5
stem(k,uk)
0.4
0.3
0.2
function [f,k]=stepseq(k0,k1,k2) %产生 f[k]=u(k-k0);k1<=k<=k2
0.1
0
-50 -40 -30 -20 -10
0
10 20 30 40 50
axis([-1 3 0 2]);
直接在命令窗口输入以上命令
建一个名字为my_file.M的文件,然后在命令窗口输
入文件名及回车。 信号与系统利用MATLAB进行信号与系统分析和 方程讲解
二、获取帮助
命令窗口输入: help+函数名 例如 help plot
信号与系统利用MATLAB进行信号与系 统分析和方程讲解
一、基本信号的MATLAB表示
%decaying exponential t=0:001:10; A=1; a=-0.4; ft=A*exp(a*t); plot(t,ft)
利用MATLAB求解系统的状态方程
A=[0 1;-2 -3];B=[3;0];C=[1 1];D=0;G=ss(A,B,C,D);
t=0:0.5:10;u=1+exp(-t).*cos(3*t);
[y,t,x]=lsim(G,u,t);plot(t,x,':',t,y,'-')
(4)系统的状态响应及输出响应曲线
-0.2968 0.5219(矩阵指数)
xt1 =
0.8187
-0.8187(状态响应)
(2)系统的状态响应和输出响应曲线:
A=[0 1;-2 -3];B=[3;0];C=[1 1];D=0;G=ss(A,B,C,D);
t=0:0.5:10;u=ones(size(t));
[y,t,x]=lsim(G,u,t);plot(t,x,':',t,y,'-')
通过本次试验,我加深了对状态转移矩阵概念的了解,学会了
[yu,t,xu]=lsim(G,u,t);
figure(2);
plot(t,xu,':',t,yu,'-')
title('零状态响应') %零状态响应曲线
y=y0+yu;x=x0+xu;
figure(3);
plot(t,x,':',t,y,'-')
title('总状态响应/输出响应') %总状态响应和输出响应
A=[0 1;-2 -3];B=[3 0]';C=[1 1];D=0;
G=ss(A,B,C,D);
t=0:0.5:10;x0=[1;2];
离散时间信号与系统实验的matlab实现
离散时间信号与系统[实验目的]1.了解信号处理的基本操作2.熟悉一些常用的序列及其应用[实验原理]我们所接触的信号大多为连续信号,为使之便于处理,往往要对其进行采样,对信号抽样并保证其能完全恢复,对抽样频率有一定的限制。
基本的离散序列的定义如下:1.单位采样序列2.单位阶跃序列3.实指数序列,;a为实数4.复数指数序列,5.正余弦序列,6.周期序列,[实验内容]1.用MATLAB实现函数impseq(n0,n1,n2),使函数实现,。
函数定义:function [x,n]=impseq(n0,n1,n2)if (n1>n2||n0>n2||n0<n1)error('parameter error');end;if (n1<=n2)for n=1:n2-n1+1if (n==n0)x(1,n)=n1-1+n;x(2,n)=1;end;x(1,n)=n1-1+n;x(2,n)=0;end;x(2,n0-n1+1)=1;end;运行结果:impseq(3,1,9)ans =6 7 8 9 10 11 12 13 140 0 0 0 1 0 0 0 0注:上面一行为自变量n,下面一行为函数值,以下运行结果为两行的,都与此题同,不在表明。
2.用MATLAB实现函数stepseq(n0,n1,n2),使函数实现u(n-n0),。
函数定义:function [x,n]=stepseq(n0,n1,n2)if (n0>n2||n0<n1||n1>n2)error('parameter error');end;for n=1:n2-n1+1if (n+n1-1<n0)x(1,n)=n1+n-1;x(2,n)=0;elsex(1,n)=n1+n-1;x(2,n)=1;end;end;运行结果:Stepseq(4,2,10)ans =2 3 4 5 6 7 8 9 100 0 1 1 1 1 1 1 1 注:与上同,上面一行是自变量,下面一行是函数值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验19 离散系统状态方程的求解
初f(k)=0.5ε(k),确定该
状态方程x(k)前10
实验19 离散系统状态方程的求解
MATLAB % %A=input(′系数矩阵A=′) %B=input(′系数矩阵B=′) %x0=input(′初始状态矩阵x0=′) %n=input(′要求计算的步长n=′)
实验19 离散系统状态方程的求解
%f=input(′输入信号f=′) %要求长度为n clear all A=[0.5 0; 0.25 0.25]; B=[1; 0]; x0=[-1; 0.5]; n=10; f=[0 0.5*ones(1,n-1)]; x(:,1)=x0; for i=1:n
x(:,i+1)=A*x(:,i)+B*f(i); end subplot(2,1,1); stem([0:n],x(1,:)); subplot(2,1,2); stem([0:n],x(2,:)); 离散系统状态方程的求解结果如图19.1所示。
实验19 离散系统状态方程的求解 图 19.1 离散系统状态方程的求解
实验19 离散系统状态方程的求解
(2) MATLAB A=[0 1; -2 3]; B=[0; 1]; % C=[1 1; 2 -1]; D=zeros(2,1); x0=[1; -1]; % N=10; f=ones(1,N);
实验19 离散系统状态方程的求解
sys=ss(A,B,C,D,[]); y=lsim(sys,f,[],x0); k=0:N-1; subplot(2,1,1); stem(k,y(:,1),′b′); subplot(2,1,2); stem(k,y(:,2),′b′); 离散系统状态方程的求解结果如图19.2
三、涉及的MATLAB
采用函数ode45可以求解微分方程。其调用格式如下: [t,y]=ode45(odefun,tspan,y0) 其中,odefun指状态方程的表达式,tspan指状态方程对 应的起止时间[t0,tf],y0
实验19 离散系统状态方程的求解
1. 验证性实验(参考程序) 采用MATLAB语言编程,求解离散系统状态方程,并绘 (1)
实验19 离散系统状态方程的求解 图 19.2 离散系统状态方程的求解
实验19 离散系统状态方程的求解
2.
(1)
x(k+1)=Ax(k)+Bf(k)
其中A=
00.2.550.025,B10,
初始状态
x1(0) x2(0)
00,
激励f(k)=δ(k),确定该状态方程x(k)前10步的解,并画出波形。
在此只对单输入的n阶离散系统的状态方程求解。一般 采用递推迭代的方式求解,由初始条件x(0)和激励f(0)求出 k=1时的x(1),然后依次迭代求得所要求的x(0),…,x(n) 编程时应注意,MATLAB中变量下标不允许为零,则初始点 的下标只能取1,第n步的x的下标为n+1
实验19 离散系统状态方程的求解
实验19 离散系统状态方程的求解
(2) 描述离散时间系统的信号流图如图所示,确定该系 统的系统函数(离散系统信号流图的形式与连续系统相同,只 不过是变量s换为z,在此不再详述。请参照上一节)
实验19 离散系统状态方程的求解 图 19.3 系统的信号流图
实验19 离散系统状态方程的求解
(1) 对于程序设计实验,要求通过对验证性实验的练习, 自行编制完整的实验程序,实现对信号的模拟,并得出实验
(2) 在计算机中输入程序,验证实验结果,并将实验结 (3) 在实验报告中写出完整的自编程序,并给出实验结
离散系统状态变量分析方法的特点。
实验19 离散系统状态方程的求解
信号与系统实验(MATLAB 西电版)实 验19 离散系统状态方程的求解
实验19 离散系统状态方程的求解
(1) 了解离散系统状态方程求解方法; (2) 了解离散系统信号流图化简的方法; (3) 了解函数ode45
x(k+1)=Ax(k)+Bf(k)
实验19 离散系统状态方程的求解
