人大附中老师谈08年中考数学命题趋势
2008年中考数学

2008年中考数学简介2008年的中考数学试卷在解题思路和题型上有一些特点。
本文将分析2008年中考数学试卷的题目类型和解题思路,并提供一些解题技巧和注意事项。
题目类型分析2008年中考数学试卷的题目类型主要包括选择题、填空题、计算题和解答题。
其中选择题和填空题占据了试卷的大部分,计算题和解答题则相对较少。
选择题涵盖了知识点的广度,主要考察学生对数学概念的理解和运用。
题目形式多样,包括判断题、单项选择题和多项选择题。
正确率较高,但需要学生具备较扎实的基础知识。
填空题主要考察学生对数学概念和公式的掌握。
题目中给出一些条件,要求学生计算出所求的变量的值,或者填入适当的表达式。
这类题目需要学生对所学的数学知识进行灵活运用。
计算题要求学生进行一系列的运算,包括四则运算、比例运算等。
这类题目较为考验学生的计算能力,需要学生具备较强的运算技巧和解题思路。
解答题是试卷中难度较高的题型之一,主要考察学生的问题分析和解决能力。
题目需要学生根据给定的条件,进行推理和证明,或者用图形进行解决,要求学生进行较为深入的思考。
解题思路与技巧1.针对选择题,注意审题和答题技巧。
细致阅读题目中的条件和要求,排除干扰项,仔细选择正确答案。
2.对于填空题,要掌握各种计算公式和方法。
遇到复杂的题目,可以适当引入变量,将问题简化为常规的计算。
3.在计算题中,要注重计算的准确性和速度。
可以通过列式计算、借位、逆向思维等方法,提高解题效率。
4.解答题需要思路清晰,逻辑性强。
在解答题之前,要认真阅读题目,明确问题的要求,合理规划解题步骤和思路。
解答过程中,要给出充分的证明和合理的推理。
5.培养良好的解题习惯,多做题、多总结。
通过大量的练习,熟悉各种题型和解题方法,提高数学解题的能力。
注意事项1.阅读理解题和应用题需要注意细节。
在解答这类题目时,要关注题目给出的信息和要求,抓住关键点,避免遗漏重要信息。
2.解答题需要注重语言的表达和结构的完整性。
2008年北京中考数学试卷解析

2008年北京市高级中等学校招生考试数学试卷答案及评分参考阅卷须知:1.一律用红钢笔或红圆珠笔批阅,按要求签名.2.第Ⅰ卷是选择题,机读阅卷.3.第Ⅱ卷包括填空题和解答题.为了阅卷方便,解答题中的推导步骤写得较为详细,考生只要写明主要过程即可.若考生的解法与本解法不同,正确者可参照评分参考给分.解答右端所注分数,表示考生正确做到这一步应得的累加分数.第Ⅰ卷(机读卷共32分)一、选择题(共8道小题,每小题4分,共32分)题号 1 2 3 4 5 6 7 8 答案ADCCBBBD第Ⅱ卷(非机读卷共88分)二、填空题(共4道小题,每小题4分,共16分)题号9101112答案12x()()a ab a b 4207ba31(1)n nnba三、解答题(共5道小题,共25分)13.(本小题满分5分)解:1182sin 45(2π)32222132··················································································· 4分22. ································································································· 5分14.(本小题满分5分)解:去括号,得51286x x ≤.···································································· 1分移项,得58612x x ≤.··········································································· 2分合并,得36x ≤. ······················································································ 3分系数化为1,得2x ≥.················································································· 4分不等式的解集在数轴上表示如下:················································································································· 5分15.(本小题满分5分)证明:AB ED ∥,B E . ····························································································· 2分在ABC △和CED △中,1 2 30 123AB CE B E BCED ,,,ABC CED △≌△.···················································································· 4分AC CD . ····························································································· 5分16.(本小题满分5分)解:由图象可知,点(21)M ,在直线3y kx 上, ············································· 1分231k .解得2k . ······························································································· 2分直线的解析式为23y x .······································································· 3分令0y,可得32x.直线与x 轴的交点坐标为302,. ······························································ 4分令0x ,可得3y.直线与y 轴的交点坐标为(03),. ······························································· 5分17.(本小题满分5分)解:222()2x y x y xxy y22()()x y x y x y ························································································ 2分2x yxy . ································································································· 3分当30xy时,3x y .·············································································· 4分原式677322y y y yyy.··············································································· 5分四、解答题(共2道小题,共10分)18.(本小题满分5分)解法一:如图1,分别过点A D ,作AEBC 于点E ,DF BC 于点F .······································1分AE DF ∥.又AD BC ∥,四边形AEFD 是矩形.2EF AD .······································2分ABCDFE 图1AB AC ,45B,42BC ,AB AC .1222AEECBC .22DF AE ,2CFECEF···················································································· 4分在Rt DFC △中,90DFC ,2222(22)(2)10DC DFCF. ··········································· 5分解法二:如图2,过点D 作DF AB ∥,分别交AC BC ,于点E F ,.···················· 1分ABAC ,90AEDBAC.AD BC ∥,18045DAEB BAC .在Rt ABC △中,90BAC,45B,42BC,2sin 454242AC BC ································································· 2分在Rt ADE △中,90AED ,45DAE,2AD ,1DEAE .3CE AC AE.·················································································· 4分在Rt DEC △中,90CED,22221310DC DECE.························································· 5分19.(本小题满分5分)解:(1)直线BD 与O 相切. ······································································· 1分证明:如图1,连结OD .OA OD ,A ADO .90C,90CBD CDB .又CBDA ,90ADO CDB .90ODB.直线BD 与O 相切.················································································· 2分DCOABE图1ABCDFE图2(2)解法一:如图1,连结DE .AE 是O 的直径,90ADE .:8:5AD AO ,4cos 5AD A AE . ···················································································· 3分90C,CBD A ,4cos 5BC CBD BD. ············································································· 4分2BC,52BD.······································································ 5分解法二:如图2,过点O 作OH AD 于点H .12AH DHAD .:8:5AD AO ,4cos 5AH A AO . ···················3分90C,CBD A ,4cos 5BC CBD BD. ································4分2BC ,52BD.································································································· 5分五、解答题(本题满分6分)解:(1)补全图1见下图. ············································································· 1分9137226311410546373003100100(个).这100位顾客平均一次购物使用塑料购物袋的平均数为3个.································· 3分200036000.估计这个超市每天需要为顾客提供6000个塑料购物袋. ········································ 4分(2)图2中,使用收费塑料购物袋的人数所占百分比为25%. ······························ 5分根据图表回答正确给1分,例如:由图2和统计表可知,购物时应尽量使用自备袋和押金式环保袋,少用塑料购物袋;塑料购物袋应尽量循环使用,以便减少塑料购物袋的使用量,为环保做贡献.6分D COABH图240 35 30 25 20 15 10 5 0图1123 4 567 4311 26379 塑料袋数/个人数/位“限塑令”实施前,平均一次购物使用不同数量塑料..购物袋的人数统计图10六、解答题(共2道小题,共9分)21.解:设这次试车时,由北京到天津的平均速度是每小时x 千米,则由天津返回北京的平均速度是每小时(40)x千米. ·························································································· 1分依题意,得3061(40)602xx . ··································································· 3分解得200x.······························································································ 4分答:这次试车时,由北京到天津的平均速度是每小时200千米.······························ 5分22.解:(1)重叠三角形A B C 的面积为3. ·················································· 1分(2)用含m 的代数式表示重叠三角形A B C 的面积为23(4)m ; ····················· 2分m 的取值范围为843m ≤.··········································································· 4分七、解答题(本题满分7分)23.(1)证明:2(32)220mxm x m 是关于x 的一元二次方程,222[(32)]4(22)44(2)m m m mm m .当0m时,2(2)0m ,即0.方程有两个不相等的实数根.········································································ 2分(2)解:由求根公式,得(32)(2)2m m xm.22m x m 或1x . ················································································· 3分0m ,222(1)1mm mm.12x x ,11x ,222m x m . ··············································································· 4分21222221m yx x m m.即2(0)ymm 为所求. ·······················5分(3)解:在同一平面直角坐标系中分别画出2(0)y mm与2(0)y m m 的图象.····························································6分由图象可得,当1m ≥时,2y m ≤. ··········7分八、解答题(本题满分7分)24.解:(1)ykx 沿y 轴向上平移3个单位长度后经过y 轴上的点C ,1 2 3 44 3 21xy O -1 -2 -3 -4 -4-3 -2-1 2(0)ymm 2(0)ym m(03)C ,.设直线BC 的解析式为3ykx .(30)B ,在直线BC 上,330k.解得1k.直线BC 的解析式为3yx. ································································· 1分抛物线2y xbx c 过点B C ,,9303b c c,.解得43b c,.抛物线的解析式为243yxx . ······························································ 2分(2)由243y xx .可得(21)(10)D A ,,,.3OB ,3OC ,1OA ,2AB.可得OBC △是等腰直角三角形.45OBC,32CB.如图1,设抛物线对称轴与x 轴交于点F ,112AF AB .过点A 作AEBC 于点E .90AEB.可得2BE AE ,22CE .在AEC △与AFP △中,90AECAFP,ACEAPF ,AEC AFP △∽△.AE CE AFPF,2221PF.解得2PF.点P 在抛物线的对称轴上,点P 的坐标为(22),或(22),. ··································································· 5分1 Oy x2 344 3 2 1-1 -2 -2-1P EBD P ACF 图1(3)解法一:如图2,作点(10)A ,关于y 轴的对称点A ,则(10)A ,.连结A C A D ,,可得10A C AC,OCAOCA .由勾股定理可得220CD,210A D .又210A C,222A DA CCD .A DC △是等腰直角三角形,90CA D,45DCA .45OCA OCD .45OCAOCD.即OCA 与OCD 两角和的度数为45. ························································ 7分解法二:如图3,连结BD .同解法一可得20CD ,10AC.在Rt DBF △中,90DFB,1BFDF,222DB DFBF.在CBD △和COA △中,221DB AO ,3223BC OC,20210CD CA.DBBCCDAO OC CA .CBD COA △∽△.BCD OCA .45OCB ,45OCAOCD.即OCA 与OCD 两角和的度数为45. ························································ 7分九、解答题(本题满分8分)25.解:(1)线段PG 与PC 的位置关系是PG PC ;1 O yx2 3 4 43 2 1-1 -2-1BDA C F 图2A 1 O y x2 3 443 2 1-1 -2 -2-1BDA C F 图3PG PC3.································································································· 2分(2)猜想:(1)中的结论没有发生变化.证明:如图,延长GP 交AD 于点H ,连结CH CG ,.P 是线段DF 的中点,FP DP .由题意可知AD FG ∥.GFP HDP .GPF HPD ,GFP HDP △≌△.GPHP ,GF HD .四边形ABCD 是菱形,CDCB ,60HDC ABC.由60ABC BEF ,且菱形BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一条直线上,可得60GBC .HDCGBC .四边形BEFG 是菱形,GF GB .HD GB .HDC GBC △≌△.CH CG ,DCH BCG .120DCHHCB BCGHCB.即120HCG .CH CG ,PH PG ,PG PC ,60GCPHCP.3PG PC.······························································································· 6分(3)PG PCtan(90). ············································································ 8分D CG P ABEFH。
2008年中考数学试题分析

2008年中考数学试题分析今年我省中考数学试题遵循《义务教育数学课程标准》的要求,命题以现行数学教材以及《山西省2008初中毕业生学业考试科目说明》为依据。
试题呈现如下特点:1.考查内容依据《课程标准》,体现基础性。
基本知识、基本技能是培养和提高学生数学素养、发展实践能力和创新精神的基础,是学生进一步学习和发展的必备条件,试题在这一点上立意明确,充分体现数学学科的教育价值。
全卷体现基础知识、基本技能、基本方法的考题覆盖面广,涉及《课程标准》主要的知识点,起点低且难易安排有序,层次合理,有助于考生较好地发挥思维水平。
这些试题的分值占全卷80%以上,有的源于课本,有的是对课本中的题目原型进行合理的加工、组合、延伸和拓展。
这样既可坚定考生考好数学的信心,又对今后的数学课堂教学起到良好的导向作用。
例如,第1题,直接考查相反数的概念,第2题考查科学记数法,第5题考查学生对众数的理解,第6题考查学生对一元一次不等式组的基本方法的掌握,第13题考查学生对视图的理解等,这样命题,既考虑了一定的覆盖面,又关注了数学的本质内涵。
2.突出了对数学思想方法的考查。
数学思想是数学的精髓,是培养学生数学思维能力的重要环节。
数学思想是对数学知识与方法,形成的规律性的理性认识,是解决问题的根本策略;数学方法则是解决问题的手段和工具。
今年试题着重考查了转化与化归思想、数形结合思想、分类讨论思想、统计思想和数学建模的思想等;考查了因式分解法、分析法、猜想与探索等思想方法。
例如,第21题突出了对学生的图表信息的收集与处理能力的考查,第24题考查学生分析问题和解决问题的能力,第25题的几何题,采用开放性的命题方法,考查学生的猜想与探索能力,要求学生运用分析法或综合法进行推理;第26题要求学生在动态中分析问题,利用转化与化归的思想、分类讨论的思想解决问题。
这些试题的内容虽在课本之外,但其根却在课本之内,考生只要认真思考分析,是不难做出正确解答的。
08中考作文命题趋势(四)选题作文

08中考作文命题趋势(四)选题作文选题作文的备选题目.可以是命题文、半命题作文、材料作文和话题作文等。
以“话题+半命题”的组合方式最常见.占选题作文%:其次为“命题十话题”。
选题作文最大限度地适应各类考生,为考生创设宽松的写作环境。
这种命题,比起单纯的话题作文更具开放性,更有利于考生自由发挥。
从笔者收集110道2007年全国各地中考作文考题来看,河南省实验区、河南非实验区、山西省、吉林省、哈尔滨市、福州、青岛、济南、长沙市、四川成都、湖北黄冈市、广州市花都区、广州番禺区白云区等共有35个省市区都采用了这种命题方式,可以预见,这种新型的命题方式,2008年必将成为各地中考作文命题人的新宠。
写作点拔1.读题审题,迅速果断地选出适合自己写作的文题选题作文命题形式具有弹性、开放性、选择性和适应性,其目的是要尽量做到让不同地域、不同层次、不同特点的学生都有话可说,正常发挥出自己的水平。
在读题审题选题阶段,同学们要准确迅速地读懂每个选题的题意,迅速果断地选出最适合自己写作的文题。
既不可仓促草率,也不能拖沓犹豫费时太长。
一般要在5分钟~8分钟之内完成。
2.煞住“惯性思维”之车.排除考前读写训练产生的不利影响考生在写选题作文时.眼睛一扫.有时会发现其中某一个作文题和考前读过的某一篇文章差不多.或者和考前写过的某篇作文很相似……受惯性思维的影响.有些考生就喜出望外,顾不得再读题审题、辨别思考,贸然选择这个作文题.把自己读过或写过的那篇文章搬来。
殊不知,失之毫厘,谬以千里。
越是遇到熟悉的题目.越需要提高警惕、仔细分辨与平时训练的题目有何异同。
3.摆脱“常规思维”的束缚.写出新鲜灵动的考场选题作文选题作文的最大特点在于提供了多角度、多层面的切入点来考查学生的写作水平.选题时必须考虑写这个题目能不能显示出独特性来,能不能使笔下文章个性十足、新鲜灵动。
构思时。
最先闪现在脑海里的往往是“常规思维”的结果。
对于中上等水平的考生来说.思考不宜就此止步,要尽量摆脱“常规思维”的束缚.或纵向,或横向.多想一想,找到最佳切人点。
近几年来中考命题的规律与2008年的命题趋势

近几年来中考命题的规律与2008年的命题趋势2008年的听力测试题仍然根据《英语课程标准》的要求,从以下几个方面进行考查:第一节(共5小题)每小题1分,满分5分,主要是听句子,选择与句子内容相关的图画。
第二节(共5小题)每小题1分,满分5分,主要是听句子,选出与所听句子内容相符的正确答案。
第三节(共10小题)每小题1分,满分10分,主要是听对话,选出能回答问题的正确选项。
第四节(共5小题)每小题2分,满分10分,主要是听对话或短文,完成下列信息表格。
听取信息”部分:从2005——2007试题来看,数字是每年必考的内容、时间、地点、人物等是考试的热点,并且难度逐渐在增加。
从题的走向来看,时间、地点、日期、星期、数字、三餐饭的食物、国家、交通工具等是历年的考试热点和重点。
“对话理解”部分:非常显然,历年此题型的考试热点是:时间、地点、人物、职业、喜好、价钱(数字)、日期、星期、交通方式、事物描述、食物水果及行为判别。
尤其是时间、地点、职业、喜好、日期、星期是历年的必考内容“短文理解”部分:从2005年——2007的短文理解看实际上仍然属于对话理解,考试热点是:数词和计算、地点和情景、职业和关系,肯定和否定、从上下文确定词义和不同场合语言的不同功能,另外还考查从整个对话中理解说话人的“弦外之音”第四节的听力试题题例请各位老师以《考试说明》题型为参考。
二、英语知识运用2005——2007三年以来的英语知识运用题型几乎没有改变,从2008年的模拟试题和《考试说明》要求的题型来看2008年的中考英语知识语言运用部分题型与前三年一致。
2008年中考英语知识运用部分也是根据《课程标准》的要求,从以下几个方面进行考查。
第一节,词语释义选出与句中画线部分相近的解释,主要考查考生对英语词语和句子的理解能力。
(5小题,每小题1分)典型题例:1. The boy was able to swim last year.A. canB. couldC. has toD. had to2. There is a lot of rain here in summer.A. muchB. manyC. moreD. lot of3. My clothes are not fashionable.A. oldB. newC. a lot of styleD. worn out第二节,单项填空/选择填空(共20小题,每小题1分,满分20分)从A、B、C、D四个选项中选择能填入空白处的正确答案。
上海08年中考数学卷题量可能微调

上海08年中考数学卷题量可能微调今年中考数学学科首次实行全市统一网上评卷,反映在卷面上,中考数学卷题量可能将有微调。
在一些学校采访时发现,学校已经开始按照新题量出模拟试卷,操练学生。
调整以后的总题量虽然增加了2道,但最后的大题目有所减少,学生们反映比以前做起来轻松。
学校的模拟卷已有变化在本市一所初级中学新出的初三数学模拟练习卷上,注意到,和去年的试卷相比,整个试卷结构、题型没有太大的差别,但试卷上各部分的题量却有些许微调,分值也将会有些变化。
其中,选择题题量从去年的4道题增加到8道题,每题3分;填空题题量虽然不变,仍然是12道题,但分值增加到了每题4分;后面的大题目数量则有所减少,从去年的9道题减少为7道题。
“调整以后的客观题部分一共占到了72分,是历年来最高的一次,这就要求学生注重客观题,增加解题的准确性。
”据这所学校的初三数学教研组组长介绍,这学期接到区里的通知,要按照新的题量出题,接下来各个区的中考模拟考也将按照这个新变化来出题,所以最近学校正在对学生反复操练,以便学生尽快适应。
数学老师认为是给学生“减负”据了解,新的初三数学试卷与今年中考数学将实行网上阅卷不无关系。
据一线教师和数学教研员说,选择题题量大也是为了便于电脑阅卷,由于网上阅卷对学生的书写要求、规范比较高,答题务必在黑色矩形边框内,而从以往答题情况看,学生在大题目解答时容易“天马行空”,不少学生还有乱涂改的习惯,所以适当减少大题目也是给予了书写的空间。
据一些初三数学教师反映,这样的调整将有利于学生得分,对学生来说是“减负”。
“因为客观题相对知识点少,答题容易,学生解题的速度因此可以加快,这也是引导学生把主要精力放在基础知识上。
”采访中,一些学生反映,本来为了保证不出错,总是要先在草稿纸上写一遍,卷子上再誊一遍,浪费了不少时间;今年数学考试选择题花费时间少,大题目少了做起来也轻松了。
数学卷将“一卷两分叉”另外,还了解到,由于二期课改到今年秋季起,就将至初三年级,目前在部分试点学校已开始使用新课程方案和新教材,所以今年中考的数学试卷也将首次出现“一卷两分叉”的情况,但具体哪些部分分叉、分叉到什么程度目前尚未确定下来。
2008年中考数学试卷分析
2008年中考数学试卷分析一、试卷总体分析2008年中考数学试卷,在继承中不断创新,对试题的内容进行了适当调整,进一步降低了填空题的难度,适当提高了主观题的难度,总体难度基本和2007年相当。
在联系实际、观察与实验、动手操作、猜想与推理等方面都有较好的体现。
1、试卷立足基础,体现学科特点。
试卷的设计充分体现了改革创新的精神,立足基础,面向全体,与大多数考生的实际能力与水平大体相适应,突出了数学作为基础学科的特点,既考查了数学基础知识的掌握程度,又加大了应用能力测试力度,充分体现了对考生数学创新意识和综合运用知识能力的考查。
卷Ⅱ中,填空题及解答题的前几道试题,考查内容从基础出发,起步较低,坡度平缓有利于的多数考生树立考试信心。
2、试卷机构科学合理试卷Ⅱ满分100分,填空题占24%,解答题占76%,总题量为16个。
试题的出现从难度、分值、位置等各方面都充分考虑到考生的接受能力。
全卷试题普遍上手容易,但解答完整、准确,则需要有较强的数学能力。
同时,还注意控制了题量为考生提供了足够的思考空间。
在知识点的覆盖上不再刻意追求覆盖面,而是围绕初中数学的核心内容以及应用性较强的知识来设计问题。
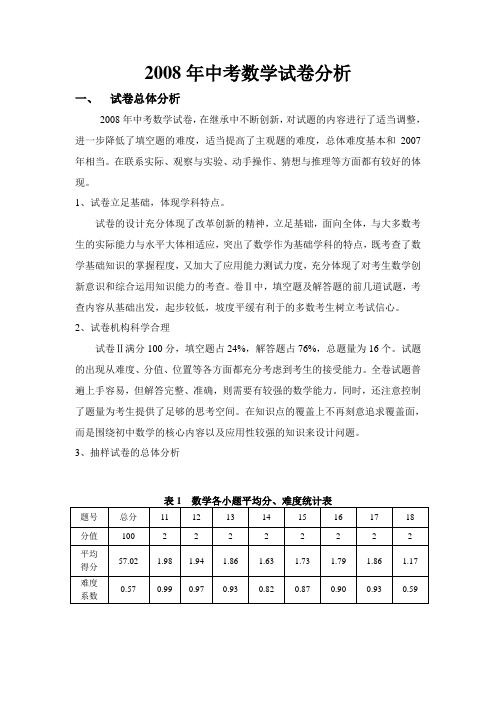
3、抽样试卷的总体分析续表全卷平均得分57.02分,难度系数0.57,和《学科说明》的要求基本一致,难度控制比较恰当。
二、试题结构分析1、知识结构及相关分析从表2可以看出,试题在考查基础知识与基本技能的同时注意了重点知识重点考察。
试题内容不是简单的、单一的内容考查,而是各部分内容互相渗透,如直线型、函数部分,难度较大的原因是,试题大多与实际应用现相结合,考查知识面广。
直线型中尤其注意了新课标中的知识考查,如:平移、对称等知识,占得分值较大。
建议教师和考生要对着方面知识注意。
2、基础试题与发展性试题比较从表3看,卷Ⅱ全卷基础试题与发展性试题的比例约为2:1,说明新课标提出的关注学生发展、注重考生能力培养的要求在试卷中已有较好的体现。
2008年中考数学试卷新特点(静安教院沈全洪)[1]
![2008年中考数学试卷新特点(静安教院沈全洪)[1]](https://img.taocdn.com/s3/m/ed014801a45177232f60a296.png)
2008年中考数学卷的导向特点及复习方法静安区教育学院沈全洪试卷结构1.命题的导向根据市教委有关文件精神,2008年初中毕业生学业考试(以下简称:中考)的指导思想是:(1)坚持有利于义务教育的均衡发展,促进本市各初中学校办学水平和质量的整体提高;(2)有利于推进本市中小学课程教材改革,构建学生全面和谐发展的初中生综合素质评价体系;(3)有利于促进本市高中阶段教育各类学校协调发展.目标是建立以初中毕业生学业考试为基础,与综合素质评价相结合的招生考试制度.今年中考将与往年基本相同:二考(毕业考和招生考)合并为一考(初中学业考).考试性质是义务教育阶段的终结性考试,目的是全面、准确反映初中毕业生学科学习方面所达到的水平.考试结果既是衡量学生是否达到毕业标准的重要依据,也是高中阶段学校招生的重要依据之一.考试命题的指导思想将有利于推进中小学实施素质教育;有利于推进中小学课程改革,促进初中教育教学改革;有利于切实减轻学业过重的课业负担,培养学生的创新精神和实践能力;有利于促进学生全面和谐、富有个性地发展.2.考查的内容由于2008年初中毕业学生中,大部分学生是在初中阶段使用一期课改的数学教材(以下简称:老教材),一部分学生使用二期课改的数学教材(以下简称:新教材),既是使用老教材的最后一年中考,又是部分学校试用新教材后的第一年中考.从有利于推进二期课改、有利于数学课堂教学、有利于社会稳定等方面考虑,命题将以上海教育出版社1998年版一期《数学课程标准(修订本)》和2002年版的二期《上海市中学数学课程标准(试验稿)》为依据,采用一卷二分叉(新老教材同一份试卷大部分相同,少部分内容不同)的形式.即对两套教教材中相同知识的内容的考查,进行同样的命题;对两套教教材中不同知识内容的考查,采用难度基本相当的不同的分叉命题;如果两套教教材中相同知识内容的教学有不同的要求或内容有较小的差异,那么按“就低不就高”的原则处理.命题将进一步突出教学的基本内容,更加注重基础.在变化中求稳定,要加强与社会实际和学生生活的联系,注重考查学生学科知识与技能、过程与方法的掌握情况,特别要注重考查在具体情景中综合运用所学知识分析和解决简单问题的能力,杜绝偏题和怪题.为明年全面使用二期课改教材的中考作好过度和衔接,进一步体现二期课改的理念.2008年中考考查的相同的知识内容:老教材为初中数学课本中七、八、九年级必学内容;新教材为初中数学课本中七、八、九年级必学内容和六年级“一次方程(组)和一次不等式(组)”全章内容,拓展内容不作为考查内容.2008年中考考查的分叉部分的知识内容:老教材为“一元二次方程的根与系数的关系(韦达定理)”、“二次函数与一元二次方程的关系”、“与圆的切线的性质与判定有关的内容”等;新教材为“概率初步”、“向量初步”等.3.试卷的结构2008年中考数学试卷总分为150分,考试的时间100分钟.总体的难易度(易、中、难题的分值比约为8:1:1)将保持与2006年、2007年相同.估计全市的平均分在120分左右.合格率在95%左右.由于2008年中考数学试卷阅卷将首次采用网上阅卷,首次使用答题纸,试卷将与答题纸分离.今年的中考数学试卷的题型及试题的编排形式的基本框架结构与往年相比将有了较大的变化,估计今年中考数学试卷总题量为三个大题27个小题左右,试题基本框架结构可能为:第一大题单项选择题(比去年增加4题),由8个小题组成,每小题3分,满分24分;第二大题填空题,由12个小题组成,每小题4分,满分48分;第三大题解答题(比去年减少2题),由4个10分题、2个12分题和1个14分题组成,满分78分.试卷特点由于今年在试卷形式有了较大的变化,估计命题指导思想会更注重在变化中求稳定,试卷可能将在以下的几个方面将继续保持稳定:1.内容比例相对稳定.考查内容除了新老教材叉的个别内容外,仍为老教材的七、八、九三个学年的主要内容,考题覆盖到每一章.在对三个学年内容全面考查的基础上,突出对一元二次方程、函数、统计初步、相似形、锐角三角比、圆这六大块内容的重点考查.每年这六大块内容的分值都在整卷分值的三分之二左右;考查的代数知识与几何知识的分值比始终控制在6:4左右.2.基础知识基本要求稳定.试卷仍将立足基础,更加着眼于基础知识、基本技能;立足课本,回归课本,更加注重课本例题、习题的作用与有效训练;立足学生,便于学生理解及思维空间的拓展与能力发展.试卷中绝大部分的试题是考查基础知识,许多试题选自新老教材课本中例题、习题,或是课本例题、习题的简单的变形.3.论证运算难度控制稳定.试题仍将体现几何论证的适度性,进一步控制几何证明题的难度,不超过课本例题、练习题的难度要求.严格控制运算量,一些繁琐的计算题不会出现在中考试卷中.新老教材分叉部分的难度将会适当的控制.4.联系生活联系实际稳定.试题仍将贴近生活,重视对数学知识在生活实际中的应用.近年来,随着对“用数学”的强调,联系生活实际的应用题成为中考的一个新的特点,试卷将加强联系实际,体现应用能力.考查在近几年的试题中,结合社会热点、结合生产、生活实际等有实际背景和意义的问题频繁的出现,要求用数学的眼光观察世界、增强应用数学的意识,突出了用数学知识、数学思想方法去分析问题、解决问题能力的考查.这类试题往往情景较为新颖,问题也较为灵活.今年的分值估计在30分左右.5.数学思想方法考查稳定.试题仍将注重了考查学生对数学思想方法的领悟.初中阶段所涉及的如:字母表示数的思想、方程思想、变量及函数思想、数形结合思想、分类讨论思想、图形运动思想、化归思想、整体代换思想、分解组合等到主要数学思想及一些常用的数学方法在试题中得到充分的体现.6.图形运动变换考查稳定.试题仍将注意对空间观念和动态图形处理能力的考查,将从对静态图形的想象、简单动态图形的想象、复杂动态图形的想象等几个不同层次对能力作恰当要求,重视图形的旋转、平移、翻折三种基本形式,体现上海教材的特色.7.信息获取能力及统计思想考查稳定.试卷仍将注意对从数学图形、图像、文字、表格等多种信息源中,获取有用的信息,通过阅读正确理解各种形式的数学语言的含意,分析问题转化的条件,概括发现规律,选择恰当的方法处理问题,体现获取信息能力和数学语言素养的考察.有关统计分值仍将在10分左右,统计的试题与往年一样不再是单纯地计算平均数、方差、标准差,而是更加注意与生活实际的联系,更加重视统计的思想方法和统计的意义.8.探索性、开放性、操作性问题的考查稳定.近年来引进了探索性问题、开放性问题、操作性问题,这类试题往往情景较为新颖,问题也较为灵活.但题目的难度不一定很大,有的在对传统题后的改变后难度大大的降低,在各种层次、类型的试题中都可出现.今年的中考数学试卷将在变化中力求稳定,在稳定中力求发展.在上述稳定之中,首先是控制试题的难度,使它体现学业水平考的性质.稳定的同时,又会有一些情景新颖、立意新颖,而且新而不难,活而不难的试题出现.复习要点1.加强基础,弥补漏洞根据中考数学试卷的特征和特点,复习时应注意对七、八、九年级(新教材还包括六年级“一次方程(组)和一次不等式(组)”)的内容进行全面系统的梳理、归纳,了解知识体系,理解知识之间的内在联系,巩固有关的概念、法则、公式、定理,掌握它们的基本应用,弥补知识漏洞.在此基础上,要突出重点,深化主干性知识和重点内容的理解、掌握和应用.2.回归教材,重视课本要回归教材,重视课本例题、习题的作用,对课本的例题、习题作进一步的反思,理解解题的思考方法,运用的数学思想方法及其问题的变形和拓展.要根据教学的基本要求,切实掌握好基础知识与基本技能,而没有必要再去做那些已经不作要求的繁难计算和证明题,及过分的追求解题技巧,在解答证明题要特别注意推理时所依据的定理、定义,关键是要写清所需要的条件.3.突出重点,针对训练要突出对一元二次方程、函数、统计初步、相似形、锐角三角比、圆这六大块重点内容,在解答题中必然出现,所占的分值较大,特别在综合性问题中,如有个别知识上产生问题必然造成大量的失分.另外还要根据自己平时学习中所出现的问题进行一些针对性的训练.4.关注热点,联系实践要关注社会热点问题,关注数学在实际中的应用,知道一些生活中的概念、数量及它们之间的关系,还需注意生活常识的积累.解题时并不是单纯地靠题型,而需将重点放在分析上,会将实际问题抽象、转化为数学问题,分清有关的数量关系、等量关系以及它们之间的内在联系,寻找解决问题的突破口,提高数学的应用意识和解决实际问题的能力.5.注重思想,体验过程要注意对数学思想和数学方法进行归纳、整理和总结,它们往往蕴含在数学知识的发生、发展和应用的全过程中,就注意认识它们的特征、思维和操作的程序,掌握思维方式并灵活运用于解决问题.重视对过程的体验.备考策略选择重方法;填空保正确;简答明算理;证明清推理;统计知思想;应用细分析;综合会分解.第一大题选择题为单项题,绝对不能多选,填涂答题纸时须特别注意题号与编排的方向.这一大题将侧重于对概念、法则的理解,解题时为了提高正确率仍要对每个选项仔细的分析,可运用直接法、排除法、比较法、特殊值法等一系列方法加以解决.第二大题填空题对解题的正确性的要求更高. 这部分试题主要考查学生对数学基础知识、基本技能、最基本的思想及方法的掌握情况,试题的主要来源是课本,在命题时主要考虑是对后面几个大题中没有涉及的知识点、方法的补充,及重点内容的突出.试题往往会涉及初中阶段各大块的知识点,因此这一部分试题的覆盖面较广,绝大部分为容易的题目.另外在这一大题中的几何题大部分不给出图形,需根据已知条件自己画出正确的图形,偶尔还会涉及作图的试题.简单的开放性问题、简单的图形运动问题也成为近几年填空题中的热点问题.解答上述两个大题要求答案正确、解题迅速,最好在二十分钟内完成.解题时尽可能地选择合理、简便的方法.第三大题解答题的前五题一般都较为容易,答题后应注意检验与反思,主要的关键的运算步骤不可缺少,证明题每一步推理的条件必须充分,必需把推理的过程写清楚,要明确每一步运算与推理的依据;对于统计问题要认真阅读文字语言、图形、表格,从中获取有用的信息,正确理解统计的意义以及统计基本的思想方法,会根据样本估计整体的情况,并会根据统计的结果作出一些简单的判断;对于应用性的问题解答仔细分析各数量之间关系、等量关系,有时可结合图形、图像,借助图形、图像的性质解决问题,还须注意各数量之间的单位是否一致.解答题的最后两题相对而言有一定难度和能力要求,主要考查数学的思想方法往往要求综合应用教材中所要求的基础知识,数与形相结合、变量与常量相结合、动与静相结合、程式性与探索性结合,解决问题时往往需要把综合性问题分解为基本的问题、把复杂的问题化归为单一性问题、把动态问题转化为静态问题,在这一系列的过程中,就要用到前面所提到的各种数学的思想方法,特别需要指出的是这类类问题中经常会涉及到分类讨论的问题,对于分类讨论的问题要做不复、不遗漏.典型试题分析一、 选择题这部分试题试题侧重于考查基本的概念、法则.例1 下列方程中有实数根的是( )(A )11=+x x ;(B )02122=++xx ;(C ) 222-=-x x x ;(D )222-=-x x x . 分析与简解:可运用“观察法”来解,通过观察可发现选项(C )中2=x 是方程的根,由于是单项选择,所以直接可选(C ).而另外的几个:方程(A )可化为012=+-x x ,△<0,方程无实数解;方程(B)中0122>+x x ,则22122>++x x ,方程无实数解;方程(D) 可化为),2()2(2-=-x x x 221==x x ,经检验2=x 是原方程的增根.说明 对于某些特殊的分式方程有无实数解问题,可运用有关的数与式的性质来判断,或转化整式方程后观察,无法直接判断时,应求出整式方程的解并检验确定是否有解.本题运用观察法解最为方便.例2 下列方程中有实数根的是( )(A )013=+-x ; (B )523-=-+-x x ;(C )x x -=-23; (D )x x -=+2.分析与简解 本题可运用“排除法”解题:方程(A )中,03≥-x 则013>+-x ,所以原方程无实数解; 方程(B )中两个二次根式的和不可能为负数,所以原方程无实数解;方程(C )中由于,03≥-x 所以必需满足⎩⎨⎧≥-≥-,02,03x x 得⎩⎨⎧≤≥,2,3x x 此不等式组无解,所以原方程无实数解.所以只能选(D ).说明 对于某些特殊的无理方程有无实数解问题,可运用根式的性质来判断,不必一个个地去解方程.常见的无实解的无理方程有一个根号或几个根号的和为负数;根据根式大于等于零及被开方数大于等于零,得未知数的取值不存在.当无法用上述方法判断时,用一般方法求解.本题中有三个选项已被排除,不必对另一个选项进行求解. 例3 如图 ,在△ABC 中,AB =AC ,AD 、AE 为高,那么下例四个角中与∠1不一定相等的角是( ) (A )∠2; (B )∠3; (C )∠4; (D )∠5. 分析与简解 应用等腰三角形三线合一及直角三角形斜边上的中线等于斜边的一半推得∠1=∠2=∠3=∠5.所以只能选择(C ). 说明 上述解法是运用了“排除法”得出结论.也可通过改变等腰三角形的形状,用“观察法”得出结论;还可以用“特殊值法”,A B C E 1 23 54设∠A =40°等,通过计算得出结论.例4如果b a >,那么下列各式中一定正确的是( )(A) 22b a >; (B )b c a c ->-; (C )c b c a +>+; (D )bc ac >. 分析与简解 本题可运用不等式性质来解.由于是单项选择所以还可以用“特殊值法”逐步排除错误的结论.如当,1,2,1时-=-=-=c b a (A )、(B )、(D )都不成立.所以只能选(C ).说明 要说明一个不等式正确需要用不等式的性质进行证明;要说明一个不等式不正确只须举出一个反例.本题用“特殊值法”和“排除法”可使问题简化.例5 已知,0a b << 那么下列不等式组中无解的是( )(A )⎩⎨⎧>>;,b x a x (B )⎩⎨⎧-<->;,b x a x (C )⎩⎨⎧-<>;,b x a x (D )⎩⎨⎧<->.,b x a x 分析与简解 先在数轴上画出表示数a 、b 、a -、b -的点,分别将每个选项中的两个不等式在数轴上表示出来,观察其是否有公共部分.不等式组A 、B 、C 、D 在数轴上表示为如图:图(C )设有公共部分就说明这两个不等式组无解.由此可知上述不等式组中无解的是(C ).说明 本题着重考查基本的概念、方法.求不等式组解集的最基本的方法就是借助于数轴找公共部分,另外本题还涉及对相反数的几何意义等基本概念的理解.本题的解题方法是“图像法”.例6 二次函数x x y 32-=的图像不经过的象限是( )(A)第一象限; (B )第二象限; (C )第三象限; (D )第四象限.分析与简解 利用x x y 32-=与x 轴的交点坐标为(0,0),(3,0)及图像的开口方向,可画出函数的大致图像,就可直接观察得出它的图像不经过第三象限.选(C ).说明 本题直接用图像法得出结论,较为简捷直观.二、 填空题这部分试题试题着重考查基础知识.例1. 不等式12)21(->-x 的解是____________________.分析与简解 本题可根据不等式的性质两边同除以21-,得2112--<x ,则1-<x . 说明:在本题解题过程中,许多学生会忽视1-等号应改变方向.例2. 写出一个图像经过第一、二、四象限的一次函数_________________.(D)分析与简解 因为一次函数的一般形式是b kx y +=(k 、b 为常数),它的图像是一条直线,由于它经过第一、二、四象限,由大致的图像可看出,y 随着x 的增大而减小,那么,0<k 而图像与x 轴的交点在y 轴的正半轴上,由此可知截矩0>b .所以只要写出一个k 为负数,b 为正数的一次函数解析式即可,如1+-=x y ,4532+-=x y 等. 说明:本题是一个简单的开放性问题,答案有无数个.解题时可画出函数的大致图形,再来确定的k 、b 取值范围.例3. 二次函数x x y 422-=的图像的顶点坐标是______________.分析与简解 求二次函数图像顶点坐标一般是用配方法,先提取二次项系数,再配上提取后的一次项系的一半的平方.2)1(2)112(2)2(2222--=-+-=-=x x x x x y ,所以它的图像的顶点坐标是(1,–2).说明:配方法是一种很重要的数学方法,是求二次函数图像顶点的一般方法.由于这个二次函数可化为)2(2-=x x y ,它的图像与x 轴的交点为(0,0)与(2,0),得它的对称轴为直线1x =,即顶点的横坐标为1,将它代入解析式可得顶点的纵坐标为-2.当二次函数解析式为两根式时,利用图像的对称性解更为迅速、简便.例4. 已知一个直角三角形的三边长是三个连续的整数,那么较长的直角边的长为__________.分析与简解 因为直角三角形的三边均未知, 可设直角三角形较长的直角边的长为x ,则较长的直角边的长为1-x ,斜边长为1+x ,由勾股定理,列出方程,)1()1(222+=-+x x x 就能求得较长的直角边的长为4.说明:本题运用了方程的思想解决几何问题.一般当一个几何量无法用几何的有关性质直接求出时,常可通过设未知,运用方程的思想进行计算.例5. 如图 ,在△ABC 中,点D 在BC 边上,△ABD 绕点A 旋转后与△ACE 重合,如果∠ECB =100°,那么旋转角的大小是_______度. 分析与简解 由题意可知∠ACE =∠B ,利用△ABC 的内角和就可求出旋转角,∠BAC =180°–(∠B +∠ACB )=180°–(∠ACE +∠ACB )=80°.说明: 本题体现了图形运动的思想, 一般地,图形经平移、旋转、翻折后的图形与原图全等,在图形平移、旋转、翻折的过程中.对应的线段、角等有关的几何量始终保持相等.例6. 已知正方形桌子桌面边长为80cm ,要买一块正方形桌布,如图铺设时,四周垂下的桌布都是等腰直角三角形,且桌面四个角的顶点恰好在桌布边上,那么要买桌布的边长是 cm (精确到个位,备用数据:73.13,41.12≈≈).分析与简解 桌布的边长正好是桌面正方形的对角线长,即113280≈(cm ).说明:本题体现了数学知识在实际生活中的应用.三、 简答题这部分试题试题侧重于考查基本的运算及统计的有关知识.例1 已知222=-x x ,将下式先化简,再求值:1)3)((3)3)((1)(2--+-++-x x x x x . 分析与简解 运用多项式的乘法公式及运算法则,先将代数式化简:原式=5632--x x =5)2(32--x x =3×2–5=1.说明 本题在化简之后应用整体代换的数学思想方法可直接求出代数式的值,也可先解方程求出x 的值后再代入代数式求值,但运算较为复杂.例2 计算:.231341651222------+-x x x x x x 分析与简解 先将各分式的分母分解因式,找出最简公分母后通分,化为同分母分式的加减法,并将结果化为最简分式.结果为.)3)(1(3--x x 说明 运算时应注意运算符号. 例3 解不等式组:⎪⎩⎪⎨⎧-≥-->+(2) .356634(1) ),1(513x x x x 分析与简解 分别解两个不等式,然后取公共部分.由(1)解得.3<x 由(2)解得.38≥x 所以原不等式组的解是.338<≤x 说明 解不等式及不等式组的试题大多为容易题,一般出现在填空题及较为容易的简答题中.解不等式时需注意不等式的两边同乘以或同除以一个负数时,不等号应改变方向.例4 解方程:.236532+--=+x x x分析与简解 本题如果直接两边平方,虽能去掉两个根号化为只有一个根号的方程,但运算较为复杂,为了运算的方便,进行适当的移项,把65-x 单独放在等号的一边得652332-=+++x x x ,两边平方后就可去掉这个根号得11)23)(32(2-=++x x , 由于方程的左边是一个非负数,右边为一个负数,不可能相等,因此此方程无实数解,从而得原方程一定无解.说明 中考试题所涉及的无理方程解题时最多需用两次两边平方,当方程中有两个含未知数根号,可将一个较为复杂的根号单独放在等号的一边,然后将它两边平方化为只有一个含未知数根号的方程,然后按只有解一个含未知数根号的方程的方法求解,本题由于得到根号为负数,所以没有必要再两边平方.例5 解方程组⎪⎩⎪⎨⎧=+-=-(2).04(1) ,04222xy x y x 分析与简解 方程(1)可分解为两个二元一次方程:.0202=-=+y x y x 或这样原方程组可化为(**) .04,02 (*) ;04,0222⎩⎨⎧=+-=-⎩⎨⎧=+-=+xy x y x xy x y x 分别解这两个方程组,可知方程组(*)无解;方程组(**)的解是⎩⎨⎧-=-=⎩⎨⎧==.4,2;4,22211y x y x 所以原方程的解是⎩⎨⎧-=-=⎩⎨⎧==.4,2;4,22211y x y x 说明 对于解二元二次方程组初中阶段只要求掌握两种类型:第一种为方程组中有一个方程为一次的方程,如方程组(*)与方程组(**)这类方程组一般可用代入消元法解;第二种为方程组中两个方程都是二次方程,但其中至少有一个方程可分解为两个一次的方程,如本例的原方程组,这类方程组一般可转化为两个第一种类型的方程组,当其中的两个方程都可分解为两个一次方程时,还可将方程组转化为四个二元一次的方程组.解二元二次方程组的方法不外是“消元”和“降次”,通过消元变为一元方程或通过降次变为一次方程.例3 抛物线x x y 422-=经过平移,能否与抛物线1622-+=x x y 重合?如果能够,请说明可以怎样平移;如果不能,请说明理由.分析 由二次项系数可知,抛物线x x y 422-=经过平移,能与抛物线1622-+=x x y 重合.分别用配方法求出两条抛物线的顶点坐标,由顶点的平移路径得到抛物线的运动路径.解 因为二次函数x x y 422-=与1622-+=x x y 的二次项系数相同,所以抛物线x x y 422-=经过平移能与抛物线10622++=x x y 重合.∵2)1(22)12(242222--=-+-=-=x x x x x y ,∴它的顶点是(1,–2).∵8)3(21018)93(21062222-+=+-++=++=x x x x x y ,∴它的顶点是(–3,–8). ∴抛物线x x y 422-=向左平移4个单位,再向下平移6个单位后与抛物线1622-+=x x y 重合.说明 配方法是一种很重要的数学方法,求二次函数图像顶点坐标一般是用配方法,先提取二次项系数,再配上提取后的一次项系的一半的平方.是求二次函数图像顶点的一般方法.抛物线平移问题中顶点是关键.例2 如果函数(2)y m x m =-+的图像不经过第三象限, 求m 的取值范围.分析与简解 由函数的象限情况可分别得到m m 与2-的符号情况,利用不等式组可求出m 的范围.由于本题没有明确这个函数是不是一次函数, 因此需要分两种情况考虑;当这个函数为一次函数时, 由于象限的情况也没有确定,还需考虑它为正比例函数时的特殊情况. 当20 2m m -==即 时, 函数为2y =, 它是一个常值函数, 图像是过点(0,2)且平行于x 轴的一条直线,经过第一、二象限,不经过第三象限,符合题意;当20m -≠时,函数为一次函数,图像是一条直线,由于它的图像不经过第三象限,那么它的图像经过第一、二、四象限或只经过第二、四象限,由此可以得到:20,0,m m -<⎧⎨≥⎩ 解得02m ≤<. 所以m 的取值范围是02m ≤≤. 说明 在本题的解题过程中,最容易遗漏常值函数及正比例函数这两种特殊的情况,或。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人大附中老师谈08年中考数学命题趋势
北京20XX中考数学命题展望与复习策略
撰稿/刘顺舟老师
纵观去年北京市的中考数学试卷,试题内容新鲜,难度适中,个别题目的关键字词添加了着重号,体现人文关怀。
考题注重考查同学们在具体情境中运用所学数学知识来分析和解决实际问题的能力,根据考试说明和试题要求,猜想20XX年中考数学命题将有如下可能
[考试范围]
由“考试说明”可以看出,数学学科考试以教育部制定的《全日制义务教育教学课程标准》规定的学习内容为考试范围,适当兼顾北京市现行不同版本教材的内容和教学实际情况,也就是说考试范围基本不会有变化。
[试卷结构]
《20XX年北京市高级中等学校招生统一考试说明》指出,试卷包括选择题、填空题和解答题,其中的解答题包括计算题、证明题和作图题。
试卷将由Ⅰ卷和Ⅱ卷组成。
Ⅰ卷为选择题,32分。
第Ⅱ卷为选择题和解答题(其中选择题16分,解答题72分)。
知识内容的分布为:数与代数约60分;空间与图形约46分;统计与概率约14分。
难易程度的分布情况为:较易试题60分;中等试题约36分;较难试题约24分。
[考试内容]数与式部分的试题将不再纯粹考查记忆的内容。
尤其是一些繁、难、偏的计算题目将不再出现,取而代之的是探索数与式的数学意义以及与实际生活的联系的问题。
在变化的图形或实际问题的背景中观察、概括出一般规律,运用数学模型解决实际问题。
2.空间与图形部分的内容难度也不会增加。
证明过程不会超过两个三段论。
在填空题和选择题中考察视图、几何体及平面展开图之间的关系以及初步的空间观念的可能性较大;几何论证题可能从常见的几何图
形中提出问题或猜想,通过对其分析、探索,发现其内在规律并能用简单的逻辑推理来证明命题的正确性,以考查学生的合理推断能力。
3.统计与概率部分的试题。
特别是与之有关的统计技能的试题,在08年的试卷将必不可少。
新课标指出,发展统计观念是新课程的重要目标。
因此“考试说明”规定这部分试题考分为14分,而这部分试题往往要求学生有较强的阅读能力。
因此我们在今后的教学中要加强培养,学生要克服畏惧心理,加强这类题目的练习即可。
其次还应该注意这类题目的开放性。
针对这些情况,比较07年与08年的考试说明,提出以下复习建议,以求达到抛砖引玉的目的。
一.重视基础。
各地中考试题均立足基础,考查学生对基本概念的理解,基本技能的把握。
且08年的考试说明增加了“了解立方根的概念、会用根号表示数的立方根”,“了解一元一
次方程的有关概念”,“理解频数,频率的概念”。
因此在复习过程中要在心中梳理知识点,使之在大脑中成像,做到胸有成竹,重视概念的实质以及概念之间的联系,在应用中加深理解。
二.重视数学方法的应用,强化数学思想的培养。
各地考题都很重视数学方法,如换元法、待定系数法、构造法、反证法、因式分解法、代入法、坐标法等等。
而数学思想是以数学方法为基础逐步形成的运用数学方法来解决数学问题的一种自觉意识。
常见的数学思想有:化归思想、数形结合思想、分类讨论思想等。
建议同学们用最快的速度重做一遍教材中的“综合运用”“拓广探索”题,并适当自我拓展,将收到较好的效果。
三.重视代数与几何等综合题的训练。
这类考题在各地的考卷中常见,考查学生的综合素质,尤其是分析问题、解决问题的能力。
因而复习阶段要重视这类题目的训练。
07年北京考题第24题是函数与几何的综合,这种题出现的可能性依然较大。
建议
同学们收集各地中考题中的这类综合题,快速突破必能事半功倍。
四.再读“考试说明”。
《20XX年考试说明》较《20XX年考试说明》提升的有“①会列一元一次方程解决实际问题;②会选择适当的方法解一元二次方程;③会用一元二次方程根的判别式判断根的情况;④提高频数、频率的概念的理解;
⑤能用概率知识解决实际问题。
”这些方面极易才出现考题。
对于梯形,07年要求会灵活的运用组合图形的知识分解梯形,而08年无要求。
这样分解梯形的习题可以适当的放弃了。
当然,命题将会受许多条件制约,尤其是受时代背景的影响。
更加关键的是,茫茫题海量大量多。
斗胆行文只希望能与同行商榷,只希望能给同学一定的帮助。
