第六章 MATLAB解曲线拟合问题
[matlab曲线拟合]MATLAB的曲线拟合
![[matlab曲线拟合]MATLAB的曲线拟合](https://img.taocdn.com/s3/m/ddca46a8c67da26925c52cc58bd63186bceb9275.png)
[matlab 曲线拟合]MATLAB的曲线拟合篇一: MA TLAB的曲线拟合MA TLAB软件提供了基本的曲线拟合函数的命令。
曲线拟合就是计算出两组数据之间的一种函数关系,由此可描绘其变化曲线及估计非采集数据对应的变量信息。
1.线性拟合函数:regress调用格式:b =regress[b,bint,r,rint,stats]= regress[b,bint,r,rint,stats] =regressx=[ones …];y=x*[10;1]+normrnd;[b,bint]=regress结果得回归方程为:y=9.9213+1.0143xx=1:20;y=x+3*sin;p=polyfitxi=linspace;z=polyval;% 多项式求值函数plotlegendfunction yy=modela=beta0;b=beta0;yy=a+*exp);拟合程序:x=[8.00 8.00 10.00 10.00 10.00 10.00 12.00 12.00 12.00 14.00 14.0014.00...16.00 16.00 16.00 18.00 18.00 20.00 20.00 20.00 20.00 22.00 22.0024.00...24.00 24.00 26.00 26.00 26.00 28.00 28.00 30.00 30.00 30.00 32.0032.00...34.00 36.00 36.00 38.00 38.00 40.00 42.00]‟;y=[0.49 0.49 0.48 0.47 0.48 0.47 0.46 0.46 0.45 0.43 0.45 0.43 0.430.44 0.43...0.43 0.46 0.42 0.42 0.43 0.41 0.41 0.40 0.42 0.40 0.40 0.41 0.400.41 0.41...0.40 0.40 0.40 0.38 0.41 0.40 0.40 0.41 0.38 0.40 0.40 0.390.39]‟;beta0=[0.30 0.02];betafit = nlinfit结果:betafit =0.3896 0.1011即:a=0.3896 ,b=0.1011 拟合函数为:x1 =[1150,1000,900,850,700,625,550,475,3350,3500,5900,5800,5700,4600,4625,4725,11650,11200,11200 ]‟;x2 =[175,100,25,0,75,100,150,200,50,600,500,225,100,1225,1600,2000,1200,1000,1550 ]‟;x = [x1,x2];y=[1.44E-02,1.80E-02,6.08E-02,5.59E-02,3.42E-02,7.74E-03,1.17E-03,6.16E-03,1.91E-04,1.,resplot3)% 值的选取没有定法,与实际问题的模型有关。
Matlab中的曲线拟合方法

Matlab中的曲线拟合方法引言在科学与工程领域,数据拟合是一个重要的技术,可用于分析实验数据、预测未知的对应关系,并量化观察到的现象。
其中,曲线拟合是一种常见的数据拟合方法,而Matlab作为一种功能强大的科学计算软件,提供了多种曲线拟合工具和函数,方便用户进行数据分析和模型建立。
本文将对Matlab中的曲线拟合方法进行详细介绍和讨论。
一、线性拟合线性拟合是最简单且常见的曲线拟合方法,其基本思想是通过一条直线拟合数据点,找到最佳拟合直线的参数。
在Matlab中,可以使用polyfit函数实现线性拟合。
该函数接受两个输入参数,第一个参数为数据点的x坐标,第二个参数为数据点的y坐标。
返回结果为一个一次多项式拟合模型的参数。
例如,我们有一组实验测量数据如下:x = [1, 2, 3, 4, 5];y = [3, 5, 7, 9, 11];通过polyfit函数进行线性拟合:coeff = polyfit(x, y, 1);其中,1表示要拟合的多项式的次数,这里我们选择了一次多项式(直线)。
coeff即为拟合得到的直线的参数,可以通过polyval函数将参数代入直线方程,得到对应x的y值。
y_fit = polyval(coeff, x);接下来,我们可以使用plot函数将原始数据点和拟合曲线都绘制在同一张图上:figure;plot(x, y, 'o', 'MarkerSize', 10); % 绘制原始数据点hold on;plot(x, y_fit); % 绘制拟合曲线xlabel('x');ylabel('y');legend('原始数据点', '拟合曲线');通过观察图像,我们可以初步判断拟合的效果如何。
如果数据点较为分散,直线拟合效果可能较差。
在此情况下,可以考虑使用更高次的多项式进行拟合。
二、多项式拟合多项式拟合是一种常见的曲线拟合方法,其基本思想是通过一个一定次数的多项式函数来拟合数据点。
曲线拟合法的Matlab实现

曲线拟合法的Matlab实现曲线拟合在许多科学和工程领域中都有广泛应用,包括机器学习,数据科学,信号处理,控制工程等。
在Matlab中实现曲线拟合的方法有多种,其中最常用的是使用fit()函数。
以下是一个基本的示例,演示如何在Matlab中使用fit()函数进行曲线拟合。
我们需要一些数据。
假设我们有一组x和y数据点,我们想要在这些点上拟合一条曲线。
y = 3*x.^2 + 2*x + 1 + randn(size(x));fitresult = fit(x, y, 'poly1');在这里,'poly1'表示我们想要拟合一个一次多项式。
你可以使用'poly2','poly3'等来拟合更高次的多项式。
同样,你也可以使用其他类型的模型,如指数、对数、自定义函数等。
然后,我们可以使用plot()函数将原始数据和拟合曲线一起绘制出来。
在这里,'hold on'命令用于保持当前图像,这样我们就可以在同一个图形上绘制多条线了。
我们可以使用fitresult来获取拟合曲线的参数和其他信息。
例如:以上就是在Matlab中进行曲线拟合的基本步骤。
需要注意的是,对于复杂的实际问题,可能需要进行更复杂的模型选择和参数优化。
也可以使用其他工具如curve fitting toolbox进行更详细的分析和拟合。
最小二乘曲线拟合是一种数学统计方法,用于根据给定数据点拟合出一条曲线或曲面,使得该曲线或曲面最小化每个数据点到拟合曲线或曲面的平方误差之和。
这种方法广泛应用于数据分析和科学计算等领域。
本文将介绍最小二乘曲线拟合的基本原理和在Matlab中的实现方法。
假设有一组数据点 (x_i, y_i),i=1,2,...,n,需要拟合出一条曲线y=f(x)。
最小二乘法要求曲线 f(x)最小化每个数据点到曲线的平方误差之和,即E = sum (f(x_i)-y_i)^2对曲线 f(x)进行求导,得到一元一次方程:f'(x)=sum(f(x)-y)*x-sum(f(x)-y)E = sum [(f'(x))^2] * x^2 - 2 * sum [f(x) * f'(x) * x] + 2 * sum [f(x)^2]令 E对 f'(x)的导数为零,可得到最小二乘曲线拟合的方程:sum [f'(x)^2] * x^2 - 2 * sum [f(x) * f'(x) * x] + 2 * n * f(x)^2 = 0在Matlab中,可以使用polyfit函数实现最小二乘曲线拟合。
用MATLAB解插值和曲线拟合问题

f=10-(10-x(1))*exp(-t/x(2));
t=[0.5 1 2 3 4 5 7 9];
v=[6.36 6.48 7.26 8.22 8.66 8.99 9.43 9.63];
x0=[0,0.05];
x=lsqcurvefit('curvefun4',x0,t,v)
Interp1(x,y,cx,’method’)
在MATLAB的线性最小二乘拟合中,用得较多的是多项式拟合,其命令为:
A=polyfit(x,y,m)
二.上机内容
1、在飞机的机翼加工时,由于机翼尺寸很大,通常在图纸上只能标出部分关键点的数据.某型号飞机的机翼上缘轮廓线的部分数据如下。用插值法求x每改变0.1时的y值,画出图形表示。
x 0 4.74 9.05 19 38 57 76 95 114 133152 171 190
y 0 5.23 8.1 11.97 16.15 17.1 16.34 14.63 12.16 6.697.03 3.99 0
2、已知观测数据点如表所示:
用3次多项式函数拟合这些数据点,画出图形。
3、教材习题1,用griddata插值函数,三次插值。
注:上机作业文件夹以自己的班级姓名学号命名,文件夹包括如下上机报告和Matlab程序。
上机报告模板如下:
佛山科学技术学院
上 机报 告
课程名称数学应用软件
上机项目用MATLAB解插值和曲线拟合问题
专业班级
一.上机目的
熟练掌握多种插值方法:线性插值,三次样条插值,三次插值和最近邻点插值(linear、spline、cubic、nearest)
f=curvefun4(x,t)
matalab曲线拟合

matalab曲线拟合MATLAB曲线拟合是指在一定条件下,利用数学模型和算法对实验数据进行拟合,以进而得出数据特征和规律的过程。
通过MATLAB曲线拟合,可以在大量数据中筛选出潜在的相关性和规律性,更好地理解实验数据,提高研究结果的分析和预测能力,为科学研究和工业应用提供理论和实践基础。
本文将探讨MATLAB曲线拟合的相关概念、方法和应用。
一、曲线拟合的概念曲线拟合是一种数学方法,利用一定的数学模型和算法对实验数据进行拟合,以得出数据之间的相互关系和规律。
在MATLAB中,曲线拟合具有很高的灵活性和适用性,可以应用于各种不同类型的数据,如线性数据、非线性数据和多项式数据等。
一般来说,拟合函数的形式和参数值将根据数据的特征和目标而变化,以实现最优的拟合效果。
常见的曲线拟合方法包括线性回归、非线性回归、多项式拟合和曲线拟合等,具体如下:1.线性回归线性回归是最简单的曲线拟合方法之一,它试图利用直线函数来拟合数据点,以揭示数据之间的线性关系。
MATLAB中提供了静态和动态线性回归模型,可以通过最小二乘法、梯度下降法等算法来确定最优的拟合函数。
线性回归只适用于线性数据,而非线性回归则可用于拟合更复杂的数据。
MATLAB中提供了非线性函数和指数函数等多种非线性拟合方法,可以根据数据分布和需求进行选择。
3.多项式拟合多项式拟合是一种常见的曲线拟合方法,可以用于拟合多项式数据。
MATLAB中常用的多项式拟合函数包括polyfit和polyval等,它们可以帮助用户通过调整曲线阶数、曲线拟合类型等参数来实现最优的拟合效果4.曲线拟合曲线拟合是将实验数据拟合到特定类型的曲线上,以确定数据之间的关系。
MATLAB中提供了许多曲线拟合函数,如spline、pchip、csape等,它们可以帮助用户根据数据的特点选择最合适的曲线拟合方法。
曲线拟合广泛应用于各种领域,如工程、物理、生物、金融和地质等领域。
下面是一些常见的应用实例:1.金融数据分析:通过曲线拟合模型,可以预测股票价格趋势、货币汇率和股票波动等金融数据的变化。
《计量经济学》与MATLAB编程-第六章多项式回归与非线性回归
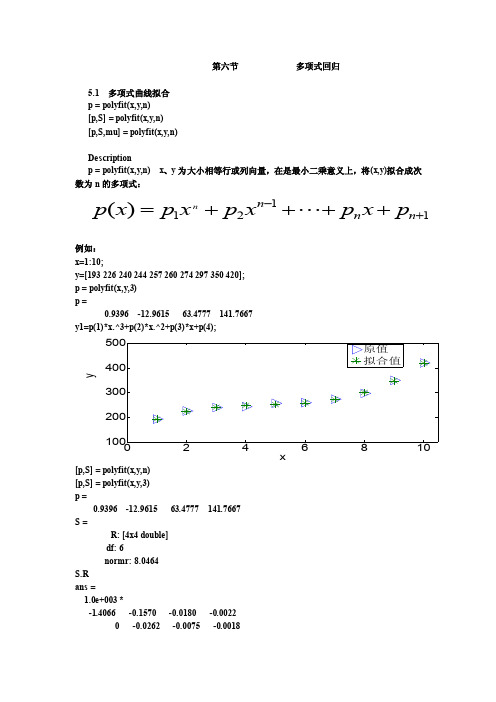
第六节 多项式回归5.1 多项式曲线拟合 p = polyfit(x,y,n) [p,S] = polyfit(x,y,n) [p,S,mu] = polyfit(x,y,n)Descriptionp = polyfit(x,y,n) x 、y 为大小相等行或列向量,在是最小二乘意义上,将(x,y)拟合成次数为n 的多项式:1121)(+-++++=n n n p x p x p x p x p n例如: x=1:10;y=[193 226 240 244 257 260 274 297 350 420]; p = polyfit(x,y,3) p =0.9396 -12.9615 63.4777 141.7667y1=p(1)*x.^3+p(2)*x.^2+p(3)*x+p(4);xy[p,S] = polyfit(x,y,n) [p,S] = polyfit(x,y,3) p =0.9396 -12.9615 63.4777 141.7667 S =R: [4x4 double] df: 6normr: 8.0464 S.R ans =1.0e+003 *-1.4066 -0.1570 -0.0180 -0.0022 0 -0.0262 -0.0075 -0.00180 0 -0.0019 -0.00140 0 0 0.0005normr是残差的模,即:norm(y-y1)ans =8.0464[p,S,MU] = polyfit(x,y,n)[p,S,MU] = polyfit(x,y,3)p =26.0768 23.2986 18.6757 255.1312S =R: [4x4 double]df: 6normr: 8.0464MU =5.50003.0277MU是x均值和x的标准差即std(x)S.Rans =5.1959 0.0000 2.7682 0.00000 -3.7926 -0.0000 -2.37310 0 1.1562 0.00000 0 0 -2.0901P它等于:[p,S] = polyfit((x-mean(x))./std(x),y,3)p =26.0768 23.2986 18.6757 255.1312S =R: [4x4 double]df: 6normr: 8.0464>> S.Rans =5.1959 0.0000 2.7682 0.00000 -3.7926 -0.0000 -2.37310 0 1.1562 0.00000 0 0 -2.09015.2 多项式估计y= polyval(p,x)[y,DELT A] = polyval(p,x,S)y= polyval(p,x) 返回给定系数p和变量x值的多项式的预测y = P(1)*x^N + P(2)*x^(N-1) + ... + P(N)*x + P(N+1)x=1:10;y= polyval([3 2],x)y =5 8 11 14 17 20 23 26 29 32[3 2]有两个数,因此为一次多项式,即y=3x+2如:x=1:10;y=[193 226 240 244 257 260 274 297 350 420];p=polyfit(x,3)y1= polyval(p,x)norm(y-y1)ans =8.0464如果是矩阵,则polyval(p,x)为对应x的每一个预测值。
7.4 用Matlab求解曲线拟合问题

2 [ f ( x ) y ] i i i 1 11
最小
12
1)输入以下命令: x=0:0.1:1;
10 8 6 4
y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66 9.56 9.48 9.30 11.2];
问题归结为,求 a1,a2, …am 使 J(a1,a2, …am) 最小。
线性最小二乘拟合 f(x)=a1r1(x)+ …+amrm(x)中 函数{r1(x), …rm(x)}的选取 1. 通过机理分析建立数学模型来确定 f(x); 2. 将数据 (xi,yi) i=1, …n 作图,通过直观判断确定 f(x): f=a1+a2x + + + + + f=a1+a2x+a3x2 + + + + + f=a1+a2x+a3x2 + + + + +
f=a1+a2/x + + +
f=aebx +
+
-bx f=ae + +
+ +
+ + +
+
+ +
一、用Matlab进行多项式曲线拟合
1. Matlab中提供函数polyfit作多项式f(x)=a1xm+ …+amx+am+1 曲线拟合,具体的调用格式如下: a=polyfit(x,y,m)
拟合多项式次数 已知数据点向量(长度相同) 输出拟合多项式系数 a=[a1, …am , am+1] (数组)
matlab 根据曲线拟合方程

【引言】曲线拟合是数学分析中一种常用的方法,通过数学模型对一系列数据点进行拟合,从而得到一个函数或曲线,使其能够很好地描述这些数据。
在工程、经济、物理、生物等领域中,曲线拟合都有着广泛的应用。
MATLAB作为一种强大的数学工具软件,提供了丰富的曲线拟合函数和工具箱,能够帮助用户实现各种复杂的曲线拟合任务。
本文将介绍MATLAB中的曲线拟合方程,并对其进行深入分析和讲解。
【一、曲线拟合的原理】1.1 数据拟合的概念在实际应用中,我们常常需要根据一系列给定的数据点,找到一个函数或曲线,使其能够很好地拟合这些数据。
这个过程就称为数据拟合。
曲线拟合是一种常用的数据拟合方法,通过拟合出的函数或曲线,我们可以进行数据的预测、趋势的分析等。
1.2 曲线拟合的方法在进行曲线拟合时,常用的方法包括线性拟合、多项式拟合、非线性拟合等。
线性拟合是最基本的拟合方法,它试图找到一条直线对数据进行拟合;多项式拟合则是试图通过一个多项式函数对数据进行拟合;非线性拟合是指通过非线性函数对数据进行拟合,可以拟合各种形状的曲线。
【二、MATLAB中的曲线拟合函数】2.1 polyfit函数MATLAB提供了polyfit函数,可以实现多项式拟合。
其语法为:p = polyfit(x, y, n)其中,x为自变量,y为因变量,n为多项式的次数,p为拟合出的多项式系数。
2.2 fit函数MATLAB的Curve Fitting Toolbox中提供了fit函数,可以实现各种曲线拟合,包括线性拟合、多项式拟合、指数拟合、幂函数拟合等。
其语法为:f = fit(x, y, 'type')其中,x为自变量,y为因变量,'type'为拟合的类型,f为拟合出的函数。
2.3 cftool工具MATLAB的Curve Fitting Toolbox还提供了cftool工具,可以通过可视化界面实现曲线拟合,用户可以方便地进行参数设定、拟合结果的可视化展示等操作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章MATLAB解曲线拟合问题曲线拟合就是计算出两组数据之间的一种函数关系,由此可描绘其变化曲线及估计非采集数据对应的变量信息。
曲线拟合有多种方式,下面是一元函数采用最小二乘法对给定数据进行多项式曲线拟合,最后给出拟合的多项式系数。
§1 线性拟合一、数学模型y=Xβ+εβ是p⨯1的参数向量;ε是服从标准正态分布的随机干扰的n⨯1的向量;y为n⨯1的向量;X为n⨯p矩阵。
二、求解线性拟合函数regress调用格式:b=regress(y,X)[b,bint,r,rint,stats]= regress(y,X)[b,bint,r,rint,stats]= regress(y,X,alpha)说明:b=regress(y,X)返回X处y的最小二乘拟合值。
bint返回β的95%的置信区间。
r 中为形状残差,rint中返回每一个残差的95%置信区间。
Stats向量包含R2统计量、回归的F 值和p值。
三、举例例1:设y的值为给定的x的线性函数加服从标准正态分布的随机干扰值得到。
即y=10x+ε;求线性拟合方程系数。
程序:编写M文件mainG.m如下:x=[ones(10,1) (1:10) '] %ones(m,n)产生一个m行n列的元素全为1的矩阵%(1:10)产生一个10行1列的元素值从1~10的矩阵% [A B] 将矩阵A和B拼接成新矩阵或者写成[A;B]y=x*[10;1]+normrnd(0,0.1,10,1)% R = normrnd(MU,SIGMA,m,n) 依据参数MU、SIGMA生成一个随机数,m和n是R的行数和列数.[b,bint]=regress(y,x,0.05)结果:x = 1 11 21 31 41 51 61 71 81 91 10x=1:20,y=x+3*sin(x)x=1:20;y=x+3*sin(x);p=polyfit(x,y,6)xi=1inspace(1,20,100);z=poyval(p,xi); %多项式求值函数plot(x,y,’o’,xi,z,’k:’,x,y,’b’)legend(‘原始数据’,’6阶曲线’)结果:p =0.0000 -0.0021 0.0505 -0.5971 3.6472 -9.7295 11.3304图 6阶曲线图10阶曲线例4:再用10阶多项式拟合程序:x=1:20;y=x+3*sin(x);p=polyfit(x,y,10)xi=linspace(1,20,100);z=polyval(p,xi);plot(x,y,'o',xi,z,'k:',x,y,'b')legend('原始数据','10阶多项式')结果:p = Columns 1 through 70.0000 -0.0000 0.0004 -0.0114 0.1814 -1.8065 11.2360 Columns 8 through 11-42.0861 88.5907 -92.8155 40.2671说明:可用不同阶的多项式来拟合数据,但也不是阶数越高拟合的越好。
§3 多项式曲线求值函数polyval( )调用格式:y=polyval(p,x)[y,DELTA]=polyval(p,x,s)说明:y=polyval(p,x)为返回对应自变量x在给定系数P的多项式的值。
[y,DELTA]=polyval(p,x,s) 使用polyfit函数的选项输出s得出误差估计Y±DELTA。
它假设polyfit函数数据输入的误差是独立正态的,并且方差为常数。
则Y±DELTA将至少包含50%的预测值。
§4 多项式曲线拟合的评价和置信区间函数polyconf( )调用格式:[Y,DELTA]=polyconf(p,x,s)[Y,DELTA]=polyconf(p,x,s,alpha)说明:[Y,DELTA]=polyconf(p,x,s)使用polyfit函数的选项输出s给出Y的95%置信区间Y±DELTA。
它假设polyfit函数数据输入的误差是独立正态的,并且方差为常数。
1-alpha 为置信度。
例5:给出上面例1的预测值及置信度为90%的置信区间。
程序:x=0:.1:1;y=[.3 .5 1 1.4 1.6 1.9 .6 .4 .8 1.5 2]n=3;[p,s]=polyfit(x,y,n)alpha=0.05;[Y,DELTA]=polyconf(p,x,s,alpha)结果:p = 16.7832 -25.7459 10.9802 -0.0035s = R: [4x4 double]df: 7normr: 1.1406Y = Columns 1 through 7-0.0035 0.8538 1.2970 1.4266 1.3434 1.1480 0.9413Columns 8 through 110.8238 0.8963 1.2594 2.0140DELTA = Columns 1 through 71.3639 1.1563 1.1563 1.1589 1.1352 1.1202 1.1352Columns 8 through 111.1589 1.1563 1.1563 1.3639§5 稳健回归函数:robust( )稳健回归是指此回归方法相对于其他回归方法而言,受异常值的影响较小。
调用格式:b=robustfit(x,y)[b,stats]=robustfit(x,y)[b,stats]=robustfit(x,y,’wfun’,tune,’const’)说明:b返回系数估计向量;stats返回各种参数估计;’wfun’指定一个加权函数;tune为调协常数;’const’的值为’on’(默认值)时添加一个常数项;为’off ’时忽略常数项。
例6:演示一个异常数据点如何影响最小二乘拟合值与稳健拟合。
首先利用函数y=10-2x加上一些随机干扰的项生成数据集,然后改变一个y的值形成异常值。
调用不同的拟合函数,通过图形观查影响程度。
程序:x=(1:10)’;y=10-2*x+randn(10,1);y(10)=0;bls=regress(y,[ones(10,1) x]) %线性拟合brob=robustfit(x,y) %稳健拟合scatter(x,y)hold onplot(x,bls(1)+bls(2)*x,’:’)plot(x,brob(1)+brob(2)*x,’r‘)结果:bls = 8.4452-1.4784brob = 10.2934-2.0006分析:稳健拟合(实线)对数据的拟合程度好些,忽略了异常值。
最小二乘拟合(点线)则受到异常值的影响,向异常值偏移。
§6 向自定义函数拟合对于给定的数据,根据经验拟合为带有待定常数的自定义函数。
二、向自定义函数拟合所用函数:nlinfit( )调用格式: [beta,r,J]=nlinfit(X,y,’fun’,betao)说明:beta 返回函数’fun’中的待定常数;r 表示残差;J 表示雅可比矩阵。
X,y 为数据;‘fun’自定义函数;beta0待定常数初值。
例7:在化工生产中获得的氯气的级分y 随生产时间x 下降,假定在x ≥8时,y 与x 之间有如下形式的非线性模型:)8()49.0(---+=x b e a a y现收集了44组数据,利用该数据通过拟合确定非线性模型中的待定常数。
x y x y x y8 0.49 16 0.43 28 0.418 0.49 18 0.46 28 0.4010 0.48 18 0.45 30 0.4010 0.47 20 0.42 30 0.4010 0.48 20 0.42 30 0.3810 0.47 20 0.43 32 0.4112 0.46 20 0.41 32 0.4012 0.46 22 0.41 34 0.4012 0.45 22 0.40 36 0.4112 0.43 24 0.42 36 0.3614 0.45 24 0.40 38 0.4014 0.43 24 0.40 38 0.4014 0.43 26 0.41 40 0.3616 0.44 26 0.40 42 0.3916 0.43 26 0.41首先定义非线性函数的m 文件:fff6.mfunction yy=model(beta0,x)a=beta0(1);b=beta0(2);yy=a+(0.49-a)*exp(-b*(x-8));程序:x=[8.00 8.00 10.00 10.00 10.00 10.00 12.00 12.00 12.00 14.00 14.00 14.00...16.00 16.00 16.00 18.00 18.00 20.00 20.00 20.00 20.00 22.00 22.00 24.00...24.00 24.00 26.00 26.00 26.00 28.00 28.00 30.00 30.00 30.00 32.00 32.00...34.00 36.00 36.00 38.00 38.00 40.00 42.00]';y=[0.49 0.49 0.48 0.47 0.48 0.47 0.46 0.46 0.45 0.43 0.45 0.43 0.43 0.44 0.43...0.43 0.46 0.42 0.42 0.43 0.41 0.41 0.40 0.42 0.40 0.40 0.41 0.40 0.41 0.41...0.40 0.40 0.40 0.38 0.41 0.40 0.40 0.41 0.38 0.40 0.40 0.39 0.39]';beta0=[0.30 0.02];betafit = nlinfit(x,y,'sta67_1m',beta0)结果:betafit =0.38960.1011即:a=0.3896 ,b=0.1011 拟合函数为: )8(1011.0)3896.049.0(3896.0---+=x e y。
