机械行业振动力学期末考试试题(doc-11页)(正式版)
机械振动试卷

机械振动测试题一、选择题(本大题共7个小题,每小题6分,共42分。
在四个选项中,至少有一个选项符合题目要求,全部选对的得6分,选不全的得3分,有错选或不选的得0分)1.水平放置的弹簧振子在做简谐运动时()A.加速度方向总是跟速度方向相同B.加速度方向总是跟速度方向相反C.振子向平衡位置运动时,加速度方向跟速度方向相反D.振子向平衡位置运动时,加速度方向跟速度方向相同2.关于简谐运动的周期,以下说法正确的是()A.间隔一个周期的两个时刻物体的振动情况完全相同B.间隔半个周期奇数倍的两个时刻,物体的速度和加速度可能同时相同C.半个周期内物体动能的变化一定为零D.一个周期内物体势能的变化一定为零3.装有砂粒的试管竖直静浮于水面,如图1所示。
将试管竖直提起少许,然后由静止释放并开始计时,在一定时间内试管在竖直方向近似做简谐运动。
若取竖直向上为正方向,则以下描述试管振动的图象中可能正确的是()图1图2 4.某质点做简谐运动,其位移与时间的关系式为:x=3sin(t+)cm,则()A.质点的振幅为3cmB.质点振动的周期为3sC.质点振动的周期为sD.t=0.75s时刻,质点回到平衡位置5.光滑的水平面上叠放有质量分别为m和m/2的两木块,下方木块与一劲度系数为k弹簧相连,弹簧的另一端固定在墙上,如图3所示。
已知两木块之间的最大静摩擦力为f,使这两个木块组成的系统像一个整体一样地振动,系统的最大振幅为()A. B.C. D.6.一砝码和一轻弹簧构成弹簧振子,图4甲所示的装置可用于研究该弹簧振子的受迫振动。
匀速转动把手时,曲杆给弹簧振子以驱动力,使振子做受迫振动。
把手匀速转动的周期就是驱动力的周期,改变把手匀速转动的速度就可以改变驱动力的周期。
若保持把手不动,给砝码一向下的初速度,砝码便做简谐运动,振动图线如图乙所示。
当把手以某一速度匀速转动,受迫振动达到稳定时,砝码的振动图线如图丙所示。
若用T0表示弹簧振子的固有周期,T表示驱动力的周期,Y表示受迫振动达到稳定后砝码振动的振幅,则()图4A.由图线可知T0=4sB.由图线可知T0=8sC.当T在4s附近时,Y显着增大;当T比4s小得多或大得多时,Y很小D.当T在8s附近时,Y显着增大;当T比8s小得多或大得多时,Y很小7.将一单摆向左拉至水平标志线上,从静止释放,当摆球运动到最低点时,摆线碰到障碍物,摆球继续向右摆动。
机械振动习题及答案完整版.docx

1.1试举出振动设计'系统识别和环境预测的实例。
1.2如果把双轴汽车的质量分别离散到前、后轴上去,在考虑悬架质量和非悬架质量两个离散质量的情况下,画出前轴或后轴垂直振动的振动模型简图,并指出在这种化简情况下,汽车振动有几个自由度?1.3设有两个刚度分别为心,心的线性弹簧如图T-1.3所示,试证明:1)它们并联时的总刚度k eq为:k eq = k x+ k22)它们串联时的总刚度匕满足:丿-畔+ 土keq & k2解:1)对系统施加力P,则两个弹簧的变形相同为X,但受力不同,分别为: P x = k x x<由力的平衡有:P = ^ + P,=(k1+k2)xp故等效刚度为:k eq^- = k1+k2x2)对系统施加力P,则两个弹簧的变形为:P%i=r 111,弹簧的总变形为:x = x}+x2= P(——I ---- )故等效刚度为:k =—Xk x k2k,2+ k、1 1=—l-------k、k21.4求图所示扭转系统的总刚度。
两个串联的轴的扭转刚度分别为心, 解:对系统施加扭矩T,则两轴的转角为:VTrx系统的总转角为:0 = G + g = Hy- + T-)褊k,i故等效刚度为:犒=二+二1.5两只减振器的粘性阻尼系数分别为q, C2,试计算总粘性阻尼系数"在两只减振器并联时,2)在两只减振器串联时。
解:1)对系统施加力P,则两个减振器的速度同为厂受力分别为:P{ - c x x<P2=C2X由力的平衡有:P=£ + E =(q+C2)Xp故等效刚度为:c eq=- = c]+c2X2)对系统施加力P,则两个减振器的速度为:p 1 1故等效刚度为:c eq=- = - + -1.6 一简谐运动,振幅为0. 5cm,周期为0.15s,求最大速度和加速度。
解:简谐运动的a>n= — = /5),振幅为5x10 3m ;= 5x10-cos(^_ 2/r即:—5x10'丽fsin(丽血/s)*610=(話讥。
机械振动试题及答案

一、填空题1、机械振动按不同情况进行分类大致可分成(线性振动)和非线性振动;确定性振动和(随机振动);(自由振动)和强迫振动,连续振动和离散系统。
2、(弹性元件)元件、(惯性元件)元件、(阻尼元件)元件是离散振动系统的三个最基本元素。
3、在振动系统中,弹性元件存储(势能)、惯性元件存储(动能)、(阻尼元件)元件耗散能量。
4、系统固有频率主要与系统的(质量)和(刚度)有关,与系统受到的激励无关。
5、研究随机振动的方法是(数理统计),工程上常见的随机过程的数字特征有:(均值)(方差)(自相关函数)和(互相关函数)。
6、周期运动的最简单形式是(简谐运动),它是时间的单一(正弦)或(余弦)函数。
7、单自由度系统无阻尼自由振动的频率只与(质量)和(刚度)有关,与系统受到的激励无关。
8、简谐激励下单自由度系统的响应由(瞬态响应)和(稳态响应)组成。
9、工程上分析随机振动用(数学统计)方法,描述随机过程的最基本的数字特征包括均值、方差、(自相关函数)和(互相关函数)。
10、机械振动是指机械或结构在(静平衡)附近的(弹性往复)运动。
11、单位脉冲力激励下,系统的脉冲响应函数和系统的(频响函数)函数是一对傅里叶变换对,和系统的(传递函数)函数是一对拉普拉斯变换对。
12、叠加原理是分析(线性振动系统)和(振动性质)的基础。
二、简答题1、什么是机械振动?振动发生的内在原因是什么?外在原因是什么?答:机械振动是指机械或结构在它的静平衡位置附近的往复弹性运动。
振动发生的内在原因是机械或结构具有在振动时储存动能和势能,而且释放动能和势能并能使动能和势能相互转换的能力。
外在原因是由于外界对系统的激励或者作用。
2、机械振动系统的固有频率与哪些因素有关?关系如何?答:机械振动系统的固有频率与系统的质量矩阵、刚度矩阵和阻尼有关。
质量越大,固有频率越低;刚度越大,固有频率越高;阻尼越大,固有频率越低。
3、从能量、运动、共振等角度简述阻尼对单自由度系统振动的影响。
机械振动期末考试题及答案

机械振动期末考试题及答案一、选择题(每题2分,共20分)1. 简谐振动的周期与振幅无关,这是由哪个定律决定的?A. 牛顿第二定律B. 牛顿第三定律C. 胡克定律D. 能量守恒定律答案:C2. 下列哪个不是阻尼振动的特点?A. 振幅逐渐减小B. 频率逐渐增大C. 能量逐渐减少D. 振幅随时间呈指数衰减答案:B3. 一个物体做自由振动,若其振幅逐渐减小,这表明振动受到了:A. 阻尼B. 共振C. 强迫振动D. 非线性振动答案:A4. 质点的振动方程为 \( y = A \sin(\omega t + \phi) \),其中\( \omega \) 表示:A. 振幅B. 频率C. 角频率D. 相位答案:C5. 弹簧振子的振动周期与下列哪个参数无关?A. 弹簧的劲度系数B. 振子的质量C. 振子的振幅D. 振子的初始相位答案:C6. 阻尼振动的振幅随时间呈指数衰减,其衰减速率与什么有关?A. 振幅大小B. 阻尼系数C. 振动频率D. 振动周期答案:B7. 以下哪个不是振动系统的自由度?A. 1B. 2C. 3D. 无穷大答案:D8. 共振现象发生在以下哪种情况下?A. 系统固有频率等于外部激励频率B. 系统阻尼系数最大C. 系统振幅最小D. 系统能量最大答案:A9. 以下哪个是简谐振动的特有现象?A. 振幅不变B. 频率不变C. 能量不变D. 周期不变答案:A10. 一个物体在水平面上做简谐振动,其振动能量主要由以下哪两个因素决定?A. 振幅和频率B. 振幅和阻尼系数C. 阻尼系数和频率D. 振幅和劲度系数答案:A二、填空题(每空2分,共20分)11. 简谐振动的周期公式为 \( T = \frac{2\pi}{\omega} \),其中\( \omega \) 为________。
答案:角频率12. 当外部激励频率接近系统的________时,系统将产生共振现象。
答案:固有频率13. 阻尼振动的振幅随时间的变化规律可表示为 \( A(t) = A_0 e^{-\beta t} \),其中 \( \beta \) 为________。
《振动力学》习题集(含答案)(完整资料).doc
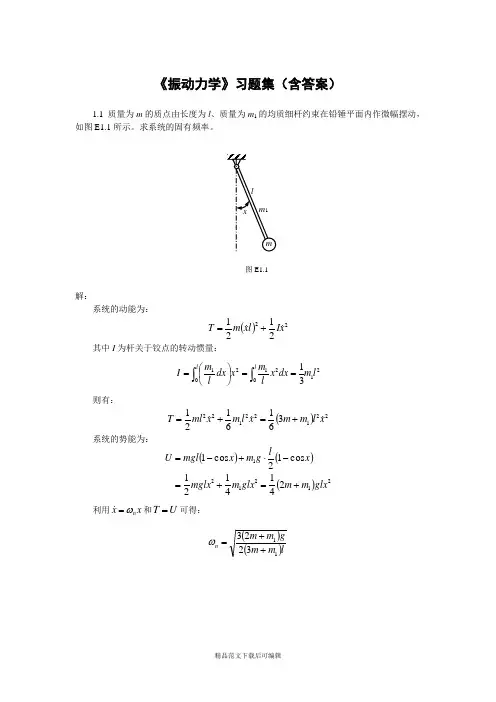
《振动力学》习题集(含答案)1.1 质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面内作微幅摆动,如图E1.1所示。
求系统的固有频率。
图E1.1解: 系统的动能为:()222121x I l x m T +=其中I 为杆关于铰点的转动惯量:2102120131l m dx x l m x dx l m I l l ⎰⎰==⎪⎭⎫⎝⎛=则有:()221221223616121x l m m x l m x ml T +=+=系统的势能为:()()()2121212414121 cos 12cos 1glx m m glx m mglx x lg m x mgl U +=+=-⋅+-=利用x xn ω= 和U T =可得: ()()lm m gm m n 113223++=ω1.2 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如图E1.2所示。
求系统的固有频率。
图E1.2解:如图,令θ为柱体的转角,则系统的动能和势能分别为:22222243212121θθθ mR mR mR I T B =⎪⎭⎫ ⎝⎛+==()[]()222212θθa R k a R k U +=+⋅=利用θωθn= 和U T =可得: ()mkR a R mR a R k n 343422+=+=ω1.3 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如图E1.3所示。
求系统的固有频率。
图E1.3解: 系统的动能为:221θ J T =2k 和3k 相当于串联,则有:332232 , θθθθθk k =+=以上两式联立可得:θθθθ32233232 , k k k k k k +=+=系统的势能为:()232323212332222*********θθθθ⎥⎦⎤⎢⎣⎡+++=++=k k k k k k k k k k U利用θωθn= 和U T =可得: ()()3232132k k J k k k k k n +++=ω1.4 在图E1.4所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
机械行业振动力学期末考试试题

机械行业振动力学期末考试试题第一大题:单自由度振动1.无阻尼自由振动系统,在初始时刻位移为A,速度为0,求解该振动系统的解析解。
2.阻尼比为0.2的单自由度振动系统受到正弦激励力,激励力的频率为系统固有频率的两倍,求解该振动系统的响应。
3.阻尼比为0.5的单自由度振动系统受到冲击激励力,激励力的持续时间为0.1秒,求解该振动系统的响应。
第二大题:多自由度振动1.有两个自由度的系统,求解其固有频率和模态振型。
2.有三个自由度的系统,求解其固有频率和模态振型。
3.给定一个多自由度振动系统的质量矩阵和刚度矩阵,求解其特征值和特征向量,进而得到固有频率和模态振型。
第三大题:振动测量与分析1.请列举常用的振动测量仪器,并对其原理进行简要说明。
2.振动信号的采样频率应该如何选择?请解释原因。
3.请说明振动信号的功率谱密度函数,并给出其计算公式。
4.请解释振动传感器的灵敏度是什么意思,并给出其计算公式。
第四大题:振动控制1.请说明主动振动控制和被动振动控制的区别。
2.请解释模态分析在振动控制中的作用。
3.请列举常用的振动控制方法,并对其原理进行简要说明。
第五大题:振动摆1.请列举用振动摆进行的实验,并对其原理进行简要说明。
2.请解释摇摆周期与摆长的关系,并给出相关公式。
3.一个摆长为1m的振动摆,其重力加速度为9.8m/s^2,求解其摇摆周期。
本文档由Markdown格式输出。
Markdown是一种轻量级的标记语言,常用于编写文档和博客。
可通过Markdown编辑器进行编辑和输出。
以上是机械行业振动力学期末考试试题的内容。
希望对您的学习有所帮助!。
机械振动期末试题及答案
机械振动期末试题及答案1. 选择题1.1 哪种情况下,系统的振动是简谐振动?A. 有耗尽能量的情况B. 存在非线性的力恢复系统中C. 无外部干扰D. 系统的振幅随时间而增长答案:C1.2 振动系统达到稳态的条件是:A. 初始位移为零B. 扰动力为零C. 初始速度为零D. 振幅随时间减小答案:B1.3 一个简谐振动的周期与振幅的关系是:A. 周期与振幅无关B. 周期与振幅成正比C. 周期与振幅成反比D. 周期与振幅正弦相关答案:A2. 判断题2.1 简谐振动的周期和角频率之间满足正比关系。
A. 对B. 错答案:B2.2 简谐振动的中心力是恒力。
A. 对B. 错答案:A2.3 当振动系统有阻尼情况时,振幅会随时间增大。
A. 对B. 错答案:B3. 简答题3.1 什么是简谐振动?它的特点是什么?答案:简谐振动是指振动系统在没有外力干扰的情况下,其平衡位置附近以某一频率固定幅度上下振动的现象。
它的特点包括振动周期与振幅无关,且系统的振动可由正弦或余弦函数进行描述。
3.2 请简要说明受迫振动的原理。
答案:受迫振动是指振动系统在外力作用下的振动。
外力的频率与系统的固有频率相近或相等时,会发生共振现象。
在共振时,外力的能量会以最大幅度传递给振动系统,导致振动幅度增大。
4. 计算题4.1 一个弹簧振子平衡位置附近的势能函数为U(x) = 4x^2 + 3,求振子的振动周期。
答案:根据简谐振动的势能函数表达式,势能函数为U(x) =1/2kx^2,其中k为弹簧的劲度系数。
将已知的势能函数与标准表达式进行比较,可得4x^2 = 1/2kx^2,解得k = 8。
由振动周期公式T =2π√(m/k),代入m和k的值,可计算出振子的振动周期。
5. 算法题设计一个程序,计算一个简谐振动系统的振动频率和振幅,并将结果打印输出。
// 输入参数float k; // 弹簧的劲度系数float m; // 系统的质量// 计算振动频率float omega = sqrt(k / m);// 计算振幅float A = 1; // 假设振幅为1// 打印输出结果print("振动频率:", omega);print("振幅:", A);经过以上计算,我们可以得到一个简谐振动系统的振动频率和振幅。
机械振动考题(完整版)
五邑大学(期末试题)院系:机电工程学院专业:机械工程年级: 12级研究生学号: 2111206011姓名:崔卫国机械振动考题1、如图所示两自由度系统。
(1)求系统固有频率和模态矩阵,并画出各阶主振型图形;(2)当系统存在初始条件⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡03.00)0()0(21x x 和⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡00)0()0(21x x 时,试采用模态叠加法求系统响应,并绘出相应曲线;(3)试合理确定k2和m2,使之构成无阻尼动力减振器。
(4)用任何一种语言编制计算程序,完成上述计算工作。
参数:m1=500kg, m2=200kg, k1=8000N/m, k2=3000N/m, F0=350N, ω=0.8解:(1)由题意及图所示可知:这是一个动力减震器问题。
1m 1k 组成的系统为主系统;2m 2k 组成的附加系统为减振器。
故可知这个组合系统的振动微分方程为:()11121221222122sin 0m x k k x k x F wt m x k x k x ⎧++-=⎪⎨-+=⎪⎩ ① 设其解为:11sin x X wt = 22sin x X wt = ② 又因为由②可得:211sin x X w wt =- 222sin x X w wt =- 把②代入方程①中可得:()()212112212112220k k w m X k X F k X k w m X ⎧+--=⎪⎨-+-=⎪⎩ 故系统的特征值问题为:2111212222220X F k k w m k X k k w m ⎡⎤+--⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦ ③ 特征方程为:2121222220k k w m k k k w m +--=-- ④由④可得:()()2222212120kw m k k w m k -+--=⇒222412*********k k k w m k w m k w m w m m ---+= ⑤ 把1k 2k 1m 2m 的值代入⑤式可得:42372400w w -+= ⑥21223720.22378.388223720.223728.61192w w -⎧==⎪⎪⎨+⎪==⎪⎩⇒ 12 2.89625.3490w w =⎧⎨=⎩计算对应二个固有频率的固有振型。
机械振动学(参考答案).docx
机械振动学试题(参考答案)一、判断题:(对以下论述,正确的打“J”,错误的打“X”,每题2 分,共20分)1、多自由度振动系统的运动微分方程组中,各运动方程间的耦合,并不是振动系统的固有性质,而只是广义坐标选用的结果。
(丁)2、一个单盘的轴盘系统,在高速旋转时,由于盘的偏心质量使轴盘做弓形回旋时,引起轴内产生交变应力,这是导致在临界转速时,感到剧烈振动的原因。
(X)3、单自由度线性无阻尼系统的自由振动频率由系统的参数确定,与初始条件无关。
(丁)4、当激振力的频率等于单自由度线性阻尼系统的固有频率时,其振幅最大值。
(X)5、一个周期激振力作用到单自由度线性系统上,系统响应的波形与激振力的波形相同,只是两波形间有一定的相位差。
(X)6、当初始条件为零,即*产;=0时,系统不会有自由振动项。
(X)7、对于多自由度无阻尼线性系统,其任何可能的自由振动都可以被描述为模态运动的线性组合。
(丁)8、任何系统只有当所有自由度上的位移均为零时,系统的势能才可能为零。
(X )9、隔振系统的阻尼愈大,则隔振效果愈好。
(X)10、当自激振动被激发后,若其振幅上升到一定程度并稳定下来,形成一种稳定的周期振动,则这种振幅自稳定性,是由于系统中的某些非线性因素的作用而发生的。
(J)二、计算题:1、一台面以f频率做垂直正弦运动。
如果求台面上的物理保持与台面接触,则台面的最大振幅可有多大?(分)解:台面的振动为:x = X sin(tyZ - cp)x = —a>2X sin(or —cp)最大加速度:无max = "X如台面上的物体与台面保持接触,贝U :九《=g (9・81米/秒2)。
所以,在f 频率(/=仝)时,最大振幅为:2nX max =x< g/4^72= 9.81/4* 严(米)2、质量为ni 的发电转子,它的转动惯量J 。
的确定采用试验方法:在转子经向Ri 的 地方附加一小质量mi 。
试验装置如图1所示,记录其振动周期。
《机械振动》测试题(含答案)
《机械振动》测试题(含答案)一、机械振动 选择题1.甲、乙两弹簧振子,振动图象如图所示,则可知( )A .甲的速度为零时,乙的速度最大B .甲的加速度最小时,乙的速度最小C .任一时刻两个振子受到的回复力都不相同D .两个振子的振动频率之比f 甲:f 乙=1:2E.两个振子的振幅之比为A 甲:A 乙=2:1 2.如图为某简谐运动图象,若t =0时,质点正经过O 点向b 运动,则下列说法正确的是( )A .质点在0.7 s 时的位移方向向左,且正在远离平衡位置运动B .质点在1.5 s 时的位移最大,方向向左,在1.75 s 时,位移为1 cmC .质点在1.2 s 到1.4 s 过程中,质点的位移在增加,方向向左D .质点从1.6 s 到1.8 s 时间内,质点的位移正在增大,方向向右3.如图所示,弹簧的一端固定,另一端与质量为2m 的物体B 相连,质量为1m 的物体A 放在B 上,212m m =.A 、B 两物体一起在光滑水平面上的N 、N '之间做简谐运动,运动过程中A 、B 之间无相对运动,O 是平衡位置.已知当两物体运动到N '时,弹簧的弹性势能为p E ,则它们由N '运动到O 的过程中,摩擦力对A 所做的功等于( )A .p EB .12p EC .13p E D .14p E 4.如图甲所示,一个有固定转动轴的竖直圆盘转动时,固定在圆盘上的小圆柱带动一个T 形支架在竖直方向振动, T 形支架的下面系着一个由弹簧和小球组成的振动系统.圆盘静止时,让小球做简谐运动,其振动图像如图乙所示.圆盘匀速转动时,小球做受迫振动.小球振动稳定时.下列说法正确的是( )A .小球振动的固有频率是4HzB .小球做受迫振动时周期一定是4sC .圆盘转动周期在4s 附近时,小球振幅显著增大D .圆盘转动周期在4s 附近时,小球振幅显著减小5.公路上匀速行驶的货车受一扰动,车上货物随车厢底板上下振动但不脱离底板.一段时间内货物在竖直方向的振动可视为简谐运动,周期为T .取竖直向上为正方向,以t =0时刻作为计时起点,其振动图像如图所示,则A .t =14T 时,货物对车厢底板的压力最大 B .t =12T 时,货物对车厢底板的压力最小 C .t =34T 时,货物对车厢底板的压力最大 D .t =34T 时,货物对车厢底板的压力最小 6.某质点做简谐运动,其位移随时间变化的关系式为5sin 4x t π=(cm) ,则下列关于质点运动的说法中正确的是( )A .质点做简谐运动的振幅为 10cmB .质点做简谐运动的周期为 4sC .在 t=4s 时质点的加速度最大D .在 t=4s 时质点的速度最大7.一位游客在千岛湖边欲乘坐游船,当日风浪较大,游船上下浮动.可把游船浮动简化成竖直方向的简谐运动,振幅为20 cm ,周期为3.0 s .当船上升到最高点时,甲板刚好与码头地面平齐.地面与甲板的高度差不超过10 cm 时,游客能舒服地登船.在一个周期内,游客能舒服登船的时间是( )A .0.5 sB .0.75 sC .1.0 sD .1.5 s8.如右图甲所示,水平的光滑杆上有一弹簧振子,振子以O 点为平衡位置,在a 、b 两点之间做简谐运动,其振动图象如图乙所示.由振动图象可以得知( )A.振子的振动周期等于t1B.在t=0时刻,振子的位置在a点C.在t=t1时刻,振子的速度为零D.从t1到t2,振子正从O点向b点运动9.下列说法中不正确的是( )A.将单摆从地球赤道移到南(北)极,振动频率将变大B.将单摆从地面移至距地面高度为地球半径的高度时,则其振动周期将变到原来的2倍C.将单摆移至绕地球运转的人造卫星中,其振动频率将不变D.在摆角很小的情况下,将单摆的振幅增大或减小,单摆的振动周期保持不变10.如图所示,一轻质弹簧上端固定在天花板上,下端连接一物块,物块沿竖直方向以O 点为中心点,在C、D两点之间做周期为T的简谐运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
…2008年振动力学期末考试试题第一题(20分)1、在图示振动系统中,已知:重物C 的质量m 1,匀质杆AB 的质量m 2,长为L ,匀质轮O 的质量m 3,弹簧的刚度系数k 。
当AB 杆处于水平时为系统的静平衡位置。
试采用能量法求系统微振时的固有频率。
解:系统可以简化成单自由度振动系统,以重物C 的位移y 作为系统的广义坐标,在静平衡位置时 y =0,此时系统的势能为零。
AB 转角: 系统动能:%m 1动能: m 2动能: m 3动能:系统势能:在理想约束的情况下,系统的主动力为有势力,则系统的机械能守恒,因而有: 上式求导,得系统的微分方程为:E y m m m ky'=+++)2131(4321固有频率和周期为:~)2131(43210m m m k++=ω2、质量为m 1的匀质圆盘置于粗糙水平面上,轮缘上绕有不可伸长的细绳并通过定滑轮A 连在质量为m 2的物块B 上;轮心C 与刚度系数为k 的水平弹簧相连;不计滑轮A ,绳及弹簧的质量,系统自弹簧原长位置静止释放。
试采用能量法求系统的固有频率。
解:系统可以简化成单自由度振动系统,以重物B 的位移x 作为系统的广义坐标,在静平衡位置时 x =0,此时系统的势能为零。
物体B 动能:22121x m T =轮子与地面接触点为速度瞬心,则轮心速度为x v c 21=,角速度为x R21=ω,转过的角度为x R21=θ。
轮子动能: )83(21)41)(21(21)41(212121212221212212x m x RR m xm J v m T c =+=+=ω \x系统势能:22228)21(21)(2121x k xR R k R k kx V c ====θ 在理想约束的情况下,系统的主动力为有势力,则系统的机械能守恒,有:E x kxm m V T =++=+22218)83(21 上式求导得系统的运动微分方程:083221=++x m m kx固有频率为:210832m m k+=ω·第二题(20分)1、在图示振动系统中,重物质量为m ,外壳质量为2m ,每个弹簧的刚度系数均为k 。
设外壳只能沿铅垂方向运动。
采用影响系数方法:(1)以x 1和x 2为广义坐标,建立系统的微分方程;(2)求系统的固有频率。
解:系统为二自由度系统。
当x1=1,x2=0时,有:k11=2k ,k21=-2k 当x2=1,x2=1时,有:k22=4k ,k12=-2k 因此系统刚度矩阵为:[⎥⎦⎤⎢⎣⎡--k k k k 4222 系统质量矩阵为:⎥⎦⎤⎢⎣⎡m m 200 系统动力学方程为:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡0042222002121x x k k k k x x m m频率方程为:024222)(Δ22=----=ωωωm k kkm k 解出系统2个固有频率:(m k )22(21-=ω,mk )22(22+=ω 2、在图示振动系统中,物体A 、B 的质量均为m ,弹簧的刚度系数均为k ,刚杆AD 的质量忽略不计,杆水平时为系统的平衡位置。
采用影响系数方法,试求:(1)以x 1和x 2为广义坐标,求系统作微振动的微分方程;(2)系统的固有频率方程。
解:系统可以简化为二自由度振动系统,以物体A 和B 在铅垂方向的位移x 1和x 2为系统的广义坐标。
当x1=1,x2=0时,AD 转角为L 3/1=θ,两个弹簧处的弹性力分别为L k θ和L k θ2。
对D 点取力矩平衡,有:kL k 91411=;另外有kL k -=21。
同理,当x2=1,x2=1时,可求得:kL k =22,kL k -=12 因此,系统刚度矩阵为:⎥⎥⎦⎤⎢⎢⎣⎡--kL kL kL kL 914 |系统质量矩阵为:⎥⎦⎤⎢⎣⎡m m 00 系统动力学方程为:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡--+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡00914002121x x kL kL kL kL x x m m频率方程为:091422=----ωωm kL kLkL m kL即:0523922242=+-L k kmL m ωω(第三题(20分)在图示振动系统中,已知:物体的质量m 1、m 2及弹簧的刚度系数为k 1、k 2、k 3、k 4。
(1)采用影响系数方法建立系统的振动微分方程;(2)若k 1= k 3=k 4= k 0,又k 2=2 k 0,求系统固有频率;(3)取k 0 =1,m 1=8/9,m 2 =1,系统初始位移条件为x 1(0)=9和x 2(0)=0,初始速度都为零,采用模态叠加法求系统响应。
解:(1)系统可以简化为二自由度振动系统。
当x1=1,x2=0时,有:k11=k1+k2+k4,k21=-k2"当x2=1,x2=1时,有:k22=k2+k3,k12=-k2。
因此,系统刚度矩阵为:⎥⎦⎤⎢⎣⎡+--++3222421k k kk k k kD/kL 32 kL 31 1⨯k11k2x 1x系统质量矩阵为:⎥⎦⎤⎢⎣⎡2100m m 系统动力学方程为:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+--+++⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡00002132224212121x x k k k k k k k x x m m(2)当0431k k k k ===,022k k =时,运动微分方程用矩阵表示为:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡003224002100002121x x k k k k x x m m "频率方程为:04)3)(4(20220210=---k m k m k ωω08)43(202021421=++-k k m m m m ωω求得:)168943(22221212121021m m m m m m m m k +--+⋅=ω)168943(22221212121022m m m m m m m m k +-++⋅=ω(3)当k 0=1,m 1=8/9,m 2 =1时,系统质量阵:⎥⎥⎦⎤⎢⎢⎣⎡=10098M :系统刚度阵:⎥⎦⎤⎢⎣⎡--=3224K 固有频率为:2321=ω,622=ω 主模态矩阵为:⎥⎥⎦⎤⎢⎢⎣⎡-=112343Φ 主质量阵:⎥⎥⎦⎤⎢⎢⎣⎡==30023M ΦΦM Tp 、主刚度阵:⎥⎥⎦⎤⎢⎢⎣⎡==180049K ΦΦK Tp 模态空间初始条件:⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-44)0()0()0()0(21121x x q q Φ,⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-00)0()0()0()0(21121x x q q Φ 模态响应:01211=+q q ω ,02222=+q q ω即:t t q 11cos 4)(ω=,t t q 22cos 4)(ω-=]因此有:⎩⎨⎧-+=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡t t t t t q t q t x t x 21212121cos 4cos 4cos 6cos 3)()()()(ωωωωΦ第四题(20分)一匀质杆质量为m ,长度为L ,两端用弹簧支承,弹簧的刚度系数为k 1和k 2。
杆质心C 上沿x 方向作用有简谐外部激励t ωsin 。
图示水平位置为静平衡位置。
(1)以x 和θ为广义坐标,采用影响系数方法建立系统的振动微分方程;(2)取参数值为m=12,L =1,k 1 =1,k 2 =3,求出系统固有频率;(2)系统参数仍取前值,试问当外部激励的频率ω为多少时,能够使得杆件只有θ方向的角振动,而无x 方向的振动 [解:(1)系统可以简化为二自由度振动系统,选x 、为广义坐标,x 为质心的纵向位移,为刚杆的角位移,如图示。
当1=x 、0=θ时:2111k k k +=,2)(1221L k k k -= 当0=x 、1=θ时:2)(1211Lk k k -=,4)(2L k k k +=|因此,刚度矩阵为: θxC t ωsin1⋅k 1⋅k k 21k、k22k1=θ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+=4)(2)(2)(221121221L k k Lk k L k k k k K 质量矩阵为:⎥⎥⎦⎤⎢⎢⎣⎡=212100mL m M 系统动力学方程:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--++⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡0sin 4)(2)(2)(121002*********t x L k k L k k L k k k k x mL m ωθθ(2)当m=12,L =,k 1 =1,k 2 =3时,系统动力学方程为:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡0sin 111410012t x x ωθθ{频率方程为:011112422=--ωω即:0316122040=+-ωω求得:67420±=ω (3)令t x x ωθθsin ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡,代入上述动力学方程,有:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡--0111112422θωωx )由第二行方程,解得21ωθ--=x,代入第一行的方程,有: 1)124(122---=ωωx ,]1)124[(2---=ωθ 要使得杆件只有θ方向的角振动,而无x 方向的振动,则需0=x ,因此1=ω。
第五题(20分)如图所示等截面悬臂梁,梁长度为L ,弹性模量为E ,横截面对中性轴的惯性矩为I ,梁材料密度为ρ。
在梁的a 位置作用有集中载荷)(t F 。
已知梁的初始条件为:)()0,(1x f x y =,)()0,(2x f x y = 。
(1)推导梁的正交性条件;(2)写出求解梁的响应),(t x y 的详细过程。
(假定已知第i 阶固有频率为i ω,相应的模态函数为)(x i φ,∞=~1i )提示:梁的动力学方程为:),(]),([222222t x f tyS x t x y EI x =∂∂+∂∂∂∂ρ,其中)()(),(a x t F t x f -=δ,δ为δ函数。
解:(1)梁的弯曲振动的动力学方程为:0),(]),([222222=∂∂+∂∂∂∂tt x y S x t x y EI x ρ ),(t x y 可写为:?)sin()()()(),(θωφφ+==t a x t q x t x y代入梁的动力学方程,有:φρωφS EI 2)(=''''设与i ω、j ω对应有i φ、j φ,有: i i i S EI φρωφ2)(=''''(1)j j j S EI φρωφ2)(=''''(2)式(1)两边乘以j φ并沿梁长对x 积分,有:⎰⎰=''''lj i i l i j dx S dx EI 02)(φφρωφφ (3)。
