浙江省绍兴市中考试题
2020年浙江省绍兴市中考物理试卷
2020年浙江省绍兴市中考物理试卷一、选择题（本题共5小题，每小题4分，共20分。
下列各小题中只有一个选项符合题意）1．（4分）端午节，小敏提着一盒粽子去看望长辈时，下列提法中手受到压强最大的是（）A．用单手提单绳B．用单手提双绳C．用双手提单绳D．用双手提双绳2．（4分）将静电球装置放在水平桌面上，未通电时，多只锡碗叠放在静电球上（图甲）。
通电后，锡碗依次向上飞起（图乙），最后落到桌面上。
下列说法正确的是（）A．图甲中，静止的锡碗受到惯性的作用B．图乙中，以空中的锡碗为参照物，静电球是运动的C．图甲中，锡碗受到自身重力和桌面对它的支持力D．图乙中，锡碗能飞起来是由于同种电荷相互吸引3．（4分）下列有关电铃（如图）说法正确的是（）A．电铃的工作原理是电磁感应B．小锤击打到铃碗时，电磁铁仍具有磁性C．要使铃声响度大一些，可适当降低电压D．滑动变阻器的滑片向左移动，电磁铁的磁性增强4．（4分）某款感应式垃圾桶如图所示。
其工作原理如下：启动开关闭合后，垃圾桶才能正常使用，此时指示灯亮起；扔垃圾时只需将手伸到感应区上方一定距离内，感应开关自动闭合，动力装置工作，垃圾桶盖缓缓打开；手离开5秒后动力装置会控制桶盖闭合，然后感应开关自动断开。
下列电路符合要求的是（）A．B．C．D．5．（4分）如图，甲、乙实验可以得出“定滑轮不能省力”这一结论。
小敏想通过一次实验既得出结论，又能直接显示出钩码的重力大小，于是在左侧加上一个相同的弹簧测力计（弹簧测力计重力不能忽略、绳和滑轮之间摩擦不计）。
下列四套装置中能实现的是（）A．B．C．D．二、填空题（本题共3小题，每空2分，共14分）6．（4分）2020年5月5日，我国自主研发的长征5号B型运载火箭圆满完成发射任务。
图为起飞阶段加速上升的火箭，该过程中，内部的新型返回舱的动能（选填“增大”、“减小”或“不变”），火箭整体的机械能（选填“增大”“减小”或“不变”）。
7．（4分）小敏将质量为20克，体积为25厘米3的塑料块放入水平平衡的容器内（图甲），放手后容器右端下降。
2022年浙江省绍兴市中考科学真题(原卷版+解析)
2022年浙江省绍兴市中考科学真题一、选择题1．实验室用于测量液体体积的仪器是（）A．刻度尺B．量筒C．温度计D．秒表2．北京冬奥会吉祥物“冰墩墩”的形象来源于熊猫。
下列生物与熊猫亲缘关系最近的是（）A．黄鲻鱼B．家兔C．海龟D．青蛙3．地球板块之间在不断地发生碰撞和张裂，下列说法正确的是（）A．图实验模拟板块碰撞形成海洋B．图实验模拟板块张裂形成山脉C．地震、火山的发生与板块的碰撞和张裂关系密切D．在流水和风的作用下板块之间发生了碰撞和张裂4．乳酸菌是一种细菌，酸菜的制作主要利用了它在无氧环境下进行发酵产生乳酸。
下列说法正确的是（）A．乳酸菌有成形的细胞核B．酸菜中所有的乳酸菌构成一个群落C．适应无氧环境的乳酸菌是自然选择的结果D．制作酸菜的植物体具有的结构层次是细胞→组织→系统→植物体5．科学研究常采用转换、模型、等效替代和控制变量等方法，下列实验中采用等效替代的是（）A．探究平面镜成像B．探究种子萌发的条件C．用石蕊试液判断酸碱性D．模拟泥石流的形成6．如图，小敏用条形磁铁使铁钉竖直静止在空中，细线紧绷且质量不计，下列说法正确的是（）A．铁钉上端被磁化成N极B．铁钉受到的磁力与自身重力大小相等C．桌面对石头的支持力和石头的重力是一对平衡力D．细线对石头的拉力和石头对细线的拉力是一对相互作用力7．制作并观察洋葱表皮细胞临时装片的部分操作与问题分析合理的是（）A．在载玻片上滴加的液体①是生理盐水B．粗准焦螺旋②可以调节显微镜的放大倍数C．视野太暗时，应该换用遮光器③中的小光圈D．视野中出现气泡④，可能是盖盖玻片时操作不当引起的8．下列关于压强的实验说法不正确的是（）A．实验甲说明大气压的存在B．实验乙说明液体的沸点随着气压的增大而升高C．实验丙说明气体的压强随着流速的增大而增大D．实验丁说明同种液体中的压强随着深度的增加而增大9．2021年，人类首次将基因编辑后的猪肾脏移植到人体中，短期内未出现强烈免疫反应，为人体器官的异种移植带来希望。
历年浙江省绍兴市中考数学试题(含答案)
2016年绍兴市初中毕业生学业考试数 学卷I （选择题）一、选择题(本大题有10小题，每小题4分，共40分，请选出每小题中一个最符合题意的选项，不选、多选、错选．均不给分） 1．－8的绝对值是A ．8B ．－8C D 2了每秒338 600 000亿次，数字338 600 000用科学记数法可简洁表示为A ．3.386×108B ．0.3386×109C ．33.86×107D ．3.386×1093．我国传统建筑中，窗框（如图1）的图案玲珑剔透、千变万化． 窗框一部分如图2，它是一个轴对称图形，其对称轴有 A ．1条 B ．2条 C ．3条 D ．4条4．如图是一个正方体，则它的表面展开图可以是5．一枚质地均匀的骰子，其六个面上分别标有数字1，2，3，4，5，6．投掷一次，朝上一A B C D 6是⊙O 的直径，点A ，C 在⊙O 上，⌒AB ＝⌒BC ，∠AOB ＝60º，则∠BDC 的 A ．60º B ．45º C ．35º D ．30º7．小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是A．①，②B．①，④C．③，④D．②，③8．如图，在Rt△ABC中，∠B＝90º，∠A＝30º．以点A为圆心，BC长为半径画弧交AB 于点D，分别以点A，D为圆心，AB长为半径画弧，两弧交于点E，连接AE，DE，则∠A B9．抛物线)过点A(2y＝O (l≤x≤3)有交点，则c的值不可能是A．4 B．6 C．8 D．1010．我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”，如图，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数．由图可知，孩子自出生后的天数是A．84 B．336C．510 D．1326卷Ⅱ（非选择题）二、填空题（本大题有6小题，每小题5分，共30分）11＝_____________．12+ 2的解是___________ ．13．如图12是它的截面图，垂直放置的脸盆与架子的交点为A，B，AB＝40cm，脸盆的最低点C到AB的距离为l0cm，则该脸盆的半径为_____ cm．14．书店举行购书优惠活动：①一次性购书不超过100元，不享受打折优惠}②一次性购书超过100元但不超过200元，一律按原价打九折；③一次性购书超过200元，一律按原价打七折．小丽在这次活动中，两次购书总共付款229.4元，第二次购书原价是第一次购书原价的3倍，那么小丽这两次购书原价的总和是_______ 元．15．如图，已知直线l：y＝－x，双曲线y．在l上取一点A（a，－a）（a＞0），过A 作x轴的垂线交双曲线于点B，过B作轴的垂线交l于点C，过C作x轴的垂线交双曲线于点D，过D作y轴的垂线交l于点E，此时E与A重合，并得到一个正方形ABCD．若原点O在正方形ABCD的对角线上且分这条对角线为1∶2的两条线段，则a的值为__________ ．16．如图，矩形ABCD 中，AB ＝4，BC ＝2，E 是AB 的中点，直线l 平行于直线EC ，且直线l 与直线EC 之间的距离为2，点F 在矩形ABCD 边上，将矩形ABCD 沿直线EF 折叠，使点A 恰好落在直线l 上，则DF 的长为 __________ ．三、解答题（本大题有8小题．第17 -ZO 小题每小题8分，第21小题10分，第22,23小题每小题12分，第24小题14分，共80分．解答需写出必要的文字说明、演算步骤17．(1)5－(2－)º＋-2．(2)＝4． 18．为了解七年级学生上学期参加社会实践活动的情况，随机抽查A 市七年级部分学生参加社会实践活动的天数，并根据抽查结果制作了如下不完整的频数分布表和条形统计图．A 市七年级部分学生参加社会 A 市七年级部分学生参加社会 实践活动天数的频数分布表 实践活动天数的条形统计图根据以上信息，解答下列问题：(l)求出频数分布表中a 的值，并补全条形统计图．(2)A 市有七年级学生20 000人，请你估计该市七年级学生参加社会实践活动不少于5天的人数．19．根据卫生防疫部门要求，游泳池必须定期换水、清洗．某游泳池周五早上8：OO打开排水孑L开始排水，排水孔的排水速度保持不变，期间因清洗游泳池需要暂停排水，游泳池的水在11：30全部排完．游泳池内的水量Q(m3)和开始排水后的时间t(h)之间的函数图象如图所示，根据图象解答下列问题：(1)暂停排水需要多少时间？排水孔的排水速度是多少？(2)当2≤t≤3.5时，求Q关于t的函数表达式．20.如图1，某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的南岸边点A处，测得河的北岸边点B在其北偏东450方向，然后向西走60m到达C点，测得点B在点C的北偏东60。
浙江省绍兴市2020年中考语文试题(解析版)
浙江省绍兴市2020年中考真题语文试卷一、书写(5分)请在答题时努力做到书写正确、工整、美观。
二、积累(16分)1.阅读下面文字,按要求完成下列题目。
(4分)近年南行的次数越来越多。
愈发喜欢看莺飞草长．(A. cháng B. zhăng)、月笼烟雨，看高涨的如欢呼般的莲叶，看富ráo▲的阳光，被照亮的事物及其纹理:喜欢临一大面湖水，看波光浩miăo ▲、葛蒲丰茂，心里即有飞鸟的喜悦:喜欢那加了糖的空气，香樟、桂花、栀子、茉莉，那份免费mì▲饯给人以幸福感，让你唇齿生津，让你觉得世间一切悲苦皆可忍受。
(节选自王开岭《南方,南方)》)(1)根据拼音写出相应的汉字。
(3分)①富(ráo)②浩(miăo)③(mì) 饯(2)给语段中加点字“长”选择正确的读音。
()(1 分)A. ChángB. zhăng2.根据语境,选出用词搭配最恰当的一项。
()(3 分)2020年春，突如其来的“新冠”疫情打破了人们的生活常态，也检测出了商人的①，专家的②，媒体的素养，医者的操守，民众的认知，以及干部的③。
A.①水平②良知③能力和状态B.①良知②水平③能力和状态C.①能力和状②良知③水平3.请在下面横线处填上合适的古诗文名句。
(9分)生活是诗。
漫步早春的钱塘湖边,闻鸟语嘤嘤，白居易写下“几处早莺争暖树，(1)”；听蛙声喧闹，感夏夜闲情，赵师秀吟出“(2) ,青草池塘处处蛙”;览山林美景，享秋野静谧，王绩提笔“树树皆秋色，(3)”;观瀚海飘雪，叹塞外奇寒，岑参挥毫“(4)，千树万树梨花开”。
诗是生活。
“新冠”来袭，使命召唤，正所谓“(5) ”，多少人胸怀”(6)，"的抱负，满怀“(7)，"的信心与决心，舍家为国，共克疫情。
(分别用孟子《生于优患，死于安乐》、范仲淹《岳阳楼记)、李白《行路难》中的句子填空。
)三、阅读(61分)(一)名著阅读(10分)4.《水浒传)中有很多与“酒"有关的故事.请仔细阅读下表，完成探究任务。
中考文言文试题 中考 文言文阅读
中考文言文试题中考文言文阅读【2023年浙江省绍兴市中考语文真题】阅读《涉园记》，完成小题。
涉园记【明】陈洪绶①涉园者，予兄己未觞槎庵来先生②请名之者也。
庚午构堂一、亭一、穿池二，余乐记之。
予忆先生名时，众以为仅取诸“日涉成趣”③之义也已。
予能广其意，当不是乎止也。
忆余十岁，兄十五岁时，读书园之前搴霞阔④中，日爱园有七樟树，经纬之以桑柘，绮绾⑤之以蔬果，幽旷若谋而成，高下咸得其所，谋为亭馆以居之。
遂因其地势之幽旷高下，择其华木之疏密高卑，又非嘉木异卉不树也。
一日而涉焉，或树一花木；一月而涉焉，又树一花木。
一日而涉焉，或去一花木；一月而涉焉，又去一花木。
至于其先必以为咸宜不改而植之，历十余年，枝干荣茂而可观，根本深固而不拔者，必树之去之，务与其地之相宜而止。
为屋则楼阁、堂轩、廊窗、亭牖、露台、曲房，图画规制，凡数十改易，务与其树之相宜而始定。
凿池则倏东倏西，随开随塞，变田成溪者十余度，务与其地与树之相宜而后成。
此非涉之之久陈迹不留新意自启能若是乎哉？夫园，细事也，能作园，末技也，不日涉则弗能为，良学固可弗日涉乎哉？故日涉经史、涉古今，予愿从兄坐此园也。
深惟⑥其涉之之义，而细察其涉之之效，种德乐善，文章用世，朝夕孜孜焉，能如其精择迁改，动与时宜之为善也。
然非日涉经史、日涉古今，能乎哉？予愿从兄坐此园也。
【注释】①陈洪绶：绍兴诸壁人，明末画家。
②予兄己未觞槎庵来先生：我哥哥己未年请槎庵来先生喝酒。
己未，古代以干支纪年，下文“庚午”同。
槎（chá）庵来先生，陈洪绶岳父来斯行，字槎庵。
③日涉成趣：语出陶渊明《归去来兮辞》，意为每天到园中散步，成为乐趣。
④搴（qiān）霞阁：阁名。
⑤绮绾：交错盘绕。
⑥惟：思，考虑。
1.根据语境推敲下列加点词的意思。
①予能广其意（）②历十余年（）③务与其地之相宜而止（）④凡数十改易（）2.用“/”给文中画横线处断句（断三处）。
此非涉之之久陈迹不留新意自启能若是乎哉？3.“涉园”的建设过程中，哪些事反复多次才得以完成？请简要概括。
浙江省绍兴市中考数学真题试卷
浙江省绍兴市2020年中考数学试卷一、选择题(本大题有10小题，每小题4分，共40分，请选出每小题中一个最符合题意的选项，不选、多选、错选，均不给分)1．实数2，0，-22中，为负数的是（）A．2B．0C．-2D22．来自动控制器的芯片，可植入2 020 000 000粒晶体管，这个数字2 020 000 000用科学记数法可表示为（）A．0．202×1010B．2．02×109C．20．2×107D．2．02×1083．将如图的七巧板的其中几块，拼成一个多边形，为中心对称图形的是( )A．B．C．D．4．如图，点A，B，C，D，E均在⊙O上，∠BAC=15°，∠CED=30°，则∠BOD的度数为（）A．45°B．60°C．75°D．90°5．如图，三角板在灯光照射下形成投影，三角板与其投影的相似比为2：5，且三角板的一边长为8cm，则投影三角板的对应边长为（）A．20cmB．10cmC．8cmD．3．2cm6．如图，小球从A入口往下落，在每个交叉口都有向左或向右两种可能，且可能性相等，则小球从E出口落出的概率是（）A．1 2B．1 3C．1 4D．1 67．长度分别为2，3，3，4的四根细木棒首尾相连，围成一个三角形(木棒允许连接，但不允许折断)，得到的三角形的最长边长为( )A．4B．5C．6D．78．如图，点O为矩形ABCD的对称中心，点E从点A出发沿AB向点B移动，移动到点B停止，延长EO交CD于点F，则四边形AECF形状的变化依次为( )A．平行四边形→正方形→平行四边形→矩形B．平行四边形→菱形→平行四边形→矩形C．平行四边形→正方形→菱形→矩形D．平行四边形→菱形→正方形→矩形9．如图，等腰三角形ABC中，∠ABC=90°，BA=BC，将BC绕点B顺时针旋转θ(0°<θ<90°)，得到BP，连结CP，过点A作AH⊥CP交CP的延长线于点H，连结AP，则∠PAH的度数（）A．随着θ的增大而增大B．随着θ的增大而减小C．不变D．随着θ的增大，先增大后减小10．同型号的甲、乙两辆车加满气体燃料后均可行驶210km，它们各自单独行驶并返回的最远距离是105km，现在它们都从A地出发，行驶途中停下来从甲车的气体燃料桶抽一些气体燃料注入乙车的气体燃料桶，然后甲车再行驶返回A地，而乙车继续行驶，到B地后再行驶返回A地．则B地最远可距离A地（）A．120kmB．140kmC．160kmD．180km卷Ⅱ(非选择题)二、填空题(本大题有6小题，每小题5分，共30分)11．分解因式：1-x2=。
浙江省绍兴市中考科学真题试题(含解析)-人教版初中九年级全册自然科学试题
某某省某某市2020年中考科学试题本卷中g取10牛/千克，可能用到的相对原子质量：H-1 C-12 O-16 Na-23 Cl-35．5 Ca-40 Fe-56 Cu-64 Zn-65试卷Ⅰ(选择题)一、选择题(本题共15小题，每小题4分，共60分。
下列各小题中只有一个选项符合题意) 1．下列表示细胞分裂的是( )A．B．C．D．【答案】A【知识点】真核细胞的分裂生殖，细胞的分裂、生长和分化【考查能力】区分细胞分裂、生长、分化特点【解析】A细胞数目变多的过程属于细胞分裂，A正确B细胞体积由小变大的过程是细胞生长，B错误；C、细胞在形态、结构和功能上发生变化是细胞分化,C错误；D、真核细胞的分裂生殖，D错误．【难度】易【题分】42．水是生命之源，有关水说法不正确的是( )A．流水是影响地形的外力作用之一B．海洋水是地球上最大的水体C．水循环的环节只有蒸发和降水D．人类需合理开发和利用水资源【答案】C【知识点】地球的外力作用，地球上水的分布，水循环的环节，水资源利用和开发【考查能力】了解相关水资源的分布、循环和利用、地球外力作用等知识【解析】A.地球的外力作用主要有风化作用、侵蚀作用（风力侵蚀、流水侵蚀、海浪侵蚀等）、搬运作用、沉积作用等，故A正确B海洋水占全球总水量的96.53%，故B正确C水循环的环节有：蒸腾、蒸发、降水、水汽输送、下渗、地表径流、地下径流，故C不正确。
D全球总水量大，但淡水总量少，水资源短缺，所以要合理开发和利用，故D正确。
【难度】易【题分】43．下列实验操作正确的是( )A．读取液体体积B．闻气味C．测定溶液pHD．稀释浓硫酸【答案】B【知识点】测量容器-量筒,闻气味的方法浓硫酸的性质及浓硫酸的稀释, 溶液的酸碱度测定【考查能力】正确的实验操作方法【解析】A读数时，量筒必须放平，视线要跟量筒内液体的凹液面的最低处保持水平，再读出液体体积.故A错；B扇气入鼻法闻气味，故B正确；C用pH试纸测定未知溶液的pH时，正确的操作方法为用玻璃棒蘸取少量待测液滴在干燥的pH试纸上，与标准比色卡对比来确定pH.不能将pH试纸伸入待测液中，以免污染待测液，故C错；D.稀释浓硫酸时，要把浓硫酸缓缓地沿器壁注入水中，同时用玻璃棒不断搅拌，以使热量及时地扩散；一定不能把水注入浓硫酸中，故D错。
(中考精品)浙江省绍兴市中考数学真题(解析版)
2022年浙江省绍兴市中考数学真题一、选择题1. 实数－6的相反数是（ ） A. 16- B. 16 C. －6 D. 6【答案】D【解析】【分析】根据只有符号不同的两个数是互为相反数求解即可．【详解】解：－6的相反数是6，故选：D ．【点睛】本题考查相反数，掌握相反数的定义是解题的关键．2. 2022年北京冬奥会3个赛区场馆使用绿色电力，减排320000吨二氧化碳．数字320000用科学记数法表示是（ ）A. 63.210⨯B. 53.210⨯C. 43.210⨯D. 43210⨯【答案】B【解析】【分析】根据科学记数法“把一个大于10的数表示成10n a ⨯的形式(其中a 是整数数位只有一位的数，即a 大于或等于1且小于10，n 是正整数)，这样的记数方法叫科学记数法”即可得．【详解】解：5320000 3.210=⨯，故选B ．【点睛】本题考查了科学记数法，解题的关键是掌握科学记数法．3. 由七个相同的小立方块搭成的几何体如图所示，则它的主视图是（ ）A. B. C. D.【答案】B【解析】【分析】根据题目中的图形，可以画出主视图，本题得以解决．【详解】解：由图可得，题目中图形的主视图是，故选：B ．【点睛】本题考查简单组合体的三视图，解题的关键是画出相应的图形．4. 在一个不透明的袋子里，装有3个红球、1个白球，它们除颜色外都相同，从袋中任意摸出一个球为红球的概率是（ ） A. 34 B. 12 C. 13 D. 14【答案】A【解析】【分析】根据概率公式计算，即可求解． 【详解】解：根据题意得：从袋中任意摸出一个球为红球的概率是33314=+． 故选：A【点睛】本题考查了概率公式：熟练掌握随机事件A 的概率P （A ）=事件A 可能出现的结果数除以所有可能出现的结果数；P （必然事件）=1；P （不可能事件）=0是解题的关键．5. 下列计算正确的是（ ）A. 2()a ab a a b +÷=+B. 22a a a ⋅=C. 222()a b a b +=+D. 325()a a = 【答案】A【解析】【分析】根据多项式除以单项式、同底数幂的乘法、完全平方公式、幂的乘方法则逐项判断即可．【详解】解：A 、2()a ab a a b +÷=+，原式计算正确；B 、23a a a ⋅=，原式计算错误；C 、222()2a b a b ab +=++，原式计算错误；D 、326()a a =，原式计算错误；故选：A ．【点睛】本题考查了多项式除以单项式、同底数幂的乘法、完全平方公式和幂的乘方，熟练掌握运算法则是解题的关键．6. 如图，把一块三角板ABC 的直角顶点B 放在直线EF 上，30C ∠=︒，AC ∥EF ，则1∠=（ ）A. 30°B. 45°C. 60°D. 75°【答案】C【解析】 【分析】根据三角板的角度，可得60A ∠=︒，根据平行线的性质即可求解．【详解】解： 30C ∠=︒，9060A C ∴∠=︒-∠=︒AC ∥EF ，160A ∴∠=∠=︒故选C【点睛】本题考查了平行线的性质，掌握平行线的性质是解题的关键．7. 已知抛物线2y x mx =+的对称轴为直线2x =，则关于x 的方程25x mx +=的根是（ ）A. 0，4B. 1，5C. 1，－5D. －1，5【答案】D【解析】【分析】根据抛物线2y x mx =+的对称轴为直线2x =可求出m 的值，然后解方程即可．【详解】 抛物线2y x mx =+的对称轴为直线2x =， 221m ∴-=⨯， 解得4m =-，∴关于x 的方程25x mx +=为2450x x --=，(5)(1)0x x ∴-+=，解得125,1x x ==-，故选：D ．【点睛】本题考查了二次函数的性质及解一元二次方程，准确理解题意，熟练掌握知识点是解题的关键．8. 如图，在平行四边形ABCD 中，22AD AB ==，60ABC ∠=︒，E ，F 是对角线BD 上的动点，且BE DF =，M ，N 分别是边AD ，边BC 上的动点．下列四种说法：①存在无数个平行四边形MENF ；②存在无数个矩形MENF ；③存在无数个菱形MENF ；④存在无数个正方形MENF ．其中正确的个数是（ ）A. 1B. 2C. 3D. 4【答案】C【解析】 【分析】根据题意作出合适的辅助线，然后逐一分析即可．【详解】如图，连接AC 、与BD 交于点O ，连接ME ，MF ，NF ，EN ，MN ，∵四边形ABCD 是平行四边形∴OA =OC ，OB =OD∵BE =DF∴OE =OF∵点E 、F 时BD 上的点，∴只要M ，N 过点O ，那么四边形MENF 就是平行四边形∴存在无数个平行四边形MENF ，故①正确；只要MN =EF ，MN 过点O ，则四边形MENF 是矩形，∵点E 、F 是BD 上的动点，∴存在无数个矩形MENF ，故②正确；只要MN ⊥EF ，MN 过点O ，则四边形MENF 是菱形；∵点E 、F 是BD 上的动点，∴存在无数个菱形MENF ，故③正确；只要MN =EF ，MN ⊥EF ，MN 过点O ，则四边形MENF 是正方形，而符合要求的正方形只有一个，故④错误；故选：C【点睛】本题考查正方形的判定、菱形的判定、矩形的判定、平行四边形的判定、解答本题的关键时明确题意，作出合适的辅助线．9. 已知112233()()()x y x y x y ，，，，，为直线23y x =-+上的三个点，且123x x x <<，则以下判断正确的是（ ）．A. 若120x x >，则130y y >B. 若130x x <，则120y y >C. 若230x x >，则130y y >D. 若230x x <，则120y y >【答案】D【解析】【分析】根据一次函数的性质和各个选项中的条件，可以判断是否正确，从而可以解答本题．【详解】解：∵直线y =−2x +3∴y 随x 增大而减小，当y =0时，=1.5∵(x 1，y 1)，(x 2，y 2)，(x 3，y 3)为直线y =−2x +3上的三个点，且x 1<x 2<x 3∴若x 1x 2>0，则x 1，x 2同号，但不能确定y 1y 3的正负，故选项A 不符合题意； 若x 1x 3<0，则x 1，x 3异号，但不能确定y 1y 2的正负，故选项B 不符合题意；若x 2x 3>0，则x 2，x 3同号，但不能确定y 1y 3的正负，故选项C 不符合题意；若x 2x 3<0，则x 2，x 3异号，则x 1，x 2同时为负，故y 1，y 2同时为正，故y 1y 2>0，故选项D 符合题意．故选：D ．【点睛】本题考查一次函数图象上点的坐标特征，解题的关键是明确题意，利用一次函数的性质解答．10. 将一张以AB 为边的矩形纸片，先沿一条直线剪掉一个直角三角形，在剩下的纸片中，再沿一条直线剪掉一个直角三角形（剪掉的两个直角三角形相似），剩下的是如图所示的四边形纸片ABCD ，其中90A ∠=︒，9AB =，7BC =，6CD =，2AD =，则剪掉的两个直角三角形的斜边长不可能是（ ）A. 252B. 454C. 10D. 354【答案】A【解析】【分析】根据题意，画出相应的图形，然后利用相似三角形的性质和分类讨论的方法，求出剪掉的两个直角三角形的斜边长，然后即可判断哪个选项符合题意．【详解】解：当△DFE ∽△ECB 时，如图，∴DF FE DE EC CB EB==， 设DF =x ，CE =y ， ∴9672x y y x +==+，解得：274214x y ⎧=⎪⎪⎨⎪=⎪⎩， ∴2145644DE CD CE =+=+=，故B 选项不符合题意； ∴2735244EB DF AD =+=+=，故选项D 不符合题意；如图，当△DCF ∽△FEB 时，∴DC CF DF FE EB FB==， 设FC =m ，FD =n ， ∴6927m n n m ==++，解得：810m n =⎧⎨=⎩， ∴FD =10，故选项C 不符合题意；8614BF FC BC =+=+=，故选项A 符合题意；故选：A【点睛】本题考查相似三角形的性质、矩形的性质，解答本题的关键是明确题意，利用分类讨论的方法解答．二、填空题11. 分解因式：2x x + ＝ ______【答案】(1)x x +【解析】【分析】利用提公因式法即可分解．【详解】2(1)x x x x +=+，故答案为：(1)x x +．【点睛】本题考查了用提公因式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解．12. 关于x 的不等式32x x ->的解是______．【答案】1x >【解析】【分析】将不等式移项，系数化为1即可得．【详解】解：32x x ->32x x ->22x >1x >，故答案为：1x >．【点睛】本题考查了解一元一次不等式，解题的关键是掌握解一元一次不等式的方法． 13. 元朝朱世杰的《算学启蒙》一书记载：“良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何追及之．” 其题意为：“良马每天行240里，劣马每天行150里，劣马先行12天，良马要几天追上劣马？”答：良马追上劣马需要的天数是______．【答案】20【解析】【分析】设良马x 天追上劣马，根据良马追上劣马所走路程相同可得：240x ＝150（x ＋12），即可解得良马20天追上劣马．【详解】解：设良马x 天追上劣马，根据题意得：240x ＝150（x ＋12），解得x ＝20，答：良马20天追上劣马；故答案为：20．【点睛】本题考查一元一次方程的应用，解题的关键是读懂题意，找到等量关系列出方程．14. 如图，在ABC 中，40ABC ∠=︒，80BAC ∠=︒，以点A 为圆心，AC 长为半径作弧，交射线BA 于点D ，连接CD BCD ∠的度数是______．【答案】10°或100°【解析】【分析】分两种情况画图，由作图可知得AC AD =，根据等腰三角形的性质和三角形内角和定理解答即可．【详解】解：如图，点D 即为所求；在ABC ∆中，40ABC ∠=︒，80BAC ∠=︒，180408060ACB ∴∠=︒-︒-︒=︒，由作图可知：AC AD =，1(18080)502ACD ADC ∴∠=∠=︒-︒=︒， 605010BCD ACB ACD ∴∠=∠-∠=︒-︒=︒；由作图可知：AC AD ='，ACD AD C ∴∠'=∠'，80ACD AD C BAC ∠'+∠'=∠=︒ ，40AD C ∴∠'=︒，1801804040100BCD ABC AD C ∴∠'=︒-∠-∠'=︒-︒-︒=︒．综上所述：BCD ∠的度数是10︒或100︒．故答案为：10︒或100︒．【点睛】本题考查了作图-复杂作图，三角形内角和定理，等腰三角形的判定与性质，解题的关键是掌握基本作图方法．15. 如图，在平面直角坐标系xOy 中，点A （0，4），B （3，4），将ABO 向右平移到CDE △位置，A 的对应点是C ，O 的对应点是E ，函数(0)k y k x=≠的图象经过点C 和DE 的中点F ，则k 的值是______．【答案】6【解析】【分析】作FG ⊥x 轴，DQ ⊥x 轴，FH ⊥y 轴，设AC=EO=BD =a ，表示出四边形ACEO 的面积，再根据三角形中位线的性质得出FG ，EG ，即可表示出四边形HFGO 的面积，然后根据k 的几何意义得出方程，求出a ，可得答案．【详解】过点F 作FG ⊥x 轴，DQ ⊥x 轴，FH ⊥y 轴，根据题意，得AC=EO=BD ，设AC=EO=BD =a ，∴四边形ACEO 的面积是4a ．∵F 是DE 的中点，FG ⊥x 轴，DQ ⊥x 轴，∴FG 是△EDQ 的中位线， ∴122FG D Q ==，1322E G E Q ==， ∴四边形HFGO 的面积为32()2a +， ∴342()2k a a ==+， 解得32a =， ∴k=6．故答案为：6．【点睛】本题主要考查了反比例函数中k 的几何意义，正确的作出辅助线构造矩形是解题的关键．16. 如图，10AB =，点C 在射线BQ 上的动点，连接AC ，作CD AC ⊥，CD AC =，动点E 在AB 延长线上，tan 3QBE ∠=，连接CE ，DE ，当CE DE =，CE DE ⊥时，BE 的长是______．【答案】5或354【解析】 【分析】过点C 作CN ⊥BE 于N ，过点D 作DM ⊥CN 延长线于M ，连接EM ，设BN =x ，则CN =3x ，由△ACN ≌△CDM 可得AN =CM =10+x ，CN =DM =3x ，由点C 、M 、D 、E 四点共圆可得△NME 是等腰直角三角形，于是NE =10-2x ，由勾股定理求得AC 可得CE ，在Rt △CNE 中由勾股定理建立方程求得x ，进而可得BE ；【详解】解：如图，过点C 作CN ⊥BE 于N ，过点D 作DM ⊥CN 延长线于M ，连接EM ，设BN =x ，则CN =BN •tan ∠CBN =3x ，∵△CAD ，△ECD 都是等腰直角三角形，∴CA =CD ，EC =ED ，∠EDC =45°，∠CAN +∠ACN =90°，∠DCM +∠ACN =90°，则∠CAN =∠DCM ，在△ACN 和△CDM 中：∠CAN =∠DCM ，∠ANC =∠CMD =90°，AC =CD ，∴△ACN ≌△CDM （AAS ），∴AN =CM =10+x ，CN =DM =3x ，∵∠CMD =∠CED =90°，∴点C 、M 、D 、E 四点共圆，∴∠CME =∠CDE=45°，∵∠ENM =90°，∴△NME 是等腰直角三角形，∴NE =NM =CM -CN =10-2x ，Rt △ANC 中，AC =，Rt △ECD 中，CD =AC ，CE CD ， Rt △CNE 中，CE 2=CN 2+NE 2，∴()()()()2222110331022x x x x ⎡⎤++=+-⎣⎦， 2425250x x -+=，()()4550x x --=，x =5或x =54， ∵BE =BN +NE =x +10-2x =10-x ，∴BE =5或BE =354； 故答案为：5或354； 【点睛】本题考查了三角函数，全等三角形的判定和性质，圆内接四边形的性质，勾股定理，一元二次方程等知识；此题综合性较强，正确作出辅助线是解题关键．三、解答题17. 计算（1）计算：6tan30°+（π+1）0（2）解方程组242.x y x y -=⎧⎨+=⎩， 【答案】（1）1（2）20x y =⎧⎨=⎩【解析】 【分析】（1）根据特殊角的三角函数值，零指数幂，二次根式的性质化简，然后进行计算即可；（2）利用加减消元法解二元一次方程组即可．【小问1详解】解：原式611=-=+-1； 【小问2详解】242x y x y -=⎧⎨+=⎩①②， ①＋②得3x ＝6，∴x ＝2，把x ＝2代入②，得y ＝0，∴原方程组的解是20x y =⎧⎨=⎩． 【点睛】本题考查了特殊角的三角函数值，零指数幂，二次根式的性质，解二元一次方程组，解决本题的关键是掌握以上知识熟练运算．18. 双减政策实施后，学校为了解八年级学生每日完成书面作业所需时长x （单位：小时）情况，在全校范围内随机抽取了八年级若干名学生进行调查，并将所收集的数据分组整理，绘制了如下两幅不完整的统计图表，请根据图表信息解答下列问题．.的八年级学生每日完成书面作业所需时长情况的统计表 组别 所需时长（小时） 学生人数（人）A 00.5x <≤ 15B 0.51x <≤ mC 1 1.5x <≤ nD 1.52x <≤5（1）求统计表中m ，n 的值．（2）已知该校八年级学生有800人，试估计该校八年级学生中每日完成书面作业所需时长满足0.5 1.5x <≤的共有多少人．【答案】（1）m 为60，n 为20（2）640人【解析】【分析】（1）先求出被调查总人数，再根据扇形统计图求出m ，用总人数减去A 、B 、D 的人数，即可得n 的值；（2）用被调查情况估计八年级800人的情况，即可得到答案．【小问1详解】解：被调查总人数：1515%100÷=（人)， 10060%60m ∴=⨯=（人)，1001560520n =---=（人)，答：m 为60，n 为20；【小问2详解】解： 当0.5 1.5x <…时，在被调查的100人中有602080+=（人)，∴在该校八年级学生800人中，每日完成书面作业所需时长满足0.5 1.5x <…的共有80800640100⨯=（人)， 答：估计共有640人．【点睛】本题考查统计图和统计表，解题的关键是掌握从图表中寻找“完整信息”从而求出被调查的总数．19. 一个深为6米的水池积存着少量水，现在打开水阀进水，下表记录了2小时内5个时刻的水位高度，其中x 表示进水用时（单位：小时），y 表示水位高度（单位：米）． x0 0.5 1 1.5 2 y 1 1.5 2 2.5 3为了描述水池水位高度与进水用时的关系，现有以下三种函数模型供选择：y kx b =+（0k ≠），y =ax 2+bx +c （0a ≠），k y x=（0k ≠）． （1）在平面直角坐标系中描出表中数据对应的点，再选出最符合实际的函数模型，求出相应的函数表达式，并画出这个函数的图象．（2）当水位高度达到5米时，求进水用时x ． 【答案】（1）y ＝x ＋1（0≤x ≤5），图见解析（2）4小时【解析】【分析】（1）观察表格数据，y 的增长量是固定的，故符合一次函数模型，建立模型待定系数法求解析式，画出函数图象即可求解；（2）根据5y =，代入解析式求得x 的值即可求解．小问1详解】（1）选择y ＝kx ＋b ，将（0，1），（1，2）代入，得12b k b =⎧⎨+=⎩，，解得11.k b =⎧⎨=⎩， ∴y ＝x ＋1（0≤x ≤5）．【小问2详解】当y ＝5时，x ＋1＝5，∴x ＝4．答：当水位高度达到5米时，进水用时x 为4小时．【点睛】本题考查了一次函数的性质，画一次函数图象，求一次函数的解析式，根据题意建立模型是解题的关键．20. 圭表（如图1)是我国古代一种通过测量正午日影长度来推定节气的天文仪器，它包括一根直立的标竿（称为“表” )和一把呈南北方向水平固定摆放的与标竿垂直的长尺（称为“圭” )，当正午太阳照射在表上时，日影便会投影在圭面上，圭面上日影长度最长的那一天定为冬至，日影长度最短的那一天定为夏至．图2是一个根据某市地理位置设计的圭表平面示意图，表AC 垂直圭BC ，已知该市冬至正午太阳高度角（即)ABC ∠为37︒，夏至正午太阳高度角（即)ADC ∠为84︒，圭面上冬至线与夏至线之间的距离（即DB 的【长）为4米．（1）求∠BAD 度数．（2）求表AC 的长（最后结果精确到0.1米）．（参考数据：sin37°≈35，cos37°≈45，tan37°≈34，tan84°≈192） 【答案】（1）47°（2）3.3米 【解析】【分析】（1）根据三角形的外角等于与它不相邻两个内角的和解答即可；（2）分别求出ADC ∠和ABC ∠的正切值，用AC 表示出CD 和CB ，得到一个只含有AC 的关系式，再解答即可．【小问1详解】解：84ADC ∠=︒ ，37ABC ∠=︒，47BAD ADC ABC ∴∠=∠-∠=︒，答：BAD ∠的度数是47︒．【小问2详解】解：在Rt △ABC 中，tan 37AC BC ︒=， ∴tan 37AC BC =︒． 同理，在Rt △ADC 中，有tan84AC DC =︒． ∵4BD =， ∴4tan 37tan84AC AC BC DC BD -=-==︒︒． ∴424319AC AC -≈，的∴ 3.3AC ≈（米）．答：表AC 的长是3.3米．【点睛】本题主要考查了三角形外角的性质和三角函数，解题的关键是熟练掌握建模思想来解决．21. 如图，半径为6的⊙O 与Rt △ABC 的边AB 相切于点A ，交边BC 于点C ，D ，∠B=90°，连接OD ，A D ．（1）若∠ACB=20°，求 AD 的长（结果保留π）． （2）求证：AD 平分∠BDO ．【答案】（1）43π （2）见解析【解析】【分析】（1）连接OA ，由20ACB ∠=︒，得40AOD ∠=︒，由弧长公式即得 AD 的长为43π； （2）根据AB 切O 于点A ，90B ∠=︒，可得//OA BC ，有OAD ADB ∠=∠，而OA OD =，即可得ADB ODA ∠=∠，从而AD 平分BDO ∠．【小问1详解】解：连接OA ，∵∠ACB ＝20°，∴∠AOD ＝40°，∴ 180n rAD π=，18040⨯π⨯6=43π=． 【小问2详解】证明：OA OD = ，OAD ODA ∠=∠∴，AB Q 切O 于点A ，OA AB ∴⊥，90B ∠=︒ ，//OA BC ∴，OAD ADB ∴∠=∠，ADB ODA ∴∠=∠，AD ∴平分BDO ∠．【点睛】本题考查与圆有关的计算及圆的性质，解题的关键是掌握弧长公式及圆的切线的性质．22. 如图，在△ABC 中，∠ABC=40°， ∠ACB=90°，AE 平分∠BAC 交BC 于点E ．P 是边BC 上的动点（不与B ，C 重合），连结AP ，将△APC 沿AP 翻折得△APD ，连结DC ，记∠BCD=α．（1）如图，当P 与E 重合时，求α的度数．（2）当P 与E 不重合时，记∠BAD=β，探究α与β的数量关系．【答案】（1）25° （2）①当点P 在线段BE 上时，2α－β＝50°；②当点P 在线段CE 上时，2α＋β＝50°【解析】【分析】（1）由∠B ＝40°，∠ACB ＝90°，得∠BAC ＝50°，根据AE 平分∠BAC ，P 与E 重合，可得∠ACD ，从而α＝∠ACB −∠ACD ；（2）分两种情况：①当点P 在线段BE 上时，可得∠ADC ＝∠ACD ＝90°−α，根据∠ADC ＋∠BAD ＝∠B ＋∠BCD ，即可得2α−β＝50°；②当点P 在线段CE 上时，延长AD 交BC于点F，由∠ADC＝∠ACD＝90°−α，∠ADC＝∠AFC＋α＝∠ABC＋∠BAD+α可得90°−α＝40°＋α＋β，即2α＋β＝50°．【小问1详解】解：∵∠B＝40°，∠ACB＝90°，∴∠BAC＝50°，∵AE平分∠BAC，∴∠EAC＝1∠BAC＝25°，2∵P与E重合，∴D在AB边上，AE⊥CD，∴∠ACD＝65°，∴α＝∠ACB－∠ACD＝25°；【小问2详解】①如图1，当点P在线段BE上时，∵∠ADC＝∠ACD＝90°－α，∠ADC＋∠BAD＝∠B＋∠BCD，∴90°－α＋β＝40°＋α，∴2α－β＝50°；②如图2，当点P在线段CE上时，延长AD交BC于点F，∵∠ADC＝∠ACD＝90°－α，∠ADC＝∠AFC＋α＝∠ABC＋∠BAD+α＝40°＋α＋β，∴90°－α＝40°＋α＋β，∴2α＋β＝50°．【点睛】本题考查三角形综合应用，涉及轴对称变换，三角形外角等于不相邻的两个内角的和的应用，解题的关键是掌握轴对称的性质，能熟练运用三角形外角的性质． 23. 已知函数2y x bx c =-++（b ，c 为常数）的图象经过点（0，﹣3），（﹣6，﹣3）．（1）求b ，c 的值．（2）当﹣4≤x ≤0时，求y 的最大值．（3）当m ≤x ≤0时，若y 的最大值与最小值之和为2，求m 的值．【答案】（1）b ＝-6，c =-3（2）x ＝－3时，y 有最大值为6（3）m ＝－2或3--【解析】【分析】（1）把（0，-3），（-6，-3）代入y ＝2x bx c -++，即可求解；（2）先求出抛物线的顶点坐标为（-3，6），再由-4≤x ≤0，可得当x ＝-3时，y 有最大值，即可求解；（3）由（2）得当x ＞-3时，y 随x 增大而减小；当x ≤-3时，y 随x 的增大而增大，然后分两种情况：当-3＜m≤0时，当m≤-3时，即可求解．【小问1详解】解：把（0，-3），（-6，-3）代入y ＝2x bx c -++，得∶33663c b c =-⎧⎨--+=-⎩，解得：63b c =-⎧⎨=-⎩； 【小问2详解】解：由（1）得：该函数解析式为y ＝263x x ---＝2(3)6x -++，∴抛物线的顶点坐标为（-3，6），∵-1＜0∴抛物线开口向下，又∵-4≤x ≤0，∴当x ＝-3时，y 有最大值为6．【小问3详解】解：由（2）得：抛物线的对称轴为直线x =-3，∴当x ＞-3时，y 随x 的增大而减小；当x ≤-3时，y 随x 的增大而增大，①当-3＜m≤0时，当x ＝0时，y 有最小值为-3，当x ＝m 时，y 有最大值为263m m ---，∴263m m ---+（-3）＝2， 的∴m ＝-2或m ＝-4（舍去）．②当m≤-3时，当x ＝-3时，y 有最大值为6，∵y 的最大值与最小值之和为2，∴y 最小值为-4，∴2(3)6m -++=-4，∴m ＝3-或m ＝3-+（舍去）．综上所述，m ＝-2或3--．【点睛】本题主要考查了二次函数的图象和性质，熟练掌握二次函数的图象和性质，并利用分类讨论思想解答是解题的关键．24. 如图，在矩形ABCD 中，6AB =，8BC =，动点E 从点A 出发，沿边AD ，DC 向点C 运动，A ，D 关于直线BE 的对称点分别为M ，N ，连结MN ．（1）如图，当E 在边AD 上且2=时，求AEM ∠的度数．（2）当N 在BC 延长线上时，求DE 的长，并判断直线MN 与直线BD 的位置关系，说明理由．（3）当直线MN 恰好经过点C 时，求DE 的长．【答案】（1）∠AEM ＝90°；（2）DE ＝103；MN ∥BD ，证明见解析；（3）DE 的长为 【解析】 【分析】（1）由DE ＝2知，AE ＝AB ＝6，可知∠AEB ＝∠MEB ＝45°，从而得出答案； （2）根据对称性得，∠ENC ＝∠BDC ，则cos ∠ENC ＝2610EN =，得EN ＝103，利用SSS 证明△BMN ≌△DCB ，得∠DBC ＝∠BNM ，则MN ∥BD ；（3）当点E 在边AD 上时，若直线MN 过点C ，利用AAS 证明△BCM ≌△CED ，得DE ＝MC；当点E在边CD上时，证明△BMC∽△CNE，可得BM MCCN EN=，从而解决问题．【小问1详解】解：∵DE=2，∴AE＝AB＝6，∵四边形ABCD是矩形，∴∠A＝90°，∴∠AEB＝∠ABE＝45°，由对称性知∠BEM＝45°，∴∠AEM=∠AEB+∠BEM＝90°；【小问2详解】如图1，∵AB=6，AD=8，∴由勾股定理得BD=10，∵当N落在BC延长线上时，BN＝BD＝10，∴CN＝2．由对称性得，∠ENC＝∠BDC，∴cos∠ENC＝2610 EN=，∴EN＝10 3，∴DE＝EN＝10 3；直线MN与直线BD的位置关系是MN∥BD．由对称性知BM＝AB＝CD，MN＝AD＝BC，又∵BN＝BD，∴△BMN≌△DCB（SSS），∴∠DBC＝∠BNM，所以MN∥BD；【小问3详解】①情况1：如图2，当E在边AD上时，直线MN过点C，∴∠BMC＝90°，∴MC=．∵BM＝AB＝CD，∠DEC＝∠BCE，∠BMC＝∠EDC＝90°，∴△BCM≌△CED（AAS），∴DE＝MC＝；②情况2：如图3，点E在边CD上时，∵BM＝6，BC＝8，∴MC＝，CN＝8-，∵∠BMC＝∠CNE＝∠BCD＝90°，∴∠BCM＋∠ECN＝90°，∵∠BCM＋∠MBC＝90°，∴∠ECN＝∠MBC，∴△BMC∽△CNE，∴BM MC CN EN=，∴ENMC CNBM⋅==∴DE＝EN．综上所述，DE的长为【点睛】本题是四边形综合题，主要考查了矩形的性质，轴对称的性质，全等三角形的判定与性质，相似三角形的判定与性质，三角函数等知识，根据题意画出图形，并运用分类讨论思想是解题的关键。
2022年浙江省绍兴市中考英语试题(含答案)
2022年绍兴市初中学业水平考试英语试卷Ⅰ（选择题共70分）（一）听力部分（共25分）一、听力（本题有15小题，第一节每小题1分，第二、三节每小题2分，共计25分）第一节：听小对话，回答问题。
1．Who took the photo?A. The boy.B. The girl.C. The girl’s sister. 2．Where does Kerry come from?A. The UK.B. Australia.C. The USA.3．Why does Betty look so weak?A. Because she is ill.B. Because she has had a test.C. Because she went to bed late last night.4．What are the speakers mainly talking about?A. Cathy’s job interview.B. Cathy’s clothes.C. Cathy’s school. 5．What’s the relationship between the two speakers?A. Doctor and patient.B. Waiter and customer.C. Teacher and student.第二节：听较长对话，回答问题。
听下面一段对话，回答下列小题。
6．When will Helen start from home tomorrow morning?A At three. B. At four. C. At five.7．What docs James mean?A. He will send Helen to the airport.B. He will call to wake Helen up.C. He will also go to Paris.听下面一段对话，回答下列小题。
浙江省绍兴市2022年中考科学试题(word版含答案)
浙江省绍兴市2022年中考科学试题(word版含答案)绍兴1．(绍兴-1)下图所示的实验操作不正确的是()A.取用液体B.称量NaCl质量C.闻气体的气味D.读取液体体积2．(绍兴-02)某军舰在东海航行时，不受参照物选择影响的是()A．航行的时间B．航行的速度C．军舰的位置D．航行的路程3．(绍兴-3)下列对如图所示某校园生态系统的描述，正确的是（）A．校园里所有的绿色植物是一个种群B．食物链：光→植物→虫→鸟→微生物C．箭头表示物质和能量是可以循环的D．绿色植物属于生产者4．(绍兴-4)2022年12月，“玉兔”号月球车由运载火箭送入太空，成功登月。
月球车质量为140千克，利用太阳能和核能工作，采用6个宽大且表面粗糙的筛网轮，具有多项现代科技成果。
以下说法中错误的是(）A．月球车在月球上重1400牛顿B．火箭发射时，受到燃气对它的推力C．采用6个宽大表面的筛网轮，可以减小月球车对月球表面的压强D．太阳能电板能将太阳能转化成电能5．(绍兴-5)下列有关水稻的说法不正确的是（）A．根向地生长是水稻对地球引力刺激作出的反应B．吸收的水分主要参与枝叶的生长和花果的发育C．水稻相邻的叶总是不重叠，增大光照面积是对光合作用的适应D．水稻体内遗传物质的结构层次：基因→DNA→染色体6．(绍兴-06)下列生活中的“小水珠”属于熔化形成的是()A.青草上的露珠B.冰凌上滴下的水珠C.山间的薄雾D.窗上的水珠7．(绍兴-7)“模拟实验”是一种常用的科学研究方法，以下不属于该研究方法的是（）A.研究气压与流速实验B.米勒实验C.研究宇宙膨胀实验D.研究地球形状实验8．(绍兴-8)某化肥包装袋上的部分说明如图所示，则下列说法不正确的是()A．硝酸铵属于氮肥B．“含氮量”中的“氮”是指氮元素C．硝酸铵受热可能会分解D．硝酸铵中氮、氢、氧元素的质量比是2∶4∶310．(绍兴-10)下列地貌形态的形成，主要是由风力侵蚀作用引起的是()A.火山湖B.海岸边的怪石C.喜马拉雅山D.沙漠中的石蘑菇11．(绍兴-11)桃形李有“江南名果”美誉,它是通过嫁接培育而成。
2023年浙江省绍兴市中考数学真题 (解析版)
2023年浙江省绍兴市中考数学真题（解析版）卷Ⅰ（选择题）一、选择题（本大题有10小题，每小题4分，共40分，请选出每小题中一个最符合题意的选项，不选、多选、错选，均不给分1.计算23-的结果是（）A.1- B.3- C.1 D.3【答案】A【解析】【分析】根据有理数的减法法则进行计算即可．【详解】解：231-=-，故选：A ．【点睛】本题主要考查了有理数的减法，解题的关键是掌握有理数的减法计算法则．减去一个数等于加上它的相反数．2.据报道，2023年“五一”假期全国国内旅游出游合计274000000人次．数字274000000用科学记数法表示是（）A.727.410⨯ B.82.7410⨯ C.90.27410⨯ D.92.7410⨯【答案】B【解析】【分析】科学记数法的表现形式为10n a ⨯的形式，其中1||10,a n ≤<为整数，确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同，由此进行求解即可得到答案．【详解】解：8274000000 2.7410=⨯，故选B ．【点睛】本题主要考查了科学记数法，解题的关键在于能够熟练掌握科学记数法的定义．3.由8个相同的立方体搭成的几何体如图所示，则它的主视图是（）A. B. C. D.【答案】D【解析】【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．【详解】从正面看第一层是三个小正方形，第二层左边一个小正方形，中间没有，右边1个小正方形，故选：D．【点睛】本题考查了三视图的知识，要求同学们掌握主视图是从物体的正面看得到的视图．4.下列计算正确的是（）A.623a a a÷= B.()52a a-=- C.()()2111a a a+-=- D.22(1)1a a+=+【答案】C【解析】【分析】根据同底数幂相除法则判断选项A；根据幂的乘方法则判断选项B；根据平方差公式判断选项C；根据完全平方公式判断选项D即可．【详解】解：A．6243a a a a÷=≠，原计算错误，不符合题意；B．()5210a a a-=-≠-，原计算错误，不符合题意；C．()()2111a a a+-=-，原计算正确，符合题意；D．222(1)211a a a a+=++≠+，原计算错误，不符合题意；故选：C．【点睛】本题考查了同底数幂相除法则、幂的乘方法则、平方差公式、完全平方公式等知识，熟练掌握各运算法则是解答本题的关键．5.在一个不透明的袋子里装有2个红球和5个白球，它们除颜色外都相同，从中任意摸出1个球，则摸出的球为红球的概率是（）A.25 B.35 C.27D.57【答案】C【解析】【分析】根据概率的意义直接计算即可．【详解】解：在一个不透明的袋子中装有2个红球和5个白球，它们除颜色外其他均相同，从中任意摸出1个球，共有7种可能，摸到红球的可能为2种，则摸出红球的概率是27，故选：C ．【点睛】本题考查了概率的计算，解题关键是熟练运用概率公式．6.《九章算术》中有一题：“今有大器五、小器一容三斛；大器一、小器五容二斛．问大、小器各容几何？”译文：今有大容器5个，小容器1个，总容量为3斛（斛：古代容是单位）；大容器1个，小容器5个，总容暴为2斛．问大容器、小容器的容量各是多少斛？设大容器的容量为x 斛，小容器的容量为y 斛，则可列方程组是（）A.5352x y x y +=⎧⎨+=⎩ B.5352x y x y +=⎧⎨+=⎩ C.5352x y x y =+⎧⎨=+⎩ D.5253x y x y =+⎧⎨=+⎩【答案】B【解析】【分析】设大容器的容积为x 斛，小容器的容积为y 斛，根据“大容器5个，小容器1个，总容量为3斛；大容器1个，小容器5个，总容量为2斛”即可得出关于x 、y 的二元一次方程组．【详解】解：设大容器的容积为x 斛，小容器的容积为y 斛，根据题意得：5352x y x y +=⎧⎨+=⎩．故选：B ．【点睛】本题考查了由实际问题抽象出二元一次方程组，根据数量关系列出关于x 、y 的二元一次方程组是解题的关键．7.在平面直角坐标系中，将点(),m n 先向右平移2个单位，再向上平移1个单位，最后所得点的坐标是（）A.()2,1m n -- B.()2,1m n -+ C.()2,1m n +- D.()2,1m n ++【答案】D【解析】【分析】把(),m n 横坐标加2，纵坐标加1即可得出结果．【详解】解：将点(),m n 先向右平移2个单位，再向上平移1个单位，最后所得点的坐标是()2,1m n ++．故选：D ．【点睛】本题考查点的平移中坐标的变换，把(),a b 向上（或向下）平移h 个单位，对应的纵坐标加上（或减去）h ，，把(),a b 向右上（或向左）平移n 个单位，对应的横坐标加上（或减去）n ．掌握平移规律是解题的关键．8.如图，在矩形ABCD 中，O 为对角线BD 的中点，60ABD ∠=︒．动点E 在线段OB 上，动点F 在线段OD 上，点,E F 同时从点O 出发，分别向终点,B D 运动，且始终保持OE OF =．点E 关于,AD AB 的对称点为12,E E ；点F 关于,BC CD 的对称点为12,F F ．在整个过程中，四边形1212E E F F 形状的变化依次是（）A.菱形→平行四边形→矩形→平行四边形→菱形B.菱形→正方形→平行四边形→菱形→平行四边形C.平行四边形→矩形→平行四边形→菱形→平行四边形D.平行四边形→菱形→正方形→平行四边形→菱形【答案】A【解析】【分析】根据题意，分别证明四边形1212E E F F 是菱形，平行四边形，矩形，即可求解．【详解】∵四边形ABCD 是矩形，∴AB CD ∥，90BAD ABC ∠=∠=︒，∴60BDC ABD ∠=∠=︒，906030ADB CBD ∠=∠=︒-︒=︒，∵OE OF =、OB OD =，∴DF EB=∵对称，∴21DF DF BF BF ==，，21,BE BE DE DE ==∴1221E F E F =∵对称，∴260F DC CDF ∠=∠=︒，130EDA E DA ∠=∠=︒∴160E DB ∠=︒，同理160F BD ∠=︒，∴11DE BF ∥∴1221E F E F ∥∴四边形1212E E F F 是平行四边形，如图所示，当,,E F O 三点重合时，DO BO =，∴1212DE DF AE AE ===即1212E E EF =∴四边形1212E E F F 是菱形，如图所示，当,E F 分别为,OD OB 的中点时，设4DB =，则21DF DF ==，13DE DE ==，在Rt △ABD 中，2,AB AD ==，连接AE ，AO ，∵602ABO BO AB ∠=︒==，，∴ABO 是等边三角形，∵E 为OB 中点，∴AE OB ⊥，1BE =，∴AE =，根据对称性可得1AE AE ==，∴2221112,9,3AD DE AE ===，∴22211AD AE DE =+，∴1DE A 是直角三角形，且190E ∠=︒，∴四边形1212E E F F 是矩形，当,F E 分别与,D B 重合时，11,BE D BDF 都是等边三角形，则四边形1212E E F F 是菱形∴在整个过程中，四边形1212E E F F 形状的变化依次是菱形→平行四边形→矩形→平行四边形→菱形，故选：A ．【点睛】本题考查了菱形的性质与判定，平行四边形的性质与判定，矩形的性质与判定，勾股定理与勾股定理的逆定理，轴对称的性质，含30度角的直角三角形的性质，熟练掌握以上知识是解题的关键．9.已知点()()()4,2,2,,2,M a N a P a ---在同一个函数图象上，则这个函数图象可能是（）A. B. C.D.【答案】B【解析】【分析】点()()()4,2,2,,2,M a N a P a ---在同一个函数图象上，可得N 、P 关于y 轴对称，当0x <时，y 随x 的增大而增大，即可得出答案．【详解】解：∵()()2,,2,N a P a -，∴得N 、P 关于y 轴对称，∴选项A 、C 错误，∵()()4,2,2,M a N a ---在同一个函数图象上，∴当0x <时，y 随x 的增大而增大，∴选项D 错误，选项B 正确．故选：B ．10.如图，在ABC 中，D 是边BC 上的点（不与点,B C 重合）．过点D 作DE AB ∥交AC 于点E ；过点D 作DF AC ∥交AB 于点F ．N 是线段BF 上的点，2BN NF =；M 是线段DE 上的点，2DM ME =．若已知CMN 的面积，则一定能求出（）A.AFE △的面积B.BDF V 的面积C.BCN △的面积D.DCE △的面积【答案】D【解析】【分析】如图所示，连接ND ，证明FBD EDC ∽，得出FB FD ED EC =，由已知得出NF BF ME DE=，则FD NF EC ME =，又NFD MEC ∠=∠，则NFD MEC ∽，进而得出MCD NDB ∠=∠，可得MC ND ∥，结合题意得出1122EMC DMC MNC S S S == ，即可求解．【详解】解：如图所示，连接ND ，∵DE AB ∥，DF AC ∥，∴,ECD FDB FBD EDC ∠=∠∠=∠，,BFD A A DEC ∠=∠∠=．∴FBD EDC ∽,NFD MEC ∠=∠．∴FB FD ED EC=．∵2DM ME =，2BN NF =，∴11,33NF BF ME DE ==，∴NF BF ME DE =．∴FD NF EC ME =．又∵NFD MEC ∠=∠，∴NFD MEC ∽．∴ECM FDN ∠=∠．∵FDB ECD∠=∠∴MCD NDB ∠=∠．∴MC ND ∥．∴MNC MDC S S = ．∵2DM ME =，∴1122EMC DMC MNC S S S == ．故选：D ．【点睛】本题考查了相似三角形的性质与判定，证明MC ND ∥是解题的关键．卷Ⅱ（非选择题）二、填空题（本大题有6小题，每小题5分，共30分）11.因式分解：m 2﹣3m ＝__________．【答案】()3m m -【解析】【分析】题中二项式中各项都含有公因式m ，利用提公因式法因式分解即可得到答案．【详解】解：()233m m m m -=-，故答案为：()3m m -．【点睛】本题考查整式运算中的因式分解，熟练掌握因式分解的方法技巧是解决问题的关键．12.如图，四边形ABCD 内接于圆O ，若100D ∠=︒，则B ∠的度数是________．【答案】80︒##80度【解析】【分析】根据圆内接四边形的性质：对角互补，即可解答．【详解】解：∵四边形ABCD 内接于O ，∴180B D �邪＝，∵100D ∠=︒，∴18080B D ∠︒∠︒＝﹣＝．故答案为：80︒．【点睛】本题主要考查了圆内接四边形的性质，掌握圆内接四边形的对角互补是解答本题的关键．13.方程3911x x x =++的解是________．【答案】3x =【解析】【分析】先去分母，左右两边同时乘以()1x +，再根据解一元一次方程的方法和步骤进行解答，最后进行检验即可．【详解】解：去分母，得：39x =，化系数为1，得：3x =．检验：当3x =时，10x +≠，∴3x =是原分式方程的解．故答案为：3x =．【点睛】本题主要考查了解分式方程，解题的关键是掌握解分式方程的方法和步骤，正确找出最简公分母，注意解分式方程要进行检验．14.如图，在菱形ABCD 中，40DAB ∠=︒，连接AC ，以点A 为圆心，AC 长为半径作弧，交直线AD 于点E ，连接CE ，则AEC ∠的度数是________．【答案】10︒或80︒【解析】【分析】根据题意画出图形，结合菱形的性质可得1202CAD DAB ∠=∠=︒，再进行分类讨论：当点E 在点A 上方时，当点E 在点A 下方时，即可进行解答．【详解】解：∵四边形ABCD 为菱形，40DAB ∠=︒，∴1202CAD DAB ∠=∠=︒，连接CE ，①当点E 在点A 上方时，如图1E ，∵1AC AE =，120CAE ∠=︒，∴()1118020802AE C ∠=︒-︒=︒，②当点E 在点A 下方时，如图2E ，∵1AC AE =，120CAE ∠=︒，∴211102AE C CAE ∠=∠=︒，故答案为：10︒或80︒．【点睛】本题主要考查了菱形的性质，等腰三角形的性质，三角形的内角和以及三角形的外角定理，解题的关键是掌握菱形的对角线平分内角；等腰三角形两底角相等，三角形的内角和为180︒；三角形的一个外角等于与它不相邻的两个内角之和．15.如图，在平面直角坐标系xOy 中，函数k y x=（k 为大于0的常数，0x >）图象上的两点()()1122,,,A x y B x y ，满足212x x =．ABC 的边AC x ∥轴，边∥BC y 轴，若OAB 的面积为6，则ABC 的面积是________．【答案】2【解析】【分析】过点A B 、作AF y ⊥轴于点F ，AD x ⊥轴于点D ，BE x ⊥于点E ，利用6AFO ABO BOE FABEO S S S S k =++=+ 五边形，AFOD FABEO ADEB ADEB S S S k S =+=+矩形五边形梯形梯形，得到6ADEB S =梯形，结合梯形的面积公式解得11=8x y ，再由三角形面积公式计算2112111111111()()22224ABC S AC BC x x y y x y x y =×=-×-=×=，即可解答．【详解】解：如图，过点A B 、作AF y ⊥轴于点F ，AD x ⊥轴于点D ，BE x ⊥于点E ，6AFO ABO BOE FABEO S S S S k =++=+ 五边形AFOD FABEO ADEB ADEBS S S k S =+=+矩形五边形梯形梯形6ADEB S ∴=梯形2121()()62y y x x +-∴= 212x x =2112y y ∴=11112121111()(2)()()32==6224y y x x y y x x y x +-+-∴=11=8x y ∴8k ∴=21121111111111()()82222244ABC S AC BC x x y y x y x y =×=-×-=×===故答案为：2．【点睛】本题考查反比例函数中k 的几何意义，是重要考点，掌握相关知识是解题关键．16.在平面直角坐标系xOy 中，一个图形上的点都在一边平行于x 轴的矩形内部（包括边界），这些矩形中面积最小的矩形称为该图形的关联矩形．例如：如图，函数()2(2)03y x x =-≤≤的图象（抛物线中的实线部分），它的关联矩形为矩形OABC ．若二次函数()21034y x bx c x =++≤≤图象的关联矩形恰好也是矩形OABC ，则b =________．【答案】712或2512-【解析】【分析】根据题意求得点()3,0A ，()3,4B ，()0,4C，根据题意分两种情况，待定系数法求解析式即可求解．【详解】由()2(2)03y x x =-≤≤，当0x =时，4y =，∴()0,4C ，∵()3,0A ，四边形ABCO 是矩形，∴()3,4B ，①当抛物线经过O B ，时，将点()0,0，()3,4B 代入()21034y x bx c x =++≤≤，∴019344c b c =⎧⎪⎨⨯++=⎪⎩解得：712b =②当抛物线经过点,A C 时，将点()3,0A ,()0,4C 代入()21034y x bx c x =++≤≤，∴419304c b c =⎧⎪⎨⨯++=⎪⎩解得：2512b =-综上所述，712b =或2512b =-，故答案为：712或2512-．【点睛】本题考查了待定系数法求抛物线解析式，理解新定义，最小矩形的限制条件是解题的关键．三、解答题（本大题有8小题，第17~20小题每小题8分，第21小题10分，第22，23小题每小题12分，第24小题14分，共80分．解答需写出必要的文字说明、演算步骤或证明过程）17.（1）计算：0(1)π---．（2）解不等式：324x x ->+．【答案】（1）1；（2）3x >【解析】【分析】（1）根据零指数幂的性质、二次根式的化简、绝对值的性质依次解答；（2）先移项，再合并同类项，最后化系数为1即可解答．【详解】解：（1）原式1=-+1=．（2）移项得36x x ->，即26x >，∴3x >．∴原不等式的解是3x >．【点睛】本题考查实数的混合运算、零指数幂、二次根式的化简和解一元一次不等式等知识，是基础考点，掌握相关知识是解题关键．18.某校兴趣小组通过调查，形成了如下调查报告（不完整）．建议……结合调查信息，回答下列问题：（1）本次调查共抽查了多少名学生？（2）估计该校900名初中生中最喜爱篮球项目的人数．（3）假如你是小组成员，请你向该校提一条合理建议．【答案】（1）100（2）360（3）答案不唯一，见解析【解析】【分析】（1）根据乒乓球人数和所占比例，求出抽查的学生数；（2）先求出喜爱篮球学生比例，再乘以总数即可；（3）从图中观察或计算得出，合理即可．【小问1详解】被抽查学生数：3030%100÷=，答：本次调查共抽查了100名学生．【小问2详解】被抽查的100人中最喜爱羽毛球的人数为：1005%5⨯=，∴被抽查的100人中最喜爱篮球的人数为：100301015540----=，∴40900360100⨯=（人）．答：估计该校900名初中生中最喜爱篮球项目的人数为360．【小问3详解】答案不唯一，如：因为喜欢篮球的学生较多，建议学校多配置篮球器材、增加篮球场地等．【点睛】本题考查从条形统计图和扇形统计图获取信息的能力，并用所获取的信息反映实际问题．19.图1是某款篮球架，图2是其示意图，立柱OA 垂直地面OB ，支架CD 与OA 交于点A ，支架CG CD ⊥交OA 于点G ，支架DE 平行地面OB ，篮筺EF 与支架DE 在同一直线上， 2.5OA =米，0.8AD =米，32AGC ∠=︒．（1）求GAC ∠的度数．（2）某运动员准备给篮筐挂上篮网，如果他站在発子上，最高可以把篮网挂到离地面3米处，那么他能挂上篮网吗？请通过计算说明理由．（参考数据：sin 320.53,cos 320.85,tan 320.62︒≈︒≈︒≈）【答案】（1）58︒（2）该运动员能挂上篮网，理由见解析【解析】【分析】（1）根据直角三角形的两个锐角互余即可求解；（2）延长,OA ED 交于点M ，根据题意得出32ADM ∠=︒，解Rt ADM △，求得AM ，根据OM OA AM =+与3比较即可求解．【小问1详解】解：∵CG CD ⊥，∴90ACG ∠=︒，∵32AGC ∠=︒，∴903258GAC ∠=︒-︒=︒．【小问2详解】该运动员能挂上篮网，理由如下．如图，延长,OA ED 交于点M ，∵,OA OB DE OB ⊥∥，∴90DMA ∠=︒，又∵58DAM GAC ∠=∠=︒，∴32ADM ∠=︒，在Rt ADM △中，sin 320.80.530.424AM AD =︒≈⨯=，∴ 2.50.424 2.9243OM OA AM =+=+=<，∴该运动员能挂上篮网．【点睛】本题考查了解直角三角形的应用，直角三角形的两个锐角互余，熟练掌握三角函数的定义是解题的关键．20.一条笔直的路上依次有,,M P N 三地，其中,M N 两地相距1000米．甲、乙两机器人分别从,M N 两地同时出发，去目的地,N M ，匀速而行．图中,OA BC 分别表示甲、乙机器人离M 地的距离y （米）与行走时间x （分钟）的函数关系图象．（1）求OA 所在直线的表达式．（2）出发后甲机器人行走多少时间，与乙机器人相遇？（3）甲机器人到P 地后，再经过1分钟乙机器人也到P 地，求,P M 两地间的距离．【答案】（1）200y x=（2）出发后甲机器人行走103分钟，与乙机器人相遇（3）,P M 两地间的距离为600米【解析】【分析】（1）利用待定系数法即可求解；（2）利用待定系数法求出BC 所在直线的表达式，再列方程组求出交点坐标，即可；（3）列出方程即可解决．【小问1详解】∵()()0,0,5,1000O A ，∴OA 所在直线的表达式为200y x =．【小问2详解】设BC 所在直线的表达式为y kx b =+，∵()()0,1000,10,0B C ，∴10000,010,b k b =+⎧⎨=+⎩解得100,1000k b =-⎧⎨=⎩．∴1001000y x =-+．甲、乙机器人相遇时，即2001001000x x =-+，解得103x =，∴出发后甲机器人行走103分钟，与乙机器人相遇．【小问3详解】设甲机器人行走t 分钟时到P 地，P 地与M 地距离200y t =，则乙机器人()1t +分钟后到P 地，P 地与M 地距离()10011000y t =-++，由()20010011000t t =-++，得3t =．∴600y =．答：,P M 两地间的距离为600米．【点睛】本题考查了一次函数的图象与性质，用待定系数法可求出函数表达式，要利用方程组的解，求出两个函数的交点坐标，充分应用数形结合思想是解题的关键．21.如图，AB 是O 的直径，C 是O 上一点，过点C 作O 的切线CD ，交AB 的延长线于点D ，过点A 作AE CD ⊥于点E ．（1）若25EAC ∠=︒，求ACD ∠的度数．（2）若2,1OB BD ==，求CE 的长．【答案】（1）115︒（2）CE =【解析】【分析】（1）根据三角形的外角的性质，ACD AEC EAC ∠=∠+∠即可求解．（2）根据CD 是O 的切线，可得90OCD ∠=︒，在Rt OCD △中，勾股定理求得CD =根据OC AE ∥，可得CD OD CE OA=，进而即可求解．【小问1详解】解：∵AE CD ⊥于点E ，∴90AEC ∠=︒，∴9025115ACD AEC EAC ∠=∠+∠=︒+︒=︒．【小问2详解】∵CD 是O 的切线，OC 是O 的半径，∴90OCD ∠=︒．在Rt OCD △中，∵2,3OC OB OD OB BD ===+=，∴CD =．∵90OCD AEC ∠=∠=︒，∴OC AE∥∴CD OD CE OA =，即32CE =，∴CE =．【点睛】本题考查了三角形外角的性质，切线的性质，勾股定理，平行线分线段成比例，熟练掌握以上知识是解题的关键．22.如图，在正方形ABCD 中，G 是对角线BD 上的一点（与点,B D 不重合），,,,GE CD GF BC E F ⊥⊥分别为垂足．连接,EF AG ，并延长AG 交EF 于点H ．（1）求证：DAG EGH ∠=∠．（2）判断AH 与EF 是否垂直，并说明理由．【答案】（1）见解析（2）AH 与EF 垂直，理由见解析【解析】【分析】（1）由正方形的性质，得到AD CD ⊥，结合垂直于同一条直线的两条直线平行，可得AD GE ∥，再根据平行线的性质解答即可；（2）连接GC 交EF 于点O SAS 证明ADG CDG ≌，再根据全等三角形对应角相等得到DAG DCG ∠=∠，继而证明四边形FCEG 为矩形，最后根据矩形的性质解答即可．【小问1详解】解：在正方形ABCD 中，AD CD⊥GE CD⊥ ∴AD GE ∥，∴DAG EGH ∠=∠．【小问2详解】AH 与EF 垂直，理由如下．连接GC 交EF 于点O ．∵BD 为正方形ABCD 的对角线，∴45ADG CDG ∠=∠=︒，又∵,DG DG AD CD ==，∴ADG CDG ≌，∴DAG DCG ∠=∠．在正方形ABCD 中，90ECF ∠=︒，又∵,GE CD GF BC ⊥⊥，∴四边形FCEG 为矩形，∴OE OC =，∴OEC OCE ∠=∠，∴DAG OEC ∠=∠．又∵DAG EGH ∠=∠，∴90EGH GEH OEC GEH GEC ∠+∠=∠+∠=∠=︒，∴90GHE ∠=°，∴AH EF ⊥．【点睛】本题考查正方形的性质、平行线的性质、全等三角形的判断与性质、矩形的判定与性质等知识，综合性较强，是重要考点，掌握相关知识是解题关键．23.已知二次函数2y x bx c =-++．（1）当4,3b c ==时，①求该函数图象的顶点坐标．②当13x -≤≤时，求y 的取值范围．（2）当0x ≤时，y 的最大值为2；当0x >时，y 的最大值为3，求二次函数的表达式．【答案】（1）①()2,7；②当13x -≤≤时，27y -≤≤（2）222y x x =-++【解析】【分析】（1）①将4,3b c ==代入解析式，化为顶点式，即可求解；②已知顶点()2,7，根据二次函数的增减性，得出当2x =时，y 有最大值7，当=1x -时取得最小值，即可求解；（2）根据题意0x ≤时，y 的最大值为2；0x >时，y 的最大值为3，得出抛物线的对称轴2b x =在y 轴的右侧，即0b >，由抛物线开口向下，0x ≤时，y 的最大值为2，可知2c =，根据顶点坐标的纵坐标为3，求出2b =，即可得解．【小问1详解】解：①当4,3b c ==时，2243(2)7y x x x =-++=--+，∴顶点坐标为()2,7．②∵顶点坐标为()2,7．抛物线开口向下，当12x -≤≤时，y 随x 增大而增大，当23x ≤≤时，y 随x 增大而减小，∴当2x =时，y 有最大值7．又()2132-->-∴当=1x -时取得最小值，最小值=2y -；∴当13x -≤≤时，27y -≤≤．【小问2详解】∵0x ≤时，y 的最大值为2；0x >时，y 的最大值为3，∴抛物线的对称轴2b x =在y 轴的右侧，∴0b >，∵抛物线开口向下，0x ≤时，y 的最大值为2，∴2c =，又∵()()241341c b ⨯-⨯-=⨯-，∴2b =±，∵0b >，∴2b =，∴二次函数的表达式为222y x x =-++．【点睛】本题考查了待定系数法求二次函数解析式，顶点式，二次函数的最值问题，熟练掌握二次函数的性质是解题的关键．24.在平行四边形ABCD 中（顶点,,,A B C D 按逆时针方向排列），12,10,AB AD B ==∠为锐角，且4sin 5B =．（1）如图1，求AB 边上的高CH （2）P 是边AB 上的一动点，点,C D 同时绕点P 按逆时针方向旋转90︒得点,C D ''．①如图2，当点C '落在射线CA 上时，求BP 的长．②当AC D ''△是直角三角形时，求BP 的长．【答案】（1）8（2）①347BP =；②6BP =或8±【解析】【分析】（1）利用正弦的定义即可求得答案；（2）①先证明PQC CHP '△≌△，再证明AQC AHC '△∽△，最后利用相似三角形对应边成比例列出方程即可；②分三种情况讨论完成，第一种：C '为直角顶点；第二种：A 为直角顶点；第三种，D ¢为直角顶点，但此种情况不成立，故最终有两个答案．【小问1详解】在ABCD Y 中，10BC AD ==，在Rt BCH 中，4sin 1085CH BC B ==⨯=．【小问2详解】①如图1，作CH BA ⊥于点H ，由（1）得，6BH ==，则1266AH =-=，作C Q BA '⊥交BA 延长线于点Q ，则90CHP PQC ∠'=∠=︒，∴90C PQ PC Q '∠+∠='︒．∵90C PQ CPH ∠+∠='︒∴PC Q CPH ∠=∠'．由旋转知PC PC '=，∴PQC CHP '△≌△．设BP x =，则8,6,4PQ CH C Q PH x QA PQ PA x ====-=-=-'．∵,C Q AB CH AB '⊥⊥，∴C Q CH '∥，∴AQC AHC '△∽△，∴C Q QA CH HA ='，即6486x x --=，∴347x =，∴347BP =．②由旋转得,PCD PC D CD C D '''='△≌△，CD C D ⊥''，又因为AB CD ，所以C D AB ''⊥．情况一：当以C '为直角顶点时，如图2．∵C D AB ''⊥，∴C '落在线段BA 延长线上．∵PC PC ⊥'，∴PC AB ⊥，由（1）知，8PC =，∴6BP =．情况二：当以A 为直角顶点时，如图3．设C D ''与射线BA 的交点为T ，作CH AB ⊥于点H ．∵PC PC ⊥'，∴90CPH TPC ∠'+∠=︒，∵C D AT ''⊥，∴90PC T TPC ∠'+∠='︒，∴CPH PC T ∠=∠'．又∵90,CHP PTC PC C P ∠=∠=='︒'，∴CPH PC T '△≌△，∴,8C T PH PT CH '===．设C T PH t '==，则6AP t =-，∴2AT PT PA t=-=+∵90,C AD C D AB ∠=︒''⊥''，∴ATD C TA '' ∽，∴AT C T TD TA=''，∴2AT C T TD '=⋅'，∴()2(2)12t t ι+=-，化简得2420t t -+=，解得2t =±∴8BP BH HP =+=±情况三：当以D ¢为直角顶点时，点P 落在BA 的延长线上，不符合题意．综上所述，6BP =或8±【点睛】本题考查了平行四边形的性质，正弦的定义，全等的判定及性质，相似的判定及性质，理解记忆相关定义，判定，性质是解题的关键．。
浙江省绍兴市2022年中考[化学]考试真题与答案解析
![浙江省绍兴市2022年中考[化学]考试真题与答案解析](https://img.taocdn.com/s3/m/0394372df68a6529647d27284b73f242336c31c4.png)
浙江省绍兴市2022年中考·化学·考试真题与答案解析一、选择题本题共3小题，每小题4分，共12分。
下列各小题中只有一个选项符合题意。
1．（4分）春秋初期，绍兴一带是南方的一个冶铁中心，其炼铁方法是在1000℃左右的温度下2O3）发生一系列的反应生成含较多杂质的海绵铁。
其中主要化学反应为：3CO+Fe2O3 2Fe+3CO2。
下列说法正确的是（ ）A．海绵铁是一种纯净物B．Fe2O3中铁元素的化合价为+3价C．上述反应中涉及的氧化物只有2种D．炼铁过程中，木炭只是作为燃料使用【分析】A、根据纯净物是由一种物质组成的，混合物有多种物质组成进行分析；B、根据在化合物中正负化合价的代数和为零分析；C、根据氧化物是由两种元素组成，其中一种是氧元素分析；D、根据木炭不完全燃烧可以生成一氧化碳分析。
【解答】解：A、纯净物是由一种物质组成的，海绵铁含有多种物质；故A错误；B、在化合物中正负化合价的代数和为零2O3中，氧元素为﹣3价；故B正确；C、氧化物是由两种元素组成，由化学方程式看出、氧化铁和二氧化碳；故C错误；D、木炭不完全燃烧还可以生成一氧化碳，用于炼铁；故D错误；故选：B。
【点评】本题主要考查了元素化合价的计算物质的分类、铁的冶炼、碳的性质等，在平时的学习中加强识记即可解答。
2．（4分）在做酸碱反应的实验时，向盛有氢氧化钠溶液的烧杯中，逐渐加入稀盐酸。
烧杯内相关物质的质量与加入稀盐酸质量的变化关系不正确的是（ ）A．B．C．D．【分析】氢氧化钠和稀盐酸反应生成氯化钠和水，随着稀盐酸的不断加入，氢氧化钠越来越少，氯化钠越来越多。
【解答】解：A、随着反应进行，当恰好完全反应后，水的质量不断增大；B、随着反应进行，当恰好完全反应后，该选项对应关系正确；C、随着反应进行，当完全反应后氢氧化钠质量是0；D、随着稀盐酸的加入，一段时间内溶液中氯化氢质量是0，溶液中的氯化氢质量不断增大；故选：D。
浙江省绍兴市2020年中考语文真题试题(含扫描答案)
浙江省绍兴市2020年中考语文真题试题一、积累1．阅读下面文字，按要求完成下面的题目坚毅刚强的性格伴随了鲁迅一生。
他没有丝毫的奴颜和（mèi）骨。
他一生顽强战斗，追求真理。
“横眉冷对千夫指，（fǔ）首甘为孺子牛．”在我心目中，他仿佛成了一块铁，一块钢，一块金刚石。
刀砍不断，石砸不破，火烧不_____，水浸不透．他的身影凛然立于宇宙之间，给人带来无限的鼓舞与力量．（节选自季羡林《访绍兴鲁迅故居》）（1）根据拼音写出相应的汉字。
mèi fǔ_____骨_____首（2）给文中划线字“横”选择正确的读音。
（）A．héng B．hèng（3）给文中横线处选择合适的汉字。
（）A．融 B．熔2．鸟影翩跹，人诗人文。
请在下列横线上填入相应的句子。
（1）独怜幽草涧边生，____________________。
（韦应物《滁州西涧》）（2）塞下秋来风景异，____________________。
（范仲淹《渔家傲·秋思》）（3）_______________，缥缈孤鸿影。
（苏拭《卜算子·黄州定慧院寓居作》）（4）晓雾将歇，_______________。
（陶弘景《答谢中书书》）（5）晏殊《烷溪沙》中惋惜与欣慰交织，又深含理趣的句子是：_______________，_______________。
（6）杜甫《春望》一诗中，“_______________，_______________”两句移情于物，因时伤怀，表达了诗人深切的爱国情怀。
（7）在美丽的绍兴乡村，浅山婀娜，暮色氤氲，群鸟纷纷归巢，再现了陶渊明笔下“_______________，_______________”的田园美景。
（《饮酒》其五）3．用现代汉语给下列句子中的划线词作注释。
（1）居①数月，其马将②胡骏马而归。
（《塞翁失马》）__________、__________ （2）策③之不以其道，食④之不能尽其材，鸣之而不能通其意。
2022年浙江省绍兴市中考数学试卷(解析版)
2022年浙江省绍兴市中考数学试卷一、选择题（本大题有10小题，每小题4分，共40分．请选出每小题中一个最符合题意的选项，不选、多选、错选，均不给分）1．（4分）实数﹣6的相反数是（）A．B．C．﹣6D．62．（4分）2022年北京冬奥会3个赛区场馆使用绿色电力，减排320000吨二氧化碳．数字320000用科学记数法表示是（）A．3.2×106B．3.2×105C．3.2×104D．32×1043．（4分）由七个相同的小立方块搭成的几何体如图所示，则它的主视图是（）A．B．C．D．4．（4分）在一个不透明的袋子里，装有3个红球、1个白球，它们除颜色外都相同，从袋中任意摸出一个球为红球的概率是（）A．B．C．D．5．（4分）下列计算正确的是（）A．（a2+ab）÷a＝a+b B．a2•a＝a2C．（a+b）2＝a2+b2D．（a3）2＝a56．（4分）如图，把一块三角板ABC的直角顶点B放在直线EF上，∠C＝30°，AC∥EF，则∠1＝（）A．30°B．45°C．60°D．75°7．（4分）已知抛物线y＝x2+mx的对称轴为直线x＝2，则关于x的方程x2+mx＝5的根是（）A．0，4B．1，5C．1，﹣5D．﹣1，58．（4分）如图，在平行四边形ABCD中，AD＝2AB＝2，∠ABC＝60°，E，F是对角线BD上的动点，且BE＝DF，M，N分别是边AD，边BC上的动点．下列四种说法：①存在无数个平行四边形MENF；②存在无数个矩形MENF；③存在无数个菱形MENF；④存在无数个正方形MENF．其中正确的个数是（）A．1B．2C．3D．49．（4分）已知（x1，y1），（x2，y2），（x3，y3）为直线y＝﹣2x+3上的三个点，且x1＜x2＜x3，则以下判断正确的是（）A．若x1x2＞0，则y1y3＞0B．若x1x3＜0，则y1y2＞0C．若x2x3＞0，则y1y3＞0D．若x2x3＜0，则y1y2＞010．（4分）将一张以AB为边的矩形纸片，先沿一条直线剪掉一个直角三角形，在剩下的纸片中，再沿一条直线剪掉一个直角三角形（剪掉的两个直角三角形相似），剩下的是如图所示的四边形纸片ABCD，其中∠A＝90°，AB＝9，BC＝7，CD＝6，AD＝2，则剪掉的两个直角三角形的斜边长不可能是（）A．B．C．10D．二、填空题（本大题有6小题，每小题5分，共30分）11．（5分）分解因式：x2+x＝．12．（5分）关于x的不等式3x﹣2＞x的解集是．13．（5分）元朝朱世杰的《算学启蒙》一书记载：“良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何追及之．”其题意为：“良马每天行240里，劣马每天行150里，劣马先行12天，良马要几天追上劣马？”答：良马追上劣马需要的天数是．14．（5分）如图，在△ABC中，∠ABC＝40°，∠BAC＝80°，以点A为圆心，AC长为半径作弧，交射线BA于点D，连结CD，则∠BCD的度数是．15．（5分）如图，在平面直角坐标系xOy中，点A（0，4），B（3，4），将△ABO向右平移到△CDE位置，A的对应点是C，O的对应点是E，函数y＝（k≠0）的图象经过点C 和DE的中点F，则k的值是．16．（5分）如图，AB＝10，点C是射线BQ上的动点，连结AC，作CD⊥AC，CD＝AC，动点E在AB延长线上，tan∠QBE＝3，连结CE，DE，当CE＝DE，CE⊥DE时，BE的长是．三、解答题（本大题有8小题，第17～20小题每小题8分，第21小题10分，第22，23小题每小题8分，第24小题14分，共80分．解答需写出必要的文字说明、演算步骤或证明过程）17．（8分）（1）计算：6tan30°+（π+1）0﹣．（2）解方程组：．18．（8分）双减政策实施后，学校为了解八年级学生每日完成书面作业所需时长x（单位：小时）的情况，在全校范围内随机抽取了八年级若干名学生进行调查，并将所收集的数据分组整理，绘制了如下两幅不完整的统计图表，请根据图表信息解答下列问题．八年级学生每日完成书面作业所需时长情况的统计表组别所需时长（小时）学生人数（人）A0＜x≤0.515B0.5＜x≤1mC1＜x≤1.5nD 1.5＜x≤25（1）求统计表中m，n的值．（2）已知该校八年级学生有800人，试估计该校八年级学生中每日完成书面作业所需时长满足0.5＜x≤1.5的共有多少人．19．（8分）一个深为6米的水池积存着少量水，现在打开水阀进水，下表记录了2小时内5个时刻的水位高度，其中x表示进水用时（单位：小时），y表示水位高度（单位：米）．x00.51 1.52y1 1.52 2.53为了描述水池水位高度与进水用时的关系，现有以下三种函数模型供选择：y＝kx+b（k ≠0），y＝ax2+bx+c（a≠0），y＝（k≠0）．（1）在平面直角坐标系中描出表中数据对应的点，再选出最符合实际的函数模型，求出相应的函数表达式，并画出这个函数的图象．（2）当水位高度达到5米时，求进水用时x．20．（8分）圭表（如图1）是我国古代一种通过测量正午日影长度来推定节气的天文仪器，它包括一根直立的标竿（称为“表”）和一把呈南北方向水平固定摆放的与标竿垂直的长尺（称为“圭”），当正午太阳照射在表上时，日影便会投影在圭面上，圭面上日影长度最长的那一天定为冬至，日影长度最短的那一天定为夏至．图2是一个根据某市地理位置设计的圭表平面示意图，表AC垂直圭BC，已知该市冬至正午太阳高度角（即∠ABC）为37°，夏至正午太阳高度角（即∠ADC）为84°，圭面上冬至线与夏至线之间的距离（即DB的长）为4米．（1）求∠BAD的度数．（2）求表AC的长（最后结果精确到0.1米）．（参考数据：sin37°≈，cos37°≈，tan37°≈，tan84°≈）21．（10分）如图，半径为6的⊙O与Rt△ABC的边AB相切于点A，交边BC于点C，D，∠B＝90°，连结OD，AD．（1）若∠ACB＝20°，求的长（结果保留π）．（2）求证：AD平分∠BDO．22．（12分）如图，在△ABC中，∠ABC＝40°，∠ACB＝90°，AE平分∠BAC交BC于点E．P是边BC上的动点（不与B，C重合），连结AP，将△APC沿AP翻折得△APD，连结DC，记∠BCD＝α．（1）如图，当P与E重合时，求α的度数．（2）当P与E不重合时，记∠BAD＝β，探究α与β的数量关系．23．（12分）已知函数y＝﹣x2+bx+c（b，c为常数）的图象经过点（0，﹣3），（﹣6，﹣3）．（1）求b，c的值．（2）当﹣4≤x≤0时，求y的最大值．（3）当m≤x≤0时，若y的最大值与最小值之和为2，求m的值．24．（14分）如图，在矩形ABCD中，AB＝6，BC＝8，动点E从点A出发，沿边AD，DC 向点C运动，A，D关于直线BE的对称点分别为M，N，连结MN．（1）如图，当E在边AD上且DE＝2时，求∠AEM的度数．（2）当N在BC延长线上时，求DE的长，并判断直线MN与直线BD的位置关系，说明理由．（3）当直线MN恰好经过点C时，求DE的长．2022年浙江省绍兴市中考数学试卷参考答案与试题解析一、选择题（本大题有10小题，每小题4分，共40分．请选出每小题中一个最符合题意的选项，不选、多选、错选，均不给分）1．（4分）实数﹣6的相反数是（）A．B．C．﹣6D．6【分析】根据相反数的定义即可得出答案．【解答】解：﹣6的相反数是6，故选：D．【点评】本题考查了相反数，掌握只有符号不同的两个数互为相反数是解题的关键．2．（4分）2022年北京冬奥会3个赛区场馆使用绿色电力，减排320000吨二氧化碳．数字320000用科学记数法表示是（）A．3.2×106B．3.2×105C．3.2×104D．32×104【分析】把较大的数写成a×10n（1≤a＜10，n为正整数）的形式即可．【解答】解：320000＝3.2×105，故选：B．【点评】本题考查了科学记数法﹣表示较大的数，掌握10的指数比原来的整数位数少1是解题的关键．3．（4分）由七个相同的小立方块搭成的几何体如图所示，则它的主视图是（）A．B．C．D．【分析】根据题目中的图形，可以画出主视图，本题得以解决．【解答】解：由图可得，题目中图形的主视图是，故选：B．【点评】本题考查简单组合体的三视图，解答本题的关键是画出相应的图形．4．（4分）在一个不透明的袋子里，装有3个红球、1个白球，它们除颜色外都相同，从袋中任意摸出一个球为红球的概率是（）A．B．C．D．【分析】根据红球可能出现的结果数÷所有可能出现的结果数即可得出答案．【解答】解：∵总共有4个球，其中红球有3个，摸到每个球的可能性都相等，∴摸到红球的概率P＝，故选：A．【点评】本题考查了概率公式，掌握P（摸到红球的概率）＝红球可能出现的结果数÷所有可能出现的结果数是解题的关键．5．（4分）下列计算正确的是（）A．（a2+ab）÷a＝a+b B．a2•a＝a2C．（a+b）2＝a2+b2D．（a3）2＝a5【分析】根据多项式除以单项式判断A选项；根据同底数幂的乘法判断B选项；根据完全平方公式判断C选项；根据幂的乘方判断D选项．【解答】解：A选项，原式＝a2÷a+ab÷a＝a+b，故该选项符合题意；B选项，原式＝a3，故该选项不符合题意；C选项，原式＝a2+2ab+b2，故该选项不符合题意；D选项，原式＝a6，故该选项不符合题意；故选：A．【点评】本题考查了整式的除法，同底数幂的乘法，幂的乘方与积的乘方，完全平方公式，掌握（a+b）2＝a2+2ab+b2是解题的关键．6．（4分）如图，把一块三角板ABC的直角顶点B放在直线EF上，∠C＝30°，AC∥EF，则∠1＝（）A．30°B．45°C．60°D．75°【分析】根据平行线的性质，可以得到∠CBF的度数，再根据∠ABC＝90°，可以得到∠1的度数．【解答】解：∵AC∥EF，∠C＝30°，∴∠C＝∠CBF＝30°，∵∠ABC＝90°，∴∠1＝180°﹣∠ABC﹣∠CBF＝180°﹣90°﹣30°＝60°，故选：C．【点评】本题考查直角三角形的性质、平行线的性质，解答本题的关键是明确题意，利用平行线的性质解答．7．（4分）已知抛物线y＝x2+mx的对称轴为直线x＝2，则关于x的方程x2+mx＝5的根是（）A．0，4B．1，5C．1，﹣5D．﹣1，5【分析】根据抛物线y＝x2+mx的对称轴为直线x＝2，可以得到m的值，然后解方程即可．【解答】解：∵抛物线y＝x2+mx的对称轴为直线x＝2，∴﹣＝2，解得m＝﹣4，∴方程x2+mx＝5可以写成x2﹣4x＝5，∴x2﹣4x﹣5＝0，∴（x﹣5）（x+1）＝0，解得x1＝5，x2＝﹣1，故选：D．【点评】本题考查二次函数的性质、解一元二次方程，解答本题的关键是明确题意，求出m的值．8．（4分）如图，在平行四边形ABCD中，AD＝2AB＝2，∠ABC＝60°，E，F是对角线BD上的动点，且BE＝DF，M，N分别是边AD，边BC上的动点．下列四种说法：①存在无数个平行四边形MENF；②存在无数个矩形MENF；③存在无数个菱形MENF；④存在无数个正方形MENF．其中正确的个数是（）A．1B．2C．3D．4【分析】根据题意作出合适的辅助线，然后逐一分析即可．【解答】解：连接AC，MN，且令AC，MN，BD相交于点O，∵四边形ABCD是平行四边形，∴OA＝OC，OB＝OD，∵BE＝DF，∴OE＝OF，只要OM＝ON，那么四边形MENF就是平行四边形，∵点E，F是BD上的动点，∴存在无数个平行四边形MENF，故①正确；只要MN＝EF，OM＝ON，则四边形MENF是矩形，∵点E，F是BD上的动点，∴存在无数个矩形MENF，故②正确；只要MN⊥EF，OM＝ON，则四边形MENF是菱形，∵点E，F是BD上的动点，∴存在无数个菱形MENF，故③正确；只要MN＝EF，MN⊥EF，OM＝ON，则四边形MENF是正方形，而符合要求的正方形只有一个，故④错误；故选：C．【点评】本题考查正方形的判定、菱形的判定、矩形的判定、平行四边形的判定，解答本题的关键是明确题意，作出合适的辅助线．9．（4分）已知（x1，y1），（x2，y2），（x3，y3）为直线y＝﹣2x+3上的三个点，且x1＜x2＜x3，则以下判断正确的是（）A．若x1x2＞0，则y1y3＞0B．若x1x3＜0，则y1y2＞0C．若x2x3＞0，则y1y3＞0D．若x2x3＜0，则y1y2＞0【分析】根据一次函数的性质和各个选项中的条件，可以判断是否正确，从而可以解答本题．【解答】解：∵直线y＝﹣2x+3，∴y随x的增大而减小，当y＝0时，x＝1.5，∵（x1，y1），（x2，y2），（x3，y3）为直线y＝﹣2x+3上的三个点，且x1＜x2＜x3，∴若x1x2＞0，则x1，x2同号，但不能确定y1y3的正负，故选项A不符合题意；若x1x3＜0，则x1，x3异号，但不能确定y1y2的正负，故选项B不符合题意；若x2x3＞0，则x2，x3同号，但不能确定y1y3的正负，故选项C不符合题意；若x2x3＜0，则x2，x3异号，则x1，x2同时为负，故y1，y2同时为正，故y1y2＞0，故选项D符合题意；故选：D．【点评】本题考查一次函数图象上点的坐标特征，解答本题的关键是明确题意，利用一次函数的性质解答．10．（4分）将一张以AB为边的矩形纸片，先沿一条直线剪掉一个直角三角形，在剩下的纸片中，再沿一条直线剪掉一个直角三角形（剪掉的两个直角三角形相似），剩下的是如图所示的四边形纸片ABCD，其中∠A＝90°，AB＝9，BC＝7，CD＝6，AD＝2，则剪掉的两个直角三角形的斜边长不可能是（）A．B．C．10D．【分析】根据题意，画出相应的图形，然后利用相似三角形的性质和分类讨论的方法，求出剪掉的两个直角三角形的斜边长，然后即可判断哪个选项符合题意．【解答】解：如右图1所示，由已知可得，△DFE∽△ECB，则，设DF＝x，CE＝y，则，解得，∴DE＝CD+CE＝6+＝，故选项B不符合题意；EB＝DF+AD＝+2＝，故选项D不符合题意；如图2所示，由已知可得，△DCF∽△FEB，则，设FC＝m，FD＝n，则，解得，∴FD＝10，故选项C不符合题意；BF＝FC+BC＝8+6＝14，故选：A．【点评】本题考查相似三角形的性质、矩形的性质，解答本题的关键是明确题意，利用分类讨论的方法解答．二、填空题（本大题有6小题，每小题5分，共30分）11．（5分）分解因式：x2+x＝x（x+1）．【分析】直接提取公因式x，进而分解因式得出即可．【解答】解：x2+x＝x（x+1）．故答案为：x（x+1）．【点评】此题主要考查了提取公因式分解因式，正确提取公因式是解题关键．12．（5分）关于x的不等式3x﹣2＞x的解集是x＞1．【分析】根据解一元一次不等式步骤即可解得答案．【解答】解：∵3x﹣2＞x，∴3x﹣x＞2，即2x＞2，解得x＞1，故答案为：x＞1．【点评】本题考查解一元一次不等式，解题的关键是掌握解一元一次不等式的基本步骤．13．（5分）元朝朱世杰的《算学启蒙》一书记载：“良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何追及之．”其题意为：“良马每天行240里，劣马每天行150里，劣马先行12天，良马要几天追上劣马？”答：良马追上劣马需要的天数是20．【分析】设良马x天追上劣马，根据良马追上劣马所走路程相同可得：240x＝150（x+12），即可解得良马20天追上劣马．【解答】解：设良马x天追上劣马，根据题意得：240x＝150（x+12），解得x＝20，答：良马20天追上劣马；故答案为：20．【点评】本题考查一元一次方程的应用，解题的关键是读懂题意，找到等量关系列出方程．14．（5分）如图，在△ABC中，∠ABC＝40°，∠BAC＝80°，以点A为圆心，AC长为半径作弧，交射线BA于点D，连结CD，则∠BCD的度数是10°或100°．【分析】分两种情况画图，由作图可知得AC＝AD，根据等腰三角形的性质和三角形内角和定理解答即可．【解答】解：如图，点D即为所求；在△ABC中，∠ABC＝40°，∠BAC＝80°，∴∠ACB＝180°﹣40°﹣80°＝60°，由作图可知：AC＝AD，∴∠ACD＝∠ADC＝（180°﹣80°）＝50°，∴∠BCD＝∠ACB﹣∠ACD＝60°﹣50°＝10°；由作图可知：AC＝AD′，∴∠ACD′＝∠AD′C，∵∠ACD′+∠AD′C＝∠BAC＝80°，∴∠AD′C＝40°，∴∠BCD′＝180°﹣∠ABC﹣∠AD′C＝180°﹣40°﹣40°＝100°．综上所述：∠BCD的度数是10°或100°．故答案为：10°或100°．【点评】本题考查了作图﹣基本作图，三角形内角和定理，等腰三角形的判定与性质，解决本题的关键是掌握基本作图方法．15．（5分）如图，在平面直角坐标系xOy中，点A（0，4），B（3，4），将△ABO向右平移到△CDE位置，A的对应点是C，O的对应点是E，函数y＝（k≠0）的图象经过点C 和DE的中点F，则k的值是6．【分析】根据反比例函数k的几何意义构造出矩形，利用方程思想解答即可．【解答】解：过点F作FG⊥x轴，DQ⊥x轴，FH⊥y轴，根据题意可知，AC＝OE＝BD，设AC＝OE＝BD＝a，∴四边形ACEO的面积为4a，∵F为DE的中点，FG⊥x轴，DQ⊥x轴，∴FG为△EDQ的中位线，∴FG＝DQ＝2，EG＝EQ＝，∴四边形HFGO的面积为2（a+），∴k＝4a＝2（a+），解得：a＝，∴k＝6．故答案为：6．【点评】本题主要考查了反比例函数中k的几何意义，正确作出辅助线构造出矩形是解决本题的关键．16．（5分）如图，AB＝10，点C是射线BQ上的动点，连结AC，作CD⊥AC，CD＝AC，动点E在AB延长线上，tan∠QBE＝3，连结CE，DE，当CE＝DE，CE⊥DE时，BE的长是5或．【分析】如图，过点C作CT⊥AE于点T，过点D作DJ⊥CT交CT的延长线于点J，连接EJ．由tan∠CBT＝3＝，可以假设BT＝k，CT＝3k，证明△ATC≌△CJD（AAS），推出DJ＝CT＝3k，AT＝CJ＝10+k，再利用勾股定理，构建方程求解即可．【解答】解：如图，过点C作CT⊥AE于点T，过点D作DJ⊥CT交CT的延长线于点J，连接EJ．∵tan∠CBT＝3＝，∴可以假设BT＝k，CT＝3k，∵∠CAT+∠ACT＝90°，∠ACT+∠JCD＝90°，∴∠CAT＝∠JCD，在△ATC和△CJD中，，∴△ATC≌△CJD（AAS），∴DJ＝CT＝3k，AT＝CJ＝10+k，∵∠CJD＝∠CED＝90°，∴C，E，D，J四点共圆，∵EC＝DE，∴∠CJE＝∠DJE＝45°，∴ET＝TJ＝10﹣2k，∵CE2＝CT2+TE2＝（CD）2，∴（3k）2+（10﹣2k）2＝[•]2，整理得4k2﹣25k+25＝0，∴（k﹣5）（4k﹣5）＝0，∴k＝5和，∴BE＝BT+ET＝k+10﹣2k＝10﹣k＝5或，故答案为：5或．【点评】本题考查全等三角形的判定和性质，四点共圆，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．三、解答题（本大题有8小题，第17～20小题每小题8分，第21小题10分，第22，23小题每小题8分，第24小题14分，共80分．解答需写出必要的文字说明、演算步骤或证明过程）17．（8分）（1）计算：6tan30°+（π+1）0﹣．（2）解方程组：．【分析】（1）根据特殊角的三角函数值，实数的运算，零指数幂，二次根式的性质与化简进行计算即可；（2）根据加减法解二元一次方程组即可．【解答】解：（1）原式＝6×+1﹣2＝＝1；（2），①+②得：3x＝6，解得x＝2，把x＝2代入②，得：y＝0，∴原方程组的解是．【点评】本题考查了特殊角的三角函数值，实数的运算，零指数幂，二次根式的性质与化简，解二元一次方程组，解决本题的关键是掌握以上知识熟练运算．18．（8分）双减政策实施后，学校为了解八年级学生每日完成书面作业所需时长x（单位：小时）的情况，在全校范围内随机抽取了八年级若干名学生进行调查，并将所收集的数据分组整理，绘制了如下两幅不完整的统计图表，请根据图表信息解答下列问题．八年级学生每日完成书面作业所需时长情况的统计表组别所需时长（小时）学生人数（人）A0＜x≤0.515B0.5＜x≤1mC1＜x≤1.5nD 1.5＜x≤25（1）求统计表中m，n的值．（2）已知该校八年级学生有800人，试估计该校八年级学生中每日完成书面作业所需时长满足0.5＜x≤1.5的共有多少人．【分析】（1）先求出被调查总人数，再根据扇形统计图求出m，用总人数减去A、B、D 的人数，即可得n的值；（2）用被调查情况估计八年级800人的情况，即可得到答案．【解答】解：（1）被调查总人数：15÷15%＝100（人），∴m＝100×60%＝60（人），n＝100﹣15﹣60﹣5＝20（人），答：m为60，n为20；（2）∵当0.5＜x≤1.5时，在被调查的100人中有60+20＝80（人），∴在该校八年级学生800人中，每日完成书面作业所需时长满足0.5＜x≤1.5的共有800×＝640（人），答：估计共有640人．【点评】本题考查统计图和统计表，解题的关键是掌握从图表中寻找“完整信息”从而求出被调查的总数．19．（8分）一个深为6米的水池积存着少量水，现在打开水阀进水，下表记录了2小时内5个时刻的水位高度，其中x表示进水用时（单位：小时），y表示水位高度（单位：米）．x00.51 1.52y1 1.52 2.53为了描述水池水位高度与进水用时的关系，现有以下三种函数模型供选择：y＝kx+b（k ≠0），y＝ax2+bx+c（a≠0），y＝（k≠0）．（1）在平面直角坐标系中描出表中数据对应的点，再选出最符合实际的函数模型，求出相应的函数表达式，并画出这个函数的图象．（2）当水位高度达到5米时，求进水用时x．【分析】（1）根据表格数对画出函数图象即可；然后利用待定系数法即可求出相应的函数表达式；（2）结合（1）的函数表达式，代入值即可解决问题．【解答】解：（1）函数的图象如图所示：根据图象可知：选择函数y＝kx+b，将（0，1），（1，2）代入，得解得∴函数表达式为：y＝x+1（0≤x≤5）；（2）当y＝5时，x+1＝5，∴x＝4．答：当水位高度达到5米时，进水用时x为4小时．【点评】本题考查了一次函数的应用，解决本题的关键是掌握一次函数的图象和性质．20．（8分）圭表（如图1）是我国古代一种通过测量正午日影长度来推定节气的天文仪器，它包括一根直立的标竿（称为“表”）和一把呈南北方向水平固定摆放的与标竿垂直的长尺（称为“圭”），当正午太阳照射在表上时，日影便会投影在圭面上，圭面上日影长度最长的那一天定为冬至，日影长度最短的那一天定为夏至．图2是一个根据某市地理位置设计的圭表平面示意图，表AC垂直圭BC，已知该市冬至正午太阳高度角（即∠ABC）为37°，夏至正午太阳高度角（即∠ADC）为84°，圭面上冬至线与夏至线之间的距离（即DB的长）为4米．（1）求∠BAD的度数．（2）求表AC的长（最后结果精确到0.1米）．（参考数据：sin37°≈，cos37°≈，tan37°≈，tan84°≈）【分析】（1）根据三角形的外角等于与它不相邻两个内角的和解答即可；（2）分别求出∠ADC和∠ABC的正切值，用AC表示出CD和CB，得到一个只含有AC 的关系式，再解答即可．【解答】解：（1）∵∠ADC＝84°，∠ABC＝37°，∴∠BAD＝∠ADC﹣∠ABC＝47°，答：∠BAD的度数是47°．（2）在Rt△ABC中，，∴．在Rt△ADC中，，∵BD＝4，∴，∴，∴AC≈3.3（米），答：表AC的长是3.3米．【点评】本题主要考查了三角形外角的性质和三角函数，熟练掌握建模思想是解决本题的关键．21．（10分）如图，半径为6的⊙O与Rt△ABC的边AB相切于点A，交边BC于点C，D，∠B＝90°，连结OD，AD．（1）若∠ACB＝20°，求的长（结果保留π）．（2）求证：AD平分∠BDO．【分析】（1）连结OA，由∠ACB＝20°，得∠AOD＝40°，由弧长公式即得的长为；（2）根据AB切⊙O于点A，∠B＝90°，可得OA∥BC，有∠OAD＝∠ADB，而OA＝OD，即可得∠ADB＝∠ODA，从而AD平分∠BDO．【解答】（1）解：连结OA，如图：∵∠ACB＝20°，∴∠AOD＝40°，∴＝＝；（2）证明：∵OA＝OD，∴∠OAD＝∠ODA，∵AB切⊙O于点A，∴OA⊥AB，∵∠B＝90°，∴OA∥BC，∴∠OAD＝∠ADB，∴∠ADB＝∠ODA，∴AD平分∠BDO．【点评】本题考查与圆有关的计算及圆的性质，解题的关键是掌握弧长公式及圆的切线的性质．22．（12分）如图，在△ABC中，∠ABC＝40°，∠ACB＝90°，AE平分∠BAC交BC于点E．P是边BC上的动点（不与B，C重合），连结AP，将△APC沿AP翻折得△APD，连结DC，记∠BCD＝α．（1）如图，当P与E重合时，求α的度数．（2）当P与E不重合时，记∠BAD＝β，探究α与β的数量关系．【分析】（1）由∠B＝40°，∠ACB＝90°，得∠BAC＝50°，根据AE平分∠BAC，P 与E重合，即得∠ACD＝∠ADC＝65°，从而α＝∠ACB﹣∠ACD＝25°；（2）分两种情况：①当点P在线段BE上时，可得∠ADC＝∠ACD＝90°﹣α，根据∠ADC+∠BAD＝∠B+∠BCD，即可得2α﹣β＝50°；②当点P在线段CE上时，延长AD 交BC于点F，由∠ADC＝∠ACD＝90°﹣α，又∠ADC＝∠AFC+∠BCD，∠AFC＝∠ABC+∠BAD可得90°﹣α＝40°+α+β，2α+β＝50°．【解答】解：（1）∵∠B＝40°，∠ACB＝90°，∴∠BAC＝50°，∵AE平分∠BAC，P与E重合，∴D在AB边上，AC＝AD，∴∠ACD＝∠ADC＝（180°﹣∠BAC）÷2＝65°，∴α＝∠ACB﹣∠ACD＝25°；答：α的度数为25°；（2）①当点P在线段BE上时，如图：∵将△APC沿AP翻折得△APD，∴AC＝AD，∵∠BCD＝α，∠ACB＝90°，∴∠ADC＝∠ACD＝90°﹣α，又∵∠ADC+∠BAD＝∠B+∠BCD，∠BAD＝β，∠B＝40°，∴（90°﹣α）+β＝40°+α，∴2α﹣β＝50°，②如图2，当点P在线段CE上时，延长AD交BC于点F，如图：∵将△APC沿AP翻折得△APD，∴AC＝AD，∵∠BCD＝α，∠ACB＝90°，∴∠ADC＝∠ACD＝90°﹣α，又∵∠ADC＝∠AFC+∠BCD，∠AFC＝∠ABC+∠BAD，∴∠ADC＝∠ABC+∠BAD+∠BCD＝40°+β+α，∴90°﹣α＝40°+α+β，∴2α+β＝50°；综上所述，当点P在线段BE上时，2α﹣β＝50°；当点P在线段CE上时，2α+β＝50°．【点评】本题考查三角形综合应用，涉及轴对称变换，三角形外角等于不相邻的两个内角的和的应用，解题的关键是掌握轴对称的性质，能熟练运用三角形内角和定理．23．（12分）已知函数y＝﹣x2+bx+c（b，c为常数）的图象经过点（0，﹣3），（﹣6，﹣3）．（1）求b，c的值．（2）当﹣4≤x≤0时，求y的最大值．（3）当m≤x≤0时，若y的最大值与最小值之和为2，求m的值．【分析】（1）将图象经过的两个点的坐标代入二次函数解析式解答即可；（2）根据x的取值范围，二次函数图象的开口方向和对称轴，结合二次函数的性质判定y的最大值即可；（3）根据对称轴为x＝﹣3，结合二次函数图象的性质，分类讨论得出m的取值范围即可．【解答】解：（1）把（0，﹣3），（﹣6，﹣3）代入y＝﹣x2+bx+c，得b＝﹣6，c＝﹣3．（2）∵y＝﹣x2﹣6x﹣3＝﹣（x+3）2+6，又∵﹣4≤x≤0，∴当x＝﹣3时，y有最大值为6．（3）①当﹣3＜m≤0时，当x＝0时，y有最小值为﹣3，当x＝m时，y有最大值为﹣m2﹣6m﹣3，∴﹣m2﹣6m﹣3+（﹣3）＝2，∴m＝﹣2或m＝﹣4（舍去）．②当m≤﹣3时，当x＝﹣3时y有最大值为6，∵y的最大值与最小值之和为2，∴y最小值为﹣4，∴﹣（m+3）2+6＝﹣4，∴m＝或m＝（舍去）．综上所述，m＝﹣2或．【点评】此题主要考查了待定系数法求二次函数解析式以及二次函数的性质等知识，正确分类讨论得出m的取值范围是解题关键．24．（14分）如图，在矩形ABCD中，AB＝6，BC＝8，动点E从点A出发，沿边AD，DC向点C运动，A，D关于直线BE的对称点分别为M，N，连结MN．（1）如图，当E在边AD上且DE＝2时，求∠AEM的度数．（2）当N在BC延长线上时，求DE的长，并判断直线MN与直线BD的位置关系，说明理由．（3）当直线MN恰好经过点C时，求DE的长．【分析】（1）由DE＝2知，AE＝AB＝6，可知∠AEB＝∠MEB＝45°，从而得出答案；（2）根据对称性得，∠ENC＝∠BDC，则cos∠ENC＝，得EN＝，利用HL 证明Rt△BMN≌Rt△DCB，得∠DBC＝∠BNM，则MN∥BD；（3）当E在边AD上时，若直线MN过点C，利用AAS证明△BCM≌△CED，得DE＝MC，当点E在边CD上时，利用△BMC∽△CNE，则，从而解决问题．【解答】解：（1）∵DE＝2，∴AE＝AB＝6，∵四边形ABCD是矩形，∴∠A＝90°，∴∠AEB＝∠ABE＝45°．由对称性知∠BEM＝45°，∴∠AEM＝90°．（2）如图2，∵AB＝6，AD＝8，∴BD＝10，∵当N落在BC延长线上时，BN＝BD＝10，∴CN＝2．由对称性得，∠ENC＝∠BDC，∴cos∠ENC＝，得EN＝，∴DE＝EN＝．∵BM＝AB＝CD，MN＝AD＝BC，∴Rt△BMN≌Rt△DCB（HL），∴∠DBC＝∠BNM，∴MN∥BD．（3）如图3，当E在边AD上时，∴∠BMC＝90°，∴MC＝．∵BM＝AB＝CD，∠DEC＝∠BCE，∴△BCM≌△CED（AAS），∴DE＝MC＝．如图4，点E在边CD上时，∵BM＝6，BC＝8，∴MC＝，CN＝8﹣．∵∠BMC＝∠CNE＝∠BCD＝90°，∴△BMC∽△CNE，∴，∴EN＝，∴DE＝EN＝．综上所述，DE的长为或．【点评】本题是四边形综合题，主要考查了矩形的性质，轴对称的性质，全等三角形的判定与性质，相似三角形的判定与性质，三角函数等知识，根据题意画出图形，并运用分类讨论思想是解题的关键．。
2020年浙江省绍兴市中考化学试卷及答案
2020年浙江省绍兴市中考化学试卷及答案一、选择题（本题共5小题，每小题4分，共20分。
下列各小题只有一个选项符合题意）1．（4分）下列实验操作正确的是（）A．读取液体体积B．闻气味C．测定溶液pH D．稀释浓硫酸2．（4分）科学研究常采用转换、模型、分类和控制变量等研究方法，下列采用转换的是（）A．模拟月相的形成B．探究种子萌发的部分条件C．纯净物的类别D．测量木块受到的摩擦力3．（4分）与图示微观变化相符的化学反应是（）A．2CO+O22CO2B．H2+CuO H2O+CuC．2H2+O22H2O D．H2CO3H2O+CO2↑4．（4分）下列实验中，能证明燃烧需要氧气的是（）A．B．C．D．5．（4分）兴趣小组按如图流程进行实验（每步均充分反应），反应结束后，将烧杯内物质进行过滤，向滤渣中加入少量稀盐酸，无明显现象，下列说法不正确的是（）A．由实验可判断出铁、铜、锌的活动性顺序B．两支试管混合后，固体总质量一定增加C．滤渣中一定有Cu，一定没有Fe和ZnD．滤液中的溶质一定有FeCl2、ZnCl2和CuCl2二、填空题（本题共2小题，每空2分，共12分）6．（6分）如图是实验室制取、收集、检验气体的常用装置。
（1）图甲中，在试管口放棉花的目的是；用图示方法收集氧气的理由是。
（2）用图乙装置制取并检验CO2性质时，澄清石灰水始终未见浑浊，原因可能是。
7．（6分）下表是A、B、C三种固体物质在不同温度下（t1＜t2＜t3）的溶解度，请回答：温度（℃）t1t2t336.036.237.3物质A（克）物质B31.636.2110.1（克）0.1650.1350.076物质C（克）（1）℃时，A、B两种物质的溶解度相同。
（2）t3℃时，分别取等量的B、C饱和溶液于试管甲、乙中（如图），将试管放入盛有水的烧杯中，向烧杯中加入一定量硝酸铵（不考虑试管中水的变化），有固体析出的试管为（选填“甲”或“乙”）。
历年浙江省绍兴市中考数学试卷(含答案)
2017 年浙江省绍兴市中考数学试卷一、选择题（本大题共 10 小题，每小题 4 分，共 40 分。
请选出每小题中一个 最符合题意的选项，不选、多选、错选，均不给分） 1．（4分）﹣5 的相反数是（ ）B ．5C ．﹣D ．﹣5 2．（4 分）研究表明，可燃冰是一种替代石油的新型清洁能源，在我国某海域已 探明的可燃冰存储量达 150000000000立方米，其中数字 150000000000 用科学 记数法可表示为（ ）A ．15×1010B ．0.15×1012C ． 1.5× 1011D ．1.5×10123．（4 分）如图的几何体由五个相同的小正方体搭成，它的主视图是（ ）4．（4分）在一个不透明的袋子中装有 4个红球和 3 个黑球，它们除颜色外其他 均相同，从中任意摸出一个球，则摸出黑球的概率是（ ） A ． B ． C ． D ．5．（4 分）下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平 均数和方差： 甲乙 丙 丁 平均数（环） 9.149.15 9.14 9.15 方差6.6 6.8 6.7 6.6 根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（）A ． A ．A．甲B．乙C．丙D．丁6．（4 分）如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7 米，顶端距离地面 2.4 米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面 2 米，则小巷的宽度为（）A．0.7米B．1.5米C．2.2米D．2.4 米7．（4 分）均匀地向一个容器注水，最后把容器注满，在注水过程中，水面高度h 随时间t 的变化规律如图所示（图中OABC 为折线），这个容器的形状可以是）D8．（4分）在探索“尺规三等分角”这个数学名题的过程中，曾利用了如图．该图中，四边形ABCD是矩形，E是BA延长线上一点，F是CE上一点，∠ACF=∠AFC，∠FAE=∠FEA．若∠ ACB=2°1，则∠ ECD的度数是（）A．7° B．21°C．23°D．24°9．（4 分）矩形ABCD的两条对称轴为坐标轴，点 A 的坐标为（2，1）．一张透明纸上画有一个点和一条抛物线，平移透明纸，使这个点与点A重合，此时抛物线的函数表达式为y=x2，再次平移透明纸，使这个点与点 C 重合，则该抛物线的函数表达式变为（）A．y=x2+8x+14 B．y=x2﹣8x+14 C．y=x2+4x+3 D．y=x2﹣4x+310．（ 4 分）一块竹条编织物，先将其按如图MN 翻转180°，再将它所示绕直线按逆时针方向旋转90°，所得的竹条编织物是（）二、填空题（本大题共 6 小题，每小题5分，共30 分）11．（ 5 分）分解因式：x2y﹣y= ．12．（5 分）如图，一块含45°角的直角三角板，它的一个锐角顶点A 在⊙O上，边AB，AC分别与⊙ O交于点D，E，则∠ DOE的度数为．13．（5 分）如图，Rt△ABC的两个锐角顶点A，B 在函数y=（x>0）的图象上，AC∥x轴，AC=2，若点A的坐标为（2，2），则点B的坐标为．14．（5 分）如图为某城市部分街道示意图，四边形ABCD为正方形，点G 在对角线BD上，GE⊥CD，GF⊥BC，AD=1500m，小敏行走的路线为B→A→G→E，小聪行走的路线为B→ A→ D→ E→F．若小敏行走的路程为3100m，则小聪行走的路程为m．15．（5分）以Rt△ABC的锐角顶点A为圆心，适当长为半径作弧，与边AB，AC 各相交于一点，再分别以这两个交点为圆心，适当长为半径作弧，过两弧的交点与点A作直线，与边BC交于点D．若∠ ADB=6°0 ，点D到AC的距离为2，则AB 的长为．16．（5 分）如图，∠ AOB=45°，点M，N 在边OA上，OM=x，ON=x+4，点P 是边OB上的点，若使点P，M，N 构成等腰三角形的点P 恰好有三个，则x 的值是．三、解答题（本大题共8小题，第17-20小题每小题8分，第21题10分，第22,23小题每小题8分，第24小题14分，共80分，解答需写出必要的文字说明、演算步骤或证明过程）17．（8分）（1）计算：（2 ﹣π）0+|4﹣3 | ﹣．（2）解不等式：4x+5≤2（x+1）18．（8 分）某市规定了每月用水18 立方米以内（含18 立方米）和用水18 立方米以上两种不同的收费标准，该市的用户每月应交水费y（元）是用水量x（立方米）的函数，其图象如图所示．（1）若某月用水量为18 立方米，则应交水费多少元？（2）求当x>18时，y关于x的函数表达式，若小敏家某月交水费81元，则这个月用水量为多少立方米？19．（8 分）为了解本校七年级同学在双休日参加体育锻炼的时间，课题小组进行了问卷调查（问卷调查表如图所示），并用调查结果绘制了图1，图 2 两幅统计图（均不完整），请根据统计图解答以下问题：（1）本次接受问卷调查的同学有多少人？补全条形统计图．（2）本校有七年级同学800人，估计双休日参加体育锻炼时间在 3 小时以内（不含 3 小时）的人数．20．（8 分）如图，学校的实验楼对面是一幢教学楼，小敏在实验楼的窗口 C 测得教学楼顶部 D 的仰角为18°，教学楼底部B的俯角为20°，量得实验楼与教学楼之间的距离AB=30m．（1）求∠ BCD的度数．（2）求教学楼的高BD．（结果精确到0.1m，参考数据：tan20 °≈0.36，tan1821．（10 分）某农场拟建一间矩形种牛饲养室，饲养室的一面靠现有墙（墙足够长），已知计划中的建筑材料可建围墙的总长为50m．设饲养室长为x（m），占地面积为y（m2）．（1）如图1，问饲养室长x 为多少时，占地面积y 最大？（2）如图2，现要求在图中所示位置留2m 宽的门，且仍使饲养室的占地面积最大，小敏说：“只要饲养室长比（1）中的长多2m 就行了．”请你通过计算，判断小敏的说法是否正确．22．（12 分）定义：有一组邻边相等，并且它们的夹角是直角的凸四边形叫做等腰直角四边形．（1）如图1，等腰直角四边形ABCD，AB=BC，∠ ABC=9°0，①若AB=CD=1，AB∥CD，求对角线BD 的长．②若AC⊥BD，求证：AD=CD，（2）如图2，在矩形ABCD中，AB=5，BC=9，点P 是对角线BD上一点，且BP=2PD，过点P 作直线分别交边AD，BC于点E，F，使四边形ABFE是等腰直角四边形，求AE 的长．23．（12 分）已知△ ABC，AB=AC，D 为直线BC上一点，E为直线AC 上一点，AD=AE，设∠ BAD=α，∠ CDE=β．（1）如图，若点D在线段BC上，点E在线段AC上．①如果∠ ABC=6°0，∠ ADE=7°0，那么α=°，β= °，②求α，β之间的关系式．（2）是否存在不同于以上②中的α，β之间的关系式？若存在，求出这个关系式（求出一个即可）；若不存在，说明理由．24．（14分）如图1，已知?ABCD，AB∥x轴，AB=6，点A的坐标为（1，﹣4），点 D 的坐标为（﹣3，4），点 B 在第四象限，点P 是?ABCD边上的一个动点．（1）若点P 在边BC上，PD=CD，求点P 的坐标．（2）若点P在边AB，AD上，点P关于坐标轴对称的点Q落在直线y=x﹣1 上，求点P 的坐标．（3）若点P在边AB，AD，CD上，点G是AD与y 轴的交点，如图2，过点P 作y轴的平行线PM，过点G作x 轴的平行线GM，它们相交于点M，将△ PGM 沿直线PG翻折，当点M 的对应点落在坐标轴上时，求点P 的坐标．（直接写出2017 年浙江省绍兴市中考数学试卷参考答案与试题解析一、选择题（本大题共10 小题，每小题 4 分，共40 分。
2021年浙江省绍兴市中考道德与法治真题试卷(含答案)
2021年浙江省绍兴市中考道德与法治真题试卷（含答案）一、单项选择题（本大题共10小题，共20.0分）1.2020年11月，由“杂交水稻之父”团队研发的杂交水稻双季亩产突破1500公斤大关。
（）A. 南仁东B. 孙家栋C. 袁隆平D. 屠呦呦2.2021年1月，中共中央印发《建设规划（2020-2025年）》，这是新中国成立以来第一个关于该主题的专门规划。
（）A. 法治中国B. 创新中国C. 美丽中国D. 和谐中国3.2021年3月，新华社受权播发了十三届全国人大四次会议批准的《中华人民共和国国民经济和社会发展第个五年规划和2035年远景目标纲要》。
（）A. 十二B. 十三C. 十四D. 十五4.读图可知，绍兴市（）①人口总数不断增长②人口素质稳步提升③教育事业取得成效④老龄化的进程加速A. ①②B. ①④C. ②③D. ③④5.疫情期间，某退休干部面对防控执勤人员的管理，情绪失控，蛮横辱骂，拒不遵守防疫规定，造成不良影响，被行政拘留5日。
该事例告诉我们（）①要学会合理调节情绪②法律面前人人平等③犯罪行为要受到刑罚处罚④言行须有度，违法必担责A. ①②③B. ①②④C. ①③④D. ②③④6.绍兴市某禁毒教育体验馆通过设定一个缉毒游戏，综合视觉、听觉、触觉上的体验，引导青少年熟知毒品危害、识别易涉毒场所、了解禁毒法律法规。
这有助于青少年（）A. 防微杜渐，尽量避免交友B. 依法自律，谨防吸毒过量C. 履行义务，共筑司法保护D. 认清危害，自觉远离毒品7.习近平说：“立宪和修宪在任何一个国家都是最为重要的政治活动和立法活动。
”这是因为宪法是（）①国家的根本法②国家法制统一的基础③一切法律的总和④一切组织和个人的根本活动准则A. ①②③B. ①②④C. ①③④D. ②③④8.2021年3月30日，第十三届全国人大常委会第二十七次会议以全票表决通过了修订后的香港基本法附件一和附件二，以确保“爱国者治港”的主旨和原则。
2020年浙江省绍兴市中考语文试卷(含答案解析)
2020年浙江省绍兴市中考语文试卷副标题1.阅读下面文字，按要求完成下列题目。
近年南行的次数越来越多。
愈发喜欢看莺飞草长．（A．cháng B．zhǎng）、月笼烟雨，看高涨的如欢呼般的莲叶，看富ráo的阳光、被照亮的事物及其纹理；喜欢临一大面湖水，看波光浩miǎo、菖蒲丰茂，心里即有飞鸟的喜悦；喜欢那加了糖的空气，香樟、桂花、栀子、茉莉，那份免费mì饯给人以幸福感，让你唇齿生津，让你觉得世间一切悲苦皆可忍受。
（节选自王开岭《南方，南方》）根据拼音写出相应的汉字。
①富（ráo）______②浩（miǎo）______③（mì）______ 饯给语段中加点字“长”选择正确的读音。
______A．cháng B．zhǎng2.根据语境，选出用词搭配最恰当的一项（）2020年春，突如其来的“新冠”疫情打破了人们的生活常态，也检测出了商人的①_____，专家的②_____，媒体的素养，医者的操守，民众的认知，以及干部的③_____。
A. ①水平②良知③能力和状态B. ①良知②水平③能力和状态C. ①能力和状态②良知③水平3.请在下面横线处填上合适的古诗文名句。
生活是诗。
漫步早春的钱塘湖边，闻鸟语嘤嘤，白居易写下“几处早莺争暖树，______”；听蛙声喧闹，感夏夜闲情，赵师秀吟出“______，青草池塘处处蛙”；览山林美景，享秋野静谧，王绩提笔“树树皆秋色，______”；观瀚海飘雪，叹塞外奇寒，岑参挥毫“______，千树万树梨花开”。
诗是生活。
“新冠”来袭，使命召唤，正所谓“______”，多少人胸怀“______，______”的抱负，满怀“______，______”的信心与决心，舍家为国，共克疫情。
（分别用孟子《生于忧患，死于安乐》、范仲淹《岳阳楼记》、李白《行路难》中的句子填空。
）4.名著阅读。
《水浒传》中有很多与“酒”有关的故事，请仔细阅读下表，完成探究任务。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2016年绍兴市初中毕业生学业考试
数 学
卷I （选择题）
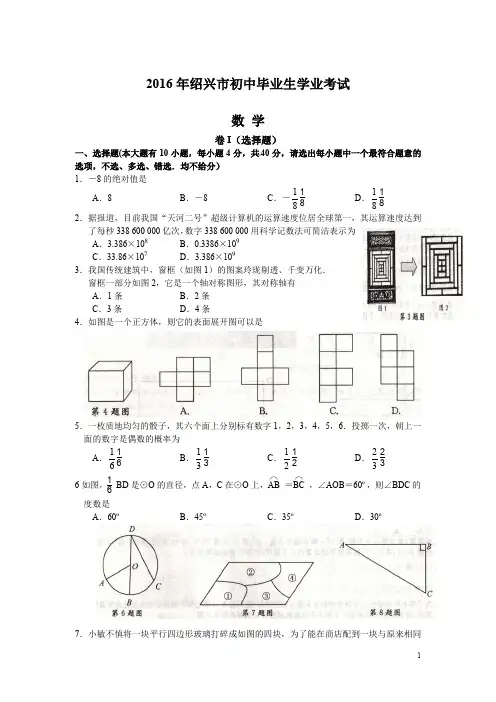
一、选择题(本大题有10小题，每小题4分，共40分，请选出每小题中一个最符合题意的选项，不选、多选、错选．均不给分） 1．－8的绝对值是
A ．8
B ．－8
C 18
18 D 18
1
8 2了每秒338 600 000亿次，数字338 600 000用科学记数法可简洁表示为 A ．3.386×108 B ．0.3386×109 C ．33.86×107 D ．3.386×109
3．我国传统建筑中，窗框（如图1）的图案玲珑剔透、千变万化． 窗框一部分如图2，它是一个轴对称图形，其对称轴有 A ．1条 B ．2条 C ．3条 D ．4条
4．如图是一个正方体，则它的表面展开图可以是
5．一枚质地均匀的骰子，其六个面上分别标有数字1，2，3，4，5，6．投掷一次，朝上一面的数字是偶数的概率为
A ．
16
16 B 13
1
3 C 12
1
2 D 23
2
3 6如图，1
6 BD 是⊙O 的直径，点A ，C 在⊙O 上，⌒AB ＝⌒BC ，∠AOB ＝60º，则∠BDC 的 A ．60º
B ．45º
C ．35º
D ．30º
7．小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是 A ．①，② B ．①，④ C ．③，④ D ．②，③
8．如图，在Rt △ABC 中，∠B ＝90º，∠A ＝30º．以点A 为圆心，BC 长为半径画弧交AB 于点D ，分别以点A ，D 为圆心，AB 长为半径画弧，两弧交于点E ，连接AE ，DE ，则∠EAD 的余弦值是
A ．错误!未找到引用源。
12
B ．错误!未找到引用源。
6
C ．错误!未找到引用源。
3
D ．错误!未找到引用源。
2
9y x 2x ，c 是常数)过点y ＝O
(l ≤x ≤3)有交点，则c 的值不可能是
A ．4
B ．6
C ．8
D ．10 10．我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”，如图，一位母亲在从右到左依次排列的绳子上打结，满七进一，用来记录孩子自出生后的天数．由图可知，孩子自出生后的天数是 A ．84 B ．336 C ．510 D ．1326
卷Ⅱ（非选择题）
二、填空题（本大题有6小题，每小题5分，共30分） 11．分解因式：a 3－ 9a ＝ _____________． 12．不等式
3
x +134
x
3
+ 2的解是 ___________ ．
13．如图1，小敏利用课余时间制作了一个脸盆架，图2是它的截面图，
垂直放置的脸盆与架子的交点为A ，B ，AB ＝40cm ，脸盆的最低点 C 到AB 的距离为l0cm ，则该脸盆的半径为 _____ cm ．
14．书店举行购书优惠活动：①一次性购书不超过100元，不享受打折 优惠}②一次性购书超过100元但不超过200元，一律按原价打九 折；③一次性购书超过200元，一律按原价打七折．小丽在这次活 动中，两次购书总共付款229.4元，第二次购书原价是第一次购书
原价的3倍，那么小丽这两次购书原价的总和是 _______ 元．
15．如图，已知直线l ：y ＝－x ，双曲线y ＝1
x
．在l 上取一点A （a ，－a ）（a ＞0），过A 作x 轴的垂线交双曲线于点B ，过B 作y 轴的垂线交l 于点C ，过C 作x 轴的垂线交双曲线于点D ，过D 作y 轴的垂线交l 于点E ， 此时E 与A 重合，并得到一个正方形
ABCD．若原点O在正方形ABCD的对角线上且分这条对角线为1∶2的两条线段，则a 的值为__________ ．
16．如图，矩形ABCD中，AB＝4，BC＝2，E是AB的中点，直线l平行于直线EC，且直线l 与直线EC之间的距离为2，点F在矩形ABCD边上，将矩形ABCD沿直线EF折叠，使点A 恰好落在直线l上，则DF的长为 __________ ．
三、解答题（本大题有8小题．第17 -ZO小题每小题8分，第21小题10分，第22,23小
题每小题12分，第24小题14分，共80分．解答需写出必要的文字说明、演算步骤或证明过程）
17．(1)计算：5
－(2－)º＋(
1
2 )
-2
．
(2)解分式方程：x
x－1＋2
1－x
＝4．
18．为了解七年级学生上学期参加社会实践活动的情况，随机抽查A市七年级部分学生参加社会实践活动的天数，并根据抽查结果制作了如下不完整的频数分布表和条形统计图．A市七年级部分学生参加社会 A市七年级部分学生参加社会实践活动天数的频数分布表实践活动天数的条形统计图
根据以上信息，解答下列问题：
(l)求出频数分布表中a的值，并补全条形统计图．
(2)A市有七年级学生20 000人，请你估计该市七年级学生
参加社会实践活动不少于5天的人数．
19．根据卫生防疫部门要求，游泳池必须定期换水、清洗．某游泳池
周五早上8：OO打开排水孑L开始排水，排水孔的排水速度保持
不变，期间因清洗游泳池需要暂停排水，游泳池的水在11：30
全部排完．游泳池内的水量Q(m3)和开始排水后的时间t(h)之
间的函数图象如图所示，根据图象解答下列问题：
(1)暂停排水需要多少时间？排水孔的排水速度是多少？
(2)当2≤t≤3.5时，求Q关于t的函数表达式．
20.如图1，某社会实践活动小组实地测量两岸互相平行的一段河的宽度，在河的南岸边点A
处，测得河的北岸边点B在其北偏东450方向，然后向西走60m到达C点，测得点B在点C的北偏东60。
方向，如图2．
(l)求∠CBA的度数．
(2)求出这段河的宽（结果精确到1m，备用数据：错误!未找到引用源。
≈l 41，错误!未找到引用源。
≈1.73）．
21．课本中有一个例题；
有一个窗户形状如图1，上部是一个半圆，下部是一个矩形，如果制作窗框的材料总长为6m，如何设计这个窗户，使透光面积最大？
这个例题的答案是：当窗户半圆的半径约为0. 35m时，透光面积的最大值约为1.05m²．我们如果改变这个窗户的形状，上部改为由两个正方形组成的矩形，如图2，材料总长仍为6m利用图3,解答下列问题：
(1)若AB为1m，求此时窗户的透光面积．
(2)与课本中的例题比较，改变窗户形状后，窗户透光面积的最大值有没有变大？请通过
计算说明．
22．如果将四根木条首尾相连，在相连处用螺钉连接，就能构成一个平面图形． (l)若固定三根木条AB，BC，AD不动，AB=AD=2cm，BC=5cm，如图，量得第
四根木条CD=5cm，判断此时∠B与∠D是否相等，并说明理由．
(2)若固定二根木条AB，BC不动，AB＝2cm，BC＝5cm，量得木条CD＝ 5cm，
∠B＝90°，写出木条AD的长度可能取到的一个值（直接写出一个即可）．(3)若固定一根木条AB不动，AB＝2cm，量得木条CD＝ 5cm．如果木条AD，
BC的长度不变，当点D移到BA的延长线上时，点C也在BA的延长线上；当点C移到AB的延长线上时，点A，C，D能构成周长为30cm的三
角形，求出木条AD，BC的长度．
23．对于坐标平面内的点，先将该点向右平移1个单位，
再向上平移2个单位，这种点的运动称为点的斜平移，
如点P(2，3)经1次斜平移后的点的坐标为 (3，5)．
已知点A的坐标为(1,0)．
(1)分别写出点A经1次、2次斜平移后得到的点的
坐标．
(2)如图，点M是直线l上的一点，点A关于点M的
对称点为点B，点B关于直线l的对称点为点C
①若A，B，C三点不在同一条直线上，判断∆ABC
是否是直角三角形？请说明理由，
②若点B由点A经n次斜平移后得到t且点C的坐标
为(7，6)，求出点B的坐标及n的值，
24．如图，在矩形ABCO中，点O为坐标原点，点B的
坐标为(4，3)，点A，C在坐标轴上，点P在BC边上，
直线l1:y=2x＋3，直线l2：y =2 x－3
(1)分别求直线l1与x轴、直线l2与AB的交点坐标．
(2)已知点M在第一象限，且是直线l2上的点，若∆APM是
等腰直角三角形，求点M的坐标．
(3)我们把直线l1和直线l2上的点所组成的图形称为图形F．
已知矩形ANPQ的顶点N在图形F上，Q是坐标平面内的
点，且N点的横坐标为x，请直接写出x的取值范围
（不用说明理由）．
数学试卷参考答案
一、选择题（本大题有10小题，共40分）
l．A 2．A 3．B 4．B 5．C 6．D 7．D 8．B 9．A 10．C。