结构力学.同济大学_朱慈勉分享资料
(完整版)完整的结构力学答案-同济大学朱慈勉
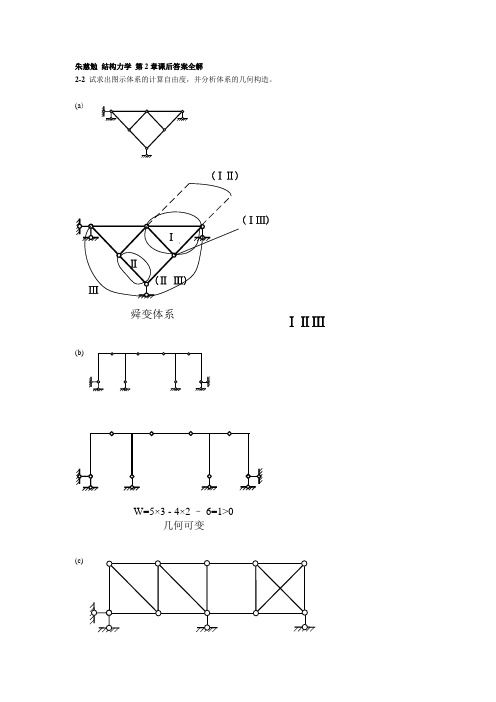
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aaaa a2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m 3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m 6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
结构力学课后习题答案(朱慈勉)

取虚线所示的两个隔离体有:
M B 0,
2 2
FN
2
a
FN 1
a
Fx 0, FN1
2 2
FN
2
4 3
a
2a
联立方程解得:FN1
a 3
,
FN 2
2a 3
杆3的内力可以通过D节点求得
a
a
a
a
FN 3 P
(c)
先去除结构中的零力杆
2
再求出支座反力
1
在A, B点用节点法可求得
43
FN1
13 2
1.5qa
FP
)
FP
FP
FP
FP
、
3-12 试求图示桁架各指定杆件的内力。 (b)
3m
3 ×3m
D
1
1
B
3
2KN
4m
7.5KN
4m
2kN
E
2 3kN
1
A F3
10.5KN
4m
然后再依次隔离A, B, D点不难求得 F2 7.5KN (), FBD 3KN , F1 4KN ()
先求出支座反力,如图所示。零杆亦示于图中。 取1-1截面以上部分分析
$
2-3 试分析图示体系的几何构造。 (a)
(ⅠⅢ) (ⅠⅡ)
Ⅰ
Ⅱ
Ⅲ
几何不变
(Ⅱ Ⅲ)
,
(b)
(ⅠⅡ) Ⅰ
(ⅡⅢ) Ⅱ
(ⅠⅢ)
Ⅲ
几何不变
<
2-4 试分析图示体系的几何构造。
(a)
(ⅠⅢ)
·
(b)
Ⅰ
Ⅱ
(ⅠⅡ)
Ⅲ
同济大学朱慈勉结构力学第10章结构动.知识题目解析

同济大学朱慈勉 结构力学 第10章 结构动..习题答案10-1 试说明动力荷载与移动荷载的区别。
移动荷载是否可能产生动力效应?10-2 试说明冲击荷载与突加荷载之间的区别。
为何在作厂房动力分析时,吊车水平制动力可视作突加荷载?10-3 什么是体系的动力自由度?它与几何构造分析中体系的自由度之间有何区别?如何确定体系的 动力自由度?10-4 将无限自由度的振动问题转化为有限自由度有哪些方法?它们分别采用何种坐标? 10-5 试确定图示各体系的动力自由度,忽略弹性杆自身的质量。
(a) (b)EI 1=∞EImyϕ分布质量的刚度为无穷大,由广义坐标法可知,体系仅有两个振动自由度y ,ϕ。
(c)(d)在集中质量处施加刚性链杆以限制质量运动体系。
有四个自由度。
10-6 建立单自由度体系的运动方程有哪些主要方法?它们的基本原理是什么? 10-7 单自由度体系当动力荷载不作用在质量上时,应如何建立运动方程?10-8 图示结构横梁具有无限刚性和均布质量m ,B 处有一弹性支座(刚度系数为k ),C处有一阻尼器(阻尼系数为c ),梁上受三角形分布动力荷载作用,试用不同的方法建立体系的运动方程。
解:1)刚度法该体系仅有一个自由度。
可设A 截面转角a 为坐标顺时针为正,此时作用于分布质量m 上的惯性力呈三角形分布。
其端部集度为..ml a 。
取A 点隔离体,A 结点力矩为: (3)121233I M ml a l l mal =⨯⨯⨯=由动力荷载引起的力矩为:()()2121233t t q l l q l ⋅⋅= 由弹性恢复力所引起的弯矩为:.2133la k l c al ⋅⋅+ 根据A 结点力矩平衡条件0I p s M M M ++=可得:()3 (322)1393t q l ka m al l c al ++=整理得:()...33t q ka c a m a l l l++= 2)力法.cα解:取AC 杆转角为坐标,设在平衡位置附近发生虚位移α。
同济大学朱慈勉 结构力学第11章_结构的稳定计算

§11-2 有限自由度体系的稳定 ——静力法和能量法
P
即 : P 3klP k l 0
2 2 2
A 1.618
1
2.618kl 3 5 特征值: P kl 2 0.382kl
B C
k
Pcr 0.382kl ---临界荷载
y1 1 ---失稳形式 y2 1.618
P A
EI
y1
k k
y2
ky1
l
B
EI
ky2
l
C
(2lk P ) y1 kly2 0 整理得 :(kl P ) y Py 0 1 2
为使y1、y2 不同时为零,令:
HB’
P
A’ B’
VB’
ky1 ky2
2kl P kl 0 ----稳定方程 kl P P
y
y(l ) l
y(l ) tanl
经试算: (l )min 4.493
2 Pcr min EI 4.493 2 EI ( ) EI 20.19 2 l l
2
3 2
5 2
l
§11-3 无限自由度体系的稳定——静力法
例11.8 求体系的临界荷载Pcr 。 P P
第十一两类稳定问题概述 §11-2 有限自由度体系的稳定 ——静力法和能量法
§11-3 无限自由度体系的稳定 ——静力法 §11-4 无限自由度体系的稳定 ——能量法
§11-1 概述
强度验算 薄壁结构 刚度验算 结构设计 高强材料结构 稳定验算——某些时候是必须的 (如钢结构) 主要受压的结构等 强度验算与刚度验算是在结构静力平衡的状态下、采用未变形的 结构的计算简图来分析的; 而稳定验算是在结构产生大变形后的几何形状和位置上进行计算 的,其方法已经属于几何非线性范畴,叠加原理不再适用。
同济大学朱慈勉版结构力学课后答案(下)-精品.pdf
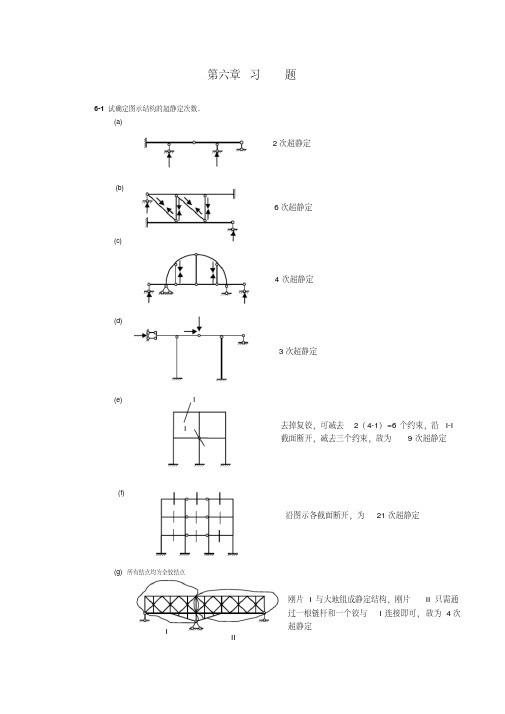
M BF 6 8.69 9 17.39 104.37 KN m
M FE 3 17.39 52.17 KN m M CG 6 8.69 52.14KN m
52.17
M
248.49
104.37 52.14
6-6 试用力法求解图示超静定桁架,并计算 (a)
1、 2 杆的内力。设各杆的 EA 均相同。 (b)
C l
解:取 1/4 结构: q
基本结构为: q
X2 X1
l
1
M1
1
1
1 M2
q2 l
2
ql2
q 2
2
Mp
1 l2
2
l3
11
EI
l 23
3EI
12
1 1 l2 1
l2
EI 2
2 EI
22 1 l 1 1 l 1 1
3l
EI 2
2EI
1p
1 1 l ql 2 l 3
EI 3
2
4
ql 4 8EI
2 p 1 1 l ql 2 1
l
11
1 12
EI 2
EI
1 1 l ql 2
l ql 2
ql 2
1p
EI 3 2
1
8
2
1 8
12EI
11 X 1
1p 0
X1
ql 2
12
M M 1 X1 M p
ql 2 24
ql 2 12
ql 2
ql 2
24
24
ql 2
12 ql 2
12
2
2
ql
ql
M
24
24
朱慈勉结构力学第一章

绪论 框架结构传力分析
绪论 桁架结构传力分析
绪论 拱结构传力分析
绪论
二、结构力学的任务
1、研究结构的组成规律:杆件如何拼装才能 成为一个结构,怎样拼装才能成为一个好的结构。
2、研究结构在外部因素作用下的强度、刚度 和稳定性的计算原理计算方法
3、结构组成举例:
绪论 1、静定结构 2、超静定结构 3、几何可变体系
A
VA
(3)固定支座(固定端支座):力作用点、方向、大小均未知。
A
HA MA VA
绪论
(4)定向支座(滑动支座):力作用点、方向、大小均未知。
A
A
HA
MA
MA
4、荷载的简化
VA
(1)体荷载:折算为作用于杆轴、沿杆轴线分布的线荷载。例如 自重。
(2)面荷载:折算为作用于杆轴的集中荷载或线荷载。例如风压、 雪压、设备重等。
A
B
CD
A:刚结点 B、D:铰结点
E
F
G
C:组合结点
杆BF与杆CD为刚结, 杆BC与杆BF为铰结。
绪论
3、支座结点的简化
支座定义:把结构与基础联结起来的装置。
(1)铰支座(固定铰支座):力作用点在铰中心,方向大小均未知。 A
HA
VA
(2)可动铰支座(辊轴支座):力作用点在铰中心,方向向上,大
小未知。
5、结构简化举例 单层工业厂房:
绪论
厂房 排架
桁架 吊车梁
绪论
1.3 平面结构的分类 一、按构造特征和受力特点分:
1、梁
梁
2、拱
3、桁架
4、刚架
拱
5、组合结构
桁架
刚架
组合结构
同济大学朱慈勉 结构力学12章
p
2
p2 3
Mu a
Mu
Mu
Mu 依 上 限 定 理 : pu 2.27 a
机构(2)
例题1 试用机动法求图示结构的极限荷载。 (1)分析弯矩与曲率的关系 : p 1.1 p
A D B E
C
1
y
M EI
(a )当M为 正 值 时 , 曲 率 为 负 ; 值
2a
例题1 试用机动法求图示结构的极限荷载。 p 1.1 p
解:
2a
a
1.1 p
Mu
a
a
p
机构( 1) 1.1p1 2a M u 3 M u 2 p1 2.27 Mu a
2
Mu
3
机构( 2) p2 a M u M u 2
机构(1)
1.1 p
Mu
塑性极限弯矩 仅与截面形状有关
截面形状
矩形 圆
截面形状 系数 1.5 16/3p=1.7
进入塑性流动区后,截面抵抗内力不在增加,但变 形继续发展,相当与承受一个极限弯矩作用的铰
塑性铰与普通铰的相同之处: 铰两侧的截面可以产生有限的相对转角
工字型
圆环
1.10~1.17
1.27~1.40
塑性铰与普通铰的不同之处: (1) 普通铰不能承受弯矩作用,而塑性铰两侧必有大小等于极限弯矩Mu的弯矩 作用。 (2) 普通铰是双向铰,可以绕着铰的两个方向自由转动,而塑性铰是单向铰, 只能沿着弯矩增大的方向自由转动,若方向转动则恢复刚性链接的特性。
三、破坏机构 由于足够多的塑性铰的出现,使原结构成为机构(几何可变体系), 失去继续承载的能力,该几何可变体系称为“机构”。 1、不同结构在荷载作用下,成为机构,所需塑性铰的数目不同。
同济大学-朱慈勉版-结构力学-课后答案(上)
2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a)(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)【W=5×3 - 4×2 – 6=1>0几何可变(c)】有一个多余约束的几何不变体系(d)|2-3 试分析图示体系的几何构造。
(a)/W=3×3 - 2×2 – 4=1>0可变体系(ⅡⅢ) (b);Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变-(b)~(ⅠⅢ)(ⅡⅢ)几何不变~W=4×3 -3×2 -5=1>0几何可变体系(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体@(e)(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系…(f)?(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(g):(h)|二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)%(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)!Ⅲ(ⅡⅢ)(ⅠⅢ)`3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)%aa *a a2P F a 2P F a4P F Q34P F 2P F(b)"2020Q10/326/310(c){2m6m`4m2m3m2m2m3m3m4m18060(d)]7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)3m2m2m2m2m2m 2m2m4kNm%6m1k N /m2kNCB{242018616MQ18(b),30303011010QM 2106m10kN>3m3m40kNmAB CD:45MQ(d)…444444/32MQN3m3m6m)2m2m(e))4481``(f)#222220M…4m2m3m4m/3-4试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)—(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
第三章-静定结构受力分析,同济大学课件,朱慈勉版教材
F
D
ql x 2
ql x 2
解:
1 2 C F ql 8 1.EBCF为基本部分,AE和FD为附属部分。 2.求铰B、E处约束力及支座反力。 3.确定铰E、F的位置。 M MC 1 1 1 根据叠加原理, B M 中 = ql 2 M B M C ql x x qx x 2 8 2 2 1 l 考虑到 M B M C M 中 , 故, M B=M C ql 2 , 从而, x 16 8
第3章
§3-1 §3-2 §3-3 §3-4 §3-5 §3-6 §3-7
静定结构受力分析
Analysis of Statically Determinate Structures
概述 多跨静定梁 静定平面刚架 三铰拱 静定平面桁架 组合结构 静定结构的一般性质
土木工程学院 结构力学
2014/10/13
为何采用多跨静定梁这种结构型式?(多跨静定梁的优点)
q
0.086ql 2
多跨静定梁
0.086ql 2
l
x
0.086ql 2
l
x 0.172l时正负弯矩相等
q
简支梁(两个并列)
1 2 ql 8
1 2 ql 0.125ql 2 8
相同跨度相同荷载作用下,与简支梁相比,多跨静定梁弯矩较小, 而且分布均匀。(节省材料,便于大跨)
土木工程学院 结构力学 2014/10/13
例:
叠加法作梁的M图。
由杆端弯矩作图
叠加q弯矩图
ql 2 32
ql 2 16 ql 2 4
M2
叠加ql2弯矩图
ql 2 2
3ql 2 4
ql 2 32
同济大学朱慈勉-结构力学第10章-结构动力学
分析过程:
第1阶段:位移时间历史 y y(x)
第2阶段: 应力、应变及内力 (如何求?)
已知荷载的类型
周期荷载: 简谐荷载
复杂荷载
F
t
F
t
建筑物上的偏心电机
内燃机连杆
任意复杂周期荷载可以用傅里叶级数展开为简谐荷载
非周期荷载:
F
t
F
t
爆破
地震
§10-2 体系振动的自由度
(动力)自由度:确定体系上全部质量位置所需的独立参 数的数目
确定体系阻尼比的一种方法
▪ 阻尼体系动力反应:
y(t) et sin(dt )
▪ 体系的阻尼比可以通过测试体 系运动的衰减规律得到:
▪ 体系从任一时刻经几个周期后 的振幅比为:
y (t)
e tk
e (tk nT )
t
0 tk
t k + nT
e t
T 2/d
y e tk
tk
n T
2nπ d
my cy ky 0
(3-2)
▪ 特征方程:
s c
c
2
2
2m 2m
▪ 如果体系的阻尼比临界阻尼小,则显然有c/2m< ,这时,特 征方程根式中的值必然为负值,则s 值成为:
s c i 2 c 2
2m
2m
▪ 引入符号: c c cc 2m
c 2m
▪ 其中 表示体系阻尼与临界阻尼的比值,称为阻尼比,则:
y3 y2
y1
忽略楼板变形
3个自由度
y1 y2
2个自由度
1个自由度
y1
忽略杆件轴向变形
4个自由度
y1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
15
三、多余约束 在体系上加上或撤除某一约束并不改变原体系的
自由度数,则该约束就是多余约束。
第一章 绪 论
§1-1 结构力学的研究对象和任务
1、结构的概念:结构是在建筑物和构筑物中,起 主要受力、传力及支承作用的部分。
2、结构的分类(按构件的几何特征):杆件结构 (空间或平面)、薄壁结构(薄板、薄壳)、实 体结构。
1
3、课程研究的对象:平面杆件结构。 4、课程的任务:
结构的组成规律、合理形式; 结构在外因作用下的强度、刚度和稳定性(即平 面杆件结构在各种外因作用下的内力、位移的计算 原理和计算方法。暂不涉及稳定问题)。
不允许有任何方向的移动和转动,产生水平、竖 直及限制转动的约束力。
5
§1-3 杆件结构的分类
1、按结构的受力特点分类: 梁:由水平(或斜向)放置杆件构成。梁构件主
要承受弯曲变形,是受弯构件。 刚架:不同方向的杆件用结点(一般都有刚结点)
连接构成。刚架杆件以受弯为主,所以又叫梁式构 件。
桁架:由若干直杆在两端用铰结点连接构成。桁 架杆件主要承受轴向变形,是拉压构件。
平面内最简体系的自由度数:
一个点:在平面内运动完全不受限制的一个点有 2个自由度。
一个刚片:在平面内运动完全不受限制的一个刚 片有3个自由度。(图2-2-1)
11
12
二、约束概念 当对体系添加了某些装置后,限制了体系的某些
方向的运动,使体系原有的自由度数减少,就说这 些装置是加在体系上的约束。约束,是能减少体系 自由度数的装置。
10
(图2-2-2)上3所示,为平面内一根链杆AB, 其一端A和大地相连,显然相对于大地来说这根链 杆在平面内只有一种运动方式,即作绕A点转动, 所以该体系只有一个自由度。同时又可看到,如果 用链杆AB与水平坐标的夹角作为表示该体系运动 方式的参变量,即表示该体系运动中任一时刻的位 置,表示体系位置的参变量数与体系的自由度数也 是相等的。所以,该体系的自由度数为1个。
§1-2 结构计算简图
1、结构计算简图的概念 2、结构计算简图的简化原则是:
1)计算简图要能反映实际结构的主要受力和变 形特点,即要使计算结果安全可靠;
2)便于计算,即计算简图的简化程度要与计算 手段以及对结果的要求相一致。
2
3
3、结构计算简图的几个要点:
空间杆件结构的平面简化 杆件构件的简化:以杆件的轴线代替杆件;
8
3、刚片:假想的一个在平面内完全不变形的刚性 物体叫作刚片。在平面杆件体系中,一根直杆、折 杆或曲杆都可以视为刚片,并且由这些构件组成的 几何不变体系也可视为刚片。
刚片中任一两点间的距离保持不变,既由刚片中 任意两点间的一条直线的位置可确定刚片中任一点 的位置。所以可由刚片中的一条直线代表刚片。
16
§2-3 平面体系的几何组成分析
一、几何不变体系的简单组成规则
规则一 (两刚片规则):(图2-3-1)
两个刚片用不全交于一点也不全平行的三根链杆
13
1、单约束(见图2-2-2) 连接两个物体(刚片或点)的约束叫单约束。
1)单链杆(链杆)(上图) 一根单链杆或一个可动铰(一根支座链杆)具
有1个约束。 2)单铰(下图)
一个单铰或一个固定铰支座(两个支座链杆) 具有两个约束。 3)单刚结点
一个单刚结点或一个固定支座具有3个约束。
14
2、复约束 连接3个(含3个)以上物体的约束叫复约束。
组合结构:由梁式构件和拉压构件构成。 拱:一般由曲杆构成。在竖向荷载作用下有水 平支座反力。
2、按计算方法分类: 静定结构, 超静定结构。
6
§1-4 荷载分类
1、按作用时间分类:
恒载:永久作用在结构上。如结构自重、永久 设备重量。
活载:暂时作用在结构上。如人群、风、雪 (在结构上可占有任意位置的可动荷载)及车辆、 吊车(在结构上平行移动并保持间距不变的移动荷 载)。 2、按作用性质分类:
9
二、研究体系几何组成的任务和目的:
1、研究结构的基本组成规则,用及判定体系是否 可作为结构以及选取结构的合理形式。
2、根据结构的几何组成,选择相应的计算方法和 计算途径。
§2-2 平面体系的自由度
一、 自由度的概念
体系可独立运动的方式称为该体系的自由度。 或表示体系位置的独立坐标数。
平面体系的自由度:用以确定平面体系在平面 内位置的独立坐标数。
刚结点与铰结点的组合体。 4
结构与支承物连接的简化: 以理想支座代替结构与其支承物(一般是大地)
之间的连结 。 1)活动铰支座:
允许沿支座链杆垂直方向的微小移动。沿支座链 杆方向产生约束力。 2)固定铰支座:
允许饶固定铰铰心的微小转动。过铰心产生任意 方向的约束力(分解成水平和竖直方向的两个力)。 3)固定支座:
本节内容:研究结构的组成规律和合理形式。
前提条件:不考虑结构受力后由于材料的应变而 产生的微小变形,即把组成结构的每根杆件都看作 完全不变形的刚性杆件。
一、术语简介(图2-1-1)
1、 几何不变体系:在荷载作用下能保持其几何形
状和位置都不改变的体系称之。
2、几何可变体系:件之间连接的简化:理想结点代替杆件与杆件 之间的连接。 1)铰结点:
汇交于一点的杆端是用一个完全无磨擦的光滑铰 连结。铰结点所连各杆端可独自绕铰心自由转动, 即各杆端之间的夹角可任意改变。 2)刚结点:
汇交于一点的杆端是用一个完全不变形的刚性结 点连结,形成一个整体。刚结点所连各杆端相互之 间的夹角不能改变。 3)组合结点(半铰):
静力荷载:荷载由零加至最后值,且在加载过 程中结构始终保持静力平衡,即可忽略惯性力的影 响。
动力荷载:荷载(大小、方向、作用线)随时 间迅速变化,并使结构发生不容忽视的惯性力。 3、按与结构的接触分类:直接荷载,间接荷载7 。
第二章 平面体系的几何组成分析 §2-1 概 述
平面杆件结构,是由若干根杆件构成的能支承荷 载的平面杆件体系,而任一杆件体系却不一定能作 为结构。
