小学数学经典试题讲解
小学数学中的13种典型例题口诀及解析
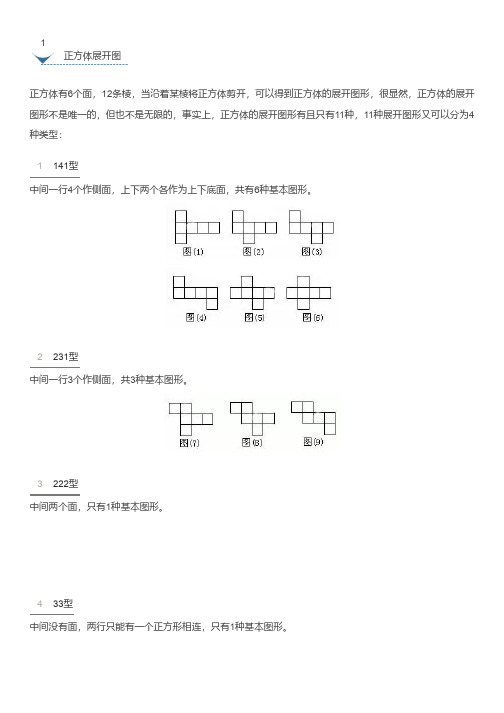
1正方体展开图正方体有6个面,12条棱,当沿着某棱将正方体剪开,可以得到正方体的展开图形,很显然,正方体的展开图形不是唯一的,但也不是无限的,事实上,正方体的展开图形有且只有11种,11种展开图形又可以分为4种类型:1141型中间一行4个作侧面,上下两个各作为上下底面,共有6种基本图形。
2231型中间一行3个作侧面,共3种基本图形。
3222型中间两个面,只有1种基本图形。
433型中间没有面,两行只能有一个正方形相连,只有1种基本图形。
2和差问题已知两数的和与差,求这两个数。
【口诀】: 和加上差,越加越大; 除以2,便是大的; 和减去差,越减越小; 除以2,便是小的。
例:已知两数和是10,差是2,求这两个数。
按口诀,则大数=(10+2)÷2=6,小数=(10-2)÷2=4。
3鸡兔同笼问题【口诀】: 假设全是鸡,假设全是兔。
多了几只脚,少了几只足? 除以脚的差,便是鸡兔数。
例:鸡免同笼,有头36 ,有脚120,求鸡兔数。
求兔时,假设全是鸡,则免子数=(120-36X2)÷(4-2)=24求鸡时,假设全是兔,则鸡数 =(4X36-120)÷(4-2)=124浓度问题(1)加水稀释【口诀】: 加水先求糖,糖完求糖水。
糖水减糖水,便是加糖量。
例:有20千克浓度为15%的糖水,加水多少千克后,浓度变为10%?加水先求糖,原来含糖为:20X15%=3(千克)糖完求糖水,含3千克糖在10%浓度下应有多少糖水,3÷10%=30(千克)糖水减糖水,后的糖水量减去原来的糖水量,30-20=10(千克)(2)加糖浓化【口诀】: 加糖先求水,水完求糖水。
糖水减糖水,求出便解题。
例:有20千克浓度为15%的糖水,加糖多少千克后,浓度变为20%?加糖先求水,原来含水为:20X(1-15%)=17(千克)水完求糖水,含17千克水在20%浓度下应有多少糖水,17÷(1-20%)=21.25(千克)糖水减糖水,后的糖水量减去原来的糖水量,21.25-20=1.25(千克)5路程问题(1)相遇问题【口诀】: 相遇那一刻,路程全走过。
小学数学30种典型题型详解

小学数学30种典型问题001归一问题002归总问题003和差问题004和倍问题005差倍问题006倍比问题007相遇问题008追及问题009植树问题010年龄问题011行船问题012列车问题013时钟问题014 盈亏问题015工程问题016正反比例问题017按比例分配问题018百分数问题019“牛吃草”问题020鸡兔同笼问题021方阵问题022商品利润问题023存款利率问题024溶液浓度问题025构图布数问题026幻方问题027抽屉原则问题028公约公倍问题029最值问题030列方程问题1 归一问题【含义】在解题时,先求出一份是多少(即单一量),然后以单一量为标准,求出所要求的数量。
这类应用题叫做归一问题。
【数量关系】总量÷份数=1份数量 1份数量×所占份数=所求几份的数量另一总量÷(总量÷份数)=所求份数【解题思路和方法】先求出单一量,以单一量为标准,求出所要求的数量。
例1 买5支铅笔要0.6元钱,买同样的铅笔16支,需要多少钱?解(1)买1支铅笔多少钱? 0.6÷5=0.12(元)(2)买16支铅笔需要多少钱?0.12×16=1.92(元)列成综合算式 0.6÷5×16=0.12×16=1.92(元)答:需要1.92元。
例2 3台拖拉机3天耕地90公顷,照这样计算,5台拖拉机6 天耕地多少公顷?解(1)1台拖拉机1天耕地多少公顷? 90÷3÷3=10(公顷)(2)5台拖拉机6天耕地多少公顷?10×5×6=300(公顷)列成综合算式 90÷3÷3×5×6=10×30=300(公顷)答:5台拖拉机6 天耕地300公顷。
例3 5辆汽车4次可以运送100吨钢材,如果用同样的7辆汽车运送105吨钢材,需要运几次?解(1)1辆汽车1次能运多少吨钢材? 100÷5÷4=5(吨)(2)7辆汽车1次能运多少吨钢材? 5×7=35(吨)(3)105吨钢材7辆汽车需要运几次?105÷35=3(次)列成综合算式 105÷(100÷5÷4×7)=3(次)答:需要运3次。
小学数学题目及答案解析大全

小学数学题目及答案解析大全一、加减法题目及答案解析1.题目:小明的铅笔盒里有9支铅笔,他送给了小红3支铅笔,还给了小华5支铅笔。
请问,小明还剩下几支铅笔?答案解析:小明的铅笔盒里一开始有9支铅笔,送给小红3支铅笔,还给小华5支铅笔,所以小明还剩下9 - 3 - 5 = 1支铅笔。
2.题目:小明在数学考试中得了72分,然后又得了88分,他一共得了多少分?答案解析:小明得了72分,又得了88分,所以他一共得了72 + 88 = 160分。
3.题目:小华的花园里有12朵红花,他又从花店买回来了8朵黄花,他一共有多少朵花?答案解析:小华原来有12朵红花,又买回来了8朵黄花,所以他一共有12 + 8 = 20朵花。
二、乘法题目及答案解析1.题目:一个农场有5个圈圈,每个圈圈里有3只鸡,请问农场一共有多少只鸡?答案解析:每个圈圈里有3只鸡,一共有5个圈圈,所以农场一共有3 x 5 = 15只鸡。
2.题目:小明用3个篮子,每个篮子放4个苹果,请问一共有多少个苹果?答案解析:每个篮子放4个苹果,一共有3个篮子,所以一共有4 x 3 = 12个苹果。
3.题目:小华每天练习写2页作业,一共练习了4天,请问一共写了多少页作业?答案解析:每天练习写2页作业,一共练习了4天,所以一共写了2 x 4 = 8页作业。
三、除法题目及答案解析1.题目:小华一共有24个糖果,他要平均分给6个朋友,请问每个朋友能分到几个糖果?答案解析:小华一共有24个糖果,要平均分给6个朋友,所以每个朋友能分到24 ÷ 6 = 4个糖果。
2.题目:小明有20元,他要买5本书,请问每本书多少元?答案解析:小明有20元,要买5本书,所以每本书需要20 ÷ 5 = 4元。
3.题目:小华一共有30个苹果,他要分给10个同学,请问每个同学能分到几个苹果?答案解析:小华一共有30个苹果,要分给10个同学,所以每个同学能分到30 ÷ 10 = 3个苹果。
三年级好题讲解

三年级好题讲解
这是一个非常好的问题,我会尽力为你提供一些适合三年级的数学题目和讲解。
1. 题目:小华和小明都有一些苹果,小华的苹果比小明多3个。
如果小明有10个苹果,那么小华有多少个苹果?
讲解:首先,我们知道小明的苹果数量是10个。
根据题目,小华的苹果比
小明多3个。
我们可以使用简单的加法来计算小华的苹果数量。
所以,小华的苹果数量 = 小明的苹果数量 + 3 = 10 + 3 = 13。
2. 题目:小红有5支铅笔,她给小丽3支后,她们两个都有一样多的铅笔。
小丽原来有多少支铅笔?
讲解:首先,我们知道小红给了小丽3支铅笔后,她们两个铅笔数量相同。
所以,我们可以知道小红给了小丽铅笔后,她自己还剩下5 - 3 = 2支铅笔。
那么,小丽原来有2 - 3 = -1支铅笔(因为小红给了她3支后和她一样多)。
但铅笔数量不能为负数,所以我们可以知道这是一个错误的问题,但我们可以通过逻辑推理知道,小丽原来有1支铅笔。
3. 题目:小华和小明一起做作业。
小华做了40道题,错了5道。
小明做了45道题,错了10道。
谁的正确率更高?
讲解:正确率是正确答案的数量除以总题目数量。
所以,小华的正确率 = (40 - 5) / 40 = 。
而小明的正确率 = (45 - 10) / 45 = 。
因为 > ,所以小华的正确率更高。
这些题目都是基于基本的数学知识和逻辑推理,适合三年级的学生进行练习和巩固知识。
小学四年级数学经典题型解析

小学四年级数学经典题型解析1. 选择题:(1)下面哪个图形是正方形?A. 长方形B. 正方形C. 圆形D. 三角形(2)计算下列等式,选择正确答案:A. 2×3=6B. 2×3=5C. 2×3=4D. 2×3=7(3)将下列数字按照从小到大的顺序排列:A. 3, 5, 1, 8B. 5, 3, 8, 1C. 1, 3, 5, 8D. 8, 5, 3, 1(4)下列哪个数字是偶数?A. 5B. 6C. 7D. 82. 填空题:(5)计算:5 + 7 = ____(6)计算:10 - 3 = ____ (7)计算:2 × 4 = ____(8)计算:8 ÷ 2 = ____3. 判断题:(9)100是一个偶数。
(对/错)(10)3的2倍等于6。
(对/错)(11)5的4倍等于20。
(对/错)(12)8除以2等于4。
(对/错)4. 解答题:(13)计算下列等式:12 + 7 = ____(14)计算下列等式:15 - 9 = ____(15)计算下列等式:4 × 6 = ____(16)计算下列等式:18 ÷ 3 = ____(17)小明有20个苹果,他每天吃3个,那么小明可以吃多少天?(18)小华有15元钱,她买了一个8元的铅笔盒,还剩多少钱?(19)一个长方形的长是6厘米,宽是4厘米,求这个长方形的面积。
(20)一个正方形的边长是5厘米,求这个正方形的面积。
答案:1. B, A, C, B2. 12, 7, 8, 43. 对, 对, 对, 对4. 19, 6, 24, 6, 6, 10, 1, 25。
小学数学试题和答案解析

小学数学试题和答案解析一、加法与减法1. 下列哪个选项的计算结果是10?A. 6 + 2B. 12 - 5C. 3 + 4D. 8 - 1答案与解析:B. 12 - 5计算12减去5的结果为7,不是10。
2. 5 + 3 - 2 = ?A. 5B. 6C. 4D. 8答案与解析:B. 6首先计算5加3等于8,再减去2得到6。
二、乘法与除法1. 4 x 7 = ?A. 28B. 30C. 32D. 24答案与解析:A. 284乘以7的结果为28。
2. 18 ÷ 3 = ?A. 6B. 5C. 4D. 3答案与解析:A. 618除以3等于6。
三、分数1. 1/2 + 1/3 = ?A. 2/3B. 3/5C. 5/6D. 1/5答案与解析:A. 2/3将分数通分得到3/6 + 2/6 = 5/6,化简后为2/3。
2. 如果将2/5化为百分数,应写成多少?A. 40%B. 35%C. 20%D. 30%答案与解析:A. 40%将2/5化为百分数,乘以100得到40%。
四、形状与图形1. 下列哪个图形是长方形?A. 三角形B. 正方形C. 梯形D. 长方形答案与解析:D. 长方形长方形具有四个直角和对边相等的特点。
2. 如果一个正方形的边长是6厘米,它的周长是多少厘米?A. 30B. 24C. 36D. 18答案与解析:B. 24正方形的周长等于4乘以边长,即4 x 6 = 24厘米。
五、时间1. 如果现在是上午8点,那么5小时后是几点?A. 上午1点B. 下午1点C. 下午3点D. 中午12点答案与解析:B. 下午1点8点到1点是5个小时,所以5小时后是下午1点。
2. 小明从下午4点玩到下午6点,他一共玩了多少小时?A. 1小时B. 2小时C. 3小时D. 4小时答案与解析:B. 2小时从下午4点到下午6点是2个小时。
以上是关于小学数学试题和答案解析的内容,希朥能帮助你更好地理解和掌握基础数学知识。
小学数学难题讲解及答案

第一讲速算与巧算例1 计算9+99+999+9999+99999解:在涉及所有数字都是9的计算中,常使用凑整法.例如将999化成1000—1去计算.这是小学数学中常用的一种技巧.9+99+999+9999+99999=(10-1)+(100-1)+(1000-1)+(10000-1)+(100000-1)=10+100+1000+10000+100000-5=111110-5=111105.例2 计算199999+19999+1999+199+19解:此题各数字中,除最高位是1外,其余都是9,仍使用凑整法.不过这里是加1凑整.(如 199+1=200)199999+19999+1999+199+19=(19999+1)+(19999+1)+(1999+1)+(199+1)+(19+1)-5=200000+20000+2000+200+20-5=222220-5=22225.例3 计算(1+3+5+...+1989)-(2+4+6+ (1988)解法2:先把两个括号内的数分别相加,再相减.第一个括号内的数相加的结果是:从1到1989共有995个奇数,凑成497个1990,还剩下995,第二个括号内的数相加的结果是:从2到1988共有994个偶数,凑成497个1990.1990×497+995—1990×497=995.例4 计算 389+387+383+385+384+386+388解法1:认真观察每个加数,发现它们都和整数390接近,所以选390为基准数.389+387+383+385+384+386+388=390×7—1—3—7—5—6—4—=2730—28=2702.解法2:也可以选380为基准数,则有389+387+383+385+384+386+388=380×7+9+7+3+5+4+6+8=2660+42=2702.例5 计算(4942+4943+4938+4939+4941+4943)÷6解:认真观察可知此题关键是求括号中6个相接近的数之和,故可选4940为基准数.(4942+4943+4938+4939+4941+4943)÷6=(4940×6+2+3—2—1+1+3)÷6=(4940×6+6)÷6(这里没有把4940×6先算出来,而是运=4940×6÷6+6÷6运用了除法中的巧算方法)=4940+1=4941.例6 计算54+99×99+45解:此题表面上看没有巧妙的算法,但如果把45和54先结合可得99,就可以运用乘法分配律进行简算了.54+99×99+45=(54+45)+99×99=99+99×99=99×(1+99)=99×100=9900.例7 计算 9999×2222+3333×3334解:此题如果直接乘,数字较大,容易出错.如果将9999变为3333×3,规律就出现了.9999×2222+3333×3334=3333×3×2222+3333×3334=3333×6666+3333×3334=3333×(6666+3334)=3333×10000=33330000.习题一1.计算899998+89998+8998+898+882.计算799999+79999+7999+799+793.计算(1988+1986+1984+…+6+4+2)-(1+3+5+…+1983+1985+1987)4.计算1—2+3—4+5—6+…+1991—1992+19935.时钟1点钟敲1下,2点钟敲2下,3点钟敲3下,依次类推.从1点到12点这12个小时内时钟共敲了多少下?6.求出从1~25的全体自然数之和.7.计算 1000+999—998—997+996+995—994—993+…+108+107—106—105+104+103—102—1018.计算92+94+89+93+95+88+94+96+879.计算(125×99+125)×1610.计算 3×999+3+99×8+8+2×9+2+9第二讲速算与巧算例1 比较下面两个积的大小:A=987654321×123456789,B=987654322×123456788.分析经审题可知A的第一个因数的个位数字比B的第一个因数的个位数字小1,但A的第二个因数的个位数字比B的第二个因数的个位数字大1.所以不经计算,凭直接观察不容易知道A和B哪个大.但是无论是对A或是对B,直接把两个因数相乘求积又太繁,所以我们开动脑筋,将A和B先进行恒等变形,再作判断.解: A=987654321×123456789=987654321×(123456788+1)=987654321×123456788+987654321.B=987654322×123456788=(987654321+1)×123456788=987654321×123456788+123456788.因为 987654321>123456788,所以 A>B.例2 不用笔算,请你指出下面哪道题得数最大,并说明理由.241×249 242×248 243×247244×246 245×245.解:利用乘法分配律,将各式恒等变形之后,再判断.241×249=(240+1)×(250—1)=240×250+1×9;242×248=(240+2)×(250—2)=240×250+2×8;243×247=(240+ 3)×(250— 3)= 240×250+3×7;244×246=(240+4)×(250—4)=240×250+4×6;245×245=(240+5)×(250— 5)=240×250+5×5.恒等变形以后的各式有相同的部分 240 × 250,又有不同的部分 1×9, 2×8, 3×7, 4 ×6, 5×5,由此很容易看出 245×245的积最大.一般说来,将一个整数拆成两部分(或两个整数),两部分的差值越小时,这两部分的乘积越大.如:10=1+9=2+8=3+7=4+6=5+5则5×5=25积最大.例3 求 1966、 1976、 1986、 1996、 2006五个数的总和.解:五个数中,后一个数都比前一个数大10,可看出1986是这五个数的平均值,故其总和为:1986×5=9930.例4 2、4、6、8、10、12…是连续偶数,如果五个连续偶数的和是320,求它们中最小的一个.解:五个连续偶数的中间一个数应为 320÷5=64,因相邻偶数相差2,故这五个偶数依次是60、62、64、66、68,其中最小的是60.总结以上两题,可以概括为巧用中数的计算方法.三个连续自然数,中间一个数为首末两数的平均值;五个连续自然数,中间的数也有类似的性质——它是五个自然数的平均值.如果用字母表示更为明显,这五个数可以记作:x-2、x—1、x、x+1、x+2.如此类推,对于奇数个连续自然数,最中间的数是所有这些自然数的平均值.如:对于2n+1个连续自然数可以表示为:x—n,x—n+1,x-n+2,…, x—1,x, x+1,…x+n—1,x+n,其中 x是这2n+1个自然数的平均值.巧用中数的计算方法,还可进一步推广,请看下面例题.例5 将1~1001各数按下面格式排列:一个正方形框出九个数,要使这九个数之和等于:①1986,②2529,③1989,能否办到?如果办不到,请说明理由.解:仔细观察,方框中的九个数里,最中间的一个是这九个数的平均值,即中数.又因横行相邻两数相差1,是3个连续自然数,竖列3个数中,上下两数相差7.框中的九个数之和应是9的倍数.①1986不是9的倍数,故不行;②2529÷9=281,是9的倍数,但是281÷7=40×7+1,这说明281在题中数表的最左一列,显然它不能做中数,也不行;③1989÷9=221,是9的倍数,且221÷7=31×7+4,这就是说221在数表中第四列,它可做中数.这样可求出所框九数之和为1989是办得到的,且最大的数是229,最小的数是213.这个例题是所谓的“月历卡”上的数字问题的推广.同学们,小小的月历卡上还有那么多有趣的问题呢!所以平时要注意观察,认真思考,积累巧算经验.习题二1.右图的30个方格中,最上面的一横行和最左面的一竖列的数已经填好,其余每个格子中的数等于同一横行最左边的数与同一竖列最上面的数之和(如方格中a=14+17=31).右图填满后,这30个数的总和是多少?2.有两个算式:①98765×98769,②98766 × 98768,请先不要计算出结果,用最简单的方法很快比较出哪个得数大,大多少?3.比较568×764和567×765哪个积大?4.在下面四个算式中,最大的得数是多少?① 1992×1999+1999② 1993×1998+1998③ 1994×1997+1997④ 1995×1996+19965.五个连续奇数的和是85,求其中最大和最小的数.第三讲等差数列及其应用许多同学都知道这样一个故事:大数学家高斯在很小的时候,就利用巧妙的算法迅速计算出从1到100这100个自然数的总和.大家在佩服赞叹之余,有没有仔细想一想,高斯为什么算得快呢?当然,小高斯的聪明和善于观察是不必说了,往深处想,最基本的原因却是这100个数及其排列的方法本身具有极强的规律性——每项都比它前面的一项大1,即它们构成了差相等的数列,而这种数列有极简便的求和方法.通过这一讲的学习,我们将不仅掌握有关这种数列求和的方法,而且学会利用这种数列来解决许多有趣的问题.一、等差数列什么叫等差数列呢?我们先来看几个例子:①l,2,3,4,5,6,7,8,9,…②1,3,5,7,9,11,13.③ 2,4,6,8,10,12,14…④ 3,6,9,12,15,18,21.⑤100,95,90,85,80,75,70.⑥20,18,16,14,12,10,8.这六个数列有一个共同的特点,即相邻两项的差是一个固定的数,像这样的数列就称为等差数列.其中这个固定的数就称为公差,一般用字母d表示,如:数列①中,d=2-1=3-2=4-3= (1)数列②中,d=3-1=5-3=…=13-11=2;数列⑤中,d=100-95=95-90=…=75-70=5;数列⑥中,d=20-18=18-16=…=10-8=2.例1下面的数列中,哪些是等差数列?若是,请指明公差,若不是,则说明理由.①6,10,14,18,22, (98)②1,2,1,2,3,4,5,6;③ 1,2,4,8,16,32,64;④ 9,8,7,6,5,4,3,2;⑤3,3,3,3,3,3,3,3;⑥1,0,1,0,l,0,1,0;解:①是,公差d=4.②不是,因为数列的第3项减去第2项不等于数列的第2项减去第1项.③不是,因为4-2≠2-1.④是,公差d=l.⑤是,公差d=0.⑥不是,因为第1项减去第2项不等于第2项减去第3项.一般地说,如果一个数列是等差数列,那么这个数列的每一项或者都不小于前面的项,或者每一项都大于前面的项,上述例1的数列⑥中,第1项大于第2项,第2项却又小于第3项,所以,显然不符合等差数列的定义.为了叙述和书写的方便,通常,我们把数列的第1项记为a1,第2项记为a2,…,第n项记为an,an。
小学数学应用题详解100例附答案(完整版)

小学数学应用题详解100例附答案(完整版)1. 小明有10 个苹果,小红的苹果数比小明多5 个,小红有多少个苹果?答案:小明有10 个苹果,小红比小明多5 个,所以小红有10 + 5 = 15 个苹果。
2. 商店里有20 支铅笔,卖出了8 支,还剩下多少支?答案:原本有20 支铅笔,卖出8 支,剩下20 - 8 = 12 支。
3. 一本书有50 页,小明已经看了20 页,还剩多少页没看?答案:总页数50 页,已看20 页,未看的页数为50 - 20 = 30 页。
4. 一辆公交车上原本有30 人,到第一站下去了10 人,又上来了5 人,现在车上有多少人?答案:原本30 人,下去10 人后剩30 - 10 = 20 人,又上来5 人,现在有20 + 5 = 25 人。
5. 小兰有8 元钱,姐姐的钱数是小兰的3 倍,姐姐有多少钱?答案:小兰有8 元,姐姐的钱是小兰的3 倍,所以姐姐有8×3 = 24 元。
6. 果园里有苹果树25 棵,梨树比苹果树少8 棵,梨树有多少棵?答案:苹果树25 棵,梨树比苹果树少8 棵,梨树有25 - 8 = 17 棵。
7. 一条绳子长15 米,剪成3 米一段,可以剪成几段?答案:15÷3 = 5 段。
8. 小明每分钟走60 米,5 分钟能走多少米?答案:速度×时间= 路程,所以60×5 = 300 米。
9. 一箱牛奶有12 瓶,3 箱牛奶一共有多少瓶?答案:一箱12 瓶,3 箱共有12×3 = 36 瓶。
10. 学校要种50 棵树,已经种了20 棵,还要种多少棵?答案:50 - 20 = 30 棵。
11. 一件衣服原价80 元,打八折后的价格是多少?答案:八折就是原价的80%,80×80% = 64 元。
12. 一个长方形的长是8 厘米,宽是5 厘米,它的周长是多少?答案:长方形周长= (长+ 宽)×2,所以(8 + 5)×2 = 26 厘米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学数学经典试题讲解
驹日二百四,驽日一百五;
驽先十二日,驹追不辞苦。
需追多少日,方可齐飞舞?
(解说)此题是依据我国古代著名算题“驹追驽”编写而成的,题目出处待查。
原来
的题目是:
“驹日行二百四十里,驽日行一百五十里。
驽先行十二日,驹随后追及。
问几何日可
及之?”
题中的“驹”是良驹,指少壮的马,就是好马,也就是会跑路的马;“驽”即劣马,
也就是不会跑路的马。
“驹日二百四”和“驽日一百五”,分别指“良驹每日能行240里”和“劣马每日能行150里”。
“里”为古代长度单位,不同时期它的进率也有所不同,最
早的1里=1800尺,后来又改为1里=150丈=1500尺( 3尺=1米)。
我们计算时,可只用“里”为单位,而不去理会“里”的长度以及它的进率。
题目如用通俗的话来表达,可以是:
有两匹马,一匹很会跑路,每日能行240里;另一匹不会跑路,每日只能行150里。
现在不会跑路的马已经先走了12天,会跑路的`马才起步追赶。
问:需要多少天才可以追上?
题目的解法是:
因为驽马每日行150里,故12日共行的路程是
150×12=1800(里)
这就是说,当良驹开始去追驽马时,它隔驽马的路程是1800里。
依据“追及问题”
的数量关系
相隔距离÷(速度差)=追及时间
所以可求得良驹追上驽马所需要的时间是
1800÷(240-150)=20(日)
如果列成综合算式,就是
150×2÷(240-150)=1800÷90=20(日)
(答略)
(思考、练习)
1.夏令营营员分成甲乙两队做军事野营活动。
他们同时同地同向出发,甲队每小时
行4千米,乙队每小时行3千米。
经过1小时,甲队停下来开展了1小时的军事游戏活动,然后去追已超过了他们的乙队。
问:需要多少小时才能追上?(答案:2小时)
2.小翔和小玲二人骑自行车同时从学校出发,同方向前进。
小翔每小时行15千米,
小玲每小时行10千米。
出发0.5小时后,小翔因事又返回学校,到校以后,又耽搁1小时,然后动身追小玲。
小翔几小时可以追上小玲?(答案:4小时)
感谢您的阅读,祝您生活愉快。
