第四节高阶系统分析
合集下载
自动控制原理 第4章第二次课

2
1s
1
试绘制以时间常数 为参变量的广义根轨迹。
解:该系统的闭环特征方程式为
ss 1s 1 2 0
s3 s2 s2 s 2 s3 s2 s2 s 2 0
用 s2 s 2 除方程的两端
1
s2s 1
s2 s 2
0
其等效开环传递函数为
GsH s
s2s 1
s2 s 2
Amplitude
0.6
0.4
0.2
0
0
2
4
11
自动控制原理
Step Response
原系统 简化后系统
6
8
10
12
14
16
18
Time (sec)
4-4 系统性能的分析
自动控制原理
二. 闭环偶极子
一对相距很近的闭环零点、极点。
如果这对偶极子不十分靠近坐标原点和其他极点,则它们对
动态性能的影响可以忽略不计。
等效开环传递函数
1 A P(s) 0 A P(s) 1
Q(s)
Q(s)
A为除K*外,系统任意变化的参数
注意:等效意义在于特征方程相同,而此时闭环零点是不同的。
1
4-3 广义根轨迹
自动控制原理
例 设单位反馈系统的开环传递函数为 G(s) 4 s(s a) 绘制以a为参变量的根轨迹
(s) G(s)
j
闭环系统具有1个实数根和一对共轭复数根, 它们均位于复平面左半部,系统有衰减振荡的 动态分量,阶跃响应呈现欠阻尼状态。
-3
-2
-1
0
30
4-4 系统性能的分析
'
s
s2
0.436 0.66s
自动控制原理(胡寿松版)课件下载

s + 2ζωn s + ω = 0
2 2 n
解方程求得特征根:
s1,2 = −ζωn ± ωn ζ − 1
2
两个参数。 s1,s2完全取决于 ζ ,ωn两个参数。
当输入为阶跃信号时,则微分方程解的形式为:
c(t ) = A0 + Aes1t + A2es2t 1
式中 A 0 , A1 , A 2 为由r(t)和初始条件确定的待定的 系数。
第三章 线性系统的时域分析法
第三节 二阶系统的时域分析 一、二阶系统的数学模型 二、二阶系统的单位阶跃响应 三、欠阻尼二阶系统的动态过程分析 四、过阻尼二阶系统的动态过程分析 五、二阶系统的单位斜坡响应 六、改善二阶系统性能的措施
第三节 二阶系统的时域分析
一、二阶系统的数学模型 二阶系统的微分方程一般式为: 二阶系统的微分方程一般式为:
第一节 系统时间响应的性能指标 ⑤正弦函数 其数学表达式为: 其数学表达式为:
sin ωt f (t ) = 0 t≥0 t<0
f(t)
其拉氏变换为: 其拉氏变换为:
st L[ f ( t )] = F ( s ) = ∫ sin ω t e dt = − 0 ∞
ω 2 2 s +ω
第一节 系统时间响应的性能指标 三、动态过程与稳态过程 (1)动态过程 系统在典型信号输入下, 系统在典型信号输入下,系统的输出量从初 始状态到最终状态的响应过程。 始状态到最终状态的响应过程。 (2)稳态过程 系统在典型信号输入下,当时间t 系统在典型信号输入下,当时间t趋于无 穷时,系统输出量的表现方式。 穷时,系统输出量的表现方式。
第二节 一阶系统的时域分析
一、一阶系统的数学模型
【2019年整理】第六节高阶系统分析
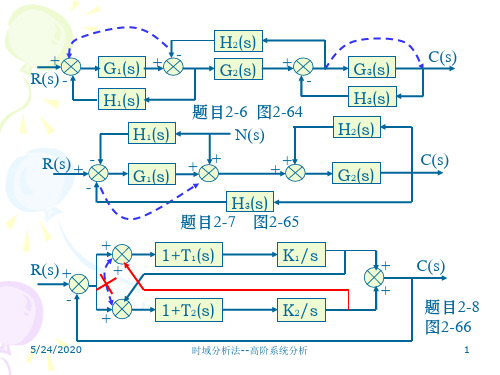
{[1+T1(s)]K1/s}+ {[1+T2(s)]K2/s} 1+ {[1+T1(s)]K1/s}+ {[1+T2(s)]K2/s}+ {[1+T1(s)]K1/s}* {[1+T2(s)]K2/s}
方法二:利用梅森公式求解C(s)/R(s)
4/15/2019 时域分析法--高阶系统分析 2
+ R(s) + + + -
1+T1(s) 1+T2(s)
K1/s K2/s
+ +
C(s) 题目2-8 图2-66
有5个单独环路,没有相互接触的环路
L1=-[1+T1(s)]K1/s,
L2=-[1+T2(s)]K2/s, L3=[1+T1(s)]K1/s*[1+T2(s)]K2/s, L4=-[1+T1(s)]K1/s*[1+T2(s)]K2/s, L5=-[1+T1(s)]K1/s*[1+T2(s)]K2/s
2
1 1 , p3 T
2
p2
p3
n 1 2
p1
4/15/2019
n 0
n 1 2
时域分析法--高阶系统分析
6
三阶系统单位阶跃响应
单位阶跃响应的表达式和曲线: n 2 p3 1 1 C (s) (s) 2 2 s ( s 2 n s n )(s p3 ) s A3 1 A1s A2 2 2 s s 2 n s n s p3 p3 A1, A2 , A3 与 , n , 式中: (实极点与共轭极点的位置关 n 系)有关。 A1e n t sin( n 1 2 t ) c (t ) 1 1 2
方法二:利用梅森公式求解C(s)/R(s)
4/15/2019 时域分析法--高阶系统分析 2
+ R(s) + + + -
1+T1(s) 1+T2(s)
K1/s K2/s
+ +
C(s) 题目2-8 图2-66
有5个单独环路,没有相互接触的环路
L1=-[1+T1(s)]K1/s,
L2=-[1+T2(s)]K2/s, L3=[1+T1(s)]K1/s*[1+T2(s)]K2/s, L4=-[1+T1(s)]K1/s*[1+T2(s)]K2/s, L5=-[1+T1(s)]K1/s*[1+T2(s)]K2/s
2
1 1 , p3 T
2
p2
p3
n 1 2
p1
4/15/2019
n 0
n 1 2
时域分析法--高阶系统分析
6
三阶系统单位阶跃响应
单位阶跃响应的表达式和曲线: n 2 p3 1 1 C (s) (s) 2 2 s ( s 2 n s n )(s p3 ) s A3 1 A1s A2 2 2 s s 2 n s n s p3 p3 A1, A2 , A3 与 , n , 式中: (实极点与共轭极点的位置关 n 系)有关。 A1e n t sin( n 1 2 t ) c (t ) 1 1 2
3-4 第五节 高阶系统分析 自动控制原理课件

法,有如下几种
• 1 特征方程法 系统稳定的充分必要条件是系统特征方程 的所有特征根或闭环传递函数的所有极点
均位于s平面的左半部。
• 2 代数判据法 根据特征方程的系数来判别特征方程根的 实部符号,从而判定系统的稳定性。常用 的代数判据有劳斯判据和胡尔维茨判据两 种。由于时间有限,仅讲劳斯判据。
退出
ess
lim sE(s)
s0
lim s
s0
s(s 1)(2s 1)
s(s 1)(2s 1) K (0.5s 1)
1 s2
1 K
由稳定的条件知:
ess
1 6
不能满足 ess 0.1 的要求
三、给定输入作用下系统的误差分析
这时,不考虑扰动的影响。
R(s)
E(s)
可以写出随动系统的误差 :
-
E(s) 1 R(s) 1 R(s)
1
1
lim
s0
Gk
(s)
1 lim
s0
1 K s
G0 (s)
1 1 Kp
式中:K p
lim
s0
当 0时,K p
Gk (s) 称为位置误差系数;
lim
s0
KG0
(s)
K
,
essr
1
1 K
当
1时,K p
lim
s0
K s
G0 (s)
,
essr 0
K p 的大小反映了系统在阶跃输入下的稳态精度。K p 越大,ess 越 小。所以说 K p 反映了系统跟踪阶跃输入的能力。
1 G1G2H
1 Gk
essr
lim
t
e(t)
lim
第四章 频域分析(第四-六节)
L( ) / dB L( ) / dB
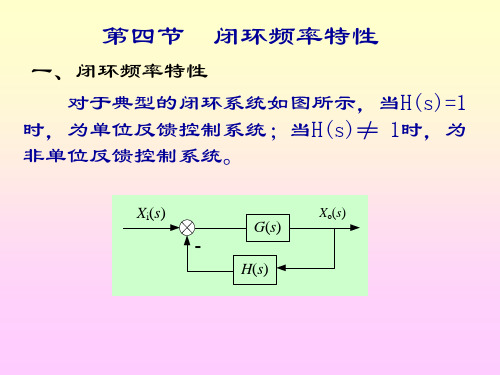
-20 -20
/(rad s 1 )
K
-40
/(rad s 1 )
K
b)
-40
a)
(3) Ⅱ 型 系 统 n = 2 , 其 低 频 段 是 斜 率 为 - 4 0 d B / d e c 的 直 线 , 该 直 线 或 其 延 长 线 与 0 d B 线 ( 横 轴 )的 交 点 频 率 为 w a , 此 时 , K = w a。
p
= e
- xp /
1- x
2
和谐振峰值M
r
= 1 / 2x 1- x
2
可 以 看 出 , 它 们 均 随 着 阻 尼 比 x的 增 大 而 减 小 。 由 此 可 见 , M r 越 大 的 系 统 , 相 应 的 M p也 越 大 , 瞬 态 响 应 的相对稳定性越差。为了减弱系统的振荡性,同时使 系 统 又 具 有 一 定 的 快 速 性 , 应 当 适 当 选 取 M r值 。 如 果 M r 取 值 在 1< M r < 1 .4 范 围 内 , 相 当 于 阻 尼 比 x 在 0 .4 < x < 0 .7 范 围 内 , 这 时 二 阶 系 统 阶 跃 响 应 的 超 调 量 M p < 25% 。
= e
由 此 可 见 , 最 大 超 调 量 M p和 谐 振 峰 值 M r都 随 着 阻 尼 比 x的 增 大 而 减 小 。 同 时 随 着 M r的 增 加 , 相 应 地 M p也 增 加 , 其 物 理 意 义 在 于 : 当 闭 环 幅 频 特 性 有 谐 振 峰 值 时 , 系 统 的 输 入 信 号 的 频 谱 在 w = w r附 近的谐波分量通过系统后显著增强,从而引起振 荡。
-20 -20
/(rad s 1 )
K
-40
/(rad s 1 )
K
b)
-40
a)
(3) Ⅱ 型 系 统 n = 2 , 其 低 频 段 是 斜 率 为 - 4 0 d B / d e c 的 直 线 , 该 直 线 或 其 延 长 线 与 0 d B 线 ( 横 轴 )的 交 点 频 率 为 w a , 此 时 , K = w a。
p
= e
- xp /
1- x
2
和谐振峰值M
r
= 1 / 2x 1- x
2
可 以 看 出 , 它 们 均 随 着 阻 尼 比 x的 增 大 而 减 小 。 由 此 可 见 , M r 越 大 的 系 统 , 相 应 的 M p也 越 大 , 瞬 态 响 应 的相对稳定性越差。为了减弱系统的振荡性,同时使 系 统 又 具 有 一 定 的 快 速 性 , 应 当 适 当 选 取 M r值 。 如 果 M r 取 值 在 1< M r < 1 .4 范 围 内 , 相 当 于 阻 尼 比 x 在 0 .4 < x < 0 .7 范 围 内 , 这 时 二 阶 系 统 阶 跃 响 应 的 超 调 量 M p < 25% 。
= e
由 此 可 见 , 最 大 超 调 量 M p和 谐 振 峰 值 M r都 随 着 阻 尼 比 x的 增 大 而 减 小 。 同 时 随 着 M r的 增 加 , 相 应 地 M p也 增 加 , 其 物 理 意 义 在 于 : 当 闭 环 幅 频 特 性 有 谐 振 峰 值 时 , 系 统 的 输 入 信 号 的 频 谱 在 w = w r附 近的谐波分量通过系统后显著增强,从而引起振 荡。
自动控制原理-第3章

响应曲线如图3-2所示。图中
为输出的稳态值。
第三章 线性系统的时域分析 法
图 3-2 动态性能指标
第三章 线性系统的时域分析 法
动态性能指标通常有以下几种:
延迟时间td: 指响应曲线第一次达到稳态值的一半所需的时间
上升时间tr: 若阶跃响应不超过稳态值, 上升时间指响应曲线从 稳态值的10%上升到90%所需的时间; 对于有振荡的系统, 上升时 间定义为响应从零第一次上升到稳态值所需的时间。上升时间越 短, 响应速度越快。
可由下式确定: (3.8)
振荡次数N: 在0≤t≤ts内, 阶跃响应曲线穿越稳态值c(∞)次 一半称为振荡次数。
上述动态性能指标中, 常用的指标有tr、ts和σp。上升时间tr 价系统的响应速度; σp评价系统的运行平稳性或阻尼程度; ts是同
时反映响应速度和阻尼程度的综合性指标。 应当指出, 除简单的一 、二阶系统外, 要精确给出这些指标的解析表达式是很困难的。
中可以看出, 随着阻尼比ζ的减小, 阶跃响应的振荡程度加剧。 ζ =0时是等幅振荡, ζ≥1时是无振荡的单调上升曲线, 其中临界阻尼 对应的过渡过程时间最短。 在欠阻尼的状态下, 当0.4<ζ<0.8时过
渡过程时间比临界阻尼时更短, 而且振荡也不严重。 因此在 控制工程中, 除了那些不允许产生超调和振荡的情况外, 通常都希
第三章 线性系统的时域分析法 4. 脉冲函数 脉冲函数(见图3-1(d))的时域表达式为
(3.4)
式中,h称为脉冲宽度, 脉冲的面积为1。若对脉冲的宽度取趋于 零的极限, 则有
(3.5) 及
(3.6)
称此函数为理想脉冲函数, 又称δ函数(见图3-1(e))。
第三章 线性系统的时域分析 法
系统工程第四章-系统分析

表4-6 等级及分数
因素 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 合计
A地
等级
最大级 4 2 1 4 4 3 最大级 4 2 3 2 2 4 1 3 2 3 2 1
B地
分数
280 176 40 6 24 32 36 10 8 8 12 8 8 8 4 6 4 30 12 4 716
第三节系统环境分析科技发展动态预期自行开发的新产品竞争对手的开发情况企业技术环境政治体制国民生产总值消费水平政府开支利率变化汇率变化货币供求量价值观念变化人口变化生活方式变化就业状况企业与政府的关政策体制政策变化企业经营管理系统环境因素分析第三节系统环境分析环境因素的评价1swot分析法环境分析分析外部存在的机会和威胁设定任务和使命决定干什么设定目标确定系统的目标和方向系统内部评价分析内部竞争能力的优势和劣势形成战略确定系统的发展战略swot分析图第三节系统环境分析企业内部条件企业外部条件产品销路好产品质量差基础管理好需求量扩大引进先进技术引进人才企业规模大企业负担重资金不足原材料价格上涨利率过高竞争激烈swot分析表第三节系统环境分析2情景分析法
③逻辑框代表“与”或“或”的逻辑关系。 ④时间箭头表明完成一项活动需要的时间。 ⑤活动框表明正进行或将要完成的动作,如运 输石油到炼油厂。 ⑥联接矩阵是表明活动框输入与输出关系的一 种简捷方便的方式。输入从矩阵的左边引入, 输出从矩阵底部引出。 ⑦接地符号是一个活动或项目的结束标记。
第四节 系统的目标和结构分析
例 要实现“有效摧毁八千公里外敌方设施”这样一个总目 标,要建立目标集 。
第四节 系统的
分解总目标,建立目标树,是由对信息库进行搜索和 辨识的活动程序确定的。从过程上看,则是运用效能原理不 断进行分析,而后逐步用组态原理进行设计的过程。 效能原理就是指对实现开发目标方向可以产生效能的科 学技术原理 。 组态原理就是实现效能原理的工程原理模型,在同一个 效能原理下,可以采用不同的工程原理 。
自动控制原理第三章二阶系统

1. ζ >1 过阻尼
1 T
e-t/T
c(t)=1-e-t/T
r(t)=t
c(t)=t-T+Te-t/T
可知: 系统输入信号导数的输出响应,等 于该输入信号输出响应的导数;根据一种 典型信号的响应,就可推知于其它。
自动控制原理第三章二阶系统
第二节 一阶系统性能分析
设例ФKk(若=s一 调 t)=s1要=阶 节000CR求系 时.1((ss:sK统 间)),=H的t=求1s+0结(反t1.11s0构0±=馈000•如/5K.系S1%HR图/s(数Ss)),。;=试(_E如0(求.则s0果)11系://K要KKS统HkH求)的S+C1(s) 解Ф:(系s)统=t s=闭CR3((T环ss=))传=3×1递+K01H1函.000=010数0•/./0K3S.1H/=SK0k .=K1HT0.s=11S00K+.0H11/KH
有性任何着 能=二对 指S2阶应 标+GR系(的 与sS1)/=统/L关 其L+CUU的1系 参rc(/(ssL动))C数。=态L间求C=性S的出2能S+2关标R+1指C2系准Sζω标+ω形,1n。2n 式S便+ω的可n动求2
ቤተ መጻሕፍቲ ባይዱ
态 得
2ζ ω n=R/L
得:
ω
2 n
=
1/LC
ω n=1/ LC
ζ=
RC 2L
一阶系统ts =单3位T 阶跃响应:
(±R5%(s))=
1 S
C(s)= tФs =(s4)•TS1
=
1 TS+1
•
1S(=±1S2%- S)+11/T
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等式两端计算: [sC(s)] |s=0
A0 = 1 留数法
同理, 等式两端计算: [(s + p3 )C(s)] |s=− p3
A3
=
ζ
2β
−1 (β −
2)
+1
两端计算:
C ( s )( s 2
+
2ζωn s
+ωn2来自)|s=−ζωn ±
jωn
1−ζ 2
可列出两个方程,求解得:
A1
=
−ζ ζ 2β
对于不能简化为低阶系统的高阶系统,可采用数值计算 的方法进行仿真,得出系统的瞬态性能指标。
Saturday, October 05, 2013
2
一个高阶系统的例子:
Φ(s) =
10
s(s +1)(s +10)
令 Φ(s) = a + b + c 部分分式法(待定系数法) s s +1 s +10
第四节 高阶系统分析
Saturday, October 05, 2013
自动控制原理B
面向专业:微电子系
授课教师:刘剑毅
1
overview 在控制工程中,几乎所有的控制系统都是高阶系统,即 用高阶微分方程描述的系统。
分析高阶系统的基本思路是将其简化为一、二阶系统。
工程上常采用闭环主导极点的概念对高阶系统进行近似 分析,得到动态性能指标的估算公式。
⎪⎩ 10a = 10
⎪⎩ c = 1/ 9
求该系统的单位脉冲响应: C(s) = Φ(s) ⋅1 = 1 − 10 1 + 1 1 s 9 s +1 9 s +10
Saturday, October 05, 2013
c(t) = 1 − 10 e−t + 1 e−10t 99
3
一、一般三阶系统的瞬态响应
∴Φ(s) = a(s +1)(s +10) + bs(s +10) + cs(s +1) s(s +1)(s +10)
= as2 +11as +10a + bs2 +10bs + cs2 + cs s(s +1)(s +10)
⎧ a+b+c=0 ∴⎨⎪11a +10b + c = 0
⎧ a =1 ⎪⎨b = −10 / 9
+
n2 k =1
Bk (s + ζ kω k ) + Ckω k
1
−
ζ
2 k
s2
+
2ζ kω
ks
+
ω
2 k
Saturday, October 05, 2013
9
查拉氏反变换表,可得其时域表达式为:
n1
∑ c(t ) = A0 + Aje− pjt
j =1
n2
∑ +
B e−ζkωkt k
cos
k=1
n2
10
[定性分析]:
⒈极点的影响 ——对于稳定的高阶系统(闭环极点全部位于s左半平面),极 点为实数或共轭复数,分别对应阶跃响应时域表达式的指数 衰减项或衰减正弦项;
——阶跃响应中,距虚轴近的极点对应项的系数大,而距虚 轴远的极点对应项的系数小。所以,距虚轴近的极点对瞬态 响应影响大。
C(s) = Φ(s)⋅ 1 =
10
= 1 − 10 1 + 1 1
s s(s + 1)(s + 10) s 9 s + 1 9 s + 10
c(t) = 1 − 10 e−t + 1 e−10t 99
Saturday, October 05, 2013
∑ 1
−
ζ
2 k
ω
kt
+
C e−ζkω kt k
sin
k=1
由此可见:
1
−
ζ
2 k
ω
kt
t≥0
⒈系数求解仍可采用留数法;
2. 高阶系统的阶跃响应总可以由简单函数项组成,即由一阶、 二阶系统的响应组成。
3. c(t)的瞬态性能同样取决于闭环极点的相对位置关系。
Saturday, October 05, 2013
这相当于在典型二阶系统振荡环节的基础上增加了一个一
阶的惯性环节
Saturday, October 05, 2013
4
三阶系统的单位阶跃响应:
部分分式法
C(s)
=
(s2
ωn2 p3 + 2ζωns + ωn2 )(s
+
⋅1 p3 ) s
=
A0 s
+
s2
A1s + A2 + 2ζωns + ωn2
+
A3 s + p3
2β (β − (β − 2)
2) +1
A2
=
− ζβ[2ζ 2(β − 2) + 1]ωn ζ 2β (β − 2) +1
式中:
β = p3 ζωn
表示实极点和共轭复极点 实部的相对位置。
5
取拉氏反变换(查表),单位阶跃响应为:
y(t
)
=
1
−
ζ
2β
e− (β
p3t
−
2)
+
1
−
1−ζ
2
ζβ e −ζω n t ζ 2β(β
图中β =∞,表示无实极点。随着实极点的靠近虚轴,超调量下
降了,但调节时间也增加了。 Saturday, October 05, 2013
7
[分析]:三阶系统的单位阶跃响应由三部分组成:稳态项,共轭 复极点形成的振荡分量,实极点构成的衰减指数项分量。
⒈当 β>>1时,表示实极点远离虚轴,共轭复极点离虚轴近,系 统的瞬态特性主要由共轭复极点决定,呈二阶系统的特性,即系 统的特性由二阶系统的特征参数ζ和 ωn 决定。
−
2)
+1
sin(ωd t
+ θ ),t
≥
0
β 大小决定着这两项的此消彼长
式中: ωd = ωn 1 − ζ 2
θ
=
tg −1 ζ
(β − 2) ζ 2(β −
1−ζ 2 2) + 1
Saturday, October 05, 2013
6
β =2 β =∞
β =4
β =1 β =0.5
β = p3 ζωn
传递函数:Φ(s)
=
(s2
+
ωn2 2ζωns + ωn2
)(Ts
+ 1)
当 0 < ζ < 1 时,极点分布如下:
− p1 = −ζωn + jωn 1 − ζ 2
− p2 = −ζωn − jωn 1 − ζ 2
−
p3
=
−
1 T
−×p1
ωn 1−ζ 2
− ×p3
−
×
ζω
n
0
− p2
−ωn 1−ζ 2
m≤n
写成零极点形式:
m
∏ kg (s + zi )
Φ(s) = n1
i=1 n2
∏ ∏ (s + pj )
(s2
+
2ζ
kω
ks
+
ω
2 k
)
j =1
k=1
n1 + 2n2 = n , m ≤ n
其单位阶跃响应函数为: 部分分式法
∑ ∑ C(s) =
Φ(s)⋅ 1 s
=
A0 s
+
n1 j=1
Aj s + pj
⒉当 β<<1时,表示实极点离虚轴近,共轭复极点离虚轴远,系 统的瞬态特性主要由实极点p决定,呈一阶系统的特性。
⒊一般情况下三阶系统的阶跃响应与实极点和共轭复极点的相对 位置有关。
一般的高阶系统的传递函数:
Φ(s)
=
bm s m an s n
+ +
bm−1sm−1 + ... + b0 an−1sn−1 + ... + a0
