2012年铜仁地区高中阶段教育招生统一考试数学卷(word含答案)
2012年贵州省铜仁市中考数学试题及答案
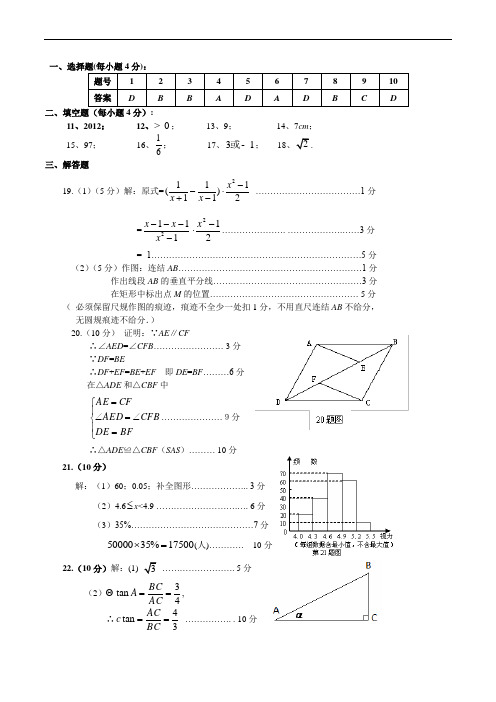
题号 1 2 3 4 5 6 7 8 9 10 答案DBBADADBCD二、填空题(每小题4分):11、2012; 12、0>; 13、9; 14、7cm ;15、97; 16、16; 17、31或-; 182三、解答题19.(1)(5分)解:原式=21)1111(2-⋅--+x x x ………………………………1分 =1112----x x x 212-⋅x …………………. ……………….……3分 = -1………………………………………………………………5分(2)(5分)作图:连结AB ………………………………………………………1分作出线段AB 的垂直平分线……………………………………………3分在矩形中标出点M 的位置…………………………………………… 5分 ( 必须保留尺规作图的痕迹,痕迹不全少一处扣1分,不用直尺连结AB 不给分, 无圆规痕迹不给分.)20.(10分) 证明:∵AE ∥CF∴∠AED =∠CFB …………………… 3分 ∵DF =BE∴DF +EF =BE +EF 即DE =BF ………6分 在△ADE 和△CBF 中⎪⎩⎪⎨⎧=∠=∠=BF DE CFB AED CF AE …………………9分 ∴△ADE ≌△CBF (SAS )……… 10分21.(10分)解:(1)60;0.05;补全图形……………….. 3分(2)4.6≤x <4.9 ……………………….…. 6分 (3)35%……………………………………7分17500%3550000=⨯(人)………… 10分22.(10分)解:(1)3……………………. 5分(2)43tan ==AC BC A Θ, ∴34tan ==BC AC c ……………. . 10分四、23.(12分)(1)证明:∵BF 是圆O 的切线,AB 是圆O 的直径∴BF ⊥AB …………………………………………3分 ∵CD ⊥AB∴CD ∥BF ………………………………….…… 6分 (2)解:∵AB 是圆O 的直径∴∠ADB =90º ………………………………… 7分 ∵圆O 的半径5∴AB =10 ……………………………………… 8分 ∵∠BAD =∠BCD …………………………… 10分∴ cos ∠BAD = cos ∠BCD =45=AD AB ∴1054cos ⨯=⋅∠=AB BAD AD =8∴AD =8…………………………………………12分五、24.(12分)解:(1)设该商店购进一件A 种纪念品需要a 元,购进一件B 种纪念品需要b 元, 根据题意得方程组⎩⎨⎧=+=+8006595038b a b a …………………………………………………………2分 解方程组得⎩⎨⎧==50100b a∴购进一件A 种纪念品需要100元,购进一件B 种纪念品需要50元…………4分(2)设该商店购进A 种纪念品x 个,则购进B 种纪念品有(100—x )个∴⎩⎨⎧≤-+≥-+7650)100(501007500)100(50100x x x x ………………………………………6分解得50≤x ≤53 …………………………………………………………7分∵ x 为正整数,∴共有4种进货方案………………………………………………8分 (3)因为B 种纪念品利润较高,故B 种数量越多总利润越高,因此选择购A 种50件,B 种50件.…………………………………………………10分总利润=250030502050=⨯+⨯(元)∴当购进A 种纪念品50件,B 种纪念品50件时,可获最大利润,最大利润是2500元………………………………………………………………………12分六、25.(14分)解(1):由题意得,A (3,0),B (0,3)∵抛物线经过A 、B 、C 三点,∴把A (3,0),B (0,3),C (1,0)三点分别代入2y ax bx c=++得方程组⎪⎩⎪⎨⎧=++==++0339c b a c c b a ……3分 解得:⎪⎩⎪⎨⎧=-==341c b a∴抛物线的解析式为243y x x =-+………………5分(2)由题意可得:△ABO 为等腰三角形,如图所示,若△ABO ∽△AP 1D ,则1DP OBAD AO = ∴DP 1=AD =4 ,∴P 1(1,4)-……………………………………………… …………7分 若△ABO ∽△ADP 2 ,过点P 2作P 2 M ⊥x 轴于M ,AD =4,∵△ABO 为等腰三角形, ∴△ADP 2是等腰三角形,由三线合一可得:DM =AM =2= P 2M ,即点M 与点C 重合∴P 2(1,2)……………………10分 (3)如图设点E (,)x y ,则||2||21y y AD S ADE =⋅⋅=∆ ①当P 1(-1,4)时,S四边形AP 1CE=S 三角形ACP 1+S 三角形ACE||2214221y ⋅⨯+⨯⨯== 4y +………………………11分∴24y y =+ ∴4y = ∵点E 在x 轴下方 ∴4y =-代入得: 2434x x -+=-,即 0742=+-x x ∵△=(-4)2-4×7=-12<0∴此方程无解……………………………………………………………12分 ②当P 2(1,2)时,S 四边形AP 2CE =S 三角形ACP 2+S 三角形ACE = 2y +∴22y y =+ ∴2y =∵点E 在x 轴下方 ∴2y =- 代入得:2432x x -+=- 即 0542=+-x x ,∵△=(-4)2-4×5=-4<0∴此方程无解综上所述,在x 轴下方的抛物线上不存在这样的点E .……………14分。
2012年贵州铜仁中考真题附答案

铜仁市2012年初中毕业生学业(升学)统一考试数学试题、选择题:(本大题共10个小题,每小题4分,共40分)本题每小题均有A、B、C、D四个备选答案,其中只有一个是正确的,请你将正确答案的序号填涂在相应的答题卡上.资料个人收集整理,勿做商业用途1. -2的相反数是(1 1A. B.--2 22. 下列四个图形中,既是轴对称图形又是中心对称图形的有(3. 某中学足球队的18名队员的年龄情况如下表:年龄(单位:岁)1415161718人数36441A . 15, 15B . 15, 15.5C . 15, 16D . 16, 154•铜仁市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果C. -2D. 2每隔6米栽1棵,则树苗正好用完. 设原有树苗x棵,则根据题意列出方程正确的是资料个人收集整理,勿做商业用途A. 5(x 21 -1) =6(x -1)C. 5(x 21 -1)=6xB. 5(x 21) =6(x -1)D. 5(x 21) =6x5.如图,正方形ABOC的边长为2,反比例函数y =色的图象经过点x则k的值是( )A . 2B . -2C . 4D . -4B . 3个6 •小红要过生日了,为了筹备生日聚会,准备自己动手用纸板制作一个底面半径为母线长为30cm 的圆锥形生日礼帽, 则这个圆锥形礼帽的侧面积为()资料个人收集整理,理,勿做商业用途6766A • 3 10B • 0.3 10C • 3.0 10D . 2.99 1010•如图,第①个图形中一共有 1个平行四边形,第②个图形中一共有 5个平行四边形,第③个图形中一共有11个平行四边形,……则第⑩个图形中平行四边形的个数是()资料个人收集整理,勿做商业用途/C7日n…LJ圈② 图③ 10题图A.54勿做商业用途B.110C.19D.109资料个人收集整理,卷II9cm,勿做商业用途2A • 270 n cm2B • 540 n cm2C • 135 n cm2资料个人收集整理,D • 216 n cm7.如图,在 △ ABC 中,/ ABC 和/ACB 的平分线 交于点E ,过点E 作MN // BC 交AB 于M ,交 AC 于N ,若BM+CN=9 ,则线段MN 的长为()C. 8D. 9&如图, 六边形ABCDEF s 六边形 GHIJKL , A •/ E=2 / KB. BC=2HIC. 六边形ABCDEF 的周长 =六边形相似比为2:1,则下列结论正确的是()GHIJKL 的周长D. S 六边形ABCDEF =2S 六边形GHIJKL9 •从权威部门获悉,中国海洋面积是 299.7万平方公里,约为陆地面积的三分之一,299.7万平方公里用科学计数法表示为()平方公里(保留两位有效数字)资料个人收集整二、填空题:(本大题共8个小题,每小题4分,共32 分)11. - 2012= __________ ;13.一个多边形每一个外角都等于 ________ 40,则这个多边形的边数是;14. 已知圆01和圆。
2012年高考真题——理科数学(全国卷)Word版含答案

2012年普通高等学校招生全国统一考试理科数学(必修+选修Ⅱ)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至2页,第Ⅱ卷第3至第4页。
考试结束,务必将试卷和答题卡一并上交。
第Ⅰ卷注意事项:全卷满分150分,考试时间120分钟。
考生注意事项:1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。
请认真核准该条形码上的准考证号、姓名和科目。
2.没小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
在试题卷上作答无效.........。
3.第I 卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
一、选择题(1)复数131i i-+=+ (A )2i + (B )2i - (C )12i + (D )12i -(2)已知集合{1A =,{1,}B m =,A B A = ,则m =(A )0(B )0或3 (C )1(D )1或3(3)椭圆的中心在原点,焦距为4,一条准线为4x =-,则该椭圆的方程为(A )2211612x y += (B )221128x y += (C )22184x y += (D )221124x y += (4)已知正四棱柱1111ABCD A BC D -中 ,2AB =,1CC =E 为1CC 的中点,则直线1AC 与平面BED 的距离为(A )2 (B(C(D )1(5)已知等差数列{}n a 的前n 项和为n S ,55a =,515S =,则数列11{}n n a a +的前100项和为(A )100101 (B )99101(C )99100 (D )101100(6)ABC ∆中,AB 边的高为CD ,若C B a = ,CA b = ,0a b ⋅= ,||1a = ,||2b = ,则AD = (A )1133a b - (B )2233a b - (C )3355a b - (D )4455a b -(7)已知α为第二象限角,sin cos αα+=,则cos 2α=(A ) (B ) (C (D (8)已知1F 、2F 为双曲线22:2C x y -=的左、右焦点,点P 在C 上,12||2||PF PF =,则12cos F PF ∠=(A )14 (B )35 (C )34 (D )45(9)已知ln x π=,5log 2y =,12z e -=,则(A )x y z << (B )z x y << (C )z y x << (D )y z x <<(10)已知函数33y x x c =-+的图像与x 恰有两个公共点,则c =(A )2-或2 (B )9-或3 (C )1-或1 (D )3-或1(11)将字母,,,,,a a b b c c 排成三行两列,要求每行的字母互不相同,每列的字母也互不相同,则不同的排列方法共有(A )12种 (B )18种 (C )24种 (D )36种(12)正方形ABCD 的边长为1,点E 在边AB 上,点F 在边BC 上,37AE BF ==。
贵州铜仁市2012年初中毕业生学业 升学 统一考试理科综合试题2

贵州铜仁市2012年初中毕业生学业升学统一考试理科综合试题2第Ⅱ卷(非选择题共114分)二、填空题(本题共4个小题,每空1分,共17分。
请将答案填写在答题卡相应的位置。
)19.(4分)用元素符号或化学式填空:(1)3个硫原子,(2)硝酸,(3)8个水分子,(4)三氧化二铁。
20.(6分)化学就在我们身边,它与我们生产、生活息息相关。
现有以下常见的物质:①CO2、②CH3COOH、③NaOH、④NaCl、⑤Na2CO3、⑥C2H5OH、⑦ SO2请选择合适物质的序号..填空:(1)俗称纯碱的是,(2)医疗上用来配制生理盐水的是,(3)属于首要空气污染物之一的是,(4)绿色植物进行光合作用需要的是,(5)食醋中含有的是,(6)国酒茅台中含有的是。
21.(4分)请写出下列反应的化学方程式,并注明反应的类型(化合、分解、置换、复分解)。
(1)铝和氧气的反应,反应类型,(2)实验室用锌和稀盐酸制取氢气,反应类型。
22.(3分)请你用具备的化学知识回答下列问题:(1)化学肥料主要有,(2)点燃氢气前必须要进行的操作是,(3)铁锅、铝锅、铜锅可用来炒菜、做饭是利用了它们的。
三、简答题(本题共2个小题,每小题3分,共6分。
请将答案填写在答题卡相应的位置。
)23.(3分)简述在实验室如何稀释浓硫酸。
24.(3分)某校课外兴趣小组同学用氯酸钾和二氧化锰混合物加热制氧气,实验完毕后发现混合物固体质量减少了,请你用学过的化学知识解释。
四.实验探究题(本题共2个小题,每空1分,共13分。
请将答案填写在答题卡相应的位置。
)25. (6分)实验室制取气体所需装置如下图所示。
(1)实验仪器a 、b 的名称是a 、b 。
(2)用大理石和稀盐酸制取二氧化碳时,所选用的发生装置是 (填序号),其反应的化学方程式是 。
(3)用高锰酸钾制取氧气,其反应的化学方程式是 。
将装置A 和C 连接进行此实验,实验结束,停止加热前要先将导管移出水面 ,目的是 。
【初中数学】贵州省各市2012年中考数学试题分类解析汇编(实数等12份) 通用2

贵州各市2012年中考数学试题分类解析汇编专题12:押轴题一、选择题1. (2012贵州贵阳3分)已知二次函数y=ax2+bx+c(a<0)的图象如图所示,当﹣5≤x≤0时,下列说法正确的是【】A.有最小值﹣5、最大值0 B.有最小值﹣3、最大值6C.有最小值0、最大值6 D.有最小值2、最大值6【答案】B。
【考点】二次函数的图象和最值。
【分析】由二次函数的图象可知,∵﹣5≤x≤0,∴当x=﹣2时函数有最大值,y最大=6;当x=﹣5时函数值最小,y最小=﹣3。
故选B。
2. (2012贵州安顺3分)下列说法中正确的是【】A.B.函数的自变量的取值范围是x>﹣1C.若点P(2,a)和点Q(b,﹣3)关于x轴对称,则a﹣b的值为1D.﹣8的立方根是2【答案】C。
【考点】无理数,函数自变量的取值范围,二次根式有意义的条件,关于x轴对称的点的坐标,立方根。
【分析】A是有理数,故此选项错误;B、函数的自变量的取值范围是x≥﹣1,故此选项错误;C 、若点P (2,a )和点Q (b ,﹣3)关于x 轴对称,则b=2,a=3,故a ﹣b=3﹣2=1,故此选项正确;D 、﹣8的立方根式﹣2,故此选项错误。
故选C 。
3. (2012贵州毕节3分)如图,在正方形ABCD 中,以A 为顶点作等边△AEF ,交BC 边于E ,交DC 边于F ;又以A 为圆心,AE 的长为半径作 EF。
若△AEF 的边长为2,则阴影部分的面积约是【 】1.414 1.732,π取3.14)A. 0.64B. 1.64C. 1.68D. 0.36 【答案】A 。
【考点】正方形和等边三角形的性质,勾股定理,扇形和三角形面积。
【分析】由图知,AEF CEF AEF S S S S ∆∆=+-扇形影部分阴。
因此,由已知,根据正方形、等边三角形的性质和勾股定理,可得等边△AEF 的边长为2Rt △AEF 的两直角边长AEF 的半径为2圆心角为600。
贵州省2012高中数学学业水平测试卷

2012年贵州省普通高中学业水平考试试题一、选择题(每小题3分,共105分)1.设集合A {1,2,3,4,5},{3,5}A B ==,则A B ⋂=A .{1,2,3,4}B .{3,5}C .{5} D.{1,2,3,4,5} 2.已知角α的终边经过点(-3,4),则tan α= A .34 B .34- C .43 D.43- 3.不等式(1)0x x ->的解集是A .{|1}x x >B .{|1}x x <C .{|01}x x << D.{|0,1}x x x <>或 4.函数cos 2y x =的最小正周期是A .4π B .2πC .π D.2π 5.已知向量(1,2),(1,1)a b ==-,则a b +=A .-1B .3C .(2,1) D.(3,0) 6.函数()2,[0,3]x f x x =∈,则()f x 的值域是 A .[0,8] B .[0,6] C .[1,6] D.[1,8] 7.若0a b >>,则下列不等式一定成立的是A .a c b c -<-B .22a b > C .ac bc > D.||||a b < 8.直线l 经过坐标原点,且斜率为-2 ,则下列各点中在直线l 上的是 A .(1,-2) B .(2,-1) C .1(1,)2- D.(-2,-4) 9.右边程序运行后的结果是A .5B .10C .15 D.A+1010.棱长为2的正方体的内切球的表面积为 A .2π B .4π C .8π D.16π11.下列四个函数中,在区间(0,)+∞上为减函数的是A .1y x= B .12y x = C .2y x = D.y x =12.函数()f x 是实数集R 上的奇函数,若(2)2f =,则(2)f -= A .2 B .-2 C .0 D.2或-2 13.不等式||1x >-的解集是510A A A PRINT A END==+A . (0,)+∞B .(,0)-∞C .∅ D. R 14.在程序框图中,图形符号” ”可用于 A .输出 B .赋值 C .判断 D.结束算法 15.已知点(2,1),(2,3)A B ,则直线AB 的倾斜角为 A .00B .300C .600D.90016.下列函数中,在区间(1,2)内有零点的函数是A .23y x =+B .23y x =-C .2x y = D.lg y x =17.右图是某职业篮球运动员在连续11场比赛中得分的茎叶统计图,则该数据的中位数是A .31B .32C .35 D.3618.某班有男同学20人,女同学30人,用分层抽样的方法抽取一个容量为10的样本,则应分别抽取A .男同学4人,女同学6人B .男同学5人,女同学5人C .男同学2人,女同学8人 D. 男同学2人,女同学3人 19.若0x >,则12x x++有 A .最小值4 B .最小值3 C .最大值4 D. 最大值320.已知5sin ,(0,)132x x π=∈,则 cos x = A .513 B .1213 C .513- D.1213-21.0cos75cos15sin 75sin15-的值为 A .0 B .12C22.函数lg y x =的值域是A .(0,)+∞B .(1,)+∞C .(,0)(0,)-∞⋃+∞ D.R 23.把二进制1011(2)化为十进制数,则此数为 A .8 B .10 C .11 D.16 24.在等比数列{}n a 中,已知119,3a q ==-,则3S = A .5 B .6 C .7 D.6325.已知向量,,||2,||4a b a b == ,且a 与b 的夹角为600,则a b ⋅=A .4 B..26.在等差数列{}n a 中,已知3510a a +=,则4a = A .4 B .5 C .10 D.201 2 52 5 43 6 5 1 9 74 75 127.抛掷两枚质地均匀的硬币,出现”两次都是反面”的概率是 A .16 B .13 C .14 D.1228.已知231232,(),log 32R P Q -===,则,,P Q R 的大小关系是A .P Q R <<B .Q R P <<C .Q P R << D.R Q P <<29.不等式组20x y x y +≤⎧⎪≥⎨⎪≥⎩表示的平面区域的面积是 A .1 B .2 C .4 D.5 30.ABC ∆中,已知33,5,cos 5AB BC B ===,这个三角形的面积等于 A .12 B .6 C .3 D.9231.正方体1111ABCD A B C D -中,11AC 与BD 所在直线所成角的大小是 A .300B .450C .600D.9032.下表显示函数值随自变量变化的一组数据,由此判断它最可能的函数模型是A .一次函数模型B .二次函数模型C .指数函数模型 D.对数函数模型 33.某人午觉醒来,发现表停了,他打开收音机,想听电台整点报时,则他等待的时间少于20分钟的概率为 A .16 B .13 C .12 D.2334.如图所示,一个空间几何体的正视图和侧视图教师边长为2的正方形,俯视图是是一个圆,那么这个几何体的体积为 A .2πB .πC .2π D.4π 35.过点(2,3),且到原点的距离最大的直线方程是A .32120x y +-=B .23130x y +-=C .2x = D.50x y +-=二、填空题36.计算lg 2lg50+=37.在ABC ∆中,02,45BC AC B ==∠=,则A ∠=38.右图程序运行后输出的结果为 39. 下列命题中,错误例题的序号是(1)平行于同一条直线的两条直线平行;(2) 垂直于同一条直线的两条直线平行;i=1WHILE i<6i=i+2s=2*i+1WEND PRINT s ENDA 1D 1B 1C 1D C BA(3)平行于同一个平面的两个平面平行;(4)垂直于同一个平面的两个平面平行. 40.某研究性学习小组要制作一个容积为0.183m ,深为0.5m 的长方体无盖水箱,箱底和箱壁的造价每平方米分别为400元和100元,那么水箱的最低总造价为 元. 三、解答题(每小题10分)41.已知函数()sin cos ,f x x x x R =+∈.(1)求函数()f x 的最大值及取得最大值的自变量x 的集合; (2)说明函数()f x 的图象可由sin y x =的图象经过的变化得到.42..数列{}n a 中,(1)已知2112,2(1)n n a a a n +=-=≥.求1a ;(2)求数列{}n a 前5项和5S . 43.已知点M(1,2)和直线:5l x y -=.(1)求以M 为圆心,且与直线l 相切的圆M 的方程; (2)过直线5y x =+上一点P 作圆M 的切线PA 、PB,其中A 、B 为切点,求当四边形PAMB 的面积最小时点P 的坐标.2012年贵州省普通高中学业水平考试试题参考答案:选择题1---35 BDDCC DBACB ABDCD BCAAB ADCCA BCBB B DCBCB填空题:36---40 2 30015 (1),(3) 264 解答题 41.解:(1)())4f x x π=+,当sin()14x π+=,即,4x k k Z ππ=+∈时,x 的取值集合为{|,}4x x k k Z ππ=+∈;(2)先将sin y x =的图象向左平移4π个单位,然后再把所得函数图象上每个点的纵坐()y f x =的图象。
2012贵州铜仁中考数学
2012铜仁市中考试题数 学(满分150分,考试时间120分钟)卷I一、选择题:(本大题共10个小题,每小题4分,共40分)本题每小题均有A 、B 、C 、D 四个备选答案,其中只有一个是正确的,请你将正确答案的序号填涂在相应的答题卡上. 1. (2012贵州铜仁,1,4分)-2的相反数是( )A .21B. -21错误!未找到引用源。
C. -2 D. 2 【答案】D2. (2012贵州铜仁,2,4分)下列四个图形中,既是轴对称图形又是中心对称图形的有( )A .4个B .3个 C.2个 D.1个 【答案】B3. (2012贵州铜仁,3,4分)某中学足球队的18名队员的年龄情况如下表:A .15,15B .15,15.5 C.15,16 D.16,15 【答案】B4. (2012贵州铜仁,4,4分) 铜仁市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x 棵,则根据题意列出方程正确的是( )A .)1(6)121(5-=-+x x B. )1(6)21(5-=+x x C. x x 6)121(5=-+ D. x x 6)21(5=+【答案】A5. (2012贵州铜仁,5,4分)如图,正方形ABOC 的边长为2,反比例函数ky x=的图象经过点A ,则k 的值是( )2题图5题图A.2 B.-2C.4 D.-4【答案】D6.(2012贵州铜仁,6,4分)小红要过生日了,为了筹备生日聚会,准备自己动手用纸板制作一个底面半径为9cm,母线长为30cm的圆锥形生日礼帽,则这个圆锥形礼帽的侧面积为()A.270πcm2B.540πcm2C.135πcm2D.216πcm2【答案】A7.(2012贵州铜仁,7,4分)如图,在ΔABC中,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( ) A.6 B.7 C.8 D.9【答案】D8.(2012贵州铜仁,8,4分)如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论正确的是()A.∠E=2∠KB.BC=2HIC.六边形ABCDEF的周长=六边形GHIJKL的周长D.S六边形ABCDEF=2S六边形GHIJKL【答案】B9.(2012贵州铜仁,9,4分)从权威部门获悉,中国海洋面积是299.7万平方公里,约为陆地面积的三分之一, 299.7万平方公里用科学计数法表示为( )平方公里(保留两位有效数字)A .6103⨯ B .7103.0⨯ C.6100.3⨯ D.61099.2⨯ 【答案】C10. (2012贵州铜仁,10,4分)如图,第①个图形中一共有1个平行四边形,第②个图形中一共有5个平行四边形,第③个图形中一共有11个平行四边形,……则第⑩个图形中平行四边形的个数是( )A .54 B.110 C.19 D.109 【答案】D卷II二、填空题:(本大题共8个小题,每小题4分,共32分)11. (2012贵州铜仁,11,4分)2012-=_________; 【答案】201212. (2012贵州铜仁,12,4分)当x ___________【答案】>013. (2012贵州铜仁,13,4分)一个多边形每一个外角都等于40,则这个多边形的边数是______; 【答案】914. (2012贵州铜仁,14,4分)已知圆O 1和圆O 2外切,圆心距为10cm ,圆O 1的半径为3cm ,则圆O 2的半径为 ______; 【答案】7cm15. (2012贵州铜仁,15,4分)照下图所示的操作步骤,若输入x 的值为5,则输出的值为_______________;【答案】97第10题图16. (2012贵州铜仁,16,4分)一个不透明的口袋中,装有红球6个,白球9个,黑球3个, 这些球除颜色不同外没有任何区别,从中任意摸出一个球, 则摸到黑球的概率为_______________; 【答案】1617. (2012贵州铜仁,17,4分)一元二次方程0322=--x x 的解为____________; 【答案】3或﹣118. (2012贵州铜仁,18,4分)以边长为2的正方形的中心O 为端点,引两条相互垂直的射线,分别与正方形的边交于A 、B 两点,则线段AB 的最小值是__________.三、解答题:(本题共4个题,19题每小题5分,第20、21、22每题10分,共40分,要有解题的主要过程)19.(1)(2012贵州铜仁,19.(1),5分)化简:12)1111(2-÷--+x x x 【答案】解:原式=21)1111(2-⋅--+x x x =1112----x x x 212-⋅x = -1(2)(2012贵州铜仁,19.(2),5分)某市计划在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M 到广场的两个入口A 、B 的距离相等,且到广场管理处C 的距离等于A 和B 之间距离的一半,A 、B 、C 的位置如图所示,请在原图上利用尺规作图作出音乐喷泉M 的位置,(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)【答案】作图如图示:19(2)题图20. (2012贵州铜仁,20,10分)如图,E 、F 是四边形ABCD 的对角线BD 上的两点, AE ∥CF ,AE =CF ,BE =DF .求证: ΔADE ≌ΔCBF . 【答案】证明:∵AE ∥CF ∴∠AED =∠CFB ∵DF =BE∴DF +EF =BE +EF 即DE =BF 在△ADE 和△CBF 中⎪⎩⎪⎨⎧=∠=∠=BF DE CFB AED CF AE ∴△ADE ≌△CBF (SAS )21. (2012贵州铜仁,21,10分)某市对参加2012年中考的50000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:(1)在频数分布表中,a 的值为__________,b 的值为__________,并将频数分布直方图补充完整;(2)甲同学说“我的视力情况是此次抽样调查所得数据的中位数”,问甲同学的视力情况应在什么范围内?(3)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是________,并根据上述信息估计全市初中毕业生中视力正常的学生有多少人?【答案】解:(1)60;0.05;补全图形(2)4.6≤x <4.9(3)35%,17500%3550000=⨯(人) 22.(2012贵州铜仁,22,10分)如图,定义:在直角三角形ABC 中,锐角α的邻边与对边的比叫做角α的余切,记作ctan α, 即ctan α=BCAC=的对边角的邻边角αα,根据上述角的余切定义,解下列问题:(1)ctan30◦= ; (2)如图,已知tan A =43,其中∠A 为锐角,试求ctan A 的值. 【答案】解:(1)(2)43tan ==AC BC A , ∴34tan ==BC AC c 四、(本题满分12分)23.. (2012贵州铜仁,23,12分)如图,已知⊙O 的直径AB 与弦CD 相交于点E , AB ⊥CD ,⊙O 的切线BF 与弦AD 的延长线相交于点F . (1)求证:CD ∥ BF ;(2)若⊙O 的半径为5, cos ∠BCD =54,求线段AD 的长.【答案(1)证明:∵BF 是圆O 的切线,AB 是圆O 的直径 ∴BF ⊥AB ∵CD ⊥AB ∴CD ∥BF(2)解:∵AB 是圆O 的直径 ∴∠ADB =90º ∵圆O 的半径5 ∴AB =10∵∠BAD =∠BCD∴ cos ∠BAD = cos ∠BCD =45=AD AB ∴1054cos ⨯=⋅∠=AB BAD AD =8∴AD =8 五、(本题满分12分)24. (2012贵州铜仁,24,12分)为了抓住梵净山文化艺术节的商机,某商店决定购进A 、B 两种艺术节纪念品.若购进A 种纪念品8件,B 种纪念品3件,需要950元;若购进A 种纪念品5件,B 种纪念品6件,需要800元. (1)求购进A 、B 两种纪念品每件各需多少元? (2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?(3)若销售每件A 种纪念品可获利润20元,每件B 种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元? 【答案】解:(1)设该商店购进一件A 种纪念品需要a 元,购进一件B 种纪念品需要b 元, 根据题意得方程组⎩⎨⎧=+=+8006595038b a b a解方程组得⎩⎨⎧==50100b a∴购进一件A 种纪念品需要100元,购进一件B 种纪念品需要50元 (2)设该商店购进A 种纪念品x 个,则购进B 种纪念品有(100—x )个∴⎩⎨⎧≤-+≥-+7650)100(501007500)100(50100x x x x解得50≤x ≤53∵ x 为正整数,∴共有4种进货方案(3)因为B 种纪念品利润较高,故B 种数量越多总利润越高, 因此选择购A 种50件,B 种50件. 总利润=250030502050=⨯+⨯(元)∴当购进A 种纪念品50件,B 种纪念品50件时,可获最大利润, 最大利润是2500元 六、(本题满分14分)25. (2012贵州铜仁,25,14分)如图已知:直线3+-=x y 交x 轴于点A ,交y 轴于点B ,抛物线y =ax 2+bx +c 经过A 、B 、C (1,0)三点. (1)求抛物线的解析式;(2)若点D 的坐标为(-1,0),在直线3+-=x y 上有一点P ,使ΔABO 与ΔADP 相似,求出点P 的坐标;(3)在(2)的条件下,在x 轴下方的抛物线上,是否存在点E ,使ΔADE 的面积等于四边形APCE 的面积?如果存在,请求出点E 的坐标;如果不存在,请说明理由.【答案】 解(1):由题意得,A (3,0),B (0,3) ∵抛物线经过A 、B 、C 三点,∴把A (3,0),B (0,3),C (1,0)三点分别代入2y ax bx c =++得方程组⎪⎩⎪⎨⎧=++==++03039c b a c c b a 解得:⎪⎩⎪⎨⎧=-==341c b a∴抛物线的解析式为243y x x =-+(2)由题意可得:△ABO 为等腰三角形,如图所示,若△ABO ∽△AP 1D ,则1DP OBAD AO =∴DP 1=AD =4 , ∴P 1(1,4)-若△ABO ∽△ADP 2 ,过点P 2作P 2 M ⊥x 轴于M ,AD =4,∵△ABO 为等腰三角形, ∴△ADP 2是等腰三角形,由三线合一可得:DM =AM =2= P 2M ,即点M 与点C 重合∴P 2(1,2) (3)如图设点E (,)x y ,则||2||21y y AD S ADE =⋅⋅=∆ ①当P 1(-1,4)时,S四边形AP 1CE=S 三角形ACP 1+S 三角形ACE||2214221y ⋅⨯+⨯⨯== 4y +∴24y y =+ ∴4y = ∵点E 在x 轴下方 ∴4y =-代入得: 2434x x -+=-,即 0742=+-x x ∵△=(-4)2-4×7=-12<0 ∴此方程无解②当P 2(1,2)时,S 四边形AP 2CE =S 三角形ACP 2+S 三角形ACE = 2y +∴22y y =+ ∴2y =∵点E 在x 轴下方 ∴2y =- 代入得:2432x x -+=- 即 0542=+-x x ,∵△=(-4)2-4×5=-4<0 ∴此方程无解综上所述,在x 轴下方的抛物线上不存在这样的点E。
2012年高考数学(理科)试卷江西卷(含答案)最完美最高清word版
2012年普通高等学校夏季招生全国统一考试数学理工农医类(江西卷)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟. 参考公式: 锥体体积公式 13V Sh =其中S 为底面积,h 为高第Ⅰ卷一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A ={-1,1},B ={0,2},则集合{z |z =x +y ,x ∈A ,y ∈B }中的元素的个数为( ) A .5 B .4 C .3 D .22.下列函数中,与函数y =定义域相同的函数为( )A .1sin y x=B .ln x y x=C .y =x e xD .sin x y x=3.若函数21,1,()lg ,1,x x f x x x ⎧+≤=⎨>⎩则f (f (10))=( )A .lg 101B .2C .1D .04.若1tan 4tan θθ+=,则sin 2θ=( ) A .15 B .14 C .13 D .125.下列命题中,假命题为( ) A .存在四边相等的四边形不.是正方形 B .z 1,z 2∈C ,z 1+z 2为实数的充分必要条件是z 1,z 2互为共轭复数 C .若x ,y ∈R ,且x +y >2,则x ,y 至少有一个大于1D .对于任意n ∈N +,01C C C nn n n +++…都是偶数6.观察下列各式:a +b =1,a 2+b 2=3,a 3+b 3=4,a 4+b 4=7,a 5+b 5=11,…,则a 10+b 10=( ) A .28 B .76 C .123 D .1997.在直角三角形ABC 中,点D 是斜边AB 的中点,点P 为线段CD 的中点,则222||||||PA PB PC +=( )A .2B .4C .5D .108.某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜和韭菜的产量、成本和售价如下表(单位:亩)分别为( )A .50,0B .30,20C .20,30D .0,509.样本(x 1,x 2,…,x n )的平均数为x ,样本(y 1,y 2,…,y m )的平均数为()y x y ≠.若样本(x 1,x 2,…,x n ,y 1,y 2,…,y m )的平均数(1)z x y αα=+-,其中0<α<12,则n ,m 的大小关系为( )A .n <mB .n >mC .n =mD .不能确定10.如下图,已知正四棱锥S -ABCD 所有棱长都为1,点E 是侧棱SC 上一动点,过点E 垂直于SC 的截面将正四棱锥分成上、下两部分.记SE =x (0<x <1),截面下面部分的体积为V (x ),则函数y =V (x )的图像大致为( )第Ⅱ卷二、(理科)填空题:本大题共4小题,每小题5分,共20分. 11.计算定积分121(sin )d x x x -=⎰+__________.12设数列{a n },{b n }都是等差数列,若a 1+b 1=7,a 3+b 3=21,则a 5+b 5=__________.13.椭圆22221xya b+=(a >b >0)的左、右顶点分别是A ,B ,左、右焦点分别是F 1,F 2.若|AF 1|,|F 1F 2|,|F 1B |成等比数列,则此椭圆的离心率为__________.14下图为某算法的程序框图,则程序运行后输出的结果是__________.三、选做题:请考生在下列两题中任选一题作答.若两题都做,则按所做的第一题评阅计分.本题共5分.15. (1)(坐标系与参数方程选做题)曲线C 的直角坐标方程为x 2+y 2-2x =0,以原点为极点,x 轴的正半轴为极轴建立极坐标系,则曲线C 的极坐标方程为__________.(2)(不等式选做题)在实数范围内,不等式|2x -1|+|2x +1|≤6的解集为__________.四、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.已知数列{a n}的前n项和S n=-12n2+kn(其中k∈N+),且S n的最大值为8.(1)确定常数k,并求a n;(2)求数列92{2nna-}的前n项和T n.17.在△ABC中,角A,B,C的对边分别为a,b,c.已知π4A=,b sin(π4+C)-c sin(π4+B)=a.(1)求证:B-C=π2;(2)若a=ABC的面积.18.如图,从A1(1,0,0),A2(2,0,0),B1(0,1,0),B2(0,2,0),C1(0,0,1),C2(0,0,2)这6个点中随机选取3个点,将这3个点及原点O两两相连构成一个“立体”,记该“立体”的体积为随机变量V(如果选取的3个点与原点在同一个平面内,此时“立体”的体积V=0).(1)求V=0的概率;(2)求V的分布列及数学期望EV.19.在三棱柱ABC-A1B1C1中,已知AB=AC=AA1BC=4,点A1在底面ABC的投影是线段BC的中点O.(1)证明在侧棱AA1上存在一点E,使得OE⊥平面BB1C1C,并求出AE的长;(2)求平面A1B1C与平面BB1C1C夹角的余弦值.20.已知三点O(0,0),A(-2,1),B(2,1),曲线C上任意一点M(x,y)满足||()2M A M B O M O A O B+=⋅++.(1)求曲线C的方程;(2)动点Q(x0,y0)(-2<x0<2)在曲线C上,曲线C在点Q处的切线为l,问:是否存在定点P(0,t)(t<0),使得l与PA,PB都相交,交点分别为D,E,且△QAB与△PDE的面积之比是常数?若存在,求t的值;若不存在,说明理由.21.若函数h(x)满足①h(0)=1,h(1)=0;②对任意a∈[0,1],有h(h(a))=a;③在(0,1)上单调递减.则称h(x)为补函数.已知函数11()()1pppxh xxλ-=+(λ>-1,p>0).(1)判断函数h(x)是否为补函数,并证明你的结论;(2)若存在m∈[0,1],使h(m)=m,称m是函数h(x)的中介元.记1pn=(n∈N+)时h(x)的中介元为x n,且1nn iiS x==∑,若对任意的n∈N+,都有12nS<,求λ的取值范围;(3)当λ=0,x∈(0,1)时,函数y=h(x)的图像总在直线y=1-x的上方,求p的取值范围.1. C 由已知,得{z |z =x +y ,x ∈A ,y ∈B }={-1,1,3},所以集合{z |z =x +y ,x ∈A ,y ∈B }中的元素的个数为3.2. D因为y =的定义域为{x |x ≠0},而1sin y x=的定义域为{x |x ≠k π,k ∈Z },ln x y x=的定义域为{x |x >0},y =x e x的定义域为R ,sin x y x=的定义域为{x |x ≠0},故D 项正确.3. B ∵f (10)=lg 10=1,∴f (f (10))=f (1)=12+1=2.4. D ∵1tan 4tan θθ+=,∴sin cos 4cos sin θθθθ+=. ∴22sin cos 4cos sin θθθθ+=,即24sin 2θ=.∴1sin 22θ=. 5. B A 项中,四边相等的空间四边形显然不是正方形,故A 项为真命题;B 项中,z 1,z 2∈C ,“z 1+z 2为实数”⇐“z 1,z 2互为共轭复数”,但“z 1+z 2为实数”D “z 1,z 2互为共轭复数”,故B 项为假命题;C 项中,假设x ,y 均小于等于1,则x +y ≤2,这与x +y >2相矛盾,故C 项为真命题;D 项中,012C C C C 2n nn n n n ++++=…,显然2n 是偶数,故D 项为真命题.6. C 利用归纳法:a +b =1,a 2+b 2=3,a 3+b 3=4=3+1,a 4+b 4=4+3=7,a 5+b 5=7+4=11,a 6+b 6=11+7=18,a 7+b 7=18+11=29,a 8+b 8=29+18=47,a 9+b 9=47+29=76,a 10+b 10=76+47=123.规律为从第三组开始,其结果为前两组结果的和.7. D 如图在Rt △ABC 中,因为D 为斜边AB 的中点,所以|CD |=12|AB |,又P 为CD 中点,所以|CP |=|PD |,以PA 、PB 为邻边作APBQ ,则有|P A |2+|PB |2=12(|PQ |2+|PB |2)而|PQ |=2|PD |=2|PC |,|AB |=2|CD |=4|PC | 故|PA |2+|PB |2=12[(2|PC |)2+(4|PC |)2]=10|PC |2 即222||||10||PA PB PC +=.8. B 设黄瓜和韭菜的种植面积分别为x 亩、y 亩,总利润为z 万元,则z 关于x ,y 的关系式为z =4x ×0.55-1.2x +6y ×0.3-0.9y =x +0.9y ,且x ,y 满足的约束条件为0,0,50,1.20.954.x y x y x y ≥⎧⎪≥⎪⎨+≤⎪⎪+≤⎩ 画可行域,如图所示:设l 0:109y x =-,将l 0上下平移可知,当直线z =x +0.9y 过点A (30,20)(注:可联立方程组500,1.20.9540,x y x y +-=⎧⎨+-=⎩解得点A 的坐标)时,z 取得最大值,因此当总利润z 最大时,x =30,y =20,即黄瓜的种植面积为30亩,韭菜的种植面积为20亩.9. A 由已知,得x 1+x 2+…+x n =n x ,y 1+y 2+…+y m =m y,1212()()(1)n m x x x y y y n x m y z x y m nm nαα++++++++===+-++……,整理,得()x y -[αm +(α-1)n ]=0, ∵x y ≠,∴αm +(α-1)n =0,即1n m αα=-.又102α<<,∴011αα<<-,∴01n m <<.又n ,m ∈N +,∴n <m .10. A 当x 从0开始,逐渐增大时,V (x )的变化不快,也不是x 的线性函数,故相排除C 、D ;当x 逐渐增大到1时,V (x )的变化也较慢,所以排除B 项,综合,选A 项.11.答案:23解析:1231112(sin )d cos 133x x x x x--⎰+=-=.12.答案:35解析:∵{a n },{b n }均是等差数列,根据等差数列的性质可得a 1+a 5=2a 3,b 1+b 5=2b 3,即a 5=2a 3-a 1,b 5=2b 3-b 1,∴a 5+b 5=2(a 3+b 3)-(a 1+b 1)=2×21-7=35.13.5解析:因为A ,B 为左、右顶点,F 1,F 2为左、右焦点,所以|AF 1|=a -c ,|F 1F 2|=2c ,|BF 1|=a +c . 又因为|AF 1|,|F 1F 2|,|BF 1|成等比数列,所以(a -c )(a +c )=4c 2,即a 2=5c 2,所以离心率5c e a ==.14.答案:3解析:当T =0,k =1时,π(1)πsin sin 22k k ->,所以a =1,T =1,k =2;当T =1,k =2时,π(1)πsin sin 22k k -<,所以a =0,T =1,k =3; 当T =1,k =3时,π(1)πsin sin 22k k -<,所以a =0,T =1,k =4; 当T =1,k =4时,π(1)πsin sin 22k k ->,所以a =1,T =2,k =5; 当T =2,k =5时,π(1)πsinsin22k k ->,所以a =1,T =3,k =6.此时k ≥6,所以输出T =3. 15.答案:(1)ρ=2cos θ (2)33{|22x x -≤≤} 16解:(1)由题知,当n =k ∈N +时,S n =-12n 2+kn 取得最大值,即8=S k =-12k 2+k 2=12k 2,故k 2=16(k ∈N +),因此k =4, 从而a n =S n -S n -1=92-n (n ≥2).又a 1=S 1=72,所以a n =92-n . (2)因为19222nn nn a n b --==,T n =b 1+b 2+…+b n =22123112222n n n n ---++++…+,所以T n =2T n -T n =2121111122144222222n n n n n nn n -----+++++-=--=-….17. (1)证明:由b sin(π4+C )-c sin(π4+B )=a ,应用正弦定理,得 sin B sin(π4+C )-sin C sin(π4+B )=sin A ,sin B(2sin C+2cos C )-sin C(2sin B+2cos B )=2,整理得sin B cos C -cos B sin C =1,即sin(B -C )=1, 由于0<B <3π4,0<C <3π4,从而B -C =π2.(2)解:B +C =π-A =3π4,又因为B -C =π2,因此5π8B =,π8C =,由a =π4A =,得sin 5π2sin sin 8a Bb A==,sin π2sin sin 8a C c A==,所以△ABC的面积15ππππ1sin sinsin288882S bc A ====.18.解:(1)从6个点中随机选取3个点总共有36C 20=种取法,选取的3个点与原点在同一个平面内的取法有1334C C 12=种,因此V =0的概率为123(0)205P V ===.(2)V 的所有可能取值为0,16,1,2,4,因此V 的分布列为由V 的分布列可得31113234190562032032032040E V =⨯+⨯+⨯+⨯+⨯=.19. (1)证明:连接AO ,在△AOA 1中,作OE ⊥AA 1于点E ,因为AA 1∥BB 1,得OE ⊥BB 1, 因为A 1O ⊥平面ABC ,所以A 1O ⊥BC . 因为AB =AC ,OB =OC ,得AO ⊥BC , 所以BC ⊥平面AA 1O ,所以BC ⊥OE , 所以OE ⊥平面BB 1C 1C . 又1AO ==,1AA =215AOAE AA ==.(2)解:如图,分别以OA ,OB ,OA 1所在直线为x ,y ,z 轴,建立空间直角坐标系,则A (1,0,0),B (0,2,0),C (0,-2,0),A 1(0,0,2),由115A E A A = 得点E 的坐标是42(0)55,,, 由(1)得平面BB1C 1C 的法向量是42(0)55O E = ,,, 设平面A 1B 1C 的法向量n =(x ,y ,z ),由10.0,AB A C⎧⋅=⎪⎨⋅=⎪⎩ n n 得20,0,x y y z -+=⎧⎨+=⎩令y =1,得x =2,z =-1,即n =(2,1,-1),所以cos ,10||||O E O E O E ⋅==⋅n n n , 即平面BB 1C 1C 与平面A 1B 1C 10.20.解:(1)由M A=(-2-x,1-y ),M B =(2-x,1-y ),得M A M B +=()O M O A O B ⋅+ =(x ,y )·(0,2)=2y ,由已知得22y =+, 化简得曲线C 的方程:x =4y .(2)(理)假设存在点P (0,t )(t <0)满足条件, 则直线P A 的方程是12t y x t -=+,PB 的方程是y =1-t2x +t . 曲线C 在点Q 处的切线l 的方程是20024x x y x =-,它与y 轴的交点为F (0,204x -).由于-2<x 0<2,因此-1<2x <1.①当-1<t <0时,11122t --<<-,存在x 0∈(-2,2),使得0122x t -=,即l 与直线P A 平行,故当-1<t <0时不符合题意.②当t ≤-1时,01122x t -≤-<,01122x t -≥>,所以l 与直线PA ,PB 一定相交.分别联立方程组2001,2,24t y x t x x y x -⎧=+⎪⎪⎨⎪=-⎪⎩和2001,2,24t y x t x x y x -⎧=+⎪⎪⎨⎪=-⎪⎩ 解得D ,E 的横坐标分别是20042(1)D x t x x t +=+-,20042(1)E x t x x t +=+-,则x E -x D =(1-t )202204(1)x t x t +--,又|FP |=-204x -t ,有S △PDE =12·|FP |·|x E -x D |=22022(4)18(1)x t t t x +-⋅--,又2200414(1)242QAB x x S ∆-=⋅⋅-=,于是22200220(4)[(1)]41(4)Q A B P D ES x x t S tx t ∆∆---=⋅-+·=42220042200[4(1)]4(1)41816x t x t tx tx t-+-+-⋅-++.对任意x 0∈(-2,2),要使Q A B P D ES S ∆∆为常数,即只须t 满足2224(1)8,4(1)16,t t t t ⎧---=⎨-=⎩ 解得t =-1.此时2Q A B P D ES S ∆∆=,故存在t =-1,使得△QAB 与△PDE 的面积之比是常数2. 21.解:(1)函数h (x )是补函数.证明如下:①110(0)()110ph -==+,111(1)()01ph λ-==+;②对任意a ∈[0,1],有111111(1)1(())(())11111pp p p pp p p ppa a a a h h a h a a a a λλλλλλ⎛⎫-- ⎪⎡⎤-++==== ⎪⎢⎥-++ ⎪⎣⎦+ ⎪+⎝⎭; ③令g (x )=(h (x ))p,有112(1)(1)()(1)p p p p ppxx x pxg'x x λλλ---+--=+=12(1)(1)p pp x x λλ--++,因为λ>-1,p >0,所以当x ∈(0,1)时,g ′(x )<0,所以函数g (x )在(0,1)上单调递减,故函数h (x )在(0,1)上单调递减. (2)当1p n=(n ∈N +)时,由h (x )=x ,得21210n n x x λ+-=.(*)(ⅰ)当λ=0时,中介元1()2nn x =;(ⅱ)当λ>-1且λ≠0时,由(*)得()10,1n x =或1[0,1]n x =;得中介元1nn x =.综合(ⅰ)(ⅱ),对任意的λ>-1,中介元为(nn x =(n ∈N +),于是,当λ>-1时,有1()1)nin n i S =⎡⎤==-<⎢⎥⎣⎦∑当n无限增大时,1n无限接近于0,S n1故对任意的n ∈N +,12n S <12≤,即λ∈[3,+∞).(3)当λ=0时,1()(1)pph x x =-,中介元为11()2pp x =, (ⅰ)当0<p ≤1时,11p≥,中介元为111()22pp x =≤,所以点(x p ,h (x p ))不在直线y =1-x 的上方,不符合条件;(ⅱ)当p >1时,依题意只须1(1)1pp x x ->-在x ∈(0,1)时恒成立, 即x p +(1-x )p <1在x ∈(0,1)时恒成立,设φ(x )=x p +(1-x )p,x ∈[0,1], 则φ′(x )=p [x p -1-(1-x )p -1], 由φ′(x )=0得12x =,且当x ∈(0,12)时,φ′(x )<0,当x ∈(12,1)时,φ′(x )>0,又因为φ(0)=φ(1)=1,所以当x∈(0,1)时,φ(x)<1恒成立.综上,p的取值范围是(1,+∞).。
2012年铜仁地区高中阶段教育招生统一考试数学卷(word有答案)
(第19题图)(第20题图)325=BD2012年温州市初中毕业学生模拟学业检测数学参考答案一、选择题(本题有10小题,每小题4分,共40分,请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)1、D2、B3、D4、A5、C6、B7、C8、D9、C 10、C 二、填空题(本题有6小题,每小题5分,共30分)11、)2)(2(-+a a 12、x=—2 13、x <—1 14、 12π 15、3216、54 三、解答题(本题有8小题,共80分)17.计算:(本题7分)0)2(45sin 28π-+- .=122222+⨯- …………………………3分=12- ……………………4分18.(本题8分)先化简,再求值:12)8()4)(4(--+-+m m m m ,其中m=21 解:原式=16—m 2+m 2—8m —12=—8m+4 ………… ……………………4分=—821⨯+4 = 0 ……………………4分19.(本题8分)(1) △ABF ≌△DCE △ABD ≌△DCB △AFD ≌△CEB ……………………3分 (2) 选择△ABD ≌△DCB ,证明如下:∵平行四边形 ABCD ∴ AB ∥CD, AB=CD, ∴ ∠ABD =∠DCB . ∵ BD=DB ∴△ABD ≌△DCB .………………5分 20.(本题10分)(2+4+4分) (1) 图①30% ,图② 20(2) 40 名, 20 人; (3) 1200×50% =600 名答:全校共有600名学生可以参加下一轮的测试。
21.(本题9分) (3+3+3分)(不需尺规作图,只要面积不同,就视为不同方案)ABCDE F6cm6cmABCD8cm6cm4cmA BCD8cmA BD8cmCO ABC M Nxy (第22题图)(第24题图)面积= 48 cm 2, 面积= 40 cm 2, 面积= 100/3 cm 2, 22(本题12分)(1)证明:如图,连结OD ,则 OD OB =∴ CBA ODB ∠=∠. ∵ AC =BC , ∴ CBA A ∠=∠.∴ ODB A ∠=∠. ∵ OD ∥AC ,∴ ODE CFE ∠=∠. ∵ DF AC ⊥于F ,∴ 90CFE ∠=.∴90ODE ∠=.∴ OD EF ⊥. ∴ EF 是⊙O 的切线. -----------6分 ( 2 ) ∵BC 是直径, ∴∠BGC =90 设 CG x =,则 6AG AC CG x =-=-. 在R t △BGA 中,222228(6)BG AB AG x =-=--.在R t △BGC 中, 222226BG BC CG x =-=-.∴ 22228(6)6x x --=-.解得 23x =.即 23CG =. 在R t △BGC 中,1sin 9GC GBC BC ∠== . --------------6分 23.(本题12分)解:(1)由题意得:98012000)2012000)(1(+=+-mm ,………2分 解得601=m 102-=m ,……………………2分经检验,601=m 102-=m ,都是原方程的解,但102-=m 不合题意,舍去 …1分 ∴ m 的值是60. (2))206012000)(4060(x x y +--= ……………………3分 )10)(20(20+--=x x y 或4000200202++-=x x y 或4500)5(202+--=x y …2分(3)2≤x ≤8……………………2分 24.(本题14分)(1) C (0,5), M (1,0)………… (2分) 55+-=x y ………… (2分) (2) S =21t 2+25t (t >0)……(2分) S =-21t 2-25t (-5<t <0)…(2分)S =21t 2+25t (t <-5)……(2分)(注:取值范围含等号,同样给分)(3) P1(2,5)…………(2分)P2(2,3)…………(2分)。
贵州省铜仁地区2012年中考数学模拟试卷
第5题图贵州省铜仁地区2012年中考数学模拟试卷友情提示:本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题.本试卷满分为120分,考试时间为120分钟.卷Ⅰ(选择题,共20分)一、选择题(本大题共10个小题;每小题2分,共20分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.计算12--的值为( )A .1-B .1C .3- D .32.如右图,从左边看图中的物体,得到的图形是( )3.小马虎在下面的计算中只做对了一道题,他做对的题目是( ) A .23a aa += B .222()ab a b -=- C .m n mn a b ab ∙= D .2362)8a a -=-(4.下列函数中,自变量x 的取值范围是x >2的函数是( ) A .2-=x y B . 12-=x y C . 21-=x y D . 121-=x y 5.如图,水平放置的一个油管的截面为圆形,其直径为26cm ,其中有油 部分油面宽AB 为24 cm ,截面上有油部分的油面高CD 为( ) A .5cm B .8cm C . 12cm D .13cm6.出售甲、乙两种商品,售价都是1800元,其中甲商品能赢利20%, 乙商品亏损20%,如果同时售出甲、乙商品各一件,那么( ) A .共赢利150元 B .共亏损150元 C .不盈也不亏 D .无法判断 7.下图是测量一物体体积的过程:步骤一,将180ml 的水装进一个容量为300ml 的杯子中. 步骤二,将三个相同的玻璃球放入水中,结果水没有满. 步骤三,同样的玻璃球再加一个放入水中,结果水满溢出.根据以上过程,推测一颗玻璃球的体积在下列哪一范围内?(1ml=1cm 3)( )A.10cm 3以上,20cm 3以下 B.20cm 3以上,3cm 3以下 C.3cm 3以上,4cm 3以下D.4cm 3以上,5cm 3以下8.如图,在△ABC 中,∠A =30º,∠B =50º ,AC =AE ,BC =BD ,则∠DCE 的度数为 ( )A .20ºB .25ºC .30ºD .40º 9.如图,反比例函数4y x =-的图象与直线13y x =-的交点为A 、B , 过点A 作y 轴的平行线与过点B 作x 轴的平行线相交于点C ,则ABC △的面积为( )A.8B.6C.4 D.210.如右上图,某运动员P 从半圆跑道的A 点出发沿APB 匀速前进到达终点B ,若以时间t 为自变量,扇形OAP 的面积S 为函数的图象大致是( )42数学试卷A.B. C.D.第2A.B.C.D.步骤一: 步骤二: 步骤三:第8题图第10题图第18题图第16题图卷Ⅱ(非选择题,共100分)二、填空题(本题8个小题,每小题3分,满分24分) 11.分解因式:22242x xy y -+= .12.用科学记数法表示0.0000106= .13.某电视台举办歌手大奖赛,每场比赛都有编号为1~10号共10道综合素质题供选手随机抽取作答.在某场比赛中,前两位选手分别抽取了2号、7号题,那么第三位选手抽中8号题的概率是 .14.某款手机连续两次降价,售价由原来的1185元降到580元,设两次降价的平均百分率为x ,则可列方程为 .15.如图,是小顺制作的一个圆锥形纸帽的示意图,则围成这个纸帽的纸的面积为 . 16.已知:如图,⊙O 的半径为1,PA 切⊙O 于A ,OP 交⊙O 于B ,且分的面积S=____________.17.瑞士中学教师巴尔末成功地从光谱数据59、1216、2125、3236…中得到巴尔末公式,从而打开了光谱奥秘的大门,请你按照这种规律写出第七个数据是______.18.如图所示,某校宣传栏(图中的AB )后面2米处种了一排树,每隔2米一棵,共种了6棵,小惠站在宣传栏中间位置的垂直距离3米处(点C 处),正好看到两端的树干,其余4棵均被挡住,那么宣传栏的长为 米.(不计宣传栏的厚度)三、解答题(本大题共8个小题;满分76分) 19.(本小题满分7分)已知12+=x ,求21111xx x ⎛⎫+÷ ⎪--⎝⎭的值. 20.(本小题满分7分)已知:如图,等边三角形ABC 中,D 为AC 边的中点,过C 作CE ∥AB ,且AE ⊥CE .求证:BD=AE .21.(本小题满分8分)如图,图(1)是某中学初三(A )班全体学生对三种蔬菜的喜欢人数的频数分布直方图.解答下列问题:(1)初三(A )班总人数为 人;(2)喜欢人数频率最高的蔬菜是 ,且频率为 ; (3)请根据各统计图中的数据,补全图(1)、(2)中的统计图;(4)根据上述统计的结果,请你为食堂的进货提出一条合理化的建议.建议: 22.(本小题满分10分)售货员:“快来买啦,特价鸡蛋,原价每箱14元,现价每箱12元,每箱有鸡蛋30个.”顾客甲:“我店里买了一些这种特价鸡蛋,花的钱比按原价买同样多鸡蛋花的钱的2倍少96元.”乙顾客:“我家买了两箱特价的鸡蛋,结果18天后,剩下的20个鸡蛋全坏了.”请你根据上面的对话,解答下面的问题: (1)顾客乙买的两箱鸡蛋合算吗?说明理由.(2)请你求出顾客甲店里买了多少箱这种特价鸡蛋,假设这批特价鸡蛋的保质期还有18天,那么甲店里平均每天至少要消费多少个鸡蛋才不会浪费? 23.(本小题满分10分)某地举行龙舟赛,甲、乙两队在比赛时,路程y (米)与时间x (分钟)的函数图象如图所示,根据函数图象填空和解答问题: (1)最先到达终点的是 队,比另一队领先 分钟到达; (2)在比赛过程中,甲队的速度始终保持为 米/分;而乙队在第分钟后第第20题图图(1) 图(2)第15题图姓名 考号_______________ 班级____________________一次加速,速度变为 米/分,在第 分钟后第二次加速; (3)图中点A 的坐标是 ,点B(424.(本小题满分10分)用两个全等的正方形ABCD 和CDFE 拼成一个矩形ABEF ,把一个足够大的直角三角尺的直角顶点与这个矩形的边AF 的中点D 重合,且将直角三角尺绕点D 按逆时针方向旋转. (1)当直角三角尺的两直角边分别与矩形ABEF 的两边BE EF ,相交于点G H ,时,如图(1),通过观察或测量BG 与EH 的长度,你能得到什么结论?并证明你的结论.(2)当直角三角尺的两直角边分别与BE 的延长线、EF 的延长线相交于点G H ,时,(如图(2)),你在(1)中得到的结论是否还成立?请说明理由.25.(本小题满分12分)某商场将进货价为30元的书包以40元售出,平均每月能售出600个,调查表明:这种书包的售价每上涨1元,其销售量就减少10个.(1)为了使平均每月有10000元的销售利润,这种书包的售价应定为多少元?(2)10000元的利润是否为最大利润?如果是,请说明理由:如果不是,请求出最大利润,并指出此时书包的售价为多少元?(3)请分析并回答售价在什么范围内商家就可以获得利润.26.(本小题满分12分)如图,平面直角坐标系中,四边形OABC 为菱形,点C 的坐标为(4,0),∠AOC =60°,垂直于x 轴的直线l 从y 轴出发,沿x 轴正方向,以每秒1个单位长度的速度运动,设直线l 与菱形的OABC 两边分别交于点M 、N (点M 在点N 的上方). (1)求A 、B 两点的坐标;(2)设△OMN 的面积为S ,直线l 运动的时间为t ,试 求S 与t 的函数关系式;(3)在题(2)的条件下,t 为何值时,△OMN 的面积S 最大?最大面积是多少?A BCO MN l xy 第26题图A BG C E HF D 图(1) A BG CE H FD 图(2)第23题图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学试卷 第 1 页 共 13 页保密★启用前铜仁市2012年初中毕业生学业(升学)统一考试数 学 试 题姓名: 准考证号:注意事项1. 答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置;2. 答题时,卷I 必须使用2B 铅笔,卷II 必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置,字体工整、笔迹清楚;3. 所有题目必须在答题卡上作答,在试卷上答题无效;4. 本试卷共8页,满分150分,考试时间120分钟;5. 考试结束后,将试题卷和答题卡一并收回.卷I一、选择题:(本大题共10个小题,每小题4分,共40分)本题每小题均有A 、B 、C 、D 四个备选答案,其中只有一个是正确的,请你将正确答案的序号填涂在相应的答题卡上.1.-2的相反数是( )A.21B. -21错误!未找到引用源。
C. -2 D. 2 2.下列四个图形中,既是轴对称图形又是中心对称图形的有()A .4个B .3个C .2个D .1个3.某中学足球队的18名队员的年龄情况如下表:则这些队员年龄的众数和中位数分别是( ) A .15,15B .15,15.5C .15,16D .16,15年龄(单位:岁)14 15 16 17 18 人数364412题图数学试卷 第 2 页 共 13 页4. 铜仁市对城区主干道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x 棵,则根据题意列出方程正确的是( ) A. )1(6)121(5-=-+x x B. )1(6)21(5-=+x x C. x x 6)121(5=-+D. x x 6)21(5=+5.如图,正方形ABOC 的边长为2,反比例函数ky x=的图象经过点A , 则k 的值是( ) A .2 B .-2 C .4D .-46.小红要过生日了,为了筹备生日聚会,准备自己动手用纸板制作一个底面半径为9cm,母线长为30cm 的圆锥形生日礼帽,则这个圆锥形礼帽的侧面积为( ) A .270πcm 2B .540πcm 2C .135πcm 2D .216πcm 27.如图,在ΔABC 中,∠ABC 和∠ACB 的平分线交于点E ,过点E 作MN ∥BC 交AB 于M , 交AC 于N ,若BM+CN=9,则线段MN 的长为( ) A . 6 B. 7 C. 8D. 98.如图,六边形ABCDEF ∽六边形GHIJKL ,相似比为2:1,则下列结论正确的是( )A .∠E=2∠K B. BC=2HIC. 六边形ABCDEF 的周长=六边形GHIJKL 的周长D. S 六边形ABCDEF =2S 六边形GHIJKL8题图7题图5题图数学试卷 第 3 页 共 13 页9.从权威部门获悉,中国海洋面积是299.7万平方公里,约为陆地面积的三分之一, 299.7万平方公里用科学计数法表示为( )平方公里(保留两位有效数字) A .6103⨯B .7103.0⨯C .6100.3⨯D .61099.2⨯10.如图,第①个图形中一共有1个平行四边形,第②个图形中一共有5个平行四边形,第③个图形中一共有11个平行四边形,……则第⑩个图形中平行四边形的个数是( )A.54B.110C.19D.109卷II二、填空题:(本大题共8个小题,每小题4分,共32分)11.2012-=_________;12.当x ___________时,二次根式1x有意义; 13.一个多边形每一个外角都等于40,则这个多边形的边数是______;14.已知圆O 1和圆O 2外切,圆心距为10cm ,圆O 1的半径为3cm ,则圆O 2的半径为 ______; 15.照下图所示的操作步骤,若输入x 的值为5,则输出的值为_______________;16.一个不透明的口袋中,装有红球6个,白球9个,黑球3个, 这些球除颜色不同外没有任何区别,从中任意摸出一个球, 则摸到黑球的概率为_______________; 17.一元二次方程0322=--x x 的解为____________;18.以边长为2的正方形的中心O 为端点,引两条相互垂直的射线,分别与正方形的边交于A 、B 两点,则线段AB 的最小值是__________.输入x加上5平方减去3输出10题图数学试卷 第 4 页 共 13 页三、解答题:(本题共4个题,19题每小题5分,第20、21、22每题10分,共40分,要有解题的主要过程) 19.(1)化简:12)1111(2-÷--+x x x(2)某市计划在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M 到广场的两个入口A 、B 的距离相等,且到广场管理处C 的距离等于A 和B 之间距离的一半,A 、B 、C 的位置如图所示,请在原图上利用尺规作图作出音乐喷泉M 的位置,(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)20.如图,E 、F 是四边形ABCD 的对角线BD 上的两点, AE ∥CF ,AE=CF ,BE=DF. 求证: ΔADE ≌ΔCBF .20题图19(2)题图数学试卷 第 5 页 共 13 页21.某市对参加2012年中考的50000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:(1)在频数分布表中,a 的值为__________,b 的值为__________,并将频数分布直方图补充完整;(2)甲同学说“我的视力情况是此次抽样调查所得数据的中位数”,问甲同学的视力情况应在什么范围内?(3)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是________,并根据上述信息估计全市初中毕业生中视力正常的学生有多少人?22.如图,定义:在直角三角形ABC 中,锐角α的邻边与对边的比叫做角α的余切,记作ctan α, 即ctan α=BCAC=的对边角的邻边角αα,根据上述角的余切定义,解下列问题:(1)ctan30◦= ; (2)如图,已知tanA=43,其中∠A 为锐角,试求ctanA 的值.21题图22题图频率数学试卷 第 6 页 共 13页四、(本题满分12分)23.如图,已知⊙O 的直径AB 与弦CD 相交于点E , AB ⊥CD ,⊙O 的切线BF 与弦AD 的延长线相交于点F . (1)求证:CD ∥ BF ;(2)若⊙O 的半径为5, cos ∠BCD=54,求线段AD 的长.23题图五、(本题满分12分)24.为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.(1)求购进A、B两种纪念品每件各需多少元?(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?数学试卷第7 页共13 页数学试卷 第 8 页 共 13 页六、(本题满分14分)25.如图已知:直线3+-=x y 交x 轴于点A ,交y 轴于点B ,抛物线y=ax 2+bx+c 经过A 、B 、C (1,0)三点. (1)求抛物线的解析式;(2)若点D 的坐标为(-1,0),在直线3+-=x y 上有一点P,使ΔABO 与ΔADP 相似,求出点P 的坐标;(3)在(2)的条件下,在x 轴下方的抛物线上,是否存在点E ,使ΔADE 的面积等于四边形APCE 的面积?如果存在,请求出点E 的坐标;如果不存在,请说明理由.25题图数学试卷 第 9 页 共 13页铜仁市2012年初中毕业生学业(升学)统一考试数学参考答案及评分标准一、选择题(每小题4分):题号 1 2 3 4 5 6 7 8 9 10 答案DBBADADBCD二、填空题(每小题4分):11、2012; 12、0>; 13、9; 14、7cm ;15、97; 16、16; 17、31或-; 18、2. 三、解答题19.(1)(5分)解:原式=21)1111(2-⋅--+x x x ………………………………1分 =1112----x x x 212-⋅x …………………. ……………….……3分= -1………………………………………………………………5分(2)(5分)作图:连结AB ………………………………………………………1分作出线段AB 的垂直平分线……………………………………………3分在矩形中标出点M 的位置…………………………………………… 5分 ( 必须保留尺规作图的痕迹,痕迹不全少一处扣1分,不用直尺连结AB 不给分, 无圆规痕迹不给分.) 20.(10分) 证明:∵AE ∥CF∴∠AED=∠CFB …………………… 3分 ∵DF=BE∴DF+EF=BE+EF 即DE=BF………6分 在△ADE 和△CBF 中⎪⎩⎪⎨⎧=∠=∠=BF DE CFB AED CF AE …………………9分 ∴△ADE ≌△CBF (SAS )……… 10分数学试卷 第 10 页 共 13页21.(10分)解:(1)60;0.05;补全图形……………….. 3分(2)4.6≤x<4.9 ……………………….…. 6分 (3)35%……………………………………7分17500%3550000=⨯(人)………… 10分22.(10分)解:(1)3 ……………………. 5分(2)43tan ==AC BC A , ∴34tan ==BC AC c ……………. . 10分四、23.(12分)(1)证明:∵BF 是圆O 的切线,AB 是圆O 的直径∴BF ⊥AB…………………………………………3分 ∵CD ⊥AB ∴CD ∥BF ………………………………….…… 6分 (2)解:∵AB 是圆O 的直径∴∠ADB=90º ………………………………… 7分 ∵圆O 的半径5 ∴AB=10 ……………………………………… 8分 ∵∠BAD=∠BCD …………………………… 10分∴ cos ∠BAD= cos ∠BCD=45=AD AB ∴1054cos ⨯=⋅∠=AB BAD AD =8∴AD=8…………………………………………12分数学试卷 第 11 页 共 13 页五、24.(12分)解:(1)设该商店购进一件A 种纪念品需要a 元,购进一件B 种纪念品需要b 元, 根据题意得方程组⎩⎨⎧=+=+8006595038b a b a …………………………………………………………2分 解方程组得⎩⎨⎧==50100b a ∴购进一件A 种纪念品需要100元,购进一件B 种纪念品需要50元…………4分(2)设该商店购进A 种纪念品x 个,则购进B 种纪念品有(100—x )个∴⎩⎨⎧≤-+≥-+7650)100(501007500)100(50100x x x x ………………………………………6分 解得50≤x ≤53 …………………………………………………………7分∵ x 为正整数,∴共有4种进货方案………………………………………………8分(3)因为B 种纪念品利润较高,故B 种数量越多总利润越高,因此选择购A 种50件,B 种50件.…………………………………………………10分总利润=250030502050=⨯+⨯(元)∴当购进A 种纪念品50件,B 种纪念品50件时,可获最大利润,最大利润是2500元………………………………………………………………………12分数学试卷 第 12 页 共 13 页六、25.(14分)解(1):由题意得,A (3,0),B (0,3)∵抛物线经过A 、B 、C 三点,∴把A (3,0),B (0,3),C (1,0)三点分别代入2y ax bx c =++得方程组⎪⎩⎪⎨⎧=++==++03039c b a c c b a ……3分 解得:⎪⎩⎪⎨⎧=-==341c b a∴抛物线的解析式为243y x x =-+………………5分(2)由题意可得:△ABO 为等腰三角形,如图所示,若△ABO ∽△AP 1D ,则1DP OB AD AO = ∴DP 1=AD=4 ,∴P 1(1,4)-……………………………………………… …………7分若△ABO ∽△ADP 2 ,过点P 2作P 2 M ⊥x 轴于M ,AD=4,∵△ABO 为等腰三角形, ∴△ADP 2是等腰三角形,由三线合一可得:DM=AM=2= P 2M ,即点M 与点C 重合∴P 2(1,2)……………………10分数学试卷 第 13 页 共 13页 (3)如图设点E (,)x y ,则||2||21y y AD S ADE =⋅⋅=∆ ①当P 1(-1,4)时, S四边形AP 1CE =S 三角形ACP 1+S 三角形ACE ||2214221y ⋅⨯+⨯⨯= = 4y +………………………11分∴24y y =+ ∴4y =∵点E 在x 轴下方 ∴4y =-代入得: 2434x x -+=-,即 0742=+-x x∵△=(-4)2-4×7=-12<0∴此方程无解……………………………………………………………12分 ②当P 2(1,2)时,S 四边形AP 2CE =S 三角形ACP 2+S 三角形ACE = 2y + ∴22y y =+ ∴2y =∵点E 在x 轴下方 ∴2y =- 代入得:2432x x -+=- 即 0542=+-x x ,∵△=(-4)2-4×5=-4<0 ∴此方程无解综上所述,在x 轴下方的抛物线上不存在这样的点E.……………14分。
