静载试验计算单
16000kN静载钢平台承载力验算书及设计书
钢平台结构计算书惠州市林浩钢结构建设有限公司钢平台结构计算书编制：审核：批准：惠州市林浩钢结构建设有限公司二〇二〇年一月钢平台结构计算书一、概述1.1 单桩竖向抗压静载试验概述单桩竖向抗压静载试验（以下简称单桩静载），适用于检测单桩的竖向抗压承载力。
既可用于设计阶段的试验桩检验，也可用于施工阶段工程桩抽样检测。
图1 静载试验现场1.2 加载反力装置概述单桩静载试验设备由包括加载系统、反力系统和量测系统三大部分组成，见图2。
常用压重平台作为反力装置，即所谓堆载法、堆重法。
堆载法反力装置由支墩、主梁、次梁、混凝土试块组成。
加载装置由千斤顶构成，通过控制仪器自动加载。
图2 压重平台反力装置示意图1.3 试验加载要求按单桩承载力特征值为8000kN，垂直静载试验加荷最大值为16000kN计。
主要受力参数如下表所示：表1 受力指标1.4 平台细部构造1.4.1 拟选用主、次梁及其尺寸主梁、次梁采用箱形钢梁，主梁长度为10m，配置2根；次梁长度为12m，配置10根。
细部尺寸见图3、图4。
图3：主梁细部尺寸图图4：次梁细部尺寸图主梁截面高度H=1000mm，宽度B=500mm，腹板厚度t w=32mm，上下翼缘厚度t f=50mm，翼缘自由外伸宽度c=18mm，不设加劲肋。
次梁截面高度H=600mm，宽度B=600mm，腹板厚度t w=20mm，上下翼缘厚度t f=20mm。
翼缘自由外伸宽度c=100mm，加劲肋间距为1000mm。
钢垫块尺寸1000mm×2000mm、厚度25mm，配置3~4块。
1.4.2 平台尺寸两支墩轴线间距8.0m，净距7.0m，并保证支墩边与桩中心距离不少于4D且不少于2.0m。
钢平台尺寸为12m×10m，次梁两端搁置于支墩上，主梁置于次梁之下，未加载时主次梁间为脱离状态；次梁两端伸出支墩轴线外长度2.0m，跨度8.0m，次梁间横向轴线间距1.0m。
水泥试块尺寸为1m×1m×2m，单块重量为50kN。
钢结构结构构件性能(静载试验)检测报告
(首页)共页第页委托单位报告编号工程名称工程部位样品名称样品编号样品数量规格型号施工单位样品状态生产厂家生产工艺代表批量生产日期委托日期委托人检测设备联系电话抽样人检测类别抽样数量检测日期抽样地点检测环境检测场所地抽样时间址检测依据抽样基数检测项目检测结论批准：审核：主检：检测单位检测专用章（盖章）签发日期：年月日(附页)共页第页样品名称报告编号检测项目样品状态检测依据检测内容项目外型尺寸（mm）主肋（mm）副肋填充体自重（kN/m2）设计实测检测项目技术要求检测结果单项结论使用性能检验挠度（mm）卸载后残余变形（%）荷载-变形曲线承载力检验卸载后变形减少（%）破坏标志破坏性检验（kN）检测说明(附页)共页第页样品名称报告编号加载简图、仪表位置（加载简图、仪表位置及编号简图）及编号简图裂缝情况及破坏特（裂缝情况及破坏特征简图）征简图检测说明见证单位：见证人：共页第页构件名称构件型号图集编号样品编号生产厂家生产工艺生产日期环境条件检测地点检测依据设备名称设备编号设备状态项目外形尺寸(mm)主肋(mm)副肋(mm)填充体自重(kN/m2)允许外加均布荷载(kN/m2)使用性能检测承载力检测标准值设计值挠度(mm)卸载后残余变形荷载—变形曲线卸载后变形减少破坏标志设计实测加载简图、仪表位置及编号裂缝情况及破坏特征记录说明校核：主检：检测日期：共页第页构件名称规格型号样品编号检测依据加荷荷载（kN）各测点位移(mm）使用性能荷载（kN）承载力（kN）承载力状态挠度最大裂缝宽度实测值(mm) 1234最大变形量卸载后变形量系数时间每级累计读数差值读数差值读数差值读数差值1234567891011121314151617181920记录说明校核：主检：检测日期：。
钢筋混凝土梁静载试验报告
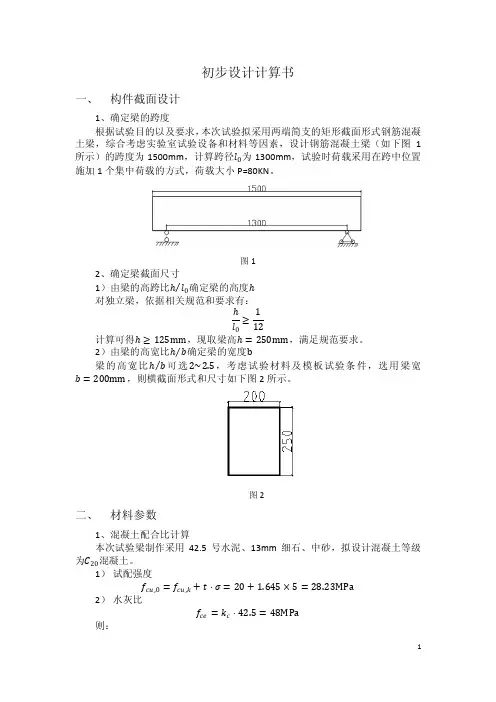
0
0
0
+
= 100 −
− 0 − 10 ·
0 0
0
0
=
0 + 0
代入数据，解得:
0 = 666kg
0 = 1238kg
则计算配合比：
0 : 0 : 0 : 0 = 316: 666: 1238: 180
2、 材料用量
根据所设计梁截面和跨度，混凝土梁及立方体试件总体积：
×
解得：ρ
sv
2 + 0.6 × 1.37
20 × × 195
= 0.0012 = 0.12%
按照规范要求，取最小配箍率为 0.18%
= 2 × 28.3 = 56.6²
=
1 × 1 × 0.56 × 10−6 × 2 + 0.6p
, b0
40.942
则，取h = 400，查 GB50010-2002： = 1.55， = 1.54Mpa
120
120
γ = 0.7 +
= 0.7 +
× 1.55 = 1.55
400
结构抗裂检验容许值：
= =
cr = 0.95
+
= 0.95 × 1.55 = 1.47
和箍筋承担。
1 截面尺寸：
○
0.51 × 10−3 fcu ,k bh0 = 0.51 × 10−3 × 20 × 200 × 20 = 100.4KN ≥ r0 ·Vd
截面尺寸满足要求。
2 箍筋：
○
0.5 × 10−3 0 = 0.5 × 10−3 × 1.06 × 200 × 20 = 23.32KN
沙田镇横流桥单梁静载试验加载力计算
沙田镇横流桥单梁静载试验加载力计算一、一期恒载计算：根据设计图纸：单块中板砼体积为11.3m3，对应自重力为11.3*26=293.8kN；单块边板砼体积为14.635m3，对应自重力为14.635*26=380.5kN。
折算为单片梁线荷载为：中板：q中=293.8/20=14.69kN/m边板：q边=380.5/20=19.03kN/m支座距跨径中心线0.35m，则计算跨径为：20-2*0.35=19.3m 中板自重内力M中=1/8*14.69*19.32=684kN-m边板自重内力M边=1/8*19.03*19.32=886kN-m二、二期恒载计算：(1)铺装层荷载：10cm厚沥青砼面层（宽15m）、10cm水泥砼铺装层（宽20m），桥梁横向共布置有15块空心板，单块空心板每延米承受的铺装重量为：(0.1*15*24+0.1*20*25)/15=5.73kN/m；(2)人行道及栏杆重量：查阅人行道及栏杆设计图：全桥人行道及栏杆柱、底座圬工量为：(68.1+28.8+9.81)=106.7m3,栏杆钢管重量为29.6kN。
桥长80米，假定人行道及栏杆重量由15块板梁平均分担，则单块空心板每延米承受的重量为：(106.7*25+29.6)/(80*15)=2.25 kN/m(3)单块空心板二期线荷载为：5.73+2.25=8.0 kN/m二期荷载产生的内力M二期=1/8*8.0*19.32=372.5kN-m三、汽车荷载作用：按公路—Ⅰ级加载。
根据现行《公路桥涵设计通用规范》（JTG D60-2004）中第4.3条之规定：对于公路—Ⅰ级汽车荷载可简化按车道荷载（均布荷载+集中力）计算。
其中，均布荷载q汽=10.5kN/m、集中力P汽=240 kN。
由于桥梁行车道宽度为15m，按规范表4.3.1-3规定：本桥设计车道数为4。
横向布置有15块板，布置有4列车时，横向分布系数平均值为：4/15=0.267。
高铁箱梁静载试验计算公式
高铁箱梁静载试验计算公式在高铁建设中，箱梁是一种常见的桥梁结构，用于支撑铁路轨道和列车的运行。
为了保证箱梁的安全性能和承载能力，需要进行静载试验来验证其设计参数和结构稳定性。
静载试验是通过施加静态荷载，观察箱梁的变形和应力情况，从而评估其承载能力和结构性能。
在进行高铁箱梁静载试验时，需要计算箱梁的承载能力和变形情况，以验证其设计参数和结构稳定性。
下面将介绍高铁箱梁静载试验计算公式，以及公式中涉及的参数和变量。
高铁箱梁静载试验计算公式如下：1. 箱梁的承载能力计算公式：P = σ× A。
其中，P为箱梁的承载能力，单位为N（牛顿）；σ为箱梁的应力，单位为Pa （帕斯卡）；A为箱梁的截面积，单位为m²（平方米）。
在静载试验中，可以通过施加不同的荷载，测量箱梁的应力情况，从而计算出其承载能力。
箱梁的应力可以通过应力传感器进行实时监测，从而得出箱梁的承载能力。
2. 箱梁的变形计算公式：δ = PL³ / 3EI。
其中，δ为箱梁的变形，单位为m（米）；P为施加在箱梁上的荷载，单位为N（牛顿）；L为箱梁的长度，单位为m（米）；E为箱梁的弹性模量，单位为Pa （帕斯卡）；I为箱梁的惯性矩，单位为m⁴（米的四次方）。
箱梁的变形是箱梁在受力后产生的形变，通过测量箱梁的变形情况，可以评估其结构的稳定性和变形能力。
在静载试验中，可以通过激光测距仪等设备实时监测箱梁的变形情况，从而得出其变形参数。
在进行高铁箱梁静载试验时，需要根据实际情况确定箱梁的设计参数和试验方案，以确保试验结果的准确性和可靠性。
同时，还需要对试验过程中的数据进行分析和处理，以得出箱梁的承载能力和变形情况，为箱梁的设计和使用提供参考依据。
总之，高铁箱梁静载试验计算公式是进行箱梁静载试验的基础，通过计算箱梁的承载能力和变形情况，可以评估其结构性能和安全性能。
在实际工程中，需要根据实际情况确定试验方案和参数，以确保试验结果的准确性和可靠性，为高铁箱梁的设计和使用提供科学依据。
桥梁静载试验载荷计算书
0.930
14499.473 417.251
八、 计算各级加载的跨中弯矩和荷载值
3‐1‐16‐1‐0‐3‐1 级别
初始状态
加载弯矩（kN.m） 0.000
第3页
加载荷载（kN） 0.000
基数级 0.6 级 0.80 级 静活载级 1.00 级 1.05 级 1.10 级 1.15 级 1.20 级
第1页
数值 23.5 0.01 0.00 0.85 1.34 1.11 1.19
1
序号 9 10 11 12 13 14 15 16 17 18 19
名称
二期恒载质量对跨中弯矩 Md(KN.m) 防水层质量对跨中的弯矩 Mf(KN.m) 活载对跨中的弯矩 Mh(KN.m) 梁体质量对跨中的弯矩 Mz(KN.m) 混凝土收缩徐变应力损失σ_L6(MPa) 钢筋松弛应力损失σ_L5(MPa) 挠跨比 f/L 抗裂安全系数 Kf 实测挠度修正系数 fφ 均布荷载剪力滞系数 Kq 集中荷载剪力滞系数 Kp
W
AA
e
3
损失的补偿弯矩ΔMs
A 10
计算基数级下跨中弯
4
矩（防水层未铺设）
已铺：M
M ∆M M
未铺：M M ∆M M M
Mka
5
计算基数级加载值 Pka
M P
α
计算各加载级下跨中 已铺：M Mz Mf Ms
未铺：M K M M M
Mk
Mf ∆Ms Mz Ms
η1=0.500
第2页
钢筋松弛应力损失σL5 的完成率：
η2=1.000
七、 各级加载弯矩参数计算
每点加载点的重量按：Ps=1000.000(kN)。 各级加载弯矩参数计算
17桥梁荷载试验与承载力评定(静载)
北京某一悬索桥静载试验时突然坍塌
每辆车的重量大概在8吨到10吨左右，10辆车加起来将近100吨
北京某一悬索桥静载试验时突然坍塌
•第10辆车上桥，突然塌了 •支架倒下劈碎桥头面包车 •10辆用来测试的卡车随桥 身坠下后报废，一名司机在 事故中骨折，另有两人轻伤。
加载时间间隔必须满足结构反应稳定对时 间的要求。在前一荷载阶段内结构反应相 对稳定后，进行了有效测试及记录后方可 进行下一荷载阶段。当进行主要控制截面 最大内力（变形）加载试验时，分级加载 的稳定时间不应少于5分钟；对尚未投入 营运的新桥，首个工况的分级加载稳定时 间不应少于15分钟。
1
2016/4/28
公路—II级的车道荷载
均布荷载：������������ = ������. ������������ × ������������. ������ = ������. ������������������
������������ ������
集中荷载：
������������＝������ ������������ + ������������������ × ������. ������������ = ������ ������������ + ������������������ × ������. ������������ = ������������������. ������������������
连 续 梁 桥
主要 内容
2.主跨最大正弯矩截面应力（应变）及挠度 3.边跨最大正弯矩截面应力（应变）及挠度 4.支点沉降
5.混凝土梁体裂缝
附加 内容
1.主跨（中）支点附近斜截面应力（应变）
5.4 试验荷载
（1）试验控制荷载确定 静载试验为验收性荷载试验时，以设计荷载为 准否则应以目标荷载标准为控制荷载。
单桩抗压静载试验吨位计算__概述及解释说明
单桩抗压静载试验吨位计算概述及解释说明1. 引言1.1 概述单桩抗压静载试验是土木工程中用来评估和设计桩基础承载能力的重要实验方法。
吨位计算是该试验中一个关键的步骤，通过对承载性能的分析，可以确定桩身在不同荷载作用下的变形特性和最大承载力。
本文将详细解释单桩抗压静载试验吨位计算的原理和方法。
1.2 文章结构本文分为引言、单桩抗压静载试验吨位计算、重要要点一、重要要点二以及结论五个部分。
其中，引言部分将介绍本文涉及的主题和目标，并概述文章结构；单桩抗压静载试验吨位计算部分将详细讲解该试验的概述、原理解释和计算方法；重要要点一和重要要点二将探讨单桩抗压静载试验中两个关键问题，并进行分析和说明；最后，结论部分将总结研究成果并提出未来发展方向。
1.3 目的本文旨在通过对单桩抗压静载试验吨位计算方法进行深入剖析，增加读者对该实验的理解和应用能力。
同时，对单桩抗压静载试验中的重要问题进行研究和分析，探索其实际应用过程中的局限性，并提出未来改进和发展的方向。
通过本文的阐述，读者将更好地理解和运用单桩抗压静载试验吨位计算方法，为工程设计提供可靠的依据。
2. 单桩抗压静载试验吨位计算2.1 单桩抗压静载试验概述单桩抗压静载试验是一种常用的地基工程试验方法，用于评估和验证单根桩柱在承受垂直荷载时的抗力性能。
该试验通过施加不同大小的垂直荷载于单根桩柱上，并测量相应的变形和应力来计算该桩柱的承载能力。
2.2 单桩抗压静载试验原理解释在进行单桩抗压静载试验时，首先需要选择合适的加载方式和加载荷载大小。
常见的加载方式包括等速加载、恒速加载和恒力加载等。
通过施加垂直荷载于待测试的单根桩柱上，可以观察到该桩柱在承受荷载作用下产生的变形和应力响应。
通过监测记录试验过程中的重要参数，如荷载-沉降曲线、侧摆位移、竖向变形等数据，可以分析单根桩柱在不同荷载水平下的承载性能。
基于这些数据，可以进一步计算出吨位值以评估该单根桩柱的承载能力。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
中铁七局集团第三工程有限公司洋浦制梁场T梁预制
预应力混凝土铁路桥简支T梁QJYP32Z-0001静载弯曲抗裂试验加载计算单
编制：
审核:
批准：
中铁七局集团第三工程有限公司洋浦制梁场
二零一四年四月九日
预应力混凝土铁路桥简支T 梁
第一次静载弯曲抗裂试验加载计算单
一、计算说明： 1、计算依据：
（1）《预应力混凝土铁路简支梁静载弯曲试验方法及评定标准》TB/T 2092-2003 附录A 的计算公式和计算规则。
（2）时速200公里客货共线铁路预制后张法简支T 梁（角钢支架方案）通桥（2012）2201-Ⅰ图纸。
（3）实测的加载设备重量。
2、适用范围：
时速200公里客货共线铁路预制后张法简支T 梁（直线边梁）静载试验。
3、试验梁基本情况
本试验梁为时速200公里客货共线铁路预制后张法简支T 梁，梁号：QJYP32Z-0001，采用C55高性能混凝土，混凝土浇筑日期为2014年1月7日，终张拉日期为2014年3月7日，静载试验日期2014年4月9日，终张拉龄期为33天；试件28天抗压强度62.4MPa ，弹性模量4.13×104 MPa ，静活载设计挠度12.389mm 。
二、详细计算单：
A.1等效集中荷载采用五点加载，跨中设一集中荷载，其余在其左右对称布置。
各荷载纵向间距均为4m 。
如图A1 X i
P 1 P 2 P 3 P 4
P 5
R A R B
图A1 加载图示
A.1.1根据加载图式计算α值
跨中弯矩：∑=-⨯=n
i i i X P L R M 1
2
各加载点载荷相等： P 1=P 2=P 3……=P i
4
4
4
4
L /2
L /2
则 ()i i n
i i i P P P P X P L R M 28482
32252211=⨯+⨯-⨯=-⨯=∑=
由 i P P M 28=⨯=α 得出：
6.552828====
i i i P P P P P M α
式中：R —— 支点反力，kN ； L —— 计算跨度，m ；
P i —— 各加载点所施加的荷载，kN ； X i —— 各加载点至跨中距离，m ；
P —— 各加载点所施加的荷载的合力，i n
i i P P P 51==∑=，kN ；
α —— 各加载点合力作用下的等效力臂，m 。
A.2 计算未完成的应力损失值 Δσs ＝（1-η
1
）σL6+（1-η2）σ
L5
＝（1-0.409）×146.55 +（1-0.90789）×12.77
＝87.787MPa 式中：σ
L6
σ
L5
—— 分别为收缩、徐变与松驰应力损失值，MPa ；
η1、η 2 —— 分别为收缩、徐变与松驰应力损失完成率，MPa 。
S σ∆ —— 未完成的预应力损失值，MPa 。
A.3 计算未完成应力损失的补偿弯矩ΔM S Δ
Ms=Δσs ×（A y +A g ）（W 0/A 0+e 0）×10
3
＝88.787×（0.0119+0）×（0.977438/1.47041+1.1821）×103
＝1929.328（kN ·m ）
式中：A y —— 跨中截面预应力钢筋截面积，m 2；
A g —— 跨中截面普通钢筋截面面积（全预应力梁取A g =0），m 2
W 0 —— 对跨中截面下边缘换算截面抵抗矩（对后张梁为扣孔换算截面抵抗矩）,m 3 A 0 —— 跨中截面换算截面面积（对后张梁为扣孔换算截面抵抗矩）,m 2
e 0 —— 跨中截面预应力合力中心至换算截面重（对后张梁为扣孔换算截面）,m
S M ∆ —— 未完成的预应力损失的补偿弯矩，kN ·m 。
S σ∆ —— 未完成的预应力损失值，MPa 。
A.4 计算基数级荷载跨中弯矩 M Ka ＝M d +ΔMs -Ms+ M f
M d ＝6480.6 kN ·m ； M f ＝368.6 kN ·m ；
ΔM s ＝1929.328 kN ·m M S =αP s
＝5.6×（g1×5+g2×5+g3×5） ＝5.6×（1.32×5+0.309×5） ＝45.612（kN ·m ）
得出: M Ka =6480.6+1929.328-45.612+368.6=8732.916（kN ·m ） *)本片静载实验梁防水层未铺设。
式中：M ka —— 基数级下跨中弯矩，kN ·m ；
M d —— 二期恒载质量对跨中弯矩，kN ·m ； M S —— 加载设备质量对跨中弯矩，kN ·m 。
其中： g 1为加载千斤顶的重量；132kg/个，共5个
g 2为加载千斤顶钢板垫块的重量； 每个垫块重量：30.9kg ，共5个 加载油泵放置在梁下地面
A.5 计算基数级荷载值
P Ka ＝M Ka /α＝8732.916/5.6＝1559.449（kN ） A.6 计算各加载级下跨中弯矩
M k ＝K(M z +M d + M h +M f ) +ΔMs -M z – M s (kN ·m) 计算列表如下：
加载级K
Ka
0.6 0.8 1.0 1.05 1.10 1.15 1.20 M k (kN ·m) 8732.916
8287.856
12266.636
16245.416
17240.111
18234.806
19229.501
20224.196
式中：K —— 加载系数 ；
M h —— 活载对跨中弯矩，本梁数据为：7512.5kN ·m ；
M
z
——梁体质量对跨中弯矩，本梁数据为：5232.2kN·m 。
A.7计算各加载等级下的加载值如下(防水未做)：
P
k
＝M k/α(kN)
加载级K Ka 0.6 0.8 1.0 1.05 1.10 1.15 1.20
M k(kN·m) 8732.916 8287.856 12266.636 16245.416 17240.111 18234.806 19229.501 20224.196
Pk (kN) 1559.449 1479.974 2190.471 2900.967 3078.591 3256.215 3433.839 3611.464
因计算出的基数级载荷大于0.6级载荷，故取消P
0.6。
A.8 计算静活载级下的荷载等级
K b＝[M h/（1+μ）+ M z+ M d]/（M h+ M z+ M d）
＝[7512.5/1.194+5532.2+6480.6]/（7512.5+5232.2+6480.6）
＝0.9386
式中: 1+μ——动力系数。
A.9 计算静活载级之跨中弯矩
Mkb = Kb(Mz+Md+ Mh+Mf) +ΔMs -Mz–Ms
=0.9386(5532.2+6480.6+7512.5+368.6)+1929.328-5532.2-45.612 =15023.931（kN·m）
A.10 计算静活载级荷载
P Kb＝M Kb/
＝15023.931/5.6＝2682.845（kN）
A.11 根据等效加载力计算各加载等级单个千斤顶加载数据统计如下：
P
i
＝P k / 5
加载级K Ka 0.8 静活载
级
1.0 1.05 1.10 1.15 1.20
P i (kN) 311.890 438.094 536.569 580.193 615.718 651.243 686.768 722.293。