第六章证明测试题

合集下载

第六章：证明(一)经典试题

第一部分：基础复习八年级数学(下)第六章：证明(一)一、中考要求：l．理解证明的必要性和设置公理的必要性．2．关注现实，并通过具体例子了解定义、命题、定理的含义，会区分命题的条件和结论，知道反倒的意义和作用．3．初步掌握用综合法证明的格式，会证明两直线平行的有关判定定理，两直线平行的有关性质定理，三角形内角和定理及其椎论．4．体会推理的严谨性和结论的确定性，初步树立步步有据的推理意识，发展推理论证能力，同时，要善于表达自己的想法，并能与同伴交流．新课标对本章的要求不高，但比较简单的几何证明题仍是2006年中考的热点．二、中考卷研究(一)中考对知识点的考查：2004、2005年部分省市课标中考涉及的知识点如下表:(二)中考热点：新课标对本章的要求不高，但比较简单的几何证明题仍是2006年中考的热点．三、中考命题趋势及复习对策本章主要考查对命题，定理等概念的理解以及运用定义、定理证明问题的过程，在中考题中以证明题的形式出现，一般占5～7分，因此同学们在复习时应注意认真理解概念，分清题目的条件和结论，正确的写出证明过程．★★★(I)考点突破★★★考点1：一、考点讲解：定义：对名称和术语的含义加以描述，作出明确的规定，就叫做定义·命题：判断一件事情的句子叫命题，每个命题都由条件和结论两部分一组成，条件是已知的事项，结论是由已知事项推断出的事项，一般地，命题都可以写成“如果……，那么……”的形式，其中“如果”引出的部分是条件，“那么”引出的部分是结论．命题分为真命题和假命题．真命题：正确的命题是真命题；假命题：不正确的命题是假命题；要说明一个命题是假命题，通常可以举出一个例子，使之具备命题的条件，而不具有命题的结论，这种例子称为反例．公理：公认的真命题称为公理．证明：除了公理外，其他真命题的正确性都通过推理的方法证实，推理的过程称为证明．定理：经过证明的真命题称为定理．逆命题：把原命题的结论作为命题的条件，原命题的条件作为命题的结论，所组成的命题叫原命题的逆命题．逆定理：如果一个定理的逆命题是真命题，那么这个逆命题就叫原定理的逆定理．二、经典考题剖析：【考题1－1】（2004、宁安，9分）如图l－6－1，四边形ABCD中，点E在边CD上，连结AE、BE。

第六章证明一练习题

第六章证明一练习题姓名1.△ABC 的三个外角度数比为4∶3∶5，则它的三个内角度数分别为 .2.如图，△ABC 中，∠ACD=115°，∠B=56°, 则∠A= , ∠ACB= 。

3.已知:直线a ,b 被直线c 所截，∠1+∠2=180°4.已知:如图，∠3=∠4, 求证：a ∥b 。

求证：∠1+∠2=180°5.如图，BD 平分∠ABC ，若∠1＝∠2，则 ( ) A 、AB ∥CD B 、AD ∥BC C 、AD=BC D 、AB=CD6.如果点P 是线段AB 的黄金分割点，且AP>PB ，则下列说法正确的是______（仅填序号）。

①AP 2＝PB ·AB ；②AB 2＝AP ·PB ；③BP 2＝AP ·AB ；④AP ：AB ＝PB ：AP7已知，如图，在△ABC 中，AD 平分外角∠EAC ，AD ∥BC ，求证：∠B =∠C8.已知△ABC 中，∠1是它的一个外角，E 是边AC 上一点，延长BC 到D ，连接DE .求证：∠1>∠5.9.如图，求证(1)∠BDC >∠A . (2)∠BDC =∠B +∠C +∠A .10．如图，已知DE∥BC，CD 是∠ACB 的平分线，∠ACB=50°，求∠EDC 的度数．ABCD11.已知a ∶b ∶c =2∶3∶4,且a +3b －2c =15.（1）求a ,b ,c 的值（2）求4a －3b +c 的值.12.（1）如图在△ABC 中，P 是AB 上一点，连结 CP ，当满足条件∠ACP= 或∠APC= 时，或时，△ACP ∽△ABC ．（2）如图，P 为△ABC 的边AB 上一点，且∠ABC =∠ACP ，AP =3 cm, AB =4 cm ，求AC 的长13.在方格中，△ABC 与△DEF 是否成位似图形？请说明你的理由。

14.把图中的四边形ABCD 以点O 为位似中心沿OA 方向放大2倍（即位似比为2：1）。

第六章习题与复习题(二次型)----高等代数

习题6.11．写出下列二次型的矩阵.（1）222123123121323(,,)f x x x x x x x x x x x x =+++++（2）12341223(,,,)f x x x x x x x x =-（3）1234135(,,,)246785T f x x x x X X ⎛⎫⎪= ⎪ ⎪⎝⎭2．将二次型2221231231223(,,)32810f x x x x x x x x x x =+-+-表成矩阵形式，并求该二次型的秩.3．设A = ⎪⎪⎪⎭⎫ ⎝⎛321000000a a a ，B = ⎪⎪⎪⎭⎫ ⎝⎛13200000a a a 证明A 与B 合同，并求可逆矩阵C ，使得B =TC A C ．4．如果n 阶实对称矩阵A 与B 合同，C 与D 合同，证明A O B O O C O D ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭与合同.习题6.21．用正交变换法化下列实二次型为标准形，并求出所用的正交变换.（1）22212312323(,,)2334f x x x x x x x x =+++2．已知二次型2221231231223(,,)222f x x x x x x cx x x x =++++的秩为2.(1) 求c;(2) 求一正交变换化二次型为标准形.3．已知二次型2212323121323(,,)43248f x x x x x ax x x x x x =-+-+经正交变换化为标准形2221236,,f y y by a b =++求的值与所用正交变换.22224. 222444,,.x x ay z bxy xy yz y Q z a b Q ξηζηζ⎛⎫⎛⎫⎪ ⎪+++++== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭+=2已知二次曲面方程可经正交变换化为椭圆柱面方程求的值与正交矩阵5．用配方法化下列二次型为标准形，并求出所用的可逆线性变换.（1）222123123121323(,,)25228f x x x x x x x x x x x x =+++++6．在二次型f （x 1，x 2，x 3 ）=213232221)()()(x x x x x x -+-+-中，令⎪⎩⎪⎨⎧-=-=-=133322211xx y x x y x x y 得f =232221y y y ++可否由此认定上式为原二次型f 的标准形且原二次型的秩为3 ？为什么？若结论是否定的，请你将f 化为标准形并确定f 的秩.7．判断矩阵01111213A B ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭与是否合同.习题6.31．判定下列实二次型的正定性.（1）2221231231223(,,)23442f x x x x x x x x x x =++-- （2）222123123121323(,,)23222f x x x x x x x x x x x x =---+-+（3）123121323(,,)5f x x x x x x x x x =+- （4）∑∑≤<≤=+nj i jini ixx x1122． a 为何值时，实二次型222123123121323(,,)(2)22f x x x x a x ax x x x x x x =++++--是正定的.21013. 020,(),101A B kE A k B k B ⎛⎫ ⎪==+ ⎪ ⎪⎝⎭ΛΛ设矩阵其中为实数.（1）求对角阵，使与相似；（2）求参数的值，使为正定矩阵.习题六 (A)一、填空题1．二次型222123123121323(,,)23246f x x x x x x x x x x x x =+-+-+的矩阵为 .2．2123123(,,)()f x x x ax bx cx =++二次型的矩阵为.3．已知二次型的矩阵为124214447-⎛⎫⎪- ⎪ ⎪--⎝⎭，则该二次型为.4．二次型213232221321)()()(),,(x x x x x x x x x f ++-++=的秩为.5．化二次型222123123(,,)43f x x x x x x =+-为规范形，所用的可逆线性变换矩阵为. 6．二次型123121323(,,)f x x x x x x x x x =++的规范形为 .7．已知实对称矩阵A 与矩阵100012022T X AX ⎛⎫⎪- ⎪ ⎪⎝⎭合同，则二次型的规范形为.8．已知2221231231223(,,)22f x x x x x x x x ax x =++++正定，则a =. 9．当t 满足, 2221231231213(,,)4242f x x x x x x tx x x x =---++是负定的. 10．已知二次型222123123121323(,,)222f x x x x ax x x x ax x x x =+++--的正、负惯性指数均为1，则a =.二、单项选择题1. 已知二次型22212312312(,,)(1)(1)22(1)f x x x a x a x x a x x =-+-+++的秩为2,则a =( ).(A) 0 (B) 1 (C) 2 (D) 32. 设100020005A ⎛⎫ ⎪= ⎪ ⎪-⎝⎭, 则下列矩阵中与A 合同的矩阵是( ).(A) ⎪⎪⎪⎭⎫ ⎝⎛-100010001 (B)100020001-⎛⎫⎪- ⎪ ⎪-⎝⎭ (C) ⎪⎪⎪⎭⎫ ⎝⎛--500010002 (D)⎪⎪⎪⎭⎫ ⎝⎛300010002 3. , T T Tn f X AX A A X CY f Y BY ====如果元二次型（其中）可经可逆线性变换化为则下列结论不正确的是（）.(A) A 与B 合同 (B) A 与B 等价 (C) A 与B 相似 (D) A 与B 的秩相等 4. 设A, B 都是正定阵, 则( ).(A) AB, A + B 一定都是正定阵 (B) AB 是正定阵, A + B 不是正定阵 (C) AB 不一定是正定阵, A + B 是正定阵 (D) AB, A + B 都不是正定阵 5. 下列条件不能保证n 阶实对称矩阵A 为正定的是( ). (A) 1A -正定(B) 二次型f=X T AX 的负惯性指数为零 (C) 二次型f=X T AX 的正惯性指数为n (D) A 合同于单位矩阵22212312323123 (,,)(2)(23)(3)( ).() 1 () 1 () 1 ()1f x x x x ax x x x x x ax A a B a C a D a =+-+++++<-≠-≠>6.二次型正定的充要条件是7. 已知实对称矩阵A 满足A 2-5A+6E=O ,则A ( ).(A) 正定 (B) 半正定 (C) 负定 (D) 不定8. 已知二次型222123123121323(,,)22248f x x x x x x ax x x x x x =--+++经正交变换化为 222123227f y y y =+-,则a =( ). (A)1 (B) -1 (C) 2 (D)-2 9. 下列矩阵合同于单位矩阵的是( ).(A) 121242363⎛⎫ ⎪⎪ ⎪⎝⎭ (B)101040101-⎛⎫⎪ ⎪ ⎪--⎝⎭(C) ⎪⎪⎪⎭⎫ ⎝⎛811172121 (D)212134244--⎛⎫ ⎪- ⎪ ⎪⎝⎭10. 设矩阵211112111120A B A B --⎛⎫⎛⎫⎪ ⎪=--= ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭与矩阵，则与( ).(A) 合同且相似 (B) 合同但不相似(C) 不合同但相似 (D) 既不合同也不相似(B)1．已知22082006B a ⎛⎫ ⎪= ⎪ ⎪⎝⎭相似于对角阵.（1）求a 的值；（2）求正交变换使二次型X T BX 为标准形.222123123121323123(,,)55266 2.(1);(2)(,,)1f x x x x x cx x x x x x x c f x x x =++-+-=2. 已知二次型的秩为求和二次型矩阵的特征值指出方程表示哪种二次曲面.3. 已知实二次型f=X T AX 中矩阵A 的特征值为1，2，5，A 属于特征值1与2的特征向量分别为12(0,1,1),(1,0,0),TTαα=-=求该二次型. 4．设二次型123(,,)f x x x 经正交变换1123212331232221231(22)31 (22)31(22)342,x y y y x y y y x y y y f y y y ⎧=++⎪⎪⎪=-++⎨⎪⎪=-+⎪⎩=+-化为了标准形求该二次型。

(完整版)第六章线性空间练习题参考答案

第六章线性空间练习题参考答案一、填空题1.已知0000,,00V a bc a b c R c b ⎧⎫⎛⎫⎪⎪ ⎪=+∈⎨⎬ ⎪⎪⎪ ⎪+⎝⎭⎩⎭是33R ⨯的一个子空间，则维（V ）＝ 3 ， V 的一组基是000000000100,100,010*********⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.2．在P 4中，若1234(1,2,0,1),(1,1,1,1),(1,,1,1),(0,1,,1)k k αααα===-=线性无关，则k 的取值范围是3k ≠（以1234,,,αααα为行或者列构成的行列式不为零）. 3．已知a 是数域P 中的一个固定的数，而1{(,,,),1,2,,}n i W a x x x P i n =∈=是P n+1的一个子空间，则a ＝ 0 ，而维(W)＝n 4．维数公式为12dim dim V V +=1212dim()dim()V V V V ++.5．设123,,εεε是线性空间V 的一组基，112233x x x αεεε=++，则由基123,,εεε到基231,,εεε的过渡矩阵T ＝001100010⎛⎫⎪⎪ ⎪⎝⎭，而α在基321,,εεε下的坐标是321(,,)x x x 由基123,,εεε到基233112,,εεεεεε+++的过渡矩阵为T ＝011101110⎛⎫⎪⎪ ⎪⎝⎭.6．数域P 上n 级对称矩阵全体构成数域P 上(1)2n n +维线性空间，数域P 上n 级反对称矩阵全体构成数域P 上(1)2n n -维线性空间，数域P 上n 级上三角矩阵全体构成数域P 上(1)2n n +维线性空间，数域P 上n 级对交矩阵全体构成数域P 上n 维线性空间，数域P 上n 级数量矩阵全体构成数域P 上 1 维线性空间.二、判断题1.设n n V P ⨯=，则{,0}n n W A A P A ⨯=∈=是V 的子空间.错.行列式为零的两个方阵的和的行列式未必为零，因此W 中矩阵关于矩阵的加法运算不封闭，不能成为子空间.）2.已知{(,),,,}V a bi c di a b c d R =++∈为R 上的线性空间，且维(V ）＝2. 错.是子空间，但是是4维的，其基为(1,0),(,0),(0,1),(0,)i i .3.设,n n A B P ⨯∈，V 是0A X B ⎛⎫= ⎪⎝⎭的解空间，V 1是AX ＝0的解空间，V 2是(A ＋B)X ＝0的解空间，则12V V V =.正确. 12V V 中的向量既满足AX ＝0，又满足(A ＋B)X ＝0，因此也满足BX ＝0，即满足0A X B ⎛⎫= ⎪⎝⎭，即为V 中的向量.反之，V 中的向量既在1V 中，又在2V 中，即为12V V 中的向量.因此12V V V =.4.设线性空间V 的子空间W 中每个向量可由W 中的线性无关的向量组12,,,s ααα线性表出，则维(W)＝s.正确.根据定理1.5.设W 是线性空间V 的子空间，如果,,V αβ∈但,W W αβ∉∉且则必有.W αβ+∉错误.可能.W αβ+∈如取,αβ为一对互为负向量，则0.W αβ=+∈ 6. }0|),,{(33321=∈=x R x x x W 是3R 的子空间.正确. 基为（1,0,0），（0,1,0），维数为2. 7.}1|),,{(23321=∈=x R x x x W 是3R 的子空间. 错误.不包含零向量.8.}|),,{(3213321x x x R x x x W ==∈= 是3R 的子空间. 正确.基为（1,1,1），维数为1.9.}|),,{(3213321x x x R x x x W -=∈= 是3R 的子空间. 正确. 基为（1,1,0），（1,0，-1），维数为2. 三、计算题1.求所有与A 可交换的矩阵组成的nn P ⨯的子空间()C A 的维数与一组基，其中100020003A ⎛⎫⎪= ⎪ ⎪⎝⎭.解：设矩阵33()ij B b ⨯=与A 可交换，即有AB BA =.即111213111213212223212223313233313233100100020020003003b b b b b b b b b b b b b b b b b b ⎛⎫⎛⎫⎛⎫⎛⎫⎪⎪⎪⎪= ⎪⎪ ⎪⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭.111213111213212223212223313233313233232222333323b b b b b b b b b b b b b b b b b b ⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭. 所以有,()0,,1,2,3.ij ij ij ib b j i j b i j =-==当i j ≠时，0ij b =，因此11223300()0000b C A b b ⎧⎫⎛⎫⎪⎪⎪=⎨⎬ ⎪⎪⎪ ⎪⎝⎭⎩⎭ 维数为3，基为112233,,E E E .2.在线性空间P 4中，求由基1234,,,αααα到基1234,,,ββββ的过渡矩阵，并求(1,4,2,3)α=在基1234,,,αααα下的坐标，其中1234(1,0,0,0),(4,1,0,0),(3,2,1,0),(2,3,2,1)αααα===-=- 1234(1,1,8,3),(0,3,7,2),(1,1,6,2),(1,4,1,1).ββββ====--- 解：令过渡矩阵为T ，则有10111432131401238761001232210001T --⎛⎫⎛⎫⎪⎪- ⎪ ⎪=⎪ ⎪- ⎪⎪-⎝⎭⎝⎭因此1143210112379801231314633100128761232100132213221T ------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪--⎪ ⎪ ⎪==⎪ ⎪ ⎪- ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭. 令1234114324012320012301x x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪- ⎪⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭112341432114113611010123401274210012200122400013000133x x x x -----⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎪ ⎪-- ⎪ ⎪ ⎪ ⎪⎪ ⎪===⎪ ⎪ ⎪ ⎪⎪ ⎪-- ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ (1,4,2,3)α=在基1234,,,αααα下的坐标为（-101,21，-4,3）四、证明题1.V 为定义在实数域上的函数构成的线性空间，令12{()(),()()},{()(),()()}W f x f x V f x f x W f x f x V f x f x =∈=-=∈=--证明：W 1、W 2皆为V 的子空间，且12.V W W =⊕证明：W 1、W 2 分别为偶函数全体及奇函数全体构成的集合，显然W 1、W 2均为非空的.由奇偶函数的性质可得W 1、W 2皆为V 的子空间.()()()()(),()22f x f x f x f x f x V f x +---∀∈=+. 而12()()()(),22f x f x f x f x W W +---∈∈，因此12.V W W =+又12{0}.W W =所以12.V W W =⊕2.设W 是P n 的一个非零子空间，若对于W 的每一个向量12(,,,)n a a a 来说，或者120n a a a ====，或者每一个i α都不等于零，证明：维(W)＝1.证明：由W 是P n 的一个非零子空间，可得W 中含有非零向量设1212(,,,),(,,,)n n a a a b b b αβ==是W 中的任二个非零向量，由题意可得每一个,i i a b 都不等于零.考虑向量11112112121211(,,,)(,,,)(0,,,)n n n n b a b a a a a b b b b a a b b a a b W αβ-=-=--∈.由题设条件有1212110n n b a a b b a a b -==-=，即有1212n na a ab b b ===.即W 中的任二个非零向量均成比例，因此维(W)＝1.。

北师大版八年级下册数学第六章平行四边形含辅助线证明题—截长补短类训练

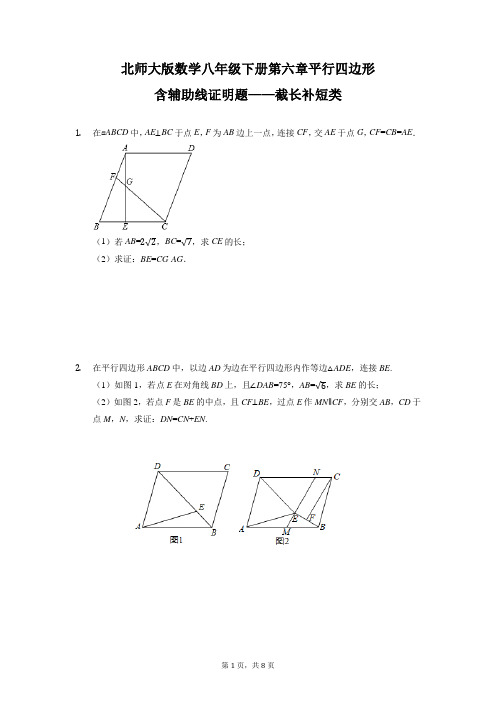
北师大版数学八年级下册第六章平行四边形含辅助线证明题——截长补短类1.在▱ABCD中，AE⊥BC于点E，F为AB边上一点，连接CF，交AE于点G，CF=CB=AE．（1）若AB=2√2，BC=√7，求CE的长；（2）求证：BE=CG-AG．2.在平行四边形ABCD中，以边AD为边在平行四边形内作等边△ADE，连接BE.（1）如图1，若点E在对角线BD上，且∠DAB=75°，AB=√6，求BE的长；（2）如图2，若点F是BE的中点，且CF⊥BE，过点E作MN∥CF，分别交AB，CD于点M，N，求证：DN=CN+EN.3.如图，在▱ABCD中，AE⊥BC，垂足为E，AE=CE.BF⊥AC，垂足为F，分别与AE，AD交于点G，H.（1）若AG=GE=BE=1，求▱ABCD的面积；（2）若CH平分∠BCD，求证：BC=AG+CH.4.已知在▱ABCD中，AE⊥CD，且AB=AE，F为AE上一点，且BF平分∠ABC，（1）若∠ABC=60°，AB=√3，求EF的长；（2）求证：AF+DE=BC.5.在平行四边形ABCD中，E为对角线AC上任意一点，连接BE（1）如图①所示，若AB=BE，AC=BC，∠BAC=75°，AB=2√2，求平行四边形ABCD的面积；（2）如图②所示，延长BE至F，使得EF=EB，连接CF，FD，求证：CE=AE+FD．6.在平行四边形ABCD中，连接BD，过点B作BE⊥BD于点B交DA的延长线于点E，过点B作BG⊥CD于点G．（1）如图1，若∠C=60°，∠BDC=75°，BD=6√2，求AE的长度；（2）如图2，点F为AB边上一点，连接EF，过点F作FH⊥FE于点F交GB的延长线于点H，在△ABE的异侧，以BE为斜边作Rt△BEQ，其中∠Q=90°，若∠QEB=∠BDC，EF=FH，求证：BF+BH=BQ．7.在平行四边形ABCD中，以AB为边作等边△ABE，点E在CD上，以BC为边作等边△BCF，点F在AE上，点G在BA延长线上且FG=FB．（1）若CD=6，AF=3，求△ABF的面积；（2）求证：BE=AG+CE．8.如图，在▱ABCD中，点F是对角线BD上一点，且满足AB=AF，过点F作EG交AD于E，交BC于G，作AH⊥BC于点H，交BD于M．（1）若F为MD中点，AF=2，AM=√3，求BC的长度；（2）若∠ABH=∠AFE，求证：BH+FG=HG．9.如图，平行四边形ABCD中，AB∥CD，AD∥BC，点G是线段BC的中点，点E是线段AD上的一点，点F是线段AB延长线上一点，连接DF，且∠ABE=∠CDG=∠FDG.（1）∠A=45°，∠ADF=75°，CD=3+√3，求线段BC的长；（2）求证：AB=BF+DF.10.如图，△ABC的高AD与中线BE相交于点F，过点C作BE的平行线，过点F作AB的平行线，两平行线相交于点G，连接BG，FG．（1）若AE＝2.5，CD＝3，BD＝2，求AB的长；（2）若∠CBE＝30°，求证：CG＝AD+EF．11.如图，在□ABCD中，E为BC边的中点，连接AE，F为CD边上一点，且满足∠DFA=2∠BAE.（1）若∠D=100°，∠DAF=30°，求∠FAE的大小；（2）求证：AF=CD+CF.12.已知在平行四边形ABCD中，过点D作DE⊥BC于点E，且AD=DE．连接AC交DE于点F，作DG⊥AC于点G．（1）如图1，若EFDF =12，AF=√13，求DG的长；（2）如图2，作EM⊥AC于点M，连接DM，求证：AM-EM=2DG．13.如图，在平行四边形ABCD中，AE⊥BC于点E，AE=AD，EG⊥AB于点G，延长GE、DC交于点F，连接AF.（1）若BE=2EC，AB=√13，求AD的长；（2）请猜想线段EG、BG、FC之间的等量关系并证明.14.如图，已知平行四边形ABCD中，DE⊥BC于点E，DH⊥AB于点H，AF平分∠BAD，分别交DC、DE、DH于点F、G、M，且DE=AD，CE=3，AB=5．(1)求线段CF的长度；(2)求证：AB=DG+CE．15.如图所示，在平行四边形ABCD中，∠DAC=60°，点E是BC边上一点，连接AE，AE=AB，点F是对角线AC边上一动点，连接EF.（1）如图1，若点F与对角线交点O重合，已知BE=4，OC：EC=5：3，求AC的长度；（2）如图2，若EC=FC，点G是AC边上一点，连接BG、EG，已知∠AEG=60°，∠AGB+∠BCD=180°，求证：BG+EG=DC.16.如图所示，平行四边形ABCD和平行四边形CDEF有公共边CD，边AB和EF在同一条直线上，AC⊥CD且AC=AF，过点A作AH⊥BC交CF于点G，交BC于点H，连接EG．（1）若AE=2，CD=5，求△BCF的周长；（2）求证：BC=AG+EG．。

统计学第六章测试题

第六章测试题A.参数估计B.统计推断C.区间估计D.假设检验 2.假设检验的概率依据是（）。

A.小概率原理B.最大似然原理C.大数定理D.中心极限定理3.下面有关小概率原则说法中正确的是（） A 小概率原则事件就是不可能事件B 它是指当一个事件的概率不大于充分小的界限α（0<α<1）时，可认为该事件为不可能事件C 基于”小概率原则”完全可以对某一事件发生与否作出正确判断D 总体推断中可以不予考虑的事件4.通常研究者想收集证据予以支持的假设称为（） A.原假设 B.备择假设 C.合理假设 D.正常假设5.当原假设为0μμ≥时，此时的假设检验称为（）A.双侧检验B.右侧检验C. 左侧检验D.显著性检验 6.研究表明，司机驾车时因接打手机而发生事故的比例超过20%，用来检验这一结论的原假设和备择假设应是（） A.%20:0≥μH %20:1<μH B.%20:0≤μH %20:1>μH C.%20:0≤P H %20:1>P H D.%20:0≥P H %20:1<P H7.如果是总体方差已知，正态分布、小样本数据的均值检验，应该采用（）A. t 检验B. z 检验C. P 检验D. 以上都不对 8.在假设检验中，原假设和备选假设（）A 都有可能成立B 都有可能不成立C 只有一个成立而且必有一个成立D 原假设一定成立，备选假设不一定成立9.一种零件的标准长度5Cm ，要检验某天生产的零件是否符合标准要求，建立的原假设和备选假设就为（） A ．0:5H μ=，1:5H μ≠ B ．0:5H μ≠，1:5H μ>C ．0:5H μ≤，1:5H μ> D ．0:5H μ≥，1:5H μ<10.若检验的假设为00H μμ≥：，10H μμ<：，则拒绝域为（）A ．z z α<- B ．z z α>C ．/2z z α<-或/2z z α<- D ．z z α>或z z α<-二、简答题1.假设检验的理论依据及推理的思想方法判断的理论依据：假设检验的理论依据是小概率事件原理。

数学分析课本(华师大三版)-习题及答案第六章

第六章微分中值定理及其应用一、填空题1．若0,0>>b a 均为常数，则=⎪⎪⎭⎫ ⎝⎛+→x x x x b a 302lim ________。

2．若21sin cos 1lim 0=-+→x x b x a x ，则=a ______，=b ______。

3．曲线x e y=在0=x 点处的曲率半径=R _________。

4．设2442-+=x x y ，则曲线在拐点处的切线方程为___________。

5．=-+→x e x xx 10)1(lim ___________。

6．设)4)(1()(2--=x x x x f ，则0)(='x f 有_________个根，它们分别位于________ 区间；7．函数x x x f ln )(=在[]2,1上满足拉格朗日定理条件的__________=ξ；8．函数3)(x x f =与21)(x x g +=在区间[]2,0上满足柯西定理条件的_____=ξ；9．函数x y sin =在[]2,0上满足拉格朗日中值定理条件的____=ξ；10．函数2)(xe xf x=的单调减区间是__________； 11．函数x x y 33-=的极大值点是______，极大值是_______。

12．设x xe x f =)(，则函数)()(x f n 在=x _______处取得极小值_________。

13．已知bx ax x x f ++=23)(，在1=x 处取得极小值2-，则=a _______，=b_____。

14．曲线22)3(-=x k y 在拐点处的法线通过原点，则=k________。

15．设)2,1()1()( =-⨯=n x n x f n ，n M 是)(x f 在[]1,0上的最大值，则=∞→n n M lim ___________。

16．设)(x f 在0x 可导，则0)(0='x f 是)(x f 在点0x 处取得极值的______条件；17．函数x bx x a x f ++=2ln )(在1=x 及2=x 取得极值，则______,==b a ；18. 函数3223)(x x x f -=的极小值是_________; 19．函数xx x f ln )(=的单调增区间为__________； 20. 函数x x x f cos 2)(+=在⎥⎦⎤⎢⎣⎡2,0π上的最大值为______，最小值为_____； 21. 设点)2,1(是曲线b a x y +-=3)(的拐点,则___________,==b a ;22. 曲线x e y =的下凹区间为_______,曲线的拐点为________;23. 曲线323x x y -=的上凹区间为________;24. 曲线)1ln(2x y +=的拐点为__________;25．曲线x y ln =在点______处曲率半径最小。

第六章证明(一)测试题

３在ＡＡＣ中，：０，曰、Ｃ的平分线交于０点，ＬＢＣ等于（．Ｂ厶４５。则Ｏ
（６。Ａ）５（１５Ｂ）１。（）０Ｃ８。
４举反例说明“ ．一个角的余角大于这个角” 假命题，是错误的是（（）Ａ设这个角是４。它的余角是４。但４。４。５，５，５＝５
（）０Ｄ５。
Ⅱ
１下列语句中，．是命题的是（（两点确定一条直线吗？Ａ）（作４的平分线ＡＣ）Ｍ
２两条平行线被第三条直线所截，．那么一组同旁内角的平分线（（相互重合Ａ）（互相平行Ｂ）（）Ｃ相互垂直
二、填空题（每小题３分，２）共４分
１．ｎ＝３当时，ｎ＋１ｎ＋，＋３以，２ｎ为线段长的三角形是直角三角形．，结论是，它是一个．．１．所有的质数都是奇数” ４“ 的题设是命题．填 “ ” “ ” （真或假）ｌ．５把命题 “ 对顶角相等 ” 改成 “ 如果 …… ，那么 ……” 的形式应为１．６若一个三角形的三个内角之比为４３２则这个三角形的最大内角为：：，
＝
．
．＋ＬＡＢ＜８。④ ＬＨＣＣ１０；Ｅ
２．Ｏ如图５下列结论：， ① Ａ＞ＬＡＤ；ＬＢ＋ＬＡＢ＝１０一Ａ；Ｃ ② Ｃ８。 ③
— —
（填上你认为正确的所有序号）．
Ａ
Ｅ
ＢＣＣ
Ｄ
圈４
图５
《新课程导学》适八级生读・学北大下）．合年学阅数（师版・册

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

福州十六中八年级下学期数学第六章证明（一）单元测试卷
命题人：段振富
班级___________ 座号 ___________ 姓名______________ 成绩________________
一、填空题（每空3分，共42分）
1、“两直线平行，同位角互补”是______ 命题（填真、假）
2、把命题“对顶角相等”改写成“如果…那么…”的形式_____________________________
3、如图所示，/ 1+ / 2=180 °，若/ 3=50 °，则/ 4= _________
4、如图所示，△ ABC 中，/ ACD=115 °，/ B=55 °，则/ A= ______ , / ACB= _______
5、_____________________________________________________ 在厶ABC 中，/ C=90 °，若/
A=30 °，则/ B= ______________________________________
6、在厶ABC 中，/ B — / C=40 °，则/ C= _____ ，/ B= _______
7、在三角形中，最多有_____ 个锐角，至少有______ 个锐角，最多有______ 个钝角（或直角）
8、A ABC的三个外角度数比为3 : 4 : 5,则它的三个外角度数分别为__________________________
9、在厶ABC中，/ ABC和/ACB的平分线交于点I,若/ A=60 °，则/ BIC= ________________
10、已知如图，平行四边形ABCD中，E为AB上一点，DE与AC交于点F, AF : FC=3 : 7,
贝H AE : EB= _____________
二、选择题（每小题3分，共18分）
11、下列命题是真命题的是（）
A、同旁内角互补
B、直角三角形的两锐角互余
C、三角形的一个外角等于它的两个内角之和
D、三角形的一个外角大于内角
12、下列语句为命题的是（）
13、命题“垂直与同一条直线的两条直线互相平行”的题设是（）
A、垂直
B、两条直线
C、同一条直线
D、两条直线垂直于同一条直线
14、已知△ ABC的三个内角度数比为2 : 3 : 4,则个三角形是（）
A、锐角三角形
B、直角三角形
C、钝角三角形
D、等腰三角形
15、如图，一个任意的五角星，它的五个内角的度数和为（）
A、90°
B、180 °
C、360°
D、120°
16、如图，AB // EF, / C=90 °,^ %、丫的关系为（
A、B = a + Y
B、a + 3 + Y =180 °
C、3 + Y-a =90
D、a + 3 - Y =90
三、完型填空（每空2分，共8分）
17、已知如图，在△ ABC中，CH是外角/ ACD的平分
线，BH是/ ABC的平分线。

求证：/ A= 2 / H
证明：I / ACD是厶ABC的一个外角,
/•Z ACD= / ABC+ / A ( ______________________________________ / 2是厶
BCD的一个外角,
/ 2= / 1 + / H ( ____________________________________ ) •/ CH是外角Z ACD的平分线，BH是Z ABC的平分线
1 1
•••Z 1= Z ABC , Z 2= - Z ACD ( ____________________________ )
2 2
•Z A = Z ACD- Z ABC= 2 (Z 2 - Z 1) (等式的性质)
而Z H= Z 2 - Z 1 (等式的性质)
•Z A= 2 Z H ( __________________ )
四、解答题（每题8分，共32 分）
18、已知如图，在△ ABC中，/ 1是它的一个外角，E为边AC上一点，延长BC到D，连接DE。

求证：/ 1 > Z 2
19、求证：两条直线平行，同旁内角的角平分线互相垂直。

（提示：先画图，写出已知，求证，然后进行证明）
19、已知如图，0是四边形ABCD的两条对角线的交点，过点0作0E // CD，交AD于E, 作OF //
BC，交AB于F,连接EF。

求证：EF // BD
20、已知如图，AB // DE。

(1 )、猜测/ A、/ ACD、/ D有什么关系，并证明你的结论。

(2)、若点C向右移动到线段AD的右侧，此时/ A、/ ACD、/ D之间的关系，仍然满
足(1)中的结论吗？若符合请你证明，若不符，请你写出正确的结论并证明。

要求画出
相应的图形。

D。