理论力学试题及答案
理论力学试题含答案
精选文档理论力学试题及答案一、是非题（每题2分。
正确用√，错误用×，填入括号内。
）1、作用在一个物体上有三个力，当这三个力的作用线汇交于一点时，则此力系必定均衡。
2、力关于一点的矩不因力沿其作用线挪动而改变。
（）3、在自然坐标系中，假如速度υ=常数，则加快度α=0。
（）4、虚位移是偶想的，极细小的位移，它与时间，主动力以及运动的初始条件没关。
5、设一质点的质量为m，其速度与x轴的夹角为α，则其动量在x轴上的投影为mvx=mvcosa。
二、选择题（每题3分。
请将答案的序号填入划线内。
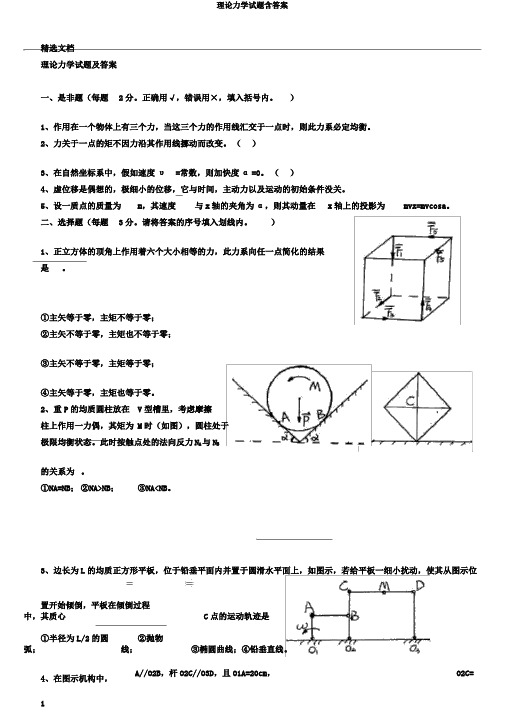
）1、正立方体的顶角上作用着六个大小相等的力，此力系向任一点简化的结果是。
①主矢等于零，主矩不等于零；②主矢不等于零，主矩也不等于零；③主矢不等于零，主矩等于零；④主矢等于零，主矩也等于零。
2、重P的均质圆柱放在V型槽里，考虑摩擦柱上作用一力偶，其矩为 M时（如图），圆柱处于极限均衡状态。
此时按触点处的法向反力N A与N B的关系为。
①N A=NB；②N A>NB；③N A<NB。
3、边长为L的均质正方形平板，位于铅垂平面内并置于圆滑水平面上，如图示，若给平板一细小扰动，使其从图示位置开始倾倒，平板在倾倒过程中，其质心C点的运动轨迹是。
①半径为L/2的圆弧；②抛物线；③椭圆曲线；④铅垂直线。
4、在图示机构中，A//O2B，杆O2C//O3D，且O1A=20cm，O2C=杆O140cm，CM=MD=30cm，若杆AO1以角速度ω=3rad/s匀速转动，则D点的速度的大小为cm/s，M点的加快度的大小为cm/s2。
①60；②120；③150；④360。
.精选文档5、曲柄OA以匀角速度转动，当系统运动到图示地点（OA//O1B。
AB |OA）时，有V A V B，A B，ωAB 0，AB 0。
①等于；②不等于。
三、填空题（每题5分。
请将简要答案填入划线内。
）1、已知A重100kN，B重25kN，A物与地面间摩擦系数为0.2。
理论力学试题库及答案(通用篇)
理论力学试题库及答案(通用篇)一、理论力学试题库（通用篇）试题一：已知一质点在平面直角坐标系中的运动方程为 x = 2t² + 3，y = 4t² - t + 1。
求该质点在t = 2s 时的速度和加速度。
试题二：一质点沿圆周运动，其半径为 r，角速度为ω，角加速度为α。
求质点在任意时刻 t 的速度和加速度。
试题三：一质点从静止开始沿直线运动，受到恒力F 的作用。
求质点在任意时刻 t 的速度和位移。
试题四：一质点在平面内做匀速圆周运动，半径为r，角速度为ω。
求质点在任意时刻 t 的速度和加速度。
试题五：一质点在平面内做匀速运动，速度大小为v，方向与水平方向成θ 角。
求质点在任意时刻 t 的位移。
试题六：一质点在重力作用下做自由落体运动，求质点在任意时刻 t 的速度和位移。
试题七：一质点在水平地面上受到一斜向上的拉力F，拉力与水平方向的夹角为θ。
求质点在任意时刻 t 的速度和加速度。
试题八：一质点在平面内做匀速圆周运动，半径为r，角速度为ω。
求质点在任意时刻 t 的切向加速度和法向加速度。
试题九：一质点在平面内做匀速运动，速度大小为v，方向与水平方向成θ 角。
求质点在任意时刻 t 的位移和速度。
试题十：一质点在水平地面上受到一恒力 F 的作用，力与水平方向的夹角为θ。
求质点在任意时刻 t 的速度和位移。
二、答案答案一：t = 2s 时，速度 v = (4t, 8t - 1) = (8, 15) m/s；加速度 a = (8, 8) m/s²。
答案二：质点在任意时刻 t 的速度v = (rω, 0)，加速度a = (0, rα)。
答案三：质点在任意时刻 t 的速度 v = (F/m)t，位移 s = (F/m)t²/2。
答案四：质点在任意时刻 t 的速度 v =(rωcos(ωt), rωsin(ωt))，加速度 a = (-rω²sin(ωt), rω²cos(ωt))。
理论力学大一试题及答案
理论力学大一试题及答案一、选择题（每题5分，共20分）1. 牛顿第一定律描述的是：A. 物体在没有外力作用下将保持静止或匀速直线运动B. 物体在受到外力作用下将改变其运动状态C. 物体在受到外力作用下将保持匀速直线运动D. 物体在受到外力作用下将保持静止答案：A2. 根据动量守恒定律，以下说法正确的是：A. 系统内所有物体的动量之和在没有外力作用下保持不变B. 系统内所有物体的动量之和在有外力作用下保持不变C. 系统内所有物体的动量之和在有外力作用下将增加D. 系统内所有物体的动量之和在有外力作用下将减少答案：A3. 角动量守恒的条件是：A. 系统不受外力矩B. 系统受外力矩C. 系统内力矩之和为零D. 系统内力矩之和不为零答案：A4. 以下哪项不是能量守恒定律的表述：A. 能量既不能被创造，也不能被消灭B. 能量可以以多种形式存在C. 能量可以以多种形式相互转化D. 能量在转化过程中总量会增加答案：D二、填空题（每题5分，共20分）1. 根据牛顿第二定律，物体的加速度与作用力成正比，与物体的质量成________。
答案：反比2. 一个物体在水平面上以初速度v0运动，受到大小为F的恒定摩擦力作用，其加速度为a=________。
答案：-F/m3. 一个质量为m的物体从高度h自由下落，其下落过程中的重力势能变化量为________。
答案：-mgh4. 根据动能定理，一个物体的动能变化量等于外力对物体做的功，即ΔK=________。
答案：W三、计算题（每题15分，共30分）1. 一个质量为2kg的物体从静止开始，受到一个大小为10N的水平拉力作用，求物体在5秒内的位移。
解：根据牛顿第二定律，F=ma，得a=F/m=10/2=5m/s²。
根据位移公式s=1/2at²，得s=1/2*5*5²=62.5m。
答案：62.5m2. 一个质量为5kg的物体从高度10m自由下落，求物体落地时的速度。
理论力学考研试题及答案
理论力学考研试题及答案一、选择题（每题2分，共20分）1. 质点系的动量守恒条件是（）。
A. 外力为零B. 外力之和为零C. 外力之和的矩为零D. 外力之和的矩不为零答案：B2. 刚体的转动惯量与（）有关。
A. 质量B. 形状C. 质量分布D. 以上都是答案：D3. 牛顿第二定律的数学表达式为（）。
A. F = maB. F = m*vC. F = m*aD. F = m*v^2答案：C4. 角动量守恒的条件是（）。
A. 外力矩为零B. 内力矩为零C. 外力矩与内力矩之和为零D. 外力矩与内力矩之差为零5. 简谐振动的周期与（）无关。
A. 振幅B. 频率C. 质量D. 刚度答案：A6. 达朗贝尔原理的实质是（）。
A. 虚功原理B. 虚位移原理C. 虚速度原理D. 虚加速度原理答案：B7. 刚体的平动与转动的区别在于（）。
A. 参考系B. 速度C. 加速度D. 角速度答案：D8. 拉格朗日方程的推导基于（）。
A. 牛顿运动定律B. 能量守恒定律C. 动量守恒定律D. 虚功原理答案：D9. 刚体转动的角动量方向与（）方向相同。
B. 力矩C. 角速度D. 线速度答案：C10. 非惯性参考系中，物体的运动方程中需要加入（）。
A. 惯性力B. 重力C. 电磁力D. 摩擦力答案：A二、填空题（每题2分，共20分）1. 质点系的动量守恒定律表明，当质点系所受外力之和为零时，其总动量保持不变。
2. 刚体的转动惯量是刚体对于某一旋转轴的惯性的量度，它与刚体的质量分布和旋转轴的位置有关。
3. 牛顿第二定律表明，物体的加速度与作用在物体上的合外力成正比，与物体的质量成反比。
4. 角动量守恒定律表明，当一个系统不受外力矩作用时，其总角动量保持不变。
5. 简谐振动的周期只与振动系统的固有频率有关，与振幅无关。
6. 达朗贝尔原理是将动力学问题转化为静力学问题的一种方法。
7. 刚体的平动是指刚体上所有点都沿着同一直线运动，而转动则是指刚体绕某一固定轴旋转。
理论力学试题及答案
理论力学试题一、填空题1．已知图示正方体边长为a , 在右侧面作用已知力F ，在顶面作用矩为M 的已知力偶矩，如图所示。
求力系对x ,y ,z 轴的力矩。
（6分）xM ∑=( )，y M ∑=( ) zM∑=( )2. 已知：图示机构位于铅垂面内，匀质杆OA 质量为m ，长为l ，且l =4R ，匀质圆盘质量为m ，半径为R ,与杆在A 端固接。
图示瞬时，杆的角速度ω=0,角加速度为α。
求惯性力系向O 点简化结果。
（6分） 主失大小=（ ），主矩大小=（ ） 方向在图中标出。
二．在图示机构中，已知：OB=OD=DA=20cm ,AC =40cm ,AB ⊥AC ,角θ=30,1F =150N,弹簧的刚度系数k =150N/cm,在图示位置已有压缩变形δ=2cm,不计各构件重量，用虚位移原理求构件在图示位置平衡时，力2F 的大小。
（用其他方法做不给分）（8分）三．已知：图示平面结构，各杆自重不计。
M =10kN ⋅m ，F =20kN ，max q =8kN/m ，2l m =，A ，B ，D 处为铰链连接，E 处为固定端。
求：Ａ，Ｅ处的约束力。
（２０分）四．已知：平面机构如图：圆轮Ａ沿水平面纯滚动，滑块Ｂ上铰链两直杆ＡＢ，ＢＤ，ＢＤ穿过做定轴转动的套筒Ｃ，15,45/,0A A R cm v cm s a ===，图示瞬时，45,30,30l cm θϕ===。
求：图示瞬时，ＡＢ，ＢＤ杆的角速度,AB BD ωω；点Ｂ的加速度B a ；ＢＤ杆的角加速度BD α。
（２０）五．已知：图示系统中，物块Ａ质量为３m ，均质圆盘Ｂ与均质圆柱Ｃ质量均为m ，半径均为Ｒ，弹簧刚度系数为k ，初始时系统静止，弹簧为原长。
系统由静止释放后，圆柱Ｃ做纯滚动。
斜面倾角为30，弹簧与绳的倾斜段与斜面平行。
求：当物块Ａ下降距离为s （未达最低位置）时的速度与加速度，两段绳中的拉力。
（２０分）理论力学试题答案一、填空题 １、Fa 22 ；0；Fa M 22- 2、ααml mR 236=；22131131696mR ml αα=；二、解：0=F W δ 120c D D B F r F r F r δδδ+-=sin A C r r δδθ= 12A C r r δδ= 1124D A C r r r δδδ== 1124B A C r r r δδδ==1211044C D C C F r F r F r δδδ+-=N 300=D F N 9002=F三、解：分析BD ，受力如图（1）所示。
专升本理论力学试题及答案
专升本理论力学试题及答案一、选择题（每题3分，共30分）1. 理论力学的研究对象是什么？A. 物体内部分子运动B. 质点的运动C. 物体在外力作用下的运动D. 物体内部结构答案：C2. 牛顿第一定律又称为A. 惯性定律B. 加速定律C. 作用力与反作用力定律D. 力的独立作用定律答案：A3. 以下哪项不是理论力学中常见的力？A. 重力B. 弹力C. 摩擦力D. 向心力答案：D4. 质点系的动量守恒定律成立的条件是A. 合外力为零B. 合外力和合外力矩都为零C. 只有重力作用D. 质点系在封闭系统内答案：A5. 刚体的转动惯量与以下哪项无关？A. 质量B. 质量分布C. 形状D. 参考点的选择答案：D6. 角速度和线速度的关系是A. 线速度是角速度的两倍B. 线速度是角速度与半径的乘积C. 角速度是线速度的一半D. 线速度与角速度无关答案：B7. 两个物体组成的系统动量守恒，以下哪项一定守恒？A. 机械能B. 内能C. 角动量D. 动能答案：C8. 以下哪项不是达朗贝尔原理的内容？A. 惯性力的概念B. 虚位移原理C. 动静法D. 力的平衡答案：B9. 科里奥利力的方向与物体的运动方向的关系是A. 垂直B. 平行C. 同向D. 反向答案：A10. 以下哪项不是理论力学中常见的稳定性问题？A. 静稳定性B. 动稳定性C. 热稳定性D. 转动稳定性答案：C二、填空题（每题2分，共20分）11. 牛顿第二定律的数学表达式为：________。
答案：F=ma12. 一个物体在水平面上做匀速直线运动，其受到的摩擦力大小等于________。
答案：物体的重力与水平面的摩擦系数的乘积13. 刚体的平面运动可以分解为________和________。
答案：平动、转动14. 一个物体从静止开始自由下落，其在前2秒内的位移与前3秒内的位移之比为________。
答案：4:915. 质点系的动能等于________。
理论力学试题及答案
理论力学试题及答案一、选择题（每题2分，共20分）1. 牛顿第一定律描述的是：A. 物体在受力时的运动状态B. 物体在不受力时的运动状态C. 物体在受力时的加速度D. 物体在受力时的位移答案：B2. 根据牛顿第二定律，物体的加速度与作用力和物体质量的关系是：A. 加速度与作用力成正比，与质量成反比B. 加速度与作用力成反比，与质量成正比C. 加速度与作用力成正比，与质量成正比D. 加速度与作用力成反比，与质量成反比答案：A3. 以下哪个不是刚体的运动特性？A. 刚体的质心保持静止或匀速直线运动B. 刚体的各部分相对位置不变C. 刚体的各部分速度相同D. 刚体的各部分加速度相同答案：C4. 角动量守恒定律适用于：A. 只有重力作用的系统B. 只有内力作用的系统C. 外力矩为零的系统D. 外力为零的系统答案：C5. 以下哪个是能量守恒定律的表述？A. 一个封闭系统的总动能是恒定的B. 一个封闭系统的总势能是恒定的C. 一个封闭系统的总能量是恒定的D. 一个封闭系统的总动量是恒定的答案：C二、简答题（每题10分，共20分）6. 简述牛顿第三定律的内容及其在实际中的应用。
答案：牛顿第三定律，又称作用与反作用定律，表述为：对于两个相互作用的物体，它们之间的作用力和反作用力总是大小相等、方向相反。
在实际应用中，例如在推门时，门对人的作用力和人对门的作用力大小相等，方向相反。
7. 描述什么是简谐振动，并给出一个生活中的例子。
答案：简谐振动是一种周期性振动，其回复力与位移成正比，且总是指向平衡位置。
生活中的例子包括弹簧振子，当弹簧被拉伸或压缩后释放，它会在原始平衡位置附近做周期性的往复运动。
三、计算题（每题15分，共30分）8. 一个质量为m的物体，从静止开始，沿着一个斜面下滑，斜面的倾角为θ。
如果斜面的摩擦系数为μ，求物体下滑的加速度。
答案：首先，物体受到重力mg的作用，分解为沿斜面方向的分力mg sinθ和垂直斜面方向的分力mg cosθ。
理论力学试题及答案
理论力学试题及答案一、选择题（每题2分，共10分）1. 一个物体在水平面上以速度v匀速直线运动，其动摩擦因数为μ，若物体所受的摩擦力为F，则F等于：A. μvB. μmgC. μND. μ(v^2)答案：B2. 根据牛顿第二定律，物体的加速度与作用在物体上的合外力成正比，与物体的质量成反比。
这一定律的数学表达式为：A. F = maB. F = m/aC. a = F/mD. a = mF答案：A3. 一个物体从静止开始自由下落，其下落的高度h与时间t的关系为：A. h = gt^2B. h = 1/2gt^2C. h = 2gtD. h = gt答案：B4. 两个物体A和B用轻杆连接，A的质量为mA，B的质量为mB，系统在水平面上以共同速度v向右做匀速直线运动。
若杆的力为F，则F的方向是：A. 向左B. 向右C. 不确定D. 无法判断答案：B5. 一个物体在竖直平面内做圆周运动，当物体通过最高点时，其向心力的来源是：A. 重力B. 杆的支持力C. 绳子的张力D. 重力和杆的支持力的合力答案：D二、填空题（每空2分，共10分）1. 一个物体的质量为2kg，受到的合外力为10N，根据牛顿第二定律，其加速度为______ m/s²。
答案：52. 一个物体做匀加速直线运动，初速度为3m/s，加速度为2m/s²，经过4秒后的速度为______ m/s。
答案：153. 在光滑水平面上，一个物体受到一个大小为5N，方向向右的恒定力作用，物体的质量为1kg，其加速度为______ m/s²。
答案：54. 一个物体在竖直上抛运动中，当其上升的最大高度为20m时，其初速度为______ m/s。
答案：205. 根据动能定理，物体的动能变化等于合外力做的功，若一个物体的动能增加了30J，合外力做的功为______ J。
答案：30三、简答题（共20分）1. 解释什么是科里奥利力，并给出其表达式。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
理论力学试题及答案、是非题（每题2分。
正确用"，错误用X,填入括号内。
）1、作用在一个物体上有三个力，当这三个力的作用线汇交于一点时，则此力系必然平衡。
2、力对于一点的矩不因力沿其作用线移动而改变。
（）3、在自然坐标系中，如果速度u =常数，则加速度a = 0。
（）4、虚位移是偶想的，极微小的位移，它与时间，主动力以及运动的初始条件无关。
5、设一质点的质量为m其速度—与x轴的夹角为a,则其动量在x轴上的投影为mv =mvcos a。
、选择题（每题3分。
请将答案的序号填入划线内。
）1、正立方体的顶角上作用着六个大小相等的力，此力系向任一点简化的结果是 ____________ 。
①主矢等于零，主矩不等于零；②主矢不等于零，主矩也不等于零；③主矢不等于零，主矩等于零；④主矢等于零，主矩也等于零。
2、重P的均质圆柱放在V型槽里，考虑摩擦柱上作用一力偶，其矩为M时（如图），圆柱处于极限平衡状态。
此时按触点处的法向反力N A与N B的关系为________________ 。
① N A = N B；② N A > N B；③ N A < N B。
3、边长为L的均质正方形平板，位于铅垂平面内并置于光滑水平面上，如图示，若给平板一微小扰动，使其从图示位置开始倾倒，平板在倾倒过程中，其质心C点的运动轨迹是___________________ 。
①半径为L/2的圆弧；②抛物线；③椭圆曲线；④铅垂直线。
4、在图示机构中，杆O A//QB,杆Q C//O3 D,且O A = 20cm , O2 C = 40cm, CM = MD = 30cm 若杆AO 以角速度co2 =3 rad / s匀速转动，则D点的速度的大小为 ________ cm/s , M点的加速度的大小为_________ c m/s 。
① 60；② 120；③ 150；④ 360。
q 2.2 22F C 0 FBy 0F x 0 F Ax F Bx0 F AX 4kNF y 0 FAy FByF 0 F AY 10kNA0 M A M F 40 M A 35kN m e [xy]T e [X 1y]T e 2 [X 2 y 2]T r r oA ip 「A r oA i pcos 45 sin 45、、2I2.2/2l 1sin 45 cos 45、、212、、2I 21cos( 30 )sin( 30 )..3/2 1/2I 2Tsin( 30 ) cos( 30 ) 1/2 3/220 q0 0 /4X O2 /2 2/2 l 1 0 l^. 2/2h 、2/2Y O■/2 .2/2 0 0l P . 2/21八 2/2M A iX A Y ATA2 F BYq1 X AY A/6Tl1I1X B X A .3/2 Y BY A1/2 1/2 .3/2 I23T l 21l2舟(2I 1..3l 2) 扑2hACl sinBC l cos V AABACl sinV B BCAB12) l cosr l sinco ta An aBAAB2 ABl(= l sin )2 22r l sin3B a At3BA n3BAa B sina A cosn3BAaBsi n 1(r cos2 2f^) l sincot2r3 l sin O 1 O 2O 2O 2O 1 O 1 O 22T T 11 212 JS 12 JO 22 (fmR 21mR 2；）寸 mR 2(3 12；）2/25、曲柄0A 以匀角速度转动，当系统运动到图 示位 置 （OA I V A V B —A—B3 | AB BCMq F C F Bx BC q F2KN.mA C 2 q 2 22 10KNBC A [F C 5KNm 2mM B 0 4kN q22 0F x F y FMRM.■AABa BAABDqrM3A2n»15OC60O it BAF BB /——2nF2魯mR2(3」4 ；）押2Q2d Tdt4M 7mR O2 L°2 F TR J O2 F T RJ S F T2R F T3mR4 3M7R ma i F TLDV D mv o i M D(F) mv o i) 0丄(mR如2R 7mR 2mR24M7mR2)7RMP R22R8M7mR21 mR24M 3M7R 7RO i F T2Rma i F T4Mm27mR2-mR223M7R 7Rma o i F S 2R M 33B 2l cos 3OA AB lxG i 3/DG 3B G 3C0 y B 2lsiny c 4 lsiny D3 -21sin 3Ci2lcos 33D■f lcosM 3 G 2l cos 3 G i 21 cos 33 G i 21 cos 2lcos2G i l cosM 2(G G) cos 0F 1 FF 1FF 20 0 F R F iF F 0 0FF 0br 2 r1 b r 20 bb0 b 0~2b0 b M o0 b 00 b b 0 bF rF b 0 0 F 0 b 0 00 F 2,.2Fe [x y z]TFF RF iFF RF z F o F R F z r 10 b b~1b 0 0bM o (F) MoM1M2~ F1b 00 ~2 F 2 bb F0 bFx~2F 2bF bF bFF iF iOOCvOyF 2OCmg .SF Sri「2 bF bF 0M o M 1 M 2 0 bF bF 0bFbFM O bF y bF z F O F R F zM O bF y bF z c 2 2 2a b 2abcossin ()sin1vOrVCV O VCO vCO~2r2 V C V2Vco 2V o V cocos2 2 1 2 :2 2 22 2/5、r (4 cos )r4 rr cosW mg 丹(1 cos )T % W2 mr (4cos ) 1 2 3・^mr sin 1mg 2 r si n3(-3 cos ) 今2sin 碁 sin 0_ 1 • 21 2.1 2 21 - J cmV -1 mr 22 2 121 2 A2— mr (- cos ) 23丄 mr 2(- cos ) 2T 023mr 2笔 cos )] 1mg^r(1 cos )V o rV o V co 2V o V co cos r 2 2*r 2 2 r 2 2cos2 2/5 \r (4 cos )T J 2 21 2 — mV c 1[mrmr (：1 1 2/42mr (- cos ) 2 3V c V o V Co cos )]1V mg 三 RcosLTV lmr 2(4 cos ) 2 mg i Rcos2 3g 丄丄o dtmr 2(4cos )imr 2 2sin1mg 2 r sin(1 cos )1 2sinsin3V o r20o ，其上作用一力Q,且已知P=Q,方向如图，则物块的状态为（A 静止（非临界平衡）状态B 临界平衡状态C 滑动状态D不能确定F 1， F 2， F 3， F 4，且 F 1 = F 2 = F 3=F 4 =4kN ，该力系 向B 点简化的结果为:主矢大小为F R = _____________ ，主矩大小为 M B = ______________ 向D 点简化的结果是什么？ _____________ 。
第1题图第2题图2. 图示滚轮，已知 R 2m ，r 1m ，30，作用于 B 点的力F 4kN ，求力F 对A 点之矩M A = _____________ 。
3. 平面力系向O 点简化，主矢F R 与主矩M O 如图。
若已知F R 10kN ，M O 20kNgm ，求合力大小及 作用线位置，并画在图上。
V s V O r V C V O V COV CO 4 rL s V s mv cM s (F)J s J c m CS 2 £mr 22 122m(r 1 r r cos )42(-3 cos )mr(4 cos )mr 2 V s mv c V s mv co V s mv co Sin()4 mr 2 2 sin(-3 cos )mrL s J sL s mr 2 2 sin(4 cos )mr 2 M s (F) mg^rs inmr 2 2sin(4 cos )mr 21 mr2 2sinmg 2 r sin (善 cos )1 2・g ・ "2sin yrsin块重P,与水面的摩擦角 第1题图2. 图（a ）、（b ）为两种结构，则（）A 图（a ）为静不定的，图（b ）为为静定的 C 图（a ）、（b ）均为静定的 D（二）填空题（每题3分，共12分）第2题图 B 图（a ）、（b ）均为静不定的图（a ）为静不定的，图（b ）为为静1•沿边长为a 2m 的正方形各边分别作用有第4题图角速度 O i A = _____________ , C 点的速度 C = ______________ 。
（三）简单计算题（每小题8分，共24分）1. 梁的尺寸及荷载如图，求 A 、B 处的支座反力。
2. 丁字杆ABC 的A 端固定，尺寸及荷载如图。
求 A 端支座反力。
3. 在图示机构中，已知 O i A O 2B r 0.4m ，O 1O 2 AB ，0/杆的角速度2rad s 2，求三角板C 点的加速度，并画出其方向。
（四）图示结构的尺寸及载荷如图所示，q= 10kN/m, q o = 20kN/m= 约束反力。
（五）多跨静定梁的支撑、荷载及尺寸如图所示。
已知 q= 20kN/m, I = 2m,求支座A 、D E 处的约束反第3题图 4.机构如图，O “A 与O 2B 均位于铅直位置，已知 O i A 3m , 0?B 5m ,O 2B3rad s ，则杆O 1A 的4rad s ，角加速度求A 、C 处力。
（六）复合梁的制成、荷载及尺寸如图所示，杆重不计。
已知q = 20kN/m, I = 2m,求1、2杆的内力以及固定端A处的约束反力。
（七）图示机构中，曲柄 0A= r，以角速度4rad/s绕0轴转动。
QC//O2D , OC= QD= r，求杆OC的角速度。
（一）单项选择题1.A2. B（二）填空题1.0 ; 16kN gm ; F R 0 , M D 16kNgm2.M A 2.93kN gm3.合力F R 10kN，合力作用线位置（通过O1 ） d 2m4. 4.5rad s ; 9m. s（三）简单计算1.取梁为研究对象，其受力图如图所示。
有F AXM A（F）0 , F B 2 P 3 M 0F B 5kNY 0 , F Ay F B P Q 0F Ay 0kN2.取丁字杆为研究对象，其受力图如图所示。