第十七章波动光学
大学物理第十七章波动光学(二)双缝干涉

3. 菲涅耳双棱镜干涉实验
pM
E
s1
ds
s2
N E`
B
C
4. 菲涅耳双面镜干涉实验
点光源 s
屏
平面镜
M1
A
C
M2
B
4. 菲涅耳双面镜干涉实验
点光源 s
屏
平面镜
s1
M1
A
虚光源
s2
C
M2
B
4. 菲涅耳双面镜干涉实验
xk红
k
D d
红
x(k 1)紫
(k
1)
D d
紫
干涉明暗条纹的位置
由 xk红 = x(k+1)紫 的临界情况可得
k红 (k 1)紫
将 红 = 7600Å, 紫 = 4000Å代入得 k=1.1
因为 k只能取整数,所以应取 k=2
这一结果表明:在中央白色明纹两侧, 只有第一级彩色光谱是清晰可辨的。
当容器未充气时,
测量装置实际上是杨氏
l
·P`
双缝干涉实验装置。其
s1
零级亮纹出现在屏上与 s
p0
S1 、S2 对称的P0点.从
s2
S1 、S2射出的光在此处
相遇时光程差为零。
容器充气后,S1射出的光线经容器时光程要增加, 零级亮纹应在 P0的上方某处P出现,因而整个条纹要向 上移动。
干涉明暗条纹的位置
高等教育大学教学课件 大学物理-波动光学
§17-2 双缝干涉 1. 杨氏双缝实验
托马斯• 杨
杨氏双缝实验
相干光的获得:分波阵面法
大学物理第十七章波动光学(一)干涉波 相干波

辐
射
(4) 化学发光
激
(5) 同步辐射光源
受
光
激
光
辐
源
(6) 激光光源
射
2.光源的发光机理
(1)普通光源的发光机理 例:氢原子光谱Fra bibliotek尔末系(可见光)
… …
n
5 4 3
2
E h hc
1
发光时间 :
E4 E3 E2
E
E1 n2
: 108 ~ 1010s
波列
E1=-13.6eV
受激辐射
E2
h
E1
频率 完
h
相位 全 偏振态 相
h
传播方向 同
二、相干光的获得
思路:将同一点光源、某一时刻发出的光分成两束,
再引导其相遇叠加
分波阵面法
将同一波面上两不同 部分作为相干光源
分振幅法(分振幅~分能 量将) 透明薄膜两个面的反射
(透射)光作为相干光源
S1
S*
S2
S
非线性光学 傅里叶光学
§17-1 光源 相干光
一、光的电磁本质
1. 光
广义:电磁波 狭义: 可见光,电磁波中的狭窄波段
光波:交变电磁场在空间传播
S EH
平面电磁波方程
E
E0
cos
(t
r u
)
H
H0
cos (t
r) u
光矢量用 E 矢量表示光矢量,它在引起人眼视觉
和底片感光上起主要作用 .
(5)起偏、检偏,马吕斯定律,布儒斯 特定律
难点: (1)光源发光机理、相干光的获得 (2)光的衍射,光的双折射 (3)光场的时间相干性、空间相干性
迈克尔逊干涉仪
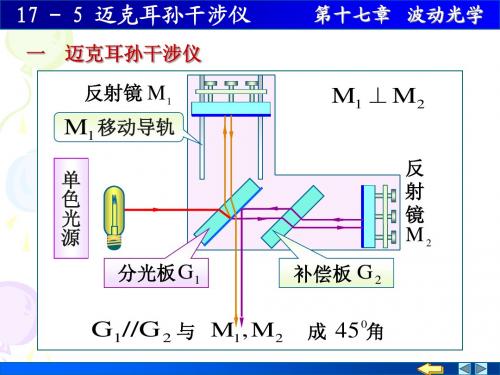
单 色 光 源 反 射 镜
G1
G2
M2
∆ = 2d
17 - 5 迈克耳孙干涉仪
M'2
反射镜M1 单 色 光 源
第十七章 波动光学 当 M1不垂直于 M2 时,可形成劈尖型 等厚干涉条纹. 等厚干涉条纹
反 射 镜
G1
G2
M2
若条纹为等厚条纹, 平移d时 若条纹为等厚条纹 ,M1平移 时, 干涉条移过N条 干涉条移过 条,则有
λ
2
G1
G2
M2
移 动 距 离
干涉 条纹 移动 数目
17 - 5 迈克耳孙干涉仪
第十七章 波动光学
干涉条纹的移动
当 M1 与 M ′ 之间 2 距离变大时 ,圆形干涉 条纹从中心一个个长出, 条纹从中心一个个长出 并向外扩张, 并向外扩张 干涉条纹 变密; 距离变小时, 变密 距离变小时,圆 形干涉条纹一个个向中 心缩进, 心缩进 干涉条纹变稀 .
∆1 − ∆2 = 2 ( n − 1)l = 107 .2 λ
−7
107.2λ 107.2 × 546 ×10 cm = 1+ n = 1+ 2l 2 ×10.0cm
= 1.00029
17 - 5 迈克耳孙干涉仪
第十七章 波动光学
2. 观察肥皂膜的干涉时,先看到彩色图样,当彩色图 观察肥皂膜的干涉时,先看到彩色图样, 消失呈现黑色时,肥皂膜破裂。试解释这一现象。 消失呈现黑色时,肥皂膜破裂。试解释这一现象。 自然光(日光)照射肥皂膜时,入射角恒定( 自然光(日光)照射肥皂膜时,入射角恒定(日 光是平行光) 由于肥皂膜厚度不均匀, 光是平行光),由于肥皂膜厚度不均匀,产生等厚 干涉条纹;又因为日光是白光,其中不同波长的光 干涉条纹;又因为日光是白光, 的干涉条纹疏密不同,所以形成彩色干涉图样。 的干涉条纹疏密不同,所以形成彩色干涉图样。当 薄膜厚度趋向零时,由于半波损失, 薄膜厚度趋向零时,由于半波损失,光程差为λ/2, , 相消干涉, 各种波长的光都是相消干涉 呈现黑色, 各种波长的光都是相消干涉,呈现黑色,此时肥皂 膜即将破裂。 膜即将破裂。
大学物理第十七章波动光学(二)双缝干涉

的极限宽度:
b B
d
d B
b
光场的空间相干性:
*描述光源线宽度对干涉条纹的影响。 *反映扩展光源不同部分发光的独立性。
光源沿y轴方向扩展时,各点光源的各套干涉纹 发生非相干性叠加,条纹更加明亮,所以用狭 缝线光源
(c)光的非单色性对条纹可见度的影响
实际光源都发出非严格单色波,
I
条纹的移动 x D
d
(1)d,D一定时,若λ变化,则Δx将怎样变化?
(2) λ,D一定时,条纹间距Δx与d的关系如何?
(3)白光照射双缝: 零级明纹:白色 其余明纹:彩色光谱
高级次重叠。 S*
零级
一级
二级 三级
(4)光源S的移动对条纹的影响
S沿x轴平移,条纹整体沿相反方向上下移动, 其余不变
I0
I0/2
L
P
可度以证有明关波系L列:长度2L与波长波宽列通过谱PO线点宽持度续时间 t
L c
干涉条纹可见度 V 1 Δ L
定义相干长度为能产生干涉条纹的最大光程差
V 1 Δ L
相干长度和相干时间越长, 光源的相干性越好,条纹 可见度越高。
相干长度: L 2
高等教育大学教学课件 大学物理
同学们好!
§17-2 双缝干涉
一、杨氏双缝实验
Thomas Young 1773--1829
英国医生、科学家托马斯.杨1801年 用双缝干涉实验证明了光的波动性, 并首先测出太阳光的平均波长:
杨氏 570 nm
现代 555 nm
该实验对光的波动说的复苏起到关键 作用,在物理学史上占重要地位。
S沿y轴平移,条纹不动
思考: (1)条纹的定域
第十七章 波动光学习题析与解答

x d
K+1 K
c
第十七章 波动光学
部分习题分析与解答
钢珠c和 、 的直径不同 的直径不同, 钢珠 和a、b的直径不同,则两平板玻璃形成 空气劈尖,由分析得,钢珠c的直径与标准件 空气劈尖,由分析得,钢珠 的直径与标准件 直径相差: 直径相差:
x = N
λ
2
= 1 . 81 × 10
6
m
改变钢珠间的距离d,将钢珠c移至 c′ 处,如图 改变钢珠间的距离 ,将钢珠 移至 所示, 与 之间条纹数目未改变, 所示,a与 c′之间条纹数目未改变,故不影响检 验结果。但由于相邻条纹间距变小, 验结果。但由于相邻条纹间距变小,从而影响观 测。
d = (2k + 1)
λ
4n2
= 2n2 d = (2k + 1)
当k = 0时,d =
λ
4n2
2 = 99.3nm.
17第十七章 波动光学 17-7另解 -
部分习题分析与解答
在折射率n3=1.52的照相机镜头表面涂有一层折射率n2= 1.38的MgF2增透膜,若此膜仅适用于波长 λ =550nm的 光,则此膜的最小厚度为多少? 解:如图示,光线1直接透射,光 2 1 线2经过两次反射后透射,有半波 n1=1.0 2 损失,故两透射光的光程差为 n2=1.38 d
第十七章 波动光学
部分习题分析与解答
解法2 解法 因双缝干涉是等间距的,故也可用以下的条纹间距 公式求入射光波长
x =
d ′ λ d
x
第5条暗纹
应注意两个第5条暗纹之间所包含的相 9 邻条纹间隔数为9,因为中央明纹是中 心(被分在两侧,如右图所示)。故 △x=22.78/9mm,把有关数据代入可得
大学物理(工科) 17-12光的偏振 马吕斯定律

自的然夹光角穿 为过60它 时们,,另出一射束光单强色为自I1然; 光当穿它过们它偏们振化, 出方射向光间 强为 I2 , 且 I1 I2 . 求两束单色自然光的强度之比 .
解 设两束单色自然光的强度分别为 I10 和 I20 .
经过起偏器后光强分别为 I10 和 I20 22
偏振片 : 涂有二向色性材料的透明薄片 .
偏振化方向 : 当自然光照射在偏振片上时, 它只让某一特定方向的光通过,这个方向叫此偏振 片的偏振化方向 .
起偏
I0
起偏器
1 2 I0 偏振化方向
17 - 12 光的偏振性 马吕斯定律 第十七章 波动光学
检偏
起偏器
检偏器
17 - 12 光的偏振性 马吕斯定律 第十七章 波动光学
的光强 I 与转角的关系 .
,
I0
p1
p3
p1
p2
p3
I0
p1
I1 p2 I2 p3
I3
I1
1 2
I0
I2
I1 cos2
I0 2
cos2
17 - 12 光的偏振性 马吕斯定律 第十七章 波动光学
I0
p1
I1 p2 I2 p3
I3
p1
p2 p3
I2
I0 2
cos2
I3
I2
cos2 (π 2
17 - 12 光的偏振性 马吕斯定律 第十七章 波动光学
光的波动性 光波是横波
机械横波与纵波的区别
光的干涉、衍射 . 光的偏振 .
机 械 波 穿 过 狭 缝
17 - 12 光的偏振性 马吕斯定律 第十七章 波动光学
哈工大大学物理课件马文蔚教材第17章波动与光学光的干涉
增透膜、多层膜
1) 增透膜
MgF2 n 1.38
对某一特定波长 ,反射干涉相 玻璃
消,透过相长。
n 1.50
ne , 3
44
2) 高反膜
对某一特定波长使反射率大大加强,透 射率相应减少。
ZnS
MgF2
ZnS
MgF2
3) 干涉滤光层
ZnS
MgF2
多层膜可使从白光中获得特定波长范围的
光。
玻璃
26
17-4 劈尖牛顿环
一 劈尖
2ne
2
劈尖干涉
亮纹 k 暗纹 (k 1 )
2
k 1,2 , k 0 , 1,2 ,
讨论: 1) e 相同的条纹在同一级上,称为等厚干涉
2) e=0 的棱边处,是暗纹,这是半波损失一例证。 3) 任意相邻明(暗)纹间距为 L
e
ek 1
ek
两个普通光源或同一普通光源的不同部分所发出的光是 不相干的
分波前法
从普通光源获得相干光方法:
分振幅法
分振动面法
7
17-2 杨氏双缝干涉实验 双镜 劳埃德镜
一 杨氏双缝干涉实验
实验装置 分波阵面干涉
8
杨氏干涉条纹
S1 和 S2 振动方向相同,
相位相同
频率相同
P点光强
I I1 I2 2
I1I2 cos
Ar: 光场振幅分布
r: 光场相位分布 设原点 0
3
Er, t Arcost r
复数表达式
E~r,t
A
r
eit r
A
r
eit ei r
E~
r
e it
复振幅:
大学物理第十七章波动光学A
例1: 波长为680 nm的平行光照射到L=12 cm长的两块
玻璃片上,两玻璃片的一边相互接触 ,另一边被厚度
D=0.048 mm的纸片隔开. 试问在这12 cm长度内会呈
现多少条暗条纹 ?
解 2d ( 2k 1 )
2
2
空气 n 1
k 0 ,1,2,
2D 2 ( 2km 1 ) 2
n1
nD
n1 L
2D
km
141.2 共有142条暗纹
b
共有141条明纹
讨论:
以明条纹条件为例
2n2e
2
k
两边取无穷小量 2n2e k
e k
2n2
当k 1 e
2n2
条纹级数改变一级某处厚度改变 2。条纹左移
r2 r1 0 由前式可知:
( r2 d nd ) r1
( n 1 )d 7
d 7 7 550 109 6 64 106 m
n 1 1 58 1
P619 17-3-2解: 光程差与干涉条纹位置的关系
r1
s1
s
r2
s2
n c u
c u '
介质中的波长 '
n
真空中的波长 介质的折射率
讨论: 分成的两个点光源S1,S2发出的光波在P点相遇
1.同一介质中相位差和波程差的关系
2
( r1
r2
)
2
r
S1
相位差
波程差
S2
r1
n
8 17-07单缝衍射
d [cot( 15 ) cot( 15 )] 153 m
x1 f
b sin ( 2 k 1)
b
f
R
第一暗纹的衍射角
L
P
1 arcsin
b
b
f
x
o
17 – 7 单缝衍射
第一暗纹的衍射角 1 arcsin
第十七章 波动光学
一定
b b 增大, 1减小 0 , 1 0 b
光直线传播 衍射最大
f
I
sin 当 较小时,
x f
3
2
b
b
o
f
b b f
2
3
b
sin
f
3
b
b
f 2
b
b
f
2
b
f
3
x
b
b
17 – 7 单缝衍射
讨论
b sin 2 k
第十七章 波动光学
2
k 干涉相消(暗纹)
干涉加强(明纹) 2 x x f , b sin b sin , f (1)第一暗纹距中心的距离
17 – 7 单缝衍射
二 光强分布
b sin 2 k
第十七章 波动光学
2
k
干涉相消(暗纹) 干涉加强(明纹)
b sin ( 2 k 1)
2
I
3
b
2
第17章波动光学
教学内容:1. 杨氏双缝干涉实验装置,获得相干光的方法;2. 光程的概念以及光程差和相位差的关系;3. 薄膜干涉中两相干光光程差的分析,确定杨氏双缝干涉条纹及薄膜等厚干涉条纹的位置; 重点难点:1. 光程的计算;2. 薄膜干涉明、暗条纹的计算; 基本要求:1. 了解获得相干光的方法;2. 掌握计算明、暗条纹的光程差条件;3. 理解薄膜干涉是由膜的上、下表面分别反射的两束光的干涉;第十七章 波动光学引言:光学的发展历史和光的本性(学生自学)光学的研究内容十分广泛,它包括光的发射、传播和接收等规律,以及光和其它物质的相互作用(如光的吸收、散射和色散,光的机械作用和光的热、电、化学和生理效应等)。
光学既是物理学中最古老的一门基础学科,又是当前科学领域中最活跃的前沿阵地之一,具有强大的生命力和不可估量的发展前途。
光学的发展过程,是人类认识客观世界的历史长河中一个重要的组成部分,是不断揭露矛盾和克服矛盾、从不完全和不确切的认识逐步走向较完善和较确切认识的过程。
它的不少规律和理论是直接从生产实践中总结出来的,也有相当多的发现来自长期的系统的科学实验。
因此,生产实践和科学实验是推动光学发展的强大动力,为光学发展提供了丰富的源泉。
从方法论上看,作为物理学的一个重要学科分支,光学研究的发展也完全符合如下的认识规律:在观察和实验的基础上,对物理现象进行分析、抽象和综合,进而提出假说,形成理论,并不断反复经受实践的检验。
光学的发展大致可划分为下列五个时期:一、萌芽时期 二、几何光学时期 三、波动光学时期 四、量子光学时期 五、现代光学时期具体发展历史请参阅阅读材料。
第一节 相干光一、光源光波列长度c t l ⨯∆=,秒810-<∆t , 1. 普通光源(1)发光的间隙性;(2)发光的随机性;2. 激光光源单色性好。
λν∆∆、表示光源单色性好坏。
二、光波的描述1. 光振动电场强度E的振动称为光振动。
)2cos(λπϕωrt A E o -+=,uT =λ,εμμμεε11==ro r o u2. 电磁场的能量密度222121H E w με+=)2(cos 222λπϕωεεr t A u E u uw S o -+===平均能流密度或称为光强:2200212111A A u Sdt T Sdt I T μεεττ====⎰⎰比较空间两处的光强,除去介质本身因素外,就是考虑两处光振动矢量的振幅大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d sin i
i
光栅 L
观察屏
p
f
o
λ d sin
>0
i>0 入射光
法线
d (sin sini )
斜入射可获得更高级次条纹(教材例4.5) 对于确定的k,i变化,则 也变化。
例如0级衍射光(k = 0), 有
sin sin i
相邻入射光的相位差: d sini d sin 2π 2π sin 2π d 改变 ,即可改变 0 级衍射光的方向。 2、相控阵雷达
设光栅的每个缝宽均为a,在夫琅禾费衍射下, 每个缝的衍射图样位置是相重叠的。
光栅衍射
N 4 , d 4a
I0 单 单缝衍射光强曲线 -2 -1 0 N2
I单
1 sin2N/sin2
2 sin (/a)
多光束干涉光强曲线
-8
-4 光栅衍射 光强曲线
0 I N2I 0单
4
8 sin (/d)
y1 = 11.9°
2k
2
NEp
d sin 2k
暗纹条件:各振幅矢量构成闭合多边形 0 2
2 2 d sin si n
N=4
2 sin 4d
4d
3 2 sin 3 4d
I 0级 1级 sin /d 2/d
-2(/d) -(/d)
3
4 d 2 d 4d
0
•主极大位置不变 •相 邻 主 极 大 间 有 3 个 暗纹和 2 个次极 •大 条纹变窄、变亮。
N个缝的暗纹,要求: N 2k π
k 1,2,… Nk d sin 而: 2π
闭合
Ep
siny 4R / a b 0.828
∴ y=55.9° (2) 红光的第二、四级与蓝光重合,且最多只能看 到四级,所以纯红光谱的第一、三级将出现.
siny 1 R /a b 0.207
siny 3 3R /a b 0.621
y3 = 38.4°
解: ∵ a+b= (1 / 300) mm = 3.33 m (1) (a + b) siny =k ∴ k= (a + b) sin24.46°= 1.38 m
∵ R=0.63─0.76 m;B=0.43─0.49 m 对于红光,取k=2 , 则R=0.69 m 对于蓝光,取k=3, 则 B=0.46 m 红光最大级次 kmax= (a + b) / R=4.8, 取kmax=4则红光的第4级与蓝光的第6级还会重 合.设重合处的衍射角为y , 则
7
( k 1) 紫 a b
k红 (k 1 )紫
7.6 10 k 4 10 (k 1 )
所以只有 k 1 才满足上式,所以只能产生一 个完整的可见光谱,而第二级和第三级光谱即有 重叠出现。
7
光栅光谱
设第二级光谱中波长为 的光与第三级中紫光开始重 叠,这样
光栅衍射
透镜 θ θ θ 衍射光相干叠加
λ
a d
I
f
衍射的影响: 多缝干涉条纹各级主极大的强度不再相等,而 是受到了衍射的调制。主极大的位置没有变化。
光栅衍射
1.3 光栅的衍射图样
不考虑衍射时, 多缝干涉的光强分布图:
多光束干涉光强曲线 N2 sin2N/sin2
-8
-4
0
4
8 sin (/d)
光栅光谱
解
(1)根据光栅方程 ( a b) sin k 得
b k a sin
按题意知,光栅常数为
ab
1 500
mm 2 10 m
sin 1
2见 k的可能最大值相应于
代入数值得
k
3 .4
k只能取整数 ,故取k=3,即垂直入射时能看到第 三级条纹。
设在美国鳕角(Cape cod)的相控阵雷达照片 阵列宽31m,有1792个辐射单元,覆盖240o视野。 能探测到5500公里范围内的10m2大小的物体。 用于搜索洲际导弹和跟踪人造卫星。
1.6干涉和衍射的联系与区别
干涉和衍射都是波的相干叠加, 但干涉是 有限多个分立光束的相干叠加, 衍射是波阵面
例:用每毫米300条刻痕的衍射光栅来检验仅含有属于红和 蓝的两种单色成分的光谱.已 知 红谱线波长 R 在 0.63─0.76m范围内,蓝谱线波长 B在0.43─0.49 m 范围内.当光垂直入射到光栅时,发现在衍射角为24.46° 处,红蓝两谱线同时出现. (1) 在什么角度下红蓝两谱线还会同时出现? (2) 在什么角度下只有红谱线出现?
上无限多个子波的相干叠加。 二者又常出现在 同一现象中。
单缝衍射
I
多缝衍射中的干涉条纹
-8 -4
a=14 d = 56
0 4 ) 8 / (º
多缝衍射中干涉条纹的强度为单缝衍射图样所影响 a=
-8 -4
d = 50
0
4
8 /(º )
多缝干涉中干涉条纹的强度受单缝衍射的影响小
光栅光谱
单缝衍射 轮廓线 8 sin (/d)
-8
-4
0
4
光栅衍射
1.3 多光束干涉
明纹条件:
缝平面G 透 镜 L
观察屏 P
d
d sin k
(k = 0,1,2,3…)
dsin
o
焦距 f
---光栅方程 设每个缝发的光在对应衍射角 方向的P点的光振 动的振幅为Ep
P点为主极大时
Ep
I单
1 sin2N/sin2
2 sin (/a)
多光束干涉光强曲线
-8
-4 光栅衍射 光强曲线
0 I N2I 0单
4
8 sin (/d)
单缝衍射 轮廓线 8 sin (/d)
-8
-4
0
4
1.5 光栅光谱 1、光栅光谱
1, 2, 正入射: d sin k,k 0,
2 sin (/a)
多光束干涉光强曲线
-8
-4 光栅衍射 光强曲线
0 I N2I 0单
4
8 sin (/d)
单缝衍射 轮廓线 8 sin (/d)
-8
-4
0
4
光栅衍射
光栅衍射的谱线特点: ( 1 )主级大明纹的位置与缝数 N 无关,它们对称 地分布在中央明纹的两侧,中央明纹光强最大;
( 2 )在相邻的两个主级大之间,有 N1 个极小 (暗纹)和N2=2个光强很小的次极大,当N 很大 时,实际上在相邻的主极大之间形成一片暗区,即 能获得又细又亮暗区很宽的光栅衍射条纹。
§17-11 光栅衍射 1. 光栅衍射
1.1 基本概念
• 光栅—大量等宽等间距的平行狭缝(或反射面) 构成的光学元件。 • 种类:
透射光栅 d 反射光栅
d
• 光栅常数
a是透光(或反光)部分的宽度
b是不透光(或不反光)部分的宽度
d=a+b 光栅常量
1.2光通过光栅后的光强分布
缝平面 G
观察屏
透镜 L
k d sin N
k 0, k Nk
相邻主极大间距: d sin 相邻暗纹间距: d sin N 相邻主极大间有N-1个暗纹和N-2个次极大
光栅衍射
N 4 , d 4a
I0 单 单缝衍射光强曲线 -2 -1 0 N2
I单
1 sin2N/sin2
k 一定时, ,不同颜色光的 主极大位置也不同,形成同一级光谱。 白光(350770nm)的光栅光谱是连续谱:
-3级
3级
-2级
-1级 0级 1级 (白 )
2级
汞的光栅光谱
2、斜入射光栅 相控阵雷达 1、光线斜入射时的光栅方程
d (sin sin i ) k
角度符号规定:由法线 转向光线,逆时针为正。
k (k 1 )紫
k 2 ,代入得
紫 4 10 m 6 10 m 600nm
3 2 3 2 7 7
光栅光谱
例题17-11 用每毫米刻有500条栅纹的光栅,观察 钠光谱线( 589.3 nm),问
平行光线垂直入射时; 最多能看见第几级条纹?总共 有多少条条纹?
的单缝衍射和光栅衍射
光栅衍射
干涉明纹位置:
d sin k,k 0,1,2,
衍射暗纹位置: a sin k ,k 1,2,3,
d k 时, ,出现缺级。 k a
干涉明纹缺级级次
d k k a
光栅衍射
N 4 , d 4a
I0 单 单缝衍射光强曲线 -2 -1 0 N2
光栅衍射
1.4 缺级
d 为整数比时,明纹会出现缺级 a I0 单 I单
-2 -1
0
I N 2 I0 单
1
2 sin ( /a)
光栅衍射 光强曲线
N=4 单缝衍射 d = 4a 轮廓线
-8
-4
此图为N = 4,
的光强分布曲线,这里主极大缺±4,±8…级。
d = 4 a
0
4
8 sin ( /d )
d
p 0
dsin
焦距 f
各缝之间的干涉和每缝自身的夫琅禾费衍射, 决定了光通过光栅后的光强分布 多 光 束 干 涉和单缝衍射联合作用的结果。
以双缝为例
透镜
sin 缝衍射:I I 0 观察屏 π a si n
