高一数学二倍角的正
吉林省吉林市高一数学 第三章第2节《二倍角的正弦、余弦、正切(2)》教案 新人教B版必修4

1吉林省吉林市高一数学 第三章第2节《二倍角的正弦、余弦、正切(2)》教案 新人教B 版必修4:(一)复习:1.二倍角的正弦、余弦、正切公式。
2.练习:①=π-ππ+π)125cos125)(sin125cos125(sin2365cos125cos125sin22=π-=π-π.②若tan 3θ=,求sin 2cos 2θθ-的值。
(解答:2222222sin cos sin cos 2tan tan 17sin 2cos 2sin cos 1tan 5θθθθθθθθθθθ+-+--===++).(二)新课讲解:例1.利用三角公式化简:)10tan 31(50sin+.解:原式10cos )10sin 2310cos 21(250sin )10cos 10sin 31(50sin +⋅=+=10cos 40sin 50sin 210cos 10sin 30cos 10cos 30sin 50sin 2=+⋅=110cos 80sin 10cos 40sin 40cos 2===.例2.求证21sin 4cos 41sin 4cos 42tan 1tan θθθθθθ+-++=-.证明:原式等价于22tan 1sin 4cos 4(1sin 4cos 4)1tan θθθθθθ+-=++-, 即:1sin 4cos 4tan 2(1sin 4cos 4)θθθθθ+-=++ (*)而(*)式右边tan 2(1cos 4sin 4)θθθ=++ 2sin 2(2cos 2sin 2cos 2)cos 2θθθθθ=+222sin 2cos 22sin 2θθθ=+ sin 41cos 4θθ=+-=左边, 所以,(*)式成立,原式得证。
【变式练习】已知223sin 2sin 1,3sin 22sin 20αβαβ+=-=,求证:cos(2)0αβ+=. 例3.求函数)7cos(2)722cos(π+-π+=x x y 的值域。
吉林省吉林市高一数学 第三章第2节《二倍角的正弦、余弦、正切(3)》教案 新人教B版必修4

1吉林省吉林市高一数学 第三章第2节《二倍角的正弦、余弦、正切(3)》教案 新人教B 版必修4(一)复习: 1.二倍角公式sin 22sin cos ααα=22cos 2cos sin ααα=-222cos 112sin αα=-=- 22tan tan 21tan ααα=-【练习1】化简:(1)cos 20cos 40cos 60cos 80 ;(2)sin 10sin 30sin 50sin 70 . ((1)(2)两题答案:116).总结:一般地,11sin(2)cos cos 2cos 4cos 22sin n nn αααααα++⋅⋅⋅=. 2.二倍角公式反映的是将二倍角的三角函数值转化为单角的三角函数值。
在倍角公式中,“倍角”与“半角”是相对的,从而有降幂公式:21cos sin 22αα-=,21cos cos 22αα+=,21cos tan 21cos ααα-=+.(二)新课讲解: 1.半角公式:sin2α=cos2α=tan2α=.说明:(1)只要知道2α角终边所在象限,就可以确定符号;(2)公式的“本质”是用α角的余弦表示2α角的正弦、余弦、正切;(3)还有一个有用的公式:αα-=α+α=αsin cos 1cos 1sin 2tan (下面给出证明)。
2.例题分析:2例1.求证:αα-=α+α=αsin cos 1cos 1sin 2tan.证法一:sin sin 2cos sin 222tan21cos cos cos 2cos222ααααααααα⋅===+⋅ .证法二:221cos (1cos )(1cos )sin tan ()21cos (1cos )(1cos )1cos ααααααααα--+===++++∴sin |sin ||tan|||21cos 1cos ααααα==++. 又由2sin 2sin cos2tancos2222ααααα==知sin α与tan2α同号,且1cos 0α+≥,∴sin tan21cos ααα=+, 同理1cos tan2sin ααα-=.【练习2】已知3sin 25θ=,且022πθ<<,求22cossin 12)4θθπθ--+的值。
高一数学必修4313二倍角的正弦余弦正切公式PPT课件

A.6
B.-34
C.-38
9 D.8
[答案] B [解析] tan2α=1-2tatannα2α=12-×332=-34.
第三章 3.1 3.1.3
成才之路 ·数学 ·人教A版 · 必修4
[拓展]倍角公式的变形公式 剖析:(1)公式的逆用: 2sinαcosα=sin2α;sinαcosα=12sin2α; cosα=s2isni2nαα; cos2α-sin2α=cos2α; 1-2tatannα2α=tan2α.
第三章 三角恒等变换
成才之路 ·数学 ·人教A版 · 必修4
课前自主预习 思路方法技巧 名师辨误做答
随堂应用练习 课后强化作业
第三章 3.1 3.1.3
成才之路 ·数学 ·人教A版 · 必修4
课前自主预习
第三章 3.1 3.1.3
成才之路 ·数学 ·人教A版 · 必修4
温故知新 1.cos(α±β)=________;sin(α±β)=________;tan(α±β) =________. [答案] cosαcosβ∓sinαsinβ sinαcosβ±cosαsinβ tanα±tanβ 1∓tanαtanβ
成才之路 ·数学 ·人教A版 · 必修4
思路方法技巧
第三章 3.1 3.1.3
成才之路 ·数学 ·人教A版 · 必修4
命题方向 倍角公式的正用 从题设出发,顺着问题的线索,符合公式的特点,直接 应用倍角公式. [例1] 已知sinα=45,求sin2α、cos2α、tan2α的值.
第三章 3.1 3.1.3
第三章 3.1 3.1.3
成才之路 ·数学 ·人教A版 · 必修4
2.sin21°cos39°+cos21°sin39°等于( )
二倍角的正弦、余弦、正切公式

归纳小结
(1)二倍角公式是和角公式的特例,体现了 二倍角公式是和角公式的特例, 二倍角公式是和角公式的特例 将一般化归为特殊的基本数学思想方法。 将一般化归为特殊的基本数学思想方法。 (2)二倍角公式与和角、差角公式一样,反 二倍角公式与和角、 二倍角公式与和角 差角公式一样, 映的都是如何用单角α的三角函数值表示 映的都是如何用单角 的三角函数值表示 复角( 的三角函数值, 复角(和、差、倍)的三角函数值,结合 前面学习到的同角三角函数关系式和诱导 公式可以解决三角函数中有关的求值、 公式可以解决三角函数中有关的求值、化 简和证明问题。 简和证明问题。
化简 sin 50 (1 + 3 tan10 )
o o
cos10o + 3 sin 10o o 解: 原式 = sin 50 ⋅ o cos10 o o 2 sin 40 = sin 50 ⋅ o cos10 o o 2 sin 40 = cos 40 ⋅ o cos10 o sin 80 = =1 o cos10
[例2]若270°<α<360°, 化简:
1 1 + 2 2
求值
1 1 + cos 2α 2 2
(1)cos80°cos40°cos20° (2)sin10°sin30°sin50°sin70°
例3
1+sin2 −cos2 θ θ 求 : 证 = tanθ 1+sin2 +cos2 θ θ
2
1 + 2 sin θ cos θ − (1 − 2 sin θ ) 证明: 证明:左边 = 2 1 + 2 sin θ cos θ + ( 2 cos θ − 1)
同样对于正切也有这样的结论
5.5.1第三课时二倍角的正弦、余弦、正切公式课件高一上学期数学人教A版(2019)必修第一册

2
+
1-cos (2 -30°)
2
+cos θsin θ
1
=1+2(cos 2θcos 30°-sin 2θsin 30°-cos 2θcos 30°-sin 2θsin 30°)
1
1
+2sin 2θ=1-sin 2θsin 30°+2sin 2θ=1.
(2)证明 左边=
(1-cos2 )+sin2
A.2sin 15°cos 15°
B.cos215°-sin215°
C.2sin215°
D.sin215°+cos215°
2.若 sin
α
3
= ,则 cos α等于
2 3
2
1
A.-
B.-
3
3
π
π
3.sin4 -cos4 等于
12
12
1
A.-
2
B.-
3
2
1
C.
3
1
C.
2
2
D.
3
D.
3
2
跟踪训练
4.cos275°+cos215°+cos 75°cos 15°的值等于
二倍关系.
(3)注意几种公式的灵活应用,如:
①sin
π
π
2x=cos2-2x=cos24-x
=2cos
②cos
π
π
2x=sin2-2x=sin24-x
π
π
=2sin4-xcos4-x.
人教版高一数学必修四第三章二倍角的正弦、余弦、正切公式
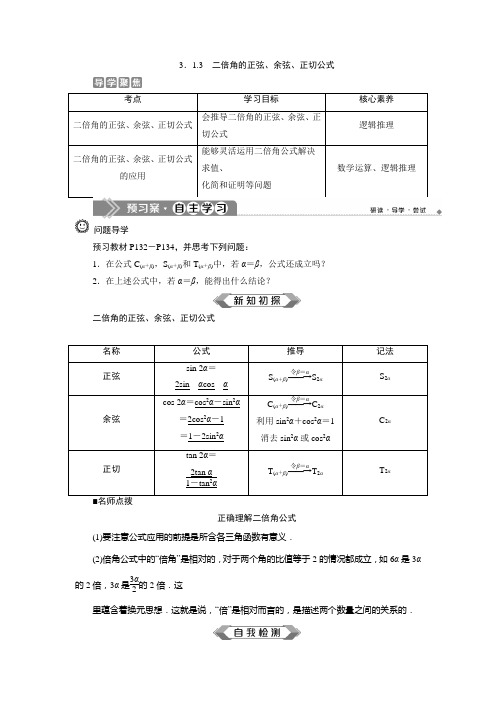
3.1.3二倍角的正弦、余弦、正切公式考点学习目标核心素养二倍角的正弦、余弦、正切公式会推导二倍角的正弦、余弦、正切公式逻辑推理二倍角的正弦、余弦、正切公式的应用能够灵活运用二倍角公式解决求值、化简和证明等问题数学运算、逻辑推理问题导学预习教材P132-P134,并思考下列问题:1.在公式C(α+β),S(α+β)和T(α+β)中,若α=β,公式还成立吗?2.在上述公式中,若α=β,能得出什么结论?二倍角的正弦、余弦、正切公式名称公式推导记法正弦sin 2α=2sin__αcos__αS(α+β)――→令β=αS2αS2α余弦cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2αC(α+β)――→令β=αC2α利用sin2α+cos2α=1消去sin2α或cos2αC2α正切tan 2α=2tan α1-tan2αT(α+β)――→令β=αT2αT2α正确理解二倍角公式(1)要注意公式应用的前提是所含各三角函数有意义.(2)倍角公式中的“倍角”是相对的,对于两个角的比值等于2的情况都成立,如6α是3α的2倍,3α是3α2的2倍.这里蕴含着换元思想.这就是说,“倍”是相对而言的,是描述两个数量之间的关系的.判断(正确的打“√”,错误的打“×”) (1)10α是5α的倍角,5α是5α2的倍角.( ) (2)二倍角的正弦、余弦、正切公式的适用范围是任意角.( ) (3)存在角α,使得sin 2α=2sin α成立.( ) (4)对于任意角α,总有tan 2α=2tan α1-tan 2α.( )答案:(1)√ (2)× (3)√ (4)×已知sin α=35,cos α=45,则sin 2α等于( )A.75 B.125 C.1225 D.2425答案:D计算1-2sin 222.5°的结果等于( ) A.12 B.22 C.33D.32 答案:B已知tan α=43,则tan 2α=________.答案:-247给角求值求下列各式的值. (1)sin π8cos π8;(2)cos 2π6-sin 2π6;(3)2tan 150°1-tan 2150°; (4)cos π5cos 2π5.【解】 (1)sin π8cos π8=12×2sin π8cos π8=12×sin π4=12×22=24.(2)cos2π6-sin2π6=cos⎝⎛⎭⎫2×π6=cosπ3=12.(3)原式=tan(2×150°)=tan 300°=tan(360°-60°)=-tan 60°=- 3.(4)原式=2sinπ5cosπ5cos2π52sinπ5=sin2π5cos2π52sinπ5=sin4π54sinπ5=sinπ54sinπ5=14.给角求值问题的两类解法(1)直接正用、逆用二倍角公式,结合诱导公式和同角三角函数的基本关系对已知式进行转化,一般可以化为特殊角.(2)若形式为几个非特殊角的三角函数式相乘,则一般逆用二倍角的正弦公式,在求解过程中,需利用互余关系配凑出应用二倍角公式的条件,使得问题出现可以连用二倍角的正弦公式的形式.1.cos4π12-sin4π12等于()A.-12B.-32C.12 D.32解析:选D.原式=⎝⎛⎭⎫cos2π12-sin2π12⎝⎛⎭⎫cos2π12+sin2π12=cos π6=32.2.求下列各式的值.(1)tan 30°1-tan2 30°;(2)1sin 10°-3cos 10°.解:(1)tan 30°1-tan230°=12×2tan 30°1-tan230°=12tan 60°=32.(2)原式=cos 10°-3sin 10°sin 10°cos 10°=2⎝⎛⎭⎫12cos 10°-32sin 10°sin 10°cos 10°=4(sin 30°cos 10°-cos 30°sin 10°)2sin 10°cos 10°=4sin (30°-10°)sin (2×10°)=4sin 20°sin 20°=4.给值求值已知cos ⎝⎛⎭⎫α+π4=35,π2≤α<3π2,求cos(2α+π4)的值. 【解】 因为π2≤α<3π2,所以3π4≤α+π4<7π4.因为cos ⎝⎛⎭⎫α+π4>0,所以3π2<α+π4<7π4. 所以sin ⎝⎛⎭⎫α+π4=-1-cos 2⎝⎛⎭⎫α+π4 =-1-⎝⎛⎭⎫352=-45. 所以cos 2α=sin ⎝⎛⎭⎫2α+π2 =2sin ⎝⎛⎭⎫α+π4cos ⎝⎛⎭⎫α+π4 =2×⎝⎛⎭⎫-45×35=-2425, sin 2α=-cos ⎝⎛⎭⎫2α+π2=1-2cos 2⎝⎛⎭⎫α+π4 =1-2×⎝⎛⎭⎫352=725.所以cos ⎝⎛⎭⎫2α+π4=22cos 2α-22sin 2α =22×⎝⎛⎭⎫-2425-725=-31250.三角函数求值问题的一般思路(1)一是对题设条件变形,将题设条件中的角、函数名向结论中的角、函数名靠拢;另一种是对结论变形,将结论中的角、函数名向题设条件中的角、函数名靠拢,以便将题设条件代入结论.(2)注意几种公式的灵活应用,如: ①sin 2x =cos ⎝⎛⎭⎫π2-2x =cos ⎣⎡⎦⎤2⎝⎛⎭⎫π4-x =2cos 2⎝⎛⎭⎫π4-x -1=1-2sin 2⎝⎛⎭⎫π4-x ; ②cos 2x =sin ⎝⎛⎭⎫π2-2x =sin ⎣⎡⎦⎤2⎝⎛⎭⎫π4-x =2sin ⎝⎛⎭⎫π4-x cos ⎝⎛⎭⎫π4-x .1.已知x ∈⎝⎛⎭⎫-π2,0,cos x =45,则tan 2x =( ) A.724 B .-724 C.247D .-247解析:选D.由cos x =45,x ∈⎝⎛⎭⎫-π2,0, 得sin x =-35,所以tan x =-34,所以tan 2x =2tan x1-tan 2x =2×⎝⎛⎭⎫-341-⎝⎛⎭⎫-342=-247,故选D.2.若α∈⎝⎛⎭⎫π2,π,且3cos 2α=sin ⎝⎛⎭⎫π4-α,则sin 2α的值为( )A.118 B .-118 C.1718D .-1718解析:选 D.cos 2α=sin ⎝⎛⎭⎫π2-2α=sin 2⎝⎛⎭⎫π4-α=2sin ⎝⎛⎭⎫π4-αcos ⎝⎛⎭⎫π4-α,代入原式,得6sin ⎝⎛⎭⎫π4-α·cos ⎝⎛⎭⎫π4-α=sin ⎝⎛⎭⎫π4-α.因为α∈⎝⎛⎭⎫π2,π,所以cos ⎝⎛⎭⎫π4-α=16,所以sin 2α=cos ⎝⎛⎭⎫π2-2α=2cos 2⎝⎛⎭⎫π4-α-1=-1718.化简与证明(1)化简2cos 2α-12tan ⎝⎛⎭⎫π4-αsin 2⎝⎛⎭⎫π4+α;(2)证明tan ⎝⎛⎭⎫π4+α-tan ⎝⎛⎭⎫π4-α=2tan 2α. 【解】 (1)原式=cos 2α2tan ⎝⎛⎭⎫π4-αcos 2⎝⎛⎭⎫π2-π4-α=cos 2α2tan ⎝⎛⎭⎫π4-αcos 2⎝⎛⎭⎫π4-α=cos 2α2sin ⎝⎛⎭⎫π4-αcos ⎝⎛⎭⎫π4-α =cos 2αsin ⎝⎛⎭⎫2×π4-2α =cos 2αcos 2α=1. (2)证明:法一:左边=sin ⎝⎛⎭⎫π4+αcos ⎝⎛⎭⎫π4+α-sin ⎝⎛⎭⎫π4-αcos ⎝⎛⎭⎫π4-α=sin ⎝⎛⎭⎫π4+αcos ⎝⎛⎭⎫π4-α-sin ⎝⎛⎭⎫π4-αcos ⎝⎛⎭⎫π4+αcos ⎝⎛⎭⎫π4+αcos ⎝⎛⎭⎫π4-α=sin ⎝⎛⎭⎫π4+α-π4+αcos ⎝⎛⎭⎫π4+αsin ⎝⎛⎭⎫π4+α=sin 2α12sin ⎝⎛⎭⎫π2+2α=2sin 2αcos 2α=2tan 2α=右边.所以等式成立.法二:左边=1+tan α1-tan α-1-tan α1+tan α=4tan α1-tan 2α=2tan 2α=右边.故原式成立.三角函数式的化简与证明(1)化简的方法①弦切互化,异名化同名,异角化同角;②降幂或升幂;③一个重要结论:(sin θ±cos θ)2=1±sin 2θ.(2)证明三角恒等式的方法①从复杂的一边入手,证明一边等于另一边;②比较法,左边-右边=0,左边右边=1;③分析法,从要证明的等式出发,一步步寻找等式成立的条件.1.若α为第三象限角,则1+cos 2αcos α-1-cos 2αsin α=________.解析:因为α为第三象限角,所以cos α<0,sin α<0, 所以1+cos 2αcos α-1-cos 2αsin α=2cos 2αcos α-2sin 2αsin α=-2cos αcos α--2sin αsin α=0.答案:02.求证:4sin αcos α1+cos 2α·cos 2αcos 2α-sin 2α=tan 2α.证明:左边=2sin 2α2cos 2α·cos 2αcos 2α=tan 2α=右边.1.已知sin α=3cos α,那么tan 2α的值为( ) A .2 B .-2 C.34D .-34解析:选D.因为sin α=3cos α,所以tan α=3, 所以tan 2α=2tan α1-tan 2α=2×31-32=-34.2.已知sin θ2+cos θ2=233,那么sin θ=________,cos 2θ=________.解析:因为sin θ2+cos θ2=233,所以⎝⎛⎭⎫sin θ2+cos θ22=43, 即1+2sin θ2cos θ2=43,所以sin θ=13,所以cos 2θ=1-2sin 2θ=1-2×⎝⎛⎭⎫132=79. 答案:13 793.已知α∈⎝⎛⎭⎫π2,π,sin α=55. (1)求sin 2α,cos 2α的值; (2)求cos ⎝⎛⎭⎫5π6-2α的值. 解:(1)因为α∈⎝⎛⎭⎫π2,π,sin α=55, 所以cos α=-1-sin 2α=-255.sin 2α=2sin αcos α=2×55×⎝⎛⎭⎫-255=-45, cos 2α=1-2sin 2α=1-2×⎝⎛⎭⎫552=35. (2)由(1)知cos ⎝⎛⎭⎫5π6-2α=cos 5π6cos 2α+sin 5π6sin 2α =⎝⎛⎭⎫-32×35+12×⎝⎛⎭⎫-45 =-4+3310.[A 基础达标]1.已知sin ⎝⎛⎭⎫π4-x =35,则cos ⎝⎛⎭⎫π2-2x 的值为( )A.1925 B.1625 C.1425D.725解析:选D.因为sin ⎝ ⎛⎭⎪⎫π4-x =35,所以cos ⎝ ⎛⎭⎪⎫π2-2x =cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫π4-x=1-2sin 2⎝ ⎛⎭⎪⎫π4-x =725.2.已知sin α=55,则cos 4α-sin 4α的值为( ) A .-35B .-15C.15D.35解析:选D.cos 4α-sin 4α=(cos 2α+sin 2α)(cos 2α-sin 2α)=cos 2α=1-2sin 2α=1-25=35.3.设-3π<α<-5π2,化简1-cos (α-π)2的结果是( )A .sin α2B .cos α2C .-cos α2D .-sin α2解析:选C.因为-3π<α<-5π2,-3π2<α2<-5π4,所以1-cos (α-π)2=1+cos α2=⎪⎪⎪⎪⎪⎪cos α2=-cos α2.4.已知cos ⎝⎛⎭⎫α-π4=-13,则sin(-3π+2α)=( )A.79 B .-79C.35D .-35解析:选A.易得cos ⎝ ⎛⎭⎪⎫2α-π2=2cos 2⎝ ⎛⎭⎪⎫α-π4-1=2×⎝⎛⎭⎫-132-1=-79.又cos ⎝⎛⎭⎪⎫2α-π2=cos ⎝ ⎛⎭⎪⎫π2-2α=sin 2α,所以sin(-3π+2α)=sin(π+2α)=-sin 2α=-⎝⎛⎭⎫-79=79.故选A. 5.化简tan 14°1-tan 214°·cos 28°的结果为( )A.sin 28°2B .sin 28°C .2sin 28°D .sin 14°cos 28°解析:选A.tan 14°1-tan 214°·cos 28°=12×2tan 14°1-tan 214°·cos 28°=12tan 28°·cos 28°=sin 28°2,故选A.6.已知sin α-2cos α=0,则tan 2α=________. 解析:由sin α-2cos α=0,得tan α=sin αcos α=2,tan 2α=2tan α1-tan 2α=2×21-22=-43. 答案:-437.已知tan α=-13,则sin 2α-cos 2α1+cos 2α=________.解析:sin 2α-cos 2α1+cos 2α=2sin αcos α-cos 2α1+2cos 2α-1=2sin αcos α-cos 2α2cos 2α=tan α-12=-56.答案:-568.1-2sin 20°cos 20°2cos 210°-1-cos 2160°-1=________.解析:1-2sin 20°cos 20°2cos 210°-1-cos 2160°-1=(cos 20°-sin 20°)2cos 20°-sin 20°=cos 20°-sin 20°cos 20°-sin 20°=1.答案:19.已知sin 2α=513,π4<α<π2,求sin 4α,cos 4α的值.解:由π4<α<π2,得π2<2α<π. 因为sin 2α=513,所以cos 2α=-1-sin 22α=-1-⎝⎛⎭⎫5132=-1213. 于是sin 4α=2sin 2αcos 2α=2×513×⎝⎛⎭⎫-1213=-120169; cos 4α=1-2sin 22α=1-2×⎝⎛⎭⎫5132=119169. 10.已知π2<α<π,sin α=45. (1)求tan 2α的值;(2)求cos ⎝⎛⎭⎫2α-π4的值. 解:(1)由题意得cos α=-35, 所以tan α=-43, 所以tan 2α=2tan α1-tan 2α=-831-169=247. (2)因为sin α=45,所以cos 2α=1-2sin 2α=1-2×⎝⎛⎭⎫452=-725, sin 2α=2sin α·cos α=2×45×⎝⎛⎭⎫-35=-2425. 所以cos ⎝⎛⎭⎪⎫2α-π4=cos 2α·cos π4+sin 2α·sin π4=⎝⎛⎭⎫-725×22+⎝⎛⎭⎫-2425×22=-31250. [B 能力提升]11.已知tan x =2,则tan ⎣⎡⎦⎤2⎝⎛⎭⎫x -π4等于( ) A.43B .-43 C.34 D .-34解析:选C.tan ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x -π4 =tan ⎝ ⎛⎭⎪⎫2x -π2=sin ⎝ ⎛⎭⎪⎫2x -π2cos ⎝ ⎛⎭⎪⎫2x -π2=-cos 2x sin 2x =-1tan 2x=-1-tan 2x 2tan x =4-12×2=34. 12.已知θ∈⎝⎛⎭⎫π2,π,1sin θ+1cos θ=22,则sin ⎝⎛⎭⎫2θ+π3=________. 解析:1sin θ+1cos θ=22⇒sin θ+cos θsin θcos θ=22 ⇒sin θ+cos θ=22sin θcos θ⇒1+sin 2θ=2sin 22θ,因为θ∈⎝ ⎛⎭⎪⎫π2,π,所以2θ∈(π,2π), 所以sin 2θ=-12,所以sin θ+cos θ<0, 所以θ∈⎝ ⎛⎭⎪⎫3π4,π,所以2θ∈⎝ ⎛⎭⎪⎫3π2,2π, 所以cos 2θ=32,所以sin ⎝⎛⎭⎪⎫2θ+π3=sin 2θ·cos π3+sin π3cos 2θ=12. 答案:1213.已知sin ⎝⎛⎭⎫π4-x =513,0<x <π4,求cos 2x cos ⎝⎛⎭⎫π4+x 的值. 解:因为0<x <π4,所以0<π4-x <π4. 又因为sin ⎝ ⎛⎭⎪⎫π4-x =513, 所以cos ⎝ ⎛⎭⎪⎫π4-x =1213. 因为cos 2x =sin ⎝ ⎛⎭⎪⎫π2-2x =2sin ⎝ ⎛⎭⎪⎫π4-x cos ⎝ ⎛⎭⎪⎫π4-x =2sin ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π4+x cos ⎝ ⎛⎭⎪⎫π4-x=2cos ⎝ ⎛⎭⎪⎫π4+x cos ⎝ ⎛⎭⎪⎫π4-x , 所以cos 2x cos ⎝ ⎛⎭⎪⎫π4+x =2cos ⎝ ⎛⎭⎪⎫π4-x =2413. 14.(选做题)已知sin x 2-2cos x 2=0. (1)求tan x 的值;(2)求cos 2xcos ⎝⎛⎭⎫5π4+x sin (π+x )的值.解:(1)由sin x 2-2cos x 2=0, 知cos x 2≠0,所以tan x 2=2, 所以tan x =2tan x 21-tan 2 x 2=2×21-22=-43. (2)由(1)知tan x =-43, 所以cos 2x cos ⎝ ⎛⎭⎪⎫5π4+x sin (π+x ) =cos 2x-cos ⎝ ⎛⎭⎪⎫π4+x (-sin x ) =cos 2x -sin 2x ⎝⎛⎭⎫22cos x -22sin x sin x =(cos x -sin x )(cos x +sin x )22(cos x -sin x )sin x =2×cos x +sin x sin x=2×1+tan x tan x =24.。
高一数学必修4: 二倍角的正弦、余弦、正切公式

能 力 提 升一、选择题1.(2013·长沙模拟)若cos2αsin (α-π4)=-22,则cos α+sin α的值为( )A .-72 B .-12 C.12 D.72[答案] C[解析] cos2αsin (α-π4)=cos 2α-sin 2α22(sin α-cos α) =(cos α+sin α)(cos α-sin α)22(sin α-cos α)=-2(cos α+sin α)=-22. ∴sin α+cos α=12.2.已知sin θ=45,sin θcos θ<0,则sin2θ的值为( ) A .-2425 B .-1225 C .-45 D.2425 [答案] A[解析] ∵sin θ=45>0,sin θcos θ<0, ∴cos θ<0.∴cos θ=-1-sin 2θ=-35.∴sin2θ=2sin θcos θ=-2425.3.若x =π12,则cos 2x -sin 2x 的值等于( ) A.14 B.12 C.22 D.32[答案] D[解析] 当x =π12时,cos 2x -sin 2x =cos2x =cos(2×π12)=cos π6=32.4.(2013·济南模拟)已知cos2θ=23,则sin 4θ+cos 4θ的值为( ) A.1318 B.1118 C.79 D .-1 [答案] B[解析] sin 4θ+cos 4θ=(sin 2θ+cos 2θ)2-2sin 2θcos 2θ =1-12sin 22θ=1-12(1-cos 22θ)=1118.5.已知向量a =⎝ ⎛⎭⎪⎫cos θ,12的模为22,则cos2θ等于( ) A.2-32 B .-14 C .-12 D.12 [答案] C[解析] |a |=cos 2θ+14=22,则cos 2θ=14,所以cos2θ=2cos 2θ-1=-12.6.(2013·新课标Ⅱ文)已知sin2α=23,则cos 2(α+π4)=( ) A.16 B.13 C.12 D.23[答案] A[解析] 本题考查半角公式及诱导公式.由倍角公式可得,cos 2(2+π4)=1+cos (2α+π2)2=1-sin2α2=1-232=16,故选A.二、填空题7.在△ABC 中,cos A =513,则sin2A =________. [答案] 120169[解析] ∵0<A <π,∴sin A =1-cos 2A =1213.∴sin2A =2sin A cos A =120169.8.(2013山东师大附中模拟)若α∈(0,π2),且sin 2α+cos2α=14,则tan α的值等于________.[答案]3[解析] 由sin 2α+cos2α=14得sin 2α+1-2sin 2α=1-sin 2α=cos 2α=14.∵α∈(0,π2),∴cos α=12,∴α=π3,∴tan α=tan π3= 3.9.2002年北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形接成的一个大正方形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为θ,那么cos2θ的值等于________.[答案] 725[解析] 设直角三角形的两直角边长分别为a ,b ,则有4×⎝ ⎛⎭⎪⎫12ab +1=25,∴ab =12.又a 2+b 2=25,即直角三角形的斜边c =5.解方程组⎩⎪⎨⎪⎧ab =12,a 2+b 2=25,得⎩⎪⎨⎪⎧a =3,b =4或⎩⎪⎨⎪⎧a =4,b =3,∴cos θ=45.∴cos2θ=2cos 2θ-1=725. 三、解答题10.已知sin(π4-x )=513,0<x <π4,求cos2xcos (π4+x )的值. [解析] 原式=sin (π2+2x )cos (π4+x )=2sin (π4+x )·cos (π4+x )cos (π4+x )=2sin(π4+x ).∵sin(π4-x )=cos(π4+x )=513, 且0<x <π4, ∴π4+x ∈(π4,π2), ∴sin(π4+x )=1-cos 2(π4+x )=1213.∴原式=2×1213=2413.11.已知cos(x -π4)=210,x ∈(π2,3π4). (1)求sin x 的值. (2)求sin(2x +π3)的值. [解析] (1)因为x ∈(π2,3π4), 所以x -π4∈(π4,π2),于是sin(x -π4)=1-cos 2(x -π4)=7210,则sin x =sin[(x -π4)+π4] =sin(x -π4)cos π4+cos(x -π4)sin π4 =7210×22+210×22=45. (2)因为x ∈(π2,3π4), 故cos x =-1-sin 2x =-1-(45)2=-35,sin2x =2sin x cos x =-2425,cos2x =2cos 2x -1=-725,所以sin(2x +π3)=sin2x cos π3+cos2x sin π3=-24+7350.12.设函数f (x )=2cos x sin(x +π3)-3sin 2x +sin x cos x ,当x ∈[0,π2]时,求f (x )的最大值和最小值.[解析] f (x )=2cos x (12sin x +32cos x )-3sin 2x +sin x cos x =2sin x cos x +3(cos 2x -sin 2x )=sin2x +3cos2x =2sin(2x +π3). ∵x ∈[0,π2],∴2x +π3∈[π3,4π3], ∴-32≤sin(2x +π3)≤1, 从而-3≤f (x )≤2π2]时,f(x)max=2,f(x)min=- 3.故当x∈[0,。
3.1.3 二倍角的正弦、余弦、正切公式

问题 2 根据同角三角函数的基本关系式 sin2α+cos2α=1, 你能否只用 sin α 或 cos α 表示 cos 2α? ∵cos 2α=cos2α-sin2α=cos2α-( 或 cos 2α=cos2α-sin2α=( 【倍角公式】 (1)S2α:sin 2α= (2)C2α:cos 2α= (3)T2α:tan 2α= , = . sin α α cos = 2 2 = ; ; - - )= )-sin2α= - - ; .
4
例3
π sin 2x-2sin2x 4 5π 7π -x =- , <x< ,求 若 cos 的值. 4 5 4 4 1+tan x
小结 本题采用的“凑角法”是解三角问题的常用技巧,解题时首先要分析已知条件和 结论中各种角之间的相互关系,并根据这种关系来选择公式.
3
鸡西市第十九中学高一数学组
;
; .
例 1 求下列各式的值: π 5 (1)cos cos π; 12 12
1 2 (2) - cos215° . 3 3
小结 解答此类题目一方面要注意角的倍数关系; 另一方面要注意函数名称的转化方法, 同角三角函数关系及诱导公式是常用方法. 训练 1 求值:(1)cos 20° · cos 40° · cos 80° ; (2)tan 70° · cos 10° · ( 3tan 20° -1).
【二倍角的正弦、余弦、正切公式的推导】 问题 1 二倍角的正弦、 余弦、 正切公式就是用 α 的三角函数表示 2α 的三角函数的公式. 根 据前面学过的两角和与差的正弦、余弦、正切公式.你能推导出二倍角的正弦、余弦、 正切公式吗?试一试? sin 2α=sin(α+α)= cos 2α=cos(α+α)= tan 2α=tan(α+α)= + - . = = ; - ;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、1、做主线任务,跟着系统提示主线任务走,经验和奖励都比较丰厚。2、2、参拜龙卫,每天两次机会,一次免费的,一次花费100元宝的,有点小贵,不过前期经验可观。3、3、石阁试炼,高额副本任务,消耗试炼凭证门票,也就是说要门票的,没有门票进不去,不过经验高呐。4、4、除魔 作为2015年最火手游,神途手机版BOSS所在地图都是不能直接飞的地图,各大BOSS地图怎么走,今天小编就为大家详细的汇总下各大BOSS地图的走法,这样小伙伴们准备起来方便点,更容易早点打到BOSS。 神途手游之骷髅精灵 1、骷髅精灵在兽人古墓三层,小伙伴们从比奇出发,首先到比奇森林。2、接着我们通过小地图到兽人古墓一层。3、打开小地图的自动导航功能,让小伙伴们跑路更方便。4、然后我们到达兽人古墓二层,到这里BOSS已经近在眼前了。5、最后我们到达兽人古墓三层,这里就是BOSS的刷新地点,
神途开服表 https://
27代理是一款专业的网络游戏代理,很多童鞋不知道27代理怎么激活使用,容易和IP代理免费版搞混淆,下面简单介绍27代理和IP代理免费版区别以及怎么激活使用。 27代理 IP代理免费版
27代理提供免费试用功能,无需填写账号,如图所示,点击试用按钮会自动填上免费的账号密码,点击登录后即可正常使用,27代理支持魔兽世界、暗黑3、神途等所有网络游戏加速。 如果要激活,请到27代理官网充值才能激活。IP代理是一款免费的网络游戏加_速_器,不支持支持魔兽世界、暗黑3、神途游戏加速。IP代理账号和27代理账号不通用,如果需要激活,请参考以下方法激活使用。 1.进入IP代理官网 2.点击网页左边新用户注册. 3.填写账号密码,姓名,电子信箱等信息后确认即可注册成功. 4.到账号管理页面,参照图2点击激活等一分钟后即可使用. 神途魔龙地图怎么走
1、魔龙旧寨→魔龙祭坛→→↑↓魔龙西郊→西魔龙关↑↓↓↑↓魔龙城西林间胜地→魔龙沼泽→魔龙岭魔龙谷→龙源血路→魔龙血域↑↓↑↓↑东魔龙关魔龙东郊→东林间胜地→魔龙旧寨→魔龙祭坛下面是三种通往魔龙血域的坐标(魔龙城老兵坐标)魔龙城()→魔龙西郊()→魔龙旧寨()→魔龙祭 相信很多人都玩过神途这款游戏,当年可是火了很久了,可以说是很多人那一段时间的回忆,现在手游版的也特别火,但是有一些玩法会与以前的老神途有许多的不同,现在我将为大家讲解一下教程,希望大家能够有所受用。 神途手游版教程如何登入游戏1、首先,在一些软件中心,搜索“神途”会出现一堆游戏,找到神途,点击下载安装。 2、安装好之后,点击进入手游界面,点击“与QQ好友玩”如何会提示你的手机QQ授权登入,点击登入,你升级跟不上他们,不利于你玩游戏。4、进入服务器之后,选择你的游戏角色,有三个角色,我选择战 随着神途手游的公测开始,一大批神途粉进入游戏,等级高必然是大家所追求的,那么怎么样才能快速升级,在游戏中领先他人一步呢,下面介绍几个方法。
