材料力学习题解答31PPT课件
材料力学习题(PPT)共17页文档
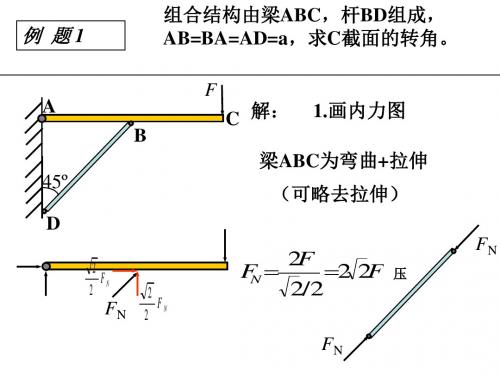
3E I
3
1
2l 1
Pll ) Pll l
2
3 GIp
fc
2Pl3 3EI
Pl3 GIp
T图
施加的单位力和P同位置、同方向, 所以M0c图、T0c图和M图、T图形 状一样
例7:图示开口刚架,EI=const。求沿P力作用线方向的相对 线位移 ΔAB 。
解:
AB2E Pa I38 11 322 12 1
2F
压
画出AC的M图,DB 的轴力图。
F
FN
FN
2 2F
A
F C 2.加单位载荷m0=1,画内力图
B
FN a
1 2/2
2 a
压
45º
D
(M)
2 2
FN
FN
2 2 FN
m0=1
1
画出AC的 M 图,DB 的FN图。
FN
2
FN
a
3.图乘法
(M)
Fa
(FN)
M
2 2F
1
2 2F 2a 2
C
例3:图示梁的抗弯刚度为EI,试求D点的铅垂位移。
vC
3 EI
Pa2 2
2a
3
Pa 3 EI
例 题4
求C处的线位移。
解: 1.画内力图
BC段为弯曲(x 轴为 中性轴)
AB段为弯曲(z 轴为 中性轴)+扭转
y
x z
Al
ql 2 2
(MT)
ql 2
qC l
B
ql 2 2
2.求 cx ,应在C处沿x方向加单位力。
qa A 2
材料力学习题及答案

材料力学-学习指导及习题答案第一章绪论1-1 图示圆截面杆,两端承受一对方向相反、力偶矩矢量沿轴线且大小均为M的力偶作用。
试问在杆件的任一横截面m-m上存在何种内力分量,并确定其大小。
解:从横截面m-m将杆切开,横截面上存在沿轴线的内力偶矩分量M x,即扭矩,其大小等于M。
1-2 如图所示,在杆件的斜截面m-m上,任一点A处的应力p=120 MPa,其方位角θ=20°,试求该点处的正应力σ与切应力τ。
解:应力p与斜截面m-m的法线的夹角α=10°,故σ=p cosα=120×cos10°=118.2MPaτ=p sinα=120×sin10°=20.8MPa1-3 图示矩形截面杆,横截面上的正应力沿截面高度线性分布,截面顶边各点处的正应力均为σmax=100 MPa,底边各点处的正应力均为零。
试问杆件横截面上存在何种内力分量,并确定其大小。
图中之C点为截面形心。
解:将横截面上的正应力向截面形心C简化,得一合力和一合力偶,其力即为轴力F N=100×106×0.04×0.1/2=200×103 N =200 kN其力偶即为弯矩M z=200×(50-33.33)×10-3 =3.33 kN·m1-4 板件的变形如图中虚线所示。
试求棱边AB与AD的平均正应变及A点处直角BAD的切应变。
解:第二章轴向拉压应力2-1试计算图示各杆的轴力,并指出其最大值。
解:(a) F N AB=F, F N BC=0, F N,max=F(b) F N AB=F, F N BC=-F, F N,max=F(c) F N AB=-2 kN, F N2BC=1 kN, F N CD=3 kN, F N,max=3 kN(d) F N AB=1 kN, F N BC=-1 kN, F N,max=1 kN2-2 图示阶梯形截面杆AC,承受轴向载荷F1=200 kN与F2=100 kN,AB段的直径d1=40 mm。
《材料力学》课后习题答案(详细)

第二章轴向拉(压)变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:(1)求指定截面上的轴力FN =-11FF F N -=+-=-222(2)作轴力图轴力图如图所示。
(b)解:(1)求指定截面上的轴力FN 211=-02222=+-=-F F N (2)作轴力图FF F F N =+-=-2233轴力图如图所示。
(c)解:(1)求指定截面上的轴力FN 211=-FF F N =+-=-222(2)作轴力图FF F F N 32233=+-=-轴力图如图所示。
(d)解:(1)求指定截面上的轴力FN =-11F F a aFF F qa F N 22222-=+⋅--=+--=-(2)作轴力图中间段的轴力方程为:x aF F x N ⋅-=)(]0,(a x ∈轴力图如图所示。
[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积2400mm A =,试求各横截面上的应力。
解:(1)求指定截面上的轴力kNN 2011-=-)(10201022kN N -=-=-)(1020102033kN N =-+=-(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力MPa mm N A N 504001020231111-=⨯-==--σMPamm N A N 254001010232222-=⨯-==--σMPa mmN A N 254001010233333=⨯==--σ[习题2-3]试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积21200mm A =,22300mm A =,23400mm A =,并求各横截面上的应力。
解:(1)求指定截面上的轴力kNN 2011-=-)(10201022kN N -=-=-)(1020102033kN N =-+=-(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力MPa mm N A N 10020010202311111-=⨯-==--σMPa mmN A N 3.3330010102322222-=⨯-==--σMPamm N A N 254001010233333=⨯==--σ[习题2-4]图示一混合屋架结构的计算简图。
章习题参考答案材料力学课后习题题解_图文

2.37 图示销钉连接中,F=100kN ,销钉材料许用剪切应力 [τj]=60MPa,试确定销钉的直径d25kN;FBA=43.3kN。查型钢表 可得:ABC=6.928cm2,
FBC=25kN;FBA=43.3kN;ABC=6.928cm2, [σ]1=160MPa;AAB=100×50mm2 ;[σ]2=8MPa。
杆BC满足强度要求,但杆BA不满足强度要求。 将[FBA]带入(1)、(2)式中求得许用荷载[F]=46.2kN
2.25 图示结构中,横杆AB为刚性杆,斜杆CD为直径d=20mm 的圆杆,材料的许用应力[σ]=160MPa ,试求许用荷载[F]。
解:CD=1.25m, sinθ=0.75/1.25=0.6
2.25 图示结构中,横杆AB为刚性杆,斜杆CD为直径d=20mm 的圆杆,材料的许用应力[σ]=160MPa ,试求许用荷载[F]。
解:受力分析如图
d1=20mm,E1=200GPa; d2=25mm,E2=100GPa。
2.15 图示结构中,AB杆和AC杆均为圆截面钢杆,材料相同 。已知结点A无水平位移,试求两杆直径之比。 解:
由两杆变形的几何关系可得
2.20 图示结构中,杆①和杆②均为圆截面钢杆,直径分别 为d1=16mm,d2=20mm ,已知F=40kN ,刚材的许用应力 [σ]=160MPa,试分别校核二杆的强度。 解:受力分析如图
解:CD=1.25m, sinθ=0.75/1.25=0.6
d=20mm [σ]=160MPa
2.27 图示杆系中,木杆的长度a不变,其强度也足够高,但 钢杆与木杆的夹角α可以改变(悬挂点C点的位置可上、下 调整)。若欲使钢杆AC的用料最少,夹角α应多大? 解:
答 45o
材料力学习题大全及答案
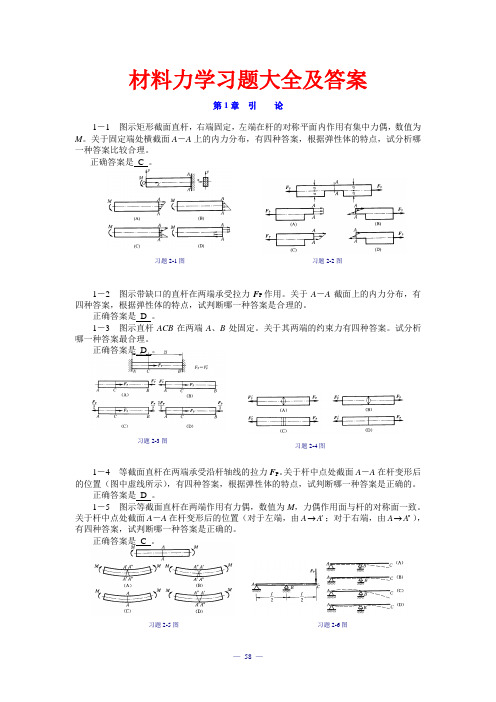
习题2-1图 习题2-2图习题2-3图 习题2-4图习题2-5图 习题2-6图材料力学习题大全及答案第1章 引 论1-1 图示矩形截面直杆,右端固定,左端在杆的对称平面内作用有集中力偶,数值为M 。
关于固定端处横截面A -A 上的内力分布,有四种答案,根据弹性体的特点,试分析哪一种答案比较合理。
正确答案是 C 。
1-2 图示带缺口的直杆在两端承受拉力F P 作用。
关于A -A 截面上的内力分布,有四种答案,根据弹性体的特点,试判断哪一种答案是合理的。
正确答案是 D 。
1-3 图示直杆ACB 在两端A 、B 处固定。
关于其两端的约束力有四种答案。
试分析哪一种答案最合理。
正确答案是 D 。
1-4 等截面直杆在两端承受沿杆轴线的拉力F P 。
关于杆中点处截面A -A 在杆变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试判断哪一种答案是正确的。
正确答案是 D 。
1-5 图示等截面直杆在两端作用有力偶,数值为M ,力偶作用面与杆的对称面一致。
关于杆中点处截面A -A 在杆变形后的位置(对于左端,由A A '→;对于右端,由A A ''→),有四种答案,试判断哪一种答案是正确的。
正确答案是 C 。
习题2-1图习题2-2图习题2-3图习题2-4图1-6 等截面直杆,其支承和受力如图所示。
关于其轴线在变形后的位置(图中虚线所示),有四种答案,根据弹性体的特点,试分析哪一种是合理的。
正确答案是 C 。
第2章 杆件的内力分析2-1 平衡微分方程中的正负号由哪些因素所确定?简支梁受力及Ox 坐标取向如图所示。
试分析下列平衡微分方程中哪一个是正确的。
(A )d d Q x F d M(B )d d Q x F (C )d d Q x F (D )d d Q xF 2-2 对于图示承受均布载荷q 的简支梁,其弯矩图凸凹性与哪些因素相关?试判断下列四种答案中哪几种是正确的。
工程力学材料力学部分课后习题详解
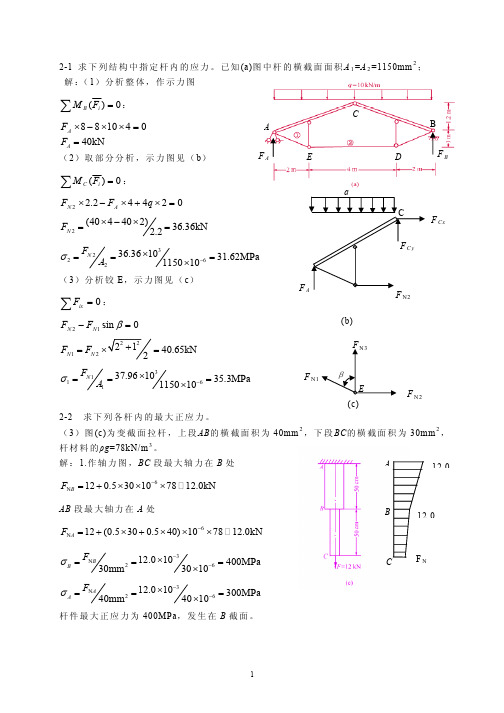
2-1 求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A 1=A 2=1150mm 2; 解:(1)分析整体,作示力图∑=0)(i BF M:CB 041088=××−×A F AF N1F N2(c)40kN A F =(2)取部分分析,示力图见(b )∑=0)(i CF M:02442.22=×+×−×q F F A N2(404402)36.36kN 2.2N F ×−×==3262236.361031.62MPa 115010N F A σ−×===×(3)分析铰E ,示力图见(c )∑=0ix F :0sin 12=−βN N F F1240.65kN N N F F == 3161137.961035.3MPa 115010N F A σ−×===×2-2 求下列各杆内的最大正应力。
(3)图(c)为变截面拉杆,上段AB 的横截面积为40mm 2,下段BC 的横截面积为30mm 2,杆材料的ρg =78kN/m 3。
解:1.作轴力图,BC 段最大轴力在B 处6N 120.530107812.0kN B F −=+×××AB 段最大轴力在A 处6N 12(0.5300.540)107812.0kN A F −=+×+×××3N 2612.010400MPa 30mm3010B B F σ−−×===× 3N 2612.010300MPa 40mm 4010AA F σ−−×===×杆件最大正应力为400MPa ,发生在B 截面。
EDF BF AF CxF N2(b)A120B120F NC2-4 一直径为15mm ,标距为200mm 的合金钢杆,比例极限内进行拉伸试验,当轴向荷载从零缓慢地增加58.4kN 时,杆伸长了0.9mm ,直径缩小了0.022mm ,确定材料的弹性模量E 、泊松比µ。
材料力学全部习题解答 ppt课件

得泊松比
' 0.33
22
解:1.轴力分析 由 F E
A
得
2.确定 F 及 值
根据节点A的平衡方程
FEA
得
23
A
l1 解:1.计算杆件的轴向变形
l2
由(2-15)可知: FN1 F50KN(拉力)
由胡克定理得
FN2 2F502KN (压力)
杆1的伸长为 l1F E N 1A 1l1 1200 50 10 9 1 03 4 00 1. 5 10 60.936m m
则,根据 Iz=Iz0+Aa2
得: Iz= I'zA y c2= 1 .7 3 1 0 -3m 4
30
(b) 沿截面顶端建立坐标轴z’,y轴不变
Z
A = 0 .8 0 .5 0 .5 5 0 .4 = 0 .1 8 m 2
ydA
yc=
A
A
0.15
0.7
0.8
0.5 ydy20.05 ydy0.5 ydy
此值虽然超过 ,但超过的百分数在5%以内,故仍符合强
度要求。
21
2-21 图示硬铝试样,厚度δ=2mm,试验段板宽b=20mm,标距l=70mm。在 轴向拉F=6kN的作用下,测得试验段伸长Δl=0.15mm,板宽缩短Δb=0.014mm。 试计算硬铝的弹性模量E与泊松比μ。
解:轴向正应变 l0.0m 15 m 1% 0 0 0.2% 14
解:1.问题分析 由于横截面上仅存在沿截面高度线性分布
的 正 应 力 , 因 此 , 横 截 面 上 只 存 在 轴 力 FN 及弯矩Mz,而不可能存在剪力和扭矩。
7
2.内力计算
根据题意,设 kya.代入数据得:
材料力学习题及答案.pptx

解 : (1) 轮 1 、 2 、 3 、 4 作 用 在 轴 上 扭 力 矩 分 别为
轴内的最大扭矩
若将轮 1 与轮 3 的位置对调,则最大扭矩变 为
最大扭矩变小,当然对轴的定的圆截面轴,承受扭力矩作用。试求支反力偶矩。设扭转刚度为已知常数。
试从强度方面考虑,建立三者间的合理比值。已知许用应力[σ]=120MPa,许用切应力[τ]=90MPa,许用挤 压应力[σbs]=240MPa。
解:由正应力强度条件 由挤压强度条件
由切应力强度条件
5
学海无 涯
D:h:d=1.225:0.333:1
式 (1) : 式 (3)得
式 (1) : 式 (2) 得
由实心轴的切应力强度条件
4-3(4-12) 某传动轴,转速 n=300 r/min,轮 1 为主动轮,输入功率 P1=50kW,轮 2、轮 3 与轮 4 为从动轮,输出功率分别为 P2=10kW,P3=P4=20kW。
(1) 试求轴内的最大扭矩; (2) 若将轮 1 与轮 3 的位置对调,试分析对轴的受力是否有利。
10
学海无 涯
解:各杆轴力及变形分别为
梁 BD 作刚体平动,其上 B、C、D 三点位移相
等
3-8(3-17) 图示桁架,在节点 B 和 C 作用一对大小相等、方
向相反的载荷 F。设各杆各截面的拉压刚度均为 EA,试计算节点 B 和 C 间的相对位移ΔB/C。
解
:
根
据
能
量
守
恒
定
律
,
有
3-9(3-21) 由铝镁合金杆与钢质套管组成一复合杆,杆、管各载面的刚度分别为 E1A1 与 E2A2。复合杆承受 轴向载荷 F 作用,试计算铝镁合金杆与钢管横载面上的正应力以及杆的轴向变形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应力
[,]许6M 用P挤a压应力
,[许b用s]切10应MPa
力
,当轴[]向1载M荷Pa 时,试确定F钢4板5k的N尺寸
与 ,以及木杆的高度L 。
h
解: 拉伸面面积:At (h2)b
F
挤压面面积: Abs 2b
剪切面面积: As 2Lh
F
L
L
h
F
b
F
拉伸,挤压以及剪切的力均为: F45kN
t
F F [] At (h2)b
F23k0N 时,试校核结构的强度。
4120
解: Fmax23k0N
F
F
Fs FbsF 5253046 kN
F s F s F s F s F s 170
危险拉伸面:
右边截面处 A tb17 10 017m 02m 0
右边第一个铆钉处 A t' (b d ) (1 7 2)0 0 1 0 15 m 0 2 m 0
与 ,以及木杆的高度L 。
h
解: (h2)b F
[]
2 Lb F [ ]
2b F [ bs ]
F
F
F
2b[ bs ]
45103 225010
9mm
L
L
h
F
b
F
L F 2b[ ]
45103
90mm
2 2501
h F 2 2b[]
45103 18 33mm 22506
7
16. 如图所示螺钉结构, D30m,md20m,mh10mm 拉杆材料的许用拉应力 []14M 0 P,a 许用挤压应力 [bs]24M 0 Pa 许用切应力 []10M 0 P。a 载荷 F45kN,试校验螺钉的强度。
解: 剪切问题。
F
剪切面为钢板中的一个圆环面。 d
Ad
F F At d
要冲出圆孔,则有:
Fbd
3 .1 4 4 3 0 1 0 3 0 .8 7 1 3 N 6 0
F
d
b
37.86kN Fmin 37.86kN
5
15. 如图所示两矩形截面的木杆,用两块钢板连
接在一起,已知木杆的截面宽度 b25,m 0许m用拉
所以,F=10kN时试 件处于弹性阶段。
l EFAlE4Fd2l
410103200 901033.14102
42 0.28m 3 m
93.14
3
13. 上题若加载到轴向应变0.8%时开始卸载, 仍然假设杆件横截面上的应力始终均匀分布, 则当载荷卸到 F时10k,N杆件中的弹性应变 以及e 塑性应变 各为 p 多少?
材料力学习题解答3
材料力学性能与 连接件的实用计算
11. 同一材料的拉伸和扭转实验的应力应变关系如 图所示,试指出哪根曲线是拉伸实验的结果?而哪根 曲线是扭转实验的结果?并根据图中的数据计算材料 的弹性模量以及泊松比。
解: ①是扭转实验曲
,(MPa)
线,②是拉伸实 验曲线。
240 ②
96
E12 2 1 0 4 6 0 0 0 0.2 160 20 10 30 MPa
① 1200
,(με)
E20G 0 Pa G 12 9 1 0 6 6 0 0 0.0 8 160 8 0 130 MPa
G E
2(1 )
G80GPa
1E12000.25
2G 160
2
12.某试件材料为如图所示的理想弹塑性材料, 若试件的直径 d10mm,长度l20m 0 ,m杆件横
截面上的应力始终均匀分布,试计算试件两端受
(h2)b F []
bsAFbs2F b[bs]
2b F [ bs ]
F F []
As 2Lb
2 Lb F [ ]
6
15. 如图所示两矩形截面的木杆,用两块钢板连
接在一起,已知木杆的截面宽度 b25,m 0许m用拉
应力
[,]许6M 用P挤a压应力
,[许b用s]切10应MPa
力
,当轴[]向1载M荷Pa 时,试确定F钢4板5k的N尺寸
拉力F10kN作用时试件的轴向伸长量,以及使试
件屈服的载荷FNs 。
解: 材料的弹性模量:
(MPa)
E1809 0130MP 9aG 0 Pa 180 0.2%
试件屈服载荷:
FNs A
s
0 0.2
(%)
FNsAs
d2s
4
3 .1 4 120 18 10 .1 4 3 130 N 1.1 4k 3N 4
解: E90GPa
(MPa)
tanE18090GPa e
e91 01830021 0 30.2%
p0.3% 0.2% 0.1%
180
0.3
0 0.2
p e
(%)
4
14. 冲床的冲压部分如图所示,冲头直径 d30m,m已知钢板的 厚度为 10mm,其剪切强度极限为 b 400MP,a若要在钢板上 冲出一个和冲头直径相同的圆孔,则至少需要多大的冲击力 F?
挤压应力 [bs]34M 0 P,a许用切应力 []12M 0 Pa。当载荷
F23k0N 时,试校核结构的强度。
4120
板中可能的最大拉伸应力:
m1 a xF A m t a x213 7 1030 0 1 03 .3M 5 P []a
m2 a xF A tF 's(23 140 5 ) 6 1 0 30 0 1.2 7M 2 P []a
10
18. 两块厚 10mm 的钢板用5个 20mm的铆钉连接。
三种构件材料相同,材料的许用拉应力 []15M 0 P,a 许用
Fs
m 2D
F A s d 422m Dd 2m 2D
Fs
Fs
Fs
Fs
2200103 3.14122 100
8.8M 5 P [a]
螺栓强度足够!
9
18. 两块厚 10mm 的钢板用5个 20mm的铆钉连接。
三种构件材料相同,材料的许用拉应力 []15M 0 P,a 许用
挤压应力 [bs]34M 0 P,a许用切应力 []12M 0 Pa。当载荷
Fs
As
F
dh
4 5130 7.6 1M P[a]
3.1 42 010
螺钉强度不够!8
17. 如图所示联轴器传递的力矩 m20N0m,两轴之间用 四个对称分布于 D10m 0 m 的圆周上的螺栓连接,螺栓直径
d12mm ,许用切应力 []60MPa,试校核螺栓的剪切强度。
解:
D m4Fs22FsD
解:
拉伸面:
At
d 2 4
挤压面:
(D2 d2)
Abs
4
D
h d
剪切面: As dh
F
拉伸力、挤压力、剪切力均为: F tF bsF sF4k 5N
t
Ft At
4F
d2
44 5130 3.1 42201
4 .3M 3 P[a]
bsF Abbss(D42Fd2)3.14 4(4 3 2 5 0 1 2 3020 )11 .6M 4 P [b a]s
