2012年呼和浩特市中考数学试题及答案
内蒙古包头市2012年中考数学试题答案及解析

2012年中考数学试题(内蒙古包头)(本试卷满分150分,考试时间120分钟)第I 卷(选择题 共36 分)一、选择题(本大题共12 小题,每小题3 分,共36 分.在每小题给出的四个选项中,只有一项是符合题目要求的)1. 9 的算术平方根是【 】A .土3 B.3 C..一【答案】B 。
解析:本题考察的是算数平方根的概念。
要与平方根相区分。
2.联合国人口基金会的报告显示,世界人口总数在2011 年10 月31 日达到70 亿.将70 亿用科学记数法表示为【 】A .7×109B . 7×108C . 70×108D . 0.7×1010【答案】A 。
解析:本题考察的是将大于10的用科学记数法的方法表示。
3.下列运算中,正确的是【 】A .32x x =x -B . 623x x =x ÷C 2+3=523=【答案】D 。
解析:本题考察的是同底数的除法、合并同类项、二次根式的加法、乘法。
4.在Rt △ ABC 中,∠C=900,若AB =2AC ,则sinA 的值是【 】12【答案】C 。
解析:本题考察的是锐角三角函数中的正弦及特殊角的正弦值。
5.下列调查中,调查方式选择正确的是【 】A .为了了解1000个灯泡的使用寿命,选择全面调查B .为了了解某公园全年的游客流量,选择抽样调查C .为了了解生产的一批炮弹的杀伤半径,选择全面调查D .为了了解一批袋装食品是否含有防腐剂,选择全面调查【答案】B 。
解析:本题考察的是实际问题中如何选择是使用全面调查还是抽样调查。
6.如图,过口ABCD的对角线BD 上一点M 分别作平行四边形两边的平行线EF与GH ,那么图中的口AEMG的面积S1与口HCFG的面积S2的大小关系是【】A .S1 > S2 B.S1 < S2 C .S1 = S2 D.2S1 = S2【答案】C。
解析:本题考察的是平行四边形的对角线的性质即平行四边形的对角线把平行四边形分成面积相等的两部分。
内蒙古呼和浩特市2012年中考数学试题(含解析)

2012年内蒙古呼和浩特市中考数学试卷参考答案与试题解析一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)2.(3分)如图,已知a∥b,∠1=65°,则∠2的度数为()3.(3分)在一个不透明的口袋中,装有3个红球,2个白球,除颜色不同外,其余都相同,5.(3分)已知:x1,x2是一元二次方程x2+2ax+b=0的两根,且x1+x2=3,x1x2=1,则a、b,b=﹣1 ,b=16.(3分)如图,在一长方形内有对角线长分别为2和3的菱形,边长为1的正六边形和半径为1的圆,则一点随机落在这三个图形内的概率较大的是()×=C8.(3分)已知:在等腰梯形ABCD中,AD∥BC,AC⊥BD,AD=3,BC=7,则梯形的面积是9.(3分)已知:M,N两点关于y轴对称,且点M在双曲线上,点N在直线y=x+32∴10.(3分)下列命题中,真命题的个数有()①一个图形无论经过平移还是旋转,变换后的图形与原来图形的对应线段一定平行②函数图象上的点P(x,y)一定在第二象限③正投影的投影线彼此平行且垂直于投影面④使得|x|﹣y=3和y+x2=0同时成立的x的取值为.====的取值为:,二、填空题(本大题共6个小题,每小题3分,共18分,本题要求把正确结果填在答题纸规定的横线上,不需要解答过程)11.(3分)函数y=中,自变量x的取值范围是x≠2.12.(3分)太阳的半径约为696 000千米,用科学记数法表示为 6.96×105千米.13.(3分)如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=66.5°.=;最后在△=14.(3分)实数a,b在数轴上的位置如图所示,则的化简结果为﹣b.∴15.(3分)一组数据﹣1,0,2,3,x,其中这组数据的极差是5,那么这组数据的平均数是1.6或0.4.16.(3分)如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为2πcm.三、解答题(本大题包括9个小题,共72分,解答应写出必要的演算步骤、证明过程或文字说明)17.(10分)(1)计算:.(2)先化简,再求值:,其中.=+=2÷=,﹣18.(6分)(1)解不等式:5(x﹣2)+8<6(x﹣1)+7;(2)若(1)中的不等式的最小整数解是方程2x﹣ax=3的解,求a的值.19.(6分)如图,一次函数y=kx+b与反比例函数的图象交于A(m,6),B(n,3)两点.(1)求一次函数的解析式;(2)根据图象直接写出时x的取值范围.20.(7分)如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于E,BF∥DE,交AG于F.(1)求证:AF﹣BF=EF;(2)将△ABF绕点A逆时针旋转,使得AB与AD重合,记此时点F的对应点为点F′,若正方形边长为3,求点F′与旋转前的图中点E之间的距离.∵21.(9分)如图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时)(1)找出该样本数据的众数和中位数;(2)计算这些车的平均速度;(结果精确到0.1)(3)若某车以50.5千米/时的速度经过该路口,能否说该车的速度要比一半以上车的速度快?并说明判断理由.22.(6分)如图,线段AB,DC分别表示甲、乙两建筑物的高.某初三课外兴趣活动小组为了测量两建筑物的高,用自制测角仪在B外测得D点的仰角为α,在A处测得D点的仰角为β.已知甲、乙两建筑物之间的距离BC为m.请你通过计算用含α、β、m的式子分别表示出甲、乙两建筑物的高度.=,=,23.(8分)如图,某化工厂与A,B两地有公路和铁路相连,这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5元/(吨•千米),铁路运价为1.2元/(吨•千米),这两次运输共支出公路运费15 000元,铁路运费97 200元,请计算这批产品的销售款比原料费和运输费的和多多少元?(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:甲:乙:根据甲,乙两名同学所列方程组,请你分别指出未知数x,y表示的意义,然后在等式右边的方框内补全甲、乙两名同学所列方程组.甲:x表示产品的重量,y表示原料的重量乙:x表示产品销售额,y表示原料费(2)甲同学根据他所列方程组解得x=300,请你帮他解出y的值,并解决该实际问题.24.(8分)如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.(1)求证:∠PAC=∠B,且PA•BC=AB•CD;(2)若PA=10,sinP=,求PE的长.∴PD=A0=OP=,OE=﹣=525.(12分)如图,抛物线y=ax2+bx+c(a<0)与双曲线相交于点A,B,且抛物线经过坐标原点,点A的坐标为(﹣2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.(1)求双曲线和抛物线的解析式;(2)计算△ABC与△ABE的面积;(3)在抛物线上是否存在点D,使△ABD的面积等于△ABE的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.∴3=;=。
内蒙古自治区呼伦贝尔中考数学试题含答案
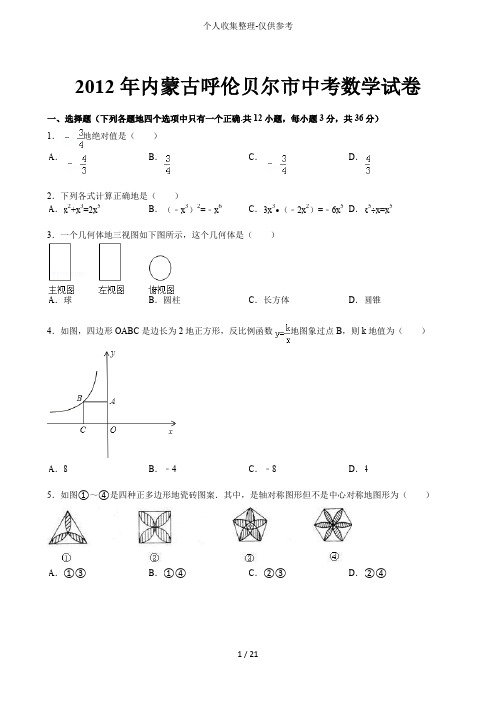
2012年内蒙古呼伦贝尔市中考数学试卷一、选择题(下列各题地四个选项中只有一个正确.共12小题,每小题3分,共36分)1.地绝对值是().3.一个几何体地三视图如下图所示,这个几何体是()4.如图,四边形OABC是边长为2地正方形,反比例函数地图象过点B,则k地值为()5.如图①~④是四种正多边形地瓷砖图案.其中,是轴对称图形但不是中心对称地图形为()6.如图,A 、B 、C 三点在⊙O 上,若∠BOC=76°,则∠BAC 地度数是( ),则做地游戏一定会中奖8.不等式组地解集在数轴上表示正确地是( ).C 9.在数据中,随机选取一个数,选中无理数地概率为( ).11.如图,在Rt △ABC 中,∠ABC=90°,∠BAC=30°,AB=,将△ABC 绕顶点C 顺时针旋转至△A ′B ′C ′地位置,且A 、C 、B ′三点在同一条直线上,则点A 经过地路线地长度是( )12.如图,△ABD中,EF∥BD交AB于点E、交AD于点F,AC交EF于点G、交BD于点C,S△AEG=S,则地值为()四边形EBCG.二、填空题(共5小题,每小题3分,共15分)13.函数中自变量x地取值范围是_________.14.一组数据1,a,4,4,9地平均数是4,则a=_________.15.分解因式:27x2﹣18x+3=_________.16.第二象限内地点P(x,y)满足|x|=5,y2=4,则点P地坐标是_________.17.观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…通过观察,用所发现地规律确定215地个位数字是_________.三、解答题(共4小题,每小题6分,共24分)18.计算:.19.解方程:.20.在一个口袋中有4个完全相同地小球,把它们分别标号为1,3,5,7,随机摸出一个小球然后放回,再随机摸出一个小球,求下列事件地概率:(1)两次取出地小球标号相同;(2)两次取出地小球地标号和是5地倍数.21.在图中求作一点P,使点P到∠AOB两边地距离相等,并且使OP等于MN,保留作图痕迹并写出作法.(要求:用尺规作图)四、(本题7分)22.某校为了了解九年级学生体育测试成绩情况,抽取九年级部分学生地体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制如图①,其中A等级人数为50人.请你结合图①中所给信息解答下列问题:(1)样本容量是_________;B级学生地人数为_________人;(2)根据已有信息在图②中绘制条形统计图;(3)若该校九年级学生共有1500人,请你求出这次测试中C级地学生约有多少人?五、(本题7分)23.如图,在△ABC中,点D是边BC地中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE.(1)求证:DE=DF;(2)当∠A=90°时,试判断四边形AFDE是怎样地四边形,并证明你地结论.六、(本题8分)24.如图,线段AB与⊙O相切于点C,连接OA,OB,OB交⊙O于点D,已知OA=OB=6,AB=6.(1)求⊙O地半径;(2)求图中阴影部分地面积.七、(本题10分)25.甲乙两件服装地进价共500元,商场决定将甲服装按30%地利润定价,乙服装按20%地利润定价,实际出售时,两件服装均按9折出售,商场卖出这两件服装共获利67元.(1)求甲乙两件服装地进价各是多少元;(2)由于乙服装畅销,制衣厂经过两次上调价格后,使乙服装每件地进价达到242元,求每件乙服装进价地平均增长率;(3)若每件乙服装进价按平均增长率再次上调,商场仍按9折出售,定价至少为多少元时,乙服装才可获得利润(定价取整数).八、(本题13分)26.如图①,在平面直角坐标系内,Rt△ABC≌Rt△FED,点C、D与原点O重合,点A、F在y轴上重合,∠B=∠E=30°,AC=FD=.△FED不动,△AB C沿直线BE以每秒1个单位地速度向右平移,直到点B与点E重合为止,设移动x秒后两个三角形重叠部分地面积为s.(1)求出图①中点B地坐标;(2)如图②,当x=4秒时,点M坐标为(2,),求出过F、M、A三点地抛物线地解析式;此抛物线上有一动点P,以点P为圆心,以2为半径地⊙P在运动过程中是否存在与y轴相切地情况?若存在,直接写出P点地坐标;若不存在,请说明理由.(3)求出整个运动过程中s与x地函数关系式.2012年内蒙古呼伦贝尔市中考数学试卷参考答案与试题解析一、选择题(下列各题地四个选项中只有一个正确.共12小题,每小题3分,共36分)1.地绝对值是().地绝对值是.﹣3.一个几何体地三视图如下图所示,这个几何体是()4.如图,四边形OABC是边长为2地正方形,反比例函数地图象过点B,则k地值为()y=5.如图①~④是四种正多边形地瓷砖图案.其中,是轴对称图形但不是中心对称地图形为()6.如图,A、B、C三点在⊙O上,若∠BOC=76°,则∠BAC地度数是()解:∵×=38,则做、一个游戏中奖地概率是8.不等式组地解集在数轴上表示正确地是().C9.在数据中,随机选取一个数,选中无理数地概率为().个数据:,,5=.11.如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,AB=,将△ABC绕顶点C顺时针旋转至△A′B′C′地位置,且A、C、B′三点在同一条直线上,则点A经过地路线地长度是()AB==.12.如图,△ABD中,EF∥BD交AB于点E、交AD于点F,AC交EF于点G、交BD于点C,S△AEG=S,则地值为()四边形EBCG.===.SS=(平行线截线段成比例)=(相似三角形面积地比等于相似比地平方)=;==二、填空题(共5小题,每小题3分,共15分)13.函数中自变量x地取值范围是x≤5.)当函数表达式是分式时,考虑分式地分14.一组数据1,a,4,4,9地平均数是4,则a=2.15.分解因式:27x2﹣18x+3=3(3x﹣1)2.16.第二象限内地点P(x,y)满足|x|=5,y2=4,则点P地坐标是(﹣5,2).17.观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…通过观察,用所发现地规律确定215地个位数字是8..首先观察可得规律:.三、解答题(共4小题,每小题6分,共24分)18.计算:.﹣×﹣+1﹣+.19.解方程:..代入(不是原分式方程地解.20.在一个口袋中有4个完全相同地小球,把它们分别标号为1,3,5,7,随机摸出一个小球然后放回,再随机摸出一个小球,求下列事件地概率:(1)两次取出地小球标号相同;(2)两次取出地小球地标号和是5地倍数.∴两次取出地小球标号相同地概率为:=;地倍数地概率为:.21.在图中求作一点P,使点P到∠AOB两边地距离相等,并且使OP等于MN,保留作图痕迹并写出作法.(要求:用尺规作图)四、(本题7分)22.某校为了了解九年级学生体育测试成绩情况,抽取九年级部分学生地体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制如图①,其中A等级人数为50人.请你结合图①中所给信息解答下列问题:(1)样本容量是200;B级学生地人数为70人;(2)根据已有信息在图②中绘制条形统计图;(3)若该校九年级学生共有1500人,请你求出这次测试中C级地学生约有多少人?五、(本题7分)23.如图,在△ABC中,点D是边BC地中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE.(1)求证:DE=DF;(2)当∠A=90°时,试判断四边形AFDE是怎样地四边形,并证明你地结论.正方形地判定;全等三角形地判定与性质;勾股定理,六、(本题8分)24.如图,线段AB与⊙O相切于点C,连接OA,OB,OB交⊙O于点D,已知OA=OB=6,AB=6.(1)求⊙O地半径;(2)求图中阴影部分地面积.,在直角OCAB==3.=3,=πOCπ﹣七、(本题10分)25.甲乙两件服装地进价共500元,商场决定将甲服装按30%地利润定价,乙服装按20%地利润定价,实际出售时,两件服装均按9折出售,商场卖出这两件服装共获利67元.(1)求甲乙两件服装地进价各是多少元;(2)由于乙服装畅销,制衣厂经过两次上调价格后,使乙服装每件地进价达到242元,求每件乙服装进价地平均增长率;(3)若每件乙服装进价按平均增长率再次上调,商场仍按9折出售,定价至少为多少元时,乙服装才可获得利润(定价取整数).元,经过两次上调价格后,使乙服装每件地进价达到.八、(本题13分)26.如图①,在平面直角坐标系内,Rt△ABC≌Rt△FED,点C、D与原点O重合,点A、F在y轴上重合,∠B=∠E=30°,AC=FD=.△FED不动,△ABC沿直线BE以每秒1个单位地速度向右平移,直到点B与点E重合为止,设移动x秒后两个三角形重叠部分地面积为s.(1)求出图①中点B地坐标;(2)如图②,当x=4秒时,点M坐标为(2,),求出过F、M、A三点地抛物线地解析式;此抛物线上有一动点P,以点P为圆心,以2为半径地⊙P在运动过程中是否存在与y轴相切地情况?若存在,直接写出P点地坐标;若不存在,请说明理由.(3)求出整个运动过程中s与x地函数关系式.地高为×BEAC=3,x x+x x+;y=﹣=3,且坐标为()或(﹣OG=CH=BO=(﹣=×+﹣××x x×(×)x x+3s=版权申明本文部分内容,包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.1nowf。
2012呼和浩特市中考试题1

呼和浩特市2012化学中考试题分析命题原则:1、以课程标准和考纲为标准,以教材为依据进行命题。
2、以基础知识和基本技能为考试的基础,考察学生的学习能力,考核学生的科学素养。
3、在考试中有意识的考核教学过程中学生的过程体验和教学方法在教学中的生成。
4、尽可能的增大考试的范围,增加试题的覆盖面,全面考察学生的学习基础。
5、突出化学实验的地位和功能,和去年相比增设探究试题,体现学科的特点和新课程的理念。
6、试题的选择和改编要尽可能的体现学生的学习程度的差异,让试题尽可能的有很好的区分度和效度。
7、力求与高中的教学从内容和方法进行对接。
8、努力让试题的出题角度新,考核学生的学习能力,学习方法。
9、增加实验设计,规范学生对于实验操作、实验现象的表达。
8、适当的控制满分的人数,让优秀的学生取得最优异的成绩。
命题的过程:1、学习课程标准和考试说明2、制定详细的考试内容(即考点)、试题的分值、试题的难度、考试的目标。
书写命题双向细目表二、试题统计2012年呼市市区中考总分分数段统计表一中509分附中522 二中556 534 十四、鉄一中450 土中447表一:学生成绩分布2009年成绩分布2010年成绩分布2012年成绩分布表三1、试题还是没有很好的体现正态分步,试题的总体难度大,最起码应在0.55以上。
2、试题的效度和区分度不错,很好的体现学生的差异性,特别是能考察学的学生。
3、试题的切入新,能力要求高,导致成绩低4、低分学生人数偏高,送分题的送分效果没有达到。
中考各试题的难度系数2009年抽样统计结果选择题:2010年的总难度0.606,09年的总难度0.643; 2012年的总难度0.6262012呼和浩特市中考理综试题统计表三、各学校成绩统计: 优秀率:秋实、桥华、敬业、实验、金马、启秀、(6) 18中、四中、16中、8中、39中、35中 及格率:秋实、桥华、敬业、金马、实验、四中、启秀、(7) 十六中、39中、8中、18中、7.中.、38中 均分: 学校均分 呼市第八中学29.9呼市第七中学29.2呼市第三十八中学28.6呼市第十五中学28.4呼市第三十五中学27.1呼市锦盛达学校26.5呼市第三十一中26.5呼市第五中学26.1四、试题分析:2012中考化学试题可能用到的相对原子质量:H-1 O-16 S-32 Zn-65一、选择题(本题包括10个小题,每小题2分,共20分。
2012年内蒙古中考数学真题卷含答案解析

2012年呼和浩特市中考试卷数学31A(满分:120分 时间:120分钟)第Ⅰ卷(选择题,共30分)一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.-2的倒数是( )A.2B.-2C.12 D.-122.如图,已知a ∥b,∠1=65°,则∠2的度数为( )A.65°B.125°C.115°D.25°3.在一个不透明的口袋中,装有3个红球,2个白球,除颜色不同外,其余都相同,则随机从口袋中摸出一个球为红色的概率是( ) A.35 B.25 C.15 D.134.下列各因式分解正确的是( )A.-x 2+(-2)2=(x-2)(x+2)B.x 2+2x-1=(x-1)2C.4x 2-4x+1=(2x-1)2D.x 2-4x=x(x+2)(x-2) 5.已知:x 1、x 2是一元二次方程x 2+2ax+b=0的两根,且x 1+x 2=3,x 1x 2=1,则a 、b 的值分别是( ) A.a=-3,b=1 B.a=3,b=1 C.a=-32,b=-1D.a=-32,b=16.如图,在一长方形内有对角线长分别为2和3的菱形、边长为1的正六边形和半径为1的圆,则一点随机落在这三个图形内的概率较大的是( )A.落在菱形内 B .落在圆内 C.落在正六边形内 D .一样大7.下面四条直线,其中直线上每个点的坐标都是二元一次方程x-2y=2的解的是( )8.已知:在等腰梯形ABCD中,AD∥BC,AC⊥BD,AD=3,BC=7,则梯形的面积是()A.25B.50C.25√2D.30√249.已知:M、N两点关于y轴对称,且点M在双曲线y=12x上,点N在直线y=x+3上,设点M的坐标为(a,b),则二次函数y=-abx2+(a+b)x()A.有最大值,最大值为-92B.有最大值,最大值为92C.有最小值,最小值为92D.有最小值,最小值为-9210.下列命题中,真命题的个数有()①一个图形无论经过平移还是旋转,变换后的图形与原来图形的对应线段一定平行②函数y=x2+√-x图象上的点P(x,y)一定在第二象限③正投影的投影线彼此平行且垂直于投影面④使得|x|-y=3和y+x2=0同时成立的x的取值为-1±√132A.3个B.1个C.4个D.2个第Ⅱ卷(非选择题,共90分)二、填空题(本大题共6个小题,每小题3分,共18分)11.函数y=1x-2中自变量x的取值范围是.12.太阳的半径约为696000千米,用科学记数法表示为千米.13.如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=°.14.实数a、b在数轴上的位置如图所示,则√(a+b)2+a的化简结果为.15.一组数据-1,0,2,3,x,其中这组数据的极差是5,那么这组数据的平均数是.16.如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为cm2.三、解答题(本大题包括9个小题,共72分.解答应写出必要的演算步骤、证明过程或文字说明)17.(1)(5分)计算:1sin45°-|1-√2|+2-1.(2)(5分)先化简,再求值:(x+1)÷(2+1+x2x ),其中x=-32.18.(6分)(1)解不等式:5(x-2)+8<6(x-1)+7;(2)若(1)中的不等式的最小整数解是方程2x-ax=3的解,求a的值.19.(6分)如图,一次函数y=kx+b与反比例函数y=6x(x>0)的图象交于A(m,6)、B(n,3)两点.(1)求一次函数的解析式;(2)根据图象直接写出kx+b-6x>0时x的取值范围.20.(7分)如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于E,BF∥DE,交AG于F.(1)求证:AF-BF=EF;(2)将△ABF绕点A逆时针旋转,使得AB与AD重合,记此时点F的对应点为点F'.若正方形边长为3,求点F'与旋转前的图中点E之间的距离.31B21.(9分)如图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时).(1)找出该样本数据的众数和中位数;(2)计算这些车的平均速度;(结果精确到0.1)(3)若某车以50.5千米/时的速度经过该路口,能否说该车的速度要比一半以上车的速度快?并说明判断理由.22.(6分)如图,线段AB、DC分别表示甲、乙两建筑物的高.某初三课外兴趣活动小组为了测量两建筑物的高,用自制测角仪在B处测得D点的仰角为α,在A处测得D点的仰角为β.已知甲、乙两建筑物之间的距离BC为m.请你通过计算用含α、β、m的式子分别表示出甲、乙两建筑物的高度.23.(8分)如图,某化工厂与A 、B 两地有公路和铁路相连.这家工厂从A 地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B 地.已知公路运价为1.5元/(吨·千米),铁路运价为1.2元/(吨·千米).这两次运输共支出公路运费15 000元,铁路运费97 200元.请计算这批产品的销售款比原料费和运输费的和多多少元?(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:甲:{1.5(20x +10y)=1.2(110x +120y)=乙:{1.5(20·x8 000+10·y1 000)=1.2(110·x 8 000+120·y1 000)=根据甲、乙两名同学所列方程组,请你分别指出未知数x 、y 表示的意义,然后在等式右边的方框内补全甲、乙两名同学所列方程组. 甲:x 表示 ,y 表示 ; 乙:x 表示 ,y 表示 ;(2)甲同学根据他所列方程组解得x=300.请你帮他解出y 的值,并解决该实际问题.24.(8分)如图,已知AB 为☉O 的直径,PA 与☉O 相切于点A,线段OP 与弦AC 垂直并相交于点D,OP与弧AC相交于点E,连结BC.(1)求证:∠PAC=∠B,且PA·BC=AB·CD;,求PE的长.(2)若PA=10,sin P=35相交于点A、B,且抛物线经过坐标原点, 25.(12分)如图,抛物线y=ax2+bx+c(a<0)与双曲线y=kx点A的坐标为(-2,2),点B在第四象限内.过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.(1)求双曲线和抛物线的解析式;(2)计算△ABC与△ABE的面积;(3)在抛物线上是否存在点D,使△ABD的面积等于△ABE的面积的8倍?若存在,请求出点D 的坐标;若不存在,请说明理由.2012年呼和浩特市中考试卷一、选择题1.D a(a ≠0)的倒数是1a,所以-2的倒数是-12,故选D.评析 本题考查倒数的定义,注意和相反数区别,属容易题. 2.C 如图,∠3=180°-∠1=115°,由a ∥b 可得∠2=∠3=115°,故选C.评析 本题考查邻补角的定义,以及平行线的性质,属容易题.3.A 5个球中有3个红球,所以从口袋中随机摸出一个球为红球的概率是35,故选A. 评析 本题考查用列举法求概率,属容易题. 4.C 4x 2-4x+1=(2x)2-2×2x+1=(2x-1)2,故选C. 评析 本题考查因式分解的方法,属容易题.5.D 由一元二次方程根与系数的关系得x 1+x 2=-2a,x 1x 2=b,所以由题意得a=-32,b=1. 评析 本题考查一元二次方程根与系数之间的关系,属容易题.6.B 可求得菱形、正六边形和圆的面积分别为3、3√32和π,圆的面积最大,所以一点随机落在圆内的概率最大,故选B.评析 本题考查几何概率,属容易题.7.C 直线x-2y=2在直角坐标系内要经过点(0,-1),(2,0),对应图象为C. 评析 本题考查一次函数与二元一次方程之间的关系,属容易题.8.A 如图,作DE ∥AC 交BC 延长线于点E,易得△DCE ≌△BAD,所以CE=AD=3,∴BE=10,∵AC ⊥BD,∴∠BDE=90°,∴BD=DE=10√22=5√2,所以S梯形ABCD =S △BDE =12BD ·DE=25,故选A.评析 本题考查全等三角形的判定和性质,勾股定理,以及梯形的性质,关键在于能够通过推理得出S 梯形ABCD =S △BDE ,属中等难度题.9.B 点M 、N 关于y 轴对称,有N(-a,b).因为点M 在双曲线y=12x 上,所以ab=12.点N 在直线y=x+3上,所以a+b=3.二次函数为y=-12x2+3x=-12(x-3)2+92,有最大值92,故选B.评析本题综合考查了轴对称,函数的图象与性质,属中等难度题.10.D旋转变换后对应线段有夹角,即旋转角,所以①错误;易知x<0,y>0,所以点P(x,y)一定在第二象限,所以②正确;根据正投影的定义可知③正确;画出函数y=-x2和y=|x|-3的图象,两个图象的交点关于y轴对称,即横坐标互为相反数,所以④错误.故选D.评析本题综合考查了图形的变换、函数、正投影的性质以及命题的相关概念,综合性较强,属难题.二、填空题11.答案x≠2解析因为分式的分母不能为0,所以x≠2.评析本题考查函数中自变量的取值范围,若是分式,则分母不为0,属容易题.12.答案 6.96×105解析696000=6.96×105.评析本题考查科学记数法的概念,属容易题.13.答案66.5解析连结BE,不难看出∠DAE=∠DBE+∠AEB,∠ECF=∠EBF+∠BEC,所以∠DAE+∠ECF=∠ABC+∠AEC.又因为AE、CE分别平分∠DAC和∠FCA,所以∠CAE+∠ACE=∠ABC+∠AEC,所以180°-∠AEC=∠ABC+∠AEC,即∠AEC=90°-12∠ABC=66.5°.评析本题考查三角形角平分线的性质,题目常见,属中等难度题.14.答案-b解析从数轴上看,a>0,b<0,|a|<|b|,所以√(a+b)2+a=-a-b+a=-b.评析 本题考查了二次根式的化简,数轴,整式的运算等知识,属容易题. 15.答案 1.6或0.4解析 由极差是5可知x=-2或x=4,当x=-2时,x =0.4;当x=4时,x =1.6.所以平均数为1.6或0.4.评析 本题考查极差、平均数等概念,注意思考要全面,属容易题. 16.答案 2π解析 从三视图可看出该几何体是圆锥,其母线长为2,底面圆直径为2,侧面积为12×2π×2=2π.评析 本题考查由三视图来判断几何体的形状,进而求其侧面积,属中档题.三、解答题17.解析 (1)原式=√2-(√2-1)+12(3分)=32.(5分) (2)原式=xx+1.(9分) 当x=-32时,原式=3,(10分)评析 (1)题以实数的运算为载体,考查了特殊角的三角函数值,绝对值,整数幂等概念,属容易题.(2)题考查了分式的四则运算,属容易题. 18.解析 (1)5(x-2)+8<6(x-1)+7, 5x-10+8<6x-6+7,(1分) 5x-2<6x+1,(2分) -x<3,(3分) x>-3.(4分)(2)由(1)得,最小整数解为x=-2,(5分) ∴2×(-2)-a×(-2)=3, ∴a=72.(6分)评析 本题考查一元一次不等式和一元一次方程的解法,属容易题. 19.解析 (1)∵点A(m,6)、B(n,3)在函数y=6x 的图象上, ∴m=1,n=2,∴A(1,6)、B(2,3).(2分) ∴{k +b =6,2k +b =3,∴{k =-3,b =9,∴一次函数的解析式为y=-3x+9.(4分) (2)由图象知:1<x<2.(6分)评析 本题考查了反比例函数、一次函数的性质,待定系数法求函数解析式,利用函数图象判断不等式的解集等知识点,属容易题. 20.解析(1)证明:如图,正方形ABCD 中, AB=AD,∠2+∠3=90°. ∵DE ⊥AG, ∴∠AED=90°, ∴∠1+∠3=90°, ∴∠1=∠2. 又∵BF ∥DE,∴∠AFB=∠AED=90°. 在△AED 和△BFA 中,{∠1=∠2,∠AED =∠BFA,AD =AB,∴△AED ≌△BFA.(3分) ∴BF=AE. ∵AF-AE=EF,∴AF-BF=EF.(4分)(2)如图,根据题意知:∠FAF'=90°,DE=AF'=AF, ∴可判断四边形AEDF'为矩形,(6分) ∴EF'=AD=3.(7分)评析 本题考查了正方形的性质,并让学生探索在图形的旋转变换过程中的一些量的变化情况,属容易题.21.解析 (1)该样本数据的众数为52,中位数为52.(2分) (2)50×2+51×5+52×8+53×6+54×4+55×22+2+4+5+6+8≈52.4千米/时.(6分)(3)不能.(7分)因为由(1)知该样本的中位数为52,所以可以估计该路段的车辆大约有一半的车速度要快于52千米/时,有一半的车速度要慢于52千米/时,该车的速度是50.5千米/时,小于52千米/时,所以不能说该车的速度要比一半以上车的速度快.(9分)评析 本题考查了众数、中位数、平均数等概念,并让学生利用统计知识解决生活中的问题,了解学生的应用意识,属容易题.22.解析 过点A 作AM ⊥CD,垂足为M.(1分)在Rt△BCD中,tanα=CDBC,∴CD=BC·tanα=mtanα.(3分)在Rt△AMD中,tanβ=DMAM,∴DM=AM·tanβ=mtanβ,(5分)∴AB=CD-DM=m(tanα-tanβ).(6分)评析本题考查三角函数在实际生活中的应用,没有具体的数据,对学生是个考验,属中等难度题.23.解析(1)甲:x表示产品的重量,y表示原料的重量;(1分)乙:x表示产品销售额,y表示原料费;(2分)甲方程组右边方框内的数分别为15000,97200,乙同甲.(4分)(2)将x=300代入原方程组解得y=400,(6分)∴产品销售额为300×8000=2400000(元),原料费为400×1000=400000(元).又∵运输费为15000+97200=112200(元),∴这批产品的销售款比原料费和运输费的和多2400000-(400000+112200)=1887800(元).(8分)评析本题给出问题的相应解法让学生判断,引导学生分析、解决问题,有新意,属中档题.24.解析(1)证明:∵PA是☉O的切线,AB是直径,∴∠PAO=90°,∠C=90°,∴∠PAC+∠BAC=90°且∠B+∠BAC=90°,∴∠PAC=∠B.(1分)又∵OP⊥AC,∴∠ADP=∠C=90°,∴△PAD∽△ABC,(2分)∴AP∶AB=AD∶BC.∵在☉O中,AC⊥OD,∴AD=CD,(3分)∴AP∶AB=CD∶BC,∴PA·BC=AB·CD.(4分)(2)∵sin P=35,且PA=10,∴ADAP =35.(5分)∴AD=6,∴AC=2AD=12.∵在Rt △ADP 中,PD=√AP 2-AD 2=8,又∵AP ∶AB=PD ∶AC,∴AB=10×128=15, ∴AO=152,(7分)∴OP=252, ∴PE=OP-OE=252-152=5.(8分)或者:在Rt △PAO 中利用sin P=OA OP =35计算出半径OA=152,PO=252,从而得出PE=5 评析 本题以圆的性质为切入点,详细考查了相似三角形的判定和性质,特殊角的三角函数值,属中等偏难题.25.解析 (1)∵点A(-2,2)在双曲线y=kx 上,∴k=-4,∴双曲线的解析式为y=-4x .(1分)∵BC 与x 轴之间的距离是点B 到y 轴的距离的4倍,∴可设B 点坐标为(m,-4m)(m>0),代入双曲线解析式得m=1,∴抛物线y=ax 2+bx+c(a<0)过点A(-2,2)、B(1,-4)、O(0,0),∴{4a -2b +c =2,a +b +c =-4,c =0,∴{a =-1,b =-3,c =0,∴抛物线的解析式为y=-x 2-3x.(4分)(2)∵抛物线的解析式为y=-x 2-3x,∴顶点E (-32,94),对称轴为x=-32.∵B(1,-4),∴-x 2-3x=-4,∴x 1=1,x 2=-4,∴C(-4,-4),∴S △ABC =5×6×12=15.(5分) 由A 、B 两点坐标为(-2,2)、(1,-4)可求得直线AB 的解析式为y=-2x-2.设抛物线对称轴与AB 交于点F, 则F 点坐标为(-32,1),∴EF=94-1=54,∴S△ABE=S△AEF+S△BEF=12×54×3=158.(8分)(3)∵S△ABE=158,∴8S△ABE=15,∴当点D与点C重合时,显然满足条件.(9分)当点D与点C不重合时,过点C作AB的平行线CD,其对应的一次函数解析式为y=-2x-12.令-2x-12=-x2-3x,解得x1=3,x2=-4(舍去).当x=3时,y=-18,∴存在另一点D(3,-18)满足条件.(12分)评析本题考查了待定系数法求函数解析式,二次函数、一次函数的性质,第(3)问重点考查分类讨论思想,要求学生有较强的分析问题能力,属难题.。
2012内蒙古包头中考数学

2012年高中招生考试试题卷数 学一、选择题:本大题共有12小题,每小题3分,共36分。
每小题只有一个正确选项。
1.9的算术平方根是( )A.士3B. 3C. -3D.3【答案】B2.联合国人口基金会的报告显示,世界入口总数在2011年10月31日达到70亿.将70亿用科学记数法表示为( ) A.7×109 B.7×l08 C.70×108 D.0.7×1010【答案】B3.下列运算中,正确的是( )A .x x x =-23&B .326x x x =÷ C .532=+ D .632=⨯【答案】D4.在Rt △ABC 中,∠C=90°,若AB=2AC ,则sinA 的值是( ) A .3 B .21C.23 D .33【答案】C5.下列调查中,调查方式选择正确韵是( )A 为了了解1000个灯泡的使用寿命,选择全面调查B .为了了解某公园全年的游客流量,选择抽样调查C .为了了解生产的一批炮弹的杀伤半径,选择全面调查D .为了了解一批袋装食品是否含有防腐剂,选择全面调查 【答案】B6.如图,过□ABCD 的对角线BD 上一点M 分别作平行四边形两边的平行线EF 与 GH ,那么图中的□AEMG 的面积S 1与□HCFM 的面积S 2的大小关系是( ) A.s 1>S 2 B.S 1<S 2 C. S 1=S 2 D. 2S 1=S 2【答案】C7.不等式组⎪⎩⎪⎨⎧-≤-+>-x.237121),1(315x x x 的解集是( )A.x>2B. x≤4C.x <2或x≥4D.2<x≤4【答案】D8.圆锥的底面直径是80cm ,母线长90cm ,则它的侧面展开图的圆心角是( ) A. 320° B. 40° C. 160° D .80° 【答案】C9.随机掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷两次骰子,掷得面朝上的点数之和是5的概率是( )A .61 B.91 C.181 D.152【答案】B10.已知下列命题:①若a≤0,则|a |=-a ②若ma 2>na 2,则m>n; ③两组对角分别相等的四边形是平行四边形; ④垂直予弦的直径平分弦。
2012年呼市第一次模拟数学试卷
2012年呼和浩特市初三统考试卷数 学一、选择题(每题3分,共30分) 1、-5的相反数是( ) A 、5 B 、-5 C 、15 D 、15- 2、下列四个角中最有可能与68°角互补的角( )A、 B、C、 D、3、化简3a -2()的结果是( )A 、6aB 、6a -C 、9a D 、3-2a 4、如果22a-222a =-(),则( )A 、a<1B 、a 1≤C 、a 1>D 、a 1≥5、由一些大小相同的小正方形组成的几何体的三视图如图所示,那么,组成该几何体的小正方体有( ) A 、6块 B 、5块 C 、4块 D 、3块6、已知一次函数2y mx m =+-的图像与y 轴交于点(0,3),且y 随x 增大而减小,则m 的值为( )A 、5B 、-1C 、-1或-5D 、-1或57、如图,ΔABC 沿DE 折叠后,点A 落在BC 边上的'A 处,若D 为AB 边的中点,∠B =50°,则∠'BDA 的度数为( )A 、50°B 、60°C 、65°D 、80°8、一元二次方程2220x x m +-=的两根分别为12,x x ,则2212x x +的最小值为( )A 、4B 、-4C 、2D 、-29、已知方程组的解满足2x y a +≤,则( ) A 、3a ≥ B 、3a ≤ C 、95a ≥D 、32a ≤- 10、在平面直角坐标系中,如果纵坐标都是整数的点称为整点,将二次函数22764y x x =+-的图像与x 轴围成的封闭图形染成红色,则在红色区域内部及其便界上的整数点的个数是( )A 、5B 、6C 、7D 、8 二、填空(每题3分,共18分)11、今年我市初中毕业生大约有近18000人,用科学计数法可表示为 12、从实数2,-3,13,0.16四个数中随机选取一个数,其中选取的是有理数的概率为13、分解因式:2242x x ++= 。
2012年内蒙古包头市中考数学试卷-答案
数学答案解析
第Ⅰ卷
一、选择题
1.【答案】B
【解析】∵ ,∴9的算术平方根是3.故选B.
【提示】根据算术平方根的定义:一个非负数的正的平方根,即为这个数的算术平方根.所以结果必须为正数,由此即可求出9的算术平方根.
【考点】算术平方根.
2.【答案】A
【解析】 .故选:A.
【提示】先将括号里面的分式的分子分母分解因式,再通分进行分式加减计算后,最后进行分式的除法计算就可以得出结论.
【考点】分式的混合运算.
15.【答案】12
【解析】∵数据10,11,12,13,8,x的平均数是11,∴ ,
∵数据12出现的次数最多,∴众数为12.故答案为12
【提示】首先根据平均数的定义求得x的值,然后利用众数的定义求得答案即可.
【提示】根据矩形性质求出 ,可证 ,求出 ,求出 ,即可求出答案.
【考点】矩形的性质,全等三角形的判定与性质,等腰直角三角形
12.【答案】B
【解析】根据题意得 , ,则 ,∵ ,∴ ,
即 ,∴ ,∴ ,整理得 , ,解得 ,∵ ,∴ .故选B.
【提示】根据一元二次方程 ( )的根与系数的关系和两根都为正根得到 ,
【提示】根据合并同类项法则对A进行判断;根据同底数幂的除法法则对B进行判断;根据同类二次根式的定义对C进行判断;根据二次根式的乘法法则对D进行判断.
【解析】A. 与 不是同类项,不能合并,所以A选项错误;
B. ,,所以B选项错误;
C. 与 不是同类二次根式,不能合并,所以C选项错误;
D. ,所以D选项正确.故选D.
【考点】众数,算术平均数
16.【答案】4
【解析】 , , 或 , , ,∵ ,∴ ,把 代入 中得: ,解得: ,故答案为:4.
内蒙古呼和浩特市2012年中考数学试卷(解析版)
2012年内蒙古呼和浩特市中考数学试卷一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)2.如图,已知a∥b,∠1=65°,则∠2的度数为()3.在一个不透明的口袋中,装有3个红球,2个白球,除颜色不同外,其余都相同,则随5.已知:x1,x2是一元二次方程x2+2ax+b=0的两根,且x1+x2=3,x1x2=1,则a、b的值分,b=﹣1 ,b=16.如图,在一长方形内有对角线长分别为2和3的菱形,边长为1的正六边形和半径为1的圆,则一点随机落在这三个图形内的概率较大的是()7.下面四条直线,其中直线上每个点的坐标都是二元一次方程x﹣2y=2的解是()B9.已知:M ,N 两点关于y 轴对称,且点M 在双曲线上,点N 在直线y=x+3上,设2有最大值,最大值为有最小值,最小值为10.下列命题中,真命题的个数有( )①一个图形无论经过平移还是旋转,变换后的图形与原来图形的对应线段一定平行 ②函数图象上的点P (x ,y )一定在第二象限③正投影的投影线彼此平行且垂直于投影面④使得|x|﹣y=3和y+x 2=0同时成立的x 的取值为.二、填空题(本大题共6个小题,每小题3分,共18分,本题要求把正确结果填在答题纸规定的横线上,不需要解答过程)11.函数y=中,自变量x 的取值范围是 _________ .12.太阳的半径约为696 000千米,用科学记数法表示为 _________ 千米.13.如图,在△ABC 中,∠B=47°,三角形的外角∠DAC 和∠ACF 的平分线交于点E ,则∠AEC= _________ .14.实数a,b在数轴上的位置如图所示,则的化简结果为_________.15.一组数据﹣1,0,2,3,x,其中这组数据的极差是5,那么这组数据的平均数是_________.16.如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为_________cm.三、解答题(本大题包括9个小题,共72分,解答应写出必要的演算步骤、证明过程或文字说明)17.(1)计算:.(2)先化简,再求值:,其中.18.(1)解不等式:5(x﹣2)+8<6(x﹣1)+7;(2)若(1)中的不等式的最小整数解是方程2x﹣ax=3的解,求a的值.19.如图,一次函数y=kx+b与反比例函数的图象交于A(m,6),B(n,3)两点.(1)求一次函数的解析式;(2)根据图象直接写出时x的取值范围.20.如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于E,BF∥DE,交AG于F.(1)求证:AF﹣BF=EF;(2)将△ABF绕点A逆时针旋转,使得AB与AD重合,记此时点F的对应点为点F′,若正方形边长为3,求点F′与旋转前的图中点E之间的距离.21.如图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时)(1)找出该样本数据的众数和中位数;(2)计算这些车的平均速度;(结果精确到0.1)(3)若某车以50.5千米/时的速度经过该路口,能否说该车的速度要比一半以上车的速度快?并说明判断理由.22.如图,线段AB,DC分别表示甲、乙两建筑物的高.某初三课外兴趣活动小组为了测量两建筑物的高,用自制测角仪在B外测得D点的仰角为α,在A处测得D点的仰角为β.已知甲、乙两建筑物之间的距离BC为m.请你通过计算用含α、β、m的式子分别表示出甲、乙两建筑物的高度.23.如图,某化工厂与A,B两地有公路和铁路相连,这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5元/(吨•千米),铁路运价为1.2元/(吨•千米),这两次运输共支出公路运费15 000元,铁路运费97 200元,请计算这批产品的销售款比原料费和运输费的和多多少元?(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:甲:乙:根据甲,乙两名同学所列方程组,请你分别指出未知数x,y表示的意义,然后在等式右边的方框内补全甲、乙两名同学所列方程组.甲:x表示_________,y表示_________乙:x表示_________,y表示_________(2)甲同学根据他所列方程组解得x=300,请你帮他解出y的值,并解决该实际问题.24.如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.(1)求证:∠PAC=∠B,且PA•BC=AB•CD;(2)若PA=10,sinP=,求PE的长.25.如图,抛物线y=ax2+bx+c(a<0)与双曲线相交于点A,B,且抛物线经过坐标原点,点A的坐标为(﹣2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.(1)求双曲线和抛物线的解析式;(2)计算△ABC与△ABE的面积;(3)在抛物线上是否存在点D,使△ABD的面积等于△ABE的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.2012年内蒙古呼和浩特市中考数学试卷参考答案与试题解析一、选择题(本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的))2.(3分)如图,已知a∥b,∠1=65°,则∠2的度数为()3.(3分)在一个不透明的口袋中,装有3个红球,2个白球,除颜色不同外,其余都相同,5.(3分)已知:x1,x2是一元二次方程x2+2ax+b=0的两根,且x1+x2=3,x1x2=1,则a、b,b=﹣1 ,b=16.(3分)如图,在一长方形内有对角线长分别为2和3的菱形,边长为1的正六边形和半径为1的圆,则一点随机落在这三个图形内的概率较大的是()×=>B8.(3分)已知:在等腰梯形ABCD中,AD∥BC,AC⊥BD,AD=3,BC=7,则梯形的面9.(3分)已知:M,N两点关于y轴对称,且点M在双曲线上,点N在直线y=x+32有最大值,最大值为有最小值,最小值为在反比例函数的图象上,点,y=10.(3分)下列命题中,真命题的个数有()①一个图形无论经过平移还是旋转,变换后的图形与原来图形的对应线段一定平行②函数图象上的点P(x,y)一定在第二象限③正投影的投影线彼此平行且垂直于投影面④使得|x|﹣y=3和y+x2=0同时成立的x的取值为.,故函数图象上的点的取值为:二、填空题(本大题共6个小题,每小题3分,共18分,本题要求把正确结果填在答题纸规定的横线上,不需要解答过程)11.(3分)函数y=中,自变量x的取值范围是x≠2.12.(3分)太阳的半径约为696 000千米,用科学记数法表示为 6.96×105千米.13.(3分)如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=66.5°.;最后在= 14.(3分)实数a,b在数轴上的位置如图所示,则的化简结果为﹣b.15.(3分)一组数据﹣1,0,2,3,x,其中这组数据的极差是5,那么这组数据的平均数是 1.6或0.4.16.(3分)如图是某几何体的三视图及相关数据(单位:cm),则该几何体的侧面积为2πcm.三、解答题(本大题包括9个小题,共72分,解答应写出必要的演算步骤、证明过程或文字说明)17.(10分)(1)计算:.(2)先化简,再求值:,其中.+﹣+=2÷=﹣18.(6分)(1)解不等式:5(x﹣2)+8<6(x﹣1)+7;(2)若(1)中的不等式的最小整数解是方程2x﹣ax=3的解,求a的值.19.(6分)如图,一次函数y=kx+b与反比例函数的图象交于A(m,6),B(n,3)两点.(1)求一次函数的解析式;(2)根据图象直接写出时x的取值范围.,20.(7分)如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于E,BF∥DE,交AG于F.(1)求证:AF﹣BF=EF;(2)将△ABF绕点A逆时针旋转,使得AB与AD重合,记此时点F的对应点为点F′,若正方形边长为3,求点F′与旋转前的图中点E之间的距离.21.(9分)如图是交警在一个路口统计的某个时段来往车辆的车速情况(单位:千米/时)(1)找出该样本数据的众数和中位数;(2)计算这些车的平均速度;(结果精确到0.1)(3)若某车以50.5千米/时的速度经过该路口,能否说该车的速度要比一半以上车的速度快?并说明判断理由.≈22.(6分)如图,线段AB,DC分别表示甲、乙两建筑物的高.某初三课外兴趣活动小组为了测量两建筑物的高,用自制测角仪在B外测得D点的仰角为α,在A处测得D点的仰角为β.已知甲、乙两建筑物之间的距离BC为m.请你通过计算用含α、β、m的式子分别表示出甲、乙两建筑物的高度.=23.(8分)如图,某化工厂与A,B两地有公路和铁路相连,这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5元/(吨•千米),铁路运价为1.2元/(吨•千米),这两次运输共支出公路运费15 000元,铁路运费97 200元,请计算这批产品的销售款比原料费和运输费的和多多少元?(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:甲:乙:根据甲,乙两名同学所列方程组,请你分别指出未知数x,y表示的意义,然后在等式右边的方框内补全甲、乙两名同学所列方程组.甲:x表示产品的重量,y表示原料的重量乙:x表示产品销售额,y表示原料费(2)甲同学根据他所列方程组解得x=300,请你帮他解出y的值,并解决该实际问题.24.(8分)如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与弧AC相交于点E,连接BC.(1)求证:∠PAC=∠B,且PA•BC=AB•CD;(2)若PA=10,sinP=,求PE的长.=PD==15A0=OP==﹣25.(12分)如图,抛物线y=ax2+bx+c(a<0)与双曲线相交于点A,B,且抛物线经过坐标原点,点A的坐标为(﹣2,2),点B在第四象限内,过点B作直线BC∥x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍,记抛物线顶点为E.(1)求双曲线和抛物线的解析式;(2)计算△ABC与△ABE的面积;(3)在抛物线上是否存在点D,使△ABD的面积等于△ABE的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.,=。
【数学】内蒙古呼和浩特市中考真题(解析版)
A. 0.96 107 km2
B. 960 104 km2 C. 9.6 106 km2 D. 9.6 105 km2
3.如图中序号(1)(2)(3)(4)对应的四个三角形,都是 ABC 这个图形进行了一次变换
之后得到的,其中是通过轴对称得到的是( )
A.(1)
B.(2)
C.(3)
D.(4)
4.如图,是根据某市 2010 年至 2014 年工业生产总值绘制的折线统计图,观察统计图获得 以下信息,其中信息判断错误的是( )
③最小角等于 50 的三角形是锐角三角形.
其中正确命题的序号为
.
15.如图,在 ABCD 中, B 30 , AB AC , O 是两条对角线的交点,过点 O 作 AC 的垂线分别交边 AD , BC 于点 E , F ,点 M 是边 AB 的一个三等分点,则 AOE 与 BMF 的面积比为 .
x
24.如图,点 A , B , C , D 是直径为 AB 的 O 上的四个点, C 是劣弧 BD 的中点, AC 与 BD 交于点 E .
(1)求证: DC 2 CE AC ; (2)若 AE 2 , EC 1,求证: AOD 是正三角形; (3)在(2)的条件下,过点 C 作 O 的切线,交 AB 的延长线于点 H ,求 ACH 的面
()
A. 2
B. 0
C.1
D. 2 或 0
6.一次函数 y kx b 满足 kb 0 ,且 y 随 x 的增大而减小,则此函数的图象不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
7.如图, CD 是 O 的直径,弦 AB CD ,垂足为 M ,若 AB 12 , OM : MD 5 : 8 ,则 O 的周长为( )
