风电出力分析中的相依概率性序列运算_张宁

合集下载

风力发电出力概率统计特性分析

1 风电场出力统计特性
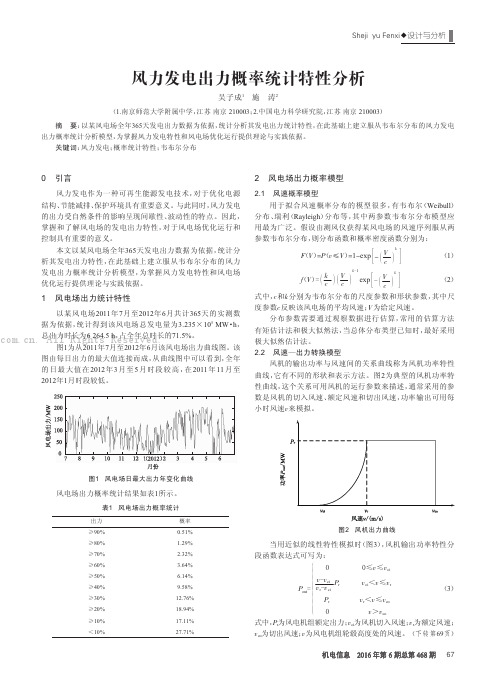
以某风电场2011年7月至2012年6月共计365天的实测数据为依据，统计得到该风电场总发电量为3.235×105 MW·h，
.总A出l力l时R长i为g6h2t6s4.5 Rh，e占s全er年v总e时d长. 的71.5%。图1为从2011年7月至2012年6月该风电场出力曲线图。该图由每日出力的最大值连接而成，从曲线图中可以看到，全年的日最大值在2012年3月至5月时段较高，在2011 年 11 月至 2012年1月时段较低。
统计查询主要包含计划完成情况查询、台区线损异常率统计、台区线损异常处置率统计、台区线损异常项统计等统计查询功能。
.4.A9 l系l系统统R管管i理g理主ht要s包含Re作s业e指rv导e书d维. 护及作业步骤维护等维
护功能。
5 平台运行效果
平台整合了低压运维、低压线损、低压用电检查等各项业务，固化了业务流程，促进了低压综合业务管理模式和业务管理流程的完善以及低压综合业务的规范化。通过计划管理与绩效管理模块相结合，为绩效评价提供了直接的客观数据支撑；以系统智能化提高管理效率，同时通过移动技术将现场作业和低压业务管理有机结合，简化了班组操作，提高了工作效率。
67
Sheji yu Fenxi◆设计与分析
异常情况的处理— ——生成用检计划工作单、生成项目库工作单、生成缺陷计划工作单。 4.4 低压用检管理
对于台区线损异常巡视计划，针对存在违约用电/窃电行为的台区，生成用检计划工作单。班长对用检计划进行派工，工作人员进行现场取证，支持上传下载图片。营销MIS系统申请登记违约窃电工作单后，在系统中进行用检结果反馈，记录营销MIS工作单号以及处理情况。 4.5 低压计量自动化管理

概率密度法在风电功率波动特性分析的应用

概率密度法在风电功率波动特性分析的应用概率密度法是基于统计学原理的一种方法，它通过对风速和风电功率数据进行分析，得到不同功率级别下的概率密度函数。

概率密度函数反映了该功率级别下的出现概率，可以用来衡量该功率级别的频率及其在总功率中的贡献程度。

通过对不同功率级别的概率密度函数进行综合分析，可以揭示功率波动的特性和规律。

概率密度法的应用过程一般包括以下几个步骤：首先，收集和整理风速和风电功率数据，并对数据进行预处理，如去除异常值和空缺值。

然后，计算不同功率级别下的概率密度函数，可以使用直方图、核密度估计等方法进行计算。

接下来，对各个功率级别的概率密度函数进行分析，可以计算平均值、方差、偏度、峰度等统计指标，以及绘制累积分布函数和风速功率曲线等。

最后，根据分析结果，可以评估风电场的功率波动特性，并采取相应的措施来降低波动风险。

概率密度法在风电功率波动特性分析中具有以下优点：首先，它可以直观地反映不同功率级别的频率和功率分布情况，有助于深入理解和研究功率波动机理。

其次，它可以揭示不同功率级别的权重和贡献程度，对评估风电场的发电能力和可靠性具有重要意义。

再次，它可以为电网调度和风电场规划提供科学依据，有利于提高风电场的经济效益和可持续发展。

下面以风电场为例，说明概率密度法在风电功率波动特性分析中的应用。

该风电场的风速和风电功率数据包括多年的观测数据，我们可以利用概率密度法计算不同功率级别下的概率密度函数。

通过对概率密度函数的分析，我们可以得到不同功率级别的频率分布、平均值、方差等统计指标，从而了解风电场的功率波动情况。

基于这些分析结果，我们可以评估该风电场的发电能力和可靠性，并采取相应的措施来降低功率波动风险，提高发电效益。

综上所述，概率密度法是一种可行的风电功率波动特性分析方法，它可以通过对风速和风电功率数据的统计分析，揭示和评估风电场的功率波动特性。

在风电场规划、电网调度和风电投资等方面具有重要的应用价值。

广东电网风电出力特性分析及其经济性评价

(1. Grid Planning & Research Center of Guangdong Power Grid Corporation, Guangzhou 510600, China; 2. Department of Electrical Engineering, Tsinghua University, Beijing 100084, China) Abstract: To study the characteristics of wind power output is very important for the planning and operation of a power system integrated with a large scale of wind power under the background of low-carbon development. Based on the simulation of the operation of a wind farm group integrated with district wind farms, this paper analyzes quantitatively the characteristics of wind power output and its economic evaluation in Guangdong Power Grid (GPG). The results show that to integrate a large scale of wind power in a power system increases the requirement of peak load regulation of the system so greatly that it must be considered carefully in the system planning and wind power policy making. The economic evaluation in terms of the system operation cost, coal consumption, pollutant discharge, etc. indicates that a large scale of wind power is of great significance to energy saving, emission reduction and low carbon development for Guangdong province though its effect of replacing the traditional units is relatively limited. Key words: a large scale of wind power; operation simulation; wind power output characteristics; capacity benefit

广东海上风电发展及出力特性分析

广东海上风电发展及出力特性分析摘要：海上风电是“十三五”及中长期广东最具规模化发展潜力的可再生能源，对于推动全省能源结构转型升级具有重要意义。

充分分析海上风电的出力特性是开展后续研究先决条件。

本文从风速、出力概率、出力特性等方面深入分析广东中部沿海某海上风电的出力情况，提出在对于电源替代及网架校核不同目的时，海上风电场出力率的选择方案并提出相关建议。

关键词：风速；出力概率；出力特性Research on the Development and Power Output Characteristics of Offshore Wind in GuangdongWANG Yijun1，LU Geng2（China Energy Engineering Group Guangdong Electric Power Design Institute Co.，Ltd.，Guangzhou 510663，China）Abstract：Offshore wind power is the renewable energy with the greatest potentialfor scale development，which has the great significance to promote the transformation and upgrading of Guangdong energy structure during “13th Five-Year” and the long-term. A thorough analysis of the output characteristics of offshore wind power is a prerequisite for the follow-up studies. This paper analyzes the wind speed characteristics，output probability，output characteristics of a certain offshore wind power in Guangdong central coast. Propose the selection scheme of the offshore wind output rate in power replacement study and grid check study，as well as the relevant suggestions.Keywords：wind speed；output probability；output characteristics引言随着能源供给侧改革的不断深入，清洁能源的开发利用已成为我国能源产业的发展方向，成为推动社会可持续绿色发展的战略举措。

基于ARMA模型的风功率数据缺失值估计方法

• 224 •内燃机与配件基于ARMA模型的风功率数据缺失值估计方法吕清泉;汪宁渤；张健美;王明松(甘肃省电力公司风电技术中心，兰州730070 )摘要：随着风电急速发展，风电功率预测准确性更加重要。

而这些技术严重依赖于风电出力，测风等基础数据，然而，在数据采集到存储过程中存在各种各样的原因会导致数据缺失或异常。

由于风功率数据具有时间序列的平稳特性，而ARMA模型具有良好的对时间序列进行建模的能力，本文将利用ARMA模型对风功率数据进行建模，并用来对序列中缺失的数据进行估计预测。

实验结果验证了该数据估计方法的有效性。

关键词：ARMA模型；功率数据;估计预测0引言目前，我国电网企业中风功率、风速、风向等基础数据采集大多通过FTP、102协议进行有线传输，在企业服务器中进行存储。

甘肃省作为新能源大省，其管理200多个风电场光伏电站数据，由于风电场站自身原因和通信网络的不稳定性，数据也会出现断点或者突变数据。

本文用 ARMA模型对风力发电中的时间序列数据进行建模，并根据建立的模型对序列中的缺失数据进行估计并恢复。

1自回归移动平均模型风力发电所依赖的风力是随时间变化的，是一种随机时间序列，并且数据传输是等时间间隔的，因此可以建立时间序列模型进行分析。

Box-Jenkins方法是随机时间序列分析的主要方法之一。

它利用历史数据来建立模型，通过一定准则来确定模型的参数和阶数，再用该模型来对时间序列中的未知数据进行预测。

ARMA模型是研究时间序列的重要方法，在Box-Jenkins方法中我们选用ARMA模型来进行风力发电的时间序列分析。

ARMA模型由自回归模型（简称A R模型）与移动平均模型（简称M A模型）为基础混合构成。

它有A R模型，M A模型和ARMA模型三种基本形式。

在新技术的研发创新中，我们应该把握住先机，以此芯片为基础，争取走在世界的前列。

我国的现实电网复杂程度是比较严重的，这种情况下的信号传输更加繁杂，载波通信技术的实现也因此增加了不少难度。

基于ARIMAX的风电功率预测研究

[８] 张晓明. 基于结构优化的风电功率单一预测模型的研究[ Ｄ] .
太原:太原理工大学ꎬ２０１４.
[９] 李进. 基于模型优选的风电功率融合预测模型[ Ｄ] . 太原:太
原理工大学ꎬ２０１３.
66
[１０] 肖峰ꎬ陈国初. 基于改进果蝇算法优化的ＳＶＭ风电功率短期
64
!"/( MW )
ＮｏｒｔｈｅａｓｔＥｌｅｃｔｒｉｃＰｏｗｅｒＵｎｉｖｅｒｓｉｔｙꎬＪｉｌｉｎ１３２０１２ꎬＣｈｉｎａ)
Ａｂｓｔｒａｃｔ:Ｔｈｅｆｌｕｃｔｕａｔｉｏｎｃｈａｒａｃｔｅｒｉｓｔｉｃｓｏｆｐｒｉｍａｒｙｅｎｅｒｇｙｈａｖｅｂｒｏｕｇｈｔａｌｏｔｏｆｔｒｏｕｂｌｅｓｔｏｔｈｅｐｏｗｅｒｇｒｉｄꎬｗｈｉｃｈ
检修公司ꎬ吉林长春１３００００ꎻ４. 东北电力大学电气工程学院ꎬ吉林吉林１３２０１２)
摘要:一次能源的波动特性给电网带来了许多麻烦ꎬ使得大量的风电、光伏都不能被充分利用ꎬ风电功率预
测技术作为有效应对风电接入的关键技术之一ꎬ对指导系统调度运行、风电场生产安排具有十分重大的意
义ꎮ 基于ＡＲＩＭＡＸ建立了风电功率预测模型ꎬ并采用实测数据对模型有效性进行验证ꎮ 研究结果表明ꎬ将
10
参考文献
[１ ] Ｊｏｓｅ′ ＬｕｉｓＤｏｍı′ꎬ ＯｒｉｏｌＧｏｍｉｓ￣Ｂｅｌｌｍｕｎｔꎬ ＦｅｒｎａｎｄｏＤ. Ｂｉａｎｃｈｉꎬ ｅｔ
5
10
20
30
40 50 60
#$%&/N
70
80
90
ａｌ. Ｐｏｗｅｒｏｓｃｉｌｌａｔｉｏｎｄａｍｐｉｎｇｓｕｐｐｏｒｔｅｄｂｙｗｉｎｄｐｏｗｅｒ:Ａｒｅｖｉｅｗ[ Ｊ] . Ｒｅ￣

风电功率波动特性分析

风电功率波动特性分析作者：张晴露何天舒来源：《中国高新技术企业》2015年第01期摘要：文章通过频率频数的直方图进行初步估计，再通过dfittool工具箱进行确认和验证，最终得出指数分布最适合风电功率波动的分布。

通过样本总体的均值和方差估计概率分布的参数，并用概率密度函数图和频率分布直方图对不同时间间隔、不同机组、每天或者一个月的概率分布之间的关系进行分析。

最终得知，各个机组在以每日为时间窗宽，每天的平均风电功率大致相同，而方差除了一些特殊的点还有这个月的最后几天外，也是大致相同。

关键词：matlab工具箱；分布拟合；回归分析；ARMA模型；平稳时间序列文献标识码：A中图分类号：TM76 文章编号：1009-2374（2015）01-0025-02 DOI：10.13535/ki.11-4406/n.2015.00131 问题描述本题研究的是风电功率的波动性问题，当前世界各国资源环境约束的日趋严苛，以化石能源为主的能源发展模式必须向绿色可再生能源转变。

风电机组发出的功率主要与风速有关。

由于风的不确定性、间歇性以及风电场内各机组间尾流的影响，使得风力发电在满足用电需求方面的确定性不如常规发电。

大规模风电基地通常需接入电网来实现风电功率的传输与消纳。

风电功率的随机波动是对电网不利的主要因素。

研究风电功率的波动特性，对改善风电预测精度、克服风电接入对电网的不利影响有重要意义。

风电场通常有几十台甚至上百台风电机组。

大型风电基地由数十甚至上百个风电场组成。

因此，风电功率的波动有很强的时空差异性。

在此我们需要研究风电功率的概率分布等一系列信息并以此对未来风电的功率进行预测，希望得到风力发电机发电功率的一般性结论。

2 模型建立与求解首先我们要研究风电机发电功率的概率分布。

对于概率分布拟合，可以在matlab软件中用dfittool来解决。

我们随机选择了五台电机作为观测对象。

将y输入dfittool里面，分别用t分布、指数分布、正态分布去拟合，然后根据拟合出来的各个分布的参数，求出三个分布的表达式，并选取一定的样本，比较三种分布的残差平方和，如表1所示：表1 时间间隔为5秒风电功率数据用t分布、指数分布、正态分布去拟合的残差平方和从分析结果可以发现指数分布的残差平方和是最小的，因此指数分布为我们推荐的最优的概率分布函数。

采用藤Copula构建风电场风速相依模型

采用藤Copula构建风电场风速相依模型徐玉琴;王莉莉;张龙【摘要】提出了采用基于Pair-Copula分解的藤Copula理论建立多元风速相依模型的方法.该方法首先考虑了风速分布的随机性,并计及风电场内部风机群风速间的相关性,采用Canonical藤描述Pair-Copula分解的逻辑结构,通过求解Canonical藤结构中的Pair-Copula概率密度函数PDF (probabilitydensity function),得到高维联合分布下的Pair-Copula多元风速相依模型;再对某实际风电场进行实证分析,得到了风电场内部6个风机群间风速的Pair-Copula联合概率密度函数JPDF(joint probability density function);最后在风电场风速相关结构的问题上进一步研究分析,为下一步建立混合Copula函数模型提供思路.【期刊名称】《电力系统及其自动化学报》【年(卷),期】2015(027)005【总页数】5页(P62-66)【关键词】Pair-Copula;藤Copula;相关结构;Kendall秩相关系数【作者】徐玉琴;王莉莉;张龙【作者单位】华北电力大学电气与电子工程学院,保定071003;华北电力大学电气与电子工程学院,保定071003;华北电力大学电气与电子工程学院,保定071003【正文语种】中文【中图分类】TM614大规模风电场接入电网后，给本已存在着负荷波动、元件故障等不确定因素的电力系统带来更多挑战[1-2]。

如何进行精确的风电功率预测成为制约风电发展的瓶颈之一。

文献[3-4]将Copula函数应用到风电不确定性分析中，采用Copula函数模拟单个风电场出力；文献[5]应用Copula理论对江苏某4个风电场出力分布之间的相依结构进行拟合，验证了相依概率性序列运算在风电场建模与计算上的有效性；文献[6]采用可以描述不对称尾部特性的Gumbel-Copula函数构建多风电场出力的联合概率分布。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

率分布的离散化以及定义相应的运算法则求解随机变量相互运算后新的概率分布，具有深刻的物理背景以及较高的计算效率，已经被成功应用于电力系
］］２４５６－－。以及其他领域中［统分析［
在现有的序列运算理论中，序列间进行各种运算的前提是参与运算的各概率性序列对应的随机变
２（），则存在一个Ｃ［］］，Ｆｏｕｌａ函数Ｃ：０，１０，１ →［ｐ ββ 使得对 α， β∈Ｒ，均有
２相依概率性序列运算原理
２．１基本序列运算序列运算理论以概率性序列表示随机变量的概率分布，并通过定义序列间的运算求解随机变量相互运算后新的概率分布，在此过程中通过对随机变巧妙地实现了计算中对状态的归量的离散化处理，并，在保证计算精度的条件下使计算速度极大提高。，其定义域设随机变量α 的概率密度函数为ｆα （ α），设离散化间隔为 Δ 为［０， α ｐ，则 α 对应的概率ｍａｘ］）性序列ａ（为ｉ）＝ａ（ｉ
Ｄｅｅｎｄｅｎｔｓｅｕｅｎｃｅｏｅｒａｔｉｏｎｓｒｏｂａｂｉｌｉｓｔｉｃｐｐｑｐｏｗｅｒｆｏｒｗｉｎｄｏｕｔｕｔａｎａｌｓｅｓｐｐｙ
，ＺＨＡＮＧＮｉｎＫＡＮＧＣｈｏｎｉｎｇｇｑｇ（，ＳｔａｔｅＫｅＬａｂｏｆＰｏｗｅｒＳｓｔｅｍｓＤｅａｒｔｍｅｎｔｏｆＥｌｅｃｔｒｉｃａｌｙｙｐ，，，）ＥｎｉｎｅｅｒｉｎＴｓｉｎｈｕａＵｎｉｖｅｒｓｉｔ１０００８４ＢｅｉｉｎＣｈｉｎａｇｙｊｇｇｇ：ＤＡｂｓｔｒａｃｔｅｅｎｄｅｎｔｓｅｕｅｎｃｅｏｅｒａｔｉｏｎｔｈｅｏｒｗａｓｒｏｂａｂｉｌｉｓｔｉｃｐｑｐｙｐｄｅｖｅｌｏｅｄｔｏｕｓｅａｒｉｔｈｍｅｔｉｃｏｅｒａｔｉｏｎｓｂｅｔｗｅｅｎｃｏｒｒｅｌａｔｅｄｓｔｏｃｈａｓｔｉｃｐｐｖａｒｉａｂｌｅｓ．ＴｈｅＣｏｕｌａｓｆｕｎｃｔｉｏｎｉｓｕｓｅｄｔｏｄｅｒｉｖｅｔｈｅｅｕａｔｉｏｎｗｉｔｈｐｑｅａｃｈｉｔｅｒａｔｉｏｎｍｕｌｔｉｌｉｎｔｈｅｖａｒｉａｂｌｅｂｔｈｅｏｆｔｈｅｒｏｂａｂｉｌｉｔｏｉｎｔｐｙｇｙｐｙｐｅａｃｈｓｅｕｅｎｃｅａｎｄｂａｎａｄｄｉｔｉｏｎａｌｍｏｄｉｆｉｅｒｄｅｔｅｒｍｉｎｅｄｂｔｈｅｏｆｑｙｙｄｅｅｎｄｅｎｔｔｒｕｃｔｕｒｅｅｌａｔｉｎｈｅａｒｉａｂｌｅｓ．Ａｒａｍｅｗｏｒｋｏｒｓｒｖｆｆｐｇｔｍｏｄｅｌｉｎｃｏｒｒｅｌａｔｅｄｓｔｏｃｈａｓｔｉｃｖａｒｉａｂｌｅｓｕｓｉｎｔｈｉｓｔｈｅｏｒｉｓａｌｓｏｇｇｙｒｅｓｅｎｔｅｄ．Ａｃａｓｅｓｔｕｄｓｈｏｗｓｉｔｓａｌｉｃａｔｉｏｎｉｎｃａｌｃｕｌａｔｉｎｔｈｅｐｙｐｐｇｄｉｓｔｒｉｂｕｔｉｏｎｏｆｔｈｅａｒｅａｔｅｏｕｔｕｔｆｒｏｍｍｕｌｔｉｌｅｗｉｎｄｆａｒｍｓｔｏｇｇｇｐｐｄｅｍｏｎｓｔｒａｔｅｉｔｓｅｆｆｅｃｔｉｖｅｎｅｓｓ．Ｔｈｅｔｈｅｏｒｅｘａｎｄｓｅｘｉｓｔｉｎｓｅｕｅｎｃｅｙｐｇｑｏｅｒａｔｉｏｎｔｈｅｏｒａｎｄｈａｓｗｉｄｅａｌｉｃａｔｉｏｎｓ．ｐｙｐｐ：；Ｃ；ｃ；Ｋｅｗｏｒｄｓｓｅｕｅｎｃｅｅｒａｔｉｏｎｈｅｏｒｏｕｌａｏｒｒｅｌａｔｉｏｎｏｔｑｐｙｐｙ；ｄｅｅｎｄｅｎｃｅｓｔｒｕｃｔｕｒｅｄｅｅｎｄｅｎｔｒｏｂａｂｉｌｉｓｔｉｃｓｅｕｅｎｃｅｑｐｐｐ；ｗｉｎｄｏｅｒａｔｉｏｎｏｗｅｒｐｐ
８］。该理论将多个随机变量的联合概率分相依结构［
而使许多实际具有复杂相关结构的物理量的建模与分析成为可能。典型的Ｃｏｕｌａ函数主要包括椭圆ｐ
［０］１１－，以及族的Ｇａｕｓｓｉａｎｃｏｕｌａ与ｔｃｏｕｌａ１ｐｐ、ＧＡｒｃｈｉｍｅｄｅｓ族的Ｃｌａｔｏｎｃｏｕｌａｕｍｂｅｌｃｏｕｌａ与ｙｐｐ［２］，更多Ｃ］。Ｆｒａｎｋｃｏｕｌａ１ｏｕｌａ函数的介绍可见文［９ｐｐ
自然科学版）ＩＳＳＮ１０００００５４清华大学学报（２０１２年第５２卷第５期－／，２１１２２２３ＮＪＴｓｉｎｈｕａＵｎｉｖ（Ｓｃｉ＆Ｔｅｃｈ）０１２，Ｖｏｌ．５２，Ｎｏ．５ＣＮ－ｇ
象出来的一种基础性的数学理论。该理论通过对概
张宁，等：风电出力分析中的相依概率性序列运算
７０５
机变量完整的相依结构信息，但联合概率分布通常难以用解析的表达式表示，特别是随机变量各自具随机变量的联合概率分布几有不同的边缘分布时，乎无法被解析地表示，其实际应用的范围有限。１．２Ｃｏｕｌａ理论及其优势ｐ１９５９年，Ｓｋｌａｒ提出Ｃｏｕｌａ理论分布的 “ 连接” 以二维为例，Ｃｏｕｌａ理论可叙述如下：ｐ（，）为随机变量 α、Ｓｋｌａｒ定理令Ｆ α β αβ β的联合、概率分布函数， α、 α） β 的边缘分布分别为Ｆα （
Ｃｏｕｌａ理论自从创立以来在统计上得到了广ｐ泛的应用，２０世纪８０年代末，Ｃｏｕｌａ理论开始应ｐ
］１３１５－。近年来，Ｃ用于金融领域［ｏｕｌａ理论被引入ｐ１６］、用于电力系统故障分析［谐波分电力系统领域，１７］１８－２１］析［以及风电不确定性［等研究中。
７］。然而，量相互独立［随机变量之间有时包含复杂
的相关关系，并不满足现有序列运算理论的前提条件，从而限制了序列运算理论的应用范围。本文应用Ｃ建ｏｕｌａ理论对现有的序列运算理论进行拓展，ｐ — — 相依概率性序列立了序列非独立时的运算理论 — 运算理论。首先根据Ｃｏｕｌａ理论推导了相依概率ｐ给出了序列之间非独立情况下性序列运算的原理，运算的形式。然后给出了利用相依概率性序列运算对非独立随机变量进行建模与计算的流程，最后将相依概率性序列运算应用于多风电场总出力概率分布的分析之中，验证了该理论的正确性和有效性。
在研究多个随机变量的相关性时，通常采用相关系数或联合概率分布等数学工具。然而，相关系数仅仅表示随机变量相关性的测度，无法描述随机变量之间详细的相依结构，即不同的相依结构可能对应同样大小的相关系数；联合概率分布包含了随
１随机变量相关性与Ｃｏｕｌａ理论ｐ
１．１随机变量的相关性随机变量的相关性描述了２个或多个随机变量之间的联系。若一个随机变量取值的概率分布受另一个随机变量取值的影响，则称这２个随机变量之间具有相关性，否则，则称这２个随机变量之间互相
７］。独立［
收稿日期：２０１１１１０７－－
１］序列运算理论［是在电力系统的研究实践中抽
）基金项目：国家 “ 八六三 ”高技术项目（２０１１ＡＡ０５Ａ１０１，男（，内蒙古，博士研究生。作者简介：张宁（汉）１９８５—）：通信作者：康重庆，教授，Ｅ－ｍａｉｌｃｋａｎｔｓｉｎｈｕａ．ｅｄｕ．ｃｎ＠ｑｇｇ
／２３２６７０９７０４－
风电出力分析中的相依概率性序列运算
张宁，康重庆