九年级数学:二次函数图象性质应用练习3
2020春北师大版九年级数学下册第二章二次函数2二次函数的图像与性质练习

2.2 二次函数的图象与性质第1课时二次函数y=x2和y=-x2的图象与性质1.填空:(1)y=x2的图像是;开口向;对称轴是;顶点坐标是;(2)y=-x2的图像是;开口向;对称轴是;顶点坐标是;(3)在抛物线y=x2的对称轴左侧y随x的减小而;而在对称轴的右侧是y随着x 的增大而;此时函数y=x2当x=时的值最是.(4)在抛物线y=-x2的对称轴左侧y随x的减小而;而在对称轴的右侧是y随着x 的增大而;此时函数y=x2当x=时的值最是.2.如图,⊙O的半径为2.C1是函数y=x2的图象,C2是函数y=﹣x2的图象,则阴影部分的面积是_________ .3.已知a≠0,在同一直角坐标系中,函数y=x与y=x2的图象有可能是()A.B.C.D.4.已知正方形的边长为ccm,面积为Scm2.(1)求S与c之间函数关系式;(2)画出图象;(3)根据图象,求出S =1cm 2时,正方形的边长; (4)根据图象,求出c 取何值时,S ≥4cm 2.2.2 二次函数的图象与性质第2课时 二次函数y =ax 2和y =ax 2+c 的图象与性质1.抛物线y=-3x 2+5的开口向________,对称轴是_______,顶点坐标是________,顶点是最_____点,所以函数有最________值是_____.2.抛物线y=4x 2-1与y 轴的交点坐标是_________,与x 轴的交点坐标是_____. 3.把抛物线y=x 2向上平移3个单位后,得到的抛物线的函数关系式为_______. 4.抛物线y=4x 2-3是将抛物线y=4x 2,向_____平移______个单位得到的.5.抛物线y=ax 2-1的图像经过(4,-5),则a=_________. 6.抛物线y=-3(2x 2-1)的开口方向是_____,对称轴是_____.7.在同一坐标系中,二次函数y=-21x 2,y=x 2,y=-3x 2的开口由大到小的顺序是______. 8.在同一坐标系中,抛物线y =4x 2,y =41x 2,y =-41 x 2的共同特点是( )A.关于y 轴对称,抛物线开口向上;B.关于y 轴对称,y 随x 的增大而增大 B.关于y 轴对称,y 随x 的增大而减小;D.关于y 轴对称,抛物线顶点在原点. 9.如图,函数y =ax 2与y =-ax+b 的图像可能是( ).10.求符合下列条件的抛物线y=ax 2-1的函数关系式: (1)通过点(-3,2);(2)与y=12x 2的开口大小相同,方向相反; (3)当x 的值由0增加到2时,函数值减少4.11..已知抛物线y=mx 2+n 向下平移2个单位后得到的函数图像是y=3x 2-1,求m,n 的值.2.2 二次函数的图象与性质第3课时 二次函数y =a (x -h )2的图象与性质1.把二次函数2x y =的图象向右平移3个单位长度,得到新的图象的函数表达式是( )A. 32+=x yB. 32-=x yC. 2)3(+=x yD. 2)3(-=x y2.抛物线2)3(2--=x y 的顶点坐标和对称轴分别是( ) A.3),0,3(-=-x 直线 B. 3),0,3(=x 直线 C. 3),3,0(-=-x 直线 D. 3),3,0(-=x 直线3.已知二次函数2)1(3+=x y 的图象上有三点 ),2(),,2(),,1(321y C y B y A - ,则321,,y y y 的大小关系为( )A.321y y y >>B. 312y y y >>C. 213y y y >>D. 123y y y >>4.把抛物线2)1(6+=x y 的图象平移后得到抛物线26x y =的图象,则平移的方法可以是( )A.沿y 轴向上平移1个单位长度B.沿y 轴向下平移1个单位长度C.沿x 轴向左平移1个单位长度D.沿x 轴向右平移1个单位长度5.若二次函数12+-=mx x y 的图象的顶点在x 轴上,则m 的值是( )A. 2B. 2-C.0D. 2± 6.对称轴是直线2-=x 的抛物线是( )A.22+-=x yB.22+=x y C.2)2(21+=x y D.2)2(3-=x y 7.对于函数2)2(3-=x y ,下列说法正确的是( )A. 当0>x 时,y 随x 的增大而减小B. 当0<x 时,y 随x 的增大而增大C. 当2>x 时,y 随x 的增大而增大D. 当2->x 时,y 随x 的增大而减小8.二次函数132+=x y 和2)1(3-=x y ,以下说法:①它们的图象都是开口向上;②它们的对称轴都是y 轴,顶点坐标都是原点(0,0); ③当0>x 时,它们的函数值y 都是随着x 的增大而增大; ④它们的开口的大小是一样的. 其中正确的说法有( )A.1个B.2个C.3个D.4个9.抛物线2)1(3--=x y 的开口向 ,对称轴是 ,顶点坐标是 。
湘教版九年级下册数学二次函数y=ax2(a>0)的图象与性质测试题

湘教版九年级数学下册测试题测试题湘教版初中数学1.2 二次函数的图象与性质第1课时二次函数)0y的图象和性质ax(2>=a1.填空:(1)y=x2的图像是;开口向;对称轴是;顶点坐标是;(2)在抛物线y=x2的对称轴左侧y随x的减小而;而在对称轴的右侧是y随着x的增大而;此时函数y=x2当x=时的值最是.2.若点A(-5,y1)、B(2,y2)都在y=2x2上,则y____2y(填“>”1或“<”)3.关于函数2y=的性质的叙述,错误的是( ).3xA.对称轴是y轴 B.顶点是原点C.当0x时,y随x的增大而增大 D.y有最大值>4.已知a≠0,在同一直角坐标系中,函数y=x与y=x2的图象有可能是()A.B.C.D.5.已知正方形的边长为ccm,面积为Scm2.(1)求S与c之间函数关系式;(2)画出图象;(3)根据图象,求出S=1cm2时,正方形的边长;(4)根据图象,求出c取何值时,S≥4cm2.6.已知直线y=-2x+3与抛物线y=ax2相交于A、B两点,且A点坐标为(-3,m).(1)求a、m的值;(2)求抛物线的表达式及其对称轴和顶点坐标;(3)x取何值时,二次函数y=ax2中的y随x的增大而减小;(4)求A、B两点及二次函数y=ax2的顶点构成的三角形的面积初中生提高做题效率的方法厚薄读书法:复习课本要厚薄结合著名数学家华罗庚先生说:“书要能从薄读到厚,还要能从厚读到薄。
”这就是厚薄读书法。
我们在复习功课时,也可以用这种方法,具体来说分为“由薄到厚”和“由厚读薄”两个部分由薄到厚第一步要“由薄到厚”地复习课本。
这就是说,我们在复习过程中对书本中的某些原理、定律、公式,不仅应该记住它的结论,而且还应该思考一下,这个定律是怎样发现的,这个公式是怎样推导的。
在阅读过程中对书中的每个概念、原理和观点要有自己的理解,对自己不懂的地方,还要查阅参考资料,通过充实书本的有关内容,使自己获得比书本上内容更为丰富、更为深刻的认识和见解,也就是把书“越读越厚”。
二次函数图像与性质练习题

二次函数图像与性质练习题二次函数是高中数学中的一个重要内容,它在数学中有着广泛的应用。
而对于学生来说,了解二次函数的图像和性质是非常重要的。
本文将通过一些练习题来帮助学生深入理解二次函数的图像和性质。
练习题一:给定函数 f(x) = 2x^2 + 3x - 2,求解以下问题:1. 求函数 f(x) 的顶点坐标和对称轴方程;2. 求函数 f(x) 的零点;3. 判断函数 f(x) 的开口方向和最值。
解答:1. 首先,我们知道二次函数的顶点坐标可以通过公式 x = -b/2a 和 y = f(-b/2a) 来求解。
将函数 f(x) 的系数代入公式中,可以得出顶点坐标为 (-3/4, -23/8)。
对称轴方程为 x = -3/4。
2. 函数 f(x) 的零点即为方程 2x^2 + 3x - 2 = 0 的解。
通过因式分解或者使用求根公式,可以得到零点为 x = 1/2 和 x = -2。
3. 由于二次函数的系数 a 大于 0,所以函数的开口方向是向上的。
同时,由于顶点坐标的 y 值为 -23/8,所以函数的最值为最小值。
练习题二:给定函数 g(x) = -x^2 + 4x + 5,求解以下问题:1. 求函数 g(x) 的顶点坐标和对称轴方程;2. 求函数 g(x) 的零点;3. 判断函数 g(x) 的开口方向和最值。
解答:1. 同样地,我们可以通过公式 x = -b/2a 和 y = g(-b/2a) 来求解顶点坐标。
将函数 g(x) 的系数代入公式中,可以得出顶点坐标为 (2, 9)。
对称轴方程为 x = 2。
2. 函数 g(x) 的零点即为方程 -x^2 + 4x + 5 = 0 的解。
通过因式分解或者使用求根公式,可以得到零点为 x = -1 和 x = 5。
3. 由于二次函数的系数 a 小于 0,所以函数的开口方向是向下的。
同时,由于顶点坐标的 y 值为 9,所以函数的最值为最大值。
通过以上练习题,我们可以看到二次函数的图像和性质是与函数的系数相关的。
苏科版九年级数学上册二次函数的图象与性质同步练习册
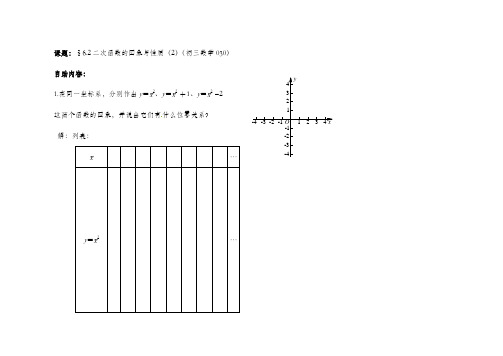
yxO1-1-112-2-223-3-334-4-44课题:§6.2二次函数的图象与性质(2)(初三数学030) 自助内容:1.在同一坐标系,分别作出y =x 2、y =x 2 +1、y =x 2 −2 这两个函数的图象,并说出它们有什么位置关系? 解:列表:x …y =x 2 [来源:学&科&…网]y=x2 +1…y=x2 −2练习:(1)函数y=x2-3是由y=x2向_____平移_____单位得到的.(2)函数y=x2+1是由y=x2-2向_____平移_____单位得到的.2. 用描点法画出y=-x2和y=-x2+3的图象并完成填空:y=-x2开口向,对称轴是,顶点坐标为,当时,y随x的增大而减小;当时,y随x的增大而增大,yx O1-1-112-2-223-3-334 -4-445 -5-55当时,y有最值,y=-x2+3 开口向,对称轴是,顶点坐标为,当时,y随x的增大而减小;当时,y随x的增大而增大,当时,y有最值.例题讲解:例1.说出抛物线y=2x2和y=2x2-2的对称轴,顶点坐标和开口方向并完成下表y=ax2+k a>0 a<0k>0k<0k>0k<0草图开口方向例2.(1)抛物线y =14x 2-9的开口 ,对称轴是 ,顶点坐标 ,它可以看作是由抛物线y =14x 2向平移 个单位得到的.(2)抛物线y =-4x 2-4的开口向 ,当x = 时,y 有最 值,最值为 .例3. 一条抛物线的形状和对称轴与y =12x 2相同,且抛物线经过点(1,1),求这条抛物线的函数关系式及其顶点坐标.例4.如图,直线l经过A(3,0),B(0,3)两点,且与二次函数y=x2+1的图象,在第一象限内相交于点C.求:(1)△AOC的面积;(2)二次函数图象顶点与点A、B组成的三角形的面积.当堂训练:1.抛物线y=-2x2-3的开口,对称轴是,顶点坐标是,当x 时,y随x的增大而增大,当x 时,y随x的增大而减小.2.将抛物线y=13x2向下平移2个单位得到的抛物线的解析式为,再向上平移3个单位得到的抛物线的解析式为,并分别写出这两个函数的顶点坐标、。
北师大版数学九年级下册y=a(x-h)2+k的函数图像和性质(3)课时对应练习(Word版含答案)

第05课时二次函数y=a(x-h)2 +k的函数图像和性质(3)1.将抛物线y=﹣2x2+1向右平移1个单位长度,再向上平移1个单位长度所得的抛物线解析式为()A.y=﹣2(x+1)2B.y=﹣2(x+1)2+2C.y=﹣2(x﹣1)2+2D.y=﹣2(x﹣1)2+12.对于抛物线y=−12(x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>1时,y随x的增大而减小;⑤抛物线与y轴的交点坐标为(0,3).其中正确的有()个.A.1B.2C.3D.43.如图,在平面直角坐标系中,有两条位置确定的抛物线,它们的对称轴相同,表达式中的h,k,m,n都是常数,则下列关系不正确的是()A.h<0,k>0B.m<0,n>0C.h=m D.k=n4.对于二次函数y=a(x﹣h)2+k,对称轴是_______,顶点坐标是_______.(1)当a>0时,图象开口_______,在对称轴左侧,y随x的增大而_______;在对称轴右侧,y 随x的增大而_______,当x=_______时,y有最_______值,是_______;(2)当a<0时,图象开口_______,在对称轴左侧,y随x的增大而_______;在对称轴右侧,y 随x的增大而_______,当x=时,y有最_______值,是_______.5.如图,把抛物线y=12x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=12x2交于点Q,则图中阴影部分的面积为_______.6.对于函数y=﹣2(x﹣1)2,当x≤a时,y随x的增大而增大,则a的范围为_______.7.抛物线y=−13(x−2)2+1的顶点为C,已知y=﹣kx+3的图象经过点C,则这个一次函数图象与两坐标轴所围成的三角形面积为_______.8.已知二次函数y=(x﹣2a)2+(a﹣1)(a为常数),当a取不同的值时,其图象构成一个“抛物线系”,如图分别是当a=﹣1,a=0,a=l,a=2时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是_______.9.已知在平面直角坐标系中,抛物线l1的解析式为y=﹣x2,将抛物线l1平移后得到抛物线l2,若抛物线l2经过点(3,﹣1),且对称轴为x=1.(1)求抛物线l2的解析式;(2)求抛物线l2的顶点坐标;(3)若将抛物线l2沿其对称轴继续上下平移,得到抛物线l3,设抛物线l3的顶点坐标为B,直线OB于抛物线l3的另一个交点为C,当OB=OC时,求C点坐标.10.已知二次函数y=(x﹣1)2﹣4的图象与x轴交于A,B两点(A在B左侧),与y轴交于点C,顶点为D.(1)求点A,B,C,D的坐标.并画出该二次函数的大致图象;(2)说出抛物线y=(x﹣1)2﹣4可由抛物线y=x2如何平移得到;(3)求四边形BOCD的面积.11.设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=3(x+1)2+4m(m为常数)上的三点,则y1,y2,y3的大小关系为()A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y3<y2<y112.已知y=12x2的图象是抛物线,若抛物线不动,把x轴,y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是()A.y=12(x﹣2)2+2B.y=12(x+2)2﹣2C.y=12(x﹣2)2﹣2D.y=12(x+2)2+213.已知抛物线C:y=12(x﹣1)2﹣1,顶点为D,将C沿水平方向向右(或向左)平移m个单位,得到抛物线C1,顶点为D1,C与C1相交于点Q,若∠DQD1=60°,则m等于()A.±4√3B.±2√3C.﹣2或2√3D.﹣4或4√3 14.当0≤x≤3时,直线y=a与抛物线y=(x﹣1)2﹣3有交点,则a的取值范围是_______.15.已知函数y={(x−1)2−1,(x<4)(x−7)2−1,(x≥4),点P(a,ka)在该函数上,若这样的点P恰好有三个,则k的值为_______.16.已知函数y={(x−2)2−2,x≤4(x−6)2−2,x>4使y=a成立的x的值恰好只有3个时,a的值为______.17.如图,在平面直角坐标系中,点A、B的坐标分别为(16,0),(0,3√10),连结AB,P是线段AO上一动点(不与点A、O重合).过A、P两点的抛物线和过P、O两点的抛物线的开口均向下,它们的顶点E、F均在线段AB上.设这两个二次函数的最大值的差为S,则S =_______.18.如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x﹣6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.(1)当h =2.6时,求y 与x 的函数关系式.(2)当h =2.6时,球能否越过球网?球会不会出界?请说明理由. (3)若球一定能越过球网,又不出边界.则h 的取值范围是多少?19.如图,二次函数y 1=(x ﹣2)2+m 的图象与y 轴交于点C ,点B 是点C 关于该二次函数图象的对称轴对称的点.已知一次函数y 2=kx +b 的图象经过该二次函数图象上点A (1,0)及点B . (1)求m 的值;(2)求二次函数与一次函数的解析式;(3)根据图象,写出满足y 2≥y 1的x 的取值范围.【参考答案】 1.C . 2.C . 3.D .4.x =h ,(h ,k ),向上,减小,增大,h ,大,k ,向下,增大,减小,h ,小,k . 5.272.6.a ≤1. 7.12×3×3=92.8.y =12x −1.9.(1)根据题意,设抛物线l 2的解析式为:y =﹣(x ﹣1)2+k , 将点(3,﹣1)代入函数解析式, ∴﹣1=﹣4+k , 解得:k =3,∴抛物线l2的解析式为:y=﹣(x﹣1)2+3;(2)∴抛物线l2的顶点坐标为(1,3);(3)设l3的解析式为:y=﹣(x﹣1)2+3+m,∴B点坐标为(1,3+m),∵B,O,C三点共线且OB=OC,∴C点坐标为(﹣1,﹣3﹣m),∵C在l3上,∴﹣(﹣1﹣1)2+3+m=﹣3﹣m,∴m=﹣1,∴C点坐标为(﹣1,﹣2).10.(1)令y=0,(x﹣1)2﹣4=0,解得x=3或﹣1,得A(﹣1,0),B(3,0),令x=0,y=﹣3,得C(0,﹣3),顶点D(1,﹣4).图象如图所示,(2)把抛物线y=x2抛向右平移1个单位,再向下平移4个单位得到抛物线y=(x﹣1)2﹣4.(3)连接OD,S四边形CDBO=S△OCD+S△OBD=12•3•1+12•3•4=152.11.A.12.B.13.A.提示:抛物线CC:y=12(x﹣1)2﹣1沿水平方向向右(或向左)平移m个单位得到y=12(x﹣m﹣1)2﹣1,∴D (1,﹣1),D 1(m +1,﹣1), ∴Q 点的横坐标为:m+22,代入y =12(x ﹣1)2﹣1求得Q (m+22,m 28−1),若∠DQD 1=60°,则△DQD 1是等边三角形, ∴QD =DD 1=|m |, 由勾股定理得,(m+22−1)2+(m 28−1+1)2=m 2,解得m =±4√3。
九年级数学下第1章二次函数1.2二次函数的图像与性质第3课时二次函数y=a2的图象与性质习题湘教

(2)求出该抛物线与坐标轴的交点坐标.
解:由(1)可知抛物线的表达式为 y=-(x-2)2. 当 y=0 时,-(x-2)2=0,解得 x1=x2=2, 所以抛物线与 x 轴的交点坐标为(2,0). 当 x=0 时,y=-4,所以抛物线与 y 轴的交点坐标为(0,-4).
17.如图,已知直线 l 经过 A(4,0)和 B(0,4)两点,抛物线 y= a(x-h)2 的顶点为 P(1,0),直线 l 与抛物线的交点为 M,连 接 PM.
3.(1)当 a__>____0 时,抛物线 y=a(x-h)2 开口向上,若 x<h(对 称轴左侧),则函数值 y 随 x 的增大而减小;若 x>h(对称轴 右侧),则函数值 y 随 x 的增大而增大.
(2)当 a__<____0 时,抛物线 y=a(x-h)2 开口向下,若 x<h(对称 轴左侧),则函数值 y 随 x 的增大而增大;若 x>h(对称轴右 侧),则函数值 y 随 x 的增大而减小.
【点拨】A.y=ax+c 中,a>0,c>0,y=a(x+c)2 中,a<0,c <0,故 A 错误;B.y=ax+c 中,a<0,c>0,y=a(x+c)2 中, a<0,c>0,故 B 正确;C.y=ax+c 中,a>0,c<0,y=a(x +c)2 中,a>0,c>0,故 C 错误;D.y=ax+c 中,a<0,c> 0,y=a(x+c)2 中,a>0,c<0,故 D 错误.
(2)将抛物线 y=(x-3)2 向上平移 1 个单位,再向左平移 t(t>0) 个单位得到新抛物线,若新抛物线的顶点 E 在△DAC 内, 求 t 的取值范围; 解:由题意可知:新抛物线的顶点坐标为(3-t,1), 设直线 AC 的表达式为 y=kx+b(k≠0). 将(1,4),(3,0)代入 y=kx+b 中, 得3kk++b= b=4, 0. 解得kb= =-6. 2,
人教版九年级数学第二十二章二次函数考点例析(三)---抛物线y=a(x-h)^2+k和y=ax^2+bx+c的图像和性质

抛物线y=a +k 和y=a 的图像和性质一、学习目标1.会画出y=a +k 这类函数的图象,通过比较,了解这类函数的性质。
2.掌握把抛物线y=a 平移至y=a +k 的规律。
3. 能通过配方把二次函数y=a 化成y=a +k 的形式,从而确定开口方向、对称轴和顶点坐标.二、知识精讲知识点1:二次函数y=a +k 的图象和性质把抛物线2y ax =向 _____平移h 个单位,向 ________平移k 个单位,可以得到抛物线2()+y a x h k =-。
【例1】巳知函数y=-3 ,y=-3 ,y=-3 -1,(1)在同一直角坐标系中画出三个函数的图象;(2)分别说出这三个函数图象的开口方向、对称轴和顶点坐标;(3)试说明:分别通过怎样的平移,可以由抛物线y=-3 得到抛物线y=-3 和抛物线y=-3 -1;(4)试讨论函数y=-3 -1的性质。
.【例2】(1)函数y=-3-1的图象可由y=-3x2的图象沿x轴向平移_____个单位再沿y轴向平移个单位得到;对称轴是______,顶点坐标是 ______;当x_________时,y随着x的增大而_______。
(2)二次函数y=-2+4的图象的开口方向________,顶点坐标是________,对称轴是_________. 当x______时,y随着x的增大而增大, 当x______时, y 随着x的增大而减少.当x=_____时,函数有最_______值是_________.(3)将抛物线y=-5x2沿y轴向下平移4个单位, 再沿x轴向右平移4个单位,所得的抛物线的函数式是_______________________(4)二次函数y=-2-1由y=-2+1向_____平移_______个单位,再向_____平移_______个单位得到.【例3】利用配方法求二次函数的顶点坐标及对称轴.(1)225y x x=-+ (2) 2y x x=-+ (3)225y x x=++【例4】用待定系数法求二次函数解析式.1.已知一个二次函数的图像的顶点在原点,且经过点(1,3),求这个二次函数的表达式.2.已知抛物线的顶点坐标是(-1,-2),且经过点(0,1),求这个二次函数的表达式.3.已知二次函数当x=3时有最大值4,并且图象经过点(4,-3),求这个二次函数的表达式.【题组训练】:1将抛物线y=2x 2向下平移1个单位,得到的抛物线是( )A .B .C .D .2抛物线y= +3的顶点坐标是( )A .(2,3)B .(-2,3)C .(2,-3)D .(-2,-3) 3二次函数y= +2的最小值是( ).A .2B .1C .-3D .4二次函数y=-3 的图象的顶点坐标是( )A .(-1,8)B .(1,8)C .(-1,2)D .(1,-4)5、将函数y= 的图象向右平移a( )个单位,得到函数y= 的图象,则a 的值为( )A .1B .2C .3D .46、两条抛物线y=x 2与y=-x 2在同一坐标系内,下列说法中不正确的是( )A .顶点相同B .对称轴相同C .开口方向相反D .都有最小值7、在抛物线y=-x 2,当y <0时,x 的取值范围应为( )A .x >0B .x <0C .x ≠0D .x ≥08、知点11()x y ,,均在抛物线y=x 2-1上,下列说法中正确的是( )A .若,则B .若,则C .若,则D .若,则9.将y=2 变为y=a +n 的形式,则=__________ 10二次函数y=a 的图象顶点在Y 轴负半轴上。
人教版九年级上册数学《二次函数的图像和性质》综合练习题【含答案】

《二次函数的图象和性质》同步练习题一、选择题(共10小题)1.下列函数中是二次函数的为 ()A .B .C .D .31y x =-231y x =-22(1)y x x =+-323y x x =+-2.二次函数与一次函数,它们在同一直角坐标系中的图象大致是2y ax bx c =++y ax c =+ ()A .B .C .D .3.已知一次函数的图象经过一、二、四象限,则二次函数的顶点y kx b =+2y kx bx k =+-在第 象限.()A .一B .二C .三D .四4.抛物线的顶点坐标是 22(3)2y x =-+()A .B .C .D .(3,2)-(3,2)(3,2)--(3,2)-5.已知,二次函数满足以下三个条件:①,②,③2y ax bx c =++24b c a >0a b c -+<,则它的图象可能是 b c <()A .B .C .D .6.把抛物线向下平移2个单位长度,再向右平移1个单位长度,所得抛物线是2(2)y x =+ ()A .B .C .D .2(2)2y x =++2(1)2y x =+-22y x =+22y x =-7.将抛物线平移得到抛物线,则这个平移过程正确的是 2y x =2(3)y x =+()A .向左平移3个单位B .向右平移3个单位C .向上平移3个单位D .向下平移3个单位8.二次函数的图象可能是 22y x x =-+()A .B .C .D .9.若点,,都在抛物线上,则下1(1,)M y -2(1,)N y 37(,)2P y 2241(0)y mx mx m m =-+++>列结论正确的是 ()A .B .C .D .123y y y <<132y y y <<312y y y <<213y y y <<10.二次函数与轴交点坐标为 23(2)5y x =--y ()A .B .C .D .(0,2)(0,5)-(0,7)(0,3)二、填空题(共4小题)11.请写出一个开口向上且与轴交点坐标为的抛物线的表达式: .y (0,1)12.若二次函数,当时,随的增大而减小,则的取值范围是 22()1y x k =-++2x - y x k .13.抛物线的对称轴是 .22247y x x =+-14.已知抛物线经过,,对于任意,点均不在抛2y ax bx c =++(0,2)A (4,2)B 0a >(,)P m n 物线上.若,则的取值范围是 .2n >m 三、解答题(共6小题)15.已知抛物线.2246y x x =--(1)请用配方法求出顶点的坐标;(2)如果该抛物线沿轴向左平移个单位后经过原点,求的值.x (0)m m >m 16.如图,在中,,,,动点从点开始沿边ABC ∆90B ∠=︒12AB mm =24BC mm =P A向以的速度移动(不与点重合),动点从点开始沿边向以AB B 2/mm s B Q B BC C 的速度移动(不与点重合).如果、分别从、同时出发,那么经过多少4/mm s C P Q A B 秒,四边形的面积最小.APQC17.已知二次函数.243(0)y ax ax b a =-++≠(1)求出二次函数图象的对称轴;(2)若该二次函数的图象经过点,且整数,满足,求二次函数的表(1,3)a b 4||9a b <+<达式;(3)对于该二次函数图象上的两点,,,,设,当时,1(A x 1)y 2(B x 2)y 11t x t + 25x 均有,请结合图象,直接写出的取值范围.12y y t 18.在平面直角坐标系中,抛物线经过点和.xOy 2(0)y ax bx c a =++>(0,3)A -(3,0)B (1)求的值及、满足的关系式;c a b(2)若抛物线在、两点间从左到右上升,求的取值范围;A B a (3)结合函数图象判断,抛物线能否同时经过点、?若能,写出(1,)M m n -+(4,)N m n -一个符合要求的抛物线的表达式和的值,若不能,请说明理由.n 19.小明利用函数与不等式的关系,对形如12()()()0n x x x x x x --⋯->为正整数)的不等式的解法进行了探究.(n (1)下面是小明的探究过程,请补充完整:①对于不等式,观察函数的图象可以得到如表格:30x ->3y x =-的范围x 3x >3x <的符号y +-由表格可知不等式的解集为.30x ->3x >②对于不等式,观察函数的图象可以得到如表表格:(3)(1)0x x -->(3)(1)y x x =--的范围x 3x >13x <<1x <的符号y +-+由表格可知不等式的解集为 .(3)(1)0x x -->③对于不等式,请根据已描出的点画出函数的(3)(1)(1)0x x x --+>(3)(1)(1)y x x x =--+图象;观察函数的图象补全下面的表格:(3)(1)(1)y x x x =--+的范围x 3x >13x <<11x -<<1x <-的符号y +- 由表格可知不等式的解集为 .(3)(1)(1)0x x x --+>⋯⋯小明将上述探究过程总结如下:对于解形如为正整数)的12()()()0(n x x x x x x n --⋯⋯->不等式,先将,,按从大到小的顺序排列,再划分的范围,然后通过列表格的1x 2x ⋯n x x 办法,可以发现表格中的符号呈现一定的规律,利用这个规律可以求这样的不等式的解y 集.(2)请你参考小明的方法,解决下列问题:①不等式的解集为 .(6)(4)(2)(2)0x x x x ---+>②不等式的解集为 .2(9)(8)(7)0x x x --->20.函数是二次函数.223y mx mx m =--(1)如果该二次函数的图象与轴的交点为,那么 ;y(0,3)m(2)在给定的坐标系中画出(1)中二次函数的图象.答案一、选择题(共10小题)1.解:、是一次函数,故错误;A 31y x =-A 、是二次函数,故正确;B 231y x =-B 、不含二次项,故错误;C 22(1)y x x =+-C 、是三次函数,故错误;D 323y x x =+-D 故选:.B 2.解:一次函数和二次函数都经过轴上的,y (0,)c 两个函数图象交于轴上的同一点,排除、;∴y B C 当时,二次函数开口向上,一次函数经过一、三象限,排除;0a >D 当时,二次函数开口向下,一次函数经过二、四象限,正确;0a <A 故选:.A 3.解:一次函数的图象经过一、二、四象限,y kx b =+,,0k ∴<0b >△,2224()40b k k b k =--=+>抛物线与轴有两个交点,∴x、异号,k b 抛物线的对称轴在轴右侧,∴y 二次函数的顶点在第一象限.∴2y kx bx k =+-故选:.A 4.解:抛物线的顶点坐标是,22(3)2y x =-+(3,2)故选:.B 5.解:二次函数满足以下三个条件:①,②,③, 2y ax bx c =++24b c a >0a b c -+<b c <由①可知当时,则抛物线与轴有两个交点,当时,∴0a >240b ac ->x 0a <240b ac -<则抛物线与轴无交点;x 由②可知:当时,,1x =-0y <由③可知:,0b c -+>,必须,0a b c -+< ∴0a <符合条件的有、,∴C D 由的图象可知,对称轴直线,,,抛物线交的负半轴,C 02b x a=->0a <0b ∴>y ,则,0c <b c >由的图象可知,对称轴直线,,,抛物线交的负半轴,D 02b x a=-<0a <0b ∴<y ,则有可能,0c <b c <故满足条件的图象可能是,D 故选:.D 6.解:抛物线的顶点坐标是,向下平移2个单位长度,再向右平移1个单2(2)y x =+(2,0)-位长度后抛物线的顶点坐标是,(1,2)--所以平移后抛物线的解析式为:2(1)2y x =+-故选:.B 7.解:抛物线的顶点坐标为,抛物线的顶点坐标为,2y x =(0,0)2(3)y x =+(3,0)-点向左平移3个单位可得到,(0,0)(3,0)-将抛物线向左平移3个单位得到抛物线.∴2y x =2(3)y x =+故选:.A 8.解:,,22y x x =-+ 0a <抛物线开口向下,、不正确,∴A C 又对称轴,而的对称轴是直线, 212x =-=-D 0x =只有符合要求.∴B 故选:.B 9.解:观察二次函数的图象可知:.132y y y <<故选:.B 10.解:23(2)5y x =-- 当时,,∴0x =7y =即二次函数与轴交点坐标为,23(2)5y x =--y (0,7)故选:.C 二、填空题(共4小题)11.解:抛物线开口方向向上,且与轴的交点坐标为,y (0,1)抛物线的解析式为.∴21y x =+故答案为.21y x =+12.解:,22()1y x k =-++对称轴为,∴x k =-,20a =-< 抛物线开口向下,∴在对称轴右侧随的增大而减小,∴y x 当时,随的增大而减小,2x - y x ,解得,2k ∴-- 2k 故.2k 13.解:抛物线的对称轴是:,22247y x x =+-24622x =-=-⨯故.6x =-14.解:依照题意,画出图形,如图所示.当时,或,2n >0m <4m >当时,若点均不在抛物线上,则.∴2n >(,)P m n 04m 故.04m三、解答题(共6小题)15.解:(1)2246y x x =--22(2)6x x =--,22(1)8x =--故该函数的顶点坐标为:;(1,8)-(2)当时,,0y =202(1)8x =--解得:,,11x =-23x =即图象与轴的交点坐标为:,,x (1,0)-(3,0)故该抛物线沿轴向左平移3个单位后经过原点,x 即.3m =16.解:设经过秒,四边形的面积最小x APQC 由题意得,,,2AP x =4BQ x =则,122PB x =-的面积PBQ ∆12BQ PB =⨯⨯1(122)42x x =⨯-⨯,24(3)36x =--+当时,的面积的最大值是,3x s =PBQ ∆236mm此时四边形的面积最小.APQC 17.解:(1)二次函数图象的对称轴是;422a x a-=-=(2)该二次函数的图象经过点,(1,3),433a a b ∴-++=,3b a ∴=把代入,3b a =4||9a b <+<得.43||9a a <+<当时,,则.0a >449a <<914a <<而为整数,a ,则,2a ∴=6b =二次函数的表达式为;∴2289y x x =-+当时,,则.0a <429a <-<922a -<<-而为整数,a 或,3a ∴=-4-则对应的或,9b =-12-二次函数的表达式为或;∴23126y x x =-+-24169y x x =-+-(3)当时,均有,25x 12y y 二次函数的对称轴是直线,243(0)y ax ax b a =-++≠2x =,12y y ①当时,有,即∴0a >12|2||2|x x -- 12|2|2x x -- ,212222x x x ∴--- ,2124x x x ∴- ,25x ,241x ∴-- 该二次函数图象上的两点,,,,1(A x 1)y 2(B x 2)y 设,当时,均有,11t x t + 25x 12y y ∴115t t -⎧⎨+⎩ .14t ∴- ②当时,,即0a <12|2||2|x x -- 12|2|2x x -- ,或,1222x x ∴-- 1222x x -- ,或12x x ∴ 124x x - ,25x ,241x ∴--该二次函数图象上的两点,,,,1(A x 1)y 2(B x 2)y 设,当时,均有,11t x t + 25x 12y y 比的最大值还大,或比的最小值还小,这是不存在的,t ∴2x 1t + 24x -故时,的值不存在,0a <t 综上,当时,.0a >14t - 18.解:(1)抛物线经过点和. 2(0)y ax bx c a =++>(0,3)A -(3,0)B ,∴3093c a b c-=⎧⎨=++⎩,.3c ∴=-310a b +-=(2)由1可得:,2(13)3y ax a x =+--对称轴为直线,132a x a -=-抛物线在、两点间从左到右上升,当时,对称轴在点左侧,如图: A B 0a >A即:,解得:,1302a a -- 13a.、两点间从左到右上升,103a ∴< A B 当时,抛物线在、两点间从左到右上升,∴103a < A B (3)抛物线不能同时经过点、.(1,)M m n -+(4,)N m n -理由如下:若抛物线同时经过点、.则对称轴为:,(1,)M m n -+(4,)N m n -(1)(4)322m m x -++-==由抛物线经过点可知抛物线经过,与抛物线经过相矛盾,A (3,3)-(3,0)B 故:抛物线不能同时经过点、(1,)M m n -+(4,)N m n -19.解:(1)②由表格可知不等式的解集为或,(3)(1)0x x -->3x >1x <故或;3x >1x <③图象如右图所示,当时,,当时,,11x -<<(3)(1)(1)0x x x --+>1x <-(3)(1)(1)0x x x --+<由表格可知不等式的解集为或,(3)(1)(1)0x x x --+>3x >11x -<<故,,或;+-3x >11x -<<(2)①不等式的解集为或或,(6)(4)(2)(2)0x x x x ---+>6x >24x <<2x <-故或或;6x >24x <<2x <-②不等式的解集为或且,2(9)(8)(7)0x x x --->9x >8x <7x ≠故或且9x >8x <7x ≠20.解:(1)该函数的图象与轴交于点, y (0,3)把,代入解析式得:,∴0x =3y =33m -=解得,1m =-故答案为;1-(2)由(1)可知函数的解析式为,223y x x =-++,2223(1)4y x x x =-++=--+ 顶点坐标为;∴(1,4)列表如下:x 2-1-01234y5-034305-描点;画图如下:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级数学:二次函数图象性质应用练习
学生做题前请先回答以下问题
问题1:a,b,c符号与图象的关系:
a的符号决定了抛物线的________,当_______时,开口________;当________时,开口________;c是抛物线与________交点的________;b的符号与a________,根据________可推导.
问题2:
①确定________符号及________的信息;
②找特殊点的___________,获取等式或不等式;
③________代入不等式,组合判断残缺式符号.(残缺型式子是指不同时含有a,b,c三个系数的式子,例如有时式子中只含有a,b时,我们就称之为残缺式或残缺型)
二次函数图象性质应用(三)
一、单选题(共6道,每道16分)
1.二次函数图象的一部分如图所示,其对称轴为直线,且过点.下列说法:①;②;③;④若是抛物线上的两点,则.其中正确的是( )
A.①②
B.②③
C.①②④
D.②③④
2.小轩从如图所示的二次函数的图象中,观察得到如下四个结论:①;②;③;④.其中正确的结论是( )
A.①②③
B.②③④
C.①②④
D.①②③④
3.已知二次函数的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0).下列结论:①;②b-2a=0;③;④.其中正确的是( )
A.③
B.②③
C.③④
D.①②
4.已知二次函数的图象如图所示,有下列结论:
①;②2a+b=0;③;④.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
5.抛物线的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图.则以下结论:①;②;
③c-a=2;④方程有两个相等的实数根.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
6.已知二次函数的图象经过(),(2,0)两点,且
,图象与y轴正半轴的交点在(0,2)的下方.则下列结论:①;②;
③;④.其中正确的是( )
A.①②
B.②③
C.①②④
D.①②③④。
