判别分析案例(鸢尾花)

合集下载

基于欧式距离的判别分析

基于欧式距离的判别分析作者：唐宇政来源：《现代商贸工业》2019年第09期摘要：分类判别问题在生活中是一个有着重要应用需求的问题。

例如根据患者肺部阴影大小，是否低烧以及其它理化指标来判断是否为肺结核患者，或是根据邮件的内容或者发件地址来判断其是否属于垃圾邮件。

在现实生活中，我们希望能够准确快速的解决这一类问题，往往需要利用历史数据来建立合理的分类器。

因此重点介绍一种常见的基于距离的判别分类方法——欧氏距离判别法。

首先在第二部分详细介绍这种分类方法以及将其和另外一种常见的基于马氏距离的判别分类法进行比较。

在第三部分，我们将进行实例分析，基于花瓣长度和花瓣宽度利用欧式距离判别法对鸢尾花进行分类。

关键词：分类问题;欧式距离;马氏距离中图分类号：TB 文献标识码：Adoi：10.19311/ki.1672-3198.2019.09.0921 背景分类判别是指根据事物的不同点加以区分辨别，确定事物所属的类别，使具有更多相似点的事物归入一类，使之在大量事物中可以根据一定规律快速鉴别各个事物的所属种类。

例如国家电网在对居民进行供电时，就可以根据以往的用电量数据对居民的用电情况进行划分，对用电量大的居民相应地收取更多的费用，从而达到促进节约用电的目的。

在解决此类问题的过程中需要准确判别个体样本所属的类别，即应该划分的组别。

本文中将介绍的是如何通过数学建模来快速准确完成这个分组判别的过程。

本文中，我们将使用鸢尾花数据集，对150个鸢尾花数据样本进行分类判别，确定样本属于三种鸢尾花中的哪一种，来实例说明欧式距离判别法在现实生活中的可行性。

2 分类方法判别分析法，是在分类确定的条件下，根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法。

常见的判别分析法主要包括基于距离的判别、Fisher判别、Bayes 判别。

本文主要研究对象是通俗易懂、应用范围广泛的基于距离的判别分析法。

2.1 基于距离的判别分析距离判别的基本思想是将距离越近的样本分为一类，距离越大的样本分为不同类。

对鸢尾花kmeans算法的总结

鸢尾花是一种常见的植物，具有多种品种和花色。

鸢尾花的种类繁多，因此如何有效地对鸢尾花进行分类成为一个研究热点。

K均值（k-means）算法是一种常用的聚类分析方法，对鸢尾花进行分类时，k-means算法可以发挥重要作用。

让我们来了解一下k-means算法的基本原理。

K均值算法通过迭代将n个数据点划分到k个集群中，使得同一集群内的点彼此距离的平方和最小。

其中，k是用户指定的聚类数目，而迭代的过程是根据每个数据点与各个中心的距离来不断更新中心点的位置，直至满足停止条件。

接下来，我们将对鸢尾花k-means算法进行总结和回顾性的探讨，以便更全面、深刻地理解这一主题。

在应用k-means算法对鸢尾花进行分类时，我们首先需要收集样本数据，包括鸢尾花的花瓣长度、花瓣宽度、花萼长度和花萼宽度等特征。

通过调用相应的数学库或算法工具，可以将这些样本数据输入到k-means算法中进行聚类分析。

当我们应用k-means算法对鸢尾花进行分类时，关键的一步是确定合适的聚类数目k。

这需要利用一些评价指标，如肘部法则（elbow method）或轮廓系数（silhouette score）来帮助确定最佳的k值。

通过数据点与各个中心的距离计算，不断迭代更新中心点的位置，最终将鸢尾花样本数据划分到不同的集群中。

对于鸢尾花k-means算法的应用而言，我们需要注意的一点是，选择合适的特征和合理地进行数据预处理是非常重要的。

另外，对聚类结果进行可视化分析也是必不可少的，可以通过绘制散点图或热力图来直观地展示聚类效果。

在我个人看来，鸢尾花k-means算法的应用不仅仅是简单的数据分析，更重要的是它可以帮助我们理解聚类分析的基本原理并掌握如何利用算法工具解决实际问题。

通过对鸢尾花k-means算法的总结和回顾性讨论，我对这一主题有了更深入的理解，也更加意识到了数据分析在实际应用中的重要性。

总结而言，通过本文的探讨，我们对鸢尾花k-means算法的原理和应用有了更全面、深刻和灵活的理解。

鸢尾花数学建模论文.

大连海事大学2014年数学建模竞赛丙组论文鸢尾花的分类研究姓名学号学院专业班级仇实2220141486 物理系应用物理学2014-1 郭杨喆2220143245 物理系应用物理学2014-1 张逸凡2220143115 物理系应用物理学2014-12014年11月23日摘要加拿大加斯帕半岛上生长着三类不同的鸢尾属的花朵,他们分别是Setosa（刚毛）、Versicolor（变色）和Virginica（弗吉尼亚）。

植物学家从三类鸢尾花中各选15株，分别测量了它们的花瓣长（Pl）、花瓣宽（Pw）、花萼长（Sl）、花萼宽（Sw）。

通过分析数据设计用于鸢尾花识别的数学算法，识别这15株花朵的类属。

本论文分析如何通过花瓣长、花瓣宽、花萼长、花萼宽建立数学模型对测试样本进行准确分类。

经过对数据的分析以及查阅资料，本题可以通过判别分析的Fisher判别模型进行计算分类，由此我们想到了利用SPSS软件对数据进行处理，最终得到Fisher线性判别函数成功地解决了对鸢尾花的分类问题。

关键词：判别分析 Fisher判别模型 SPSS软件 Fisher线性判别函数目录摘要 (1)一、问题重述 (3)二、问题分析 (3)三、建立费歇尔模型 (3)四、检验 (7)五、测试样本的分类结果 (7)六、参考文献 (8)七、附录（SPSS的操作过程） (8)一、问题重述本题是根据观测样本中刚毛、变色、弗吉尼亚的四个度量花瓣长（Pl）、花瓣宽（Pw）、花萼长（Sl）、花萼宽（Sw）对测试样本的鸢尾花进行分类。

二、问题分析根据这个问题，我们可以按照一定的判别准则，建立一个或多个判别函数，用观测样本数据确定判别函数中的待定系数，并计算判别指标，据此可以确定测试样本中的某一样本属于何类。

这类问题属于判别分析问题。

三、建立费歇尔模型1.数据分析在建立模型之前进行一些数据处理。

包括：平均向量、协方差、先验概率、错分成本，这样费歇尔判别函数的期望错判率能达到最小化。

2.判别分析

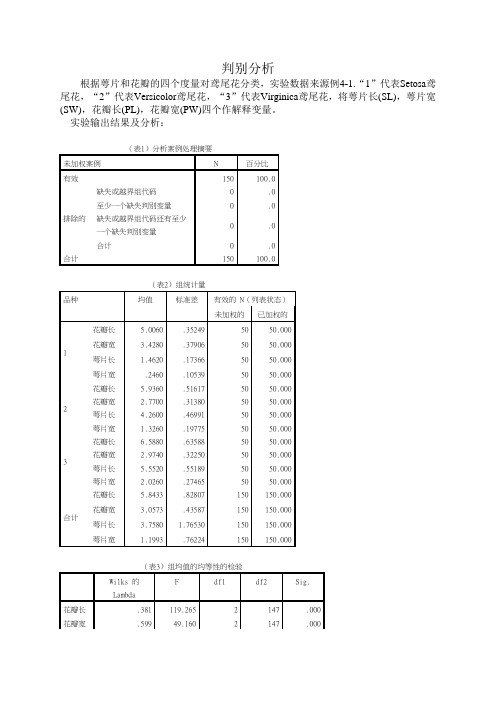
判别分析根据萼片和花瓣的四个度量对鸢尾花分类，实验数据来源例4-1.“1”代表Setosa 鸢尾花，“2”代表Versicolor 鸢尾花，“3”代表Virginica 鸢尾花，将萼片长(SL)，萼片宽(SW)，花瓣长(PL)，花瓣宽(PW)四个作解释变量。

实验输出结果及分析：（表1）分析案例处理摘要未加权案例 N 百分比有效150 100.0排除的缺失或越界组代码 0 .0 至少一个缺失判别变量0 .0 缺失或越界组代码还有至少一个缺失判别变量 0 .0 合计0 .0 合计150100.0（表2）组统计量品种均值标准差有效的 N （列表状态）未加权的已加权的 1花瓣长5.0060 .35249 50 50.000 花瓣宽3.4280.379065050.000萼片长 1.4620 .17366 50 50.000 萼片宽 .2460 .10539 50 50.000 2花瓣长5.9360 .51617 50 50.000 花瓣宽 2.7700 .31380 50 50.000 萼片长 4.2600 .46991 50 50.000 萼片宽 1.3260 .19775 50 50.000 3花瓣长6.5880 .63588 50 50.000 花瓣宽 2.9740 .32250 50 50.000 萼片长 5.5520 .55189 50 50.000 萼片宽 2.0260 .27465 50 50.000 合计花瓣长 5.8433 .82807 150 150.000 花瓣宽3.0573.43587150150.000萼片长 3.7580 1.76530 150 150.000 萼片宽1.1993.76224150150.000表1反映的是有效样本量及变量缺失的情况。

表 2是各组变量的描述统计分析。

表3是对各组均值是否相等的检验。

由表3 可以看出，在0.01的显著水平上，我们拒绝变量萼片长，萼片宽，花瓣长和花瓣宽在三组的均值相等的假设，即认为这四个变量在三组的均值是有显著差异的。

人工智能基础与应用-物以类聚发现新簇群-人工智能案例探究鸢尾花品种

授课人：目录•提出问题•解决方案01•预备知识02•任务1——确定鸢尾花最佳的品种数k值03•任务2——绘制鸢尾花聚类后的结果散点图0405随着数据收集和数据存储技术的不断进步，我们可以迅速积累海量数据，然而，如何提取有用信息和甄别不同数据种群对普通人来说存在不小的挑战。

幸运的是，现在借助一些数据挖掘工具可以较为轻松地完成一些预测任务，例如，预测新物种、探究新信息种类是聚类算法最经典的应用案例。

本案例是基于一群鸢尾花（如下图所示）的数据集（无类别标签），根据花的特征探究将这些鸢尾花分为几个品种是比较合适的。

各式各样的鸢尾花如果你是一名植物学家，这个问题对于你来说是轻而易举的。

但在很多情况下，数据的主人或使用者并不具备本领域丰富的专业知识，那能否可以利用一种人工智能技术，让机器来帮助人类发现新的信息呢？为找到一种相对最佳的鸢尾花品种数k，•首先尽可能获得关于鸢尾花的特征知识，也许它能引导我们找到品种k的有效初值，因为花的特征反映了花的独特之处和一些重要信息，具有重要的参考价值；•然后，选用k-means算法对鸢尾花数据集进行聚类，从性能指标数据和样本可视化分布方面对聚类效果进行评价，•最后，在对比不同k值聚类效果的前提下，确定鸢尾花最佳的品种数量。

本案例的解决方案如下图所示：解决方案1.鸢尾花形态特征猜测：从鸢尾花的形态结构来看，也许花瓣能更好地帮助我们分辨鸢尾花的种类一种鸢尾花植物2.数据降维在衡量采用什么方法来分析数据之前，最好能对数据的全貌有一个可视化的了解，能从中发现一些内在规律或启示，以便能更好地指导我们选择相对合理的方法来解决问题。

我们通常只在二维或三维的空间可视化数据，但原始数据的实际维度可能是四维甚至更多，所有要采用数据降维的方法将原始数据的维度降为二维或三维，以便进行可视化来直观了解数据的分布。

除此之外，降维还可以提高计算、提高模型拟合度等好处。

如何保证原高维空间里的数据关系，经降维后仍然在低维空间保持不变或者近似呢？【引例5-1】降维鸢尾花数据集iris，绘制样本点图。

sklearn iris 案例

sklearn iris 案例Scikit-learn Iris 数据集：机器学习中的经典案例研究Scikit-learn Iris 数据集是一个经典的机器学习数据集，它被广泛用于分类任务的教学和评估。

该数据集包含 150 个鸢尾花样本，属于三个不同的物种：山鸢尾、变色鸢尾和维吉尼亚鸢尾。

数据探索数据集包含以下特征：萼片长度 (sepal length)萼片宽度 (sepal width)花瓣长度 (petal length)花瓣宽度 (petal width)这些特征描述了鸢尾花的物理特性，可用于区分不同的物种。

数据可视化为了可视化数据并理解不同物种之间的关系，我们可以使用散点图或平行坐标图。

这些可视化工具有助于识别不同特征之间的模式和相关性。

数据预处理在将数据用于机器学习模型之前，需要进行一些预处理步骤。

这些步骤包括：标准化：对特征进行缩放，使它们具有相同的量级。

划分训练集和测试集：将数据分成用于训练模型的训练集和用于评估模型的测试集。

模型训练与评估Scikit-learn 提供了各种分类算法，可用于训练鸢尾花数据集。

常见的算法包括：逻辑回归支持向量机决策树随机森林训练模型后，使用测试集评估模型的性能。

评估指标包括：准确性：模型正确预测的样本的比例。

召回率：模型正确识别目标类的样本的比例。

F1 分数：准确率和召回率的加权平均值。

基于鸢尾花数据集的应用鸢尾花数据集已被用于广泛的机器学习应用，包括：分类：将鸢尾花样本分类到正确的物种。

特征重要性：确定不同特征对分类的影响程度。

模型选择：通过比较不同模型的性能来确定最佳模型。

超参数调优：优化模型的超参数以提高性能。

总结Scikit-learn Iris 数据集是机器学习中的一个宝贵资源，它提供了以下好处：简单且易于理解：数据集相对较小，具有明确定义的特征和类别。

广泛使用：该数据集已被广泛用于教学和研究目的。

算法评估：该数据集可用于评估和比较不同的机器学习算法。

降维分析报告

降维分析报告引言降维分析是一种在机器学习和数据科学领域广泛应用的方法，它可以帮助我们从高维数据中提取主要特征，减少数据的维度，并保留尽可能多的有用信息。

在本报告中，我们将介绍降维分析的基本概念和常用算法，并通过一个具体的案例来示范如何应用降维分析。

降维分析的背景和意义在现实生活中，许多问题都涉及大量的特征或变量，这些特征可能存在冗余、噪声或不具有明确的解释。

此时，使用原始高维数据进行分析和建模将导致过拟合、维度灾难等问题。

因此，通过降维分析可以将复杂的高维数据转化为更加简洁、易理解的低维表示，帮助我们更好地理解数据并提取重要特征。

常用的降维分析方法主成分分析（PCA）主成分分析是一种常用的无监督降维算法，它通过线性变换将原始数据投影到新的正交特征空间，使得数据在新特征空间上的方差最大化。

通过计算主成分之间的协方差矩阵的特征值和特征向量，我们可以确定新特征空间的基向量，进而进行降维操作。

线性判别分析（LDA）线性判别分析是一种经典的监督降维算法，它将高维数据映射到一个低维空间中，使得不同类别的数据在该空间中的投影能够最大程度地区分开来。

和PCA相比，LDA在进行降维时考虑了类别信息，因此可能更适用于分类问题。

t分布邻域嵌入（t-SNE）t-SNE是一种非线性降维算法，它通过构建高维数据点之间的概率分布和低维数据点之间的概率分布，来保持高维数据的邻域结构。

t-SNE通常被应用于可视化高维数据，特别是在探索复杂数据集时非常有用。

降维分析的案例应用为了更好地理解降维分析的实际应用，我们以鸢尾花数据集为例进行分析。

鸢尾花数据集是一个经典的多分类问题，其中包含了四个特征：花萼长度、花萼宽度、花瓣长度和花瓣宽度。

我们可以使用降维分析方法对鸢尾花数据集进行可视化，并探索数据的结构和分布。

首先，我们使用主成分分析（PCA）对鸢尾花数据进行降维。

通过计算主成分之间的协方差矩阵的特征值和特征向量，我们可以选择保留的主成分数量，从而实现数据降维。

关于如何分辨鸢尾花的判别分析报告

关于如何分辨鸢尾花的判别分析报告一、目的与背景：鸢尾花为法国的国花，Setose，Versicolour，Virginica 是三种有名的鸢尾花，其萼片是绚丽多彩的，和向上的花瓣不同，花萼是下垂的。

这三种鸢尾花很像，根据萼片和花瓣的四个度量对鸢尾花分类。

二、分析过程1、组间均值分析H0：组间均值是相等的H1：组间均值是不等的Tests of Equality of Group Means表1的显著性水平上，拒绝在三组均值相等的原假设，即花萼长、花萼宽、花瓣长、花瓣宽在三组的均值是有显著性差异的。

2、协方差阵分析H0：各组协方差阵是相等的H1：各组协方差阵是不相等的Test Results表2Box's M 92.993F Approx. 4.332df1 20df2 23344.026Sig. .000Tests null hypothesis of equal population covariance matrices.表2是对各总体协方差阵是否相等的统计检验。

在0.05的显著性水平下拒绝原假设，即各总体协方差阵不相等。

3、确定非标准化典型判别函数Canonical Discriminant Function Coefficients表3是非标准化的典型判别函数，表示为y1=-2.063-0.083*Sepal.Lenght-0.132*Sepal.Width+0.212*Petal.Leng th+0.239* Petal.Widthy2=-8.045+0.037*Sepal.Lenght+0.211*Sepal.Width-0.104*Petal.Len gth+0.273* Petal.Width4、函数的显著性检验Eigenvalues表4-1Wilks' Lambda差的比例和典型相关系数。

第一判别函数解释了99%的方差，第二判别函数解释了1%的方差，两个判别函数解释了全部的方差。

BP算法实例—鸢尾花的分类（Python）

BP算法实例—鸢尾花的分类（Python）⾸先了解下Iris鸢尾花数据集：Iris数据集（https:///wiki/Iris_flower_data_set）是常⽤的分类实验数据集，由Fisher,1936收集整理。

Iris也称鸢尾花卉数据集，是⼀类多重变量分析的数据集。

数据集包含150个数据集，分为3类，每类50个数据，每个数据包含4个属性。

可通过花萼长度，花萼宽度，花瓣长度，花瓣宽度4个属性预测鸢尾花卉属于（Setosa，Versicolour，Virginica）三个种类中的哪⼀类。

iris以鸢尾花的特征作为数据来源，常⽤在分类操作中。

该数据集由3种不同类型的鸢尾花的50个样本数据构成。

其中的⼀个种类与另外两个种类是线性可分离的，后两个种类是⾮线性可分离的。

该数据集包含了4个属性：Sepal.Length（花萼长度），单位是cm;Sepal.Width（花萼宽度），单位是cm;Petal.Length（花瓣长度），单位是cm;Petal.Width（花瓣宽度），单位是cm;种类：Iris Setosa（1.⼭鸢尾）、Iris Versicolour（2.杂⾊鸢尾），以及Iris Virginica（3.维吉尼亚鸢尾）。

Python源码：1from__future__import division2import math3import random4import pandas as pd567 flowerLables = {0: 'Iris-setosa',8 1: 'Iris-versicolor',9 2: 'Iris-virginica'}1011 random.seed(0)121314# ⽣成区间[a, b)内的随机数15def rand(a, b):16return (b - a) * random.random() + a171819# ⽣成⼤⼩ I*J 的矩阵，默认零矩阵20def makeMatrix(I, J, fill=0.0):21 m = []22for i in range(I):23 m.append([fill] * J)24return m252627# 函数 sigmoid28def sigmoid(x):29return 1.0 / (1.0 + math.exp(-x))303132# 函数 sigmoid 的导数33def dsigmoid(x):34return x * (1 - x)353637class NN:38""" 三层反向传播神经⽹络 """3940def__init__(self, ni, nh, no):41# 输⼊层、隐藏层、输出层的节点（数）42 self.ni = ni + 1 # 增加⼀个偏差节点43 self.nh = nh + 144 self.no = no4546# 激活神经⽹络的所有节点（向量）47 self.ai = [1.0] * self.ni48 self.ah = [1.0] * self.nh49 self.ao = [1.0] * self.no5051# 建⽴权重（矩阵）52 self.wi = makeMatrix(self.ni, self.nh)53 self.wo = makeMatrix(self.nh, self.no)54# 设为随机值55for i in range(self.ni):56for j in range(self.nh):57 self.wi[i][j] = rand(-0.2, 0.2)58for j in range(self.nh):59for k in range(self.no):60 self.wo[j][k] = rand(-2, 2)6162def update(self, inputs):63if len(inputs) != self.ni - 1:64raise ValueError('与输⼊层节点数不符！')6566# 激活输⼊层67for i in range(self.ni - 1):68 self.ai[i] = inputs[i]6970# 激活隐藏层71for j in range(self.nh):72 sum = 0.073for i in range(self.ni):74 sum = sum + self.ai[i] * self.wi[i][j]75 self.ah[j] = sigmoid(sum)7677# 激活输出层78for k in range(self.no):79 sum = 0.080for j in range(self.nh):81 sum = sum + self.ah[j] * self.wo[j][k]82 self.ao[k] = sigmoid(sum)8384return self.ao[:]8586def backPropagate(self, targets, lr):87""" 反向传播 """8889# 计算输出层的误差90 output_deltas = [0.0] * self.no91for k in range(self.no):92 error = targets[k] - self.ao[k]93 output_deltas[k] = dsigmoid(self.ao[k]) * error 9495# 计算隐藏层的误差96 hidden_deltas = [0.0] * self.nh97for j in range(self.nh):98 error = 0.099for k in range(self.no):100 error = error + output_deltas[k] * self.wo[j][k] 101 hidden_deltas[j] = dsigmoid(self.ah[j]) * error 102103# 更新输出层权重104for j in range(self.nh):105for k in range(self.no):106 change = output_deltas[k] * self.ah[j]107 self.wo[j][k] = self.wo[j][k] + lr * change 108109# 更新输⼊层权重110for i in range(self.ni):111for j in range(self.nh):112 change = hidden_deltas[j] * self.ai[i]113 self.wi[i][j] = self.wi[i][j] + lr * change114115# 计算误差116 error = 0.0117 error += 0.5 * (targets[k] - self.ao[k]) ** 2118return error119120def test(self, patterns):121 count = 0122for p in patterns:123 target = flowerLables[(p[1].index(1))]124 result = self.update(p[0])125 index = result.index(max(result))126print(p[0], ':', target, '->', flowerLables[index]) 127 count += (target == flowerLables[index])128 accuracy = float(count / len(patterns))129print('accuracy: %-.9f' % accuracy)130131def weights(self):132print('输⼊层权重:')133for i in range(self.ni):134print(self.wi[i])135print()136print('输出层权重:')137for j in range(self.nh):138print(self.wo[j])139140def train(self, patterns, iterations=1000, lr=0.1):141# lr: 学习速率(learning rate)142for i in range(iterations):143 error = 0.0144for p in patterns:145 inputs = p[0]146 targets = p[1]147 self.update(inputs)148 error = error + self.backPropagate(targets, lr) 149if i % 100 == 0:150print('error: %-.9f' % error)151152153154def iris():155 data = []156# 读取数据157 raw = pd.read_csv('iris.csv')158 raw_data = raw.values159 raw_feature = raw_data[0:, 0:4]160for i in range(len(raw_feature)):161 ele = []162 ele.append(list(raw_feature[i]))163if raw_data[i][4] == 'Iris-setosa':164 ele.append([1, 0, 0])165elif raw_data[i][4] == 'Iris-versicolor':166 ele.append([0, 1, 0])167else:168 ele.append([0, 0, 1])169 data.append(ele)170# 随机排列数据171 random.shuffle(data)172 training = data[0:100]173 test = data[101:]174 nn = NN(4, 7, 3)175 nn.train(training, iterations=10000)176 nn.test(test)177178179if__name__ == '__main__':180 iris()。

判别分析1

2.实验内容（1）自选数据或者使用例题4-1、4-2数据完成判别分析。

（2）对判别分析结果进行分析。

（3）选定两个样本，对样本进行分类。

3.实验步骤例4-1：判别分析的一个重要应用是动植物的分类，最著名的一个例子是1936年费歇的鸢尾花数据。

鸢尾花为法国的国花，Setosa、erisolor、Virginica是三种有名的鸢尾花，其萼片是绚丽多彩的，和向上的花瓣不同，花萼是下垂的。

这三种鸢尾花很像，人们试图建立模型，根据萼片和花瓣的四个角度来对鸢尾花分类。

该数据给出150朵鸢尾花的萼片长（sepal length）、萼片宽(sepal length)、花瓣长(petal width)、花瓣宽(petal width)以及这些分别属于的种类共五个变量。

萼片和花瓣的长度为四个定量变量，而种类为分类变量。

这里三种鸢尾花各有50个观测值。

对数据进行判别分析的得到的分析结果如下：表1-1 分析觀察值處理摘要未加權的觀察值N 百分比有效150 100.0已排除遺漏或超出範圍群組代碼0 .0至少一個遺漏區別變數0 .0遺漏或超出範圍群組代碼及至0 .0少一個遺漏區別變數總計0 .0總計150 100.0输出结果表1-1分析的是各组变量的描述统计量和对各组均值是否相等的检验。

反应的是有效样本变量及变量缺失情况。

表1-2 群組統計資料被解释变量平均數標準偏差有效的 N (listwise)表1-5 測試結果Box's M 共變異等式檢定146.663F 近似值7.045df1 20df2 77566.751顯著性.000檢定相等母體共變異數矩陣的虛無假設。

输出结果1-4和表1-5是对各组协方差矩阵是否相等的Boxs’M检验。

表1-4反映协方差矩阵的秩和行列式的对数值。

由行列式值可以看出，协方差矩阵不是病态矩阵。

表1-5是对个总体协方差矩阵是否相等的统计检验。

由F值及其显著性水平，我们在0.05的显著性水平下拒绝原假设。

有导师学习神经网络的分类——鸢尾花种类识别

有导师学习神经网络的分类——鸢尾花种类识别1、案例背景有导师学习神经网络以其良好的学习能力广泛应用于各个领域中，其不仅可以解决拟合回归问题，亦可以用于模式识别、分类识别。

本章将继续介绍两种典型的有导师学习神经网络（GRNN和PNN），并以实例说明其在分类识别中的应用。

植物的分类与识别时植物学研究和农林业生产经营中的重要基础工作，对于区分植物种类、探索植物间的亲缘关系、阐明植物系统的进化规律具有重要意义。

目前常用的植物种类鉴别方法是利用分类检索表进行鉴定，但该方法花费时间较多，且分类检索表的建立是一件费时费力的工作，需投入大量的财力物力。

叶片的识别植物的重要组成部分，叶子的外轮廓是其主要形态特征。

在提取叶子形态特征的基础上，利用计算机进行辅助分类与识别成为当前的主要研究方向，同时也是研究的热点与重点。

现采集到150组不同类型鸢尾花（Setosa、Versicolour和Virginica）的四种属性：萼片长度、萼片宽度、花瓣长度和花瓣宽度，样本编号与四种属性的关系如图26-3所示（其中，样本编号1-50为Setosa，51-100为Versicolour，101-150为Virginica）。

从图中大致可以看出，花瓣长度、花瓣宽度与鸢尾花类型间有较好的线性关系，而萼片长度、萼片宽度与鸢尾花类型间呈现出非线性的关系。

现要求：（1）利用GRNN和PNN分别建立鸢尾花种类识别模型，并对模型的性能进行评价。

（2）利用GRNN和PNN分别建立各个属性及属性组合与鸢尾花种类间的识别模型，并与（1）中所建模型的性能及运算时间进行对比，从而探求各个属性及属性组合与鸢尾花种类的相关程度。

2、案例目录：26.1 理论基础26.1.1 广义回归神经网络（GRNN）概述1. GRNN的结构2. GRNN的学习算法3. GRNN的特点4. GRNN的MATLAB工具箱函数26.1.2 概率神经网络（PNN）概述1. PNN的结构2. PNN的学习算法3. PNN的MATLAB工具箱函数26.2 案例背景26.2.1 问题描述26.2.2 解决思路及步骤26.3 MATLAB程序实现26.3.1 清空环境变量26.3.2 训练集/测试集产生26.3.3 模型建立26.3.4 性能评价26.3.5 绘图26.3.6 结果分析26.4 延伸阅读26.5 参考文献3、主程序：%% 清空环境变量clear allclc%% 训练集/测试集产生% 导入数据load iris_data.mat% 随机产生训练集和测试集P_train = [];T_train = [];P_test = [];T_test = [];for i = 1:3temp_input = features((i-1)*50+1:i*50,:);temp_output = classes((i-1)*50+1:i*50,:);n = randperm(50);% 训练集——120个样本P_train = [P_train temp_input(n(1:40),:)'];T_train = [T_train temp_output(n(1:40),:)'];% 测试集——30个样本P_test = [P_test temp_input(n(41:50),:)'];T_test = [T_test temp_output(n(41:50),:)']; end%% 模型建立result_grnn = [];result_pnn = [];time_grnn = [];time_pnn = [];for i = 1:4for j = i:4p_train = P_train(i:j,:);p_test = P_test(i:j,:);%% GRNN创建及仿真测试t = cputime;% 创建网络net_grnn = newgrnn(p_train,T_train);% 仿真测试t_sim_grnn = sim(net_grnn,p_test);T_sim_grnn = round(t_sim_grnn);t = cputime - t;time_grnn = [time_grnn t];result_grnn = [result_grnn T_sim_grnn'];%% PNN创建及仿真测试t = cputime;Tc_train = ind2vec(T_train);% 创建网络net_pnn = newpnn(p_train,Tc_train);% 仿真测试Tc_test = ind2vec(T_test);t_sim_pnn = sim(net_pnn,p_test);T_sim_pnn = vec2ind(t_sim_pnn);t = cputime - t;time_pnn = [time_pnn t];result_pnn = [result_pnn T_sim_pnn'];endend%% 性能评价% 正确率accuracyaccuracy_grnn = [];accuracy_pnn = [];time = [];for i = 1:10accuracy_1 = length(find(result_grnn(:,i) == T_test'))/length(T_test);accuracy_2 = length(find(result_pnn(:,i) == T_test'))/length(T_test);accuracy_grnn = [accuracy_grnn accuracy_1];accuracy_pnn = [accuracy_pnn accuracy_2];end% 结果对比result = [T_test' result_grnn result_pnn]accuracy = [accuracy_grnn;accuracy_pnn]time = [time_grnn;time_pnn]%% 绘图figure(1)plot(1:30,T_test,'bo',1:30,result_grnn(:,4),'r-*',1:30,result_pnn(:,4),'k:^')grid onxlabel('测试集样本编号')ylabel('测试集样本类别')string = {'测试集预测结果对比(GRNN vs PNN)';['正确率:' num2str(accuracy_grnn(4)*100) '%(GRNN) vs ' num2str(accuracy_pnn(4)*100) '%(PNN)']};title(string)legend('真实值','GRNN预测值','PNN预测值')figure(2)plot(1:10,accuracy(1,:),'r-*',1:10,accuracy(2,:),'b:o')grid onxlabel('模型编号')ylabel('测试集正确率')title('10个模型的测试集正确率对比(GRNN vs PNN)')legend('GRNN','PNN')figure(3)plot(1:10,time(1,:),'r-*',1:10,time(2,:),'b:o')grid onxlabel('模型编号')ylabel('运行时间(s)')title('10个模型的运行时间对比(GRNN vs PNN)') legend('GRNN','PNN')4、运行结果：。

SAS学习系列36.判别分析

36. 判别分析（一）基本原理判别分析，是用以判别个体所属类的一种统计方法。

其原理是根据已掌握的一批分类明确的样品，建立一个较好的判别函数，使得用该判别函数进行判别时错判事例最少，进而能用此判别函数对给定的一个新样品判别它来自哪个总体。

判别分析方法通常要给出一个判别指标（判别函数），同时还要指定一种判别规则。

一、距离判别法未知总体的样品x离哪个总体的距离最近，就判断它属于哪个总体。

1. 对于两个正态总体G1, G2距离选用马氏（Mahalanobis）距离：d2(x, G1) = (x-μ1)T∑1-1(x-μ1)d2(x, G2) = (x-μ2)T∑2-1(x-μ2)其中，μ1, μ2, ∑1, ∑2分别为总体G1, G22的均值和协差矩阵。

令W(x) = d2(x, G1) - d2(x, G2)称为判别函数，若∑1=∑2时，W(x)是线性函数，此时称为线性判别；若∑1≠∑2，W(x)是二次函数。

2. 多总体情况设有m个总体：G1, …, G m，其均值、协差阵分别为μi, ∑i. 对给定的样品x，按距离最近的准则对x进行判别归类：首先计算样品x到m个总体的马氏距离d i2(x), 然后进行比较，把x判归距离最小的那个总体，即若d h2(x) = min{ d i2(x) | i = 1,…,m}，则x∈G h.二、Fisher线性函数判别法为了方便使用，需要寻找尽量简单的判别函数，其中在Fisher 准则下的线性判别函数就是只利用总体的一、二阶矩就可求得的判别函数。

图1 Fisher线性判别分析示意图下面以两个总体为例来说明Fisher判别的思想。

设有两个总体G1、G2，其均值分别为μ1和μ2，协方差阵分别∑1和∑2，并假定∑1 = ∑2 = ∑，考虑线性组合：y = L T x。

通过寻求合适的L向量，使得来自两个总体的数据间的距离较大，而来自同一个总体数据间的差异较小。

为此，可以证明，当选L=c∑–1(μ1–μ2)，其中c ≠ 0时，所得的投影即满足要求。

Fisher判别操作手册

11.4案例分析——鸢尾花种类费希尔于1936年发表的鸢尾花（Iris）数据，被广泛用于判别分析的例子。

数据是对3种鸢尾花：刚毛鸢尾花（第一组）、变色鸢尾花（第二组）和弗吉尼亚鸢尾花（第三组），各自抽取一个容量为50的样本。

在R软件中，可以直接调用命令iris来查看数据集，每种花都有四个外观指标，部分数据如下：R软件操作安装含有Fisher判别法命令的package，即包MASSinstall.packages(“MASS”) # 安装MASS包也可以使用手动安装法安装，具体参考第零章的基本操作演示调用包library(MASS) # 调用MASS包，此时就可以调用Fisher判别了查看原始数据iris # 查看鸢尾花数据选取其中Sepal.Width和Petal.Length两个变量，绘制二维散点图，观察不同鸢尾花的分类情况plot(iris$Sepal.Width,iris$Petal.Length,col=iris$Species)画图结果部分鸢尾花的种类不能通过该两个指标区分调用Fisher判别法程序lda()，将结果命名为resultlda(Species~Sepal.Length+Sepal.Width+Petal.Length+Petal.Width,data=iris)构建一个新的鸢尾花数据，new <- data.frame(Sepal.Length=6.4,Sepal.Width=3.1,Petal.Length=4.7,Petal.Width=1.2)判断新的鸢尾花属于哪一类pre <- predict(result,new)pre结果为在Levels的三个分类中，这朵未知品种的花被分到versicolor类中，即变色鸢尾花。

距离判别法在鸢尾花亚属类型判定中的应用初探

参考文献
1. Edgar Anderson. The irises of the Gaspé Peninsula. Bulletin of the American Iris Society. 1935, 59: 2–5. 2. Fisher, R.A.. The Use of Multiple Measurements in Taxonomic Problems. Annals of Eugenics. 1936, 7: 179–188. 3. 黄利文.改进的距离判别分析法.江南大学学报（自然科学版），2011,10（6）：745-748
⎡14.21 3.23 10.51 1.12⎤
⎡8.23 3.02 5.07 2.01⎤
L(1) xx
=
⎢ ⎢
3.23
⎢10.51
2.69 2.68
2.68 10.17
0.91⎥⎥ ，
0.98⎥
L(2) xx
=
⎢⎢3.02 ⎢5.07
3.53 2.81
2.81 5.20
1.72⎥⎥ ，C
2.24⎥
=
本文主要利用马氏距离判别方法，依据鸢尾花 virginica 和 versicolor 亚属中典型个体的不同性状特征（花萼和花瓣的长度和宽度），对未知鸢尾花个体进行所属类型的判别分析，以探究距离判别法在鸢尾属的分类中应用。
1. 判别分析原理
本文采用的方法是马氏距离判别分析法，假定各总体为正态分布，并通过对总体间的协方差阵和均值向量的显著性进行检验，以进一步确定具体判别分析方法，其具体原理解析见《多元统计分析-第二版》（袁志发和宋世德编著，2009）。
距离判别是将待判样本 X=（x1, x2, x3, x4）T 到各总体 Gi (i=1、2、……、k)的距离远近作为判据的一种直观判别方法。而判别分析的方法也有很多，并且每种方法都有其自己的特点。相对于 Fisher 判别和贝叶斯判别等方法，距离判别法具有操作简单，对数据要求较少，适用范围广。但是在一般的应用中，很少涉及其判别函数的显著性检验和错判率的分析，仅在《实用判别分析》（孙尚拱和潘恩沛编著，1990）一书中有简单叙述，即利用霍特林 T2 统计量通过 F 检验对判别进行统计学意义分析和利用刀切估计法对错判率进行分析。

判别分析案例(鸢尾花)

Wilks的Lambda函数检验Wilks的Lambda 卡方df Sig.1到2 .025 538.950 8 .0002 .774 37.3513 .000标准化的典型判别式函数系数函数1 2花萼长-.346 .039花萼宽-.525 .742花瓣长.846 -.386花瓣宽.613 .555=0.613-⨯⨯0.8460.525+.0346-1花萼长z花萼宽花瓣长⨯z花瓣宽+zD⨯z=0.555⨯0.386⨯0.742⨯20.039-+花萼宽花瓣长花瓣宽+花萼长zD⨯zzz结构矩阵函数1 2花瓣长.726*.165花萼宽-.121 .879*花瓣宽.651 .718*花萼长.221 .340*判别变量和标准化典型判别式函数之间的汇聚组间相关性按函数内相关性的绝对大小排序的变量。

*.每个变量和任意判别式函数间最大的绝对相关性典型判别式函数系数0.155=0.299---.01.2526⨯0630.196花萼长zz花萼宽⨯花瓣宽z花瓣长⨯z++D⨯=0.2710.089-+-0.0072.6978⨯0.218花萼宽z+花瓣长花瓣宽z花萼长z⨯⨯+D⨯z区域图典则判别函数2-16.0-12.0-8.0-4.0.04.08.012.016.0+---------+---------+---------+---------+---------+---------+---------+---------+16.0+13+I13II13II123II123II1223I12.0++++1223++++I1223II1223II1223II1223II1223I8.0++++12+23++++I1223II1223II1223II1223II1223I4.0++++12+23++++I1223II1223II1223II1223II1223*I.0+++*+12+23+++I12*23II1223II1223II1223II1223I-4.0++++12++23+++I1223II1223II1223II1223II1223I-8.0++++12++23+++I1223II1223II1223II1223II1223I-12.0+++12++23++I1223II1223II1223II1223II1223I-16.0+1223++---------+---------+---------+---------+---------+---------+---------+---------+-16.0-12.0-8.0-4.0.04.08.012.016.0典则判别函数1区域图中使用的符号符号组标签--------------------11刚毛鸢尾花22变色鸢尾花33佛吉尼亚鸢尾花*表示一个组质心。

鸢尾花分析

35.61
51.80
11.18
36.27
142.72
山东
18.27
88.34
19.07
43.19
72.98
12.59
42.16
200.18
河南
19.07
73.18
18.01
29.38
64.51
8.91
38.14
155.45
湖北
18.76
102.67
21.87
30.47
64.33
11.99
42.14
600601
4.42
3.16
43.95
1.40
4.67
3.06
-13.58
4.73
复旦复华
600624
4.44
3.68
49.44
.53
.85
3.19
13.57
2.60
习题3.今选取内蒙古、广西、贵州、云南、西藏、宁夏、新疆、甘肃和青海等9个内陆边远省份。选取人均GDP、第三产业比重、人均消费支出、人口自然增长率及文盲半文盲人口占15岁以上人口的比例等五项能够较好的说明各地区社会经济发展水平的指标。验证一下边远及少数民族聚居区的社会经济水平与全国平均水平有无显著差异。
168.17
湖南
20.25
104.45
20.72
38.15
62.98
12.67
39.16
213.56
广东
23.68
173.30
17.43
43.59
53.66
16.86
65.02
385.94
广西
18.70
131.35

Pythonsklearn库实现PCA教程（以鸢尾花分类为例）

Pythonsklearn库实现PCA教程（以鸢尾花分类为例）PCA简介主成分分析（Principal Component Analysis，PCA）是最常⽤的⼀种降维⽅法，通常⽤于⾼维数据集的探索与可视化，还可以⽤作数据压缩和预处理等。

矩阵的主成分就是其协⽅差矩阵对应的特征向量，按照对应的特征值⼤⼩进⾏排序，最⼤的特征值就是第⼀主成分，其次是第⼆主成分，以此类推。

基本步骤：具体实现我们通过Python的sklearn库来实现鸢尾花数据进⾏降维，数据本⾝是4维的降维后变成2维，可以在平⾯中画出样本点的分布。

样本数据结构如下图：其中样本总数为150，鸢尾花的类别有三种，分别标记为0，1，2代码import matplotlib.pyplot as plt #加载matplotlib⽤于数据的可视化from sklearn.decomposition import PCA #加载PCA算法包from sklearn.datasets import load_irisdata=load_iris()y=data.targetx=data.datapca=PCA(n_components=2) #加载PCA算法，设置降维后主成分数⽬为2reduced_x=pca.fit_transform(x)#对样本进⾏降维red_x,red_y=[],[]blue_x,blue_y=[],[]green_x,green_y=[],[]for i in range(len(reduced_x)):if y[i] ==0:red_x.append(reduced_x[i][0])red_y.append(reduced_x[i][1])elif y[i]==1:blue_x.append(reduced_x[i][0])blue_y.append(reduced_x[i][1])else:green_x.append(reduced_x[i][0])green_y.append(reduced_x[i][1])#可视化plt.scatter(red_x,red_y,c='r',marker='x')plt.scatter(blue_x,blue_y,c='b',marker='D')plt.scatter(green_x,green_y,c='g',marker='.')plt.show()结果图知识拓展：python sklearn PCA 实例代码-主成分分析python sklearn decomposition PCA 主成分分析主成分分析（PCA）1、主成分分析（Principal Component Analysis,PCA）是最常⽤的⼀种降维⽅法，通常⽤于⾼维数据集的探索与可视化，还可以⽤作数据压缩和预处理2、PCA可以把具有相关性的⾼维变量合成为线性⽆关的低维变量，称为主成分。