上宝中学(初三)(精编文档).doc

合集下载

上海市上宝中学物理电流和电路章末训练(Word版含解析)

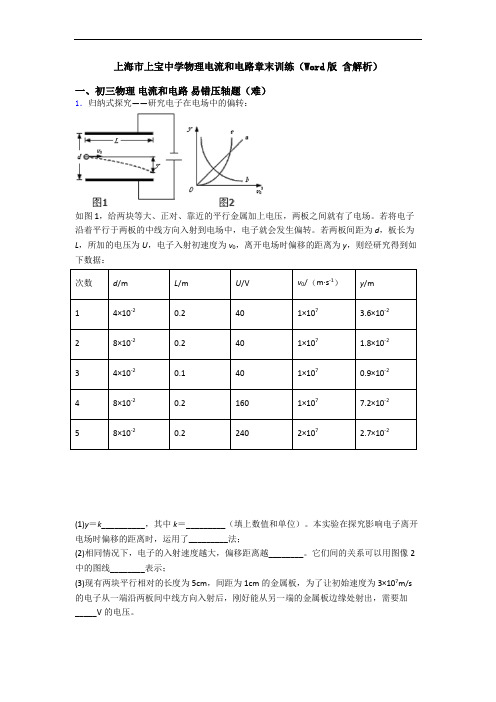
上海市上宝中学物理电流和电路章末训练（Word版含解析）一、初三物理电流和电路易错压轴题（难）1．归纳式探究——研究电子在电场中的偏转：如图1，给两块等大、正对、靠近的平行金属加上电压，两板之间就有了电场。

若将电子沿着平行于两板的中线方向入射到电场中，电子就会发生偏转。

若两板间距为d，板长为L，所加的电压为U，电子入射初速度为v0，离开电场时偏移的距离为y，则经研究得到如下数据：次数d/m L/m U/V v0/（m·s-1）y/m14×10-20.2401×107 3.6×10-228×10-20.2401×107 1.8×10-234×10-20.1401×1070.9×10-248×10-20.21601×1077.2×10-258×10-20.22402×107 2.7×10-2(1)y＝k__________，其中k＝_________（填上数值和单位）。

本实验在探究影响电子离开电场时偏移的距离时，运用了_________法；(2)相同情况下，电子的入射速度越大，偏移距离越________。

它们间的关系可以用图像2中的图线________表示；(3)现有两块平行相对的长度为5cm，间距为1cm的金属板，为了让初始速度为3×107m/s 的电子从一端沿两板间中线方向入射后，刚好能从另一端的金属板边缘处射出，需要加_____V的电压。

【答案】220UL dv ()1022910m /V s ⨯⋅ 控制变量小 b 200【解析】【分析】【详解】(1)[1]分析表中数据可知，1与2相比L 、U 、0v 均相同，而d 增大一倍，y 减小为原来的12，可知y 与d 成反比；同理，1与3相比，y 与2L 成正比；2与4相比，y 与U 成正比；将第2次实验电压U 增大至6倍，则y 增大至6倍，此时240V U =210.810m y -=⨯将此时的数据与第5次实验相比，y 与20v 成反比，综上所述可得220UL y k dv =[2]将表格中第3次数据（其他组数据也可）代入220UL y k dv =计算可得 ()1022910m /V s k =⨯⋅[3]本实验在探究影响电子离开电场时偏移的距离时，运用了控制变量法。

上海市上宝中学物理电压电阻章末训练(Word版含解析)

上海市上宝中学物理电压电阻章末训练（Word版含解析）一、初三物理电压电阻易错压轴题（难）1．小明手边有6节同种型号的新锂电池（电池电压相同）和一个电流表，他想知道把这些电池串联起来接入长度为480m、横截面积为64mm2的电阻丝A时通过的电流是多少，他想到：通过电阻丝的电流大小与电池节数、电阻丝的长度、横截面积、材料都有关系。

于是他就对由同种材料组成的不同规格的电阻丝样品进行了测试，实验数据如下：(1)分析数据可知，电阻丝中通过电流大小与电阻丝的长度成______，与电阻丝的横截面积成______。

（填“正比”或“反比”）(2)经过对样品数据的分析，得出把电阻丝A接入6节该锂电池做为电源的电路中时通过的电流为______A。

【答案】反比正比 1.6【解析】【分析】【详解】(1)[1]由第一组和第四组的实验数据可知，电源电压相同，横截面积相同，长度变为原来的四倍，电流变为原来的四分之一，说明电电阻大了四倍，由此可得：在电压相同，材料和横截面积也相同时，电阻丝中通过电流大小与电阻丝的长度成反比。

[2]由第五组和第二组的实验数据可知，电源电压相同，长度相同，横截面积变为原来的四倍，电流也变为原来的四倍，说明电阻小为了原来的四分之一，由此可得：在电压相同，材料和长度也相同时，电阻丝中通过电流大小与电阻丝的横截面积成正比。

(2)[3]由第三组和第四组的实验数据可知，电源电压不相同，电阻丝的材料、长度和横截面积相同，电源电压大为原来的二倍，电流也变为原来的二倍，由此可得：在材料、长度和横截面积相同时，电阻丝中通过电流大小与电源电压成正比。

A的横载面积为64mm2，为第一组横截面积的40倍，A的长度为480m，为第一组长度的120倍，则电阻为第一组的3倍，电阻丝A两端的电池节数是6节，为第一组电池节数的3倍，即电压变为原来的3倍，则电流为1.6A×13×3=1.6A2．在“探究串联电路电压的特点”活动中：(1)如图所示，连接电路时，至少需要______根导线；实验中应选择规格______（相同/不同）的小灯泡；(2)在测L1两端电压时，闭合开关，发现电压表示数为零，原因可能是________________（填出一种即可）；(3)小芳保持电压表的B连接点不动，只断开A连接点，并改接到C连接点上，测量L2两端电压。

上海上宝中学九上第一次月考化学试卷(Word版)

2019 学年上宝中学第一学期初三化学九月考试卷20190928 相对原子质量：H-1 O-18 C-12 P-31 Fe-56一、选择题1. 2019 年10 月，因发现抗疟疾药青蒿素而获诺贝尔自然科学类的中国本土科学家是（）A.莫言B.杨振宁C.屠呦呦D.林巧稚2. 物质的变化是多种多样的，其中属于化学变化的是（）A. 抹在墙上的石灰浆逐渐变硬B. 用活性炭消除冰箱中的异味C. 用玻璃刀切割玻璃D. 由空气制氧气3. 氧元素由化合态转化为游离态的变化是（）A. 2C H + 5O −点−燃−→ 2H O+4COB. H CO −∆−→H O+CO ↑C. 4P+5O −点−燃−→ 2P OD. 2H O −通−电−→ 2H ↑+O ↑4. 以下化学符号里的“3”，表示分子个数的是（）A. 3HB. NH3C. 3H2D. O35. 下列实验操作中正确的是（）6. 下列说法正确的是（）A. 4mol H2 中含8mol 氢B. 1mol 磷酸(H3 PO4 )的质量为98 克/摩尔C. 0.5mol H2O2 中含有1mol O2D. 等质量的O2 和O3 中所含氧原子的物质的量相同7. 在空气中易变质，且变质过程与氧气没有关系的物质是（）A. 铁B. 生石灰C. 白磷D. 木炭8. 下列对实验现象的描述，正确的是（）A. 铁丝在空气中剧烈燃烧，火星四射，生成黑色固体B. 向滴有酚酞试液的氢氧化钠溶液中滴加过量的盐酸，试液由红色变为无色C. 硫在氧气中燃烧产生微弱的淡蓝色火焰，并生成刺激性气味的气体D. 红磷在氧气中燃烧产生大量浓厚的白色烟雾9. 溶解适量的固体碘制成消毒液，应该使用（）A. 蒸馏水B. 酒精C. 汽油D. 生理盐水）A. 玫瑰花汁B. 万寿菊花汁C. 大红花汁D. 万年青花汁11. 下列各组物质加入水中，充分混合后，能得到溶液的是（）A. 氧化铁B. 汽油C. 硫酸铜D. 花生油12. 影响固体物质在溶剂中溶解度大小的因素是（）①溶质的性质②温度③压强④溶质的质量⑤溶剂的质量⑥溶剂的性质A. ①②⑥B. ①③⑤C. ①④⑤D. ②④⑥13. 给下列溶液蒸发时，溶液溶质的质量分数可能降低的是（）A. 食盐溶液B. 盐酸C.稀硫酸D.硝酸钾溶液14. 某溶液200g，蒸发20g 水后，析出8g 晶体；又蒸发20g 水后析出晶体12g，则该温度下，某物质的溶解度是（）A. 40g/100g 水B. 50g/100g 水C. 60g/100g 水D. 100g/100g 水15. 要使氢氧化钙不饱和溶液转化为饱和溶液，可采取的方法为（）①升温②降温③加水④加生石灰⑤加熟石灰⑥蒸发溶剂A. ②⑤⑥B. ①④⑤⑥C. ①⑤⑥D. ②④⑤⑥16. 下列有关溶液的认识中，不正确的是（）A. 析出晶体后的溶液是该温度下的饱和溶液B. 溶液中的化学反应通常较快C. 同种溶质的饱和溶液一定比它的不饱和溶液浓度大D. 食物里的营养成分经消化变成溶液，易被人体吸收17. 实验室用氯化钠配制 50.0g 溶质的质量分数为 10%的氯化钠溶液，下列说法错误的是（） A. 用天平称取 5.0g 氯化钠 B. 用量程为 10ml 的量筒量取所需的水C. 溶解氯化钠时，使用的玻璃仪器有烧杯、玻璃棒D. 将配制好的溶液装入细口瓶中，塞好瓶塞并贴上标签 18. 浓度为 10%的氢氧化钠溶液 100g ，如果浓度要增加一倍，应采用（） A. 将溶液蒸发掉一半 B. 加入 100g10%的氢氧化钠溶液 C. 增加 10g 氢氧化钠固体 D. 溶剂蒸发掉 45g 19. 现有 20℃时 200g 硝酸钾饱和溶液，以下操作中，溶质与溶剂的质量比发生变化（） A. 温度不变蒸发掉 20g 水 B. 温度不变加入 10g 硝酸钾 C. 温度不变加入 20g 水 D. 升温到 40℃ 20. 将 wg KNO 3 的不饱和溶液恒温蒸发水分，直到有晶体析出。

上宝中学初三上初中试卷范例

Part 3 Reading and writing(第三部分读写)VI. Reading comprehension(阅读理解)（共50分）A.Choose the best answer(根据短文内容，选择最恰当的答案)（12分）Do you want to live with a strong sense of peacefulness, happiness, goodness, and self-respect? The collection of happiness actions broadly categorized as “honor” help you create this life of good feelings.Here’s an example to show how honorable actions create happiness.Say a store clerk fails to charge us for an item. If we keep silent and profit from the clerk’s mistake, we wou ld drive home with a senseof sneaky excitement. Later we might tell our family or friends aboutout good fortune. On the other hand, if we tell the clerk about the uncharged item, the clerk would be grateful and thank us for our honesty. We would leave the store with a quiet sense of honor that we might never share with another soul.Then, what is it to do with our sense of happiness?In the first case, where we don’t tell the clerk, a couple ofthings would happen. Deep down inside we would know ourselves as a typeof thief. In the process, we would lose some peace of mind and self-respect. We would also demonstrate that we cannot be trusted, since we advertise we advertise our dishonor by telling our family and friends.We damage our own reputations by telling others. In contrast, bringing error to the clerk’s attention causes different things to happen. Immediately the clerk knows us to be honorable. Upon leaving the store,we feel honorable and our self-respect is increased. Whenever we take honorable action we gain the deep internal rewards of goodness and a sense of nobility.There is a beautiful positive cycle that is created by living alife of honorable actions. Honorable thoughts lead to honorable actions. Honorable actions lead us to a happier e xistence. And it’s easy tothink and act honorably again when we’re happy. While the positivecycle can be difficult to start, one it’s easy to continue. Keeping on doing good deeds brings us peace of mind, which is important to our happiness.1.According to the passage, the positive action in the example contributes to our ________ .A. self-respectB. sneaky excitementC. financial rewardsD. friendly relationship2.The author thinks that keeping silent about the uncharged item is equal to ________ .A. lyingB. stealingC. cheatingD. advertising3.What dose the underlined word “sneaky” mean in paragraph 3?A. secretB. unnoticeableC.silent D. public4.The phrase “bringing the error to the clerk’s attention” (in Para.5) means ________ .A. telling the truth to the clerkB. offering advice to the clerkC. blaming the clerk for the errorD. reminding the clerk of the charged item5. How will we feel if we let the clerk know the mistake?A. We’ll be very excitedB. We’ll feel unfortunateC. We’ll have a sense of honorD. We’ll feel sorry for the clerk6. What is the article mainly about?A. How to live truthfully.B. Importance of peacefulness.C. Ways of gaining self-respect.D. Happiness through honorable actions.【答案】1-6 ABAACD【分析】1.细节题。

上海民办上宝中学中考物理试题含答案

上海民办上宝中学中考物理试题含答案一、选择题1．中国空军中个头最大，被称为“胖妞”的Y-20运输机，其起飞质量能达220t，航程大于7800km，曾在2020年2月13日驰援武汉，运送了大量医疗物资，如图所示。

关于该运输机下列说法中正确的是（）A．起飞时，飞行员相对于机舱是运动的B．飞行时，机翼上方的空气流速较大，压强较大C．轮胎上的花纹，着地时可以增大与地面的摩擦力D．轮胎较多，停放时可以减小飞机对地面的压力2．为了检测学校周围声音的强弱，某同学利用声敏电阻制作了一个可以检测声音强度的仪器，电路图如图，电源电压保持不变，R1是一个声敏电阻，声敏电阻随着声音强度的增大而减小。

闭合开关S后，当学校周围的声音强度增大时，下列对电表示数变化的分析判断正确的是A．电流表和电压表示数均变小B．电流表和电压表示数均变大C．电流表示数变小，电压表示数变大D．电流表示数变大，电压表示数变小3．如图，在2019年央视春晚上的武术表演《少林魂》中，演员们排列整整齐齐：“行是行，列是列”。

如果同一列的演员，后面的人只能看到前面的人，说明队伍就排列成了一条直线，下列成语中也包含了此原理的是（）A．镜花水月B．鱼翔浅底C．立竿见影D．海市蜃楼4．如图所示，电源电压保持不变，闭合开关S，将滑动变阻器的滑片P向右移动的过程中A．电流表的示数变小B．电压表的示数变大C．电压表的示数不变D．电压表与电流表示数的比值变大5．如图所示，某一型号的锁设置了三种打开方式：密码（S1）、特定指纹（S2）或应急钥匙（S3），三者都可以单独使电动机M工作而打开门锁，下列电路设计符合要求的是A．B．C．D．6．如图，将甲，乙两灯电联在电路中闭合开关，发现甲灯发光，乙灯不发光。

则乙灯不发光的原因可能是A．乙灯灯丝断了B．乙灯的实际功率太小C．乙灯的额定电压太低D．通过乙灯的电流小于甲灯的电流7．在水平桌面上有甲、乙两个完全相同的杯子盛满不同浓度的盐水，将两个完全相同的小球分别放入其中，当小球静止时，两个杯子中小球所处的位置如图所示，则（）A．甲杯中溢出的盐水质量较小B．乙杯底部所受的液体压强较大C．甲杯底部所受的液体压力较大D．小球在乙杯中受到的浮力较大8．如图所示，压在杯底的乒乓球，上浮时会弹离水面后又落回水面。

上海民办上宝中学中考化学试题含答案

上海民办上宝中学中考化学试题含答案一、选择题1．下列物质能在 pH=13 的无色溶液中大量共存的是( )A．HCl、AgNO3、Na2CO3B．NaNO3、KNO3、NH4ClC．K2SO4、K2CO3、NaOH D．KMnO4、CuSO4、NaNO32．除去下列各物质中的少量杂质，所选用的试剂、方法能达到目的的是选项物质杂质(少量)试剂操作方法A N2O2碳粉将混合气体通过灼热的碳粉B NaOH溶液Na2CO3溶液氢氧化钙溶液加入适量氢氧化钙溶液，过滤C氯化钠固体泥沙水加水溶解，蒸发结晶D KC1溶液K2SO4溶液Ba(NO3)2溶液加入适量Ba(NO3)2溶液，过滤A．A B．B C．C D．D3．下列图像能正确反映相关实验过程中量的变化关系的是( )A．氢氧化钠溶液加水稀释B．一定压强下，CO2气体在水中的溶解度与温度的变化关系C．一定温度下，向饱和的氯化钠溶液中加入氯化钠固体D．向生锈的铁钉缓慢滴加稀盐酸4．下列有关物质的鉴别、检验、除杂所用的试剂或方法正确的是（）A．A B．B C．C D．D5．图示的四个图像分别对应四个变化过程的一种趋势，下列分析正确的是A．甲图：可能是双氧水溶液制氧气，a未使用催化剂，b使用了催化剂B．乙图：可能是加热一定质量的氯酸钾和二氧化锰固体混合物制取氧气过程C．丙图：可能是硫酸铜溶液中滴加氢氧化钠溶液D．丁图：可能是向一定量的氢氧化钠溶液中加水稀释，溶液的pH变化6．归纳总结能使知识系统化，有利于提高素质和能力，下面是一同学对部分化学知识的归纳，其中都正确的一项是A．A B．B C．C D．D7．下列四个图像反映了对应实验过程中相关量的变化，其中错误的是A．部分变质的NaOH溶液中滴加稀盐酸B．HCl气体的溶解度受温度影响的变化曲线C．等质量的Mg粉和Fe粉A．A B．B C．C D．D8．下列是四种实验操作中各量变化关系的图像，能正确反映其对应操作的图像有①电解水②向一定量pH=3的盐酸溶液中不断加水稀释③向等质量的镁和锌中分别加入溶质质量分数相同的稀盐酸至过量④向盐酸和氯化铜的混合溶液中不断滴加氢氧化钾溶液A．4个B．3个C．2个D．1个9．除去下列各物质中的少量杂质，所用方法不可行的是（）选项物质杂质除去杂质的方法A Al2(SO4)3溶液H2SO4溶液加入足量Al2O3粉末后过滤B Cu CuO通入氧气并加热C CaO CaCO3高温煅烧D H2气体HCl气体先通过NaOH溶液，再通过浓硫酸A．A B．B C．C D．D10．下列物质的溶液，不另加试剂就不能鉴别出来的一组是A．CuSO4、BaCl2、H2SO4B．Na2CO3、Ca(NO3)2、HClC．Na2SO4、KNO3、HClD．FeCl3、NaOH、 KMnO411．下列实验方案不合理的是（）选项实验目的所用试剂和方法A鉴别浓盐酸和浓硫酸打开瓶塞，观察是否有白雾产生B鉴别氯化钡溶液和硝酸钾溶液分别加入硫酸钠溶液C除去二氧化碳气体中少量的一氧化碳将气体点燃D除去氧化铝粉末中的铝粉在干燥空气中加热A．A B．B C．C D．D12．实验小组将未打磨的铝片和稀盐酸放入密闭容器中，用传感器探究反应过程中温度和压强的变化，结果如下图。

上海市民办上宝中学2024-2025学年九年级上学期期中数学试卷(含解析)

2024-2025学年上海市闵行区上宝中学九年级（上）期中数学试卷一、选择题：（本大题共6题，每题4分，满分24分）1．（4分）如果x：y＝2：3，那么下列各式不成立的是（）A．＝B．＝﹣C．＝D．＝2．（4分）在比例尺为1：2000的地图上测得A、B两地间的图上距离为5cm，则A、B两地间的实际距离为（）A．10m B．25m C．100m D．10000m3．（4分）若两个相似三角形的面积之比为1：4，则它们的最长边的比是（）A．1：2B．1：4C．1：16D．无法确定4．（4分）如图，已知抛物线y＝x2+bx+c的对称轴为直线x＝2，点A，B均在抛物线上，且AB与x轴平行，其中点A的坐标为（0，3），则点B的坐标为（）A．（2，3）B．（3，2）C．（3，3）D．（4，3）5．（4分）如图所示，△ABC的顶点是正方形网格的格点，则sin A的值为（）A．B．C．D．6．（4分）如图，在菱形ABCD中，AB＝AC，点E、F分别为边AB、BC上的点，且AE＝BF，连接CE、AF交于点H，连接DH交AC于点O，则下列结论：①△ABF≌△CAE；②∠FHC＝∠B；③△AEH∽△DAH；④AE•AD＝AH•AF；其中正确的结论个数是（）A．1个B．2个C．3个D．4个二、填空题：（本大题共12题，每题4分，满分48分）7．（4分）cos30°＝．8．（4分）把长度为4cm的线段进行黄金分割，则较长线段的长是 cm．9．（4分）如果两个相似三角形的对应角平分线之比为1：4，那么它们的周长之比是．10．（4分）如果抛物线y＝（m﹣1）x2+2mx+1的图象开口向下，那么m的取值范围是．11．（4分）将二次函数y＝﹣2x2的图象向右平移1个单位，再向下平移2个单位，所得图象的解析式为．12．（4分）二次函数y＝ax2+bx+c中，函数y与自变量x的部分对应值如表，则m的值为．x﹣2﹣101234y72﹣1﹣2m2713．（4分）在Rt△ABC中，∠C＝90°，∠B＝α，AB＝2，那么BC＝．（结果用α的锐角三角函数表示）14．（4分）如图，点D、E、F分别是△ABC三边的中点，那么与相等的向量是．15．（4分）已知在平面直角坐标系xOy中，抛物线与x轴交于点A（﹣4，0）和点B，与y轴交于点C（0，3），抛物线的对称轴与x轴交于点D．点P是直线AC上方抛物线上一点，过点P 作PG⊥x轴，垂足为点G，PG与直线AC交于点H．如果PH＝AH，则点P的坐标是．16．（4分）如图，在▱ABCD中，点F在边AD上，AF＝2FD，直线BF与对角线AC相交于点E，交CD 的延长线于点G，如果BE＝2，那么EG的长是．17．（4分）如图，已知在四边形ABCD中，∠ADC＝90°，AB＝AD，点E、F分别在线段CD、AD上．如果AE⊥BF，，那么cot∠ABD＝．18．（4分）如图，已知在矩形ABCD中，连接AC，，将矩形ABCD绕点C旋转，使点B 恰好落在对角线AC上的点B′处，点A、D分别落在点A′、D′处，边A′B′、A′C分别与边AD 交于点M、N，MN﹣AM＝5，那么线段MN的长为．三、解答题：（本大题共7题，满分78分）19．（10分）计算：．20．（10分）如图，在梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，BC＝2AD，OD＝1．（1）求BD的长：（2）如果，，试用、表示向量．21．（10分）如图所示，BA和CD表示前后两幢楼，按照有感规定两幢楼间的间距不得小于楼的高度，即图中AC大于等于CD，小明想测量一下他家所著AB楼与前面CD楼是否符合规定，于是他在AC间的点M处架了测角仪，测得CD楼顶D的仰角为45°，已知AM＝4米，测角仪距地面MN＝1.5米．（1）问：两楼的间距是否符合规定？并说出你的理由；（2）为了知道前面CD楼的高度，小明又到家里（点P处），用测角仪再次测得CD楼顶D的仰角为α，如果AP＝7.5米，sinα＝0.6，请你来计算一下CD楼的高度．22．（10分）如图，在平面直角坐标系xOy中，抛物线M：y＝﹣x2+bx+c过点A（2，2）、点B（0，2），顶点为点C，抛物线M的对称轴交x轴于点D．（1）直接写出抛物线M的表达式和点C的坐标；（2）点P在x轴上，当△AOP与△ACD相似时，求点P坐标．23．（12分）已知：如图，在梯形ABCD中，AD∥BC，AB⊥BC，点M在边BC上，且∠MDB＝∠ADB，BD2＝AD•BC．（1）求证：BM＝CM；（2）作BE⊥DM，垂足为点E，并交CD于点F．求证：2AD•DM＝DF•DC．24．（12分）已知，如图，抛物线y＝x2+bx+c与x轴正半轴交于A、B两点，与y轴交于点C，直线y ＝x﹣2经过A、C两点．（1）直接写出抛物线的解析式；（2）P为抛物线上一点，若点P关于直线AC的对称点Q落在y轴上，求P点坐标；（3）现将抛物线平移，保持顶点在直线y＝x﹣，若平移后的抛物线与直线y＝x﹣2交于M、N两点．①求：MN的长度；②结合（2）的条件，直接写出△QMN的周长的最小值．25．（14分）如图，已知正方形ABCD，点H是边BC上的一个动点（不与点B、C重合），点E在DH上，满足AE＝AB，延长BE交CD于点F．（1）求：sin∠FED；（2）点M、N分别是边AB、AD的中点，已知点P在线段MN上，连结AP、BP，此时∠APB＝90°，求：cot∠ABP；（3）连结CE．如果△CEF是以CE为腰的等腰三角形，求∠FBC的正切值．2024-2025学年上海市闵行区上宝中学九年级（上）期中数学试卷参考答案与试题解析一、选择题：（本大题共6题，每题4分，满分24分）1．（4分）如果x：y＝2：3，那么下列各式不成立的是（）A．＝B．＝﹣C．＝D．＝【分析】根据比例的基本性质，可分别设出x和y，分别代入各选项进行计算即可得出结果．【解答】解：设x＝2k，y＝3k．通过代入计算，进行约分，A，B，C都正确；D不能实现约分，故错误．故选：D．【点评】此题考查了比例的性质，已知几个量的比值时，常用的解法是：设一个未知数，把题目中的几个量用所设的未知数表示出来，实现约分．2．（4分）在比例尺为1：2000的地图上测得A、B两地间的图上距离为5cm，则A、B两地间的实际距离为（）A．10m B．25m C．100m D．10000m【分析】设A、B两地间的实际距离为xm，根据比例线段得＝，然后解方程即可．【解答】解：设A、B两地间的实际距离为xm，根据题意得＝，解得x＝100．所以A、B两地间的实际距离为100m．故选：C．【点评】本题考查了比例线段：对于四条线段a、b、c、d，如果其中两条线段的比（即它们的长度比）与另两条线段的比相等，如a：b＝c：d（即ad＝bc），我们就说这四条线段是成比例线段，简称比例线段．3．（4分）若两个相似三角形的面积之比为1：4，则它们的最长边的比是（）A．1：2B．1：4C．1：16D．无法确定【分析】根据相似三角形的性质求出答案即可．【解答】解：∵两个相似三角形的面积之比为1：4，∴它们的最长边的比是1：2，故选：A．【点评】本题考查了相似三角形的性质，能熟记相似三角形的面积之比等于相似比的平方是解此题的关键．4．（4分）如图，已知抛物线y＝x2+bx+c的对称轴为直线x＝2，点A，B均在抛物线上，且AB与x轴平行，其中点A的坐标为（0，3），则点B的坐标为（）A．（2，3）B．（3，2）C．（3，3）D．（4，3）【分析】已知抛物线的对称轴为直线x＝2，知道A的坐标为（0，3），由函数的对称性知B点坐标．【解答】解：由题意可知抛物线的y＝x2+bx+c的对称轴为直线x＝2，∵点A的坐标为（0，3），且AB与x轴平行，可知A、B两点为对称点，∴B点坐标为（4，3）故选：D．【点评】本题主要考查二次函数的对称性．5．（4分）如图所示，△ABC的顶点是正方形网格的格点，则sin A的值为（）A．B．C．D．【分析】直接连接DC，得出CD⊥AB，再结合勾股定理以及锐角三角函数关系得出答案【解答】解：连接DC，由网格可得：CD⊥AB，则DC＝，AC＝，故sin A＝．故选：D．【点评】此题主要考查了锐角三角函数关系，正确构造直角三角形是解题关键．6．（4分）如图，在菱形ABCD中，AB＝AC，点E、F分别为边AB、BC上的点，且AE＝BF，连接CE、AF交于点H，连接DH交AC于点O，则下列结论：①△ABF≌△CAE；②∠FHC＝∠B；③△AEH∽△DAH；④AE•AD＝AH•AF；其中正确的结论个数是（）A．1个B．2个C．3个D．4个【分析】由菱形ABCD中，AB＝AC，易证得△ABC是等边三角形，则可得∠B＝∠EAC＝60°，由SAS 即可证得△ABF≌△CAE，可得∠BAF＝∠ACE，EC＝AF，由外角性质可得∠FHC＝∠B，可判断①②，由点A，H，C，D四点共圆，可得∠AHD＝∠ACD＝60°，∠ACH＝∠ADH＝∠BAF，可证△AEH∽△DAH，可判断③，通过证明△AEH∽△CEA，可得，可得AE•AD＝AH•AF，可判断④，即可求解．【解答】解：∵四边形ABCD是菱形，∴AB＝BC，∵AB＝AC，∴AB＝BC＝AC，即△ABC是等边三角形，同理：△ADC是等边三角形∴∠B＝∠EAC＝60°，在△ABF和△CAE中，，∴△ABF≌△CAE（SAS）；∴∠BAF＝∠ACE，EC＝AF，∵∠FHC＝∠ACE+∠FAC＝∠BAF+∠FAC＝∠BAC＝60°，∴∠FHC＝∠B，故①正确，②正确；∵∠AHC+∠ADC＝120°+60°＝180°，∴点A，H，C，D四点共圆，∴∠AHD＝∠ACD＝60°，∠ACH＝∠ADH＝∠BAF，∴∠AHD＝∠FHC＝∠AHE＝60°，∴△AEH∽△DAH，故③正确；∵∠ACE＝∠BAF，∠AEH＝∠AEC，∴△AEH∽△CEA，∴，∴AE•AC＝AH•EC，∴AE•AD＝AH•AF，故④正确；故选：D．【点评】本题考查了相似三角形的判定与性质，菱形的性质，等边三角形的判定与性质以及全等三角形的判定与性质．此题难度较大，注意数形结合思想的应用．二、填空题：（本大题共12题，每题4分，满分48分）7．（4分）cos30°＝．【分析】根据特殊角的三角函数值即可求解．【解答】解：cos30°＝．故答案为：．【点评】考查了特殊角的三角函数值，是基础题目，比较简单．8．（4分）把长度为4cm的线段进行黄金分割，则较长线段的长是　（2﹣2）　cm．【分析】根据黄金分割的定义得到较长线段的长＝×4，然后进行二次根式的运算即可．【解答】解：较长线段的长＝×4＝（2﹣2）cm．故答案为．【点评】本题考查了黄金分割：把线段AB分成两条线段AC和BC（AC＞BC），且使AC是AB和BC 的比例中项（即AB：AC＝AC：BC），叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点，其中AC＝AB≈0.618AB，并且线段AB的黄金分割点有两个．9．（4分）如果两个相似三角形的对应角平分线之比为1：4，那么它们的周长之比是　1：4　．【分析】直接根据相似三角形的性质进行解答．【解答】解：∵两个相似三角形的对应角平分线之比为1：4，∴那么它们的周长之比是1：4．故答案为：1：4．【点评】本题考查的是相似三角形的性质，即相似三角形对应边的比、对应角平分线的比、周长的比等于相似比．10．（4分）如果抛物线y＝（m﹣1）x2+2mx+1的图象开口向下，那么m的取值范围是　m＜1　．【分析】根据二次函数的性质可知，当抛物线开口向下时，二次项系数m﹣1＜0，然后解一元一次不等式即可求出m的取值范围．【解答】解：∵抛物线y＝（m﹣1）x2+2mx+1的图象开口向下，∴m﹣1＜0，解得：m＜1．故答案为：m＜1．【点评】本题主要考查了二次函数的图象与性质，明确二次函数图象的开口方法有二次项系数决定是解题的基础．11．（4分）将二次函数y＝﹣2x2的图象向右平移1个单位，再向下平移2个单位，所得图象的解析式为　y＝﹣2（x﹣1）2﹣2　．【分析】根据“左加右减，上加下减”的法则即可得出结论．【解答】解：二次函数y＝﹣2x2的图象向右平移1个单位，再向下平移2单位后，所得二次函数的解析式为y＝﹣2（x﹣1）2﹣2．故答案为：y＝﹣2（x﹣1）2﹣2．【点评】本题考查的是二次函数的图象与几何变换，熟知“上加下减，左加右减”的法则是解答此题的关键．12．（4分）二次函数y＝ax2+bx+c中，函数y与自变量x的部分对应值如表，则m的值为　﹣1　．x﹣2﹣101234y72﹣1﹣2m27【分析】利用待定系数法求出二次函数的解析式，即可求解．【解答】解：把点（﹣2，7）（﹣1，2），（0，﹣1）代入y＝bx+c，得：，解得：，∴二次函数的解析式为y＝x2﹣2x﹣1，当x＝2时，y＝m＝22﹣2×2﹣1＝﹣1．故答案为：﹣1．【点评】本题主要考查了求二次函数的性质，二次函数图象上点的坐标特征，熟练掌握用待定系数法求出二次函数的解析式的方法是解题的关键．13．（4分）在Rt△ABC中，∠C＝90°，∠B＝α，AB＝2，那么BC＝　2cosα　．（结果用α的锐角三角函数表示）【分析】根据余弦的定义可得BC＝AB•cos B＝2cosα．【解答】解：在Rt△ABC中，∠C＝90°，∠B＝α，AB＝2，∵cos B＝，∴BC＝AB•cos B＝2cosα．故答案为：2cosα．【点评】本题主要考查了锐角三角函数的定义，熟练掌握锐角三角函数的定义是关键．14．（4分）如图，点D、E、F分别是△ABC三边的中点，那么与相等的向量是　和　．【分析】由点D、E、F分别是△ABC三边的中点，根据三角形中位线的性质，即可得DF∥AC，DF＝CE＝EA＝CA，从而可得与相等的向量．【解答】解：∵D、F分别是BC、BA的中点，∴DF是△ABC的中位线，∴DF∥AC，DF＝CE＝EA＝CA，故与相等的向量是和．故答案为：和．【点评】本题考查了向量及三角形的中位线定理，属于基础题，解答本题的关键是熟练掌握三角形中位线的性质及向量相等的含义．15．（4分）已知在平面直角坐标系xOy中，抛物线与x轴交于点A（﹣4，0）和点B，与y轴交于点C（0，3），抛物线的对称轴与x轴交于点D．点P是直线AC上方抛物线上一点，过点P 作PG⊥x轴，垂足为点G，PG与直线AC交于点H．如果PH＝AH，则点P的坐标是．【分析】用待定系数法可得，由A（﹣4，0），C（0，3）可得直线AC解析式为，，设，可得，由△AHG∽△ACO，可得，故，即可解得P点坐标．【解答】解：把A（﹣4，0），C（0，3）代入得：，解得，∴；如图：设直线AC解析式为y＝px+q，由A（﹣4，0），C（0，3）可得：，解得，∴直线AC解析式为，，设，则，∴，，∵∠HAG＝∠CAO，∠AGH＝90°＝∠AOC，∴△AHG∽△ACO，∴，即，∴，∵PH＝AH，∴，解得或m＝﹣4（与A重合，舍去），∴，故答案为：．【点评】本题考查抛物线与x轴的交点，一次函数图象上点的坐标特征，二次函数的综合应用，涉及待定系数法，相似三角形的判定与性质，解题的关键是掌握相似三角形的判定定理．16．（4分）如图，在▱ABCD中，点F在边AD上，AF＝2FD，直线BF与对角线AC相交于点E，交CD 的延长线于点G，如果BE＝2，那么EG的长是　3　．【分析】由平行四边形的性质得AD∥BC，AD＝BC，再证△AEF∽△CEB，求出EF的长，然后证△GFD ∽△GBC，求出GF的长，即可解决问题．【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∵AF＝2FD，∴AF＝AD＝BC，DF＝AD＝BC，∵AD∥BC，∴△AEF∽△CEB，∴＝＝，∴EF＝EB＝×2＝，∵AD∥BC，∴△GFD∽△GBC，∴＝＝，即＝，解得：GF＝，∴EG＝EF+GF＝+＝3，故答案为：3．【点评】本题考查了相似三角形的判定与性质以及平行四边形的性质，熟练掌握平行四边形的性质和相似三角形的性质，求出EF和GF的长是解题的关键．17．（4分）如图，已知在四边形ABCD中，∠ADC＝90°，AB＝AD，点E、F分别在线段CD、AD上．如果AE⊥BF，，那么cot∠ABD＝．【分析】过B作BG⊥AD于G，交AE于点H，证明△BGF∽△ADE，即可得，设BG＝2t，则AB＝AD＝3t，由勾股定理可得，最后求出cot∠ABD的值即可．【解答】解：如图，过B作BG⊥AD于G，交AE于点H，∵BG⊥AD，AE⊥BF，∴∠BOA＝∠BGA＝90°，∵∠BHO＝∠AHG，∴∠GBF＝∠DAE，又∵∠BGF＝∠ADE．∴△BGF∽△ADE．∴，设BG＝2t，则AB＝AD＝3t，∴，∴，∵AB＝AD，∴∠ABD＝∠ADB，∴．故答案为：．【点评】本题考查等腰三角形的性质，相似三角形的判定与性质，解直角三角形，勾股定理，解题的关键是作辅助线，构造相似三角形解决问题．18．（4分）如图，已知在矩形ABCD中，连接AC，，将矩形ABCD绕点C旋转，使点B 恰好落在对角线AC上的点B′处，点A、D分别落在点A′、D′处，边A′B′、A′C分别与边AD 交于点M、N，MN﹣AM＝5，那么线段MN的长为　15　．【分析】连接BD，作A′E⊥AD于E，设AB＝CD＝3x，AD＝BC＝4x，则AC＝5x，由旋转的性质可得：B′C＝BC＝4x，A′B′＝AB＝3x，∠A′B′C＝∠ABC＝90°，证明△B′AM∽△DAC，得出，由勾股定理得出，推出，证明△AMB′∽△A′ME，求出，，得到，证明△A′EN∽△CDN，得出，求出，结合MN﹣AM ＝5得到关于x的方程，求出x的值即可得解．【解答】解：如图，连接BD，作A′E⊥AD于E，∵四边形ABCD为矩形，∴∠BAD＝∠ADC＝∠ABC＝90°，AB＝CD，AD＝BC，∵，∴设AB＝3x，AD＝4x，∴AB＝CD＝3x，AD＝BC＝4x，∴，由旋转的性质可得：B′C＝BC＝4x，A′B′＝AB＝3x，∠A′B′C＝∠ABC＝90°，∴AB′＝AC﹣B′C＝x，∠AB′M＝180°﹣∠A′B′C＝90°，∵∠B′AM＝∠DAC，∴△B′AM∽△DAC，∴，∴，∴，∴，∵A′E⊥AD，∴∠A′EM＝∠AB′M＝90°，∵∠AMB′＝∠A′ME，∴△AMB′∽△A′ME，∴，∴，，∴，∵∠A′EN＝∠CDN＝90°，∠A′NE＝∠CND，∴△A′EN∽△CDN，∴，∴，∴，∵MN﹣AM＝5，∴，∴x＝8，∴，故答案为：15．【点评】本题考查了旋转的性质，矩形的性质、解直角三角形，熟练掌握以上知识点并灵活运用是解此题的关键．三、解答题：（本大题共7题，满分78分）19．（10分）计算：．【分析】先将各个特殊角度的锐角三角函数值化简，再进行计算即可．【解答】解：原式＝＝＝＝0．【点评】本题考查了实数的运算，零指数幂，特殊角的三角函数值，掌握相应的运算法则是关键．20．（10分）如图，在梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，BC＝2AD，OD＝1．（1）求BD的长：（2）如果，，试用、表示向量．【分析】（1）由题意可得△AOD∽△COB，则，即可得OB＝2，根据BD＝OB+OD 可得答案．（2）由题意得，＝，则＝，由（1）知，OB＝，进而可得答案．【解答】解：（1）∵AD∥BC，∴∠DAO＝∠BCO，∠ADO＝∠CBO，∴△AOD∽△COB，∴，∵OD＝1，∴OB＝2，∴BD＝OB+OD＝3．（2）∵，BC＝2AD，∴＝，∴＝，由（1）知，OB＝，∴＝＝．【点评】本题考查平面向量、相似三角形的判定与性质，熟练掌握三角形法则、相似三角形的判定与性质是解答本题的关键．21．（10分）如图所示，BA和CD表示前后两幢楼，按照有感规定两幢楼间的间距不得小于楼的高度，即图中AC大于等于CD，小明想测量一下他家所著AB楼与前面CD楼是否符合规定，于是他在AC间的点M处架了测角仪，测得CD楼顶D的仰角为45°，已知AM＝4米，测角仪距地面MN＝1.5米．（1）问：两楼的间距是否符合规定？并说出你的理由；（2）为了知道前面CD楼的高度，小明又到家里（点P处），用测角仪再次测得CD楼顶D的仰角为α，如果AP＝7.5米，sinα＝0.6，请你来计算一下CD楼的高度．【分析】（1）过点N作NG⊥DC于点G，在Rt△DNG中，由∠DNG＝45°得到NG＝DG，比较AM+NG 与DG+GC即可；（2）延长DP，GN交于H，由sinα＝0.6，可得tanα＝，由正切函数可求得HJ，设NG＝DG＝x，则HG＝8+4+x＝12+x，tanα＝，列方程可求得结论．【解答】解：（1）过点N作NG⊥DC于点G，在Rt△DNG中，∵∠DNG＝45°∴NG＝DG，∵AC＝AM+NG，DC＝DG+GC，AM＝4m，MN＝1.5m，AC＞DC，∴两楼的间距符合规定；（2）延长DP，GN交于H，则∠H＝α，PJ＝AP﹣MN＝7.5m﹣1.5m＝6m，∵sinα＝0.6，∴tanα＝，∴HJ＝＝8m，设NG＝DG＝x，则HG＝8+4+x＝12+x，∵tanα＝，∴＝，解得+x＝36，即DG＝36m，∴DC＝DG+GC＝36+1.5＝37.5（米），∴CD楼的高度为37.5米．【点评】本题考查了解直角三角形的应用，题目中涉及到了仰俯角和坡度角的问题，解答本题的关键是根据仰角构造直角三角形，利用三角函数的知识求解．22．（10分）如图，在平面直角坐标系xOy中，抛物线M：y＝﹣x2+bx+c过点A（2，2）、点B（0，2），顶点为点C，抛物线M的对称轴交x轴于点D．（1）直接写出抛物线M的表达式和点C的坐标；（2）点P在x轴上，当△AOP与△ACD相似时，求点P坐标．【分析】（1）由待定系数法即可求解；（2）当△OAP∽△CAD时，则，即，即可求解；当△OAP∽△CDA时，同理可解．【解答】解：（1）由题意得：，解得：，∴抛物线的表达式为y＝﹣x2+2x+2，∵y＝﹣x2+2x+2＝﹣（x﹣1）2+3，∴顶点C（1，3）；（2）由（1）知，y＝﹣x2+2x+2＝﹣（x﹣1）2+3，又∵抛物线M的对称轴交x轴于点D，如图，∴点D（1，0），∵A（2，2）、B（0，2），C（1，3），D（1，0），∴，CD＝3，，，∠AOD＝∠DCA＝45°，又∵△AOP与△ACD相似，∴点O与点C对应，分两种情况讨论：当△OAP∽△CAD时，则，即，解得：OP＝6，即点P（6，0）；当△OAP∽△CDA时，则，即，解得：，则点，综上，点P的坐标为或（6，0）．【点评】本题考查的是二次函数综合运用，涉及到待定系数法求二次函数解析式，二次函数图象性质，相似三角形的判定性质等知识，熟练运用分类讨论的思想解决问题是解题的关键．23．（12分）已知：如图，在梯形ABCD中，AD∥BC，AB⊥BC，点M在边BC上，且∠MDB＝∠ADB，BD2＝AD•BC．（1）求证：BM＝CM；（2）作BE⊥DM，垂足为点E，并交CD于点F．求证：2AD•DM＝DF•DC．【分析】（1）首先证明BM＝DM，再根据已知条件证明△ADB∽△DBC，由相似的性质可得∠BDC＝∠A＝90°，进而证明DM＝CM，所以BM＝CM；（2）由（1）可知M是BC的中点，所以DM是三角形BDC斜边上的中线，由直角三角形的性质可知BC＝2DM，证明Rt△DFB∽Rt△DBC可得，所以BD2＝DF•DC，又因为BD2＝AD•BC，所以BD2＝AD•BC＝AD•（2DM）＝2AD•DM．【解答】证明：（1）∵AD∥BC，AB⊥BC，∠MDB＝∠ADB，∴∠ADB＝∠DBC＝∠MDB，∠A＝90°，∴BM＝DM，又∵BD2＝AD•BC，即，∴△ADB∽△DBC，∴∠BDC＝∠A＝90°，∴∠C＝∠MDC＝90°﹣∠DBC，∴DM＝CM，∴BM＝CM，（2）∵∠MDC+∠DFB＝90°，∴∠DFB＝∠DBC，∴Rt△DFB∽Rt△DBC，∴，∴DF•DC＝BD2∵BD2＝AD•BC＝AD•（2DM）＝2AD•DM，∴2AD•DM＝DF•DC．【点评】本题考查了梯形的性质、直角三角形的性质、相似三角形的判定和性质以及比例式的证明，题目的综合性很强，难度不小．24．（12分）已知，如图，抛物线y＝x2+bx+c与x轴正半轴交于A、B两点，与y轴交于点C，直线y ＝x﹣2经过A、C两点．（1）直接写出抛物线的解析式；（2）P为抛物线上一点，若点P关于直线AC的对称点Q落在y轴上，求P点坐标；（3）现将抛物线平移，保持顶点在直线y＝x﹣，若平移后的抛物线与直线y＝x﹣2交于M、N两点．①求：MN的长度；②结合（2）的条件，直接写出△QMN的周长的最小值　4+2　．【分析】（1）求出A，C点的坐标，再将点坐标代入y＝x2+bx+c，即可得解；（2）先求出∠OCA＝45°，再由对称性可知PC⊥y轴，即可求出点P的纵坐标，最后利用二次函数的解析式求出结果；（3）①先求出平移后的抛物线，再利用（x﹣m）2+m﹣＝x﹣2，得出x1+x2＝2m﹣4，x1•x2＝m2﹣4m+3，最后利用两点间的距离公式求解即可；②作KQ⊥MN，连接MK，MP，先求出KM+MP的最小值，即KP的长，最后根据△QMN的周长的最小值，即KQ+KP，得解．【解答】解：（1）在y＝x﹣2中，令y＝0，得x＝2，令x＝0，得y＝﹣2，∴A（2，0），C（0，﹣2）；抛物线y＝x2+bx+c与x轴正半轴交于A、B两点，与y轴交于点C，将A，C点坐标代入得：，解得，∴抛物线的解析式为：y＝x2+x﹣2；（2）如图，∵OA＝OC＝2，∴∠OCA＝45°，∵点P关于AC的对称点Q在y轴上，∴∠OCA＝∠PCA＝45°，∴PC⊥y轴，∴点P的纵坐标为﹣2，令x2+x﹣2＝﹣2，解得x＝6或x＝0（舍去），∴P（6，﹣2）；（3）①设平移后的抛物线的顶点为（m，m﹣），∴平移后的抛物线的解析式为：y＝（x﹣m）2+m﹣，令（x﹣m）2+m﹣＝x﹣2，整理得x2+（4﹣2m）x+m2﹣4m+3＝0，设M（x1，y1），N（x2，y2），∴x1+x2＝2m﹣4，x1•x2＝m2﹣4m+3，∴MN＝＝＝＝2，∴MN的长度为2；②如图，作KQ∥MN，并令KQ＝MN，连接MK，MP，由题可知，P（6，﹣2），Q（0，4），KQ＝MN ＝2，则只需要求QM+QN的最小值即可．∵KQ∥MN，KQ＝MN，∴KM＝QN即KM+MP的最小值，即KP的长，∴K（﹣2，2），∴KP＝4，∴△QMN的周长的最小值为4+2．故答案为：4+2．【点评】本题属于二次函数综合题，主要考查了二次函数的图象与性质，抛物线的平移，待定系数法求函数解析式，掌握二次函数的图象及性质，轴对称的性质，正确作出图形是解题关键．25．（14分）如图，已知正方形ABCD，点H是边BC上的一个动点（不与点B、C重合），点E在DH上，满足AE＝AB，延长BE交CD于点F．（1）求：sin∠FED；（2）点M、N分别是边AB、AD的中点，已知点P在线段MN上，连结AP、BP，此时∠APB＝90°，求：cot∠ABP；（3）连结CE．如果△CEF是以CE为腰的等腰三角形，求∠FBC的正切值．【分析】（1）由正方形的性质得AB＝AD，∠BAD＝90°，则AE＝AD＝AB，所以∠AEB＝∠ABE，∠AED＝∠ADE，则2∠AEB+2∠ADE+90°＝360°，所以∠AEB+∠ADE＝135°，进而得到∠FED＝45°，即可得到sin∠FED的值；（2）连接AC交MN于点O，作ME⊥AP，MF⊥BP，设正方形ABCD的边长为2，根据题意可得到，△MAN为等腰直角三角形，所以AM＝AN＝1，由直角三角形中线的性质可得AM＝MP＝BM＝1，在Rt△AOM中，由勾股定理得：，可求出，在Rt△AOP中，由勾股定理求出，进而得到，在Rt△AEM中，由勾股定理求出，由平行线的性质得到∠AME＝∠ABP，从而得到，代入即可得到答案；（3）分两种情况：①FE＝CE，则∠EFC＝∠ECF，可推出∠EBC＝∠ECB，所以BE＝CE＝FE，作EL ⊥AD于点L，可证明AL＝DL，所以AE＝DE＝AD，则∠EAD＝60°，可求得∠CBF＝15°，在BC上取一点K，连接FK，使FK＝BK，则∠CKF＝∠KFB+∠CBF＝30°，所以FK＝BK＝2CF，，；②CF＝CE，则∠CEF＝∠CFE，可证明点E在正方形ABCD的对角线AC上，则∠BAE＝∠DAE＝45°，求得∠ABE＝∠ADE＝67.5°，则∠CBF＝∠CDP＝22.5°，进而证明△BCF≌△DCP（ASA），得到CF＝CP，可证明∠PFB＝∠CBF＝22.5°，则，即可求得．【解答】解：（1）∵四边形ABCD为正方形，AE＝AB，∴AB＝AD，∠BAD＝90°，∴AE＝AD，∴∠AEB＝∠ABE，∠AED＝∠ADE，∵∠AEB+∠ABE+∠AED+∠ADE+∠BAD＝360°，∴2∠AEB+2∠AED+90°＝360°，∴∠AEB+∠AED＝135°，∴∠BED＝135°，∴∠FED＝180°﹣135°＝45°，∴．（2）由题可得，连接AC交MN于点O，作ME⊥AP，MF⊥BP，如图：设正方形ABCD的边长为2，∵点M、N分别是边AB、AD的中点，∴△MAN为等腰直角三角形，∴AM＝AN＝1，∠AMO＝45°，∵∠APB＝90°，∴AM＝MP＝BM＝1，∵∠AMO＝∠MAO＝45°，∴AO⊥MN，∴在Rt△AOM中，由勾股定理得：，∴，在Rt△AOP中，由勾股定理得：，∴，在Rt△AEM中，由勾股定理得：，∵ME⊥AP，AP⊥BP，∴∠AME＝∠ABP，∴．（3）由题可得，①当△CEF是等腰三角形，且FE＝CE，如图：∴∠EFC＝∠ECF，∵∠BCF＝90°，∴∠EBC+∠EFC＝90°，∠ECB+∠ECF＝90°，∴∠EBC＝∠ECB，∴BE＝CE＝FE，作EL⊥AD于点L，则∠ELD＝∠BAD＝90°，∴EL∥AB∥CD，∴，∴AL＝DL，∴AE＝DE＝AD，∴∠EAD＝60°，∴∠BAE＝90°﹣60°＝30°，∴，∴∠CBF＝90°﹣75°＝15°，在BC上取一点K，连接FK，使FK＝BK，则∠KFB＝∠CBF＝15°，∴∠CKF＝∠KFB+∠CBF＝15°+15°＝30°，∴FK＝BK＝2CF，∴，∴，∴，②△CEF是等腰三角形，且CF＝CE，如图：∴∠CEF＝∠CFE，∵CD∥AB，∴∠CFE＝∠ABE＝∠AEB，∴∠CEF＝∠AEB，∴∠CEB+∠AEB＝∠CEB+∠CEF＝180°，∴点E在正方形ABCD的对角线AC上，∵AB＝AD＝BC＝CD，∠ABC＝∠ADC＝∠BCD＝90°，∴∠BAE＝∠DAE＝∠BCA＝∠DCA＝45°，∴，∴∠CBF＝∠CDP＝90°﹣67.5°＝22.5°，∵CB＝CD，∠BCF＝∠DCP，∴△BCF≌△DCP（ASA），∴CF＝CP，∴∠CPF＝∠CFP＝45°，∴∠PFB＝∠CPF﹣∠CBF＝45°﹣22.5°＝22.5°，∴∠PFB＝∠CBF，∴，∴，∴，综上所述：∠FBC的正切值为或．【点评】本题考查正方形的性质，等腰直角三角形的性质，全等三角形的判定与性质，等边三角形的性质，三角形内角和定理，平行线分线段成比例定理，勾股定理，锐角三角函数与解直角三角形，数形结合与分类讨论数学思想的运用等知识与方法，熟练掌握正方形的性质，等腰直角三角形的性质，全等三角形的判定与性质，锐角三角函数和数形结合是解题的关键．。

上海市上宝中学初三九年级物理中考物理电学实验汇编

上海市上宝中学初三九年级物理中考物理电学实验汇编一、电压电阻中考物理电学实验1．在探究“串联电路电压的规律”实验中.(1)小珊想电压表测灯L1的两端电压,连接电路如图所示,分析小灯泡的发光情况：______电压表实际测哪两端电压_______(2)图中只有一根导线连错,请在连错的导线上画“X”,并用笔画线表示导线将电路连接正确. ________________(3)改正电路后,闭合开关,如图所示,电压表示数为________________,若电源电压为3V, 则L2两端的电压为______．2．物理小组探究导电液体的导电性与接入电路中液体横截面积大小的关系．他们用长方体水槽、浓度一定的食盐水、电源、滑动变阻器、电压表及电流表等器材进行了探究．实验电路连接如图－1所示，将电极M、N分别固定在水槽左右两侧底部的中央．（1）闭合开关前，为保护电路，应将滑动变阻器的滑片P移到最_____（选填“左”或“右”）端．（2）实验中，通过调节______来保持电极M、N间的电压恒为3V．控制其他条件不变，通过向水槽中添加食盐水，从而达到改变食盐水的_______的目的，用电流表测出相应的电流值．食盐水导电性的强弱可以由_______来判断．实验数据如下表：实验序号横截面积S/cm2电流I/A1500.0221000.0431500.0742000.0852500.1163000.1373500.1484000.1494500.14（3）依据表格中的数据在图－2中描点，做出电流I随横截面积S变化的I－S图像．（______）（4）分析表格中的数据或图像，可得到初步结论：其他条件不变，横截面积增大时，食盐水的导电性_______．（5）为验证实验结论是否具有普遍性，应采取的做法是：______.3．“探究串联电路的电压关系”的实验电路如图甲所示．（1）为了使探究得出的结论具有普遍意义，L1、L2应该选择_____（选填“相同”或“不相同”）的小灯泡．（2）小明根据图甲连接好电路，闭合开关，电压表示数如图乙所示，为了使实验结果更准确，接下来他应该_____．（3）测出L1两端的电压后，小明断开开关，准备拆下电压表，改装在B、C之间．小聪认为小明的操作太麻烦，只需将与A点相连的导线改接到C点即可．小聪的办法是否正确？_____．为什么？_____．（4）测量完成后，进行小组交流讨论，如表选录了四个小组的数据，你认为这些数据是否合理？_____．理由是_____．4．“探究串联电路的电压关系”的实验电路如图甲所示．（1）为了使探究得出的结论具有普遍意义，L1、L2应该选择_____（相同/不同）的小灯泡．（2）小明根据图甲连接好电路，闭合开关，电压表示数如图乙所示，为了使实验结果更准确，接下来他应该_____．（3）测出L1两端的电压后，小明断开开关，准备拆下电压表，改接在B、C之间．小聪认为小明的操作太麻烦，只需将与A点相连的导线改接到C点即可．小聪的办法是否正确？答：_____（正确/不正确）．（4）测量完成后，进行小组交流讨论．下表选录了四个小组的数据，你认为这些数据是否合理？答：_____（合理/不合理）．请说明理由：_____．实验小组L1两端电压/V L2两端电压/V串联总电压/V1 1.6 2.9 4.52 2.1 2.4 4.43 2.5 2.0 4.44 1.8 2.7 4.55．某物理兴趣小组利用图甲所示实验电路图同时测量电源电压U0的大小和电阻R x的阻值，电源电压U0约为2V～3V，R x的阻值约为6Ω～7Ω．实验室提供如下器材：导线若干、开关、电流表（量程0～0.6A，0～3A）、电压表（量程0～3V，0～15V）、滑动变阻器R （最大阻值为30Ω）．请你思考完成下列问题：（1）按照图甲用笔画线代替导线，连接好图乙中的实物图_________．（2）用物理量U0、R x、电流表的示数I写出表示电压表示数U大小的关系式：U=_____．（3）①正确连接电路后，闭合开关前应使滑动变阻器连入电路的阻值为_____（选填“最大”或“零”）；②移动滑动变阻器的滑片，读出4组电流表和电压表示数，分别以电流表的示数I和电压表的示数U为横坐标和纵坐标，在坐标纸上描点，把这4个点连接起来大致为一条直线（并虚线延长到纵轴），如图丙所示．从图丙中信息可求得：电源电压U0=_____V，电阻R x=_____Ω．6．某实验小组探究金属丝电阻大小与横截面积的关系，实验室提供了下列器材：小灯泡、电压表、电流表、电池组、滑动变阻器、刻度尺、开关和导线若干。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

【最新整理，下载后即可编辑】上宝中学2013学年第一学期期中考试初三数学试卷一、选择题(本大题共6题，每题4分，满分24分)1. 已知在△ABC 中，点D 、E 、F 分别在边AB 、AC 和BC 上，且DE ∥BC ，DF ∥AC ，那么下列比例式中，正确的是（）A.BCDEEC AE =； B.FBCFEC AE =； C .BCDEACDF=； D.BCFCAC EC =2. 已知在Rt△ABC 中，∠C=90°，∠A、∠B、∠C 的对边分别是a 、b 、c ，则下列关系式错误的是（）A ．a =b tan A ；B ．b =ccos A ；C ．a =c sin A ；D ．c =sin b A3. 如图，平行四边形ABCD 中，过点B 的直线与对角线AC 、边AD 分别交于点E 和F ．过点E 作EG∥BC，交AB 于G ，则图中相似三角形有（） A ．7对； B ．6对； C ．5对； D ． 4对第3题第4题 4. 二次函数y =ax 2+bx +c （a ，b ，c 是常数，a ≠0）图象的对称轴是直线x =1，其图象的一部分如图所示．对于下列说法：①abc >0； ②a －b +c ＜0； ③3a +c ＜0； ④当－1＜x ＜3时，y ＞0．其中正确的结论是（）．A ．①②；B ．①④；C ．②③；D ．②③④ 5. 下列说法正确的个数有（）①平分弦的直径，平分这条弦所对的弧；②在等圆中，如果弦相等，那么它们所对的弧也相等； ③等弧所对的圆心角、弦、弦心距都分别相等； ④过三点可以画一个圆.A．1个； B ．2个； C ．3个； D ．4个 6. 下列命题中，错误命题的个数有（） ①如图，若AB DE BCEF=，则////AD BE CF ；②已知一个单位向量e ，设a 是非零向量，则1a e a=；③在△ABC 中，D 在AB 边上，E 在AC 边上，且△ADE和△ABC 相似，若AD = 3，DB = 6，AC = 5，则它们的相似比为13或35；④对于抛物线f (x )=x 2－4x +c ，有f (1)>f (－1)； ⑤在△ABC 中，AB =23，AC =2，BC 边上的高AD =3，则BC =4，∠B =30°． A ．5个； B ．4个； C ．3个； D ．2个二、填空题(本大题共12题，每题4分，满分48分)7. 在比例尺为1：50000的地图上，某地区的图上面积为20平方厘米，则实际面积为平方千米. 8. 在△ABC 中，|cosA –32|+(1– cotB)2 = 0 ，则△ABC 的形状是 .9.将二次函数5422+-=x x y 图象向左平移1个单位，再向下平移2个单位后，所得图象的解析式是 .10. 如图，梯形ABCD 中，AD ∥BC ，E 、F 分别是AB 、CD 上的点，且EF ∥BC ，53AE BC BEAD==，若AB a =，DC b =，则向量EF 可用a 、b 表示为_____________________.第10题第11题第12题第6题DBCAE第13题11. 如图，在△ABC 中，点D 是AB 的黄金分割点（AD ＞BD ），BC=AD ，如果∠ACD=90°，那么tanA= .12．如图AD 是△ABC 的中线，E 是AD 上一点，且AE=13AD ，CE 的延长线交AB 于点F ，若AF=1.2，则AB= .13. 如图所示，在△ABC 中，DE∥AB∥FG，且FG 到DE 、AB 的距离之比为1：2．若△ABC 的面积为32，△CDE 的面积为2，则△CFG 的面积S=14. 在△ABC 中，AB=3，AC=4，△ABC 绕着点A 旋转后能与△AB′C′重合，那么△ABB′与△ACC′的周长之比为 .15.如图，△ABC 中，AB ＝AC ，AD ⊥BC 于D ，AE ＝EC ，AD ＝18，BE ＝15，tan∠EBC = ．16.如图，AC 是高为30米的某一建筑，在水塘的对面有一段以BD 为坡面的斜坡，小明在A 点观察点D 的俯角为30°，在A 点观察点B 的俯角为45°，若坡面BD 的坡度为1：3，则BD 的长为 . 17. ⊙O 的半径为5cm ，弦AB//CD ，AB=6cm ，CD=8 cm ，则AB 与CD 的距离为 cm.18.如图，在Rt △ABC 中，∠C =90°，AB=5，BC =3，点D 、E 分别在BC 、AC 上，且BD=CE ，设点C 关于DE 的对称点为F ，若DF ∥AB ，则BD 的长为．三、解答题(本大题共7题，满分78分)19.（本题第（1）题3分，第（2）题7分，满分10分）ACBD在平面直角坐标系中，抛物线过原点O，且与x轴交于另一点A（A 在O右侧），顶点为B．艾思轲同学用一把宽3cm的矩形直尺对抛物线进行如下测量：（1）量得OA=3cm；（2）当把直尺的左边与抛物线的对称轴重合，使得直尺左下端点与抛物线的顶点重合时（如图），测得抛物线与直尺右边的交点C的刻度读数为4.5cm．艾思轲同学将A的坐标记作（3，0），然后利用上述结论尝试完成下列各题：（1）写出抛物线的对称轴；（2）求出该抛物线的解析式．20.（本题每小题5分，满分10分）在Rt△ABC中，∠ACB=90°，AB=5，sin∠CAB＝4，D是斜边AB5上一点，过点A作AE⊥CD，垂足为E，AE的延长线交BC于点F．时，求线段BF的长；（1）当tan∠BCD＝12时，求线段AD的长．（2）当BF＝5421.（本题每小题5分，满分10分）如图，已知⊙O 的半径为5，弦AB 的长等于8，OD ⊥AB ，垂足为点D ，DO 的延长线与⊙O 相交于点C ，点E 在弦AB 的延长线上，CE 与⊙O 相交于点F ，cos C =35.求：（1）CD 的长；（2）EF 的长.22.（本题每小题5分，满分10分）如图，在一笔直的海岸线l 上有AB 两个观测站，A 在B 的正东方向，AB=2（单位：km ）．有一艘小船在点P 处，从A 测得小船在北偏西60°的方向，从B 测得小船在北偏东45°的方向．（1）求点P 到海岸线l 的距离；（2）小船从点P 处沿射线AP 的方向航行一段时间后，到点C 处，此时，从B 测得小船在北偏西15°的方向．求点C 与点B 之间的距离．（上述两小题的结果都保留根号）D AE B C O F23.（本题第（1）题5分，第（2）题7分，满分12分）如图，在△ABC 中，AB =AC ，D 是BC 的中点，DF⊥AC，E 是DF 的中点，联结AE 、BF. 求证：(1)2DF CF AF =⋅； (2)AE⊥BF .24. （本题第（1）题3分，第（2）题4分，第（3）题5分，满分12分）已知抛物线y =x 2－2x +c 与x 轴交于A ．B 两点，与y 轴交于C 点，抛物线的顶点为D 点，点A 的坐标为（－1，0）．（1）求D 点的坐标；（2）如图1，连接AC ，BD 并延长交于点E ，求∠E 的度数；（3）如图2，已知点P （－4，0），点Q 在x 轴下方的抛物线上，直线PQ 交线段AC 于点M ，当∠PMA=∠E 时，求点Q 的坐标．C25. （本题第（1）题3分，第（2）题5分，第（3）题6分，满分14分）如图，在矩形ABCD中，AB=3，BC=4，动点P从点D出发沿DA向终点A运动，同时动点Q从点A出发沿对角线AC向终点C运动．过点P 作PE∥DC，交AC于点E，动点P、Q的运动速度是每秒1个单位长度，运动时间为x秒，当点P运动到点A时，P、Q两点同时停止运动．设PE=y. （1）求y关于x的函数关系式；（2）探究：当x为何值时，四边形PQBE为梯形？（3）是否存在这样的点P和点Q，使P、Q、E为顶点的三角形是等腰三角形？若存在，请求出所有满足要求的x的值；若不存在，请说明理由．备用图备用图25、解：（1）∴∠D=90° ∴AC=225AD CD +=∵PE ∥CD ∴⊿APE ∽⊿ADC ----------- 2分∴AP AE PEAD AC DC ==即：4453x AE y -==∴353,544y x AE x =-+=-+ ----------- 4分（2）①显然，当QB ∥PE 时，四边形PQBE 是矩形，非梯形，不合题意，舍去；②当QP ∥BE 时，∠PQE=∠BEQ ∴∠AQP=∠CEB ∵AD ∥BC ∴∠PAQ=∠BCE ∴⊿PAQ ∽⊿BCE ----------- 6分∴PA AQ AQ BCCE AC AE==- 即：445455(5)4x x xxx -==--+∴45x = ----------- 8分∴当45x =时，QP ∥BE 而QB 与PE 不平行，四边形PQBE是梯形。

（3）存在。

分四种情况：当Q 在线段AE 上时：QE=AE-AQ=595544x x x -+-=-①当QE=PE 时，935344x x -=-+ ∴43x =②当QP=QE 时，∠QPE=∠QEP∵∠APQ+∠QPE=90° ∠PAQ+∠QEP=90° ∴∠APQ=∠PAQ ∴AQ=QP=QE∴954x x =-∴2013x =③当QP=PE 时，过P 作PF ⊥QE于F ，则FE=12QE=19209(5)248x x --=∵PE ∥DC ∴∠AEP=∠ACD ∴cos ∠AEP= cos ∠ACD=35CD AC=∵cos ∠AEP=209383534xFE PE x -==-+∴2827x =④当点Q 在线段EC 上时，⊿PQE 只能是钝角三角形， ∴PE=EQ 即：PE=AQ-AE∴353(5)44x x x -+=--+ ∴83x =综上，当43x =或2013x =或2827x =或83x =时，⊿PQE 为等腰三角形。

[评分标准：第（3）小题共6分，答对2个给3分，答对3个给5分，全对给6分。

]。