五年级奥数(分数的巧算)
五年级奥数基础教程巧算24小学

五年级奥数基础教程巧算24小学同学们可能都玩过“数学24”的游戏,它把枯燥的基本数字计算变得趣味盎然,能大大提高计算能力和速度,使得思维灵活敏捷,是一种寓教于乐的智力竞赛游戏。
游戏规则:给定四个自然数,通过+,-,×,÷四则运算,可以交换数的位置,可以随意地添括号,但规定每个数恰好使用一次,连起来组成一个混合运算的算式,使最后得数是24。
“数学24”游戏通常是用扑克牌进行的,此时,给定的四个自然数就被限定在1~13范围内了。
“数学24”游戏可以1个人玩,也可以多个人玩,比如四个人玩,把扑克牌中的大、小王拿掉,剩下的52张牌洗好后,每人分13张,然后每人出一张牌,每张牌的点数代表一个自然数,其中J,Q,K分别代表11,12和13,四张牌表示四个自然数。
谁最先按游戏规则算出24,就把这四张牌赢走。
然后继续进行。
最后谁的牌最多谁获胜。
要想算得又快又准,这就要靠平时的基本功了。
最重要的有两条:一是熟悉加法口诀和乘法口诀,二是利用括号。
括号既能改变运算顺序,也可以改变运算符号。
请用下面例题中给出的四个数,按规则算出24。
例1 3,3,5,6。
解一:根据3×8=24,3已有,将另三个数凑成8,得3×(5+6-3)=24。
解二:根据6×4=24,6已有,将另三个数凑成4,得6×(5-3÷3)=24或6×(3×3-5)=24。
解三:还是根据3×8=24,把3和8各分成两数,得(6-3)×(3+5)=24。
解四:先把其中两数相乘,积不足24的用另两数补足,得3×5+3+6=24。
解五:先把其中两数相乘,积超过24的用另两数割去,得5×6-3-3=24。
例2 2,2,4,8。
解一:根据8×3=24,得8×[(2+4)÷2]=24或8×(4-2÷2)=24。
五年级奥数题:分数的巧算

五年级奥数题:分数的巧算一、引言本文将介绍一些在五年级奥数中常见的关于分数的巧算方法,帮助学生们更好地理解和运用分数知识。
二、分数的概念分数是数学中的一种表示方法,由一个整数和一个分母构成。
分数可以表示一个数与一个单位的比值,通常用分子除以分母的形式表示,如$\frac{1}{2}$。
三、分数的基本运算1. 分数的加法分数的加法可以通过找到它们的公共分母进行计算。
例如,计算$\frac{1}{3} + \frac{2}{3}$,我们可以将两个分数的分母统一为3,然后将分子相加,得到$\frac{3}{3}$,再简化为$1$。
2. 分数的减法分数的减法也可以通过找到它们的公共分母进行计算。
例如,计算$\frac{4}{5} - \frac{2}{5}$,我们可以将两个分数的分母统一为5,然后将分子相减,得到$\frac{2}{5}$。
3. 分数的乘法分数的乘法可以直接将它们的分子相乘,分母相乘。
例如,计算$\frac{2}{3} \times \frac{4}{5}$,我们可以得到$\frac{8}{15}$。
4. 分数的除法分数的除法可以通过将被除数乘以倒数的方式进行计算。
例如,计算$\frac{2}{3} \div \frac{4}{5}$,我们可以将它转化为$\frac{2}{3} \times \frac{5}{4}$,然后得到$\frac{10}{12}$,再简化为$\frac{5}{6}$。
四、分数的化简有时候,我们可以将分数化简为最简形式,即分子与分母没有公因子。
例如,对于$\frac{4}{6}$,我们可以将分子和分母都除以2,得到$\frac{2}{3}$,这就是它的最简形式。
五、分数的比较当需要比较两个分数的大小时,我们可以将它们的分母统一,然后比较分子的大小。
例如,比较$\frac{1}{2}$和$\frac{2}{3}$,我们可以将它们的分母统一为6,然后比较$\frac{3}{6}$和$\frac{4}{6}$,可以得出$\frac{3}{6} < \frac{4}{6}$,即$\frac{1}{2} < \frac{2}{3}$。
五年级《速算与巧算》奥数教案

板书:
原式= + + +
=2
练习2:(5分)
计算: + + + -
分析:
将算式中的分数先化成最简分数,然后会发现化简后每个分数都是 。
板书:
原式= + + + -
=1
三、小结:(5分)
整数的加法交换律、结合律对分数的加减计算同样适用。
第二课时(50分)
师:那么我们可不可以将式子写成这种形式。
板书:
原式=(1- )+( - )+( - )+……+( - )
=1- + - + - +……+ -
=1-
=
师:从式子中我们发现中间的分数都是一加一减刚好抵消的。将数列中的每一
项分解,然后重新组合,使之能消去一些项,最终达到求和的目的,我们
把这种解题方法叫做裂项相消法。
生: ,老师,我知道了,给式子加上一个 ,再在最后减去一个 ,
+ = , + = , + = ,最后式子变成1+2+3+4+5+ + - 。
师:恩恩,同学的反应能力很快,那么请你将过程板书到黑板上。
板书:
原式=1+2+3+4+5+ + + + +( + )-
=15+ + + +( + )-
=15+ + +( + )-
练习1:(5分)
计算: - + +
分析:
五年级奥数小数的巧算和分数的分拆

计算式时,利用整数四则运算中简便计算的技巧,还可以利用小数本身的特点,对算式适当变形,将其中的数转化成整数,或者使计算中的一些数易于口算,从而达到速算与巧算。
1、3.9+0.39+0.039+0.0039+0.000392、20.36-7.98-5.02-4.363、42.1+(27.9-12.5)4、3.28-(1.98-1.72)5、42.7×4×0.256、0.125×0.25×0.5×647、4.92÷0.25÷4 8、66.66÷12.5÷0.4÷0.8÷0.39、222×4.4+8.9×888 10、9.56×4.18-7.3×4.18-0.26×4.18单位分数:分子为2、分母是自然数的分数叫单位分数。
分数的分拆:把一个分数分拆成几个分数相加的和,叫做分数的分拆。
一、将下列各分数写成两个单位分数:()()11114=+、()()11125=+、 二、将下列各分数写成三个单位分数之和。
()()()111115=++、()()()1111216=++、 三、将下列等式中的括号里填上适当的各不相同的自然数,使等式成立。
()()()()11111112=+++、 ()()()()11111221=+++、 四、将下列各分数写成两个单位分数之差。
()()11116=-、 ()()11121995=-、 3、已知A 、B 、C 是三个自然数,且C B A 1113851--= ,试求A 、B 、C 三个数之和。
五、计算 :10043211432113211211+⋅⋅⋅++++⋅⋅⋅+++++++++。
奥数5_简便运算2

第五周 简便运算(四)专题简析:前面我们介绍了运用定律和性质以及数的特点进行巧算和简算的一些方法,下面再向同学们介绍怎样用拆分法(也叫裂项法、拆项法)进行分数的简便运算。
运用拆分法解题主要是使拆开后的一些分数互相抵消,达到简化运算的目的。
一般地,形如1a ×(a+1) 的分数可以拆成1a -1a+1 ;形如1a ×(a+n )的分数可以拆成1n ×(1a -1a+n ),形如a+b a ×b 的分数可以拆成1a +1b 等等。
同学们可以结合例题思考其中的规律。
例题1。
计算:11×2 +12×3 +13×4 +…..+ 199×100原式=(1-12 )+(12 -13 )+(13-14 )+…..+ (199 -1100 )=1-12 +12 -13 +13 -14 +…..+ 199 -1100=1-1100=99100练习1计算下面各题: 1. 14×5 +15×6 +16×7 +…..+ 139×402.110×11 +111×12 +112×13 + 113×14 +114×153. 12 +16 +112 +120 + 130 +1424. 1-16 +142 +156 +172例题2。
计算:12×4 +14×6 +16×8 +…..+ 148×50原式=(22×4 +24×6+26×8 +…..+ 248×50 )×12=【(12 -14 )+(14 -16 )+(16 -18)…..+ (148 -150 )】×12=【12 -150 】×12=625练习2计算下面各题:1. 13×5 +15×7 +17×9 +…..+ 197×99 2. 11×4 +14×7 +17×10 +…..+ 197×100 3.11×5 +15×9 +19×13 +…..+ 133×374. 14 +128 +170 +1130 +1208例题3。
五年级奥数——巧算与速算(含解析)
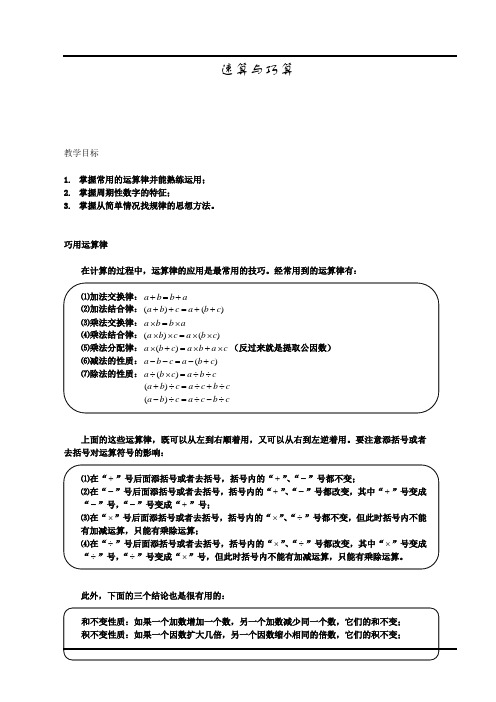
速算与巧算教学目标1.掌握常用的运算律并能熟练运用;2.掌握周期性数字的特征;3.掌握从简单情况找规律的思想方法。
巧用运算律在计算的过程中,运算律的应用是最常用的技巧。
经常用到的运算律有:⑴加法交换律:a b b a+=+⑵加法结合律:()()++=++a b c a b c⑶乘法交换律:a b b a⨯=⨯⑷乘法结合律:()()⨯⨯=⨯⨯a b c a b c⑸乘法分配律:()⨯+=⨯+⨯(反过来就是提取公因数)a b c a b a c⑹减法的性质:()--=-+a b c a b c⑺除法的性质:()÷⨯=÷÷a b c a b c+÷=÷+÷a b c a c b c()-÷=÷-÷()a b c a c b c上面的这些运算律,既可以从左到右顺着用,又可以从右到左逆着用。
要注意添括号或者去括号对运算符号的影响:⑴在“+”号后面添括号或者去括号,括号内的“+”、“-”号都不变;⑵在“-”号后面添括号或者去括号,括号内的“+”、“-”号都改变,其中“+”号变成“-”号,“-”号变成“+”号;⑶在“⨯”号后面添括号或者去括号,括号内的“⨯”、“÷”号都不变,但此时括号内不能有加减运算,只能有乘除运算;⑷在“÷”号后面添括号或者去括号,括号内的“⨯”、“÷”号都改变,其中“⨯”号变成“÷”号,“÷”号变成“⨯”号,但此时括号内不能有加减运算,只能有乘除运算。
此外,下面的三个结论也是很有用的:商不变性质:如果除数和被除数同时扩大或缩小相同的倍数,它们的商不变。
【例1】(“走进美妙的数学花园”初赛)计算:11353715⨯-⨯【分析】根据“一个因数扩大若干倍,另一个因数缩小相同的倍数,积不变”的道理,进行适当变换,再提取公因数,进而凑整求和。
原式11353735=⨯-⨯⨯=⨯-⨯11351115=-⨯(113111)5=10【例2】(武汉明心奥数挑战赛)计算:1234567981⨯【分析】原式123456799912345679(101)9(12345679012345679)9=⨯⨯=⨯-⨯=-⨯=⨯=1111111119999999999[巩固] 计算:123456789876543219⨯[分析] 原式12345678987654321(101)=⨯-=-12345678987654321012345678987654321=111111110888888889【例3】(“走进美妙的数学花园”决赛)计算:⨯+⨯+÷-⨯+2237.522.312.523040.7 2.51【分析】原式2233 2.522.35 2.523 2.50.7 2.50.4 2.5=⨯⨯+⨯⨯+⨯-⨯+⨯=⨯⨯+⨯+-+2.5(223322.35230.70.4)2.5(669111.5230.70.4)=⨯++-+=⨯2.5803.2=⨯÷803.2104=÷80324=2008[巩固] 计算:199.919.98199.819.97⨯-⨯[分析] (法1)原式199.919.9819.98199.7=⨯-⨯=⨯-19.98(199.9199.7)=⨯19.980.2(法2)也可以用凑整法来解决。
奥数题分数的巧算

华夏教育(渝北校区)内部资料 未经允许 不得使用 咨询电话:86008666小学六年级奥数训练一. 分数的巧算复习。
41994197454341+++++ 1009811081861641⨯++⨯+⨯+⨯2000199919991999÷ 900230001111⨯二. 分数和比。
例1:小明和小强的图书本数比是12:7,如果分别加上6本,他们的本数比为3:2。
原来他们各有多少本?巩固练习:1. A 、B 两种商品的价格比是7:3。
如果分别上涨70元,它们的价格比是7:4。
这两种商品原来的价格各是多少元?2. 甲书架上的书与乙书架上的书本数比是5:6,后来都借走了15本,则甲乙书架上本数比为4:7。
则甲乙两书架上原有书多少本?例2:菜市场运来的萝卜比白菜多1.52吨,卖出0.2吨萝卜和0.4吨白菜后,白菜和萝卜的重量比是7:9,原来白菜、萝卜各原来多少吨?1. 粮店原有大米比面粉多3.4吨,卖出大米1.6吨,面粉0.6吨后,大米与面粉的重量比为8:5。
原有大米面粉各多少吨?2. 声乐组人数比舞蹈组人数多14人,后来从声乐组调4人到舞蹈组后,声乐组与舞蹈组人数的比为13:10,声乐组和舞蹈组共有多少人?3. 甲乙两个生产小组每天加工零件指标一样,有一天甲组超额725个,乙组超额175个,已知这一天甲乙两组加工的总数比是7:5。
每天生产指标是多少个?例3:一、二两队人数的比是4:5,一队调72到二队后,二队比一队多46人。
原来两队各多少人?巩固练习:1. 甲乙两队的人数比是8:5,甲队调41到乙队后,甲队人数比乙队少12人,原来甲队比乙队多多少人?2. 甲乙两堆煤重量比是5:4,各运走51后,剩下的甲堆比乙堆多44吨,甲乙各运走了多少吨?例4:一项工程,甲乙合做20天完成。
已知甲乙两队的工作效率之比是4:5,甲乙两队单独完成这项工程各需多少天?1.甲乙两车同时从A、B两地相向而行,5小时相遇。
五年级奥数教案

五年级奥数教课设计第 2 单元巧算乞降(二)教课目的:奇妙的运用分数的拆分来进行简易运算。
教课内容:教科书第 10 页例 1、例 2 和自主检测。
教课重难点:能够灵巧运用此方法进行这一种类的简易计算。
教课方法:讲解法、练习法教课过程:步骤新课教课教师行为学生行为出示例 1计算 1/2+1/6+1/12+1/20惯例剖析:依据旧规方法,这是一题一般的异分母分数加法,我们一般采纳通分的方法。
1/2+1/6+1/12+1/20=60/120+20/120+10/120+6/120=96/120=4/5创新点拨:认真察看每个分数有什么特别的地方,不难看出,分子都是1,而分母能够写成1×2, 2 × 3, 3× 4, 4 × 5 ,即每个分母都能够写成两个连续自然数的积,于是每个分数都能够拆成两个分数的差:1/2 = 1/1 × 2= 1-1/2 ,1/6= 1/2× 3 = 1/2 - 1/3 , 1/12= 1/3 × 4 =1/3-1/4, 1/20 = 1/4 × 5 = 1/4-1/5。
所以能够指引学生作以下解答:1/2+1/6+1/12+1/20=1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 + 1/4 - 1/5=1 - 1/5=4/5出示例 2计算 2/3 × 5 + 2/5 × 7 + 2/7 × 9+ 2/9 × 11惯例剖析:异分母分数相加,先通分,再相加,比较麻烦。
创新点拨:认真察看不难发现,每个分数的分子都是 2,而分母都是两个自然数的积,而分子恰巧等于分母的两个自然数的差。
5- 3= 2, 7- 5= 2 , 9 - 7= 2, 11 - 9 = 2,于是有解答:2/3 × 5 + 2/5 × 7+ 2/7 × 9+ 2/9 × 11=1/3 - 1/5 + 1/5 - 1/7 + 1/7 - 1/9 + 1/9 -1/11=1/3 - 1/11=8/33在做分数加法运算时,将此中一些分数适小当打开后的一些分数能够互相抵消,以达到简结:化运算的目的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分数的计算技巧
一、知识要点
五年级所学习的简便计算主要是有关分数的巧算,除与整数、小数简便计算相同外,还有其独特的巧算方法。
1. 运算定律规律:加法的交换律、结合律,乘法的交换律、结合律和分配律,还有加、减法的运算性质、商不变的规律等。
2. ()a b c d a c b ÷±÷=±÷
3. (1)111(1)1
n n n n =-⨯++ (2)11()d n n d n n d
=-⨯++ (3)
1111()()n n d d n n d =⨯-⨯++ (4)1(1)(2)n n n ⨯+⨯+1112(1)(1)(2)n n n n ⎡⎤=⨯-⎢⎥⨯++⨯+⎣⎦
(5)将
1A 分拆成两个分数单位和的方法:先找出A 的两个约数a 和b ,然后分子、分母分别乘()a b +,再拆分,最后进行约分。
11()()()()
a b a b A A a b A a b A a b ⨯+==+⨯+⨯+⨯+ 4. 等差数列求和法:(首项+末项)×项数2÷=和。
5. 约分法简章:将写成分数形式的算式中的分子部分与分母部分同时除以它们的公有因数或公有因式,从而简化计算过程。
例1. 计算 172928
⨯
拓展一 计算 :443745⨯ 2255(97)()7979+÷+ 1998199819981999÷
例2. 计算 362548361362548186
+⨯⨯-
拓展一 计算:
198819891987198819891+⨯⨯- 1.2 2.3 3.4 4.5 5.6 6.7122334455667++++++++++
例3. 计算 11111223344950++++⨯⨯⨯⨯ 357911132612203042-+-+-
拓展一 计算:
11111198619871987198819881989198919901990++++⨯⨯⨯⨯
11111144771010131316++++⨯⨯⨯⨯⨯ 179111315131220304256-+-+-
1111123234345
9899100++++⨯⨯⨯⨯⨯⨯⨯⨯
112123125859()()()233444
60606060+++++++++++
例4. 计算 5211111111125(3)()()3()()9369126912691239+-⨯++--+⨯+++⨯-
拓展一 计算 11111111111111(1)()(1)()23423452345234
+
++⨯+++-++++⨯++
11111111111111111111234523456234562345⎛⎫⎛⎫⎛⎫⎛⎫++++⨯++++-+++++⨯+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭
1998减去它的12,再减去余下的13,再减去又余下的14,依此类推,一直减到最后余下的11998
,最后得多少?。
