第4讲 倒角模型(教师版)
倒圆角和倒斜角ppt课件
工程图中，经常要绘制圆角和斜角，用户可 分别利用FILLET和CHAMFER命令创建这些几何特征。
倒圆角
倒
圆角是利用指定半径的圆弧光滑地连接两个对象，操作的对
象包括直线、多段线、样条线、圆和圆弧等。对于多段线可
一次将多段线的所有顶点都光滑地过渡 。
“雪亮工程"是以区（县）、乡（镇） 、村（ 社区） 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
“雪亮工程"是以区（县）、乡（镇） 、村（ 社区） 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
主要内容
1 倒圆角的方法 2 倒斜角的方法
“雪亮工程"是以区（县）、乡（镇） 、村（ 社区） 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
打开素材文件“4-7.dwg”，如左图所示，用FILLET命令将 左图修改为右图。
“雪亮工程"是以区（县）、乡（镇） 、村（ 社区） 三级综 治中心 为指挥 平台、 以综治 信息化 为支撑 、以网 格化管 理为基 础、以 公共安 全视频 监控联 网应用 为重点 的“群 众性治 安防控 工程” 。
倒斜角
倒
斜角是用一条斜线连接两个对象，倒角时既可以输入每条边的倒角距离，
也可以指定某条边上，如左图所示，用CHAMFER命令将左图修改为右
图。
第4讲.全等三角形的经典模型(二).培优
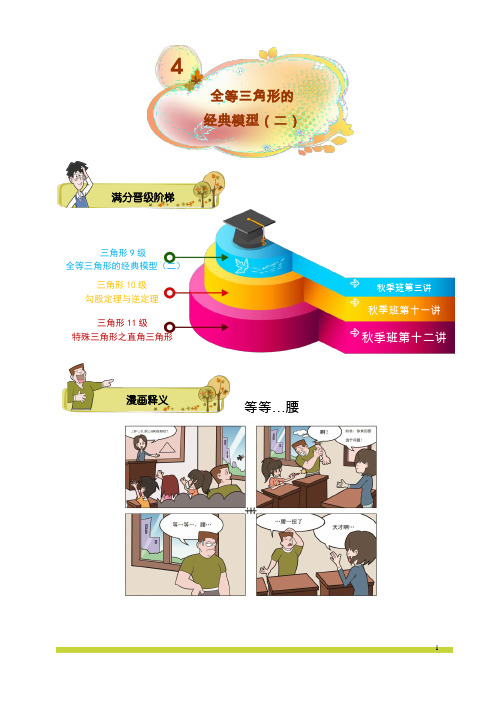
等等…腰漫画释义满分晋级阶梯4全等三角形的 经典模型（二）三角形11级特殊三角形之直角三角形 三角形10级 勾股定理与逆定理 三角形9级全等三角形的经典模型（二）OFEC BA A F COBEDHABCDO EO GFE CB A“手拉手”数学模型：⑴ ⑵ ⑶【引例】 如图，等边三角形ABE 与等边三角形AFC 共点于A ，连接BF 、CE ，求证：BF =CE 并求出∠EOB 的度数.【解析】 ∵△ABE 、△AFC 是等边三角形∴AE =AB ，AC =AF ，60∠=∠=︒EAB FAC知识互联网思路导航例题精讲题型一：“手拉手”模型NM C B A B N CN∴∠+∠=∠+∠EAB BAC FAC BAC 即∠=∠EAC BAF ∴AEC ABF △≌△ ∴BF =EC ∠=∠AEC ABF又∵AGE BGO ∠=∠ ∴60∠=∠=︒BOE EAB ∴60∠=︒EOB【例1】 如图，正方形BAFE 与正方形ACGD 共点于A ，连接BD 、CF ，求证：BD =CF 并求出∠DOH 的度数.【解析】 同引例，先证明ABD AFC △≌△∴BD =FC ，∠=∠BDA FCA ∵∠=∠DHO CHA ∴90∠=∠=︒DOH CAD【例2】 如图，已知点C 为线段AB 上一点，ACM △、BCN △是等边三角形．⑴ 求证：AN BM =.⑵ 将ACM △绕点C 按逆时针方向旋转180°，使点A 落在CB 上，请你对照原题图在图中画出符合要求的图形；⑶ 在⑵得到的图形中，结论“AN BM =”是否还成立，若成立，请证明；若不成立，请说明理由；⑷ 在⑵所得的图形中，设MA 的延长线交BN 于D ，试判断ABD △的形状，并证明你的结论．【分析】 这是一个固定后运动变化的探索题，且在一定的条件下，探究原结论的存在性（不变性）； 需要画图分析、判断、猜想、推理论证．【解析】 ⑴ ∵ACM △、BCN △是等边三角形∴AC CM =，BC CN = 60ACM BCN ∠=∠=° ∴∠=∠ACN MCB在ACN △和MCB △中典题精练OHG DFE CB ADNMCBA=⎧⎪∠=∠⎨⎪=⎩AC MC ACN MCB CN CB ∴ACN MCB △≌△（SAS ） ∴AN BM =⑵ 将ACM △绕点C 旋转如图：⑶ 在⑵的情况，结论AN BM =仍然成立．证明：∵60BCM NCA ∠=∠=°，CA CM =，CN CB =． ∴CAN CMB △≌△（SAS ），∴AN MB =．⑷ 如图，延长MA 交BN 于D ，则ABD △为等边三角形． 证明：∵60CAM BAD ABD ∠=∠=∠=°． ∴ABD △是等边三角形．【例3】 在ABC △中，90∠=BAC °，⊥AD BC 于D ，BF 平分∠ABC 交AD 于E ，交AC 于F .求证：AE=AF .54321A BCDE F【解析】 90∠=BAC °，390∴∠+∠=DAC °90⊥∴∠=︒AD BC ADC 90∴∠+∠=︒C DAC 3∴∠=∠C43152∠=∠+∠∠=∠+∠C ，BF 是ABC ∠的角平分线 12∴∠=∠ 45∴∠=∠∴=AE AF【例4】 如图，已知ABC △中，90ACB ∠=°，CD AB ⊥于D ，ABC ∠的角平分线BE 交CD 于G ，交AC 于E ，GF AB ∥交AC 于F ．典题精练题型二：双垂+角平分线模型ENMD CBA NMD CBA 求证：AF CG =．【分析】 要证AF CG =，一般想到证明这两条线段所在的三角形全等，由图形可知，不存在直接全等三角形，因此要想到添加辅助线构造全等三角形．【解析】 作EH AB ⊥于H∵12∠=∠，90ACB ∠=°∴EC EH =（角平分线定理） 又∵CD AB ⊥ ∴3A ∠=∠∵431∠=∠+∠，52A ∠=∠+∠ ∴45∠=∠ ∴CE CG = ∴CG EH =又∵GF AB ∥，90∠=∠=AHE FGC ° ∴A CFG ∠=∠∴CFG EAH △≌△（AAS ） ∴=CF EA ，∴-=-CF EF EA EF ， ∴CE AF = ∴AF CG =【例5】 已知：正方形ABCD 中，45MAN ∠=︒，MAN ∠绕点A 顺时针旋转，它的两边分别交线段CB DC 、于点M N 、.求证BM DN MN +=.【解析】 延长ND 到E 使DE BM =∵四边形ABCD 是正方形 ∴AD =AB在ADE △和ABM △ =⎧⎪∠=∠⎨⎪=⎩AD AB ADE B DE BM ∴ADE ABM △≌△∴AM =AE ∠=∠BAM DAE典题精练题型三：半角模型54321HG FE DCBA54321G FE DCBADHFECBA∵45MAN ∠=︒ ∴45∠+∠=︒BAM NAD ∴45∠=∠=︒MAN EAN在AMN △和AEN △中 =⎧⎪∠=∠⎨⎪=⎩MA EA MAN EAN AN AN ∴AMN AEN △≌△ ∴MN =EN∴DE +DN =BM +DN=MN【例6】 如图，在四边形ABCD 中，180∠+∠=︒=B D AB AD ，，E 、F 分别是线段BC 、CD 上的点，且BE +FD =EF . 求证：12∠=∠EAF BAD .ABCDEF【解析】 延长FD 到H ，使DH =BE ，易证ABE ADH △≌△， 再证AEF AHF △≌△1122∴∠=∠=∠=∠EAF FAH EAH BAD【例7】 在等边三角形ABC 的两边AB 、AC 所在直线上分别有两点M 、N ，D 为三角形ABC 外一点，且︒=∠60MDN ,︒=∠120BDC ,BD=DC . 探究：当M 、N 分别在直线AB 、AC 上移动时，BM 、NC 、MN 之间的数量关系．AM N BCDCBN M A图1 图2⑴如图1，当点M 、N 在边AB 、AC 上，且DM=DN 时，BM 、NC 、MN 之间的数量关系是 ； ⑵如图2，点M 、N 在边AB 、AC 上，且当DM ≠DN 时，猜想⑴问的结论还成立吗？写出你的猜想并加以证明.【解析】 ⑴如图1， BM 、NC 、MN 之间的数量关系BM +NC=MN ．⑵猜想：结论仍然成立．证明：如图，延长AC 至E ，使CE=BM ，连接DE ． BD=CD 且120BDC ∠=．∴ 30=∠=∠DCB DBC ． 又△ABC 是等边三角形，∴90MBD NCD ECD ∠=∠=∠=． 在MBD △与ECD △中：BM CE MBD ECD BD CD =⎧⎪∠=∠⎨⎪=⎩∴MBD △≌ECD △(SAS ) ． ∴DM=DE , BDM CDE ∠=∠ ∴60EDN BDC MDN ∠=∠-∠=在△MDN 与△EDN 中：⎪⎩⎪⎨⎧=∠=∠=DN DN EDN MDN DE DM ∴MDN EDN △≌△(SAS) ∴MN NE NC BM ==+第04讲精讲：典型的旋转全等构图：“手拉手”全等模型探究； 【探究一】“手拉手”模型基本构图；如图1，若ABC ∆与ADE ∆旋转全等，则必有ABD ∆与ACE ∆为两个顶角相等的等腰三角形（即相似的等腰三角形）；反之，如图2，若有两个顶角相等的等腰三角形ABD ∆与ACE ∆共顶角顶点，则必有ABC ∆与ADE ∆旋转全等；而图2正是“手拉手”模型的基本构图；图1EDC BA图2EDC BA【探究二】将探究一中的普通等腰三角形换成特殊的图形，例如等边三角形、等腰直角三角形、正方形，然后再探究结论如何变化；ENM DC BA图3EDCBA 图4E D CB A FG 图5ED CB A如图3、图4、图5，当两个等边三角形、等腰直角三角形、正方形共顶点时，ABC ∆与ADE ∆仍然旋转全等，并且有两个共同的结论； 结论1：ABC ∆≌ADE ∆；DE BC =；结论2：BC 与DE 所夹锐角等于两个等腰三角形的顶角；（倒角方法如下图6、图7、图8的八字模型）图6图7图8【探究三】将探究二中的特殊图形旋转后结论是否仍然成立； 如下图9、图10、图11易得探究二中的两个结论仍然成立；图9E图10图11【探究四】深化探究二中图3的结论； 如图12，可得结论1：ABC ∆≌ADE ∆；DE BC =；结论2：︒=∠=∠=∠=∠60CAE BAD COE BOD ； 结论3：如图12、图13、图14，可得三对三角形全等（ABC ∆≌ADE ∆；AHD ∆≌AGB ∆；AGC ∆≌AHE ∆）图12图13图14结论4：如图15，连接GH ，可得AGH ∆为等边三角形；（由结论3可得AH AG =）图15NM O 图16EDC BA 结论5：BE GH ∥；（由结论4可得︒=∠=∠60BAD AGH ） 结论6：连接AO ，可得AO 平分BOE ∠；（如图16，分别作BC AM ⊥、DE AN ⊥，AM 与AN 分别是全等三角形ABC ∆与ADE ∆对应边BC 和DE 上的高，故相等）SFEDCBA MP N MH GFE DCBA N M DCBA题型一 手拉手模型 巩固练习【练习1】 如图，DA ⊥AB ，EA ⊥AC ，AD=AB ，AE=AC ，则下列正确的是（ ）A. ABD ACE △≌△B. ADF AES △≌△C. BMF CMS △≌△D. ADC ABE △≌△【解析】 D【练习2】 如图，正五边形ABDEF 与正五边形ACMHG 共点于A ，连接BG 、CF ，则线段BG 、CF 具有什么样的数量关系并求出∠GNC 的度数． 【解析】 先证ABG AFC △≌△ 可得BG =CF ，∠=∠ACF AGB∵∠=∠NPG APC∴108∠=∠=︒GNC GAC题型二 双垂+角平分线模型 巩固练习【练习3】 已知AD 平分∠BAC ，⊥DE AB ，垂足为E ，⊥DF AC ,垂足为F ，且DB =DC ，则EB 与FC 的关系（ ）A. 相等B. EB <FCC. EB >FCD.以上都不对 【解析】 A题型三 半角模型 巩固练习【练习4】 如图，△ABC 是边长为3的等边三角形，△BDC 是等腰三角形，且∠BDC ＝120°．以D 为顶点作一个60°角，使其两边分别交AB 于点M ，交AC 于点N ，连接MN ，则△AMN 的周长为 ． 【解析】 6【练习5】 如图，在四边形ABCD 中，180∠+∠=︒B ADC ，AB AD =，E 、F 分别是边BC 、CD 延长线上的点，且复习巩固F E DCBAFD BAE H GD CBA FDEGCB A12EAF BAD =∠∠，求证：EF BE FD =-【解析】 证明：在BE 上截取BG ，使BG DF =，连接AG ．∵180B ADC +=︒∠∠，180ADF ADC +=︒∠∠， ∴B ADF =∠∠． ∵AB AD =，∴ABG ADF △≌△．∴BAG DAF =∠∠，AG AF =．∴12BAG EAD DAF EAD EAF BAD +=+==∠∠∠∠∠∠．∴GAE EAF =∠∠． ∵AE AE =，∴AEG AEF △≌△． ∴EG EF =∵EG BE BG =-，∴EF BE FD =-．训练1. 如图，C 为线段AB 上一点，分别以AC 、CB 为边在AB 同侧作等边ACD △和等边BCE △，AE 交DC 于G 点，DB 交CE 于H 点，求证：GH AB ∥．【分析】 本题中，ACD △与BCE △是等边三角形，因此AC CD =，BC CE =，60ACD ECB ∠=∠=°，因为A 、C 、B 在同一条直线上，故60DCE ∠=°．这样可以得到ACE DCB △≌△，AEC DBC ∠=∠，故可以得到CEG CBH △≌△，则GC HC =，60CGH CHG ∠=∠=°，所以60ACG CGH ∠=∠=°，故GH AB ∥．【解析】 ∵ACD △和BCE △是等边三角形（已知）∴AC CD =，BC CE =（等边三角形的各边都相等）思维拓展训练(选讲)A B C DH QNM60ACD BCE ∠=∠=°（等边三角形的每个角都等于60°） ∵180ACD DCE BCE ∠+∠+∠=°∴60DCE ∠=°，120ACE DCB ∠=∠=°．在ACE △和DCB △中，=⎧⎪∠=∠⎨⎪=⎩AC DC ACE DCB CE CB∴ACE DCB △≌△（SAS ）∴AEC DBC ∠=∠（全等三角形的对应角相等）在BCH △和ECG △中，60∠=∠=⎧⎪=⎨⎪∠=∠⎩BCH ECG BC CE CBH CEG °∴BCH ECG △≌△（ASA ）∴CH CG =（全等三角形的对应边相等） ∴CGH CHG ∠=∠（等边对等角）∵180GCH GHC CGH ∠+∠+∠=°（三角形内角和定理） ∴60GHC CGH ∠=∠=°．∴60ACG CGH ∠=∠=°（等量代换） ∴GH AB ∥（内错角相等，两直线平行）训练2. 条件：正方形ABCD ，M 在CB 延长线上，N 在DC 延长线上，45MAN ∠=︒．结论：⑴ MN DN BM =-；⑵ AH AB =.【解析】 ⑴在CD 上取一点Q ，使DQ =BM先证AMB AQD △≌△可得AM =AQ再证AMN AQN △≌△∴MN =NQ∴DN DQ DN BM NQ MN -=-==⑵可证△ANH ≌△AND ，∴AH=AD=AB训练3. 如图，在Rt ABC △中，锐角ACB ∠的平分线交对边于E ，又交斜边的高AD 于O ，过O引OF BC ∥，交AB 于F ，请问AE 与BF 相等吗？理由是什么？A B M C H N DDOEOO 12ABCD E F FEDCBA21543G O54321G FE DC BA【解析】 相等．理由如下：如图，过E 作EG BC ⊥于G ∵EC 平分ACB ∠，∴12∠=∠ ∵90EAC ∠=°，AD BC ⊥∴1490∠+∠=°，2390∠+∠=° ∴34∠=∠ ∵35∠=∠， ∴45∠=∠ ∴AE AO =∵EC 平分ACB ∠，EA AC ⊥，EG BC ⊥ ∴EA EG =，∴AO EG =，∵FO BC ∥∴AFO B ∠=∠，90BDA FOA ∠=∠=° ∴BEG FAO ∠=∠∴AFO EBG △≌△（AAS ） ∴AF BE =∴AF EF BE EF -=- ∴AE BF =．训练4. 如图，△ABD 为等腰直角三角形，45∠=︒MAN ，求证：以BM 、MN 、DN 为边的三角形是直角三角形.【解析】 过B 作BD 的垂线并取BQ =ND ，连接AQ 、QM先证∴=AQB AND AQ AN △≌△， 再证∴=AQM ANM MN QM △≌△∴以BM 、MN 、DN 为边的三角形是直角三角形.测试1. 如图，等腰直角△ADB 与等腰直角△AEC 共点于A ，连接BE 、CD ，则线段BE 、CD具有什么样的数量关系和位置关系【解析】 先证明ABE ADC △≌△∴BE =CD ，再类似例1倒角即可得到BE ⊥CD课后测N M DBA测试2. 如图，△ABD 为等腰直角三角形，45∠=︒MAN ，求证：以BM 、MN 、DN 为边的三角形是直角三角形.【解析】 过B 作BD 的垂线并取BQ =ND ，连接AQ 、QM先证∴=AQB AND AQ AN △≌△， 再证∴=AQM ANM MN QM △≌△∴以BM 、MN 、DN 为边的三角形是直角三角形.N M DA第十五种品格：创新学会变通，变则通一天早上，一位贫困的牧师，为了转移哭闹不止的儿子的注意力，将一幅色彩缤纷的世界地图，撕成许多细小的碎片，丢在地上，许诺说：“小约翰，你如果能拼起这些碎片，我就给你二角五分钱。
第二章 角外角四大模型(1)(1)
第二章角外角四大模型(1)(1)第二章角外角四大模型本章将介绍角外角四大模型，包括模型的定义、特点和应用等内容。
通过研究本章，读者将对角外角四大模型有一个更全面的了解。
1. 模型一1.1 定义模型一是一种用于分析角外角关系的工具。
它通过比较角内角和角外角的大小关系，来解析和验证角外角四大定理。
1.2 特点模型一具有以下特点：- 简单易懂，可以直观地展示角内角和角外角之间的关系；- 可以应用于各种角的情况，包括锐角、直角和钝角；- 可以帮助我们理解和证明角外角四大定理。
1.3 应用模型一在几何学中有广泛的应用，主要用于以下方面：- 证明和解析角外角四大定理；- 求解与角外角相关的几何问题；- 帮助学生理解和掌握角外角的概念。
2. 模型二2.1 定义模型二是一种基于角外角的数学模型。
它通过数值计算和绘图分析，来研究和解决与角外角相关的问题。
2.2 特点模型二具有以下特点：- 数值计算精确，可以得到角外角的具体数值；- 绘图分析直观，可以清晰地展示角外角的关系；- 可以应用于各种复杂角的情况，包括多角形和三维角。
2.3 应用模型二在数学研究和实际问题中有广泛的应用，主要用于以下方面：- 研究和验证角外角的数学性质；- 解决与角外角相关的数学问题；- 支持其他模型和方法的应用和发展。
3. 模型三3.1 定义模型三是一种几何模型，用于描述角外角的空间关系。
它通过几何图形的构建和推导，来研究和解决与角外角相关的空间问题。
3.2 特点模型三具有以下特点：- 几何图形直观，可以帮助我们理解角外角的空间关系；- 推导过程严谨，可以用于证明和推广角外角的性质；- 可以应用于三维几何和立体图形的研究。
3.3 应用模型三在几何学和物理学中有广泛的应用，主要用于以下方面：- 解决与角外角相关的几何和物理问题；- 推广和应用角外角的空间性质；- 支持三维几何和立体图形的研究和发展。
4. 模型四4.1 定义模型四是一种统计模型，用于分析角外角的分布和变化规律。
苏教版七年级数学下册三角形倒角专练冲刺学案设计（无答案）
苏教版七年级数学下册三⾓形倒⾓专练冲刺学案设计（⽆答案）三⾓形倒⾓专练必备⽅法：1.三⾓形内⾓和180°2.三⾓形外⾓定理必备技巧：设元必备法宝：9 种基本模型模型在⼿，思路我有！上课之前的你：上课之后的你：-----掌握它，满分不再是问题O(∩_∩)O第1页（共9页）题型⼀：常规倒⾓1. 如图， ?ABC 中， AD 是⾼， AE 、 BF 是⾓平分线，它们相交于点O ，∠BAC = 60? ，∠C = 50? ，则∠DAC = ∠BOA =．2. 如图，在?ABC 中， EF / / B C ，∠ACG 是?ABC 的外⾓，∠BAC 的平分线交 BC 于点 D ，若∠1 = 150? ，∠2 = 110? ，则∠3 = ?．3. 如图，在第 1 个?ABA 1 中，∠B = 40? ，∠BAA 1 = ∠BA 1 A ，在 A 1 B 上取⼀点C ，延长 AA 1 到 A 2 ，使得在第 2 个△ A 1CA 2 中，∠A 1CA 2 = ∠A 1 A 2C ；在 A 2C 上取⼀点 D ，延长 A 1 A 2 到 A 3 ，使得在第 3 个△ A 2 DA 3 中，∠A 2 DA 3 = ∠A 2 A 3 D ；，按此做法进⾏下去，第 3 个三⾓形中以 A 3 为顶点的内⾓的度数为；第 n个三⾓形中以 A n 为顶点的内⾓的度数为．4. ?ABC 中，∠C = 80? ，点 D 、 E 分别是?ABC 边 AC 、 BC 上的点，点 P 是⼀动点，令∠PDA = ∠1 ，∠PEB = ∠2 ，∠DPE = ∠α．（1）若点 P 在边 AB 上，且∠α= 50? ，如图 1，则∠1 + ∠2 = ?；（2）若点 P 在边 AB 上运动，如图 2 所⽰，则∠α、∠1 、∠2 之间的关系为．（3）若点 P 运动到边 AB 的延长线上，如图 3，则∠α、∠1 、∠2 之间有何关系？猜想并说明理由5.如图，四边形ABCD 中，∠A =∠B =∠C ，点E 在AB 边上，且∠ADE =1∠EDC ，∠BED =110?，3则∠A = ?．6.探究与发现：如图①，在?ABC 中，∠B =∠C = 45?，点D 在BC 边上，点E 在AC 边上，且∠ADE =∠AED ，连接DE ．（1）当∠BAD = 60?时，求∠CDE 的度数；（2）当点D 在BC （点B 、C 除外）边上运动时，试猜想∠BAD 与∠CDE 的数量关系，并说明理由．（3）深⼊探究：如图②，若∠B =∠C ，但∠C ≠ 45?，其他条件不变，试探究∠BAD 与∠CDE 的数量关系．7.如图，AE 、OB 、OC 分别平分∠BAC 、∠ABC 、∠ACB ，OD ⊥BC ，求证：∠1 =∠2 ．题型⼆：与翻折相关的倒⾓1.如图，在?ABC 中，点D 是BC 边上的⼀点，∠B = 50?，∠BAD = 30?，将?ABD 沿AD 折叠得到?AED ，AE 与BC 交于点F ，求∠AFC 的度数；求∠EDF 的度数.2.问题1现有⼀张?ABC 纸⽚，点D 、E 分别是?ABC 边上两点，若沿直线DE 折叠．研究（1）：如果折成图①的形状，使A 点落在CE 上，则∠1 与∠A 的数量关系是研究（2）：如果折成图②的形状，猜想∠1 +∠2 和∠A 的数量关系是研究（3）：如果折成图③的形状，猜想∠1 、∠2 和∠A 的数量关系，并说明理由．问题2研究（4）：将问题1 推⼴，如图④，将四边形ABCD 纸⽚沿EF 折叠，使点A 、B 落在四边形EFCD 的内部时，∠1 +∠2 与∠A 、∠B 之间的数量关系是．3 ．如图所⽰，把⼀个三⾓形纸⽚ABC 的三个顶⾓向内折叠之后(3 个顶点不重合），图中∠1 +∠2 +∠3 +∠4 +∠5 +∠6 =?．题型三：与模型相关的倒⾓1．如图，把⼀个三⾓尺的直⾓顶点D 放置在?ABC 内，使它的两条直⾓边DE ，DF 分别经过点B ，C ，如果∠A = 30?，则∠ABD +∠ACD =．2．如图，∠1 +∠2 +∠3 +∠4 +∠5 +∠6 +∠7= ．3.如图，已知?ABC 中，∠A = 60?，BD ⊥AC 于D ，CE ⊥AB 于E ，BD 、CE 交于点F ，∠FBC 、∠FCB 的平分线交于点O ，则∠BOC 的度数为．4.如图，BE 平分∠ABD ，CF 平分∠ACD ，BE 、CF 交于G ，若∠BDC =150?，∠BGC =120?，则∠A =．5.问题情景如图1，?ABC 中，有⼀块直⾓三⾓板PMN 放置在?ABC 上(P 点在?ABC 内），使三⾓板PMN 的两条直⾓边PM 、PN 恰好分别经过点B 和点C ．试问∠ABP 与∠ACP 是否存在某种确定的数量关系？（1）特殊探究：若∠A = 50?，则∠ABC +∠ACB = ?度，∠PBC +∠PCB = ?度，∠ABP +∠ACP = ?度；（2）类⽐探索：请探究∠ABP +∠ACP 与∠A 的关系．（3）类⽐延伸：如图2，改变直⾓三⾓板PMN 的位置；使P 点在?ABC 外，三⾓板PMN 的两条直⾓边PM 、PN 仍然分别经过点B 和点C ，（2）中的结论是否仍然成⽴？若不成⽴，请直接写出你的结论．6.直线MN 与直线PQ 垂直相交于点O ，点A 在射线OP 上运动（点A 不与点O 重合），点B 在射线OM 上运动（点B 不与点O 重合）．（1）如图1，已知AE 、BE 分别是∠BAO 和∠ABO 的⾓平分线，①当∠ABO = 60?时，求∠AEB 的度数；②点A 、B 在运动的过程中，∠AEB 的⼤⼩是否会发⽣变化？若发⽣变化，请说明变化的情况：若不发⽣变化，试求出∠AEB 的⼤⼩；（2）如图2，延长BA ⾄G ，已知∠BAO 、∠OAG 的⾓平分线与∠BOQ 的⾓平分线所在的直线分别相交于 E 、F ，在?AEF 中，4，请直接写出∠ABO 的度数．7.如图1，在?ABC 中，CD 、CE 分别是?ABC 的⾼和⾓平分线，∠BAC =α，∠B =β(α>β) ．（1）若∠BAC = 70?，∠B = 40?，求∠DCE 的度数；（2）若∠BAC =α，∠B =β(α>β) ，则∠DCE = ?（⽤α、β的代数式表⽰）；（3）若将?ABC 换成钝⾓三⾓形，如图2，其他条件不变，试⽤α、β的代数式表⽰∠DCE 的度数并说明理由；（4 ）如图3 ，若CE 是?ABC 外⾓∠ACF∠DCE = ?．（直接写出结果）的平分线，交BA 延长线于点 E ．且α-β= 30?，则8.探究⼀：我们知道，三⾓形的⼀个外⾓等于与它不相邻的两个内⾓的和．那么，三⾓形的⼀个内⾓与它不相邻的两个外⾓的和之间存在何种数量关系呢？如图甲，∠FDC 、∠ECD 为?ADC 的两个外⾓，则∠A 与∠FDC +∠ECD 的数量关系．探究⼆：三⾓形的⼀个内⾓与另两个内⾓的平分线所夹的钝⾓之间有何种关系？如图⼄，在?ADC 中，DP 、CP 分别平分∠ADC 和∠ACD ，则∠P 与∠A 的数量关系．探究三：若将?ADC 改为任意四边形ABCD 呢？已知：如图丙，在四边形ABCD 中，DP 、CP 分别平分∠ADC 和∠BCD ，则∠P 与∠A +∠B 的数量关系．探究四：若将上题中的四边形ABCD 改为六边形ABCDEF 呢？如图丁则∠P 与∠A +∠B +∠E +∠F 的数量关系．愉快的课后作业1．如图，?ABC 中，∠A = 40?∠B = 76? ，CE 平分∠ACB ，CD ⊥ AB 于点 D ，DF ⊥ CE 于点 F ，求∠CDF的度数．2．如图，∠A + ∠B + ∠C + ∠D + ∠E + ∠F + ∠G + ∠H + ∠I + ∠J = ?? ．3. 如图，在折纸活动中，⼩明制作了⼀张?ABC 的纸⽚，点 D ， E 分别在边 AB ， AC 上，将?ABC 沿着 DE 折叠压平， A 与A ' 重合，若∠A = 75? ，则∠1 + ∠2 =．4. 如图，在四边形 ABCD 中，∠A + ∠B = 200? ，作∠ADC 、∠BCD 的平分线交于点O 1 称为第 1 次操作，作∠O 1DC 、∠O 1CD 的平分线交于点O 2 称为第 2 次操作，作∠O 2 DC 、∠O 2CD 的平分线交于点O 3 称为第 3 次操作，，则第 5 次操作后∠CO 5 D 的度数是．5．（1）如图 1 所⽰， ?ABC 中，∠ACB 的⾓平分线CF 与∠EAC 的⾓平分线 AD 的反向延长线交于点 F ；①若∠B = 90?则∠F = ?；②若∠B = a ，求∠F 的度数（⽤ a 表⽰）；（2）如图 2 所⽰，若点G 是CB 延长线上任意⼀动点，连接 AG ，∠AGB 与∠GAB 的⾓平分线交于点 H ，随着点G 的运动，∠F +∠H 的值是否变化？若变化，请说明理由；若不变，请求出其值．第9页（共9页）。
第4讲 倒角模型(学生版)
巩固1
如图，
，
，
，则
．
巩固2
如下图，
，
，
，则 的度数为
度．
巩固3 如图，
度．
巩固4
如图，点 和点 分在
的边 和 的延长线上， ， 分别平分
和
，若
，
，则 的大小是
．
巩固5
如图，点 是
两个内角平分线的交点，点 是
，则
的度数为（ ）
两个外角平分线的交点，如果
A.
B.
C.
D.
巩固6
如图，在
中，
交于点 ，依次类推，
，
与
的角平分线交于 ，
与
的角平分线交于点 ，则
与
的角平分线
的度数是
度．
巩固7
如图⑴， 、 是任意
的 、 的角平分线．
(1) 探求
与 的数量关系.
(2)
能等于 吗？说明理由.
(3) 当 为多少度时，
？
(4) 把图⑴中的
变成图⑵中的四边形
， 、 仍然是 ， 的平分线，猜想
与 、 有何数量关系？（只写出猜想结果，不写过程）
首先得到：当 时，如图 ，
，
当 时，如图 ，
，
如图 ，猜想
．
A
B
C
图
图
图
三、数学万花筒
帕斯卡12岁证明任意三角形内角和180度 帕斯卡12岁证明任意三角形内角和180度。 任意两个相同直角三角形一定能拼成长方形，每一个长方形的内角和是360（四个直角）恰好包含了直 角三角形的6个内角，所以一个直角三角形的内角和是360÷2=180。
；
的平
三角形中的倒角模型——飞镖模型、风筝模型以及翻角模型 学生版
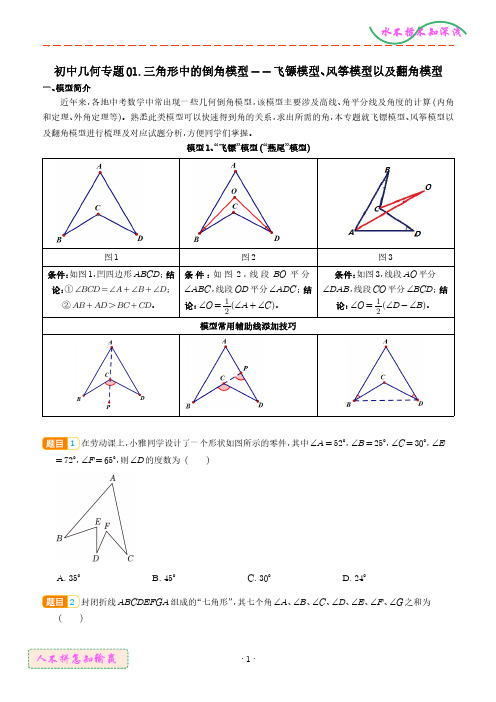
初中几何专题01.三角形中的倒角模型--飞镖模型、风筝模型以及翻角模型一、模型简介近年来，各地中考数学中常出现一些几何倒角模型，该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
熟悉此类模型可以快速得到角的关系，求出所需的角，本专题就飞镖模型、风筝模型以及翻角模型进行梳理及对应试题分析，方便同学们掌握。
模型1、“飞镖”模型(“燕尾”模型)图1图2图3条件：如图1，凹四边形ABCD；结论：①∠BCD=∠A+∠B+∠D；②AB+AD>BC+CD。
条件：如图2，线段BO平分∠ABC，线段OD平分∠ADC；结论：∠O=12(∠A+∠C)。
条件：如图3，线段AO平分∠DAB，线段CO平分∠BCD；结论：∠O=12(∠D-∠B)。
模型常用辅助线添加技巧1在劳动课上，小雅同学设计了一个形状如图所示的零件，其中∠A=52°，∠B=25°，∠C=30°，∠E =72°，∠F=65°，则∠D的度数为()A.35°B.45°C.30°D.24°2封闭折线ABCDEFGA组成的“七角形”，其七个角∠A、∠B、∠C、∠D、∠E、∠F、∠G之和为()A.180°B.270°C.360°D.720°3请阅读下列材料，并完成相应的任务：有趣的“飞镖图”如图，这种形似飞镖的四边形，可以形象地称它为“飞镖图”．当我们仔细观察后发现，它实际上就是凹四边形．那么它具有哪些性质呢？又将怎样应用呢？下面我们进行认识与探究：凹四边形通俗地说，就是一个角“凹”进去的四边形，其性质有：凹四边形中最大内角外面的角等于其余三个内角之和．(即如图1．∠ADB=∠A+∠B+∠C)理由如下：方法一：如图2，连结AB，则在△ABC中，∠C+∠CAB+∠CBA=180°，即∠1+∠2+∠3+∠4+∠C=180°，又∵在△ABD中，∠1+∠2+∠ADB=180°，∴∠ADB=∠3+∠4+∠C，即∠ADB=∠CAD+∠CBD+∠C．方法二：如图3，连结CD并延长至F，∵∠1和∠3分别是△ACD和△BCD的一个外角，⋯大家在探究的过程中，还发现有很多方法可以证明这一结论．任务：(1)填空：“方法一”主要依据的一个数学定理是；(2)探索及应用：根据“方法二”中辅助线的添加方式，写出该证明过程的剩余部分．2、风筝模型(鹰爪模型)或角内翻模型图1图21)风筝(鹰爪)模型：结论：∠A+∠O=∠1+∠2；2)风筝(鹰爪)模型(变形)：结论：∠A+∠O=∠2-∠1。
第4讲 倒角模型(教师版)
A.
B.
C.
D.
答案 C
解析
根据三角形外角性质，可得：
，
，
，
，
∴
，
，
∴
又∵ 、 分别平分
、
∴
，
，
∴
，
∴
，
即
故选 ．
． ，
．
二、角平分线模型
知识总结
模型
图形
双内角分线模型
模型
图形
双外角分线模型
模型
图形
结论 结论 结论
一内一外角分线模型
注：角平分线模型在大题中不可直接使用，必须证明后再用．
典型例题
例题4
的平分线相交于点 ，得 ；…，
于点 ，得
，则
．
的平分线交于点 ，得 的平分线与
；
的平
的平分线相交
A1
答案
解析 ∵ ∴
， 的角平分线与
角平分线交于点 ， ，
∴
．
∴依此类推得：
，
∴
．
故答案为：
．
…，
4 如图，已知射线
， 、 为 、 上两动点，
中
的平分线与
的外角
平分线所在的直线交于点 ，则 （ ）．
A.
第4讲 倒角模型
一、“飞镖”与“8字模型”
知识总结
模型
图形
结论
飞镖模型
∠BDC=∠A+∠B+∠C
模型
图形
结论
“8”字模型
∠A+∠B=∠C+∠D
【注】1．证明思路：构造三角形，利用三角形内角和定理证明； 2．飞镖模型、“8”字模型在大题中不可直接使用，必须证明后再用．
solidworks第4章 实体编辑
第4章实体编辑前面一章中介绍的是实体建模，而实体编辑就是在不改变基体特征主要形状的前提下，对已有的特征进行局部修饰的建模方法，本章就来介绍这一部分。
在SolidWorks中实体编辑主要包括圆角、倒角、孔、抽壳、圆顶、拔模以及特型特征等，本章将对这些特征的造型方法进行逐一介绍。
4.1 倒角特征倒角特征是机械加工过程中不可缺少的工艺，倒角特征是对边或角进行倒角。
在零件设计过程中，通常在锐利的零件边角处进行倒角处理，便于搬运、装配以及避免应力集中等。
4.1.1 距离倒角当需要在零件模型上生成距离倒角特征时，可按如下的操作步骤进行：（1）单击“特征”工具栏上的（倒角）按钮，或选择菜单栏中的“插入”|“特征”|“倒角”命令，此时会出现如图4-1所示的“倒角”PropertyManager设计树。
图4-1 “倒角”设计树（2）在“倒角”PropertyManager设计树中选择倒角类型，确定生成距离倒角的方式：“角度-距离”、“距离-距离”两种。
“角度-距离”选项：选择该选项后面板后会出现“距离”及“角度”参数项，利用“角度-距离”选现生成的倒角效果如图4-2所示。
距离"：应用到第一个所选的草图实体。
角度"：应用到从第一个草图实体开始的第二个草图实体。
图4-2 选择角度-距离类型生成倒角“距离-距离”选项：选择该选项后面板中会出现“距离1”或“距离1”及“距离2”参数项，利用“角度-距离”选现生成的倒角效果如图4-3所示。
距离1"：相等距离复选框被选择后，该选项表示应用到两个草图实体。
距离1"及距离2：相等距离复选框被消除后，距离1选项表示应用到第一个所选的草图实体。
距离2选项表示应用到第二个所选的草图实体。
图4-3 选择距离-距离类型生成倒角（3）单击“倒角参数”面板中图标右侧的显示框，然后在图形区域中选择实体（边线和面或顶点）。
（4）在下面对应的微调框中指定距离或角度值。
专题 三角形中的倒角模型之平行线+拐点模型(学生版)-2025年中考数学常见几何模型
三角形中的倒角模型之平行线+拐点模型近年来各地中考中常出现一些几何倒角模型，该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
平行线+拐点模型在初中数学几何模块中属于基础工具类问题，也是学生必须掌握的一块内容，熟悉这些模型可以快速得到角的关系，求出所需的角。
本专题就平行线+拐点模型(猪蹄模型(M型)、铅笔头模型、牛角模型、羊角模型、“5”字模型)进行梳理及对应试题分析，方便掌握。
拐点(平行线)模型的核心是一组平行线与一个点，然后把点与两条线分别连起来，就构成了拐点模型，这个点叫做拐点，两条线的夹角叫做拐角。
通用解法：见拐点作平行线；基本思路：和差拆分与等角转化。
目录例题讲模型模型1.猪蹄模型(M型与锯齿型)模型2.铅笔头模型模型3.牛角模型模型4.羊角模型模型5.蛇形模型(“5”字模型)习题练模型例题讲模型模型1.猪蹄模型(M型与锯齿型)先说说这个名字的由来，为什么叫猪蹄模型呢？因为它长得像猪蹄，也有叫M模型或锯齿模型的，都是根据外形来取的，只要你喜欢，叫什么都无所谓，掌握其中的核心才是关键。
①注意：拐角为左右依次排列；②若出现不是依次排列的，应进行拆分。
图1图2图3条件：如图1，①已知：AM∥BN，结论：∠APB=∠A+∠B；②条件：∠APB=∠A+∠B，结论：AM∥BN.证明：如图1，过点P作PQ∥AM，∵PQ∥AM，AM∥BN，∴PQ∥AM∥BN，∴∠A=∠APQ，∠B=∠BPQ，∴∠A+∠B=∠APQ+∠BPQ=∠APB，即：∠APB=∠A+∠B．条件：如图2，已知：AM∥BN，结论：∠P1+∠P3=∠A+∠B+∠P2.证明：根据图1中结论可得，∠A+∠B+∠P2=∠P1+∠P3，条件：如图3，已知：AM∥BN，结论：∠P1+∠P3+...+∠P2n+1=∠A+∠B+∠P2+...+∠P2n.证明：由图2的规律得，∠A+∠B+∠P2+⋯+P2n=∠P1+∠P3+∠P5+⋯+∠P2n+11.(2024·山西·二模)如图是一种卫星接收天线的轴截面示意图，卫星波束AB与DC平行射入接收天线，经反射聚集到焦点O处，若∠ABO=38°，∠DCO=45°，则∠BOC的度数为()A.90°B.83°C.76°D.73°2.(2024九年级下·辽宁·学业考试)如图，AB∥CD，AE=EF,∠A=25°,∠EFC=130°，则∠C的度数为．3.(2023春·河南驻马店·九年级专题练习)已知AB∥CD，∠EAF=13∠EAB，∠ECF=13∠ECD，若∠E=66°，则∠F为()A.23°B.33°C.44°D.46°4.(2023·广东深圳·校联考模拟预测)北京冬奥会掀起了滑雪的热潮，谷爱凌的励志故事也激励着我们青少年，很多同学纷纷来到滑雪场，想亲身感受一下奥运健儿在赛场上风驰电掣的感觉，但是第一次走进滑雪场的你，如果不想体验人仰马翻的感觉，学会正确的滑雪姿势是最重要的，正确的滑雪姿势是上身挺直略前倾，与小腿平行，使脚的根部处于微微受力的状态，如图所示，AB∥CD，当人脚与地面的夹角∠CDE=60°时，求出此时上身AB与水平线的夹角∠BAF的度数为()A.60°B.45°C.50°D.55°5.(23-24七年级下·广东云浮·期末)小明学习了角平分线的定义以及平行线的判定与性质的相关知识后，对角之间的关系进行了拓展探究．如图，直线AB∥CD，直线AC是直线AB，CD的第三条截线，AK，CK分别是∠BAC，∠DCA的平分线，并且相交于点K．问题解决：(1)∠BAC，∠DCA的平分线AK，CK所夹的∠K的度数为；问题探究：(2)如图2，∠BAK，∠DCK的平分线相交于点K1，请写出∠AK1C与∠AKC之间的等量关系，并说明理由；拓展延伸：(3)在图3中作∠BAK1，∠DCK1的平分线相交于点K，作∠BAK2，∠DCK2的平分线相交于点K3，依此类推，作∠BAK2023，∠DCK2023的平分线相交于点K2024，求出∠K2024的度数．6.(2024·上海·八年级校考期中)已知，直线AB∥CD。
三角形倒角模型结论和证明
三角形倒角模型结论和证明1. 引言好啦，今天咱们聊聊三角形倒角模型！这个名字听起来挺高大上的，但其实说白了就是把一个三角形的角给“修整”一下，让它看起来更柔和，更圆润。
就像我们在生活中总是希望把事情搞得圆滑一点，避免那些尖锐的冲突一样，倒角模型的主要目的是为了优化、提高效率，简直是“顺其自然”的典范嘛。
接下来，我会跟大家细说这个模型的结论和证明，保证你听完后，不仅会觉得有趣，还能带点干货回家。
2. 三角形倒角模型的基本概念2.1 什么是倒角？首先，咱得弄明白啥叫“倒角”。
通俗点说，就是把三角形的角切掉，留下一个小平面。
你可以想象一下，如果你有一个三角形的饼干，把那尖尖的角削平，这样就不会刮到嘴巴，吃起来也更爽口了。
倒角的目的是为了降低尖锐的边界，给人一种更加温和、亲切的感觉。
这就像我们在社交场合中，总是希望用更柔和的方式与人交流，不让人觉得不适。
2.2 倒角的应用在很多地方，倒角都是一个关键的设计元素。
比如说，在工业设计中，很多产品的边角都是经过倒角处理的，这样既好看，又能提高安全性。
想象一下，家里的家具如果都有尖角，那可真是个安全隐患。
小孩玩耍时不小心撞到，家长可就要心疼得直叫唤了！而且，倒角还可以让产品在生产时更容易加工，减少磨损，简直是一举两得，聪明得不得了。
3. 三角形倒角模型的结论3.1 模型的结论通过对三角形倒角模型的分析，我们得出一个结论：倒角处理可以有效提升结构的稳定性，同时降低受力集中现象。
这听起来可能有点抽象，简单来说，就是给三角形的角“减负”，让它在受到外力时不容易崩溃。
就像一个团队，大家都团结一致，才能更好地面对外部挑战，毕竟“团结就是力量”嘛！3.2 生活中的反思再说说这个模型在生活中的启示吧。
我们每个人都是一座小小的三角形，在生活中不可避免地会遇到各种冲突和挑战。
如果我们能够像倒角那样，适度地“软化”自己的态度，处理问题时就会更有智慧，减少不必要的摩擦。
比如说，当朋友之间有误会时，咱不妨先放下架子，真诚沟通，总比剑拔弩张要强得多。
初中数学倒角模型讲解教案
初中数学倒角模型讲解教案一、教学目标：1. 让学生理解倒角的概念，掌握倒角的计算方法。
2. 培养学生运用倒角模型解决实际问题的能力。
3. 提高学生对初中数学几何知识的兴趣和积极性。
二、教学内容：1. 倒角的概念及分类2. 倒角的计算方法3. 倒角模型的应用三、教学过程：1. 导入：利用现实生活中的事物，如建筑物、道路等，引导学生发现其中的倒角现象，引发学生对倒角的兴趣。
2. 倒角的概念及分类：（1）倒角的概念：解释倒角的概念，即两条直线相交，形成的非相邻的两个角。
（2）倒角的分类：交叉倒角、相邻倒角、对顶倒角等。
3. 倒角的计算方法：（1）交叉倒角：交叉倒角的计算公式为：交叉倒角 = 180° - (角1 + 角2)。
（2）相邻倒角：相邻倒角的计算公式为：相邻倒角 = 180° - 角1 - 角2。
（3）对顶倒角：对顶倒角的计算公式为：对顶倒角 = 角1 = 角2。
4. 倒角模型的应用：（1）解决实际问题：利用倒角模型解决生活中的实际问题，如计算道路的夹角、建筑物的倾斜度等。
（2）几何证明：运用倒角模型进行几何证明，如证明两条直线平行、证明三角形全等等。
5. 练习与巩固：设计一些有关倒角的练习题，让学生独立完成，巩固所学知识。
6. 总结与拓展：总结本节课所学内容，强调倒角的概念、计算方法和应用。
拓展学生思维，引导学生发现倒角在其他学科和生活中的应用。
四、教学评价：1. 课堂表现：观察学生在课堂上的参与程度、提问回答等情况，了解学生的学习状态。
2. 练习完成情况：检查学生练习题的完成质量，评估学生的掌握程度。
3. 课后反馈：收集学生的课后反馈，了解学生对倒角模型的理解和应用情况。
五、教学资源：1. 课件：制作倒角模型的课件，展示倒角的概念、计算方法和应用。
2. 练习题：设计一些有关倒角的练习题，巩固学生的知识。
3. 现实生活中的例子：收集一些现实生活中的倒角现象，作为教学素材。
三角形中的倒角模型-双角平分线(三角形)模型(学生版)
三角形中的倒角模型-双角平分线(三角形)模型模型1、双角平分线模型图1图2图31)两内角平分线的夹角模型条件：如图1，在△ABC 中，∠ABC 和∠ACB 的平分线BE ，CF 交于点G ；结论：∠BGC =90°+12∠A ．2)两外角平分线的夹角模型条件：如图2，在△ABC 中，BO ，CO 是△ABC 的外角平分线；结论：∠O =90°-12∠A ．3)一个内角一个外角平分线的夹角模型条件：如图3，在△ABC 中，BP 平分∠ABC ，CP 平分∠ACB 的外角，两条角平分线相交于点P ；结论：∠P =12∠A ．图4图5图64)凸多边形双内角平分线的夹角模型条件：如图4，BP 、CP 平分∠ABC 、∠DCB ，两条角平分线相交于点P ；结论：2∠P =∠A +∠D5)两内角平分线的夹角模型条件：如图5，BP 、DP 平分∠BCD 、∠CDE ，两条角平分线相交于点P ；结论：2∠P =∠A +∠B +∠E -180°6)一个内角一个外角平分线的夹角模型(累计平分线)条件：如图6，∠A =α，∠ABC ,∠ACD 的平分线相交于点P 1，∠P 1BC ,∠P 1CD 的平分线相交于点P 2，∠P 2BC ，∠P 2CD 的平分线相交于点P 3⋯⋯以此类推；结论：∠P n 的度数是α2n．7)旁心模型旁心：三角形的一条内角平分线与其他两个角的外角平分线交于一点条件：如图，BD平分∠ABC，CD平分∠ACB的外角，两条角平分线相交于点D；结论：AD平分∠CAD1(2022秋·安徽阜阳·八年级统考期中)如图，在△ABC中，点P是△ABC内一点，且点P到△ABC三边的距离相等，若∠BPC=124°，则∠A=．2(2022·湖北十堰·八年级统考期末)如图，在五边形ABCDE中，∠A+∠B+∠E=a，DP，CP分别平分∠EDC，∠BCD，则∠P的度数是．3(2023·山东济南·校考模拟预测)如图1，在△ABC中，∠BAC的平分线AD与∠BCA的平分线CE交于点O．(1)求证：∠AOC=90°+12∠ABC；(2)当∠ABC=90°时，且AO=3OD(如图2)，判断线段AE，CD，AC之间的数量关系，并加以证明．4(2023秋·成都市·八年级专题练习)如图，在△ABC中，∠B=58°，三角形两外角的角平分线交于点E，则∠AEC=．5(2023·湖北·八年级专题练习)如图，已知在ΔABC中，∠B、∠C的外角平分线相交于点G，若∠ABC =m°，∠ACB=n°，求∠BGC的度数.6(2023·辽宁葫芦岛·八年级统考期中)如图，CD、BD分别平分∠ACE、∠ABC，∠A=70°，则∠BDC =()A.35°B.25°C.70°D.60°7(2022秋·八年级课时练习)如图，BA1和CA1分别是△ABC的内角平分线和外角平分线，BA2是∠A1 BD的平分线，CA2是∠A1CD的平分线，BA3是∠A2BD的平分线，CA3是∠A2CD的平分线，⋯⋯以此类推，若∠A=α，则∠A2020=．8(2023春·成都市七年级课时练习)如图在△ABC中，BO，CO分别平分∠ABC，∠ACB，交于O，CE 为外角∠ACD的平分线，交BO的延长线于点E，记∠BAC=∠1，∠BEC=∠2，则以下结论①∠1=2∠2，②∠BOC =3∠2，③∠BOC =90°+∠1，④∠BOC =90°+∠2，正确的是．(把所有正确的结论的序号写在横线上)9(2023秋·广东佛山·八年级校考期末)(1)如图1所示，在△ABC 中，∠ABC 和∠ACB 的平分线将于点O ，则有∠BOC =90°+12∠A ，请说明理由．(2)如图2所示，在△ABC 中，内角的平分线∠ABC 和外角∠ACD 的平分线交于点O ，请直接写出∠BOC 与∠BAC 之间的关系，不必说明理由．(3)如图3所示，AP ，BP 分别平分∠CAD ，∠CBD ，则有∠P =12(∠C +∠D )，请说明理由．(4)如图4所示，AP ，BP 分别平分∠CAM ，∠CBD ，请直接写出∠P 与∠C ，∠D 之间的关系，不必说明理由．10(2023·江苏八年级课时练习)(1)如图所示，在△ABC 中，BO ,CO 分别是∠ABC 和∠ACB 的平分线，证明：∠BOC =90°+12∠A ．(2)如图所示，△ABC 的外角平分线BD 和CD 相交于点D ，证明：∠BDC =90°-12∠A ．(3)如图所示，△ABC 的内角平分线BD 和外角平分线CD 相交于点D ，证明：∠D =12∠A ．课后专项训练1(2023·成都·八年级月考)如图，ΔABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP 交于点P，若∠BPC=40°，则∠CAP=()A.40°B.45°C.50°D.60°2(2023秋·绵阳市·八年级专题练习)如图，在△ABC中，∠ABC=50°，∠ACB=60°，点E在BC的延长线上，∠ABC的平分线BD与∠ACE的平分线CD相交于点D，连接AD，下列结论中不正确的是()A.∠BAC=70°B.∠DOC=90°C.∠BDC=35°D.∠DAC=55°3(2022春·北京海淀·七年级校考期中)如图，在平面直角坐标系中，直线AB与y轴在正半轴、x轴正半轴分别交A、B两点，点C在BA的延长线上，AD平分∠CAO，BD平分∠ABO，则∠D的度数是()A.30°B.45°C.55°D.60°4(2022秋·河北张家口·八年级统考阶段练习)如图，点O在△ABC内，且到三边的距离相等，连接OB,OC．若∠BOC=120°，则∠A的度数是()A.30°B.45°C.60°D.70°5(2022秋·四川绵阳·八年级统考期末)如图，在△ABC中，∠A=30°，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，则∠D等于()A.10°B.15°C.20°D.30°6(2023春·福建漳州·七年级统考期末)如图，在△ABC中，∠ACB<∠A,BD是角平分线，BE是边AC上的高，延长BD与外角∠ACF的平分线交于点G．以下四个结论：①∠ABD=∠CBD；②∠ABE+∠A=90°；③∠G=45°；④∠A-∠ACB=2∠EBD．其中结论正确的个数是()A.1B.2C.3D.47(2022秋·贵州遵义·八年级校考阶段练习)如图，Rt△ABC中，∠ACB=90°，∠BAC=16°，∠ACB的平分线与外角∠ABD的平分线交于点E，连接AE，则∠AEC的度数为．8(2023春·江苏南通·七年级统考阶段练习)如图，BA 1和CA 1分别是△ABC 的内角平分线和外角平分线，BA 2是∠A 1BD 的平分线，CA 2是∠A 1CD 的平分线，BA 3是∠A 2BD 的平分线，CA 3是∠A 2CD 的平分线，若∠A =α，则∠A 999=．9(2022秋·北京大兴·八年级统考期末)如图，在△ABC 中，AB <AC ，∠BAC 的平分线与外角∠BCD 的平分线相交于点M ，作AB 的延长线得到射线AE ，作射线BM ，有下面四个结论：①∠MCD >∠MAB ；②BM =CM ；③射线BM 是∠EBC 的角平分线；④∠BMC =90°-12∠BAC ．所有正确结论的序号是．10(2023春·河北·七年级专题练习)如图，在△ABC 中，∠ABC 和∠ACB 的角平分线交于点O ，延长BO 与∠ACB 的外角平分线交于点D ，若∠BOC =130°，则∠D =11(2023·浙江杭州·八年级期末)如图，在四边形中，，的平分线与的平分线交于点，则．(用含字母的代数式表示)12(2023春·河南·七年级专题练习)如图，点M是△ABC两个内角平分线的交点，点N是△ABC两外角平分线的交点，如果∠CMB：∠CNB=3：2，那么∠CAB=．13(2023·黑龙江八年级课时练习)(1)如图(1)所示，已知在△ABC中，O为∠ABC和∠ACB的平分线BO，CO的交点．试猜想∠BOC和∠A的关系，并说明理由．(2)如图(2)所示，若O为∠ABC的平分线BO和∠ACE的平分线CO的交点，则∠BOC与∠A的关系又该怎样？为什么？14(2023·北京昌平·八年级校考阶段练习)认真阅读下面关于三角形内外角平分线所夹角的探究片段，完成所提出的问题.探究1：如图l，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC =90°+12∠A,理由如下：∵BO和CO分别是∠ABC和∠ACB的角平分线∴∠1=12∠ABC, ∠2=12∠ACB∴∠l+∠2=12(∠ABC+∠ACB)=12(180°-∠A)=90°-12∠A∴∠BOC=180°-(∠1+∠2)=180°-90°-12∠A=90°+12∠A(1)探究2；如图2中，O是12∠ABC与外角12∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由．(2)探究3：如图3中, O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？(直接写出结论)(3)拓展：如图4，在四边形ABCD中，O是∠ABC与∠DCB的平分线BO和CO的交点，则∠BOC与∠A+∠D有怎样的关系？(直接写出结论)15(2023春·江苏无锡·七年级校考阶段练习)如图1，点A、B分别在射线OM、ON上运动(不与点O重合)，AC、BC分别是∠BAO和∠ABO的角平分线，BC延长线交OM于点G．(1)若∠MON=60°，则∠ACG=°；若∠MON=90°，则∠ACG=°；(2)若∠MON=n°，请求出∠ACG的度数；(用含n的代数式表示)(3)如图2，若∠MON=n°，过C作直线与AB交于F，若CF∥OA时，求∠BGO-∠ACF的度数．(用含n的代数式表示)．16(2023·山西晋城·七年级统考期末)在△ABC中，已知∠A=α．(1)如图1，∠ABC、∠ACB的平分线相交于点D．①当α=70°时，∠BDC度数=度(直接写出结果)；②∠BDC的度数为(用含α的代数式表示)；(2)如图2，若∠ABC的平分线与∠ACE角平分线交于点F，求∠BFC的度数(用含α的代数式表示)．(3)在(2)的条件下，将△FBC以直线BC为对称轴翻折得到△GBC，∠GBC的角平分线与∠GCB的角平分线交于点M(如图3)，求∠BMC的度数(用含α的代数式表示)．17(2023·江苏连云港·七年级统考期中)在数学学习过程中，对有些具有特殊结构，且结论又具有一般性的数学问题我们常将其作为一个数学模型加以识记，以积累和丰富自己的问题解决经验．【结论发现】小明在处理教材第43页第21题后发现：三角形的一个内角平分线与另一内角的外角平分线的夹角的度数是三角形第三内角度数的一半．【结论探究】(1)如图1，在△ABC中，点E是△ABC内角∠ACB平分线CE与外角∠ABD的平分线BE的交点，则有∠E=12∠A．请补齐下方的说理过程．理由如下：因为∠EBC+∠EBD=180°，又因为在△EBC中，∠EBC+∠E+∠ECB=180°，所以∠EBC+∠EBD=∠EBC+∠E+∠ECB．所以∠EBD=∠E+∠．(理由是：等式性质)同理可得：∠ABD=∠A+∠．又因为BE和CE分别是∠ABD和∠ACB的角平分线，所以∠EBD=12∠ABD，∠=12∠ACB．所以12∠ABD=∠E+12∠ACB．即∠E=12∠ABD-12∠ACB=12(∠ABD-∠ACB)．所以∠E=12∠A．请直接应用上面的“结论发现”解决下列问题：【简单应用】(2)如图2，在△ABC中，∠ABC=40°．延长BA至G，延长AC至H，已知∠BAC、∠CAG 的角平分线与∠BCH的角平分线及其反向延长线交于E、F，求∠F的度数；【变式拓展】(3)如图3，四边形ABCD 的内角∠BCD 与外角∠ABG 的平分线形成如图所示形状．①已知∠A =150°，∠D =80°，求∠E +∠F 的度数；②直接写出∠E +∠F 与∠A +∠D 的关系．18(2023春·江苏南京·七年级期中)(1)问题发现：如图1，在△ABC 中，∠A =40°，∠ABC 和∠ACB 的平分线交于P ，则∠BPC 的度数是(2)类比探究：如图2，在△ABC 中，∠ABC 的平分线和∠ACB 的外角∠ACE 的角平分线交于P ，则∠BPC 与∠A 的关系是，并说明理由．(3)类比延伸：如图3，在△ABC 中，∠ABC 外角∠FBC 的角平分线和∠ACB 的外角∠BCE 的角平分线交于P ，请直接写出∠BPC 与∠A 的关系是．19(2023春·河南周口·七年级统考期末)【基本模型】(1)如图1，在△ABC 中，BP 平分∠ABC ，CP平分外角∠ACD ，试说明∠P =12∠A ．【变式应用】(2)如图2，∠MON=90°，A，B分别是射线ON，OM上的两个动点，∠ABO与∠BAN的平分线的交点为P，则点A，B的运动的过程中，∠P的大小是否会发生变化？若不发生变化，请求出其值；若发生变化，请说明理由．【拓展应用】(3)如图3，∠MON=90°，作∠MON的平分线OD，A是射线OD上的一定点，B是直线OM上的任意一点(不与点O重合)，连接AB，设∠ABO的平分线与∠BAO的邻补角的平分线的交点为P，请直接写出∠P的度数．20(2023春·江苏淮安·七年级统考期末)【定义】在一个三角形中，如果有一个角是另一个角的3倍，我们称这两个角互为“和谐角”，这个三角形叫做“和谐三角形”．例如：在△ABC中，∠A=75°，∠B= 25°，则∠A与∠B互为“和谐角”，△ABC为“和谐三角形”．【理解】(1)若△ABC为和谐三角形，∠A=140°，则这个三角形中最小的内角为°；(2)若△ABC为和谐三角形，∠A=90°，则这个三角形中最小的内角为°；(3)已知∠A是和谐△ABC中最小的内角，并且是其中的一个和谐角，试确定∠A的取值范围，并说明理由；(4)【应用】如图，△ABC中，AC=BC，∠EBC=13∠ABC，EB交AC于点F，点D是BC延长线上一点，∠ECD=13∠ACD，若∠FCB是和谐△BCF中的一个和谐角，设∠E=α，则α=．。
三角形中的倒角模型之双角平分线(三角形)模型(学生版)
三角形中的倒角模型之双角平分线(三角形)模型近年来各地考试中常出现一些几何倒角模型，该模型主要涉及高线、角平分线及角度的计算(内角和定理、外角定理等)。
熟悉这些模型可以快速得到角的关系，求出所需的角。
本专题就三类双角平分线模型进行梳理及对应试题分析，方便掌握。
大家在掌握几何模型时，多数同学会注重模型结论，而忽视几何模型的证明思路及方法，导致本末倒置。
要知道数学题目的考察不是一成不变的，学数学更不能死记硬背，要在理解的基础之上再记忆，这样才能做到对于所学知识的灵活运用，并且更多时候能够启发我们解决问题的关键就是基于已有知识、方法的思路的适当延伸、拓展，所以学生在学习几何模型要能够做到的就是：①认识几何模型并能够从题目中提炼识别几何模型；②记住结论，但更为关键的是记住证明思路及方法；③明白模型中常见的易错点，因为多数题目考察的方面均源自于易错点。
当然，以上三点均属于基础要求，因为题目的多变性，若想在几何学习中突出，还需做到的是，在平时的学习过程中通过大题量的训练，深刻认识几何模型，认真理解每一个题型，做到活学活用！目录例题讲解模型模型1双角平分线模型(双内角)模型2.双角平分线模型(一内角一外角)模型3.双角平分线模型(双外角)习题练模型例题讲解模型模型1双角平分线模型(双内角)双角平分线模型1：当这两个角为内角时，这夹角等于90°与第三个角的一半的和。
1)两内角平分线的夹角模型图1图2图3条件：如图1，在△ABC 中，∠ABC 和∠ACB 的平分线BP ，CP 交于点P ；结论：∠P =90°+12∠A 。
证明：∵∠ABC 和∠ACB 的平分线BP ，CP 交于点P ，∴∠PBC =12∠ABC ，∠PCB =12∠ACB 。
∴∠P=180°-(∠PBC+∠PCB)=180°-12(∠ABC+∠ACB)=180°-12(180°-∠A)=90°+12∠A。
倒角特征创建范例一完整ppt
铸造CAD/CAE技术
倒角特征创建范例一
主讲教师：张光明 四川程职业技术学院
职业教育材料成型与控制技术专业教学资源库
一、使用拉伸、拐角倒角命令创建图1所示零件
图1
职业教育材料成型与控制技术专业教学资源库
二、首先建立如图2所示拉伸坯料特征
图2
职业教育材料成型与控制技术专业教学资源库
三、然后先建立拉伸坯料一个拐角倒角特征，利用特 职业教征育材复料成型制与控命制技令术专业复教学制资源该库 拐角倒角特征到其他三个顶点上， 尺寸不变，完成后的模型如图3所示 职业教育材料成型与控制技术专业教学资源库
一、使用拉伸、拐角倒角命令创建图1所示零件 职业教育材料成型与控制技术专业教学资源库 职业教育材料成型与控制技术专业教学资源库 职业教育材料成型与控制技术专业教学资源库 一、使用拉伸、拐角倒角命令创建图1所示零件 二、首先建立如图2所示拉伸坯料特征 职业教育材料成型与控制技术专业教学资源库 四川工程职业技术学院 四川工程职业技术学院 职业教育材料成型与控制技术专业教学资源库 职业教育材料成型与控制技术专业教学资源库 四川工程职业技术学院 二、首先建立如图2所示拉伸坯料特征 四川工程职业技术学院
图3
倒角和筋PPT课件
拔模特征用于在模型上加入斜度结构，必须深刻理解拔模特征的4个 基木设计要素的含义与设计方法。此外，还应该掌握获得加材料和减 材料拔模特征的方法。
壳特征用来创建中空的薄壁结构。特别注意壳特征通常安排在拔模特 征、倒圆角以及倒角特征之后进行。
.
1
本次课程重点
第7章 创建工程特征
创建倒角特征； 创建筋特征 工程特征创建总结
第8章 特征的基本操作
特征阵列 特征的复制 特征之间的父子关系 删除特征 编辑特征 编辑定义特征 插入特征 编辑特征参照 重排特征顺序 模型的可见性控制 特征再生失败及其处理 特征基本操作总结
上次课程内容回顾
第7章 创建工程特征
工程特征必须以基础实体特征作为载体。都需要定形和定位参数；
孔特征是常用的工程特征之一。Pro/E捉供了直孔、草绘孔和标准孔 等3种孔类型，在设计时一可以根据需要选取。在放置孔特征时，用 户要掌握系统提供的4种放置孔特征的方法及各自的应用特点，其中 【线性】、【径向】和[同轴】都比较常用。
.
8
下次课程预习内容
曲面及其应用
什么是曲面特征； 基本曲面特征； 填充曲面特征； 边界混合曲面特征； 螺旋扫描曲面特征； 扫描混合曲面特征； 可变剖面扫描曲面特征； 编辑曲面特征 使用曲面特征构建实体特征
组件装配设计
组件装配概述； 由底向上的装配设计 由顶向下的装配设计 创建组件分解图；
来决定参照尺寸；通过加亮进行显示；
.
6
创建筋特征
筋特征是连接实体 表面的薄翼或腹板 伸出项，也是机械 零件中的重要结构 之一，通常用来加 固设计中的零件， 也常用来防止零件 上出现不需要的结
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
知识总结
典型例题1
如图，
2
如图，
3
如图
1
如下图，已知2
如图
1
如图，在凹四边形
2
如图，3
如图，
知识总结典型例题
题型：三角形-外角角分线
如图所示，1如图，点两个外角平分线的交点，如果
2
3
如图，在
D.
如图，已知射线4
1
如图，
2
如图，
，
三、数学万花筒
帕斯卡12岁证明任意三角形内角和180度
帕斯卡12岁证明任意三角形内角和180度。
任意两个相同直角三角形一定能拼成长方形，每一个长方形的内角和是360（四个直角）恰好包含了直角三角形的6个内角，所以一个直角三角形的内角和是360÷2=180。
任意两个相同的直角三角形一定能拼成长方形
在此基础上证明任意锐角三角形内角和是180°. 在三角形内作一条高，会分割出两个不同的直角三角形。
因为直角三角形的内角和是180°，所以除直角外的两个锐角和为180°-90°=90°.两个直角三角形中共有4各锐角，恰好组成了原来大锐角三角形的三个内角，即可得出任意锐角三角形内角和为
90°+90°=180°.同理可证，任意钝角三角形内角和也是180°，因为只有一条高在其内部，所以作高是没有选择余地了。
任意锐角三角形内作高
任意钝角三角形内作高
既然任意直角三角形、锐角三角形钝角三角形的内角和都是180°，小帕斯卡才会非常肯定地说：任意三角形的内角和是都是180°。
这里有个误区，有的教师以为学生在三种类型的三角形中各选择一个分别测量，就是代表了全部的三角形，实际上具体的锐角三角形不能代表所有的锐角三角形，这与帕斯卡证明方法中的任意三角形有本质的不同。
四、巩固加油站
三角形>三角形及多边形>多边形>题型：不规则图形的多角求和
题型：三角形内角的应用
两个外角平分线的交点，如果
D.。