河南理工大学材料力学 试题分解
河南理工大学大二机械专业材料力学试卷及答案1
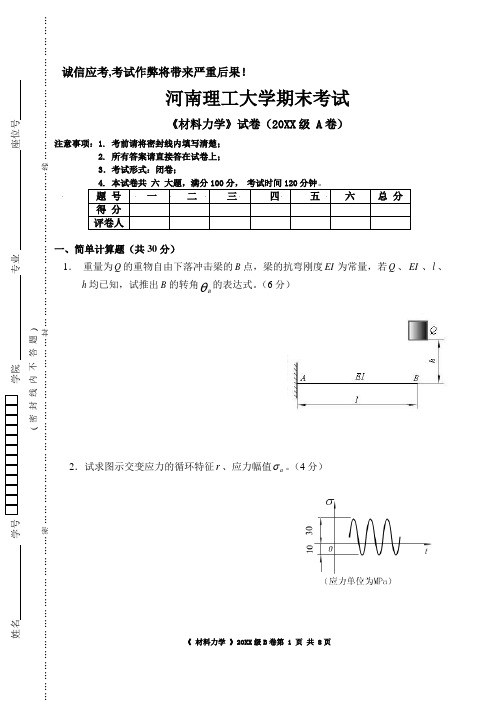
诚信应考,考试作弊将带来严重后果!河南理工大学期末考试《材料力学》试卷(20XX 级 A 卷)注意事项:1. 考前请将密封线内填写清楚; 2. 所有答案请直接答在试卷上; 3.考试形式:闭卷;4. 本试卷共 六 大题,满分100分, 考试时间120分钟。
题 号 一 二 三 四 五 六 总 分 得 分 评卷人一、简单计算题(共30分)1. 重量为Q 的重物自由下落冲击梁的B 点,梁的抗弯刚度EI 为常量,若Q 、EI 、l 、h 均已知,试推出B 的转角θB 的表达式。
(6分)2.试求图示交变应力的循环特征r 、应力幅值a σ。
(4分)姓名 学号学院 专业 座位号( 密 封 线 内 不 答 题 ) …………………………密………………………………………………封………………………………………线……………………………………3.图示为某构件内危险点的应力状态(图中应力单位为MPa ),试分别求其第二、第四强度理论的相当应力2r σ、4r σ(3.0=ν)。
(6分)4. 直径为d 的圆柱放在直径为D =3d 、厚为t 的圆形基座上,地基对基座的支反力为均匀分布,圆柱承受轴向压力P ,试求基座剪切面的剪力Q 。
(6分)5. 试求图示悬臂梁自由端B 的挠度。
(4分)P Ddt6.如下结构中,OA 为刚性杆,杆2的长度短了δ,现强行将三杆装配,试写出变形协调方程。
(4分)xBAy二、已知q、a,试作梁的剪力图和弯矩图。
(12分)三、平面刚架如图所示,EI为常量,试用能量法求出A、C处的约束力。
(16分)四、横截面为b×h的矩形截面梁如图所示,已知:h=2b=5.2cm,F=1kN,q=1kN/m,材料的许用应力为[ ]=140MPa。
试校核该梁的正应力强度。
(10分)F=1C h五、圆截面杆,受横向外力F 和绕轴线的外力偶0m 作用。
由实验测得杆表面A 点处沿轴线方向的线应变40104-⨯= ε,杆表面B 点处沿与轴线成45︒方向的线应变4451075.3-⨯= ε。
材料力学习题解答

解: (3) 梁可简化, 为图示简朴支梁。
B
(m / 2)a 6EI
ma 12EI
(逆时针)
wC 0
mm
m
2
B
C
m
m
2a a a a a 2a
4.如图所示各梁旳抗弯刚度为EI,试用叠加法计算梁 B截面旳转角以及C点旳挠度。
解: (4) 梁可简化,为图示简朴支梁。 B
q
2qqaa22
C
B
qa3 24EI
φ w3 w2
q EI a
A a/4
θ w1
w1
a 4
qa3 a qa4 24EI 4 96EI
w2
q 8EI
a 4
4
qa 4 2048EI
φ w3
w3
a 4
a 3EI
1 2
q
a 4
2
a 4
qa 4 384EI
w2
w
w1
w2
w3
15qa 4 2048EI
7.试用叠加法计算图示各梁C点旳挠度。
解: (1) 梁可简化, 为图示悬臂梁。
A
B
F (2a)2 2EI
Fa 2 2EI
B
3Fa 2 2EI
(逆时针)
wC
wA
F (2a)3 3EI
( Fa3 3EI
Fa 2 2EI
a)
F
F
B C
Fa
a
a
F
a
BF
C
F
11Fa3 wC 6EI (向下)
4.如图所示各梁旳抗弯刚度为EI,试用叠加法计算梁 B截面旳转角以及C点旳挠度。
A
先考虑载荷作用下梁旳变形。
材料力学典型例题与详解(经典题目)
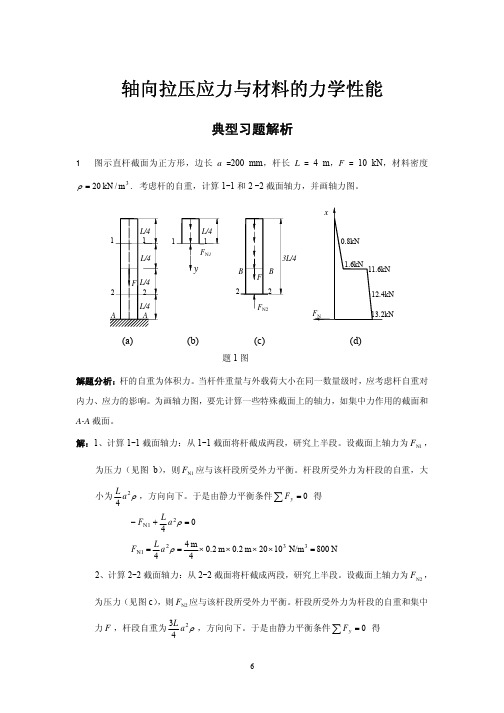
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18,或 1.33∶1.09∶1。 讨论:计算结果表明,采用等强度石柱时最节省材料,这是因为这种设计使得各截面的正应 力均达到许用应力,使材料得到充分利用。 3 滑轮结构如图,AB 杆为钢材,截面为圆形,直径 d = 20 mm ,许用应力 [σ ] = 160 MPa ,BC 杆为木材,截面为方形,边长 a = 60 mm ,许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
解:1、计算 1-1 截面轴力:从 1-1 截面将杆截成两段,研究上半段。设截面上轴力为 FN1 ,
为压力(见图 b),则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重,大
材料力学复习考试题及答案解析
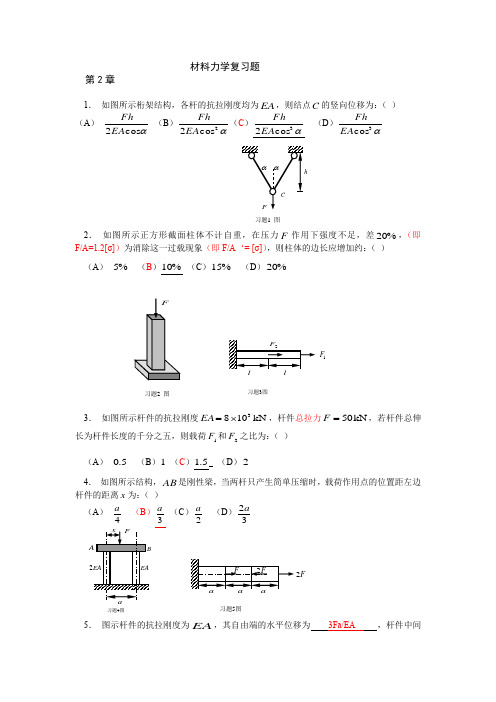
材料力学复习题第2章1. 如图所示桁架结构,各杆的抗拉刚度均为EA ,则结点C 的竖向位移为:( )(A ) αcos 2EA Fh (B )α2cos 2EA Fh (C )α3cos 2EA Fh (D )α3cos EA Fh2. 如图所示正方形截面柱体不计自重,在压力F 作用下强度不足,差%20,(即F/A=1.2[σ])为消除这一过载现象(即F/A ‘= [σ]),则柱体的边长应增加约:( ) (A ) %5 (B )%10 (C )%15 (D )%203. 如图所示杆件的抗拉刚度kN 1083⨯=EA ,杆件总拉力kN 50=F ,若杆件总伸长为杆件长度的千分之五,则载荷1F 和2F 之比为:( ) (A ) 5.0 (B )1 (C )5.1 (D )24. 如图所示结构,AB 是刚性梁,当两杆只产生简单压缩时,载荷作用点的位置距左边杆件的距离x 为:( )(A ) 4a (B )3a (C )2a (D )32a5. 图示杆件的抗拉刚度为EA ,其自由端的水平位移为 3Fa/EA ,杆件中间习题5图F2习题4图习题3图1F习题2 图习题1 图截面的水平位移为 Fa/EA 。
6.图示桁架结构各杆的抗拉刚度均为EA ,则节点C 的水平位移为 F l cos45/EA ,竖向位移为 F l cos45/EA 。
7. 图示结构AB 为刚性梁,重物重量kN 20=W ,可自由地在AB 间移动,两杆均为实心圆形截面杆,1号杆的许用应力为MPa 80,2号杆的许用应力为MPa 100,不计刚性梁AB 的重量。
试确定两杆的直径。
8. 某铣床工作台进油缸如图所示,油缸内压为MPa 2=p ,油缸内径mm 75=D ,活塞杆直径mm 18=d ,活塞杆材料的许用应力MPa 50][=σ,试校核活塞杆的强度。
9.如图所示结构,球体重量为F ,可在刚性梁AB 上自由移动,1号杆和2号杆的抗拉刚度分别为EA 和EA 2,长度均为l ,两杆距离为a 。
河南理工材料力学_试题

材料力学试题()01.(8分)
试画出低碳钢拉伸的应力应变图,并简述各阶段的主要特点。
02.(15)
图示结构中,钢索BC由一组直径d= 2 mm
的钢丝组成。
若钢丝的许用应力为[σ] =160
Mpa,AC梁自重Q = 3 KN,小车承载P = 10
KN,且小车可在梁上自由移动,求钢索需几
根钢丝组成?
试用叠加法求悬臂梁
B端的挠度。
04.(18分)
图示梁,已测得45º方向的线应变为ε 45º,求外力P。
设l、b、h及E、υ均为已知。
传动轴由电机带动,装有直径D= 1 m重G=6 KN 的皮带轮,皮带张力为水平方向,T=6 KN,t=3 KN,轴的直径d=100 mm,[σ]=60Mpa。
试按第三强度理论校核轴的强度。
06.(15分)
悬臂梁AB和简支梁CD均为矩形截面,尺寸和材料均相同。
AB梁的B端置于CD梁的中点。
今有重为Q的重物在B处上方高H处自由下落。
试求B处的最大动位移。
图示各压杆的材料和截面均相同,试问哪
根杆能承受的压力最大,哪根最小?
08.(8分)
简述金属材料疲劳破坏的主要特征及破坏机理。
河南理工大学材料力学 (1)

河南理工大学 《材料力学》试卷一、 图示力N 1000 F ,求该 力对于z 轴之矩z M 。
二、 示圆截面,在其中挖掉一个边长为a 的正方形。
x 轴与圆周相切,求图中阴影部分对x 轴的惯性矩。
三、 某塑性材料制成的构件中有图a 和图b 所示的两种应力状态。
试按第四强度理论分析比较两者的危险程度(σ与τ的数值相等)。
四、图示支架由杆AC 、ED 和滑轮组成,各处均由铰链连接。
滑轮半径r =30 cm ,上面吊着重P =1000 N 的物体。
试求A 、E 处的约束反力。
五、如图所示刚性梁AB 由三根材料相同,截面均为A 的杆 悬挂,求P 力作用下两杆的轴力。
六、图示铸铁T 形截面梁,已知:Z I =7.65×106mm 4,材料的许用拉应力[t σ]=40MPa ,许用压应力[C σ]=60MPa ,试确定此梁的许用载荷P 。
七、 图示梁,已测得中性层上K 点处45º 方向的线应变为ε45º ,求梁中点C 处外力P 的大小。
设b 、h 及E 、μ均为已知。
八、图示铰接杆系结构由两根具有相同截面和同样材料的细长杆组成。
若由于杆件在ABC 平面内失稳而引起毁坏,试确定荷 载F 为最大时的θ角(假设0<θ<90º)。
九、在图示机构中,杆AB 以速度u 向左匀速运动。
求当角45=ϕ时,OC 杆的角速度。
十、一均质圆柱C ,质量为M ,半径为R 。
其上缠绕绳子,绳子沿水平经定滑轮D 后,吊有一质量为m 的重物A ,绳子和滑轮的质量不计。
试求重物A 由静止开始下降时重物的加速度a 和绳的张力T F 。
设圆柱沿水平轨道滚动而不滑动。
河南理工大材料力学期末试题

河南理工大学 学年第 学期《材料力学》试卷( 卷)一、如图结构,AB 、AC 两杆的横截面积均为A =160mm 2,铅垂荷载P =80kN ,60=α。
若许用应力[σ]=70MPa ,试校核强度。
(10分)二、结构如图,在A 端受到压力P 的作用,杆件的横截面150=h mm ,100=b mm ,材料的弹性模量为GPa E 200=,试计算杆件的失稳临界压力P cr 。
(5分)三、应力单元如图(图中应力单位:MPa),试计算该单元:1)主应力;(8分)2)主方向;(4分)3)在图中作出主平面及主应力。
(3分)四、连续梁如图(图中集中力单位:kN,力偶单位:kNm,分布荷载单位:kN/m,长度单位:m),试作此梁的剪力图和弯矩图。
(10分)五、矩形截面外伸梁尺寸及荷载如图示,q=1.3kN/m,h=120mm,b=80mm,[σ]=10Mpa,[τ]=2MPa。
试校核该梁的正应力强度和剪应力强度。
(20分)六、图示圆截面悬臂梁同时受到轴向拉力P,横向分布荷载q和扭转力矩M的作用。
悬臂梁抗弯截面因数W、抗扭截面因数W T,试指出:1)危险截面和危险点的位置;(6分)2)危险点的应力状态(用单元体图画出);(4分)3)危险点的强度条件(用第三强度理论)。
(10分)七、如图所示AB 、CD 二梁在自由端连接,集中力Q 作用在二梁的连接处。
已知二梁的长度比为2321=l l ,二梁的抗弯刚度均为EI 。
试求AB 、CD 二梁在连接处分别受到多大的力?(提示:悬臂梁在自由端受集中力作用时自由端的挠度为EIPl w 33=)(20分)。
河南理工大学材料力学试卷

河南理工大学 2010-2011 学年第 二 学期《材料力学》试卷(A 卷)一、基本概念题。
1. 图示单元体,试求三个主应力和最大切应力。
(5分)2. 影响构件疲劳极限的因素有哪些?(5分)3. 图示正方形,边长为a ,试求该图形对z 轴的惯性矩Z I 。
(5分)4. 从钢构件内某一点的周围取出一部分如图所示。
根据理论计算已求得30M P a σ=,15M P aτ=。
材料的弹性模量200G P aE=,泊松比0.3μ=。
试求对角线AC 的长度改变量A C l ∆。
(10分)25m mA30στC5.已知某解放牌汽车主传动轴传递的最大扭矩1930N m T =,传动轴外径89m m D=,壁厚25m m .δ=,其许用应力[]70M Pa τ=。
试校核此轴。
(10分)二、图示结构,AB 杆的弹性模量GPa 200=E ,比例极限MPa200=pσ,试由AB杆的稳定条件确定许可载荷Q 。
设稳定安全系数为5。
(15分)三、一工字钢截面梁如图所示,已知18kN P =,220kN P =,06ma.=;已知低碳钢的强度极限540M Pa b σ=,取安全系数3n =,试选择工字钢的号码。
工字钢号;抗弯截面系数10;49.0cm^312.6;77.5cm^314;102cm^316;141cm^3aaaAC BD 1P 2P四、求解图示静不定问题各杆的轴力,各杆抗拉刚度相同,均为EA 。
(15分)ααl123FF F N 3N 3ααl123F(a )(b (c五、如图所示,重量100Q =N 的物体从高度50m mH=处自由下落到钢质水平直角曲拐上,试用第三强度理论校核曲拐的强度。
已知:水平AB 杆是圆杆,水平BC 杆是矩形截面杆,并且0.4ma=,1m l =,40m md =, 15m mb=,20m mh =,200G P aE =,80G P a G =,[]120MPa σ=。
(20分)labhH dQABC河南理工大学 2010-2011 学年第 二 学期《材料力学》试卷(A 卷)一、基本概念题(每小题4分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Fs
(+)
Fs Fs
Fs
(-)
b. 弯矩的正负
使梁微段发生上凹下凸变形的 弯矩 M 为正,反之为负。
M
(+)
M M
(-)
M
第四章 弯曲内力(孙教材中,与弯曲应力合为一章) 常见荷载下FS,M图的一些特征 q c 0 (向上) q c 0 (向下)
强度计算的三类问题:
强度校核:
FN A
FN A
截面设计:
A
FN
许用载荷计算:
四、杆件的变形与超静定问题求解
超静定问题的求解步骤: 建立静力平衡方程 建立变形协调方程 —— 得到补充方程
建立物理方程(胡克定律)
将平衡方程与补充方程联立求解
第二章 拉伸和压缩
3.各向同性假设 4.小变形假设
第一章 绪 论 材料力学所研究的四个基本变形 1.轴向拉伸或压缩 2.剪切 3.扭转 4.弯曲
第二章 拉伸和压缩
一、基本概念及基本量
轴力:FN —— 截面法(或快速算法)、轴力图
FN A Fl 变形: l N EA
应力:
应变:
E
(轴向应变) (横向应变)
五、剪切与挤压的实用计算
FS A
Fbs bs bs Abs
特别要注意计算挤压面面积的计算方法 (什么时候 等于实际挤压面面积,什么不等?)
第三章 扭转
1、传动轴的外力偶矩计算
M N m
2、扭矩与扭矩图 3、薄壁圆筒的扭转应力
PkW 9.55 10 nr / min
材料力学内容 总复习
总 复 习
第一部分 第二部分 第三部分 专题部分 基本变形部分 组合变形部分 压杆稳定 能量方法 动载荷与交变应力 第四部分 应力状态与强度理论
第一章 绪 论
材料力学的任务是解决构件安全与经济间的矛盾。
1、强度
2、刚度
保证构件正常工作
3、稳定性
材料力学中可变形固体的四个基本假设 1.连续性假设 2.均匀性假设
二、材料的力学性能 (材料的力学性质)
低碳钢拉伸与压缩试验 4个阶段; 5个指标: p , s , b , , 几种现象; 铸铁拉伸与压缩试验
三、拉压强度条件及其应用
F N 的确定:试验 A
s
ns
或
b
nb
第二章 拉伸和压缩
2
M 2 ( x) V dx L 2 EI
内
力
计
算
拉
压 扭 转 平 面 弯 曲
快速计算方法:看笔记
快速计算方法:看笔记
快速计算方法:看笔记
第五章 弯曲应力 1 纯弯曲:
q0
FS cx b (c 0)
M
FS cx b (c 0)
FS c
M cx b
1 2 1 cx bx d (c 0) M cx 2 bx d (c 0) 2 2
第四章 弯曲内力 集中力作用处 集中力偶作用处
若某截面的剪力FS(x)=0,根据
FS (b) FS (a ) Aq
第四章 弯曲内力
q(x)
dM ( x ) FS ( x ) dx
若横截面 A,B 间无集中力偶作用则得
b b
a
b
a
dM FS ( x )dx
a
M (b) M (a ) AFS
M (b) M (a ) AFS
拉 /压 A
扭
转 A M n T>0
FN ( x) dL dx L EA( x )
AB
T dx L AB GI p
q f´
拉(压) 强 度 条 件 刚 度 条 件 变 形 能
2
扭
转
平 面 弯 曲
max [ ]
max [ ]
|M n|max Wt [ ] M n|max Wt [ ]
max [ ] max [ ]
Tl GI p
max
b 圆轴扭转的刚度条件:
一定要注意转角单位的 Tmax 180 一致(弧度与角度的转换) GI p
第四章 弯曲内力 1、平面弯曲的概念
若梁上的外载荷都作用在纵向对称平面内,则梁弯曲变形后的轴 线为纵向对称平面内的平面曲线。
—— 这种弯曲称为平面弯曲或对称弯曲。 2、剪力与弯矩 a. 剪力的正负
3
T 2 2 r
4、圆轴扭转横截面上的应力
T Ip
5 极惯性矩与抗扭截面系数
a. 实心圆截面
max
D4
32
T Wp
Wp
Ip
D3
16
第三章 扭转
b. 空心圆截面 c. 薄壁圆截面
Ip
D4
32 3 I p 2 R0
(1 4 )
Wp
D3
16 2 Wp 2 R0
(1 4 )
6 圆轴扭转破坏与强度条件
脆性材料扭转破坏: 塑性材料扭转破坏: 沿 450 螺旋曲面被拉断 沿横截面被剪断
圆轴扭转的强度条件为:
max
Tmax Wp Ti li GI pi
7 圆轴扭转变形与刚度条件
a 圆轴扭转时的变形:
平 面 弯 曲 M M>0 F >0 x—平行于杆轴 s
A Fs
内 力
N
FN > 0
x—杆轴 x
应 力
FN ( x) A
x—杆轴
O
T ( ) Ip
My x Iz
x
F S y y S z bI z
变 形
L
A
B
n
f
f ( x)
q
M ( x) EI
x w f
d M ( x) FS ( x) 0,该 dx
截面的弯矩为极值。
第四章 弯曲内力
3. 分布荷载集度、剪力和弯矩之间的积分关系
dFS ( x ) q( x ) dx
a
若在 a 和 b 两个横截面之间无集中力,则
q(x) b
b
a
dFS( x ) q( x )dx
a
b a
b
FS (b) FS (a ) q( x )dx Aq
M max Wz [ ] M max Wz [ ]
| wmax | w l l
N max Amin [ ] N max A[ ]
[ ] max
q max [q ]
FN ( x) V dx L 2 EA
V T ( x) dx L 2GI p
