大物实验亥姆赫兹实验报告
亥姆霍兹线圈实验报告

亥姆霍兹线圈实验报告亥姆霍兹线圈实验报告引言:亥姆霍兹线圈是一种由两个同轴圆形线圈组成的实验装置,广泛应用于物理学、电子学以及医学等领域。
本实验旨在通过观察亥姆霍兹线圈在不同电流条件下的磁场分布,探究其在磁场研究中的应用。
实验目的:1. 了解亥姆霍兹线圈的基本结构和工作原理;2. 掌握亥姆霍兹线圈的实验操作方法;3. 研究不同电流条件下亥姆霍兹线圈的磁场强度分布。
实验装置:1. 亥姆霍兹线圈:由两个同轴圆形线圈组成,线圈间距与半径相等;2. 电源:提供电流供给;3. 磁场测量仪器:如磁力计或霍尔效应传感器。
实验步骤:1. 将亥姆霍兹线圈放置在水平桌面上,并调整两个线圈的间距与半径相等;2. 将电源与亥姆霍兹线圈相连,确保电流正常通路;3. 将磁场测量仪器放置在亥姆霍兹线圈的中心位置,并进行校准;4. 开始实验前,先设置电流大小为零,观察磁场测量仪器的示数是否为零;5. 逐步增加电流,记录不同电流下磁场测量仪器的示数;6. 根据记录的数据,绘制电流与磁场强度的关系曲线。
实验结果:通过实验观察和数据记录,我们得到了电流与磁场强度之间的关系曲线。
根据曲线的形状,我们可以得出以下结论:1. 在亥姆霍兹线圈内部,磁场强度随着电流的增大而增大;2. 在亥姆霍兹线圈中心位置,磁场强度较为均匀,呈现出近似于匀强磁场的分布;3. 在亥姆霍兹线圈外部,磁场强度随着距离线圈中心的增加而减小。
讨论:亥姆霍兹线圈的实验结果与理论预期相符。
根据安培定律和比奥-萨伐尔定律,我们可以推导出亥姆霍兹线圈内部的磁场强度与电流的关系。
在实验中,我们观察到了磁场强度与电流成正比的关系,这与理论计算结果一致。
亥姆霍兹线圈的磁场分布特性使其在物理学研究中具有广泛的应用。
例如,在粒子加速器中,亥姆霍兹线圈可以用来产生稳定的磁场,用于粒子束的聚焦和偏转。
在医学影像学中,亥姆霍兹线圈被用于磁共振成像(MRI)设备中,通过产生均匀的磁场来激发人体组织中的核磁共振信号。
亥姆霍兹线圈磁场实验报告

亥姆霍兹线圈磁场实验报告亥姆霍兹线圈磁场实验报告引言:磁场是我们日常生活中常常接触到的物理现象之一。
为了更好地理解和研究磁场的特性,科学家们进行了许多实验。
本实验报告将介绍亥姆霍兹线圈磁场实验的过程和结果,并探讨其在科学研究和应用中的意义。
实验目的:本实验的目的是通过制作亥姆霍兹线圈并测量其磁场强度,验证亥姆霍兹线圈的磁场特性,并了解磁场对物体的影响。
实验装置和原理:实验中使用的主要装置是亥姆霍兹线圈,它由两个平行的同轴线圈组成,每个线圈上有N个匝数。
当通过线圈的电流为I时,可以产生均匀的磁场。
亥姆霍兹线圈的磁场强度可以通过以下公式计算得出:B = (μ0 * N * I) / (2 * R)其中,B表示磁场强度,μ0是真空中的磁导率,N是线圈的匝数,I是通过线圈的电流,R是线圈半径。
实验步骤:1. 制作亥姆霍兹线圈:根据实验要求,选择合适的线圈半径和匝数,使用导线绕制两个平行的同轴线圈,并将其固定在一个支架上。
2. 连接电路:将线圈的两端与电源连接,确保电流可以通过线圈。
3. 测量磁场强度:使用磁场强度计或霍尔效应传感器等仪器,在不同位置上测量磁场强度,并记录测量结果。
4. 改变电流强度:通过调节电源的电流大小,改变线圈的电流强度,再次测量磁场强度,并记录结果。
实验结果与分析:根据实验步骤,我们制作了亥姆霍兹线圈并进行了磁场强度的测量。
通过将磁场强度计放置在不同位置上,我们得到了一系列的测量结果。
随着距离线圈中心的距离增加,磁场强度逐渐减小,符合亥姆霍兹线圈的磁场分布特性。
通过改变线圈的电流强度,我们可以观察到磁场强度的变化。
根据磁场强度与电流的线性关系,我们可以验证亥姆霍兹线圈的磁场公式。
实验结果与理论计算值相符,进一步验证了亥姆霍兹线圈的磁场特性。
实验意义:亥姆霍兹线圈磁场实验是研究磁场特性的重要手段之一。
通过实验,我们可以更好地理解磁场的分布规律和影响因素。
亥姆霍兹线圈的磁场特性研究对于电磁学的发展和应用具有重要意义。
亥姆霍兹线圈磁场测定-实验报告

亥姆霍兹线圈磁场测定-实验报告实验目的:1. 掌握亥姆霍兹线圈原理及其构造;2. 熟悉磁场测定的基本方法;3. 使用亥姆霍兹线圈测定磁场的强度,了解其精度;4. 熟悉使用万用表和数字万用表进行电量测量。
实验原理:亥姆霍兹线圈是一种特殊的线圈结构,由两个同轴的环形线圈组成,两个线圈的半径相等,通电方向相反,电流强度相等,在同一轴向上构成匀强磁场。
如果通过两线圈流同向电流,其磁场强度将会倍增。
由于外界物体的磁场强度对线圈的磁场有一定的影响,因此在实验过程中,需要先测定环境中的磁场强度,再将线圈放置于恒定的磁场中,通过测量线圈中的磁场强度差,求得外磁场的强度。
实验器材:亥姆霍兹线圈、数字万用表、长板子、短板子、直流电源等。
实验步骤:1. 将亥姆霍兹线圈放置于平稳的桌面上,用数字万用表测定环境中的磁场强度,记录下读数。
2. 在同一位置,保持线圈不动,通过调节直流电源输出电压,使亥姆霍兹线圈中的磁场强度降低至为0。
记录下此时的电压值,并将其记作$U_0$。
5. 测量亥姆霍兹线圈本身的参数:使用数字万用表测量亥姆霍兹线圈中圈数,环半径等参数。
6. 计算环境中的磁场强度B0:根据数字万用表测量得到的环境磁场强度读数,使用其对应的磁场表值作为环境磁场强度B0。
7. 计算磁场强度B:由均匀磁场的定义,设线圈中磁场$B_1$和$B_2$分别为直流电源输出电压为$U_1$和$U_2$时线圈中磁场的强度,则有$B=\frac{1}{2}(B_1+B_2)$。
8. 计算外界磁场的强度B': 由于亥姆霍兹线圈内自带磁场,需要在计算磁场强度B 时,减去线圈的自感磁场强度$B_{self}$。
因此,有$B'=B-B_{self}$。
9. 计算磁场强度的不确定度:需考虑设备测量误差和环境影响因素的影响,根据不确定度的综合误差计算公式$U=\sqrt {\sum_{i=1}^n u_i}$,其中n为误差项的数目,$u_i$为每一误差项的保守评估。
亥姆霍兹线圈实验报告
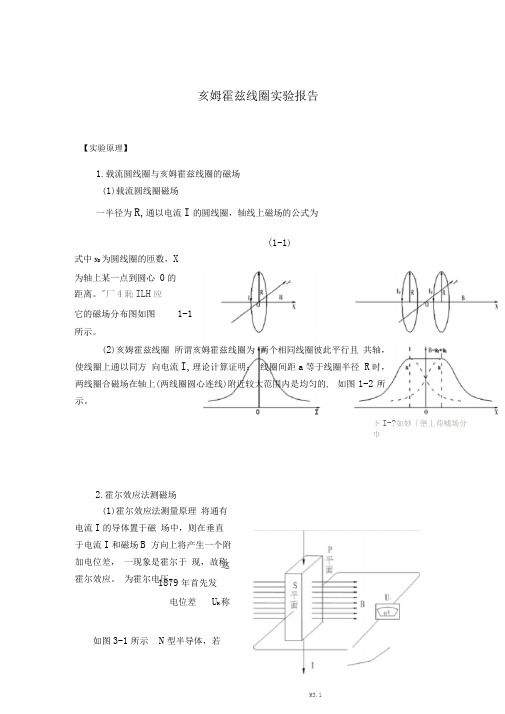
亥姆霍兹线圈实验报告【实验原理】1.载流圆线圈与亥姆霍兹线圈的磁场(1)载流圆线圈磁场一半径为R,通以电流I 的圆线圈,轴线上磁场的公式为式中N D 为圆线圈的匝数,X 为轴上某一点到圆心 0的 距离。
"厂4恥ILH 应 它的磁场分布图如图 1-1 所示。
(1-1) 0 I(2)亥姆霍兹线圈 所谓亥姆霍兹线圈为 两个相同线圈彼此平行且 共轴,使线圈上通以同方 向电流I,理论计算证明: 线圈间距a 等于线圈半径 R 时,两线圈合磁场在轴上(两线圈圆心连线)附近较大范围内是均匀的, 如图1-2所示。
卜I-?如妙「巒丄荀噓场分巾2.霍尔效应法测磁场 (1)霍尔效应法测量原理 将通有电流I 的导体置于磁 场中,则在垂直于电流I 和磁场B 方向上将产生一个附加电位差, 一现象是霍尔于 现,故称霍尔效应。
为霍尔电压。
这 1879年首先发 电位差 U H 称 如图3-1所示 N 型半导体,若 M3.1在MN 两端加上电压U,则有电流I 沿X 轴方向流动(有速度为V 运动的电子), 此时在Z 轴方向加以强度为 B 的磁场后,运动着的电子受洛伦兹力F B 的作用而偏移、聚集在 S 平面;同时随着电子的向 S 平面(下平面)偏移和聚集, 在 P 平面(上平面)出现等量的正电荷,结果在上下平面之间形成一个电场 E H (此电场称之为霍尔电场)。
这个电场反过来阻止电子继续向下偏移。
当 电子受到的洛伦兹力和霍尔电场的反作用力这二种达到平衡时,就不能向下 偏移。
此时在上下平面(S 、P 平面)间形成一个稳定的电压 U H (霍尔电压)。
2)霍尔系数、霍尔灵敏度、霍尔电压设材料的长度为I ,宽为b ,厚为d ,载流子浓度为 n ,载流子速度v , 则与通过材料的电流 I 有如下关系:I=nevbdR H =1/ne ,单位为 m3/c ;霍尔灵敏度 KH=RRZd ,单位为 mV/mA I 为常数时,有U H = K H IB =k o B ,通过测量霍尔电压 U H ,就本实验使用的仪器用集成霍尔元件,已经与显示模块联调,直接显示磁 场强度。
亥姆霍兹线圈实验报告

亥姆霍兹线圈实验报告【实验原理】1.载流圆线圈与亥姆霍兹线圈的磁场(1)载流圆线圈磁场一半径为R,通以电流I的圆线圈,轴线上磁场的公式为(1-1)式中N0为圆线圈的匝数,X为轴上某一点到圆心O的距离。
它的磁场分布图如图1-1所示。
(2)亥姆霍兹线圈所谓亥姆霍兹线圈为两个相同线圈彼此平行且共轴,使线圈上通以同方向电流I,理论计算证明:线圈间距a等于线圈半径R时,两线圈合磁场在轴上(两线圈圆心连线)附近较大范围内是均匀的,如图1-2所示。
2.霍尔效应法测磁场(1)霍尔效应法测量原理将通有电流I的导体置于磁场中,则在垂直于电流I和磁场B方向上将产生一个附加电位差,这一现象是霍尔于1879年首先发现,故称霍尔效应。
电位差U H称为霍尔电压。
如图3-1所示N型半导体,若在MN两端加上电压U,则有电流I沿X轴方向流动(有速度为V运动的电子),此时在Z轴方向加以强度为B的磁场后,运动着的电子受洛伦兹力F B的作用而偏移、聚集在S平面;同时随着电子的向S平面(下平面)偏移和聚集,在P平面(上平面)出现等量的正电荷,结果在上下平面之间形成一个电场E H(此电场称之为霍尔电场)。
这个电场反过来阻止电子继续向下偏移。
当电子受到的洛伦兹力和霍尔电场的反作用力这二种达到平衡时,就不能向下偏移。
此时在上下平面(S、P平面)间形成一个稳定的电压U H(霍尔电压)。
(2)霍尔系数、霍尔灵敏度、霍尔电压设材料的长度为l,宽为b,厚为d,载流子浓度为n,载流子速度v,则与通过材料的电流I有如下关系:I=nevbd霍尔电压 U H=IB/ned=R H IB/d=K H IB式中霍尔系数R H=1/ne,单位为m3/c;霍尔灵敏度K H=R H/d,单位为mV/mA由此可见,使I为常数时,有U H= K H IB =k0B,通过测量霍尔电压U H,就可计算出未知磁场强度B。
本实验使用的仪器用集成霍尔元件,已经与显示模块联调,直接显示磁场强度。
亥姆赫兹实验报告

实验项目名称亥姆霍兹线圈磁场测量一. 实验目的1. 学习和掌握霍尔效应原理测量磁场的方法;2. 测量载流圆线圈和亥姆霍兹线圈轴线上的磁场分布。
二. 实验原理载流圆线圈与亥姆霍兹线圈1、载流圆线圈磁场半径为 R 通以电流为 I 的圆线圈,周线上磁场的公式为B = μ0 N 0 IR 22( R 2 + x 2 )2/3式中 N 0 为线圈的匝数; x 为轴上某一点到圆心O 的距离; μ0 = 4π ⨯107 H ⋅ m -1 .本次实验取 I = 69.7 mA.2、亥姆霍兹线圈两个相同线圈彼此靠近,使线圈上通以同向电流理论计算证明:线圈间距a 等于线圈半径 R 时,两线圈合场在轴 附近较大范围内是均匀的.这时线圈称为亥姆霍兹线圈。
电磁感应法测磁场1. 电磁感应法测磁场的原理设由交流信号驱动的交变磁场的强度 B = B m sin ωt ,设有一个探测线圈放在这个磁场中,通过这个探测线圈的有效磁通量为Φ = NSB m cos θ sin ωt式中, N 为探测线圈的匝数,S 为线圈的截面积;θ 为 B 与线圈法线夹角.线圈产生的感应电动势为 t t B NS dt d m m ωεωθωφεcos cos cos --===当θ = 0 时,εmax = NS ωB m .用数字式毫伏表测量此时线圈的电动势,则其示值U max 应为 2maxε ,则 m m m U NS NS B ωωε2==由(1)式可以计算出 B m .2 探测线圈的技术指标试验中探测线圈的长度L 和D 有L=2/3D 的关系,线圈内径为d, D=0.012m, N=800匝,线圈在磁场中的有效面积经过理论计算为210813D S π三. 实验仪器磁场测试仪、亥姆霍兹线圈架、亥姆霍兹磁场实验控制箱四. 实验内容及步骤1.测量圆电流线圈轴上磁场的分布(1)仪器使用前,请先开机预热5min 接好电路,调零;(2) 调节磁场试验仪的输出功率,使励磁电流有效值为I=200mA ,以圆电流线圈中心为坐标原点,每隔10.0mm 测一个Bm 值,测量过程中注意保持励磁电流值不变,记录数据并作出磁场分布曲线图。
亥姆赫兹实验报告模板
南昌大学物理实验报告课程名称:大学物理基础试实验实验名称:亥姆霍茨一、实验目的:1,、学习和掌握霍尔效应原理测量磁场的方法2、测量载流圆线圈和亥姆霍兹线圈的磁场分布二、实验原理:1. 载流圆线圈与亥姆霍兹线圈的磁场:(1)载流圆线圈:其中,R为线圈半径,I为电流,N0为线圈匝数,X为轴上某一点到圆心的距离,为真空磁导率。
(2)亥姆霍兹线圈:2. 电磁感应法测量磁场: ;;ωωεωεεωθφωNS U NS B t t NSB tB B mm m m m 2cos sin cos sin m ==-===; 。
线圈等效面积为210813D S π=3. 霍尔效应法:IBK d IB R ned IB U nevbdI H h h ====//其中,材料宽b ,厚d ,载流子浓度n ,载流子速度v ,通过材料电流I 。
霍尔电压:;其中,霍尔系数R H =1/ne 单位m 3/c ,霍尔灵敏度K H =R h /d 。
三、实验仪器:亥姆霍茨线圈磁场实验仪四、实验内容和步骤:1、测量圆电流线圈轴线上磁场的分布 (1)先预热5分钟,调零(2)调节磁场实验仪的输出功率,使励磁场电流为200mA,每隔10mm 测量一个B 值,记录数据并 作出磁场分布图2、测量亥姆霍茨线圈轴线磁场的分布五、实验数据与处理:六、误差分析:1. 其他磁场对线圈磁场强度测量的干扰;2. 亥姆霍兹线圈的两个线圈的圆心不在同一水平线上,导致实验误差;3. 实验仪器本身具有一定的误差。
七、原始数据:八实验总结磁场感应器难以放在线圈中心,桌子对面的仪器对我有误差,一开始我做这个实验忽略了移动装置自带瞄准刻度的线,导致实验重新做,做实验前要注重对实验器具的了解,不能盲目动手。
大物实验亥姆赫兹实验报告
大学物理实验报告 课程名称: 大学物理实验 实验名称: 亥姆霍兹线圈磁场一.实验项目名称:亥姆霍兹线圈磁场二.实验目的1.学习和掌握霍尔效应原理测量磁场的方法2.测量载流圆线圈和亥姆霍兹轴线上的磁场分布三.实验原理1.载流圆线圈与亥姆霍兹线圈的磁场(1) 载流圆线圈磁场一半径为R,通以电流I的圆线圈,轴线上磁场的公式为23222002/)X R (IR N B +=μ(1-1)式中0N 为圆线圈的匝数,X 为轴上某一点到圆心O 的距离。
,/10470m H -⨯=πμ 它的磁场分布图如图1-1所示。
(2)亥姆霍兹线圈所谓亥姆霍兹线圈为两个相同线圈彼此平行且共轴,使线圈上通以同方向电流I,理论计算证明:线圈间距a等于线圈半径R时,两线圈合磁场在轴上(两线圈圆心连线)附近较大范围内是均匀的,如图1-2所示。
2. 电磁感应法测量磁场:;;;。
线圈等效面积为。
3. 霍尔效应法:其中,材料宽b,厚d,载流子浓度n,载流子速度v,通过材料电流I。
霍尔电压:; 其中,霍尔系数R H,霍尔灵敏度K H。
四.实验仪器亥姆霍兹实验仪由二部分组成。
它们分别为励磁线圈架部分(见图〈一〉)和磁场测量仪器部分(见图〈二〉)。
二个励磁线圈:线圈有效半径 105mm线圈匝数 500匝二线圈中心间距 105mm测量磁场传感器:4501A使用霍尔元件测量磁场。
移动装置:横向可移动距离150mm,纵向可移动距离50mm距离分辨力0.5mm五.实验内容及步骤1.一起使用前,先开机预热5min,接好电路,调零。
2. 测量圆电流线圈轴线上磁场的分布接好电路。
调节磁场实验仪的输出功率,使励磁电流有效值为I=200mA,以圆电流线圈中心为坐标原点,每隔10.0 mm测一个Bm值,测量过程中注意保持励磁电流值不变,记录数据并作出磁场分布曲线图。
3.测量亥姆霍兹线圈轴线上磁场的分布把磁场实验仪的两组线圈串联起来(注意极性不要接反),接到磁场测试仪的输出端钮。
亥姆赫兹实验报告模板
时, m NSBm 用数字式毫伏表测量此时线圈的电动 势,则其示值 U m 应为 计算出 Bm 。
m 2U m ,则 Bm m ,由此可 NS NS 2
三、实验仪器: 磁场测试仪、 亥姆霍兹线圈架和亥姆霍兹磁场实验控 制箱.工作温度 10~35℃,相对湿度 25%~75%. 两 个励磁线圈各 500 匝, 圆线圈的平均半径 105R mm, 两 线 圈 中 心 间 距 105mm. 感 应 线 圈 距 离 分 辨 率 0.5mm。
四、实验内容及步骤:1. 测量亥姆霍兹线圈周线上的磁场分布 2.验证公式 m NSBmcos 3. 研究励磁电流频率改变对磁场强度的影响 。 五.数据记录及处理: 亥姆霍兹线圈 轴向距离/cm -110 实测 B/mT 0.474 I=200mA -100 0.532 -50 0.793 0 0.852 50 0.792 100 0.533 -90 0.593 -40 0.816 10 0.844 60 0.754 110 0.475 -80 0.650 -30 0.834 20 0.842 70 0.704 -70 0.706 -20 0.841 30 0.835 80 0.651
I=200mA 10 0.465 60 0.566 110 0.394 20 0.508 70 0.540 30 0.539 80 0.520
七、附上原始实验数据(拍照)
号驱动的交变磁场的强度 B Bmsint 设有一个探测线 圈放在这个磁场中,通过这个探测线圈的有效磁通量 为 NSBmcossint 式中,N 为探测线圈的匝数,S 为 线圈的截面积; 为 B 与线圈法线夹角.线圈产生的感 应电动势为
d NSBm cos cos t m cos t 当 =0 dt
亥姆霍兹线圈实验报告
亥姆霍兹线圈实验报告一、实验目的1.1 探索亥姆霍兹线圈的磁场特性亥姆霍兹线圈,听起来是不是有点高大上?其实,它是由两个相同的圆形线圈组成,彼此平行且间距固定。
这个实验的目的就是想看看在不同电流下,亥姆霍兹线圈会产生怎样的磁场。
我们要找出这些磁场的分布情况,以及它们和电流之间的关系。
1.2 磁场测量磁场的测量是个细致活。
我们用到的工具叫“霍尔效应传感器”。
它可以精确测量磁场的强度和方向。
搭配一些简单的仪器,比如电源和电流表,我们就可以开始实验了。
这个过程既复杂又刺激,充满了探索的乐趣。
二、实验步骤2.1 准备工作首先,得把亥姆霍兹线圈搭建好。
线圈的直径和线圈之间的距离都是有讲究的。
我们得确保它们完美对称,这样才能得到理想的磁场。
接着,连接电源,调试电流的大小。
小心翼翼,生怕弄错了。
2.2 测量磁场接下来就是关键环节。
把霍尔传感器放在线圈中间,调节电流,从小到大逐步增加。
每一次变化都让我心跳加速。
随着电流的增大,磁场强度也随之变化。
这种直接的因果关系让人惊叹。
2.3 数据记录记录数据的时候,得保持专注。
每一个数字背后都藏着宝贵的信息。
磁场强度、位置、时间,一一不落。
看着一串串数据在纸上排列开来,真有种小小的成就感。
实验的每一步,都是一次新的发现。
三、结果分析3.1 磁场分布根据记录的数据,我们可以绘制出磁场的分布图。
这张图,就像是一幅艺术作品,清晰地展现了磁场的特性。
中心区域的磁场强度最大,逐渐向外减弱。
这个过程让人深刻体会到“物极必反”的道理。
3.2 电流与磁场的关系接下来,我们分析电流和磁场之间的关系。
数据表明,电流越大,磁场强度也越强。
简单明了,像极了生活中的许多道理——投入越多,收获越大。
这种线性关系不仅符合我们的预期,更加坚定了我们对物理规律的信心。
四、总结亥姆霍兹线圈的实验让我感受到了科学的魅力。
每一个步骤都让我更加理解了磁场的本质,体会到了实验的重要性。
科学不仅仅是冷冰冰的公式,更是充满了无限可能的探索之旅。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学物理实验报告 课程名称: 大学物理实验 实验名称: 亥姆霍兹线圈磁场
一.实验项目名称:亥姆霍兹线圈磁场
二.实验目的
1.学习和掌握霍尔效应原理测量磁场的方法
2.测量载流圆线圈和亥姆霍兹轴线上的磁场分布
三.实验原理
1.载流圆线圈与亥姆霍兹线圈的磁场
(1) 载流圆线圈磁场
一半径为R,通以电流
I的圆线圈,轴线上磁
场的公式为
23222
002/)X R (IR N B +=μ
(1-1)
式中0N 为圆线圈的匝数,X 为轴上某一点到圆心O 的距离。
,/10470m H -⨯=πμ 它的磁场分布图如图1-1所示。
(2)亥姆霍兹线圈
所谓亥姆霍兹线圈为两个相同线圈彼此平行且共轴,使线圈上通以同方向电流I,理论计算证明:线圈间距a等于线圈半径R时,两线圈合磁场在轴上(两线圈圆心连线)附近较大范围内是均匀的,如图1-2所示。
2. 电磁感应法测量磁场:
;;
;。
线圈等效面积为。
3. 霍尔效应法:
其中,材料宽b,厚d,载流子浓度n,载流子速度v,通过材料电流
I。
霍尔电压:; 其中,霍尔系数R H,霍尔灵敏度K H。
四.实验仪器
亥姆霍兹实验仪由二部分组成。
它们分别为励磁线圈架部分(见图〈一〉)和磁场测量仪器部分(见图〈二〉)。
二个励磁线圈:线圈有效半径 105mm
线圈匝数 500匝
二线圈中心间距 105mm
测量磁场传感器:4501A使用霍尔元件测量磁场。
移动装置:横向可移动距离150mm,纵向可移动距离50mm
距离分辨力0.5mm
五.实验内容及步骤
1.一起使用前,先开机预热5min,接好电路,调零。
2. 测量圆电流线圈轴线上磁场的分布
接好电路。
调节磁场实验仪的输出功率,使励磁电流有效值为I=200mA,以圆电流线圈中心为坐标原点,每隔10.0 mm测一个Bm值,测量过程中注意保持励磁电流值不变,记录数据并作出磁场分布曲线图。
3.测量亥姆霍兹线圈轴线上磁场的分布
把磁场实验仪的两组线圈串联起来(注意极性不要接反),接到磁场测试仪的输出端钮。
调节磁场测试仪的输出功率,使励磁电流有效值仍为I=200mA。
以两个圆线圈轴线上的中心点为坐标原点,每隔10.0mm测一个Bm 值。
记录数据并作出磁场分布曲线图。
六.数据记录及处理(包括数据表格、数据计算、画图等)
1. 圆电流线圈轴线上磁场分布的测量数据(注意坐标原点在-53处)。
单线圈
刻度/mm到中心的距离x/mm测量值/mT理论值B/mT 10630.3020.377
0530.3390.426 -10430.3810.474
-20330.4230.519
-30230.4600.557
-40130.4930.585
-5030.5160.597
-5300.5190.598
-60-70.5240.594
-70-170.5200.575
-80-270.5020.543
-90-370.4740.502
-100-470.4380.455
-110-570.3970.406
2.亥姆霍兹线圈轴线上的磁场分布的测量数据,(注意坐标原点设在两个线圈圆心连线的中点0处)。
双线圈
刻度/mm 测量值/mT
-1100.505
-1000.571
-900.622
-800.667
-700.708
-600.730
-500.748
-400.761
-300.767
-200.768
-100.769
00.769
100.769
200.765
300.754
400.734
500.705
600.665
700.614
800.565
900.505
1000.447
1100.395
七.实验结果分析与小结
单线圈轴线上磁感应强度分布的理论值和实验值的误差产生的原因是: 1.线圈可能歪斜,并不在竖直平面;
2.对环心位置估计有误差;
3.仪器原因。
亥姆霍兹线圈轴线上的磁场分布误差产生的原因是:
1. 其他磁场对线圈磁场强度测量的干扰;
2. 亥姆霍兹线圈的两个线圈的圆心不在同一水平线上,导致实验误差;
3. 实验仪器本身具有一定的误差。
八.附上原始实验数据(拍照)。
