直方图规定化
直方图规定化过程
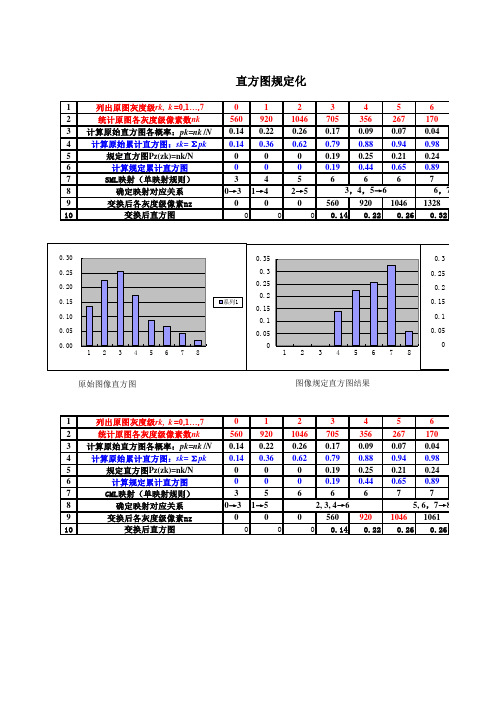
2 1046 0.26 0.62 0 0 6 0
3 705 0.17 0.79 0.19 0.19 6 2, 3, 4→6 560 0 0.14
4 356 0.09 0.88 0.25 0.44 6 920 0.22
6 170 0.04 0.98 0.24 0.89 7 5, 6，7→8 1046 1061 0.26 0.26
0.30
0.35
0.3
0.3
0.25
0.25 0.20 0.15 0.10 0.05 0.00 1 2 3 4 5 6 7 8
系列1
0.25 0.2 0.15 0.1
0.05
0.2 0.15 系列1 0.1 0.05 0 1 2 3 4 5 6 7 8
0
原始图像直方图
图像规定直方图结果
1 2 3 4 5 6 7 8 9 10
直方图规定化
1 2 3 4 5 6 7 8 9 10 列出原图灰度级rk, k =0,1…,7 统计原图各灰度级像素数nk 计算原始直方图各概率：pk=nk /N 计算原始累计直方图：sk= Σpk 规定直方图Pz(zk)=nk/N 计算规定累计直方图 SML映射（单映射规则） 确定映射对应关系 变换后各灰度级像素nz 变换后直方图 0 1 560 920 0.14 0.22 0.14 0.36 0 0 0 0 3 4 0→ 3 1→ 4 0 0 0 0 2 1046 0.26 0.62 0 0 5 2→ 5 0 0 3 705 0.17 0.79 0.19 0.19 6 4 356 0.09 0.88 0.25 0.44 6 3， 4， 5→ 6 560 920 0.14 0.22 5 267 0.07 0.94 0.21 0.65 6 1046 0.26 6 170 0.04 0.98 0.24 0.89 7 6， 7→ 8 1328 0.32
Matlab实现直方图规定化
Matlab实现直⽅图规定化直⽅图规定化算法分析1. 求出原图的累积概率分布2. 求出规定图的累积概率分布3. 求出原图中每⼀个灰度级累积概率与规定图的累积概率最接近的灰度级4. 根据第3步的⽅法将原图的灰度映射到标准图中距离最近的灰度值伪代码function outputimg = my_histspec(A,B)% 灰度图的直⽅图规定化% 输⼊：A是读⼊的原图，B是读⼊的规定化的标准图% 输出：outputimg是将A规定化到B之后的图像[HA,WA] = 原图的⼤⼩[HB,WB] = 标准图的⼤⼩统计原图灰度级频数统计标准图灰度级频数计算原图灰度级概率计算标准图灰度级概率计算原图灰度级累积概率分布计算标准图灰度级累积概率分布%求原图和标准图的映射关系，找到两个累积概率最接近的灰度级遍历原图的每个灰度级value{j} = 求标准图当前灰度级累积概率与原图所有灰度级累积概率之差的绝对值[temp{j},index(j)] = index中存的是vlaue中最⼩值的下标outputimg = 开辟⼀个和原图⼤⼩⼀致的新矩阵存放规定化后的图像遍历outputimgoutputimg(i,j) = 根据映射关系为每⼀个新矩阵的像素点赋灰度值转换outputimg成uint8数据类型end代码function outputimg = my_histspec(A,B)% 灰度图的直⽅图规定化% 输⼊：A是读⼊的原图，B是读⼊的规定化的标准图% 输出：outputimg是将A规定到B之后的图像[HA,WA] = size(A);[HB,WB] = size(B);PA = imhist(A) / (HA * WA);PB = imhist(B) / (HB * WB);%求累积概率分布for i = 2 : 256PA(i) = PA(i - 1) + PA(i);PB(i) = PB(i - 1) + PB(i);end%求原图和映射图的映射关系，找到两个累积直⽅图距离最近的点for j = 1:256value{j} = abs(PB - PA(j));[temp{j},index(j)] = min(value{j}) %index中存的是最⼩值的下标，temp中存的是最⼩值endoutputimg = zeros(HA, WA);for i = 1:HAfor j = 1:WAoutputimg(i,j) = index(A(i,j) + 1)-1;endendoutputimg = uint8(outputimg);end实验结果%调⽤⽰例：A = imread('pout.tif');B = imread('coins.png');C = my_histspec(A,B);subplot(2,3,1);imshow(A);title('原图');subplot(2,3,2);imshow(B);title('标准图');subplot(2,3,3);imshow(C);title('匹配到标准图后');subplot(2,3,4);imhist(A);title('原图直⽅图');subplot(2,3,5);imhist(B);title('标准图直⽅图');subplot(2,3,6);imhist(C);title('匹配到标准图后直⽅图');实验分析直⽅图均衡化是直⽅图规定化的特例，理想状态下原图直⽅图均衡化和标准图均衡化后对应的直⽅图应该是相等的，通过求得原图累积概率和标准图累积概率最接近的灰度值映射，最后的效果是原图的直⽅图和标准图的直⽅图接近。
【数字图像处理】直方图的均衡与规定化
【数字图像处理】直⽅图的均衡与规定化很多情况下，图像的灰度级集中在较窄的区间，引起图像细节模糊。
通过直⽅图处理可以明晰图像细节，突出⽬标物体，改善亮度⽐例关系，增强图像对⽐度。
直⽅图处理基于概率论。
直⽅图处理通常包括直⽅图均衡化和直⽅图规定化。
直⽅图均衡化可实现图像的⾃动增强，但效果不易控制，得到的是全局增强的结果。
直⽅图规定化可实现图像的有选择增强，只要给定规定的直⽅图，即可实现特定增强的效果。
直⽅图均衡化直⽅图均衡化借助灰度统计直⽅图和灰度累积直⽅图来进⾏。
灰度统计直⽅图灰度统计直⽅图反映了图像中不同灰度级出现的统计情况。
灰度统计直⽅图是⼀个⼀维离散函数，可表⽰为h (k )=n k ,k =0,1,...L −1，其中k 为某个灰度级，L 为灰度级的数量，最⼤取256，n k 为具有第k 级灰度值的像素的数⽬。
灰度直⽅图归⼀化概率灰度统计直⽅图的归⼀化概率表达形式给出了对s k 出现概率的⼀个估计，可表⽰为p s (s k )=n k /N ,k =0,1,2..,L −1式中，k 为某个灰度级；L 为灰度级的数量，最⼤取256；s k 为第k 级灰度值的归⼀化表达形式，s k =k /255，故s k ∈[0，1]；n k 为具有第k 级灰度值的像素的数⽬；N 为图像中像素的总数，故（n k /N ）∈[0，1]。
灰度累计直⽅图灰度累积直⽅图反映了图像中灰度级⼩于或等于某值的像素的个数。
灰度累积直⽅图是⼀个⼀维离散函数，可表⽰为H (k )=k ∑i =0n i ,k =0,1,2..,L −1式中，k 为某个灰度级；L 为灰度级的数量，最⼤取256；n i 为具有第i 级灰度值的像素的数⽬。
累积分布函数可以表⽰为：t k =k ∑i =0p s (s i )相对的，灰度累积直⽅图的归⼀化表⽰如下图：Processing math: 100%原理步骤直⽅图均衡化主要⽤于增强动态范围偏⼩的图像的反差。
直方图规定化
直方图规定化直方图规定化是指将一幅图像的像素值分布规定到另一幅图像的像素值分布上的过程。
其基本思想是通过将目标图像的像素值分布函数变换为规定分布函数，再将原始图像的像素值进行相应的变换，从而实现两幅图像的像素值分布逼近或一致。
直方图规定化可以用于图像处理的许多应用，例如图像增强、图像融合、图像匹配等。
下面将详细介绍直方图规定化的原理和实现步骤。
直方图规定化的原理如下：1. 给定一幅原始图像和一幅目标图像，分别计算它们的像素值频率分布函数H1(i)和H2(i)。
2. 对于每一个像素值i，计算原始图像和目标图像的积累密度函数C1(i)和C2(i)。
3. 构造映射关系，将原始图像的像素值映射到目标图像的像素值上。
可以通过计算C1(i)和C2(i)的差值，得到原始图像像素值i在目标图像上的对应像素值j。
4. 使用这个映射关系，对原始图像的每个像素值i进行变换，得到规定化后的图像。
直方图规定化的实现步骤如下：1. 计算原始图像和目标图像的像素值频率分布函数H1(i)和H2(i)。
2. 对原始图像和目标图像的分布函数进行归一化处理，得到归一化分布函数P1(i)和P2(i)。
3. 计算归一化分布函数的积累密度函数C1(i)和C2(i)。
4. 对于每一个像素值i，计算C1(i)和C2(i)之间的差值。
5. 找到C2(i) - C1(i)绝对值的最小值，并记录对应的像素值j。
6. 将原始图像的像素值i映射到目标图像的像素值j。
7. 使用这个映射关系，对原始图像的每个像素值i进行变换，得到规定化后的图像。
直方图规定化要求原始图像和目标图像的像素值范围相同，并且分布函数的积累密度函数单调递增。
如果原始图像和目标图像的像素值范围不同，可以通过直方图均衡化等方法进行一定的预处理。
在实际应用中，直方图规定化是一个重要的图像处理技术，可以根据目标图像的特点调整原始图像的像素值分布，从而实现图像的增强和融合效果。
此外，直方图规定化还可以用于图像匹配，将不同图像的像素值分布规定为一致，方便后续的图像匹配和目标检测等任务。
图像直方图均衡的标准化与规定化处理
图像直方图均衡的标准化处理均衡化基本原理：对在图像中像素个数多的灰度值（即对画面其主要作用的灰度值）进行展宽，而对像素个数少的灰度值进行归并，从而达到清晰图像的目的。
代码：img=imread('tim.jpg');figure,imshow(img);[m,n]=size(img); %测量图像尺寸参数h=zeros(1,256) %预创建存放灰度出现概率的向量for k=0:255h(k+1)=length(find(img==k))/(m*n);endfigure,bar(0:255,h,'k') %绘制直方图title('原图像直方图')xlabel('灰度值')ylabel('出现概率')S1=zeros(1,256);for i=1:256for j=1:iS1(i)=h(j)+S1(i); %计算SkendendS2=round(S1*256); %将Sk归到相近级的灰度for i=1:256heq(i)=sum(h(find(S2==i))); %显示均衡化后的直方图endfigure,bar(0:255,heq,'k') %显示灰度变化曲线title('均衡化后的直方图')xlabel('灰度值')ylabel('出现概率')figure,plot(0:255,S2,'r') %显示灰度变化曲线legend('灰度变化曲线')xlabel('原图像灰度级')ylabel('均衡化后灰度级')TR=img;for i=0:255TR(find(img==i))=S2(i+1); %将各个像素归一化后的灰度值付给这个像素endfigure,imshow(TR) %将各个像素归一化后的灰度值赋给这个像素 title('均衡化后图像')imwrite(TR,'tim.jpg');实验效果图：原图像原图像直方图标准化后图像标准化后直方图：灰度变化曲线图像直方图均衡的规定化处理直方图规定化的基本原理：有目的地增强某个灰度区间的图像，即能够人为地修正直方图的形状，使之与期望的形状相匹配。
2.2.4 直方图规定化 _多媒体信息处理技术_[共3页]
![2.2.4 直方图规定化 _多媒体信息处理技术_[共3页]](https://img.taocdn.com/s3/m/8d29d0da6c85ec3a87c2c5f5.png)
第章 图像增强 4122.2.4 增强整幅图像的对比度，但它的具体增强效果不易控制，处理的结果总是得到近似均匀分布的直方图。
实际应用中，在不同的情况下，并不总是需要具有均匀直方图的图像，即希望找到灰度变换函数，使原直方图即是找一种变换，使得原图像r 之间的是直()d r 直方图规定化直方图均衡化的优点是能有时要求突出图像中人们感兴趣的灰度范围，图像的直方图变成所要求的特定形状，从而有选择地增强某个灰度值范围内的对比度。
直方图规定化就是针对上述要求提出来的一种直方图修正方法。
实际上，直方图均衡化是直方图规定化中给定直方图为均匀分布的一种特例。
下面仍然从研究连续灰度的概率密度函数入手来讨论直方图规定化的基本思想。
设()r p r 是待增强的原始图像的灰度分布概率密度函数，()z p z 是直方图规定化后的新图像（即希望得到的图像）的灰度分布概率密度函数。
规定化经变换后，变成了具有灰度分布概率密度函数()z p z 的新图像。
如何建立()z p z 和p ()r 联系方图规定化处理的关键。
首先对原始图像进行直方图均衡化处理，即()r 0s T r p ==∫ （）x x 2-16灰度分布概率密度函数为，并对其作直方图均衡化处理，即为 ()z p z 假定已经得到了所希望的规定化后的图像，其也0()()d z u G z p x x ==∫ （2-17）式（2-17）的反变换函数z 1()z G u −= （2-18）根据前面关于连续图像直方图均衡化的讨论，若对原始图像和期望图像都进行一次直方图均衡化处理，将会得到相同的归一化均匀灰度分布的概率密度函数，即()()1s u p s p u ==（2-19） 也就是说，均匀分布的随机变量s 和u 有完全相同的统计特性。
换句话说，在统计意义上说，它们是完全相同的。
为此，可用s 来代替式（2-18）中的u ，即)11()(G u G s −−== z （2-20） 这样，得到的灰度值z 便是所希望的规定化后的图像的灰度值。
直方图规定化
• 由于都是进行均衡化处理，处理后的原图 像概率密度函数Ps（S）及理想图像概率密 度函数PV（V）是相等的。于是，我们可 以用变换后的原始图像灰度级S代替（2） 式中的V。即 Z G 1 ( S ) ( 4) • 这时的灰度级Z 便是所希望的图像的灰度级。 • 此外，利用（1）与（3）式还可得到组合 变换函数
一个例子
序 号 1
2 3 4 5 6 7 8 9
运算
原始图像灰度级 原始直方图各灰度级像素 原始直方图P(r) 原始累积直方图V1 规定直方图P(z) 规定累积直方图V2 映射| V2 -V1|最小 确定映射关系 变换后直方图 0 790 0.19 0.19 0 0 3 0->3 0 1 1023 0.25 0.44 0 0 4 1->4 0 2 850 0.21 0.65 0 0 5 2->5 0
• 由 v k s k可知，所找的z值必须满足等式 G ( z k ) s k 因此要找 s k 所对应的 z k 只需在 z值上迭代，以满足等式。因为处理的是整 数，所能得到的满足等式 G ( z k ) sk 0 最接近的整数即可。
算法描述
• • • • 对源图像的直方图进行灰度级上的概率密度统计 对源图像的直方图概率密度进行直方图均衡化 对规定的直方图概率密度进行直方图均衡化 确定源图像直方图与规定直方图的对应映射关系， 原则是针对源图像均衡化后的直方图的每一个灰 度级概率密度，查找最接近的规定直方图灰度概 率密度，建立灰度映射表。 • 根据映射结果对像素点进行处理
直方图规定化
什么是直方图规定化
指定希望处理的图像所具有的直方图形状 用于产生处理后有特殊直方图的图像的方法 称为直方图匹配或直方图规定化处理 目的：实现对输入图像进行有目的地增强
数字图像的直方图规定化处理实验
XX 大学实验报告
（一） 掌握数字图像的直方图规定化处理的算法和方法。
（二） 熟悉数字图像的直方图规定化处理的算法原理。
按照实验内容及参考程序，独立完成此次实验，记下不懂的知识点，查阅资料或者向老 师咨询。
直方图规定化是用于产生处理后有特殊直方图的图像方法。
学院:
专业: 班级: 姓名 实验时间 实验项目名称
实验二：数字图像的直方图规定化处理
令
p r （r ）和Pz （z ）分别为原始图像和期望图像的灰度概率密度函数。
和期望图像均作直方图均衡化处理，应有：
r
s T （r ） 0 p r （r ）dr ，V G （Z ）
对原始图像
z 0
P z
(z )dz ，z
G
1
(V)
由于都是作直方图均衡化处理，所以处理后的原图像的灰度概率密度函数
p S （s ）及理
想图像的灰度概率密度函数 P V （V ）是相等的。
因此，可以用变换后的原始图像灰度级
S
代替上式中的V, 即Z G 1[T （r ）]。
利用此式可以从原始图像得到希望的图像灰度级。
对离散图像，有
P Z (ZJ
虹，V i G (乙)^P z (Z i )， Z i
G 1(S i ) G 1[T(r i )]
n
i 0
综上所述，数字图像的直方图规定化就是将直方图均衡化后的结果映射到期望的理想直 方图上，使图像按人的意愿去变换。
数字图像的直方图规定的算法如下：
（一）将原始图像作直方图均衡化处理， 求出原图像中每一个灰度级 r i 所对应的变
学号 指导教师
实验组 成绩。
(精品)数字图像处理实验报告--直方图规定化
数字图像处理实验报告直方图匹配规定化直方图均衡化能够自动增强整个图像的对比度，但它的具体增强效果不容易控制，处理的结果总是得到全局均匀化的直方图。
实际上有时需要变换直方图，使之成为某个特定的形状，从而有选择地增强某个灰度值范围内的对比度。
这时可以采用比较灵活的直方图规定化。
一般来说正确地选择规定化的函数可以获得比直方图均衡化更好的效果。
所谓直方图规定化，就是通过一个灰度映像函数，将原灰度直方图改造成所希望的直方图。
所以，直方图修正的关键就是灰度映像函数。
直方图匹配方法主要有3个步骤（这里设M和N分别为原始图和规定图中的灰度级数，且只考虑N≤M的情况）：(1) 如同均衡化方法中，对原始图的直方图进行灰度均衡化：(2) 规定需要的直方图，并计算能使规定的直方图均衡化的变换：(3) 将第1个步骤得到的变换反转过来，即将原始直方图对应映射到规定的直方图，也就是将所有pf(fi)对应到pu(uj)去。
一、A图直方图规定B图Matlab程序:%直方图规定化clear allA=imread('C:\Users\hp\Desktop\A.tif'); %读入A图像imshow(A) %显示出来title('输入的A图像')%绘制直方图[m,n]=size(A); %测量图像尺寸B=zeros(1,256); %预创建存放灰度出现概率的向量for k=0:255B(k+1)=length(find(A==k))/(m*n); %计算每级灰度出现的概率，将其存入B中相应位置endfigure,bar(0:255,B,'g'); %绘制直方图title('A图像直方图')xlabel('灰度值')ylabel('出现概率')axis([0,260,0,0.015])C=imread('C:\Users\hp\Desktop\B.tif');%读入B图像imshow(C) %显示出来title('输入的B图像')%绘制直方图[m,n]=size(C); %测量图像尺寸D=zeros(1,256); %预创建存放灰度出现概率的向量for k=0:255D(k+1)=length(find(C==k))/(m*n); %计算每级灰度出现的概率，将其存入D中相应位置endfigure,bar(0:255,D,'g'); %绘制直方图title('B图像直方图')xlabel('灰度值')ylabel('出现概率')axis([0,260,0,0.015])S1=zeros(1,256);for i=1:256for j=1:iS1(i)=D(j)+S1(i); %计算B灰度图累计直方图endendcounts=Bfigure,bar(0:255,counts,'r')title('A图像直方图 ')S2=zeros(1,256);for i=1:256for j=1:iS2(i)=counts(j)+S2(i);endend; %"累计"规定化直方图%对比直方图，找到相差最小的灰度级for i=1:256for j=1:255if S1(j)<=S2(i)&S1(j+1)>=S2(i)if abs(S1(j)-S2(i))<=abs(S1(j+1)-S2(i)) T(i)=j;else T(i)=j+1;endendendend%确定变换关系，重组直方图H=zeros(1,256);H(1)=S2(1);for i=2:255if T(i-1)>0for k=(T(i-1)+1):T(i)H(i)=H(i)+D(k);endelse H(i)=0;endendfigure,bar(0:255,H,'g') %显示规定化后的直方图title('A规定B后的直方图')xlabel('灰度值')ylabel('出现概率')axis([0,260,0,0.6])%显示规定图PA=C; %将各个像素归一化后的灰度值赋给这个像素for i=1:mfor j=1:nfor k=2:255if T(k-1)<=C(i,j)&C(i,j)<=T(k)PA(i,j)=k;break;endendendendfigure,imshow(PA) %显示规定化后的图像title('A规定B后图像')imwrite(PA,'guidinghua.bmp');二、用已知直方图规定A图规定灰度为[zeros(1,49),0.3,zeros(1,49),0.1,zeros(1,49),0.2,zeros(1,49),0.1,zeros(1,49 ),0.2,zeros(1,49),0.1]Matlab程序：clear allA=imread('C:\Users\hp\Desktop\B.tif'); %读入A图像imshow(A) %显示出来title('输入的A图像')%绘制直方图[m,n]=size(A); %测量图像尺寸B=zeros(1,256); %预创建存放灰度出现概率的向量for k=0:255B(k+1)=length(find(A==k))/(m*n); %计算每级灰度出现的概率，将其存入B中相应位置endfigure,bar(0:255,B,'g'); %绘制直方图title('A图像直方图')xlabel('灰度值')ylabel('出现概率')axis([0,260,0,0.015])S1=zeros(1,256);for i=1:256for j=1:iS1(i)=B(j)+S1(i); %计算原灰度图累计直方图endendcounts=[zeros(1,49),0.3,zeros(1,49),0.1,zeros(1,49),0.2,zeros(1,49),0.1,zer os(1,49),0.2,zeros(1,49),0.1];%规定化直方图figure,bar(1:300,counts,'r')title('规定化直方图')S2=zeros(1,256);for i=1:256for j=1:iS2(i)=counts(j)+S2(i);endend; %"累计"规定化直方图%对比直方图，找到相差最小的灰度级for i=1:256for j=1:256if S1(j)<=S2(i)&S1(j+1)>=S2(i)if abs(S1(j)-S2(i))<=abs(S1(j+1)-S2(i)) T(i)=j;else T(i)=j+1;endendendend%确定变换关系，重组直方图H=zeros(1,256);H(1)=S2(1);for i=2:256if T(i-1)>0for k=(T(i-1)+1):T(i)H(i)=H(i)+B(k);endelse H(i)=0;endendfigure,bar(0:255,H,'g') %显示规定化后的直方图title('规定化后的直方图')xlabel('灰度值')ylabel('出现概率')axis([0,260,0,0.6])%显示规定图PA=A; %将各个像素归一化后的灰度值赋给这个像素for i=1:mfor j=1:nfor k=2:256if T(k-1)<=A(i,j)&A(i,j)<=T(k)PA(i,j)=k;break;endendendendfigure,imshow(PA) %显示规定化后的图像title('规定化后图像')imwrite(PA,'guidinghua.bmp');。
直方图均衡化及规定化
直方图均衡化
直方图均衡化示意图
图(a) 原图灰度级直方图；图(b) 累积变换后的直方图； 图(c) 均衡化后的直方图；
直方图均衡化
直方图均衡化
直方图规定化
直方图规定化的原因： 在实际应用中，希望能够有目的地增强某 个灰度区间的图像， 即能够人为地修正直 方图的形状， 使之与期望的形状相匹配， 这就是直方图规定化的基本思想。
s G( z ) ( L 1) q(t )dt
0 z
3.由于它们的直方图均衡化图像理论上是一样的，即：
G( z ) s T (r ), z G 1[T (r )] G 1[s]
于是就得到了根据指定直方图来变换图像的直方图匹配变换。
直方图规定化
直方图规定化
直方图规定化
原图 均衡化的图像
直方图规定化
例如：Pr (r)为原图像的灰度密度函数, Pz (z)为希 望得到的增强图像的灰度密度函数,二者的直方图 如下:
直方图规定化
直方图规定化基本步骤：
1.先对原图做直方图均衡化，得到
s T (r ) ( L 1) p(t )dt
0 r
2.再对规定的直方图均衡化，得到
就给出了一个函数图形，称为直方图。
直方图未规范化 规范化直方图均衡化均衡化的原因： 大多数自然图像，其灰度分布集中在较窄的区间，引起 图像细节不够清晰，采用直方图修正后可使图像的灰度间距 拉开或使灰度分布均匀，从而增大反差，使图像细节清晰，
达到增强的目的。
直方图均衡化
直方图均衡化处理的“中心思想”： 把原始图像的灰度直方图从比较集中的某个灰度区间
变成在全部灰度范围内的均匀分布。
直方图均衡化就是对图像进行非线性拉伸，重新分配
直方图均衡化及直方图规定化
《数字图像处理》实验报告（二）学号：____________ 姓名：__________ 专业：____ 课序号：__________计算机科学与技术学院实验2直方图均衡化一、实验学时：4学时（本部分占实验成绩的40%）二、实验目的：1、理解直方图均衡化的原理及步骤；2、编程实现图像（灰度或彩色）的直方图均衡化。
三、必须学习和掌握的知识点：直方图均衡化是一种快速有效且简便的图像空域增强方法，在图像处理中有着非常重要的意义，因此要求掌握。
四、实验题目：编程实现灰度图像的直方图均衡化处理。
要求给出原始图像的直方图、均衡化图像及其直方图和直方图均衡化时所用的灰度级变换曲线图。
五、思考题：（选做，有加分）实现对灰度图像的直方图规定化处理。
六、实验报告：请按照要求完成下面报告内容并提交源程序、可执行程序文件和实验结果图像。
1、请详细描述本实验的原理：1.直方图均衡化概述图像对比度增强的方法可以分成两类:一类是直接对比度增强方法;另一类是间接对比度增强方法。
直方图拉伸和直方图均衡化是两种最常见的间接对比度增强方法。
直方图拉伸是通过对比度拉伸对直方图进行调整，从而“扩大”前景和背景灰度的差别，以达到增强对比度的目的，这种方法可以利用线性或非线性的方法来实现;直方图均衡化则通过使用累积函数对灰度值进行“调整”以实现对比度的增强。
直方图均衡化的英文名称是Histogram Equalization.直方图均衡化是图像处理领域中利用图像直方图对对比度进行调整的方法。
这种方法通常用来增加许多图像的局部对比度，尤其是当图像的有用数据的对比度相当接近的时候。
通过这种方法，亮度可以更好地在直方图上分布。
这样就可以用于增强局部的对比度而不影响整体的对比度，直方图均衡化通过有效地扩展常用的亮度来实现这种功能。
2基本思想直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。
直方图规定化及其实现
■ MATLAB中的函数J=histeq(I，hgram)可以实现 直方图规定化，它来源于MATLAB图像处理工 具箱imagetoolbox
■ I代表待处理的图片
■ Hgram是由自己指定的矢量，规定将原始图 像I的直方图变换成hgram，hgram中的每个 元素都在[0，1]之间。
参考文献 张阳德，胡智渊，叶茂英，王吉伟，潘一峰，尹翔．扩大显微镜下细菌图片的灰度分布范围--基于MATLAB 直方图增强方法[J]．《中国医学工程》,2006,14(3)：228—233．
■ X=imread(‘ibm．bmp‘)； ％读取图片 ■ Y=rgb29ray(X)； ％将RGB图像转换为灰
度图像
■ L=127：255； ％设置规定化函数量 ■ G=histeq(Y，L)； ％调用函数求直方图规
定化
■ N=imadjust(G，[0．867，1]，[])；％调整 图像的灰度级范围
直方图规定
直方图增强
直方图均衡 直方图规定化
直方图规定化的定义
■ 直方图均衡实现了图像灰度的均衡分布，对 提高图像对比度、提升图像亮度具有明显的 作用。
■ 在实际应用中，有时并不需要图像的直方图 具有整体的均匀分布，而希望直方图与规定 要求的直方图一致，这就是直方图规定化。
■ 它可以人为地改变原始图像直方图的形状， 使其成为某个特定的形状，即增强特定灰度 级分布范围内的图间映射规则
逐次接近映射规则
直方图规定化的应用
——乳腺钼靶图像直方图增强
乳腺钼靶摄影是诊断乳腺疾病，特别是发现早期乳腺癌 的一种重要和有效的检查方法。
参考文献 昊杨韬,刘春,王娟,汤乐民．基于MATLAB的乳腺钼靶图像直方图增强方法的比较[J]．《生物医学工程学进 展》,2009,30(2)：90—93．
直方图修正法
直方图修正法分为直方图均衡化和直方图规定化目的：采用直方图修整后可使图像的灰度间距拉开或使灰度分布均匀，从而增大反差，使图像细节清晰，从而增强图像。
1.直方图均衡化通过对原图像进行某种变换使原图像的灰度直方图修正为均匀的直方图的一种方法以r 和s 分别表示归一化了的原图像灰度和经直方图修正后的图像灰度。
即 1,0≤≤s r 在[]1,0区间内的任一个r ，经变换T （r ）都可产生一个S ，且 S=T(r)T(r)为变换函数，应满足下列条件：（1）在10≤≤r 内为单调递增函数（保证灰度级从黑到白的次序不变）；（2）在10≤≤r 内，有1)(0≤≤r T 。
（确保映射后的像素灰度在允许的范围内） 由概率论理论可知，如果已知随机变量r 的概率密度为)(r p r ,而随机变量s 是r 的函数，则s 的概率密度)(s p s 可以由)(r p r 求出。
假定随机变量s 的分布函数用)(s F s 表示，根据分布函数定义，则有⎰⎰∞-∞-==s r r s s dr r ds s s p p F )()()([])()(1s dsd s T p p r s -=⇒ （1） 因为归一化假定 1)(=s p s由（1）得dr r ds p r )(= 两边积分得 ⎰==rrdr r r T s p 0)()( （变换函数） 上式表明当变换函数T （r ）是原图像直方图累积分布函数时，能达到直方图均衡化的目的。
对于灰度级为离散的数字图像，用频率来代替概率。
∑∑=====k j k j j j r k k n r T n r p s 00)()(1,,2,1,0,10-=≤≤L k r k2.直方图规定化（直方图匹配）使原图像灰度直方图变成规定形状的直方图而对图像作修正的增强方法。
假设)(r p r 和)(z p z分别表示已归一化的原图像灰度概率密度函数和希望得到的图像概率密度函数。
首先对原图像进行直方图均衡化处理，即求变换函数：⎰==rrdr r r T s p 0)()( 假定已得到了所希望的图像，对它也进行均衡化处理，即⎰==zzdr r z G v p 0)()( （2） 它的逆变换是 )(1v z G -=即由均衡化后的灰度级得到希望图像的灰度级。
直方图规定化计算
直方图规定化计算直方图规定化是一种图像处理技术，通过对图像的亮度分布进行调整来改变图像的视觉效果。
它可以用于增强图像的对比度和细节，使图像更加清晰和易于观察。
在直方图规定化过程中，我们需要计算原始图像和目标图像的累积分布函数，并将原始图像的像素值映射到目标图像的像素值。
首先，我们需要计算原始图像的直方图。
直方图是一个反映图像亮度分布的统计图，它描述了图像中各个亮度级别的像素数量。
我们可以通过统计图像中每个像素值的出现次数来得到直方图。
然后，我们将直方图进行归一化，以便进行比较和计算。
接下来，我们计算原始图像直方图的累积分布函数（CDF）。
CDF描述了累积到某个亮度级别的像素数量与图像总像素数量之间的关系。
通过计算CDF，我们可以得到原始图像的亮度累积分布。
同样，我们也需要计算目标图像的直方图和CDF。
然后，我们使用原始图像的CDF和目标图像的CDF来计算映射函数。
映射函数将原始图像的像素值映射到目标图像的像素值。
在计算映射函数时，我们可以使用线性插值方法，即通过对两个CDF之间的差异进行比例缩放来得到映射函数。
这样，我们就可以将原始图像的每个像素值映射到目标图像的相应像素值。
最后，我们将经过映射函数处理的原始图像和目标图像进行比较。
通过观察比较后的图像，我们可以看到一些改进的细节和对比度。
如果比较后的图像满足我们的期望，那么我们就可以将规定化后的图像保存下来。
直方图规定化是一种非常有用的图像处理技术，它可以用于改善图像的质量和视觉效果。
通过调整图像的亮度分布，我们可以增强图像的对比度和细节，使其更加清晰和易于观察。
同时，直方图规定化还可以用于图像的风格转换和图像的特征提取等应用领域。
在实际应用中，直方图规定化往往需要一定的计算时间和处理能力。
对于大尺寸的图像和高分辨率的图像，计算直方图和累积分布函数需要耗费较多的时间和计算资源。
因此，在实际应用中，我们需要根据具体需求和计算能力选择合适的图像处理方法和算法，以获得满意的结果。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（6）以新值替代原灰度值，形成均衡化后的新图像。
（7）根据原图像像元统计值对应找到新图像像元统计值， 做出新直方图。
采用近似方法选择最邻近的对应值，再找到新 灰度值。新像元统计值由其所对应的像元统计值 合并得到。
4.实例
计算实例（P135） 应用实例
用变换后的地形湿度指数建立土壤水分模型
BEA Confidential. | 10
直方图规定化原理
均衡化的变换函数均采用归一化的形式，即拉伸 因子为1。此时，像元总数为1，均衡化后的最大灰度值 也为1，其他相应变为小数或分数。因此，均衡化的变 换函数即为该图像的累积直方图本身。
直方图规定化
3.直方图规定化步骤
原图直方图
累积直方图 参考图直方图 参考累积直方图 Step 3
均衡化
计算实例（P135）
原始图像
参考图像
用变换后的地形湿度指数建立土壤水分模型
BEA Confidential. 11用变换后的地形湿度指数建立土壤水分模型
BEA Confidential. | 12
表中的灰度值和累积像元统计值均采用归 一化数据。 用变换后的地形湿度指数建立土壤水分模型
BEA Confidential. | 13
对应累积值 均衡化新图像
新直方图
具体步骤
（1）做出原图像的直方图。 （2）做出原图像的累积直方图，对原图像进行均衡化变换。 （3）做出参考图像的直方图或确定参考直方图。
（4）做出参考累积直方图，进行均衡化变换。
（5）对原图像找到参考累积直方图中对应的累积值；如参 考图有数学公式，直接求的新灰度值。
增强方法。
就是通过一个灰度映像函数，将原灰度 直方图改造成所希望的直方图。所以，直方
图修正的关键就是灰度映像函数。
直方图规定化概念
规
定
直 方 图
一幅参考图像的直方图
Service Bus
特定函数形式的直方图
2. 直方图规定化原理
直方图规定化原理是对两个直方图都做均 衡化，变成相同的归一化的均匀直方图。以此 均匀直方图起到媒 介作用，再对参考图像做均 衡化的逆运算即可。
相同的投影)
现有的图像增强方法各有利弊，同一种方法 能突出图像的某些特征，又会掩盖或消除图像别 用变换后的地形湿度指数建立土壤水分模型 的特征，因此应根据需要加以选用。
（2）直方图规定化应用
图像镶嵌
相邻图像拼接
遥感图像动态变化研究
用变换后的地形湿度指数建立土壤水分模型
BEA Confidential. | 19
直方图规定化
杜婷
直方图均衡化能够自动增强整个图像的对比度，
但它的具体增强效果不容易控制，处理的结果总是
得到全局均匀化的直方图。实际上有时需要变换直
方图，使之成为某个特定的形状，从而有选择地增
强某个灰度值范围内的对比度。 这时可以采用比较
灵活的直方图规定化。一般来说正确地选择规定化
的函数可以获得比直方图均衡化更好的效果。
原始图像直方图
规定化后直方图
参考图像直方图
用变换后的地形湿度指数建立土壤水分模型
BEA Confidential. | 14
应用实例
用变换后的地形湿度指数建立土壤水分模型
BEA Confidential. | 15
应用实例
用变换后的地形湿度指数建立土壤水分模型
BEA Confidential. | 16
应用实例
用变换后的地形湿度指数建立土壤水分模型
BEA Confidential. | 17
5.总结分析
（1）直方图规定化优缺点 优点：消除由于太阳高度角或大气影响造成的图像色调差 异。 缺点：图像是离散函数，同时近似运算存在误差，规定化 变换只能接近参考直方图，不可能完全相同。两幅亮度相 差很大的图像，无法做规定化。(注：两幅图像必须具有
Thank you
直方图规定化
所以，直方图规定化可以看作是均衡化的改进。
内容
1 2 3 4 5
直方图规定化概念
直方图规定化原理
直方图规定化步骤 实例 总结分析
1. 直方图规定化概念
直方图规定化（ histogram specification ） 又称直方图匹配，是指使一幅图像的直方图 变成规定形状的直方图而对图像进行变换的