管理运筹学(第四版)第九章习题答案
《管理运筹学》第4版课后习题解析(韩伯棠)
10 x1 2 x2 s1 20 3x1 3x2 s2 18 4 x1 9 x2 s3 36 x1 , x2 , s1 , s2 , s3 ≥ 0
2
《管理运筹学》第四版课后习题解析
韩伯棠
剩余变量（0, 0, 13） 最优解为 x1=1，x2=5。 6．解： （1）最优解为 x1=3，x2=7。 （2） 1 c1 3 。 （3） 2 c2 6 。 （4）
x1 6。 x2 4。
（5）最优解为 x1=8，x2=0。 （6）不变化。因为当斜率 1 ≤
c1 1 ≤ ，最优解不变，变化后斜率为 1，所以最优解不变。 c2 3
7.解： 设 x，y 分别为甲、乙两种柜的日产量， 目标函数 z=200x＋240y， 线性约束条件： 6 x 12 y 120 8 x 4 y 64 x 0 y 0 x 2 y 20 2 x y 16 x 0 y 0
作直线 960x＋360y=0． 即 8x＋3y=0，向上平移至过点 B(10，8)时，z=960x ＋360y 取到最小值． z 最小=960×10＋360×8=12480 答：大卡车租 10 辆，农用车租 8 辆时运费最低，最低运费为 12480 元． 11．解： 设圆桌和衣柜的生产件数分别为 x、y，所获利润为 z，则 z=6x＋10y． 0.18 x 0.09 y 72 2 x y 800 0.08 x 0.28 y 56 2 x 7 y 1400 即 x 0 x 0 y 0 y 0
． 但 E 不是可行域内的整点，在可行域的整点中，点 ( 4,8) 使 z 取得最小值。 答：应截第一种钢板 4 张，第二种钢板 8 张，能得所需三种规格的钢板，且使所 用钢板的面积最小． 9．解： 设用甲种规格原料 x 张，乙种规格原料 y 张，所用原料的总面积是 zm2，目标函 x 2 y 2 2 x y 3 数 z=3x＋2y，线性约束条件 作出可行域．作一组平等直线 3x＋ x 0 y 0 x 2 y 2 2y=t． 解 得 C ( 4 / 3,1 / 3) 2 x y 3
《管理运筹学》第四版课后习题答案
《管理运筹学》第四版课后习题解析（上）第2章线性规划的图解法1．解：（1）可行域为OABC。
（2）等值线为图中虚线部分。
? （3）由图2-1可知，最优解为B 点，最优解 x =12 ， x ??15 7 2 7 图2-1；最优目标函数值 69 。
72．解：（1）如图2-2所示，由图解法可知有唯一解?x 1 ??0.2 ，函数值为3.6。
?x 2 图2-2（2）无可行解。
（3）无界解。
（4）无可行解。
? （5）无穷多解。
?x ? （6）有唯一解 ??1 ? 203 ，函数值为 92 。
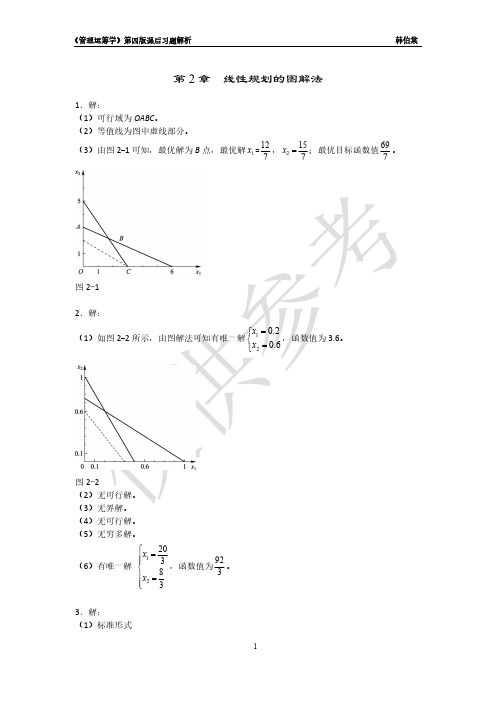
8 3x ? ??2 3 3．解：（1）标准形式max f ??3x 1 ??2x 2 ??0s 1 ??0s 2 ??0s 39x 1 ??2x 2 ??s 1 ??303x 1 ??2x 2 ??s 2 ??132x 1 ??2x 2 ??s 3 ??9x 1, x 2 , s 1, s 2 , s 3 ≥ 0（2）标准形式min f ??4x 1 ??6x 2 ??0s 1 ??0s 23x 1 ??x 2 ??s 1 ??6x 1 ??2x 2 ??s 2??10 7x 1 ??6x 2??4x 1, x 2 , s 1, s 2 ≥ 0（3）标准形式min f ??x 1????2x 2????2x 2??????0s 1 ??0s 2?3x 1 ??5x 2????5x 2??????s 1 ??702x 1????5x 2????5x 2??????503x 1????2x 2????2x 2??????s 2 ??30x 1?, x 2??, x 2????, s 1, s 2 ≥ 0 4．解：标准形式max z ??10x 1 ??5x 2 ??0s 1 ??0s 23x 1 ??4x 2 ??s 1??95x 1 ??2x 2 ??s 2 ??8x 1, x 2 , s 1, s 2 ≥ 0≤ 松弛变量（0，0）最优解为 x 1 =1，x 2=3/2。
《管理运筹学》第4版课后习题解析(韩伯棠)
《管理运筹学》第四版课后习题解析
韩伯棠
（2）模型变为 max z 5 xA 4 xB
50 xA 100 xB ≤ 1 200 000 100 xB ≥ 300 000 xA , xB ≥ 0
推导出 x1 18 000 ， x2 3 000 ，故基金 A 投资 90 万元，基金 B 投资 30 万元。
第 2 章 线性规划的图解法
1．解： （1）可行域为 OABC。 （2）等值线为图中虚线部分。 （3）由图 2-1 可知，最优解为 B 点，最优解 x1 =
12 15 69 ， x2 ；最优目标函数值 。 7 7 7
图 2-1 2．解： （1）如图 2-2 所示，由图解法可知有唯一解
8
《管理运筹学》第四版课后习题解析
韩伯棠
第 3 章 线性规划问题的计算机求解
1．解： ⑴甲、乙两种柜的日产量是分别是 4 和 8，这时最大利润是 2720 ⑵每多生产一件乙柜，可以使总利润提高 13.333 元 ⑶常数项的上下限是指常数项在指定的范围内变化时， 与其对应的约束条件的对偶价格不变。 比如油漆时间变为 100，因为 100 在 40 和 160 之间，所以其对偶价格不变仍为 13.333 ⑷不变，因为还在 120 和 480 之间。 2．解： ⑴不是，因为上面得到的最优解不为整数解，而本题需要的是整数解 ⑵最优解为 (4，8) 3 ．解： ⑴农用车有 12 辆剩余 ⑵大于 300 ⑶每增加一辆大卡车，总运费降低 192 元 4．解： 计算机得出的解不为整数解，平移取点得整数最优解为(10，8) 5．解： 圆桌和衣柜的生产件数分别是 350 和 100 件，这时最大利润是 3100 元 相差值为 0 代表，不需要对相应的目标系数进行改进就可以生产该产品。 最优解不变，因为 C1 允许增加量 20-6=14；C2 允许减少量为 10-3=7，所有允许增加百分比 和允许减少百分比之和（7.5-6）/14+（10-9）/7〈100%，所以最优解不变。 6．解： （1） x1 150 ， x2 70 ；目标函数最优值 103 000。 （2）1、3 车间的加工工时数已使用完；2、4 车间的加工工时数没用完；没用完的加工工时 数为 2 车间 330 小时，4 车间 15 小时。 （3）50，0，200，0。 含义：1 车间每增加 1 工时，总利润增加 50 元；3 车间每增加 1 工时，总利润增加 200 元； 2 车间与 4 车间每增加一个工时，总利润不增加。 （4）3 车间，因为增加的利润最大。 （5）在 400 到正无穷的范围内变化，最优产品的组合不变。 （6）不变，因为在 0,500 的范围内。 （7）所谓的上限和下限值指当约束条件的右边值在给定范围内变化时，约束条件 1 的右边 值在 200,440 变化，对偶价格仍为 50（同理解释其他约束条件） 。 （8）总利润增加了 100×50=5 000，最优产品组合不变。 （9）不能，因为对偶价格发生变化。
《管理运筹学》第4版课后习题解析(韩伯棠)
《管理运筹学》第四版课后习题解析
韩伯棠
C 不是整点，C 不是最优解．在可行域内的整点中，点 B(1，1)使 z 取得最小 值． z 最小=3×1＋2×1=5， 答：用甲种规格的原料 1 张，乙种原料的原料 1 张，可使所用原料的总面积最 小为 5m2． 10．解： 设租用大卡车 x 辆， 农用车 y 辆， 最低运费为 z 元． 目标函数为 z=960x＋360y．
即
作
出
可
行
域． x 2 y 20 解 得 Q ( 4,8) 2 x y 16
z最大 200 4 240 8 2720
3
《管理运筹学》第四版课后习题解析
韩伯棠
答：该公司安排甲、乙两种柜的日产量分别为 4 台和 8 台，可获最大利润 2720 元．
8．解：
设需截第一种钢板 x 张，第二种钢板 y 张，所用钢板面积 zm2． 目标函数 z=x＋2y， 线性约束条件： x y 12 2 x y 15 x 3 y 27 x 0 y 0 x 3 y 27 作出可行域，并做一组一组平行直线 x＋2y=t．解 得 E ( 9 / 2,15 / 2) x y 12
． 但 E 不是可行域内的整点，在可行域的整点中，点 ( 4,8) 使 z 取得最小值。 答：应截第一种钢板 4 张，第二种钢板 8 张，能得所需三种规格的钢板，且使所 用钢板的面积最小． 9．解： 设用甲种规格原料 x 张，乙种规格原料 y 张，所用原料的总面积是 zm2，目标函 x 2 y 2 2 x y 3 数 z=3x＋2y，线性约束条件 作出可行域．作一组平等直线 3x＋ x 0 y 0 x 2 y 2 2y=t． 解 得 C ( 4 / 3,1 / 3) 2 x y 3
管理运筹学(第四版)第九章习题答案
关键路线为：H-B-G-A- Du3-F-K，总工期为20方案Ⅰ：按正常工时工作，总工期15天，关键路线为：B-Du2-G-H直接费用为20＋30＋15＋5＋18＋40＋10＋15＝153百元，间接费用为5×15＝75百元，总费用为153＋75＝228百元方案II：G工时缩短1天，总工期14天直接费用为153＋3×1＝156百元，间接费用为5×14＝70百元，总费用为156＋70＝226百元关键路线为：B-Du2-G-H、A-F-Du1-H和B-C最低成本日程为226百元，总工期14天。
直接费用为100＋200＋80＋0＋150＋250＋120＋100＋180＋130＝1310元，间接费用为15×27＝405元，总费用为1310＋405＝1715元方案II：1－2工序工时缩短2天，总工期25天直接费用为1310＋10×2＝1330元，间接费用为15×（27－2）＝375元，总费用为1330＋375＝1705元关键路线为：关键路线为：1－2－3－4－6－8方案III：2－3工序工时缩短4天，总工期21天直接费用为1330＋20×4＝1410元，间接费用为15×（25－4）＝315元，总费用为1410＋315＝1725元最低成本日程为1705元，总工期25天。
9.5解：网络图如下：方案Ⅱ：E工时缩短2天，总工期17天，变化费用＝30－50×2＝－70；关键路线为：B-E-F和C-F方案Ⅲ：C工时缩短1天，E工时缩短1天，总工期16天，变化费用＝－70＋30＋15－50×1＝－75；关键路线为：A-D-F、B-E-F和C-F方案Ⅳ：F工时缩短1天，总工期15天，变化费用＝－75＋40－50＝－85；关键路线为：A-D-F、B-E-F和C-F方案Ⅴ：B工时缩短3天，C工时缩短3天，D工时缩短2天，A工时缩短1天，总工期12天，变化费用＝－85＋25×3＋30×3＋10×2＋20×1－50×3＝－30；关键路线为：A-D-F、B-E-F和C-F所以正常计划工期是19天，最少工期是12天，最佳工期是15天，各项工作的相应工时如上表方案Ⅳ所示。
最新《运筹学》第四版课后习题答案
作出可行域．
x2y20
2xy16
得Q(4,8)
z最大200424082720
答：该公司安排甲、乙两种柜的日产量分别为4台和8台，可获最大利润2720元．
8．解：
设需截第一种钢板x张，第二种钢板y张，所用钢板面积zm2． 目标函数z=x＋2y，线性约束条件：
xy12
2xy15
x3y27
x0
y0
x3y27
（4）x16。
x24。
（5）最优解为x1=8，x2=0。
（6）不变化。因为当斜率1≤c1
c2
1，最优解不变，变化后斜率为1，所以最优解3
不变。
7.解：
设x，y分别为甲、乙两种柜的日产量， 目标函数z=200x＋240y，线性约束条件：
6x12y120
8x4y64
即
x0
y0
x2y20
2xy16
x0
y0
x350
得ቤተ መጻሕፍቲ ባይዱ
y100
即C(350，100)．当直线6x＋10y=0即3x＋5y=0平移到
经过点C(350，100)时，z=6x＋10y最大
12．解：
模型maxz500x1400x2
2x1≤300
3x2≤540
2x12x1≤440
1.2x11.5x2≤300
x1,x2≥0
（1）x1150，x270，即目标函数最优值是103000。
《管理运筹学》第四版课后习题解析（上
）
第
1．解：
（1）可行域为OABC。
（2）等值线为图中虚线部分。
（3）由图2-1可知，最优解为B点，最优解x=12，x15
最新《运筹学》第四版课后习题答案
收集于网络，如有侵权请联系管理员删除⎨= 0.6《管理运筹学》第四版课后习题解析（上）第2章 线性规划的图解法1．解：（1）可行域为OABC 。
（2）等值线为图中虚线部分。
（3）由图2-1可知，最优解为B 点，最优解 x =12， x = 15 1727图2-1；最优目标函数值 69。
72．解：（1）如图2-2所示，由图解法可知有唯一解 ⎧x 1 = 0.2，函数值为3.6。
⎩x 2图2-2（2）无可行解。
（3）无界解。
（4）无可行解。
⎨ （5）无穷多解。
⎧x = （6）有唯一解 ⎪ 1⎪ 203 ，函数值为 92 。
8 3 x = ⎪⎩ 2 33．解： （1）标准形式max f = 3x 1 + 2x 2 + 0s 1 + 0s 2 + 0s 39x 1 + 2x 2 + s 1 = 303x 1 + 2x 2 + s 2 = 13 2x 1 + 2x 2 + s 3 = 9x 1, x 2 , s 1, s 2 , s 3 ≥ 0（2）标准形式min f = 4x 1 + 6x 2 + 0s 1 + 0s 23x 1 - x 2 - s 1 = 6 x 1 + 2x 2 + s 2 = 10 7x 1 - 6x 2 = 4x 1, x 2 , s 1, s 2 ≥ 0（3）标准形式min f = x 1' - 2x 2' + 2x 2'' + 0s 1 + 0s 2-3x 1 + 5x 2' - 5x 2'' + s 1 = 70 2x 1' - 5x 2' + 5x 2'' = 50 3x 1' + 2x 2' - 2x 2'' - s 2 = 30 x 1', x 2' , x 2'' , s 1, s 2 ≥4．解： 标准形式max z = 10x 1 + 5x 2 + 0s 1 + 0s 23x 1 + 4x 2 + s 1 = 9 5x 1 + 2x 2 + s 2 = 8 x 1, x 2 , s 1, s 2 ≥ 0≤松弛变量（0，0）最优解为 x 1 =1，x 2=3/2。
运筹学教程答案第九章
A B C D E
page 13 22 May 2012
5 8 3 6 10
A,C A C B,C
F G H I J
4 8 2 4 5
B,C C F,G E,H F,G
School of Management
运筹学教程
第九章习题解答
page 14 22 May 2012
School of Management
运筹学教程
第九章习题解答
表9-12 工时（ ） 工作 工时（d） 紧前工作 工时（ ） 工作 工时（d） 紧前工作
A B C D E F G H
page 15 22 May 2012
18 6 5 21 27 15 24 13
A A B B D,E
I J K L M N P Q
6 15 6 3 12 5 3 6
运筹学教程
第九章习题解答
9.1 有A，B，C，D，E，F 6项工作，关系分别 项工作， ， ， ， ， ， 项工作 如图9-38(a)，(b)，试画出网络图。 如图 ， ，试画出网络图。
page 1 22 May 2012
School of Management
运筹学教程
第九章习题解答
page 2 22 May 2012
School of Management
运筹学教程
第九章习题解答
9.4 绘制表 绘制表9-11，表9-12所示的网络图，并用表 所示的网络图， ， 所示的网络图 上计算法计算工作的各项时间参数、确定关键路线。 上计算法计算工作的各项时间参数、确定关键路线。
表9-11 工时（ ） 工作 工时（d） 紧前工作 工时（ ） 工作 工时（d） 紧前工作
《管理运筹学》第四版课后习题答案
《管理运筹学》第四版课后习题解析（上）第2章线性规划的图解法1．解：（1）可行域为OABC。
（2）等值线为图中虚线部分。
? （3）由图2-1可知，最优解为B 点，最优解 x =12， x ??15 727图2-1 ；最优目标函数值 69。
72．解：（1）如图2-2所示，由图解法可知有唯一解?x 1 ??0.2，函数值为3.6。
?x 2图2-2（2）无可行解。
（3）无界解。
（4）无可行解。
? （5）无穷多解。
?x ? （6）有唯一解 ??1? 203，函数值为 92 。
8 3x ? ??2 33．解： （1）标准形式max f ??3x 1 ??2x 2 ??0s 1 ??0s 2 ??0s 39x 1 ??2x 2 ??s 1 ??30 3x 1 ??2x 2 ??s 2 ??13 2x 1 ??2x 2 ??s 3 ??9 x 1, x 2 , s 1, s 2 , s 3 ≥ 0（2）标准形式min f ??4x 1 ??6x 2 ??0s 1 ??0s 23x 1 ??x 2 ??s 1 ??6x 1 ??2x 2 ??s 2 ??10 7x 1 ??6x 2 ??4x 1, x 2 , s 1, s 2 ≥ 0（3）标准形式min f ??x 1????2x 2????2x 2??????0s 1 ??0s 2?3x 1 ??5x 2????5x 2??????s 1 ??70 2x 1????5x 2????5x 2??????50 3x 1????2x 2????2x 2??????s 2 ??30 x 1?, x 2??, x 2????, s 1, s 2 ≥ 0 4．解： 标准形式max z ??10x 1 ??5x 2 ??0s 1 ??0s 23x 1 ??4x 2 ??s 1 ??95x 1 ??2x 2 ??s 2 ??8x1, x2 , s1, s2 ≥0≤松弛变量（0，0）最优解为 x 1 =1，x 2=3/2。
《管理运筹学》第四版课后习题答案
（4）3 车间 ，因为增加的利 润最大。
（5）在400 到正无 穷的范 围内 变化，最优产 品的 组合不 变。
（6）不变，因为在 0,500 的范 围内。
（7）所谓的上限和下限 值指当 约束条件的右 边值 在 给定范 围 内变化 时，约束条件 1 的右 边值 在 200,440 变化，对 偶价格仍 为 50（同理解释 其他 约 束条件）。
当 c1 不变时 ，c2 在 负无穷 到 6.4 的范 围内变 化，最优 解不 变。 （5）约 束条件 1 的右 边值 在 780 000,1500 000 变化，对偶价格仍 为 0.057（其他同理） 。 （6）不能，因为允 许减少的百分比与允 许 增加的百分比之和 4 2 100% ，理由
4.25 3.6
11．解： 设圆 桌和衣柜的生 产件数分 别为 x、y，所获 利润为 z，则 z=6x＋10y．
0.18x 0.08x
x0 y0
0.09 y 0.28 y
72 2x y 800
56 2x 7 y 即 x0
1400 作出可行域．平移 6x＋ 10y=0 ，如图
y0
2x y 800
x 350
得
即 C(350，100) ．当直线 6x＋ 10y=0 即 3x＋ 5y=0 平移
x1
0.2
，函数值为 3.6。
x2 0.6
图 2-2
（2）无可行解。 （3）无界解。 （4）无可行解。
（5）无穷多解。
x1
（6）有唯一解
x2
20
3 ，函数值为 92 。
8
3
3
3．解： （1）标 准形式
max f 3x1 2x2 0s1 0s2 0s3
《管理运筹学》第四版课后习题答案
2x 7 y 1400 y 100 到
经过 点 C(350，100) 时 ，z=6x＋10y 最大
12．解：
模型 max z 500 x1 400 x2
2 x1 ≤ 300 3x2 ≤ 540 2 x1 2 x1 ≤ 440 1.2x1 1.5x2 ≤ 300 x1, x2 ≥ 0
（1）x1 150 ，x2 70 ，即目 标 函数最 优值 是 103 000。
（2）无可行解。 （3）无界解。 （4）无可行解。
（5）无穷多解。
x1
（6）有唯一解
x2
20
3 ，函数值为 92 。
8
3
3
3．解： （1）标 准形式
max f 3x1 2x2 0s1 0s2 0s3
9 x1 2 x2 s1 30 3x1 2 x2 s2 13 2 x1 2 x2 s3 9 x1, x2 ,s1, s2, s3 ≥ 0
3x＋2y，线性 约束条件
x 2y 2x y
x0 y0
2 3 作出可行域．作一 组平等直 线 3x＋ 2y=t ． 解
x 2y 2 得 C (4 / 3,1/ 3)
2x y 3
C不是整点，C不是最 优 解．在可行域内的整点中，点 B(1，1) 使 z 取得最小 值． z 最小 =3×1＋2×1=5，
50 xA 100xB ≤ 1 200 000 5 xA 4 xB ≥ 60 000 100xB ≥ 300 000 xA , xB ≥ 0
基金 A，B 分别为 4 000 元，10 000 元，回报额为 62000 元。
（2）模型变为 max z 5xA 4 xB
50 xA 100xB ≤ 1 200 000 100xB ≥ 300 000 xA ,xB ≥ 0
《管理运筹学》第四版课后习题解析
《管理运筹学》第四版课后习题解析(上)第2章线性规划的图解法1•解：(1) 可行域为OABG(2) 等值线为图中虚线部分。
图2-1 2•解：3•解:12，X215上;最优目标函数值769~7X20.206,函数值为3、6。
X1⑹有唯一解X2 203，函数值为92。
8 3 3(3)由图2-1可知,最优解为B点,最优解图2-2(2) 无可行解。
(3) 无界解。
(4) 无可行解。
(1)如图2-2所示，由图解法可知有唯一解(1) 标准形式max 3x1 2x2 0s1 0s2 0s39x1 2x2 s1 303x1 2x2 s2 132x1 2x2 s3 9X i，X2，®,S2，S3 > 0(2) 标准形式min f 4X1 6X2 0S1 0S23X1 X2 S1 6X1 2X2 S2 107X1 6X2 4X1, X2，S1, S2》(3) 标准形式min f X1 2X2 2X2 0S1 0S23X1 5X2 5X2 S1 702X1 5X2 5X2 503X1 2X2 2X2 S2 30X i，X2，X2，q,S2 > 0 4.解: 标准形式maX z 10X1 5X2 0S1 0S23X1 4X2 S1 95X1 2X2 S2 8X1, X2,s1,s2> 0松弛变量(0，0)最优解为X1=1,X2=3/2。
5.解: 标准形式min f 11X1 8X2 0S1 0S2 0S310X1 2X2 S1 203X1 3X2 S2 184X1 9X2 S3 36X i，X2，S i，S2，S3 > 0剩余变量(0, 0, 13)最优解为X i=1,X2=5。
6•解：(1) 最优解为X I=3,X2=7。
(2) 1 q 3。
⑶ 2 C2 6。
Xi 6。
⑷4X 4。
⑸最优解为X1=8,X2=0。
(6)不变化。
因为当斜率1 < 9 < 1,最优解不变,变化后斜率为1,所以最优解不变。
《管理运筹学》第四版课后习题答案解析
学习资料整理⎨= 0.6《管理运筹学》第四版课后习题解析（上）第2章 线性规划的图解法1．解：（1）可行域为OABC 。
（2）等值线为图中虚线部分。
（3）由图2-1可知，最优解为B 点，最优解 x =12， x15 1727图2-1；最优目标函数值 69。
72．解：（1）如图2-2所示，由图解法可知有唯一解 x 10.2，函数值为3.6。
x 2图2-2（2）无可行解。
（3）无界解。
（4）无可行解。
⎨ （5）无穷多解。
x（6）有唯一解 120 3，函数值为 92 。
8 3x2 33．解：（1）标准形式max f3x 12x 20s 10s 20s 39x 1 2x 2 s 1 30 3x 1 2x 2 s 2 13 2x 12x 2s 39x 1, x 2 , s 1, s 2 , s 3 ≥ 0（2）标准形式min f4x 16x 20s 10s 23x 1x 2 s 16 x 12x 2s 210 7x 16x2 4x 1, x 2 , s 1, s 2 ≥ 0（3）标准形式min fx 12x 22x 20s 1 0s 23x1 5x 25x 2s 1702x 15x 25x 250 3x 12x 22x 2s 230x 1, x 2, x 2, s 1, s 2 ≥ 04．解： 标准形式max z10x 15x 20s 10s 2范文范例 指导参考学习资料整理3x 14x 2s 19 5x 12x 2s 28x 1, x 2 , s 1, s 2 ≥ 0≤松弛变量（0，0）最优解为 x 1 =1，x 2=3/2。
5．解： 标准形式min f11x 18x 20s 10s 20s 310x 1 2x 2 s 1 20 3x 1 3x 2 s 2 18 4x 19x 2s 336x 1, x 2 , s 1, s 2 , s 3 ≥ 0剩余变量（0, 0, 13）最优解为 x 1=1，x 2=5。
管理运筹学》-第四版课后习题答案.docx
.《管理运筹学》第四版课后习题解析（上）第 2 章线性规划的图解法1．解：（1）可行域为 OABC。
（2）等值线为图中虚线部分。
（）由图2-1可知，最优解为 B 点，最优解x=12，69。
315；最优目标函数值7x1277图 2-12．解：x10.2（ 1）如图 2-2 所示，由图解法可知有唯一解，函数值为 3.6 。
x20.6图2-2（2）无可行解。
（3）无界解。
（4）无可行解。
word 资料.（ 5）无穷多解。
x2092（ 6）有唯一解3，函数值为。
183x2 33．解：（ 1）标准形式maxf 3 12x2010s20s3 x s9 x12x2s1303x12x2s2132 x12x2s39x1,x2, s1,s2,s3≥0（ 2）标准形式min f4x16x20 s10s23x1x2s16x1 2 x2s2107 x16x24x1, x2, s1, s2≥0（ 3）标准形式min f x12x22x20 s10s23x15x25x2s1702 x15x25x2503x1 2 x2 2 x2s230x1, x2, x2, s1 , s2≥ 04．解：标准形式max z10 x15x20 s10s2word 资料.3x14x2s195 x12x2s28x1, x2, s1, s2≥0word 资料.松弛变量（ 0，0）最优解为 x 1 =1，x 2=3/2 。
5．解： 标准形式min f11x 18 x 20 s 10s 20s 310x 1 2x 2 s 1 20 3x 1 3x 2 s 2 18 4 x 19x 2s 336x 1, x 2 , s 1 , s 2 , s 3 ≥ 0剩余变量（ 0, 0, 13 ）最优解为 x 1=1，x 2=5。
6．解：（ 1）最优解为 x 1=3，x 2=7。
（ 2） 1 c 1 3 。
（ 3） 2 c 26 。
（ 4）x 16。
x 24。
（ 5）最优解为 x 1=8，x 2=0。
《管理运筹学》第四版课后习题
《管理运筹学》第四版课后习题答案第2章 线性规划的图解法1．解：（1）可行域为OABC 。
（2）等值线为图中虚线部分。
（3）由图2-1可知，最优解为B 点，最优解1x =127，2157x =；最优目标函数值697。
图2-12．解：（1）如图2-2所示，由图解法可知有唯一解120.20.6x x =⎧⎨=⎩，函数值为3.6。
图2-2（2）无可行解。
（3）无界解。
（4）无可行解。
（5）无穷多解。
（6）有唯一解 1220383x x ⎧=⎪⎪⎨⎪=⎪⎩，函数值为923。
3．解：（1）标准形式12123max 32000f x x s s s =++++1211221231212392303213229,,,,0x x s x x s x x s x x s s s ++=++=++=≥（2）标准形式1212min 4600f x x s s =+++12112212121236210764,,,0x x s x x s x x x x s s --=++=-=≥（3）标准形式12212min 2200f x x x s s ''''=-+++ 1221122122212212355702555032230,,,,0x x x s x x x x x x s x x x s s '''-+-+=''''-+=''''+--=''''≥4．解：标准形式1212max 10500z x x s s =+++1211221212349528,,,0x x s x x s x x s s ++=++=≥松弛变量（0，0）最优解为 1x =1，x 2=3/2。
5．解：标准形式12123min 118000f x x s s s =++++121122123121231022033184936,,,,0x x s x x s x x s x x s s s +-=+-=+-=≥剩余变量（0, 0, 13）最优解为 x 1=1，x 2=5。
《管理运筹学》第四版课后习题解析[下]
![《管理运筹学》第四版课后习题解析[下]](https://img.taocdn.com/s3/m/97cbd28969dc5022aaea006f.png)
0
900
最大利润为13500。
17．解：
最优策略为（1,2,3）或者（2,1,3），即该厂应订购6套设备，可分别分给三个厂1,2,3套或者2,1,3套。每年利润最大为18万元。
第11章 图与网络模型
1、解：
破圈法的主要思想就是在图中找圈，同时去除圈中权值最大的边。因此有以下结果：
圈 去除边 ；圈 去除边 ；圈 去除边 ；圈 去除边 ；得到图(a1)。0 Nhomakorabea0
9.解：
前两年生产乙，后三年生产甲，最大获利2372000元。
10．解：
最优解（0，200，300，100）或（200，100，200，100）或者（100，100，300，100）或（200，200，0，200）。总利润最大增长额为134万。
11．解：
在一区建3个分店，在二区建2个分店，不在三区建立分店。最大总利润为32。
得 ，将其作为约束条件求解下述问题。
得最优值 ，将其作为约束条件计算下述问题。
得最优值 ，将其作为约束条件计算下述问题。
得
所以，食品厂商为了依次达到4个活动目标，需在电视上发布广告9.474次，报纸上发布广告20次，广播中发布广告2.105次。（使用管理运筹学软件可一次求解上述问题）
5、解：
（1）设该化工厂生产 升粘合剂A和 升粘合剂B。则根据工厂要求，建立以下目标规划模型。
图解法略，求解得 。
（2）目标规划模型如下。
图解法略，求解得 。
由此可见，所得结果与（1）中的解是不相同的。
（3）加权目标规划模型如下，
求解得 。
9、解：
假设甲乙两种洗衣机的装配量分别是x1,x2,建立数学规划模型如下。
用管理运筹学软件解得：
《管理运筹学》第四版课后习题答案
《管理运筹学》第四版课后习题解析（上）第2章线性规划的图解法1.解：（1）可行域为OABC。
（2）等值线为图中虚线部分。
（3）由图2-1可知，最优解为3点，最优解x上；最优目标函数値_?9。
12 15 7,x17 272.解：⑴如图2-2所示，由图解法可知有唯咚。
;吟函数值为36（2）无可行解。
（3）无界解。
（4）无可行解。
（5）无穷多解。
x 20（62有唯一解J ,函数值珂翌~。
3.解：（1）标准形式max f3为2X20》0s2°Ss9禺2X2§303马2x,S?132x\2x?习9坷，屯,S2 »$0（2）标准形式min f4也6-v2 Os】0s23址x2勺 6画2X2s2107 X、 6 Ao4X\, X2 , q, S2 Mo（3）标准形式4.解: 标准形式0 S] 0 S23曲5 Ao5^2q702冯5X25X2503西 2 An 2X2S2禺，x?,X2，勺，S2 Mo30 max z3 禺4x z勺 95 禺 2 Ab s2 8 Aj, X2 , S2 $0松弛变量（0, 0）最优解为禺二1, X2=3/2O5.解：标准形式min f llAj 8X2 0勺0s210题 2 Ao L203羽3也184禺9疋S336禺，勺，S?,习$0x2,剩余变量（0,0,13)最优解为X1=1, X2=5O6.解：(1)最优解为禺二3, A2=7O(2) 1 q 3 o(3) 2 c2 6 o（5）最优解为^1=8, ^2=0o（6）不变化。
因为当斜率J最篇掣解不变，变化后斜率为】，所以iw q不变。
7.解：设x, y分别为甲、乙两种柜的日产量，目标函数z=200x +240y,线性约束条件:12 y x2120 f20作出可行域.n4y1 2x y6416即X0x0y0y2x y16z 仆 200 4 240 8 2720答：该公司安排甲、乙两种柜的日产量分别为4台和8台，可获最大利润2720 元.8.解：设需截第一种钢板x张，第二种钢板y张，所用钢板面积zm2.目标函数z二x + 2y, 线性约束条件：x y122x y15x 3y27x 0 x 3y 27y作出可行域，并做一组一组平行直线x+2y=t.解x y 12得£(9 / 2,15 / 2)答：应截第一种钢板4张，第二种钢板8张，能得所需三种规格的钢板，且使所用钢板的面积最小.9.解：设用甲种规格原料x张，乙种规格原料y张，所用原料的总面积是zm2,目标函数z=X 2 y23x + 2y r线性约束条件Xy作出可行域.作一组平等直线3x + 2y=t・解x 22 得C(4 / 3,1 / 3) 2xy3C不是整点，C不是最优解.在可行域内的整点中，点B(l, 1)使Z取得最小值. z 垠小=3X14-2X1=5,答：用甲种规格的原料1张，乙种原料的原料1张，可使所用原料的总面积最小为 5 m2.10.解：设租用大卡车x辆，农用车y辆，最低运费为z元.目标函数为z二960x + 360y.0 x 10线性约束条件是＜y作出可行域，并作直线960x + 360y=0.208x 2.5 y 100即8x+3y=0,向上平移sly)\V>=X（T）+（T）-12-16x10由得最佳点为&108x 2.5y 100作直线960x +360y=0.即8x+3y=0,向上平移至过点B（10, 8）时,z=960x + 360y取到最小值.z 垠小=960X10+360X8=12480答：大卡车租10辆，农用车租8辆时运费最低，最低运费为12480元.11.解:设圆桌和衣柜的生产件数分别为X、y,所获利润为z,则z=6x + 10y.0. 18x0. 092x y800y720. 08x0. 28y56作出可行域.平移6x+10y=0 ,如2x7 y1400 即x x 0°y 02x y X即C(350, 100).当直线6x+10y二0 即3x+5y二0 平移800得350到2x7 y y1400100经过点C(350, 100)时,z=6x+10y 最大12.解：模型max z 500为400JV22X\ W3003也<5402x\ 2x\ W4401.2x\ 1. 5Ao W 300Aj, x2 ^0(1)x、 150 , x? 70 ,即目标函数最优值是103 000o(2)2, 4有剩余，分别是330, 15,均为松弛变量。
《管理运筹学》第四版课后习题答案
《管理运筹学》第四版课后习题解析（上）第2章线性规划的图解法1 •解：1 ）可行域为OABC2）等值线为图中虚线部分2•解：『X =0 21）女图2-2所示，由图解法可知有唯一解X1 _ . ,函数值为3.6凶=°.6图2-22） 无可行解。
3） 无界解。
4） 无可行解。
3）由图2-1可知，最优解为B 点，最优解辿=12，丿 最优目标函数值 _152 _ 76975）无穷多解3•解:1）标准形式max f =3x i 2x 2 0s i - 0s 2 - 0s 39xi 2x 2 si =303x 1 亠2X 2 亠s =132x i 亠2x 2 亠S 3 =9x i , x 2 ,S 1, S 2, S 3》02） 标准形式min f =4x 1 亠6x 2 亠0$ 亠0s 23x i - X 2 - Si — 6x 1 2x 2 S 2 =i07x i -6x 2 =4x i , x , S i , S 2 A 03） 标准形式min f =xi —2X 2 亠2X 2 亠0s 1 亠0S 2-3x i 5x 2 -5x 2 S i =702x i -5x 2 5X 2： =503x i 2x 2 —2x 2 -S 2 =30x i , xl X 2： Si, S 2 A 0 4•解：标准形式max z =10x i ' 5x 2 ' 0s i 0S 23x 1 4x 2 Si =95xi 2x 2 S 2 =8x i , x , S i , S 2 A 06）有唯一解■: X 2=20 3，函数值为 83 92 3松弛变量0,0） 最优解为x i =1, X 2=3/2。
5•解：标准形式min f =11x i 8x 2 - 0s i - 0s 2 - 0S 310X 1 2X 2 -s 1 =203X I 亠 3X2 -S 2 =184X1 9X2 —S3 =36X 1, X 2 , S 1, S 2 , S3》0剩余变量0, 0, 13)最优解为X 1=1 , X 2=5。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
关键路线为：H-B-G-A- Du3-F-K，总工期为20
关键路线为：a-f-i-n-o-q，总工期为152
2
直接费用为20＋30＋15＋5＋18＋40＋10＋15＝153百元，间接费用为5×15＝75百元，总费用为153＋75＝228百元
方案II：G工时缩短1天，总工期14天
直接费用为153＋3×1＝156百元，间接费用为5×14＝70百元，总费用为156＋70＝226百元
关键路线为：B-Du2-G-H、A-F-Du1-H和B-C
最低成本日程为226百元，总工期14天。
直接费用为100＋200＋80＋0＋150＋250＋120＋100＋180＋130＝1310元，间接费用为15×27＝405元，总费用为1310＋405＝1715元
方案II：1－2工序工时缩短2天，总工期25天
直接费用为1310＋10×2＝1330元，间接费用为15×（27－2）＝375元，
总费用为1330＋375＝1705元
关键路线为：关键路线为：1－2－3－4－6－8
方案III：2－3工序工时缩短4天，总工期21天
直接费用为1330＋20×4＝1410元，间接费用为15×（25－4）＝315元，
总费用为1410＋315＝1725元
最低成本日程为1705元，总工期25天。
9.5解：网络图如下：
方案Ⅰ：按正常工时工作，总工期19天，关键路线为：B-E-F
方案Ⅱ：E工时缩短2天，总工期17天，变化费用＝30－50×2＝－70；
关键路线为：B-E-F和C-F
方案Ⅲ：C工时缩短1天，E工时缩短1天，总工期16天，变化费用＝－70＋30＋15－50×1＝－75；
关键路线为：A-D-F、B-E-F和C-F
方案Ⅳ：F工时缩短1天，总工期15天，变化费用＝－75＋40－50＝－85；
关键路线为：A-D-F、B-E-F和C-F
方案Ⅴ：B工时缩短3天，C工时缩短3天，D工时缩短2天，A工时缩短1天，总工期12天，变化费用＝－85＋25×3＋30×3＋10×2＋20×1－50×3＝－30；
关键路线为：A-D-F、B-E-F和C-F
所以正常计划工期是19天，最少工期是12天，最佳工期是15天，各项工作的相应工时如上表方案Ⅳ所示。
9.6网络图如下：
方差和5111112
=++++=σ
提前3天的概率为：
34.15
3229-=-=
-=
σ
λE
K T T ，()%01.934.1=-=λP
推迟5天的概率为：
24.25
32
37=-=
-=
σ
λE
K T T ，()%74.9824.2==λP
关键路线：B-E-G
从上表可以知道，第11至14天，工人数超出9人，第6至9天的工人数过剩，而D工序最早开始时间为第2天，所以把D工序的开始时间从原来的第9天改为第6天，这样，第6至9天工作的工序为D、E，所需工人数为8+12=20，不会超过现有劳动力。
修改后工序与
关键路线：A-B-虚工序-E-H
若所有工序均按最早开始时间开始，各个时间的工序及需要的工人数如下表所示：
从上表可以知道，第6至8天，工人数超出1人，第9至19天的工人数过剩，而F工序最迟开始时间为第17天，所以把F工序的开始时间从原来的第6天改为第9天以后的任何一
9.9网络图如下：
（2）关键路线是完工期的期望值为36.5天； 方差和25.23125.21642
=+++=σ
（3）不迟于40天的概率为：
73.025
.235.3640=-=
-=
σ
λE
K T T ，()%73.7673.0==λP
（4）完工概率至少为0.95，则：
%95=⎪
⎭
⎫
⎝⎛
-=σλE K
T T P ，即645.125.235.36=-K T ，解得454.44≈=K T 天 完工日期应定为45天。