小学五年级奥数_找规律
五年级奥数找规律1

1.找规律
在2、3两数之间,第一次写上5,第二次在2、5和5、3之间分别写上7、8(如下所示),每次都在已写上的两个相邻数之间写上这两个相邻数之和.这样的过程共重复了六次,问,纸上所有数之和是 .
2.火车过桥
两列火车相向而行,甲车每小时行36千米,乙车每小时行54千米.两车错车时,甲车上一乘客发现:从乙车车头经过他的车窗时开始到乙车车尾经过他的车 窗共用了14秒,乙车上也有一乘客发现:从甲车车头经过他的车窗时开始到甲车车尾经过他的车窗共用了11秒,那么站在铁路旁的的丙,看到两列火车从车头相 齐到车尾相离时共用多少时间?
虽然排列顺序不同,但只要找到十分位上的数字后,再依验算以上结论成立。
2.计算
一个三位小数四舍五入后成为4.80,原来的三位小数可能是哪些小数?
分析与解答 我们分两种情况考虑:四舍;五入。
四舍不进位得4.80,那么原来千分位上数字只能是1,2,3,4,所以原数为4.801,4.802,4.803,4.804。
五入进位后得4.80,那么原数百分位上的数为9,十分位上的数字为7,而千分位上的数字只能是5、6、7、8、9。所以原数为4.795,4.796,4.797,4.798,4.799。
答:原来的三位小数可能是4.801,4.802,4.803,4.804,4.795,4.796,4.797,4.798,4.799。
1.找规律
用循环小数表示1÷7,2÷7,3÷7的商,比较一下它们的循环节中的数字有什么特点,从中可以找出什么规律?应用找出的规律,写出4÷7,5÷7,6÷7的循环节后,再除一下,看看找到的规律对不对?
分析与解答 通过计算知,用7分别去除1,2,3后所得到循环节的位数相同,所出现的数字也相同
五年级上册数学试题-奥数:小数除法的应用-2.找规律计算人教版 (1)

第五周小数除法的应用2.找规律计算[题型概述]有些计算不需要一部一步地计算,只要通过你的观察,就能直接写出结果。
[典型例题]先计算下面一组算式前三题的结果,然后找出其中的规律,并根据规律直接写出后面几题的得数。
1×0.8+0.1=()12×0.8+0.2=()123×0.8+0.3=()……12345678×0.8+0.8=()123456789×0.8+0.9=()思路点拨通过计算,我们先得出前面三题的得数:1×0.8+0.1=(0.9);12×0.8+0.2=(9.8);123×0.8+0.3=(98.7)。
不难发现得数的变化规律:得数的位数与第一个因数一样,最高位上是9,其余数位上的数依次是8,7,6,5,4,3…,因此12345678×0.8+0.8=(9876543.2)123456789×0.8+0.9=(98765432.1)[举一反三]1.观察算式,找出规律,在括号里填上适当的数。
1.9+9×0.9=1011.8+98×0.9=100111.7+987×0.9=1000……11111.5+()×0.9=()11111111.2 +()×0.9=()2.找出规律后直接填出括号内的数。
199999.8÷9=22222.2299999.7÷9=33333.3()99999.()÷9=44444.4()99999.()÷9=55555.5()99999.()÷9=66666.63.运用发现的规律,在括号内填上合适的数:9×6=5499×96=9504999×996=99550049999×()=99950004[拓展提高]先找出规律,再填空:1×0.9+0.2=1.112×0.9+0.3=11.1123×0.9+0.4=111.1……()×0.9+()=1111111.1思路点拨通过观察前三题,我们可以发现:第二个因数都是0.9;得数整数部分“1”的个数与第一个因数是几位数一样,得数的十分位都是“1”;整个得数部分有几个“1”,加数就是零点几。
小学五年级奥数练习找规律

小学五年级奥数精选一、数列规律的应用--找规律(四)按一定的顺序排列的一串数,叫做数列,每一个数是数列的一项,排在第几个位置就叫第几项。
要找到数列的规律,必须善于观察,一般可以从以下几方面去观察数列: ①数列的每一项怎样随项数变化而变化; ②后面的项与前面的项有什么关系; ③数列分组后有什么规律。
注意:同一个数列,从不同的方面去观察,可以有不同的规律性。
如数列:1,4,9,16,25,36,……规律1:从第2项起每一项比前一项依次大3,5,7,9,11,……规律2:每一项=它的项数的平方。
把这个数列看作:12,22,32,42,52,62,…… 例1、准备题,按规律填数。
(1) 2,9,16,23, , ; (2) 1,2,4,7,11, , ;(3) 21,32,43,54, , ;(4) 2,4,5,10,11,22,23, , ;例2、把自然数中的偶数:2,4,6,8,……依次排成5列(如图)从上到下为列,从左到右为行,最左边的一列叫第一列,最上面一行叫第一行,那么数1994出现在第几行第几列?2 4 6 8 16 14 12 10 18 20 22 24 32 30 28 26 34 36 38 40 … … … …例3、把自然数如右图排列, ①第10行正中的数是哪个? ②1999在第几行左起第几个 数?例4、自然数如右图排列:①第一行中自左至右第8个数是几? ②自上至下第10行中第8个数是几?例5、把所有自然数按下图规律排列后,从上到下分成A,B,C,D,E 五类,问1991在哪一类?第一行 1 第二行23 4第三行5 67 8 9第四行 10 11 12 1314 15 16…1 3 6 10 15 21 … 2 5 9 14 20 …4 8 13 19 …712 18 …11 17 (1)6…A B C DE12 3 4 8 7 6 5 9 10 11 12 16 15 14 13 17 … … ………… …例6、所有自然数如右图排列, ①300应位于哪个字母下面? ②字母F 下面,从上往下数 第6个数是多少?例7、有列数:2,3,6,8,8, …,从第3个数起,每个数都是前两个数乘积的个位数字,那么这一列数的第80个数是多少?例8、有一列数:1,1989,1988,1,1987, …,从第3个数起,每一个数都是前两个数中大数减小数的差,那么第1989个数是多少?例9、如数表,第n 行有一个数A,它的下一行(第n+1行)有一个数B,且A 和B 在同一竖列,如果A+B=394,那么n 是多少?1 2 3 4 7 6 5 8 9 10 11 14 13 12 15 16 … … … …第1行1 2 3 4 5 … 14 15第2行 30 29 28 27 26 … 17 16第3行 31 32 33 3435 … 44 45……………………………………………………例10、右图是一个由数字组成的三角形。
五年级找规律(经典30道)

五年级找规律一.选择题1.按的方式摆放在桌面上.8个按这种方式摆放,有()个面露在外面.A.20B.23C.26D.292.按下列规律印刷笑脸图案,第8幅图案有()个笑脸.A.8B.32C.363.将一些小圆球如图摆放,第六幅图有()个小圆球.A.30B.36C.424.古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是()A.13=3+10B.25=9+16C.36=15+21D.49=18+315.找规律填空3、5、8、10、13、()、18、20.A.14B.15C.16D.176.按规律填数:2,3,5,9,(),33,…….A.13B.15C.17D.307.找规律:19.8,18.6,17.4,()A.17.2B.16.8C.16.2D.15.28.按如图规律摆放三角形则第⑥个图三角形的个数为()A.15B.17C.20D.249.观察下面的点阵图,按规律,第(9)个点阵图中有()个点.A.27B.30C.33D.54二.填空题(共19小题)10.摆一个需要4根小棒,摆需要7根小棒,摆需要10根小棒…,像这样摆n个正方形需要根小棒,当n=20时,需要根小棒.11.如图方式摆放桌子和椅子,一张桌子能坐6人,3张桌子能坐人.12.下图编号为(1),(2),(3),(4)这四幅图分别由1,4,9,16个小等边三角形拼成,它们的周长分别为3,6,9,12.按这个规律.由100个小等边三角形拼成的图形,周长为.13.如图,它是由火柴棒拼成的图案,如果在这个图案中用了51根火柴棒,可拼成个三角形.14.找规律填数.(1)1,4,7,10,,,.(2)2,4,6,8,,,.(3)1,1,2,3,5,8,,.(4)2,5,4,7,6,9,8,,.(5)1,﹣4,9,﹣16,25,,.15.△□□△□□△□□…,这一组图形中第16个是,第21个是.16.●●〇●〇〇〇●●〇●〇〇〇…,黑白两色棋子是按的规律摆放的,第51枚棋子是,前20枚棋子中,白色棋子有枚.17.按规律填数:,,,,,,.18.先找规律,再填数:1,,,,,,.19.照下图排列的规律,第10幅图有个圆点,第n个图有个圆点.20.用同样长的小木棒摆成如图,照这样摆下去,第6幅图需要根这样的小木棒.21.下图是小亮在沙滩上用石子摆成的小房子,观察图形的变化规律,写出第7个小房子用了块石子.22.将一些▲按一定的规律摆放,(如图所示).图中▲的个数依次是6、10、16、24……第10个图形共有个▲.第m个图形中共有个▲.23.用边长为1的小三角形按如图方式摆图形.摆第7个图形需要个小三角形,第7个图形的周长是.24.将一些半径相同的小圆按如图所示的規律摆放:第1个图形中有6个小圆,第2个形中有10个小圆,第3个图形中有16个小圆,第4个图形中有24个小圆,…依此律,第6个图形有个小圆.25.仔细观察如图,照这样排列下去,第六个图形中共有个三角形,其中涂色的三角形有个.26.数形结合是一种重要的数学思想.请你仔细观察,找出下面图形与算式的关系,再直接填空.(1)推算:1+3+5+…+19=2(2)概括:=2(3)拓展应用:1+3+5+7+9+11+13+15+13+11+9+7+5+3+1=27.奇思用小棒这样摆三角形:…,一共用了27根小棒,摆出了个三角形.28.如图,每个图案都是由若干个棋子摆成,依照此规律,第100个图案中棋子的总个数是.三.解答题(共2小题)29.学校准备了40000元,够不够?30.摆放易拉罐,(如图)看图回答问题.(1)摆两层一共有:1+2=3个摆三层一共有1+2+3=6个摆四层一共有个.摆五层一共有个.摆六层一共有个.…(2)用n表示摆的层数,你能总结出一个计算公式吗?.五年级找规律参考答案与试题解析一.选择题(共9小题)1.按的方式摆放在桌面上.8个按这种方式摆放,有()个面露在外面.A.20B.23C.26D.29【解】根据题干分析可得,n个正方体有5+(n﹣1)×3=3n+2;所以8个小正方体时,露在外部的面有:3n+2=3×8+2=26(个)故选:C.2.按下列规律印刷笑脸图案,第8幅图案有()个笑脸.A.8B.32C.36【解】1+2+3+4+5+6+7+8,=(1+8)+(2+7)+(3+6)+(4+5),=9×4,=36;答:第8副图案有36个笑脸.故选:C.3.将一些小圆球如图摆放,第六幅图有()个小圆球.A.30B.36C.42【解】观察图形可知:第一个图形中有1×2=2个小圆球,第二个图形中有2×3=6个小圆球,第三个图形中有3×4=12个小圆球,第四个图形中有4×5=20个小圆球,…所以第六幅图有6×7=42个小圆球.故选:C.4.古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是()A.13=3+10B.25=9+16C.36=15+21D.49=18+31【解】这些三角形数的规律是1,3,6,10,15,21,28,36,45,…,且正方形数是这串数中相邻两数之和,很容易看到:恰有36=15+21.故选:C.5.找规律填空3、5、8、10、13、()、18、20.A.14B.15C.16D.17【解】10+5=15故选:B.6.按规律填数:2,3,5,9,(),33,…….A.13B.15C.17D.30【解】2×9﹣1=18﹣1=17所以:2,3,5,9,17,33,…….故选:C.7.找规律:19.8,18.6,17.4,()A.17.2B.16.8C.16.2D.15.2【解】17.4﹣1.2=16.2.故选:C.8.按如图规律摆放三角形则第⑥个图三角形的个数为()A.15B.17C.20D.24【解】图①三角形的个数:2×3﹣1=5(个)图②三角形的个数:3×3﹣1=8(个)图③三角形的个数:4×3﹣1=11(个)……图n三角形的个数:3(n+1)﹣1=(3n+2)个……第⑥个图三角形的个数为:3×6+2=18+2=20(个)答:第⑥个图三角形的个数为20个.故选:C.9.观察下面的点阵图,按规律,第(9)个点阵图中有()个点.A.27B.30C.33D.54【解】由分析可知,第n项是(3n+3)个点3×9+3=27+3=30答:第(9)个点阵图中有30个点.故选:B.二.填空题(共19小题)10.摆一个需要4根小棒,摆需要7根小棒,摆需要10根小棒…,像这样摆n个正方形需要3n+1根小棒,当n=20时,需要61根小棒.【解】第一个正方形由四根火柴摆成,以后加三根就可加一个正方形,摆n个正方形需要3n+1根小棒,当n=20时,需要3×20+1=61根小棒.故答案为:3n+1,61.11.如图方式摆放桌子和椅子,一张桌子能坐6人,3张桌子能坐14人.【解】有1张桌子时有6把椅子,有2张桌子时有10把椅子,10=6+4×1,有3张桌子时有14把椅子,14=6+4×2,答:3张桌子可以坐14人.故答案为:14.12.下图编号为(1),(2),(3),(4)这四幅图分别由1,4,9,16个小等边三角形拼成,它们的周长分别为3,6,9,12.按这个规律.由100个小等边三角形拼成的图形,周长为30.【解】因为:100=102所以由100个小等边三角形拼成的图形编号为(10),所以周长为:3×10=30.故答案为:30.13.如图,它是由火柴棒拼成的图案,如果在这个图案中用了51根火柴棒,可拼成25个三角形.【解】第一个三角形有1+2=3根火柴棒组成,以后每多一个三角形就多用2根火柴棒,所以组成n个三角形就需要1+2n根火柴棒;当1+2n=51时2n=50n=25答:可拼成25个三角形.故答案为:25.14.找规律填数.(1)1,4,7,10,13,16,19.(2)2,4,6,8,10,12,14.(3)1,1,2,3,5,8,13,21.(4)2,5,4,7,6,9,8,11,10.(5)1,﹣4,9,﹣16,25,49,﹣64.【解答】解(1)10+3=1313+3=1616+3=19(2)8+2=1010+2=1212+2=14(3)5+8=138+13=21(4)72=49﹣16×4=﹣64故答案为:13,16,19;10,12,14,13,21,49,﹣64.15.△□□△□□△□□…,这一组图形中第16个是△,第21个是□.【解】16÷3=5…1,所以这一组图形中第16个是△;21÷3=7,所以这一组图形中第21个是□;故答案为:△,□.16.●●〇●〇〇〇●●〇●〇〇〇…,黑白两色棋子是按●●〇●〇〇〇的规律摆放的,第51枚棋子是黑色的,前20枚棋子中,白色棋子有11枚.【解】51÷7=7(周)…2(个)第51枚棋子是黑色的.20÷7=2(周)…6(个)2×4+3=11(个)所以前20枚中一共有11个白色的.答:第51枚棋子是黑色的,前20枚棋子中,白色棋子有11枚.故答案为:黑色的,11.17.按规律填数:,,,,,,.【解】==故答案为:;.18.先找规律,再填数:1,,,,,,.【解】1=,由前几个分数可知,分子是从1开始的连续奇数,分母是项数的平方;所以,第6项的分子是11,分母是62=36,是.故答案为:.19.照下图排列的规律,第10幅图有33个圆点,第n个图有(3n+3)个圆点.【解】第一幅图圆点个数:1+2+3=6(个)第二副图圆点个数:2+3+4=9(个)第三幅图圆点个数:3+4+5=12(个)……第10幅图圆点个数:10+11+12=33(个)……第n幅图圆点的个数:n+(n+1)+(n+2)=(3n+3)个答:第10幅图有33个圆点,第n个图有(3n+3)个圆点.故答案为:33;(3n+3).20.用同样长的小木棒摆成如图,照这样摆下去,第6幅图需要34根这样的小木棒.【解】由分析可得:第n幅图需要小棒:4+6(n﹣1)根.所以第6幅图需要小棒:4+6(n﹣1)=4+6×(6﹣1)=4+30=34(根)答:第6幅图需要34根这样的小木棒.故答案为:34.21.下图是小亮在沙滩上用石子摆成的小房子,观察图形的变化规律,写出第7个小房子用了77块石子.【解】第一个图形有5块小石子,5=1×(1+4)第二个图形有12块小石子,12=2×(2+4)第三个图形由21块小石子,21=3×(3+4)……由此推出:第n个图形有n(n+4)块石子7×(7+4)=7×11=77(块)答:第7个小房子用了77块石子.故答案为:77.22.将一些▲按一定的规律摆放,(如图所示).图中▲的个数依次是6、10、16、24……第10个图形共有114个▲.第m个图形中共有m(m+1)+4个▲.【解】∵第1个图形有1×2+4=6个三角形,第2个图形有4+2×3=10个三角形,第3个图形有4+3×4=16个三角形,…,∴第m个图形中有m(m+1)+4个三角形,∴第10个图形棋子的颗数为:10×(10+1)+4=10×11+4=110+4=114(个)故答案为:114,m(m+1)+4.23.用边长为1的小三角形按如图方式摆图形.摆第7个图形需要49个小三角形,第7个图形的周长是21.【解】根据题干分析可得:第一个图形是12=1个三角形,边长是1;第二个图形是22=4个三角形,边长是2;第三个图形是32=9个三角形,边长是3;…,第七个图形是72=49个三角形,边长是7,周长是7×3=21.答:摆第7个图形需要49个小三角形,第7个图形的周长是21.故答案为:49;21.24.将一些半径相同的小圆按如图所示的規律摆放:第1个图形中有6个小圆,第2个形中有10个小圆,第3个图形中有16个小圆,第4个图形中有24个小圆,…依此律,第6个图形有44个小圆.【解】第1个图形中有6个小圆第2个形中有10个小圆第3个图形中有16个小圆第4个图形中有24个小圆……第n个图形为:[n(n+1)+4]个小圆所以,第6个图形小圆的个数为:6×7+4=42+2=44(个)答:第6个图形有44个小圆.故答案为:44.25.仔细观察如图,照这样排列下去,第六个图形中共有49个三角形,其中涂色的三角形有21个.【解】根据题干分析可得:第n个图形涂色的小三角形个数为1+2+3+…+n,没有涂色的小三角形个数为1+2+3+…+n+n+1,当n=6时,1+2+3+4+5+6=21(个)没有涂色小三角形有1+2+3+4+5+6+7=28(个)21+28=49(个)故答案为:49,21.26.数形结合是一种重要的数学思想.请你仔细观察,找出下面图形与算式的关系,再直接填空.(1)推算:1+3+5+…+19=102(2)概括:=n2(3)拓展应用:1+3+5+7+9+11+13+15+13+11+9+7+5+3+1=113【解】(1)1+3+5+…+19=(19+1)÷2=10(个),即1+3+5+…+19由10个加数其和是102即1+3+5+…+19=102(2)=n2(3)1+3+5+7+9+11+13+15+13+11+9+7+5+3+1=(1+3+5+7+9+11+13+15)+(1+3+5+7+9+11+13)=82+72=64+49=113故答案为:10,n,113.27.奇思用小棒这样摆三角形:…,一共用了27根小棒,摆出了13个三角形.【解】当有n个三角形时小棒的数量就是:3+2(n﹣1)=3+2n﹣2=2n+1(根);当有27根小棒时:2n+1=272n=26n=13;答:摆27根小棒能摆出13个三角形.故答案为:13.28.如图,每个图案都是由若干个棋子摆成,依照此规律,第100个图案中棋子的总个数是10100.【解】由分析可得:每个图案的纵队棋子个数是:n,每个图案的横队棋子个数是:n+1,那么第n个图案中棋子的总个数与n的关系式为:总个数=n(n+1).那么第100个图案中棋子的总个数:100×(100+1)=100×101=10100(个)答:第100个图案中棋子的总个数是10100个.故答案为:10100.三.解答题(共2小题)29.学校准备了40000元,够不够?【解】172×42+328×45=7224+14760=21984(元)21984<40000答:学校准备了40000元,够.30.摆放易拉罐,(如图)看图回答问题.(1)摆两层一共有:1+2=3个摆三层一共有1+2+3=6个摆四层一共有1+2+3+4=10个.摆五层一共有1+2+3+4+5=15个.摆六层一共有1+2+3+4+5+6=21个.…(2)用n表示摆的层数,你能总结出一个计算公式吗?n(n+1).【解】(1)摆两层一共有:1+2=3个摆三层一共有1+2+3=6个摆四层一共有1+2+3+4=10个.摆五层一共有1+2+3+4+5=15个.摆六层一共有1+2+3+4+5+6=21个(2)用n表示摆的层数:n(n+1)故答案为:1+2+3+4=10;1+2+3+4+5=15;1+2+3+4+5+6=21;n(n+1)。
五年级奥数8数列中的规律

8、数列中的规律姓名:按某种规律排列的一组数,叫作数列。
数列中常见的规律有以下几种:①规律蕴含在相邻两数的差中。
1,2,3,4,5,发6,7,…后一项减去前面与其相邻的一项,差为1。
100,95,90,85,80,…前一项减去后面与其相邻的一项,差为5。
像这样的一组数,从第二项起,每一项与其前一项的差都相等的数列,叫作等差数列。
后一项与前一项的差,叫作这个数列的公差,通常用d表示。
在等差数列a1,a2,a3,…,an中,数列的公差为d,则:a 2=a1+da 3=a2+d=(a1+d)+d=a1+2da 4=a3+d=(a1+2d)+d=a1+3d由此可见,等差数列从第二项起,每一项都等于第一项加上公差的若干倍,这个倍数等于该项的项数减1的差,即,an =a1+(n-1)×d。
这个公式,我们称之为等差数列的通项公式,利用它可以求出等差数列中的任何一项。
等差数列中的基本公式还包括:项数(n)=(末项-首项)÷公差+1首项(a1)=末项-(项数-1)×公差末项(an)=首项+(项数-1)×公差和(S)三(首项+末项)×项数÷2奇数项等差数列的和=中间项×项数奇数项等差数列的中间项=(首项+末项)÷2②规律蕴含在相邻两数的倍数中。
像1,2,4,8,16,32,…这样的一组数,相邻两数为2倍关系,即前一项乘2等于与其相邻的后一项,也就是说相邻两项的比值相同,我们把它称作等比数列或等倍数列。
③前后几项为一组,以组为单位蕴含一定的规律。
例:1,0,0,1,1,0,0,1,…从左到右,每四项为一组,每组都是“1,0,0,1”四个数字。
④数列中间隔的项之间存在着一定的规律。
例:12,15,17,30,22,45,27,60,…第1,3,5项依次相差5,第2,4,6项依次相差15。
⑤相邻两数的关系中隐含着规律。
例:18,20,24,30,38,48,60,…此数列中相邻两数依次相差2,4,6,8,10,12,…例:2,5,11,23,47,…此数列从第二个数开始,每个数都是它前面那个数的2倍再加1。
五年级奥数讲义-第7讲(找规律-a的n次方的个位数是几)
整数a与它本身的乘积,即a×a叫做这个数的平方,记作a2,即a2=a×a;同样,三个a 的乘积叫做a的三次方,记作a3,即a3=a×a×a。
一般地,n个a相乘,叫做a的n次方,记作a n,即本讲主要讲a n的个位数的变化规律,以及a n除以某数所得余数的变化规律。
因为积的个位数只与被乘数的个位数和乘数的个位数有关,所以a n的个位数只与a的个位数有关,而a的个位数只有0,1,2,…,9共十种情况,故我们只需讨论这十种情况。
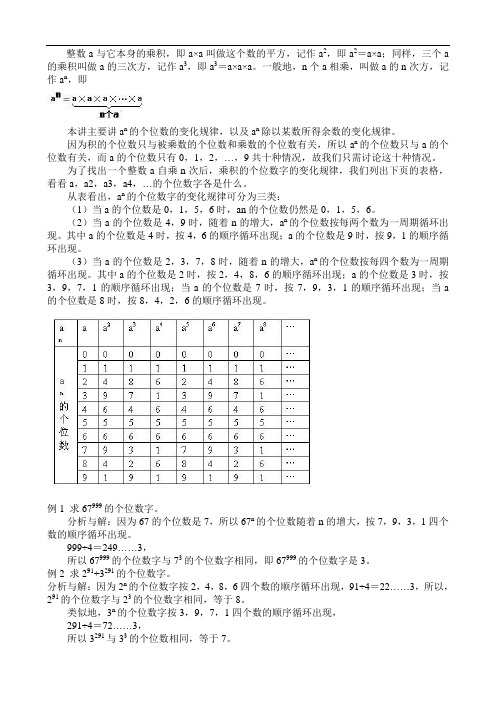
为了找出一个整数a自乘n次后,乘积的个位数字的变化规律,我们列出下页的表格,看看a,a2,a3,a4,…的个位数字各是什么。
从表看出,a n的个位数字的变化规律可分为三类:(1)当a的个位数是0,1,5,6时,an的个位数仍然是0,1,5,6。
(2)当a的个位数是4,9时,随着n的增大,a n的个位数按每两个数为一周期循环出现。
其中a的个位数是4时,按4,6的顺序循环出现;a的个位数是9时,按9,1的顺序循环出现。
(3)当a的个位数是2,3,7,8时,随着n的增大,a n的个位数按每四个数为一周期循环出现。
其中a的个位数是2时,按2,4,8,6的顺序循环出现;a的个位数是3时,按3,9,7,1的顺序循环出现;当a的个位数是7时,按7,9,3,1的顺序循环出现;当a 的个位数是8时,按8,4,2,6的顺序循环出现。
例1 求67999的个位数字。
分析与解:因为67的个位数是7,所以67n的个位数随着n的增大,按7,9,3,1四个数的顺序循环出现。
999÷4=249……3,所以67999的个位数字与73的个位数字相同,即67999的个位数字是3。
例2 求291+3291的个位数字。
分析与解:因为2n的个位数字按2,4,8,6四个数的顺序循环出现,91÷4=22……3,所以,291的个位数字与23的个位数字相同,等于8。
类似地,3n的个位数字按3,9,7,1四个数的顺序循环出现,291÷4=72……3,所以3291与33的个位数相同,等于7。
奥数培优 五年级 第5讲 有趣的找规律

第五讲有趣的找规律例1、一串数按规律排列如下:1,2,3,2,3,4,3,4,5,4,5,6,5,6,7,...... 从第一个数算起,前100个数的和是多少?例2 、在平面上画1994条直线,这些直线最多能形成多少个交点?例3、在一个长方形中,如果没有一条直线,则长方形可以看作一个部分,如果在长方形中画一条直线,这个长方形就被分成两个部分,在长方形中画两条直线最多可以将长方形分成四个部分,如果画三条直线最多可以将长方形分成七个部分(如图)。
如果在长方形中画100条直线,最多可以将长方形分成多少个部分?例4、小明放学回家要路过一个有10个台阶的广场,如果上台阶时每步跨一个或两个台阶,要跨上第10个台阶共有多少种不同的走法?例5、在方格纸上画折线(如下图),小方格的边长是1,图中的1,2,3,4,......,分别表示折线的第1,2,3,4,......段,求折线中第1994段的长度。
思考与练习1、找规律,在括号内填上合适的数。
(1)1,3,9,27,(),243;(2)1,3,2,4,3,5,4,();(3)6,3,8,5,10,7,12,9,(),11;(4)81,64,(),36,(),16,9,4,1;(5)1,8,9,17,26,(),69.2、一串数按下面规律排列:1,3,5,2,4,6,3,5,7,4,6,8,5,7,9,......,从第一个算起,前100个数的和是多少?3、有一串黑白相间的珠子(如图),第100个黑珠前面一共有多少种取法?4、从1—9中每次取两个不同的数相加,和大于10的共有多少种取法?5、(1)在平面中任意作20条直线,这些直线最多可把这个平面分成多少个部分?(2)在平面上任意作6个圆,这些圆最多可把这个平面分成多少个部分?序号 1 2 3 4 5算式1+1 2+3 3+5 1+7 2+9序号 6 7 8 9 ......算式3+11 1+13 2+15 3+17 .......7、已知小正方形的边长是1厘米,依次作出下面这些图形。
小学奥数 图形找规律 精选例题练习习题(含知识点拨)
找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题: ⑴图形数量的变化; ⑵图形形状的变化; ⑶图形大小的变化; ⑷图形颜色的变化; ⑸图形位置的变化; ⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.模块一、图形规律——数量规律【例 1】 观察这几个图形的变化规律,在横线上画出适当的图形.【例 2】 请找出下面哪个图形与其他图形不一样.(1)(2)(3)(4)(5)【例 3】 观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【例 4】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【巩固】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?例题精讲知识点拨4-1-2.图形找规律【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【例5】观察下面的图形,按规律在“?”处填上适当的图形.(4)?【例6】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【例7】观察下图中的点群,请回答:(1)方框内的点群包含个点;(2)推测第10个点群中包含个点;(3)前10个点群中,所有点的总数是。
【例8】观察下面由点组成的图形(点群),请回答:(1)方框内的点群包含个点;(2)第(10)个点群中包含个点;(3)前十个点群中,所有点的总数是。
【例9】下图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:(1)五层的“宝塔”的最下层包含多少个小三角形?(2)整个五层“宝塔”一共包含多少个小三角形?【例 10】 在纸上画5条直线,最多可有 个交点。
模块二、图形规律—— 旋转、轮换型规律【例 11】 相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗? ○ □ ☆ △ ○ □ ☆ △ △ ○ □ ☆ △ ○ □ ☆ ☆ △ ○ □ ☆ △ ○ □ ()()()()()()()()【例 12】 下面的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形.(1)(2)(3)【例 13】 观察下图的变化规律,画出丙图.甲DA乙BC丙【例 14】 图中的三个图形都是由A 、B 、C 、D (线段或圆)中的两个组合而成,记为A ★B 、C ★D 、A ★D .请你画出表示A ★C 的图形.A★B C★D A★D【例15】(希望杯五年级一试第7题,6分)下列四个图形是由四个简单图形A、B、C、D(线段和正方形)组合(记为*)而成。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
找规律
1、找出下列各列数的排列规律,然后在括号里填上适当的数。
(1)2,6,10,14,(),22,26
(2)3,6,9,12,(),18,21
(3)33,28,23,(),13,(),3
(4)55,49,43,(),31,(),19
(5)3,6,12,(),48,(),192
(6)2,6,10,14,(),22,26
(7)33,28,23,(),13,(),3
(8)55,49,43,(),31,(),19
(9)3,6,12,(),48,(),192
(10)2,6,18,(),162,()
(11)128,64,32,(),8,(),2
(12)19,3,17,3,15,3,(),(),11,3
(13)1,2,4,7,(),16,22
(14)3,6,9,12,(),18,21
2、找出下列数排列的规律,然后在括号里填上适当的数。
(1)10,11,13,16,20,(),31
(2)1,4,9,16,25,(),49,64
(3)3,2,5,2,7,2,(),(),11,2
(4)53,44,36,29,(),18,(),11,9,8
(5)81,64,49,36,(),16,(),4,1,0
3、有一串很长的珠子,它是按照5颗红珠、3颗白珠、4颗黄珠、2颗绿珠的顺序重复排列的。
问:第100颗珠子是什么颜色?前200颗珠子中有多少颗红珠?
4、节日的夜景真漂亮,街上的彩灯按照5盏红灯、再接4盏蓝灯、再接3盏黄灯,然后又是5盏红灯、4盏蓝灯、3盏黄灯、……这样排下去。
问:
(1)第100盏灯是什么颜色?
(2)前150盏彩灯中有多少盏蓝灯?
5、有一串数,任何相邻的四个数之和都等于25。
已知第1个数是3,第6个数是6,第11个数是7。
问:这串数中第24个数是几?前77个数的和是多少?。
