求几何图形的阴影部分的面积及答案
小升初数学几何求阴影部分面积题带解析
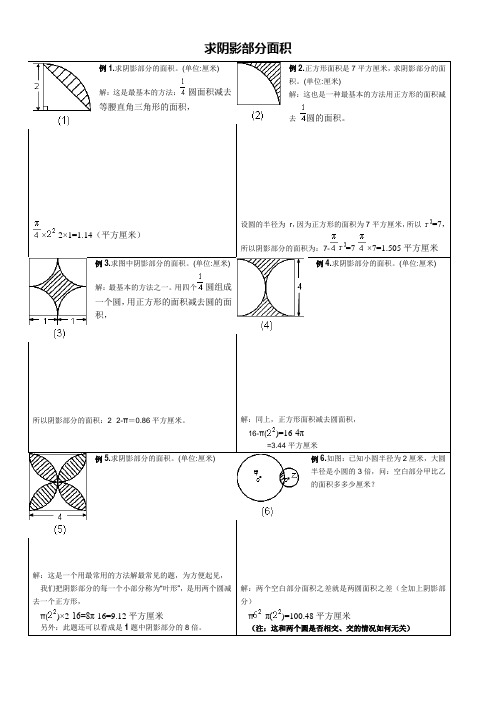
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解：这是最基本的方法：圆面积减去等腰直角三角形的面积，×-2×1=1.14（平方厘米）例2.正方形面积是7平方厘米，求阴影部分的面积。
(单位:厘米)解：这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r，因为正方形的面积为7平方厘米，所以=7，所以阴影部分的面积为：7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解：最基本的方法之一。
用四个圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π()×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。
例6.如图：已知小圆半径为2厘米，大圆半径是小圆的3倍，问：空白部分甲比乙的面积多多少厘米？解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π-π()=100.48平方厘米（注：这和两个圆是否相交、交的情况如何无关）解：正方形面积可用(对角线长×对角线长÷2，求)正方形面积为：5×5÷2=12.5所以阴影面积为：π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为圆，所以阴影部分面积为：π()=3.14平方厘米例9.求阴影部分的面积。
(单位:厘米)解：把右面的正方形平移至左边的正方形部分，则阴影部分合成一个长方形，所以阴影部分面积为：2×3=6平方厘米例10.求阴影部分的面积。
平面几何图形中阴影部分面积的求法
平面几何图形中阴影部分面积的求法
平面几何图形中阴影部分面积的求法是一个重要而经典的问题，它被广泛应用于各种数学研究有关的方面。
求阴影面积的方法有很多，其中最常用的是用分割法。
分割法的思想是：将实体图形分割成一些相对便于计算的小部分，然后分别求出每个小部分的面积，最后累加所有小面积之和即为实体图形阴影面积。
例如：一条无穷长的矩形线段，将其分割成N个等长的矩形，根据三角形的面积公式，可求出矩形面积 S = (a*b)/2（a和b分别为等长的矩形的边长），由此可以由可以得到矩形线段的阴影面积为 S1 + S2 + S3 + ... + SN。
依据此方法，对复杂的几何图形，可把其分割为一些相对简单的图形，例如：三角形、矩形等图形，然后通过计算这些简单图形的阴影面积，再累加求得几何图形的阴影面积。
以上就是用分割法来求解平面几何图形中阴影部分面积的方法，它不仅直观，而且是一个经典而又重要的问题，它是很多数学研究有关方面应用的基础性工作。
阴影部分的面积
一、相加相减法【点拨】：这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，相加求出整个图形的面积. 或者将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.【例题1】：求组合图形的面积。
（单位：厘米）【分析与解答】：上图中，要求整个图形的面积，只要先求出上面半圆的面积，再求出下面正方形的面积，然后把它们相加就可以了.4÷2=2（米）4×4+2×2×3.14÷2=22.28（平方厘米）【例题2】：长方形长6厘米，宽4厘米，求阴影部分的面积。
【分析与解答】：上图中，若求阴影部分的面积，只需先求出正方形面积再减去里面圆的面积即可.4÷2=2（米）6×4-2×2×3.14÷218.28（平方厘米）二、用比例知识求面积【点拨】：利用图形之间的比例关系解题。
【例题3】一块长方形耕地，它由四个小长方形拼合而成，其中三个小长方形的面积分别为15、18、30公顷，图中阴影部分的面积是多少？【分析与解答】：因为阴影部分也是一长方形，所以只要求出它的长、宽是多少就行，为此设它的长、宽分别为a、b，面积为18公顷的长方形的长、宽分别为c、d.直接按比例关系来理解。
因为（a×c）:(d×c)=(a×b):(d×b),a:d=15：18=阴影面积：30，阴影面积为15×30÷18＝25（公顷）。
三、等分法【点拨】：根据所求图形的对称性，将所求图形面积平均分成若干份，先求出其中的一份面积，然后求总面积。
【例题4】：求阴影部分的面积（单位：厘米）【分析与解答】：把原图平均分成八分，就得到下图，先求出每个小扇形面积中的阴影部分：3.14×22÷4－2×2÷2=1.14(平方厘米 )阴影部分总面积为：1.14×8=9.12(平方厘米 )四、等积变形【点拨】：将题中的条件或问题替换成面积相等的另外的条件或问题，使原来复杂的图形变为简单明了的图形。
小升初复习专题求阴影部分面积(含答案)
小升初复习专题求阴影部分面积(含答案)2017年小升初复专题-求阴影部分面积（含答案）本专题旨在巩固小学几何图形计算公式，并通过复加强学生对于图形面积计算的灵活运用。
首先列出了几何图形计算公式，包括正方形、正方体、长方形、长方体、三角形、平行四边形、梯形、圆形、圆柱体和圆锥体。
然后介绍了面积求解的大致分类方法，包括从整体图形中减去局部和割补法，强调了观察图形特点并选择合适的方法求解图形面积的重要性。
例题部分包含多个图形，要求求出阴影部分的面积，其中有些题目给出了已知条件，有些则需要自行推导。
学生需要灵活运用所学过的基本的平面图形的面积求解方法，根据图形特点选择合适的方法求解阴影部分的面积。
以下是例题部分，已经修正了格式错误并删除了明显有问题的段落：例1.求阴影部分的面积。
(单位:厘米)图片显示了一个正方形，其中一角被割去，求剩余部分的面积）解：由于正方形是一个规则图形，我们可以直接计算出整个正方形的面积，然后减去被割去的部分的面积即可。
设正方形边长为a，则正方形的面积为a×a，被割去的部分是一个直角三角形，底边长为a，高为a/2，面积为a×a/2×1/2=a²/4.将两个面积相减，得到阴影部分的面积为3a²/4.例2.正方形面积是7平方厘米，求阴影部分的面积。
(单位:厘米)图片显示了一个正方形，其中一角被割去，求剩余部分的面积）解：设正方形边长为a，则根据题意可得a²=7，解得a=√7.同样地，我们可以计算出被割去的部分的面积为a²/4=7/4.将整个正方形的面积减去被割去的部分的面积，得到阴影部分的面积为21/4.例3.求图中阴影部分的面积。
(单位:厘米)图片显示了一个矩形，其中一角被割去，求剩余部分的面积）解：设矩形长为a，宽为b，则根据题意可得a=6，b=4.被割去的部分是一个直角三角形，底边长为4，高为2，面积为4×2/2=4.将整个矩形的面积减去被割去的部分的面积，得到阴影部分的面积为20.例4.求阴影部分的面积。
求阴影部分面积九字决
求阴影部分面积九字决河北张家口市第十九中学 贺峰关于求几何图形阴影部分面积的计算问题是初中数学“空间与图形”中一道亮丽的风景，历年来常考不衰，这类试题往往将多边形与圆结合，并且多由一些不规则图形组合、重叠而成；既能考查同学们观察能力、分析能力、计算能力、空间想象能力，同时又能考查同学们合理选择和运用数学思想方法的技能。
解决这类问题时，要善于抓住图形的特点，灵活采用作“差”、重“组”、“去”重、求“和”巧“移”、“翻”折、旋“转”、“设”参、转“化”等方式进行，从而使问题得到解决。
一、作“差”例1如图1，正六边形ABCDEF 的边长是a ，分别以C 、F 为圆心，a 为半径画弧，则图中阴影部分的面积是（ ）(A)223332a ⎪⎪⎭⎫ ⎝⎛π- (B)23333a ⎪⎪⎭⎫ ⎝⎛π-(C)232233a ⎪⎪⎭⎫⎝⎛-π (D)23223a ⎪⎭⎫ ⎝⎛π- 析解：依题意，由于给出的阴影部分是由规则图形围成的，因此解决此题可利用“作差法”解决，即S 阴影=S 正六边形－2S 扇形=232233a ⎪⎪⎭⎫⎝⎛-π。
因此答案选C 。
二、重“组”例2 如图2，⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离，它们的半径都是1，顺次连接五个圆心得到五边形ABCDE ，则图中五个扇形的面积和是_______。
析解：由于不知道每个扇形圆心角的具体角度，故无法直接计算，而五边形的内角和为5400=3600＋1800，因此可将阴影部分的面积“重新组合”成一个圆和一个半圆的面积，即1.5个圆的面积。
因此结果为1.5π。
三、“去”重例3(2005湖北武汉) 如图3，Rt △ABC 中，∠C=900，AC ＝2，AB ＝4，分别以AC 、BC 为直径作半圆，则图中阴影部分的面积为 。
析解：观察图形，发现两个半圆覆盖了一个三角形，而且中间阴影部分重叠了两次，故采用“图形去重法”解决，即阴影部分的面积等于大、小半圆面积之和与Rt △ABC 面积的差：12×π×12＋12×π×(42－22÷2)2－12×2×3，故结果为2π－23。
求平面几何阴影部分面积的三种方法
思路探寻求平面几何阴影部分的面积问题是平面几何中的典型问题.大部分求平面几何阴影部分面积问题中的几何图形都是不规则的图形，对此，我们要学会灵活运用和差法、等积法、割补法来解题.一、和差法和差法就是把所求图形的面积问题转化为若干个图形的面积的和或差来进行计算的方法.而运用和差法解题的关键是弄清楚阴影部分的面积可以由哪些图形的面积的差或和构成.针对某些较为复杂图形的阴影面积问题，可以通过不改变图形的位置，将它的面积用几个规则图形的面积的和或差表示出来，再通过计算求得图形的面积.例1.如图1所示，B 是AC 上的一点，分别以AB ,BC ,AC 为直径作半圆，过B 作BD ⊥AC 与半圆交于点D .求证：图中阴影部分面积等于以BD 为直径的圆的面积.分析：通过观察图形可以发现，将大半圆的面积减去两个小半圆的面积，就可以得到阴影部分的面积，可用和差法来解答本题.证明：∵AC =AB +BC ，∴S 阴影=π2∙æèöøAC 22-π2∙æèöøAB 22-π2∙æèöøBC 22=π4AB ∙BC ，而以BD 为直径的圆的面积为S 圆=π∙æèöøBD 22=π4BD 2，∵BD ⊥AC ,∠ADC =90°，∴BD 2=AB ∙BC ，∴阴影部分面积等于以BD 为直径的圆的面积.二、等积法当图形的面积很难求出或者无法利用和差法来求解时，我们通常运用等积法，即将问题转化为求与其等面积的图形的面积来求解.运用等积法解题的关键是弄清楚哪两个图形的面积相等.可借助同底等高或等底同高的两个三角形、平行四边形面积相等的性质来解答有关问题.例2.如图2所示，⊙0的半径为1，C 是⊙0上一点，以C 为圆心，以1为半径作弧与⊙0相交于A ,B 两点，求图中阴影部分的面积.分析：我们无法直接求出本题中阴影部分的面积，可运用等积法来求解，连接分割线AB ，将问题转化为求两个弓形图形的面积.解：连接AB ，则S 阴影=2×S 弓形ACB ，∵OD =12OC =12，可得∠OAB =30°，从而∠AOB =120°∴S 弓形=120π360-12×3×12=π3，∴S 阴影=23π-.三、割补法割补法就是把图形割补成几个规则图形，使题目便于解答的方法.有些图形较为复杂，我们可以结合题意将图形割补为规则图形，如三角形、平行四边形、圆、扇形等，然后运用三角形、平行四边形、圆、扇形等的面积公式进行求解.例3.如图3所示，已知菱形ABCD 的两条对角线分别为a ，b ，分别以每条边为直径向菱形内作半圆，求四条半圆弧围成的花瓣形面积，即图中阴影部分的面积.分析：所求阴影部分的面积是由几个图形叠加而成，我们需要运用割补法来求解.将阴影部分面积看作是四个半圆与菱形重叠之后的面积，割去重叠的部分，便可求出阴影部分的面积.解：设以BC 为直径的半圆面积为S 半圆，则S 半圆-S △OBC =14S 花瓣，S 花瓣=4S 半圆-S 菱形ABCD =4×12π2-ab 2=π()a 2+b 2-4ab 8.作差法、等积法和割补法都是求平面几何图形阴影部分面积的基本方法.无论运用哪种方法进行求解，我们都需要仔细观察阴影部分的图形，寻找它与规则图形之间的联系，将问题转化为求规则图形面积的问题.（作者单位：新疆特克斯县高级中学）朱家燕图2图1图3A B C D 53Copyright©博看网 . All Rights Reserved.。
中考数学：求阴影部分面积的几种常见方法
阴影部分面积的几种常见方法在初中数学中，求阴影部分的面积问题是一个重要内容，在近年来的各地中考试题中屡见不鲜．这类试题大多数都是求不规则图形的面积,具有一定的难度，因此，正确把握求阴影部分面积问题的解题方法,显得尤为重要．本文举例介绍解决这类问题的常见方法．一、直接求解法例1 如图1,有一矩形纸片ABCD，AB＝10，AD＝6，将纸片折叠，使AD边落在AB 边上，AD变到AD1位置,折痕为AE．再将△AED1以D1E为折痕，向右折叠，AE变到A1E 位置,且A1E交BC于点F．求图中阴影部分的面积．分析因为阴影部分是一个规则的几何图形Rt△CEF，故根据已知条件可以直接计算阴影部分面积．解如图1,根据对称性可得AD＝AD1＝A1D1＝6．由已知条件易知：EC＝D1B＝4,BC＝6;Rt△FBA1∽Rt△FCE．设FC为x，则FB＝6－x．二、间接求解法例2 如图2,⊙O1与⊙O2外切于点C，且两圆分别和直线l相切于A、B两点,若⊙O1半径为3cm；⊙O2半径为1cm，求阴影部分面积．分析这是求一个不规则图形的面积,没有现成的面积公式，因此应采用间接的方法,设法转化为规则图形的面积的和或差去计算．三、整体合并法例3 如图3，⊙A、⊙B、⊙C两两不相交，且半径都是0.5cm，求三个阴影部分面积之和．分析所求的阴影部分面积是三个扇形面积之和，因为三个扇形圆心角度数不知道,所以无法单独求解，但仔细观察发现，三个扇形的圆心角分别是△ABC的三个内角,其和为180°，而扇形半径都相等，所以三个扇形能合并成一个半圆．于是问题获解．解如图3,因为三个圆的半径相等，三个扇形圆心角之和是180°，所以其面积就是半圆面积．四、等积变换法例4 如图4,A是半径为R的⊙O外一点，弦BC为3R,OA∥BC，求阴影部分面积．分析本题的阴影部分是不规则的图形,求其面积较困难,但灵活运用等积变换，就可以把它的面积转化为扇形OBC的面积，从而获解．解连接OC，OB，五、分割法例5 如图5，在Rt△ABC中，∠C＝90°，AC＝4，BC＝2,分别以AC、BC为直径画半圆，求阴影部分面积．分析阴影部分图形不规则，不能直接求面积，可以把它分割成几个部分求面积的和．解如图5，连接CD．∵AC、BC是直径,∴∠ADC＝∠BDC＝90°，∴A、D、B三点共线．设阴影部分面积被分割为S1、S2、S3、S4四部分．则六、转化法例6如图（1),大半圆O与小半圆O1相切于点C，大半圆的弦AB与小半圆相切于点F，且AB∥CD，AB＝4cm,求阴影部分面积．分析如果想直接求阴影部分面积，无法求解，因为它不是规则图形．但要采取转化思想，把小半圆平移到与大半圆的圆心重合的位置，作OE⊥AB于点E．连接OB，可知BE＝2cm,阴影部分面积等于大半圆面积减去小半圆的面积．解如图(2)，将小半圆O1移至与大半圆圆心重合，作OE⊥AB于点E，则BE＝12AB＝2cm．设大圆半径为R，小圆半径为x,在Rt△OEB中，有七、割补法例7 如图7，点P（3a，a）是反比例函数y＝12x与⊙O在第一象限内的一个交点，求阴影部分的面积．分析阴影部分分两部分，难于逐一求解,但考虑反比例函数的对称性,结合割补原理，问题变得特别简单．解如图7，把右上角的S1部分分割下来,移到左下方补在S3处,与S2就组成了一个扇形OAB．易知:∵P(3a，a)在反比例函数y＝12x的图象上，∴3a＝12a．解得:a1＝2,a2＝－2（舍去）．∴P坐标为(6，2)．连接OP,作PC⊥x轴于点C,得：八、方程建模法例8如图8，正方形边长为a,以每边为直径在正方形内画四个半圆，求阴影部分的面积．分析本题直接求阴影部分面积较复杂，但观察图形特点引入方程的思想，问题变得非常简单．解正方形由四个阴影花瓣和四个空白图形组成，如图8，设一个阴影花瓣面积为x，一个空白图形面积为y．根据题意得:因此阴影部分面积为．222aaπ-．。
【2020】小升初数学几何图形阴影部分面积题型大全(详细答案解析)
六年级阴影部分的面积1.求阴影部分的面积。
(单位:厘米)解：割补后如右图，易知，阴影部分面积为一个梯形。
梯形上底DE=7-4=3厘米，1S =S =DE AB)AD 2⨯+⨯阴梯形（=137)42⨯+⨯（=20(平方厘米)2、求阴影部分的面积。
<解：S =S 阴梯形，梯形的上底是圆的直径，下底、高是圆的半径，S =S 阴梯形=124)22⨯+⨯（=6(2cm )3、如图，平行四边形的高是6厘米，面积是54平方厘米，求阴影三角形的面积。
【解：S =AD AO ⨯ABCD =54平方厘米，且AO=6厘米，所以AD=9厘米。
由图形可知AED ∆是等腰直角三角形，所以AE=AD ，OE=OF=AE-AO=9-6=3cm ，BO=BC-OC=9-3=6cm 。
1S =BO OF 2⨯⨯阴=1S =632⨯⨯阴=92cm 。
4、如图是一个平行四边形，面积是50平方厘米，求阴影积分的面积。
解：方法一：过C 点作CF AD ⊥交AD 于点F ，可知AECF 是长方形，面积=5×6=302cm ，ABE CFD S =S ∆∆=(50-30)÷2=102cm 。
方法二：BC=S ABCD ÷AE=50÷5=10cm ，BE=BC-EC=10-6=4cm ，ABE S ∆=BE ×AE ÷2 =4×5÷2=102cm,5、下图是一个半圆形，已知ＡＢ＝10厘米，阴影部分的面积为平方厘米，求图形中三角形的高。
解：S =S -S ∆阴半圆=21AB 22π⎛⎫⨯⨯ ⎪⎝⎭=21103.1422⎛⎫⨯⨯ ⎪⎝⎭=152cm ， 三角形的高=2S ∆÷AB=2×15÷10=3cm 。
@6、如图，一个长方形长是10cm ，宽是4cm ，以A 点和C 点为圆心各画一个扇形，求画中阴影部分的面积是多少平方厘米解：BECD 1S =S -S 4阴大圆=ABCD 11S -S S 44⎛⎫- ⎪⎝⎭大圆小圆=ABCD 11S +S -S 44大圆小圆=()2213.1410-4-1044⨯⨯⨯ =2cm 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
求几何图形的阴影部分的面积1.如图，大圆半径为5厘米，小圆半径为3厘米,求阴影部分的面积,2.如图，已知两同心圆（圆心相同，半径不相等的两个圆），大圆半径为3厘米，小圆半径为1厘米，求阴影部分的面积3.如图，大圆半径为6cm，小圆半径为4cm，求阴影部分的面积4.已知如图大圆的半径为4cm，小圆的半径为3cm，求两个圆阴影部分的面积的差5.求阴影部分的面积(单位:厘米)6.正方形面积是7平方厘米，求阴影部分的面积(单位:厘米)7.求图中阴影部分的面积(单位:厘米)8.求阴影部分的面积(单位:厘米)9.求阴影部分的面积(单位:厘米)10.如图,已知小圆半径为2厘米，大圆半径是小圆的3倍，问空白部分甲比乙的面积多多少厘米？11.求阴影部分的面积(单位:厘米)12.求阴影部分的面积(单位:厘米)13.求阴影部分的面积(单位:厘米)14.求阴影部分的面积(单位:厘米)15.求阴影部分的面积(单位:厘米)16.求阴影部分的面积(单位:厘米)17.求阴影部分的面积(单位:厘米)18.求阴影部分的面积(单位:厘米)19.已知直角三角形面积是12平方厘米，求阴影部分的面积20.求阴影部分的面积(单位:厘米)21.图中圆的半径为5厘米,求阴影部分的面积(单位:厘米)22.如图，在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长23.正方形边长为2厘米，求阴影部分的面积24.如图，正方形ABCD的面积是36平方厘米，求阴影部分的面积25.图中四个圆的半径都是1厘米，求阴影部分的面积26.如图，正方形边长为8厘米，求阴影部分的面积27.图中的4个圆的圆心是正方形的4个顶点，它们的公共点是该正方形的中心，如果每个圆的半径都是1厘米，那么阴影部分的面积是多少？28.如图，有8个半径为1厘米的小圆，用他们的圆周的一部分连成一个花瓣图形，图中的黑点是这些圆的圆心。
如果圆周π率取3.1416，那么花瓣图形的的面积是多少平方厘米？29.如图，四个扇形的半径相等，求阴影部分的面积(单位:厘米)30.如图，等腰直角三角形ABC和四分之一圆DEB，AB=5厘米，BE=2厘米，求图中阴影部分的面积31.如图，正方形ABCD的对角线AC=2厘米，扇形ACB是以AC为直径的半圆，扇形DAC是以D为圆心，AD为半径的圆的一部分，求阴影部分的面积32.求阴影部分的面积(单位:厘米)33.图中直角三角形ABC的直角三角形的直角边AB=4厘米，BC=6厘米，扇形BCD所在圆是以B为圆心，半径为BC的圆，∠CBD=500,问阴影部分甲比乙面积小多少？34.如图，三角形ABC是直角三角形，阴影部分甲比阴影部分乙面积大28平方厘米，AB=40厘米,求BC的长度35.如图是一个正方形和半圆所组成的图形，P为半圆周的中点，Q为正方形一边上的中点，求阴影部分的面积36.如图，大正方形的边长为6厘米，小正方形的边长为4厘米。
求阴影部分的面积37.求阴影部分的面积(单位:厘米)38.求阴影部分的面积(单位:厘米)39.如图，三角形OAB是等腰三角形，OBC是扇形，OB=5厘米，求阴影部分的面积40.如图,大小正方形的边长分别是3厘米和2厘米，求阴影部分的面积41.如图，大小正方形的边长分别是12厘米和10厘米,求阴影部分面积42.如图，求图中阴影部分图形的面积及周长43.如图,阴影部分三角形的面积是5平方米，求圆的面积44.如图,圆的直径是2厘米，求阴影部分的面积45.如图，求阴影部分图形的面积及周长。
46.如图，求图中阴影部分的面积（单位：厘米）47.如图，求图中阴影部分的面积48.如图，求图中阴影部分的面积49.如图，求图中阴影部分的面积。
50.如图，求图中阴影部分的面积。
51.如图，两个直角三角形完全相同，求图中阴影部分的面积52.求阴影部分的面积（单位：厘米）求几何图形阴影部分的面积答案1.5×5-3×3=25-9=16（平方厘米）2.分析：如图，根据圆的对称性，大圆与小圆之间的部分全等，故阴影部分的面积是两圆面积差的一半． 解：观察图形，发现：阴影部分的面积是两圆面积差的一半，即S 阴影=（S 大圆﹣S 小圆）=π（32﹣12）=4π，=4×3.14=12.56（平方厘米）；答：阴影部分的面积是12.56平方厘米3.阴影部分的面积=21×3.14×（62-42）=1.57×（36-16）=1.57×20=31.4（平方厘米） 4.分析：观察图形可知，空白处是两个圆的公共部分，所以两个圆的阴影部分的面积的差，就是这两个圆的面积之差，据此利用圆的面积公式计算即可解答问题解：3.14×42﹣3.14×32=3.14×16﹣3.14×9=3.14×（16﹣9）=3.14×7=21.98（平方厘米）5.解：这是最基本的方法：1／4 圆面积减去等腰直角三角形的面积，（π／4）× 22-2×1=1.14（平方厘米） 6.解：这也是一种最基本的方法用正方形的面积减去41圆的面积。
设圆的半径为 r ，因为正方形的面积为7平方厘米，所以 =7，所以阴影部分的面积为：7-πr 2／4=7-7π／4=1.505平方厘米7.解：最基本的方法之一.用四个1／4圆组成一个圆，用正方形的面积减去圆的面积，所以阴影部分的面积：2×2-π＝0.86平方厘米8.解：同上，正方形面积减去圆面积，16-π()=16-4π=3.44平方厘米9.解：这是一个用最常用的方法解最常见的题，为方便起见，我们把阴影部分的每一个小部分称为“叶形”，是用两个圆减去一个正方形，π×22×2-16=8π-16=9.12平方厘米另外：此题还可以看成是1题中阴影部分的8倍。
10.解：两个空白部分面积之差就是两圆面积之差（全加上阴影部分）π×62-π×22=100.48平方厘米 （注：这和两个圆是否相交、交的情况如何无关）11.解：正方形面积可用(对角线长×对角线长÷2，求)，正方形面积为：5×5÷2=12.5所以阴影面积为：π×52÷4-12.5=7.125平方厘米12.解：右面正方形上部阴影部分的面积，等于左面正方形下部空白部分面积，割补以后为1／4圆，所以阴影部分面积为：41π×22=3.14平方厘米 13.解：把右面的正方形平移至左边的正方形部分，则阴影部分合成一个长方形，所以阴影部分面积为：2×3=6平方厘米14.解：同上，平移左右两部分至中间部分，则合成一个长方形，所以阴影部分面积为2×1=2平方厘米15.解：这种图形称为环形，可以用两个同心圆的面积差或差的一部分来求，（π×42 -π×32）×36060=67×3.14=3.66平方厘米 16.解：三个部分拼成一个半圆面积．π×32÷2＝14.13平方厘米17.解: 连对角线后将"叶形"剪开移到右上面的空白部分,凑成正方形的一半.，所以阴影部分面积为：8×8÷2=32平方厘米18.解：梯形面积减去41圆面积， 21 (4+10)×4-41π=28-4π=15.44平方厘米 . 19.分析: 此题比上面的题有一定难度,这是"叶形"的一个半.解: 设三角形的直角边长为r ，则21=12，2)2(r =6 圆面积为：π2)2(r÷2=3π。
圆内三角形的面积为12÷2=6，阴影部分面积为：(3π-6)×23=5.13平方厘米 20.解：21［π×102＋π×42－π×62］=21π(116-36)=40π=125.6平方厘米 21.解：上面的阴影部分以AB 为轴翻转后，整个阴影部分成为梯形减去直角三角形，或两个小直角三角形AED 、BCD 面积和，所以阴影部分面积为：5×5÷2+5×10÷2=37.5平方厘米22.解：阴影部分的周长为三个扇形弧，拼在一起为一个半圆弧，所以圆弧周长为：2×3.14×3÷2=9.42厘米23.解：右半部分上面部分逆时针，下面部分顺时针旋转到左半部分，组成一个矩形，所以面积为：1×2=2平方厘米24.解：设小圆半径为r ，4=36, r=3，大圆半径为R ， R 2=2=18,将阴影部分通过转动移在一起构成半个圆环,所以面积为:π(R 2-)÷2=4.5π=14.13平方厘米 25.解：把中间部分分成四等分，分别放在上面圆的四个角上，补成一个正方形，边长为2厘米，所以面积为：2×2=4平方厘米26.解法一: 将左边上面一块移至右边上面,补上空白,则左边为一三角形,右边一个半圆.阴影部分为一个三角形和一个半圆面积之和. π×42÷2+4×4=8π+16=41.12平方厘米解法二: 补上两个空白为一个完整的圆. 所以阴影部分面积为一个圆减去一个叶形,叶形面积为:π×42÷2-4×4=8π-16，所以阴影部分的面积为: π×42-8π+16=41.12平方厘米 27.解：根据图可得四个空白中的一个空白部分1／2的面积为：π×12×41－21×1×1=41π－21，所以一个空白部分的面积是21π－1，两个空白色部分的面积为：2×﹙21π－1﹚＝π－2，所以阴影部分的面积为：4×﹛π×12－﹙π－2﹚﹜＝8（平方厘米），答：阴影部分的面积是8平方厘米28.分析：连接角上四个小圆的圆心构成一个正方形，各个小圆被切去3／4个圆，这四个部分正好合成3个整圆，而正方形中的空白部分合成两个小圆。
解：阴影部分为大正方形面积与一个小圆面积之和为4×4+π=19.1416平方厘米29.分析：四个空白部分可以拼成一个以2为半径的圆．所以阴影部分的面积为梯形面积减去圆的面积，4×(4+7)÷2-π×22=22-4π=9.44平方厘米30.解: 将三角形CEB 以B 为圆心，逆时针转动90度，到三角形ABD 位置,阴影部分成为三角形ACB 面积减去个小圆面积为:5×5÷2-π÷4=12.25-3.14=9.36平方厘米31.解: 因为2（AD ）2=（AC ）2=4，所以（AD ）2=2， 以AC 为直径的圆面积减去三角形ABC 面积加上弓形AC 面积，21π×12-2×2÷4+[π（AD ）2÷4-2] =21π-1+(21π-1)=π-2=1.14平方厘米 32.解法一：设AC 中点为B,阴影面积为三角形ABD 面积加弓形BD 的面积, 三角形ABD 的面积为:5×5÷2=12.5，弓形面积为:[π÷2-5×5]÷2=7.125，所以阴影面积为:12.5+7.125=19.625平方厘米解法二：右上面空白部分为小正方形面积减去41小圆面积，其值为：5×5-41π×52=25-425π阴影面积为三角形ADC 减去空白部分面积，为：10×5÷2-（25-425π）=425π=19.625平方厘米 33.解: 甲、乙两个部分同补上空白部分的三角形后合成一个扇形BCD ，一个成为三角形ABC ，此两部分差即为：π××36050－21×4×6＝5π-12=3.7平方厘米 34.解：两部分同补上空白部分后为直角三角形ABC ，一个为半圆，设BC 长为X ，则40X÷2-π÷2=28 ，所以40X-400π=56 则X=32.8厘米35.解：连PD 、PC 转换为两个三角形和两个弓形，两三角形面积为：△APD 面积+△QPC 面积=21（5×10+5×5）=37.5两弓形PC 、PD 面积为：21π×52-5×5，所以阴影部分的面积为：37.5+225π-25=51.75平方厘米 36.解：三角形DCE 的面积为: 21×4×10=20平方厘米，梯形ABCD 的面积为: 21(4+6)×4=20平方厘米 从而知道它们面积相等,则三角形ADF 面积等于三角形EBF 面积，阴影部分可补成圆ABE 的面积，其面积为：π÷4=9π=28.26平方厘米37.解:用41大圆的面积减去长方形面积再加上一个以2为半径的41圆ABE 面积，为41 (π×32+π×22)-6=41×13π-6=4.205平方厘米 38.解：两个弓形面积为：π2)25(-3×4÷2=425π-6，阴影部分为两个半圆面积减去两个弓形面积，结果为π×+π×2)23(-（425π-6）=π（4+49-425）+6=6平方厘米39.解：将两个同样的图形拼在一起成为41圆减等腰直角三角形 [π×52÷4-21×5×5]÷2=（425π-225）÷2=3.5625平方厘米40.（2+3）×2÷2+3×3÷2－（2+3）×2÷2=4.5（平方厘米）41.（10+12）×10÷2+3.14×12×12÷4－（10+12）×10÷2=113.04（平方厘米） 42.面积：6×（6÷2）－3.14×（6÷2）×（6÷2）÷2=3.87（平方厘米） 周长： 3.14×6÷2+6＋（6÷2）×2=21.42（厘米）43.2r ×r ÷2=5,即r ×r=5,圆的面积πr 2=3.14×5=15.7（平方厘米） 44.3.14×（2÷2）×（2÷2）－2×2÷2=1.14（平方厘米）45.面积：3.14×6×6÷4－3.14×（6÷2）×（6÷2）÷2=14.13 （平方厘米） 周长：2×3.14×6÷4+3.14×6÷2+6=24.84 （厘米）46.（6+4）×4÷2－（4×4－3.14×4×4÷4）=16.56（平方厘米） 47.6×3－3×3÷2=13.5（平方厘米） 48.8×（8÷2）÷2=16（平方厘米）49.3.14×4×4÷4－4×4÷2=4.56（平方厘米） 50.5×5÷2=12.5（平方厘米）51.﹙8+8-2﹚×3÷2＝21（平方厘米）52.阴影部分的面积=以6厘米为半径的圆的面积+以4厘米为半径的圆的面积﹣长方形的面积，长方形的长和宽分别为6厘米和4厘米，于是利用长方形和圆的面积公式即可求解．×3.14×62+×3.14×42﹣﹣4×6=28.26+12.56﹣24=16.82（平方厘米）答：阴影部分的面积16.82平方厘米。