2016高中数学人教A版必修四第一章41单位圆与任意角的正弦函数余弦函数的定义42单位圆与周期性训练
《单位圆与任意角的正弦函数、余弦函数定义》精品课件

解析
先考虑角的终边不在坐标轴上的情形如图设角的终边与单
位圆交于点P,则点P的坐标为 ,且 = .
点 在角的终边上,则 = + 分别过点P,Q作x轴的垂线
PM,QN,垂足为M,N.易知△ ∼△ .
所以
=
.即
学而优 ·教有方
典例剖析
高中数学
GAOZHONGSHUXUE
师生互动
教师出示例2,组织学生分组讨论,确定利用定义解题的思路,然后安排一名学生上黑板演
示例2的解答过程,其他学生在练习本上完成.教师巡视,收集信息,及时评价,纠错,讲解,规
范解题过程.
教师引导学生完成“思考交流”,根据角的范围安排学生分四组讨论交流,完成填空并回
(1)画出角;
(2)求角的正弦函数值和余弦函数值.
解析
(1)如图,以原点为角的顶点,以x轴的非负半轴为始边,顺时针旋转,
与 单 位 圆 交 于 点 P, 过 点 P 作 x 轴 的 垂 线 交 x 轴 于 点 M. 于 是 =
∠ = − 即为所作的角.
(2)设点 ,则 =
答问题,集体评价,教师归纳总结.
设计意图
通过例2和思考交流,加深学生对定义的理解,培养学生的直观想象和数学运算核心素养.
学而优 ·教有方
课堂小结
高中数学
GAOZHONGSHUXUE
1.锐角的正弦函数和余弦函数的定义.
2.任意角的正弦函数和余弦函数的两个定义:是用单位圆上点的坐标定义;
二是用终边上除原点外任意一点的坐标的比值定义.
学而优 ·教有方
+ .
单位圆与任意角的正弦函数、余弦函数定义 课件

(2)在单位圆中,若角α= ,求 sin α与 cos α的值;
例 2 已知任意角α终边上除原点外的一点 Q(x,y),求角α的正弦函数
值、余弦函数值.
例 2 已知任意角α终边上除原点外的一点 Q(x,y),求角α的正弦函数
值、余弦函数值.
例 2 已知任意角α终边上除原点外的一点 Q(x,y),求角α的正弦函数
把点P的横坐标u叫作角α的余弦值,记作u=cos α.
2.任意角的正余弦函数值的计算方法
= , =
其中 =
2 + 2
课后思考
已知角α的终边过点 P(-3a,4a)(a≠0),求 2sin α+cos α的值.
课后思考
已知角α的终边过点 P(-3a,4a)(a≠0),求 2sin α+cos α的值.
值、余弦函数值.
y
N
M
x
抽象概括
设任意角终边上除原点外的另外一点 , ,则角的正弦函数值和余
弦函数值分别为:
= , =
其中 =
2 + 2
学以致用
例3.若角α的终边经过点P(5,-12),则sin α=
解析因为 x=5,y=-12,
所以 r= 52 + (-12)2=13,
单位圆与任意角的正弦函数,余弦函数
2023.02.20情Fra bibliotek导入在初中我们是如何定义锐角的正弦值和余弦值?
P
O
M
MP
sin α
OP
OM
cos α
OP
新知探究
下面我们在直角坐标系中,利用单位圆来进一步研究锐角α的
人教A版高中数学必修四课件第一章1.4.2正弦函数余弦函数的性质

练一练
练习 2、函数 y=3sin(π3-2x)在什么区间是减函数? [解析]令 u=π3-2x,则 u 是 x 的减函数. ∵y=sinu 在[-π2+2kπ,π2+2kπ](k∈Z)上为增函数, ∴原函数 y=3sin(π3-2x)在区间[-2π+2kπ,2π+2kπ](k∈Z)上递减, ∴-π2+2kπ≤3π-2x≤π2+2kπ, 即-1π2+kπ≤x≤152π+kπ(k∈Z).
[分析] (1)先将异名三角函数化为同名三角函数,并且利用诱导 公式化到同一单调区间上.(2)先比较 sin38π与 cos38π的大小,然后利用 正弦函数单调性求解.
练一练
[解析] (1)sin194°=sin(180°+14°)=-sin14°, cos160°=cos(180°-20°)=-cos20°=-sin70°. ∵0°<14°<70°<90°,∴sin14°<sin70°, 从而-sin14°>-sin70°,即 sin194°>cos160°. (2)∵cos38π=sinπ8,∴0<cos38π<sin38π<1. 而 y=sinx 在(0,1)内递增, ∴sincos38π<sinsin38π.
作业布置
[分析] (1)将2x看成一个整体,利用余弦函数的值域求得;(2) 把sinx看成一个整体,利用换元法转化为求二次函数的值域.
典例精析
[解析] (1)∵-1≤cos2x≤1,∴-2≤-2cos2x≤2. ∴1≤3-2cos2x≤5,即1≤y≤5. ∴函数y=3-2cos2x,x∈R的值域为[1,5]. (2)y=cos2x+2sinx-2=-sin2x+2sinx-1=-(sinx-1)2. ∵-1≤sinx≤1,∴函数y=cos2x+2sinx-2,x∈R的值域为[-4,0].
人教A版高中数学必修四课件第一章三角函数1.4.2正弦函数、余弦函数的性质(二).pptx

偶函数
单调递减区间: [2kπ, π 2kπ](k Z) 单调递增区间: [2kπ π, 2kπ 2π](k Z)
例1 不通过求值,指出下列各式大于0还是小于0:
(1)
sin(
)
18
–
sin(
10)
解:
2 10 18 2
又
y=sinx
在[
2
,
2
]上是增函数.
sin( ) < sin( )
10
18
即:sin(
18
)
–
sin(
10
)>0
例1 不通过求值,指出下列各式大于0还是小于0:
2
,
2
上是减函
答案:B
小结:
我们把正弦函数、余弦函数的 性质总结一下,列成表格为:
定义域 值域 周期 奇偶性
单调性
正弦函数
R
[-1,1]
2π
奇函数
单调递增区间:
[ π 2kπ, π 2kπ](k Z)
2
2
单调递减区间:
[ π 2kπ, 3π 2kπ](k Z)
2
2
余弦函数 R
[-1,1]
y=cosx (xR) 是偶函数
2
3
4
5 6 x
3.正弦函数的单调性
组卷网
y
1
x
-3 5 -2 3
2
2
-
o 2
2
3
2
2
5 2
3
7 2
4
-1
…x
0
2
…
… …
2
3 2
sinx -1
0
高中数学第1章三角函数4.1单位圆与任意角的正弦函数、余弦函数的定义4.2单位圆与周期性课件北师大版必修4

(2)根据正弦、余弦在各个象限的符号确定2α的象限,进而确定α所在的象 限.
1.正弦、余弦函数值在各象限内取正数的规律可概括为“正弦上为正、余 弦右为正”,即当角α的终边在x轴的上方时sin α>0;当角α的终边在y轴的右侧 时,cos α>0.
2.一般地,对于函数f(x),如果存在 非零实数T ,对定义域内的 任意一个 x值,都有 f(x+T)=f(x) ,则称f(x)为周期函数,T称为这个函数的周期.
3.特别地,正弦函数、余弦函数是周期函数,称2kπ(k∈Z,k≠0)是正弦函 数、余弦函数的周期,其中2π是正弦函数、余弦函数正周期中 最小 的一个, 称为 最小正周期 .
2.对于确定角α所在象限的问题,应首先界定题目中所有三角函数的符号, 然后根据各三角函数的符号来确定角α所在象限,则它们的公共象限即为所求.
3.由kπ<θ<kπ+π2(k∈Z)确定θ所在象限时应对k进行分类讨论.
[探究共研型] 利用正弦、余弦函数的周期性求值
探究1 30°与390°的终边相同,两角的同一三角函数值相等吗? 【提示】 相等. 探究2 终边相同的角的同一函数值都相等吗?为什么? 【提示】 都相等.因两角终边相同,其始边与单位圆交于同一点,由三角 函数定义知函数值相等.
(2)错误.因为f(-2+6)≠f(-2).
(3)错误.fπ+π2≠f(π)不满足任意性. 【答案】 (1)× (2)× (3)×
[小组合作型] 正弦、余弦函数的定义
已知θ的终边经过点P(a,a),a≠0,求sin θ,cos θ. 【精彩点拨】 利用正弦函数、余弦函数的定义可求sin θ,cos θ.
人教版A版高中数学必修4:1.4.2 正弦函数、余弦函数的性质(6)

=2sinx3-π6, ∴y=2sinx3-π6的周期是 6π.
(3)y=|sinx|的图象如图所示.
第一章 三角函数
∴周期T=π.
第一章 三角函数
【名师点评】 求三角函数的周期,通常有三 种方法. (1)定义法; (2)公式法,对 y=Asin(ωx+φ)或 y=Acos(ωx +φ)(A,ω,φ 是常数,且 A≠0,ω≠0),T=|2ωπ|;
第一章 三角函数
1.4.2 正弦函数、余弦函数的 性质
第一章 三角函数
预习目标
学习导航
重点难点 重点:正、余弦函数的性质. 难点:利用正、余弦函数的性质,求正、 余弦函数的周期、奇偶性、单调性、最值 等问题.
第一章 三角函数
新知初探思维启动
正、余弦函数的图象和性质
函数
y=sinx
y=cosx
图象
第一章 三角函数
解:(1)函数应满足 1+sinx≠0,
∴函数 f(x)=1+s1i+nx-sincxos2x的定义域为{x∈
R|x≠2kπ+3π, k∈ Z}. 2
显然定义域不关于原点对称,
故函数
f(x)=1+
sinx- cos 2 x为非奇非偶函数. 1+sinx
第一章 三角函数
1-cosx≥0 (2)由cosx-1≥0,得 cosx=1,故 f(x)=0,
第一章 三角函数
单调减区间为[34π+2kπ,74π+2kπ](k∈Z). 所以原函数 y=2sin(π4-x)的单调增区间为[34π +2kπ,74π+2kπ](k∈Z); 单调减区间为[-π4+2kπ,34π+2kπ](k∈Z).
第一章 三角函数
变式训练
3.求函数 y=2sin(x+π4)的单调区间. 解:y=sinx 的单调增区间为[-π2+2kπ,π2+ 2kπ],k∈Z;单调减区间为[π2+2kπ,32π+2kπ], k∈Z. 由-π2+2kπ≤x+π4≤π2+2kπ,k∈Z,
高中数学必修四文档:第一章§4.1单位圆与任意角的正弦函数、余弦函数的定义
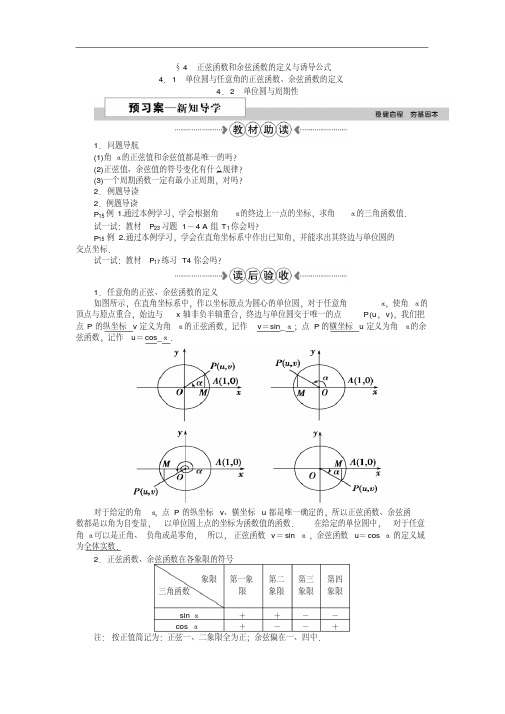
4. 2 单位圆与周期性
1. 问题导航 (1)角 α的正弦值和余弦值都是唯一的吗? (2)正弦值、余弦值的符号变化有什么规律? (3)一个周期函数一定有最小正周期,对吗? 2. 例题导读 2.例题导读 P15 例 1.通过本例学习,学会根据角 α的终边上一点的坐标,求角 α的三角函数值. 试一试:教材 P23 习题 1- 4 A 组 T1 你会吗? P15 例 2.通过本例学习,学会在直角坐标系中作出已知角,并能求出其终边与单位圆的 交点坐标. 试一试:教材 P17 练习 T4 你会吗?
1. 对正弦函数、余弦函数定义的理解
(1)定义中, α是一个任意角,同时它也可以是一个实数 (弧度数 ). (2)角 α的终边与单位圆 O 交于点 P(u, v),实际上给出了两个对应关系,即 实数 α(弧度 )对应于点 P 的纵坐标 v―对―应→正弦
பைடு நூலகம்对应
实数 α(弧度 )对应于点 P 的横坐标 u――→余弦
1. 任意角的正弦、余弦函数的定义
如图所示,在直角坐标系中,作以坐标原点为圆心的单位圆,对于任意角
α,使角 α的
顶点与原点重合,始边与 x 轴非负半轴重合,终边与单位圆交于唯一的点
P(u, v),我们把
点 P 的纵坐标 v 定义为角 α的正弦函数,记作 v=sin_α;点 P 的横坐标 u 定义为角 α的余
2. 正弦函数、余弦函数在各象限的符号
象限 第一象
三角函数
限
第二 象限
第三 第四 象限 象限
sin α
+
+
-
-
cos α
+
-
-
人教版高一数学 A版 必修4 教学课件:第一章 《1.4.2 正弦函数、余弦函数的性质》

终边重合,也具有周而复始的变化规律,为定量描述这种变 化规律,需引入一个新的数学概念——函数周期性.
探究点一 周期函数的定义
思考1 观察正弦函数图象知,正弦曲线每相隔2π个单位重复出 现其理论依据是什么?
答 诱导公式sin(x+2kπ)=sin x(k∈Z)当自变量x的值增加2π的
公式得,sin(-x)=-sin x,cos(-x)=cos x均对一切x∈R恒成
立.
例1 求下列三角函数的周期.
(1)y=3cos x,x∈R; 解 ∵3cos(x+2π)=3cos x, ∴自变量x只要并且至少要增加到x+2π, 函数y=3cos x,x∈R的值才能重复出现, 所以,函数y=3cos x,x∈R的周期是2π.
∴f(-x)=lg[1-sin(-x)]-lg[1+sin(-x)]
=lg(1+sin x)-lg(1-sin x)=-f(x). ∴f(x)为奇函数.
1+sin x-cos2x
(3)f(x)=
.
1+sin x
解 ∵1+sin x≠0,∴sin x≠-1,
∴x∈R 且 x≠2kπ-π2,k∈Z.
∵定义域不关于原点对称,
(2)y=sin 2x,x∈R;
解 ∵sin(2x+2π)=sin2(x+π)=sin 2x, ∴自变量x只要并且至少要增加到x+π, 函数y=sin 2x,x∈R的值才能重复出现, 所以,函数y=sin 2x,x∈R的周期是π.
(3)y=2sin12x-π6,x∈R. 解 ∵2sin12x+4π-π6=2sin12x-π6+2π=2sin12x-π6,
第一章 三角函数
§1.4 三角函数的图象与性质
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
活学巧练跟踪验证
[A、基础达标]
1、cos错谋!的值为( )
A、-错误! B.错误!
C、扌
D、i错误!
解析:选D、-yn的终边与错误!rr的终边重合,故cos错误!=cos错误!= 一错误!、
2、若a的终边过点(2sin 30°,一2cos30° ),则sin。
的值为( )
A、错误! B. 一错误!
C、一错误!
D、-错误!
解析:选C.因为sin 30° =错误!,cos 30° =错误!,
所以a的终边过点(1, 一错谋!),所以厂=错误!=2, 所以sin a=错误!= 一错误!,故选C、
3、尸错误! +错误!的值域为()
A、{2,0} B. {一2, 0}
C、{2-2}
D、{2, 一2.0}
解析:选D、x为第一象限角吋,y=2\x为第二象限角时』=0: x为第三象限角时,y =—2丸为第四象限角时,)=0:
所以值域为{2, -2, 0}、
4、若点P的坐标为(cos 2 015° , sin 2 015° ),则点P在( )
A、第一象限 B.第二象限
C、第三象限
D、第四象限
解析:选C、因为2015° =5X360° +215° ,所以角2 015°的终边在第三象限,所以cos 2 015° <0, sin 2 015° <0,所以点P在第三象限、
5、有下列命题:
①存在函数f (x)^义域中的某个自变M AC使f (xo+T) =f (xo),则f(x)为周期函数:
②存在实数7:使得对f (x)泄义域内的任意一个上都满足Ax+T) =f C则心) 为周期函数;
③周期函数的周期就是唯一的、
其中,正确命题的个数就是()
A、0 B. 1
C、 2
D、 3
解析:选A、①由周期函数的定义,可知f (A +D =/ (x)对定艾域内的任意一个A都成立,且TH0,故不正确;
②由周期函数的定狡可知TH0,故不正确;
③若T为周期,则.心+2门=/[(x+70 +门=心+卩)=/ (x),所以2T也就是周期,故不正确、
6、已知角a为第二象限角,贝I]错误!化简的结果为________ > ______________
解析:因为角a为第二象限角,故sin a>0, cos a <0,因此y] (sin a—cos a2)= I sin a—cos
al=sin a—cos a.
答案:sin o—cos a
7、若a就是第三象限角,则sin(cos 〃)・cos (sin a) _______ 0、
解析:因为a就是第三象限角,
所以一lvcos a<0, — 1 <sin a〈0、
所以sin(cos a) <0, cos(sin a) >0,
所以sin(cos a)-cos (sin a )〈0、
答案:<
8、已知角&的顶点为坐标原点,始边为x轴的非负半轴,若P(4, y)就是角&终边上一
点,且sin 〃 = 一错误!,则y=______ 、
解析/=错误!=错误!,且sin & =—错误!,所以sin 8=错误!=错误!= 一错误!,)<0,所以&为第四象限角,解得〉,=一8、
答案:-8
9、已知角a的终边过点P(—4加,3加)伽工0),求2sin ”+cosa的值、解:①当加>0时,
点P在第二象限,10PI = 5g
有2sin a+cos a =错误! +错误!=错误!:
②当加V0吋,点P在第四象限,10戸丨=一5加,
有2sin a+cos a =错误! +错误!= 一错误!、
10、已知函数Ax)的左义域就是R对任意实数;v,满足八兀+2)=—心人当圧[0, 4) 时
/(A)=X2+ 2¥x
t
(1)求证:函数沧)就是周期函数;
(2)求/(一7)、
解:(1)证明:对任意实数x,有•心+4) =/[(x+2)+2] =—心+2) = —[一/U)]=/(切、所以函数夬切就是周期函数、
(2)由(1)知,函数f (%)的周期为4,
所以/ (一7)=/(—7+2X4)=/(l)、
因为当xG[0,4)吋,/ (A) =/+2丫,
所以f (-7)=/ (1) =3、
IB、能力提升]
1、已知点Hsin geos在第二象限,则角a的终边在( )
A、第一象限
B、第二象限
C、第三象限
D、第四象限
解析:选D、因为P(sin a, cos a)在第二象限,
所以错误!
由sin a〈0,得a在第三或第四象限或y轴非正半轴上,
由cos a>0,得a在第一或第四象限或x轴非负半轴上,
所以a就是第四象限角.
2、已知角a终边经过点P( —8加,—6cos 60° )且cos。
= ~错误!,则加的值为( )
A、错误! B.-错误!
C、一错误!
D、错谋!
解析:选A、点P的坐标可化为(一8心一3),
由广=错误!=错误!,
由三角函数的定狡知cos Q=错误!=错误!= 一错误!、
即100川=64加?+9,解得加=±错误!,
当加=—[吋,点、P的坐标为(4, —3),则cos a为正,不符合题意,故加=错误匚
3、已知泄义在R上的函数.心)就是以2为周期的奇函数,则方程心)=0在[一2,2]上至少有________ 个实数根、
解析:因为函数7U)就是定义在R上的奇函数,
所以f (0) =0,又因为函数f (x)以2为周期,
所以f (2)=A-2) =/(0)=0,且错误!
解得•代一1) =/(1)=0,故方程f (x)=0在[一2, 2]上至少有5个实数根、答案:5
4、设。
就是第二象限角,且Icos错误!l=-cos错误!,则角错误!就是第 __________ 象限角、
解析:因为角a就是第二象限角,
所以2«TT+错误!va〈2kn + Ti g®,
所以E+错误!v错误!〈5+错误!UGZ),
当k为偶数时,错误!就是第一象限角;
当k为奇数时,错误!就是第三象限角,
又因为错误! = -cos错误!,
即cos错误!<0,
所以错误!就是第三象限角、
答案:三
5、已知角a的终边过点(3加一9,加+2),且cos a<0, sin &>0,求加的取值范围. 解:因为
cos a<0,
所以a的终边在第二或第三象限,或x轴的非正半轴上、
又因为sin a>09
所以a的终边在第一或第二象限,或y轴的非负半轴上、
所以a就是第二象限角,
即点(3/n—9,加+ 2)在第二象限、
所以错误!
解得一2</“〈3,
即加的取值范围就是(一2, 3).
6、(选做题)已知角a的顶点在原点,始边与x轴的非负半轴重合•错误!= 一错误!,且lg (cos有意义、
(1)试判断角a所在象限;
(2)若角。
的终边与单位圆相交于点M错误!,求加的值及sin "的值.
解:⑴由一=一- 可知sin a<0,所以。
就是第三或第四象限角或终边在y轴
I sin a\ sin a
非正半轴上的角、
由lg(cos a)有意艾可知cos a>09所以a就是第一或第四象限角或终边在x轴的非负半轴上的角、
综上可知角a就是第四象限角.
(2)因为点M错误!在单位圆上,
所以错误!错谋!+川=1,解得加=±错误!、
又a就是第四象限角,故加〈0,从而加=一错误!、
由正弦函数的定狡可知sin a =—错谋!、。
