江西省南昌市NCS20200607项目第一次模拟测试卷文科数学参考答案和评分标准
2020年江西省第一次高考模拟考试文科数学试题与答案

2020年江西省第一次高考模拟考试文科数学试题与答案(满分150分,考试时间120分钟)注意事项:1.答题前,考生务必将自己的姓名、准考证号码填写在答题卡和试卷指定位置上,并将条形码准确粘贴在条形码区域内。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
|﹣1<x<5},集合A={1,3},则集合∁U A的子集的个数是()1. 设全集U={x NA. 16B. 8C. 7D. 42. 下列各式的运算结果为纯虚数的是()A. i(1+i)2B. i2(1﹣i)C. (1+i)2D. i(1+i)3. 为比较甲、以两名篮球运动员的近期竞技状态,选取这两名球员最近五场比赛的得分制成如图所示的茎叶图,有以下结论:①甲最近五场比赛得分的中位数高于乙最近五场比赛得分的中位数;②甲最近五场比赛得分平均数低于乙最近五场比赛得分的平均数;③从最近五场比赛的得分看,乙比甲更稳定;④从最近五场比赛的得分看,甲比乙更稳定。
其中所有正确结论的编号为()A. ①③B. ①④C. ②③D. ②④4. 已知直线,直线为,若则( )A.或 B.C .D .或5. 已知,条件甲:;条件乙:,则甲是乙的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件6. 轴截面为正方形的圆柱的外接球的体积与该圆柱的体积的比值为( ) A . B .C .D .7. 在中,a ,b ,c 分别是角A ,B ,C 的对边,,则角B=( )A.B. C.D.8. 执行如图所示的程序框图,输出的S=( )A. 25B. 9C. 17D. 209. 设直线1:210l x y -+=与直线A 的交点为A ;,P Q 分别为12,l l 上任意两点,点M 为,P Q 的中点,若12AM PQ =,则m 的值为( ) A. 2B. 2-C. 3D. 3-10.在V ABC 中,sin B A =,BC =4C π=,则=AB ( )B. 5C. D.11. 已知函数,若,且函数存在最小值,则实数的取值范围为( ) A.B.C. D. 12.已知三棱锥的底面的顶点都在球的表面上,且,,,且三棱锥的体积为,则球的体积为( ) A.B.C.D.二、填空题:本题共4小题,每小题5分,共20分。
江西高三-月考模拟文科数学试卷及答案解析

南昌市高三第一次模拟考试文科数学考试时间:____分钟题型单选题填空题简答题总分得分单选题(本大题共12小题,每小题____分,共____分。
)1.在复平面内,复数(1+对应的点位于()A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.已知集合A={x|y=),B= {y| y-l<0),则A B=()A. (一∞,1)B. (一∞,1]C. [0,1)D. [0,1]3.已知命题p:函数f (x)=|cosx|的最小正周期为2π;命题q:函数y=x3+sinx的图像关于原点中心对称,则下列命题是真命题的是()A. p qB. p qC. (p) ( q)D. p (q)4.已知变量x与y正相关,且由观测数据算得样本平均数x=3,y=3.5,则由该观测数据算得的线性回归方程可能是()A. =0.4x+2.3B. =2x - 2.4C. =-2x+9.5D. =-0.3x+4.45.执行如图所示的程序框图.若输出的结果为3,则可输入的实数x的个数为()A. 1B. 2C. 3D. 46.已知函数f(x)= 则下列结论正确的是()A. f(x)是偶函数B. f(x)是增函数C. f(x)是周期函数D. f(x)的值域为[-1,+∞)7.设α为平面,a、b为两条不同的直线,则下列叙述正确的是()A. 若a∥α,b∥α,则a∥bB. 若a⊥α,a∥b,则b⊥αC. 若a⊥α,a⊥b,则b∥αD. 若a∥α,a⊥b,则b⊥α8.若等比数列的各项均为正数,前4项的和为9,积为,则前4项倒数的和为()A.B.C. 1D. 29.已知抛物线C:y2 =8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点,若FP=3FQ,则|QF|=()A.B.C. 3D. 210.如图网格纸上小正方形的边长为l,粗实线画出的是某几何体的三视图,则这个几何体的体积为()A. 2B. 3C. 4D. 511.已知点P在直线x+3y-2=0上,点Q在直线x+3y+6=0上,线段PQ的中点为M(x0,y0),且y0<x0 +2,则的取值范围是()A. [一,0)B. (一,0)C. (一,+∞)D. (一∞,一)(0,+∞)12.已知函数f(x)= ,若|f(x)|≥ax,则a的取值范围是()A. (-∞,0]B. (一∞,1]C. [一3,0]D. [一3,1]填空题(本大题共4小题,每小题____分,共____分。
2023届江西省南昌市高三上学期摸底测试(零模)数学(文)试题(解析版)

江西省南昌市2023届高三上学期摸底测试(零模)数学(文)试题一、单选题1.已知集合{2,1,0,1,2}A =--,2{|20}B x x x =+-<,则A B =( ) A .{1,0,1}- B .{1,0}-C .{21,1,2}--,D .{01,2}, 2.复数112i+的虚部是( ) A .25-B .15-C .15D .253.抛物线22y x =的焦点到准线的距离为( ) A .4B .2C .1D .124.若变量,x y 满足约束条件200x y y x y +≤⎧⎪-≤⎨⎪≥⎩,则2z x y =+的最大值为( )A .0B .1C .2D .35.“0ab >”是“2b aa b +≥”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.已知点,,A B C 是球O 的小圆1O 上的三点,若133,4AB BC CA OO ====,则球O 的表面积为( ) A .64πB .100πC .144πD .200π7.若直线2232x y =-与圆224x y +=相交于,A B 两点,O 为坐标原点,则OA AB ⋅=( ) A .22B .4C .22-D .-48.如图,正四棱台1111ABCD A B C D -中,点,,E F G 分别是棱111111,,C D D A A B 的中点,则下列判断中,不正确的是( )A .11,,,B B D D 共面 B .F ∈平面ACEC .FG ⊥平面ACED .11//A C 平面ACE9.冬残奥会闭幕式上,中国式浪漫再现,天干地支时辰钟表盘再现,由定音鼓构成的“表盘”形象上,60名残健共融表演者用行为模拟“指针”每圈60个时间刻度的行进轨迹.若以图中12点与圆心连线为始边,某时刻指向第1,21,41名残健共融表演者的“指针”为终边的角分别记为,,αβγ,则cos cos cos αβγ++的值为( )A .1-B .0C .1D .cos α10.设函数()f x 的定义域为R ,且(2)f x +是奇函数,(1)f x +是偶函数,则一定有( ) A .(4)0f =B .(1)0f -=C .(3)0f =D .(5)0f =11.若2221(2)x x y -=-+,则2222(2)(2)x y x y +++-+的最小值为( ) A .1B .2C .3D .412.已知函数()()2sin f x x ωϕ=+的部分图象如图所示,则下列判断正确的是( )A .函数()f x 的周期为4πB .对任意的x ∈R ,都有()2π3f x f ⎛⎫≤ ⎪⎝⎭C .函数()f x 在区间[]0,5π上恰好有三个零点D .函数π4f x ⎛⎫- ⎪⎝⎭是偶函数二、填空题13.若函数()()sin f x x a x =+在πx =时取得极值,则=a _____. 14.执行如下程序框图,输出i 的值为_____.15.某工厂10名工人某天生产同一类型零件,生产的件数分别是7,8,9,10,11,12,12,12,13,14,则这组数据的方差为_____.(参考数据:这组数据的平方和为1212)16.已知,OA OC 为正交基底,且,,1OB OA OD OC λμλμ==>>,,P Q 分别为,AC BD 的中点,若1AB CD =,则||PQ 的最小值为_____.三、解答题17.已知公差大于0的等差数列{}n a 满足11a =,且124,,a a a 成等比数列. (1)求数列{}n a 的通项公式; (2)令22na nb =,求数列{}n b 的前n 项和.18.如图是飞行棋部分棋盘图示,飞机的初始位置为0号格,抛掷一个质地均匀的骰子,若拋出的点数为1,2,飞机在原地不动;若抛出的点数为3,4,飞机向前移一格;若抛出的点数为5,6,飞机向前移两格.记抛掷骰子一次后,飞机到达1号格为事件A .记抛两次骰子后,飞机到达2号格为事件B .(1)求()P A ; (2)求()P B .19.如图,桌面上摆放了两个相同的正四面体PABD 和QABC .(1)求证:PQ AB ⊥;(2)若2AB =,求四面体APQB 的体积.20.已知函数()e (1)ln ln (0)x f x a x a x a =+--⋅>. (1)若e a =,求函数()f x 的极值; (2)讨论函数()f x 的单调性. 21.已知()2,0A ,()0,1B 是椭圆()2222:10x y E a b a b +=>>的两个顶点. (1)求椭圆E 的标准方程;(2)过点()2,1P 的直线l 与椭圆E 交于C ,D ,与直线AB 交于点M ,求PM PMPC PD+的值. 22.已知曲线1C 的参数方程为3x ty t=⎧⎪⎨=⎪⎩(t 为参数),以O 为极点,x 轴的非负半轴为极轴建立极坐标系,曲线2C 的极坐标方程为21sin ρθ=-.(1)求曲线1C 的普通方程,曲线2C 的直角坐标方程; (2)设曲线12,C C 的交点为,A B ,求||AB 的值. 23.已知函数()|26||36|f x x x =---. (1)求不等式()1f x >的解集;(2)若不等式()||f x k x ≤恒成立,求实数k 的取值范围参考答案:1.B【分析】由题可得{}|21B x x =-<<,再求A B 即可.【详解】∵{}{}2|20|21B x x x x x =+-<=-<<,{2,1,0,1,2}A =--所以{}1,0A B ⋂=-. 故选:B. 2.A【分析】根据复数的运算法则即可得到结果 【详解】22112i 12i 12i 12i 12i (12i)(12i)1(2i)555---====-++-- 所以虚部为25-故选:A 3.C【分析】利用抛物线的标准方程可得1p =,由焦点到准线的距离为p ,从而得到结果. 【详解】抛物线22y x =的焦点到准线的距离为p , 由抛物线标准方程22y x =可得1p =, 故选:C. 4.D【分析】作出可行域,由2z x y =+可得122zy x =-+,根据数形结合求最值即可.【详解】作出可行域,如图,由2z x y =+可得122zy x =-+,根据截距的几何意义可知,故当2z x y =+过点A 时,z 有最大值,由020y x x y -=⎧⎨+-=⎩解得1,1x y ==,即(1,1)A , 所以max 1213z =+⨯=. 故选:D 5.C【分析】利用作差法、不等式的基本性质结合充分条件、必要条件的定义判断可得出结论.【详解】由2b a a b +≥可得()220a b b a a b ab-+-=≥, 由已知0a ≠且0b ≠,若0ab <,则0a b -≠,所以,()20a b ->,则()20a b ab-<,矛盾.若0ab >,则()20a b -≥,从而()220a b b a a b ab-+-=≥,合乎题意.综上所述,“0ab >”是“2b aa b +≥”的充要条件.故选:C. 6.B【分析】根据题意,求出小圆的半径r ,由1OO ⊥平面ABC ,结合勾股定理,可求得球O 的半径,计算其表面积得答案.【详解】因为AB BC CA ===ABC 是正三角形,1O 是其外接圆圆心,所以ABC 的外接圆半径1233r O A ==,球O的半径5R ==,所以球O 的表面积为24π4π25100πR =⨯=.故选:B. 7.D【分析】先求出圆心到直线的距离,再利用弦心距,半径和弦的关系可求出AB ,然后利用向量的数量积的定义及几何意义可求得结果.【详解】由题意得圆224x y +=的圆心(0,0)O到直线x =-d ==所以2AB=AB =所以()cos OA AB OA AB OAB π⋅=-∠ cos OA AB OAB =-∠242AB =-=-,故选:D 8.C【分析】根据正棱台的概念及正棱锥的性质结合条件逐项分析即得. 【详解】延长正四棱台1111ABCD A B C D -的侧棱相交于S , 则三棱锥S ABCD -为正四棱锥,连接BD ,11,,,B B D D 都在平面SBD 内,故A 正确; 因为,E F 分别是棱1111,C D D A 的中点,所以11//EF A C ,由正棱锥的性质可知11//AC A C , 所以//EF AC ,即F ∈平面ACE ,故B 正确; 因为点,E G 分别是棱1111,C D A B 的中点, 所以11//EG D B ,11EG AC ⊥,设1111A B C D O =,则SO ⊥平面1111D C B A ,EG ⊂平面1111D C B A , ∴SO EG ⊥,11,SOAC SO O =⊂平面SAC ,11A C ⊂平面SAC ,∴EG ⊥平面SAC ,显然平面SAC 与平面ACE 不平行,故C 错误;因为11//AC A C ,AC ⊂平面ACE ,11A C ⊄平面ACE , 所以11//A C 平面ACE ,故D 正确. 故选:C. 9.B【分析】根据两角和的余弦公式化简计算. 【详解】由已知得126030παπ=⨯=,212260330ππβπ=⨯=+,414260330ππγπ=⨯=+, 所以24cos cos cos coscos cos 30330330πππππαβγ⎛⎫⎛⎫++=++++ ⎪ ⎪⎝⎭⎝⎭2244cos cos cos sin sin cos cos sin sin30330330330330πππππππππ=+-+-11coscos cos 0302303023030πππππ=--+=, 故选:B. 10.A【分析】根据图象平移变换与奇偶性,可得函数的对称性,可得答案. 【详解】()2f x +图象向右平移2个单位,可得()f x 的图象,且()2f x +是奇函数,()f x ∴的图象关于点()2,0成中心对称,()20f =,()1f x +图象向右平移1个单位,可得()f x 的图象,且()1f x +是偶函数, ()f x ∴的图象关于直线1x =成轴对称,由对称性,对称轴直线1x =关于()2,0成中心对称的直线为3x =, 对称中心()2,0关于直线3x =成轴对称的点为()4,0,即()40f =. 故选:A. 11.D【分析】求解定义域,确定1≥x ,用x 的表达式表示y 4x =,结合1≥x ,求出最小值.【详解】21x -210x -≥,解得:12x ≥, 两边平方得:()22222221(2143)4443x y x x x x x x ==-+-+-=----, 其中2330x -≥,解得:1≥x 或1x ≤-,综上:1≥x ,2121x x ===++-,因为1≥x ,所以210,210x x +>->, 所以原式212144x x x =++-=≥. 故选:D 12.C【分析】利用图象求出函数()f x 的解析式,利用正弦型函数的周期性可判断A 选项;利用正弦型函数的最值可判断B 选项;在[]0,5πx ∈时,解方程()0f x =可判断C 选项;利用正弦型函数的奇偶性可判断D 选项.【详解】因为()02sin 1f ϕ==,可得1sin 2ϕ=, 因为函数()f x 在0x =处附近单调递增,所以,()π2πZ 6k k ϕ=+∈, ()ππ2sin 2π2sin 66f x x k x ωω⎛⎫⎛⎫∴=++=+ ⎪ ⎪⎝⎭⎝⎭,因为3π3ππ2sin 1226f ω⎛⎫⎛⎫=+=- ⎪⎪⎝⎭⎝⎭,则3ππ1sin 262ω⎛⎫+=- ⎪⎝⎭, 因为函数()f x 在3π2x =处附近单调递减,且()f x 在0x >时在3π2x =处第一次取值为12-, 所以,3ππ7π266ω+=,可得23ω=, ()2π2sin 36x f x ⎛⎫∴=+ ⎪⎝⎭.对于A 选项,函数()f x 的最小正周期为2π3π23T ==,A 错; 对于B 选项,2π4ππ2sin 2396f ⎛⎫⎛⎫=+≠ ⎪⎪⎝⎭⎝⎭, 所以,2π3⎛⎫⎪⎝⎭f 不是函数()f x 的最大值,B 错;对于C 选项,当05πx ≤≤时,π2π7π6362x ≤+≤, 由()0f x =可得{}2ππ,2π,3π36x +∈,可得5π11π17π,,444x ⎧⎫∈⎨⎬⎩⎭, 所以,函数()f x 在区间[]0,5π上恰好有三个零点,C 对;对于D 选项,π2ππ22sin 2sin 43463x f x x ⎡⎤⎛⎫⎛⎫-=-+= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,故函数π4f x ⎛⎫- ⎪⎝⎭是奇函数,D 错.故选:C. 13.π-【分析】求出函数的导数,由题意令导数等于0,求得a 的值,验证确定答案. 【详解】由()()sin f x x a x =+可得()sin ()cos f x x x a x '=++,函数()()sin f x x a x =+在πx =时取得极值,故(π)sin π(π)cos π0f a '=++=, 解得πa =- ,当π,πx x <→时,sin 0,(π)cos 0,()0x x x f x '>->∴>, 当π,πx x >→时,sin 0,(π)cos 0,()0x x x f x '<-<∴<, 即在πx =时,函数取得极值, 故πa =-, 故答案为:π- 14.5【分析】模拟运行循环体即可求解.【详解】第一次循环:121,=3233a i =⨯=,不满足15a =,第二次循环:131,=4344a i =⨯=,不满足15a =,第三次循环:141,=5455a i =⨯=,满足15a =,此时输出5i =,故答案为:5 15.4.56##11425【分析】将方差公式展开整理,代入相关数据计算,可得答案. 【详解】由题意得1(78910111231314)10.810x =+++++⨯++= , 根据方差公式22222222121211[()()()][]n n s x x x x x x x x x nx nn=-+-++-=+++- ,可得221(12121010.8) 4.5610s =-⨯= , 故答案为:4.5616【分析】由,OA OC 为正交基底,且,,1OB OA OD OC λμλμ==>>,结合向量的线性运算和数量积运算可得0AB CD ⋅=,再由,P Q 分别为,AC BD 的中点,可得()()1122PQ OB OD OA OC =+-+12AB CD =+,再利用基本不等式可求得其最小值.【详解】因为,OA OC 为正交基底,所以0OA OC ⋅=,因为,,1OB OA OD OC λμλμ==>>,所以(1),(1)AB OA CD OC λμ=-=-,所以(1)(1)0AB CD OA OC λμ⋅=--⋅=,因为,P Q 分别为,AC BD 的中点,PQ OQ OP =-, 所以()()1122PQ OB OD OA OC =+-+ 12AB CD =+ ()2AB CD =+ 222AB AB CD CD =+⋅+ 2212222AB CD AB CD =+≥=, 当且仅当AB CD 时取等号,所以||PQ17.(1)n a n =;(2)1443n +-.【分析】(1)利用等比中项的概念及等差数列基本量的运算即得;(2)利用等比数列求和公式即得.(1)设公差为d ,因为1a ,2a ,4a 成等比数列,则2214a a a =,即2(1)1(13)d d +=⨯+,即20d d -=,解得1d =或0d =(舍),所以()1111n a a n d n n =+-=+-=;(2)由题可知22224n a n n n b ===,14b =,14n nb b +=, 所以{}n b 是以4为首项,4为公比的等比数列,所以()11241444143n n n n S b b b +⨯--=+++==-. 18.(1)13(2)13【分析】(1)直接利用古典概型的概率公式求解即可;(2)对事件B 的发生分三种情况:①第一次抛3,4,第二次抛3,4;②第一次抛1,2,第二次抛5,6;③第一次抛5,6,第二次抛1,2;可用独立事件的概率乘法公式求解,也可用列举法套用古典概型的概率公式求解;(1)抛掷一次骰子,出现的点数有1,2,3,4,5,6共6种等可能结果,事件A 包含3,4两种结果,所以()2163P A ==; (2)抛一次骰子,记点数为1,2是D ,点数为3,4是E ,点数为5,6是F ,抛一次骰子,D ,E ,F 等可能发生,抛两次骰子所有可能结果有(),D D ,(),D E ,(),D F ,(),E D ,(),E E ,(),E F ,(),F D ,(),F E ,(),F F 9种可能情况,其中到达2号格有(),E E ,(),D F ,(),F D 三种结果,所以()3193P B ==. 19.(1)证明见解析【分析】(1)连接CD 与AB 相交于点O ,证得O 为AB 的中点,连接PO ,QO ,利用线面垂直的判定定理证得AB ⊥平面POQ ,即可得到PQ AB ⊥;(2)过点,P Q 分别作11,PP CD QQ CD ⊥⊥,得到11,P Q 分别为ABD △和ABC 的中心,分别求得1,,PP PQ OA 的长度,结合AO ⊥平面POQ ,及2A PQB A POQ V V --=,即可求解.(1)证明:因为ABD △与ABC 共面,所以连接CD 与AB 相交于点O ,因为PABD 和QABC 是相同的正四面体,所以四边形ACBD 为菱形,则O 为AB 的中点,连接PO ,QO ,因为PA PB =,QA QB =,所以,Q PO AB O AB ⊥⊥,又因为PO QO O ⋂=,所以AB ⊥平面POQ ,所以PQ AB ⊥;(2)解:在四边形DPQC 中,过点,P Q 分别作11,PP CD QQ CD ⊥⊥,垂足分别为11,P Q ,如图所示,可得11,P Q 分别为等边ABD △和等边ABC 的中心,因为2AB =,在等边ABD △中,可得3OD =,则1233DP =,133OP =, 在直角1DPP 中,可得2211263PP DP DP =-=, 同理可得133OQ =,所以1111233PQ PQ OQ OP ==+=, 由(1)知,AB ⊥平面POQ ,可得AO ⊥平面POQ , 所以1422239A PQB A POQ POQ V V S OA --==⨯⨯⨯=△.20.(1)极小值为1,无极大值;(2)当01a <≤时,()f x 在()0,∞+上单调递增;当1a >时,()f x 的单调递减区间为()0,ln a ,单调递增区间为()ln ,a +∞.【分析】(1)根据题意求得()'1()e e 1x f x x ⎛⎫=-+- ⎪⎝⎭,分01x <<和1x >讨论'()f x 的正负,从而确定函数()f x 的单调区间和极值;(2)求导得'e (1)ln ()(0)x x a x af x x x +--=>,令()e (1)ln xg x x a x a =+--,对()g x 求导,当01a <≤时,通过对()g x 的正负判断,从而得'()f x 的正负及()f x 的单调区间;当1a >时,求得'(ln )0f a =,从而分ln x a>和0ln x a <<讨论'()f x 的正负,从而确定函数()f x 的单调区间即可.(1)解:e a =时,()e (1e)ln x f x x x =+--,()'11()e (1e)e e 1x x f x x x ⎛⎫=+--=-+- ⎪⎝⎭, 当1x >时,e e 0x ->,110x->,所以()'0f x >,即()f x 在()1,+∞上单调递增, 当01x <<时,e e 0x -<,110x -<,所以()'0f x <,即()f x 在()0,1上单调递减, 则()f x 的单调递增区间为()1,+∞,单调递减区间为()0,1;所以函数()f x 的极小值为()11f =,无极大值.(2) 解:因为'ln e (1)ln ()e (1)(0)x xa x a x a f x a x x x +--=+--=>, 令()e (1)ln x g x x a x a =+--,则'()(1)x x g x e xe a =++-,(i )当01a <≤时, '()0g x > ,()g x 在()0,∞+上单调递增,则()()0ln 0g x g a >=->,所以()'0f x >在()0,∞+上恒成立,所以()f x 在()0,∞+上单调递增;(ii )当1a >时,()'ln ln ln (ln )e 0ln a a a f a a a-=-+=, 当ln x a >时,e 0x a ->,ln 0x a x->,()'0f x >,即()f x 在()ln ,a +∞上递增, 当0ln x a <<时,e 0x a -<,ln 0x a x -<,()'0f x <,即()f x 在()0,ln a 上递减. 综上,当01a <≤时,()f x 在()0,∞+上单调递增;当1a >时,()f x 的单调递减区间为()0,ln a ,单调递增区间为()ln ,a +∞.21.(1)2214x y += (2)2PM PM PC PD+= 【分析】(1)根据椭圆顶点坐标直接可得椭圆方程;(2)设直线方程,可得点M ,联立直线与椭圆结合韦达定理,再根据两点间距离化简可得解.(1)由()2,0A ,()0,1B 是椭圆()2222:10x y E a b a b +=>>的两个顶点, 得2a =,1b =, 即22:14x E y +=; (2)当直线l 的斜率不存在时,直线l 与椭圆有且只有一个公共点,不成立,所以设()11,C x y ,()22,D x y ,()33,M x y ,直线l 的斜率为k ,则(12P x x PC x =-- 同理(22x P D =-(32x P M =-33122222PM P x x x x M PC PD +--=+--. 设l :()12y k x -=-,而AB :12x y +=,联立解得3421k x k =+, 所以342222121k x k k -=-=++; 联立直线l 与椭圆E 方程,消去y 得:()()2224182116160k x k k x k k +--+-=, 所以()12282141k k x x k -+=+,2122161641k k x x k -=+, 所以()()()1212121212124411222224x x x x x x x x x x x x +-+-+=-=------++()()2222821441218211616244141k k k k k k k k k k --+=-=+---⨯+++, 所以()33122222122221x x k x x k --+=⨯+=--+, 即2PM PM PC PD+=. 【点睛】(1)解答直线与椭圆的题目时,时常把两个曲线的方程联立,消去x (或y )建立一元二次方程,然后借助根与系数的关系,并结合题设条件建立有关参变量的等量关系.(2)涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率为0或不存在等特殊情形.22.0y -=,244x y =+(2)16【分析】(1)消参可得曲线1C 的普通方程,再根据极坐标与直角坐标的互化可得2C 的直角坐标方程;(2)根据极坐标的几何意义,将曲线1C 化成极坐标3πθ=,再分别代入3πθ=和43πθ=到2C 的极坐标方程求解即可.(1) 因为曲线1C的参数方程为y ==⎪⎩(t 为参数),所以曲线1C0y -=. 因为曲线2C 的极坐标方程为21sin ρθ=-,即sin 2ρρθ-=2y =,()()2222,2x y y y +=+≥-,所以曲线2C 的直角坐标方程为244x y =+;(2)因为曲线1C0y -=,所以曲线1C 的极坐标方程为3πθ=, 令3πθ=,则21sin 3A ρπ==-43πθ=,则241sin 3B ρπ==-所以16AB ==. 23.(1)111,5⎛⎫ ⎪⎝⎭(2)[)1,+∞【分析】(1)分类讨论去绝对值后再求解不等式即可;(2)讨论0x =,当0x ≠时6623x k x ---≥,利用绝对值的三角不等式求解6623x x---的最大值即可; (1) (),22636512,23,3x x f x x x x x x x <⎧⎪=---=-+≤≤⎨⎪->⎩,当2x <时,1x >,即12x <<,当23x ≤≤时,5121x -+>,解得115x <,即1125x ≤<, 当3x >时,1x ->,解得1x <-,此时无解,综上:不等式()1f x >的解集为111,5⎛⎫ ⎪⎝⎭; (2)0x =时上述不等式显然成立,当0x ≠时,上述不等式可化为()26362366x x f x x k xx x ---=---≥=, 令()()666623231x x x f g x x xx ==---≤--+=,当且仅当02x <≤时等号成立, 所以1k,即实数k 的取值范围为[)1,+∞.。
2020届江西省南昌市第一次模拟测试数学(文)试题(解析版)

2020届江西省南昌市第一次模拟测试数学(文)试题一、单选题1.己知集合A ={0,1,2),B ={x ∈N A },则B =( ) A .{0} B .{0,2}C .{0,12, 2} D .{0, 2, 4}【答案】B【解析】12,,,根据x ∈N ,可得结果. 【详解】由题可知:A ={0,1,2),B ={x ∈N A }时,则0x N =∈,符合时,则12x N =∉,不符合时,则2x N =∈,符合 所以{}0,2B = 故选:B 【点睛】本题考查集合元素的求法,审清题意,细心计算,属基础题.2.在复平面内,复数1z =对应的点为Z ,将向量OZ uuu r绕原点O 按逆时针方向旋转23π,所得向量对应的复数是( )A .122-+ B .122i -+ C .122-- D .122i -- 【答案】A【解析】根据复数,可得点Z 坐标,进一步可得OZ uuu r以及OZ u u u r ,然后根据三角函数的定义,可得旋转后所求复数的终点坐标,最后可得结果. 【详解】由题可知:()1,0Z ,()1,0OZ =u u u r且1OZ =u u u r设旋转后的所求复数的终点(),P x y则21cos 32x OZ π==-u u u r ,2sin 32y OZ π==u u u r所以13,2P⎛⎫-⎪⎝⎭,则所求的复数为132i-+故选:A【点睛】本题考查复数的几何意义,掌握复数在复平面中点的表示以及向量的表示,同时识记三角函数的概念,审清题意,耐心计算,属基础题.3.一个正三棱柱的正(主)视图如图,则该正三棱柱的侧面积是()A.16 B.12 C.8 D.6【答案】B【解析】根据正三棱柱的主视图,以及长度,可知该几何体的底面正三角形的边长,然后根据矩形的面积公式,可得结果.【详解】由题可知:该几何体的底面正三角形的边长为2所以该正三棱柱的三个侧面均为边长为2的正方形,所以该正三棱柱的侧面积为32212⨯⨯=故选:B【点睛】本题考查正三棱柱侧面积的计算以及三视图的认识,关键在于求得底面正三角形的边长,掌握一些常见的几何体的三视图,比如:三棱锥,圆锥,圆柱等,属基础题. 4.《聊斋志异》中有:“挑水砍柴不堪苦,请归但求穿墙术”.在数学中,我们称形如以下形式的等式具有“穿墙术”:22334422,33,4,33881515===则按照以上规律,若m mmn n=“穿墙术”,则m,n满足的关系式为()A.n =2m-1 B.n=2(m-1) C.n=(m-1)2D.n=m2 -1【答案】D【解析】根据不完全归纳法,以及根式中的分子和分母的关系,可得结果.【详解】由题可知:==,====则可归纳:==, 所以21n m =- 故选:D 【点睛】本题考查不完全归纳法的应用,仔细观察,发现特点,对选择题以及填空题,常可采用特殊值以及不完全归纳法解决问题,化繁为简,属基础题.5.己知{a n }是等差数列,且a 3+a 4=-4,a 7+a 8=-8,则这个数列的前10项和等于( ) A .-16 B .-30C .-32D .-60【答案】B【解析】计算3478a a a a +++,然后根据等差数列的性质,可得56a a +,最后根据等差数列的前n 项公式,计算10S ,并结合11056a a a a +=+,可得结果. 【详解】 由题可知:数列{a n }是等差数列且34784,8a a a a +=-+=-则347812a a a a +++=-,又3754862,2a a a a a a +=+= 所以565622126a a a a +=-⇒+=- 由()11010102a a S +⨯=,且11056aa a a +=+所以()1101010302a a S +⨯==-故选:B 【点睛】本题主要考查等差数列的性质,在等差数列中,若m n p q +=+,则m n p q a a a a +=+,熟练使用性质,以及对基本公式的记忆,属基础题.6.己知抛物线C :y 2=4x 的焦点为F ,抛物线上一点的M 的纵坐标y 0,则y 0>2是|MF |>2A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 【答案】A【解析】根据点M 的纵坐标的范围,可得其横坐标的范围,然后根据抛物线的定义,可知MF 的范围,然后根据充分、必要条件的概念,可得结果. 【详解】由题可知:()1,0F ,设()00,M x y 由点M 的纵坐标02y >,则其横坐标01x > 由01MF x =+,所以2MF > 可知02y >是2MF >的充分条件 若2MF >,则00121MF x x =+>⇒>则20042y y >⇒<-或02y >所以02y >不是2MF >的必要条件 故02y >是2MF >的充分不必要条件 故选:A 【点睛】本题考查抛物线的定义以及充分、必要条件的概念,对抛物线问题经常要联想到焦点和准线,简单计算,属基础题.7.2013年至201 9年我国二氧化硫的年排放量(单位:万吨)如下表,则以下结论中错误的是( )A .二氧化硫排放量逐年下降B .2018年二氧化硫减排效果最为显著C .2017年至2018年二氧化硫减排量比2013年至2016年二氧化硫减排量的总和大D .2019年二氧化硫减排量比2018年二氧化硫减排量有所增加 【答案】D【解析】采用逐一验证法,根据数据的简单分析,可得结果.A 正确根据数据可知,二氧化硫排放量逐年下降 B 正确从2017年到2018年,下降了756.24万吨, 是所有相邻年份二氧化硫减排量最大的, 所以2018年二氧化硫减排效果最为显著 C 正确2017年至2018年二氧化硫减排量为756.24万吨2013年至2016年二氧化硫减排量的总和为2217.9-1974.4=243.5万吨 所以243.5<756.24,故C 正确 D 错2017年至2018年二氧化硫减排量为756.24万吨2018年至2019年二氧化硫减排量为1102.86-1014.6=88.26万吨 故2019年二氧化硫减排量比2018年二氧化硫减排量有所减少. 故选:D. 【点睛】本题考查对数据的分析,审清题意,简单计算,属基础题.8.已知双曲线C : 2222x y a b-=1(a >0,b >0)的右焦点为F ,过原点O 线交C 的右支于点A ,若|OA |=|OF |,则双曲线的离心率为( )A B C .2D +l【答案】D【解析】假设已知直线的倾斜角为θ3πθ=,可得sin ,cos θθ,然后根据OF OA =,可得点A 坐标,最后代入双曲线方程化简并结合()1ce e a=>,可得结果. 【详解】设已知直线的倾斜角为θ由题可知:tan 3πθθ==,所以31sin ,cos 22θθ== 又OA OF c ==,所以cos ,sin 33A c c ππ⎛⎫ ⎪⎝⎭,即3,2c c A ⎛⎫ ⎪ ⎪⎝⎭所以2222222232321144c c c c a b a b ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭-=⇒-= 又222b c a =-,所以()222223144c c a c a -=-,又c e a= 所以()22231441e e e -=- 化简可得:42840e e -+=,所以()2228816423312e ±-==±=±所以31e =±,又1e >,所以31e =+ 故选:D 【点睛】本题考查双曲线的离心率,关键在于得到点A 坐标,考验计算能力,属中档题.9.函数cos 1ln(),1,(),1x x x f x xex π⎧->⎪=⎨⎪≤⎩的图象大致是( ) A . B .C .D .【答案】A【解析】根据复合函数的单调性,同增异减以及采用排除法,可得结果.当1x >时,()1ln()f x x x=-,由1,y y x x =-=在()1,+∞递增, 所以1t x x=-在()1,+∞递增又ln y t =是增函数,所以()1ln()f x x x=-在()1,+∞递增,故排除B 、C 当1x ≤时()cos xf x eπ=,若()0,1x ∈,则()0,x ππ∈所以cos t x π=在()0,1递减,而ty e =是增函数所以()cos xf x e π=在()0,1递减,所以A 正确,D 错误故选:A 【点睛】本题考查具体函数的大致图象的判断,关键在于对复合函数单调性的理解,记住常用的结论:增+增=增,增-减=增,减+减=减,复合函数单调性同增异减,属中档题. 10.台球是一项国际上广泛流行的高雅室内体育运动,也叫桌球(中国粤港澳地区的叫法)、撞球(中国台湾地区的叫法)控制撞球点、球的旋转等控制母球走位是击球的一项重要技术,一次台球技术表演节目中,在台球桌上,画出如图正方形ABCD ,在点E ,F 处各放一个目标球,表演者先将母球放在点A 处,通过击打母球,使其依次撞击点E ,F 处的目标球,最后停在点C 处,若30,40,30,AE cm EF cm FC cm ===60AEF CFE ∠=∠=o 则该正方形的边长为( )A .40cmB .6cmC .2cmD .14cm【答案】D【解析】利用向量的方法,将AC u u u r 用,,AE EF FC u u ur u u u r u u u r 来进行表示,然后进行平方,可计算AC u u u r,最后可得结果.由题可知:60AEF CFE ∠=∠=o ,所以AE //FC 由E C EF FC A A +=+u u u r u u u u r u u r u u u r则2222222AE EF FC AE EF A AC E FC EF FC +++=⋅+⋅+⋅u u u r u u u r u u u r u u u r u u u u u u r u u u r u u u r u u u r r u u u rcos120600AE EF AE EF ⋅==-o u u u r u u u r u u u r u u u rcos0900AE FC AE FC ⋅==o u u u r u u u r u u u r u u u rcos120600EF FC EF FC ⋅==-o u u u r u u u r u u u r u u u r所以22223040301200180012002800AC =++-+-=u u u r则AC =u u u r,所以sin 45AB AC =⋅=o故选:D 【点睛】本题考查向量的线性表示以及数量积公式的应用,关键在于E C EF FC A A +=+u u u r u u u u r u u r u u u r,考验观察能力以及计算能力,属中档题. 11.己知x >y >0,x ≠1,y ≠1,则( ) A .x a> y a(a ∈R ,a ≠0)B .yx e e y x> C .x y > y xD .1132x y -->【答案】B【解析】采用逐一验证法,对,,a x y 取特殊值,进行比较可得,,A C D 错,通过构造函数()mf m me =,利用函数单调性进行比较,可得结果.【详解】A 错误,当1a =-时,1111,x y x y--==, 由0x y >>,11x y< 所以A 错误 B 正确令()mf m me = ,则()'m m fm e me =+当0m >时,()'0fm >,所以函数()f m 在()0,∞+单调递增,且0x y >>,所以有()()f x f y >,即x yxye e xe ye y x>⇒>, C 错误当4,3x y ==时,34464,381==,3443<, 所以C 错误D 错误,当11,23x y ==时,21321111263611113,2327416--====由11662716>,所以1166112716<,故213232--<所以D 错误 故选B 【点睛】本题考查式子比较大小,选择题可使用对未知数取特殊值,化繁为简,熟练掌握比较式子大小的常用方法,比如:作差法,函数单调性等,属基础题.12.如图,点E 是正方体ABCD -A 1B 1C 1D 1的棱DD 1的中点,点F ,M 分别在线段AC ,BD 1(不包含端点)上运动,则( )A .在点F 的运动过程中,存在EF //BC 1B .在点M 的运动过程中,不存在B 1M ⊥AEC .四面体EMAC 的体积为定值D .四面体FA 1C 1B 的体积不为定值 【答案】C【解析】采用逐一验证法,根据线线、线面之间的关系以及四面体的体积公式,可得结果. 【详解】 A 错误由EF ⊂平面AEC ,1BC //1AD 而1AD 与平面AEC 相交,故可知1BC 与平面AEC 相交,所以不存在EF //BC 1 B 错误,如图,作11B M BD ⊥由11,,AC BD AC BB BD BB B ⊥⊥⋂=又1,BD BB ⊂平面11BB D D ,所以AC ⊥平面11BB D D 又1B M ⊂平面11BB D D ,所以1B M AC ⊥ 由OE //1BD ,所以1B M OE ⊥AC OE O =I ,,AC OE ⊂平面AEC所以1B M ⊥平面AEC ,又AE ⊂平面AEC 所以1B M AE ⊥,所以存在 C 正确四面体EMAC 的体积为13M AEC AEC V S h -∆=⋅⋅ 其中h 为点M 到平面AEC 的距离,由OE //1BD ,OE ⊂平面AEC ,1BD ⊄平面AEC所以1BD //平面AEC ,则点M 到平面AEC 的距离即点B 到平面AEC 的距离, 所以h 为定值,故四面体EMAC 的体积为定值D 错误由AC //11A C ,11A C ⊂平面11A C B ,AC ⊄平面11A C B 所以AC //平面11A C B ,则点F 到平面11A C B 的距离1h 即为点A 到平面11A C B 的距离, 所以1h 为定值所以四面体F A 1C 1B 的体积1111113F A C B A C B V S h -∆=⋅⋅为定值 故选:C 【点睛】本题考查线面、线线之间的关系,考验分析能力以及逻辑推理能力,熟练线面垂直与平行的判定定理以及性质定理,中档题.二、填空题13.已知向量a r ,b r =(1),且a r 在b r 方向上的投影为12,则a b ⋅r r 等于__________【答案】1【解析】利用向量的投影概念,计算出向量b r的模长,结合向量的数量积,可得结果. 【详解】a r 在b r 方向上的投影为12,所以有1cos 2a θ⋅=r,且2b =u u r ,所以1cos 212b a b a θ⋅=⋅⋅=⨯=uu r r r r故答案为:1 【点睛】本题考查向量的投影的概念,以及向量数量积公式的应用,属基础题. 14.已知函数31()f x x x=-,则''1(lg 2)(lg )2f f -=__【答案】0【解析】对函数求导后,利用对数的运算结合偶函数的性质可得结果. 【详解】由题可知:函数的定义域为()(),00,-∞⋃+∞ 由'221()3f x x x=+, 可知()()f x f x -=,所以()f x 是偶函数, 且''''1(lg 2)(lg )(lg 2)(lg 2)2f f f f -=--, 又因为''(lg 2)(lg 2)f f =-, 则有''1(lg 2)(lg )02f f -= 故答案为:0. 【点睛】本题考查函数的求导运算,偶函数的性质和对数的运算,属基础题. 15.己知1sin()43x π+=,则5cos()4x π-=_____【答案】13-【解析】利用特殊角配凑出题中已知角,再结合诱导公式可得结果. 【详解】553cos()cos()cos 444424x x x ππππππ⎡⎤⎛⎫-=--+=-+ ⎪⎢⎥⎝⎭⎣⎦, 即51cos()sin .443x x ππ⎛⎫-=-+=- ⎪⎝⎭ 故答案为:1.3- 【点睛】本题考查诱导公式,角度的配凑法,属基础题.16.如图,一列圆C n :x 2 +(y -a n )2=r n 2(a n >0,r n >0)逐个外切,且所有的圆均与直线y =±相切,若r 1=1,则a 1=___,r n =______【答案】3 12n -【解析】采用第n 个圆,并假设切点n A ,利用22221,n n nn A C n A C r k -==,可得3n n a r =,代值计算可得1a ,然后根据圆与圆相切,可得()122n n r r n -=≥,利用等比数列通项公式可得结果. 【详解】设第n 个圆心为()0,n n C a ,半径为n r , 且与22y x =的切点为(),22n n n A x x 则直线n n A C 的斜率为22n n n nA C nx a k x -=所以22221922n nn n nx a x a x -⋅=-⇒=①又()222222n n n n nn A C x x a r =+-=②由①②可知:3n n a r =③, 所以当11r =时,则13a = 又113n n a r --=④由③-④可知:()113n n n n a a r r ---=- 又11n n n n a a r r ---=+, 所以()122n n r r n -=≥所以数列{}n r 是以1为首项,2为公比的等比数列所以12n n r -=故答案为:3,12n - 【点睛】本题考查直线与圆几何关系以及等比数列,本题难点在于找到3n n a r =,考验分析能力以及逻辑推理能力,属难题.三、解答题17.如图,D 是在△ABC 边AC 上的一点,△BCD 面积是△ABD 面积的2倍,∠CBD =2∠ABD =2θ.(Ⅰ)若θ=6π,求sin sin A C的值; (Ⅱ)若BC =4,AB 2,求边AC 的长. 【答案】(Ⅰ)sin 23sin 3A C =;(Ⅱ)210AC =【解析】(Ⅰ)利用三角形面积公式以及2BCD ABD S S ∆∆=并结合正弦定理sin sin AB BCC A=,可得结果.(Ⅱ)根据2BCD ABD S S ∆∆=,可得θ,然后使用余弦定理2222sin AC AB BC AB BC ABC =+-⋅∠,可得结果.【详解】(Ⅰ)23CBD ABD π∠=∠=,所以11sin 2sin 2326BC BD AB BD ππ⋅=⨯⋅ 所以sin 23sin 333BC A AB C =⇒==; (Ⅱ)11sin 22sin 22BC BD AB BD θθ⋅=⨯⋅, 所以242sin cos 222cos 2θθθθ⨯=⨯⇒=,所以4πθ=,334ABC πθ∠==, 所以22168242240AC ⎛⎫=+-⨯⨯⨯-= ⎪⎝⎭,所以边210AC =. 【点睛】本题考查三角形面积公式,正弦定理以及余弦定理的应用,关键在于识记公式,属中档题.18.如图,三棱柱ABC -A 1B 1C 1中,A -BCB 1是棱长为2的正四面体.(Ⅰ)求证:AC ⊥CC 1; (Ⅱ)求三棱锥B -ACC 1的体积. 【答案】(Ⅰ)见解析;(Ⅱ22 【解析】(Ⅰ)取1BB 的中点E ,根据正四面体特点,可知AO ⊥平面11BCC B ,1BCB ∆为正三角形,然后根据11,BB AO BB CE ⊥⊥,可得1BB ⊥平面AEC ,最后可得结果. (Ⅱ)计算1BCC S △以及AO ,使用等体积法11B ACC A BCC V V --=,并结合锥体体积公式,可得结果. 【详解】(Ⅰ)如图,取1BB 的中点E ,连接CE 交1BC 于点O , 则点O 为1BCB △的重心,连接AO ,设1BC 交1B C 于点F .依题意点A 在底面的投影为1BCB △的重心O , 即AO ⊥平面11BCC B ,所以1AO BB ⊥. 因为1BCB △是正三角形,所以1CE BB ⊥,,,AO CE O AO CE ⋂=⊂平面AEC则1BB ⊥平面AEC ,又AC ⊂平面AEC ,则1BB AC ⊥,由1BB //1CC 所以1CC AC ⊥.(Ⅱ)由1A BCB -是棱长为2的正四面体, 所以2333CO CE ==,2AC =, 22263AO AC CO =-=因为12BC CC ==,1120BCC ∠=︒, 得111113sin 223222BCC S BC CC BCC =⋅⋅∠=⨯⨯⨯=△所以1112622333B ACC A BCC V V --===. 【点睛】本题考查线面、线线位置关系,还考查等体积法的使用,熟练掌握线面垂直的判定定理以及性质定理,考验推理论证能力,属中档题.19.某市2013年至2019年新能源汽车y (单位:百台)的数据如下表:(Ⅰ)求y 关于x 的线性回归方程,并预测该市2021年新能源汽车台数;(Ⅱ)该市某公司计划投资600台“双枪同充”(两把充电枪)、“一拖四群充”(四把充电枪)的两种型号的直流充电桩.按要求,充电枪的总把数不少于该市2021年新能源汽车预测台数,若双枪同充、一拖四群充的每把充电枪的日利润分别为25元,10元,问两种型号的充电桩各安装多少台时,才能使日利润最大,求出最大日利润.77211140,364i i i i i x x y ==⎛⎫== ⎪⎝⎭∑∑附:回归直线的斜率和截距的最小二乘法估计公式分别为717221ˆ,i ii ii x y nxybxnx ==-=-∑∑ˆa y bx=- 【答案】(Ⅰ)ˆy =23x +,2100台;(Ⅱ)双枪同充安装150台,一拖四群充安装450台时,每天的利润最大,最大利润为25500元.【解析】(Ⅰ)计算,x y ,根据7172217ˆ7i ii ii x y xybxx ==-=-∑∑,可得ˆb,进一步可得a ,然后可得方程,最后代值计算,可得结果.(Ⅱ)假设一拖四群充,双枪同充分别安装m 台,600m -台,根据42(600)2100m m +-≥,可得m 的范围,然后计算日利润4050(600)z m m =+-,依据不等式可得结果. 【详解】(Ⅰ)依题意知123456747x ++++++==,58810141517117y ++++++==,77211140,364ii i i i xx y ====∑∑,71722173647411ˆ21407167i ii ii x yxybxx ==--⨯⨯===-⨯-∑∑,ˆ11243a y bx=-=-⨯=, 则y 关于x 的线性回归方程23y x =+.令9x =得:ˆ29321y=⨯+=, 故预测2021年该市新能源汽车大约有2100台.(Ⅱ)设一拖四群充,双枪同充分别安装m 台,600m -台, 每天的利润为z 元,则42(600)2100m m +-≥,即450m ≥4050(600)z m m =+-300001030000450025500z m =-≤-=所以当450m =时,z 取最大值25500.故当双枪同充安装150台,一拖四群充安装450台时, 每天的利润最大,最大利润为25500元. 【点睛】本题考查线性回归方程,本题关键在于识记公式,考验计算能力,属基础题.20.已知函数,f (x )=33x -mx 2-m +ln (1-m ),(m <1).(Ⅰ)当m =12时,求f (x )的极值; (Ⅱ)证明:函数f (x )有且只有一个零点. 【答案】(Ⅰ)函数极大值为1ln 22--,极小值为 2ln 23--;(Ⅱ)见解析 【解析】(Ⅰ)利用导数,通过'()f x 的符号,判断出函数的单调性,找到极值点,可得结果.(Ⅱ)计算'(())2x f x x m =-,采用分类讨论的方法,0m =,0m <以及01m <<,判断函数的单调性,可得结果. 【详解】(Ⅰ)32111()ln 3222x f x x =--+'2()f x x x =-,则()f x 在(,0)-∞递增,在(0,1)递减,在(1,)+∞上递增, 所以函数极大值为1(0)ln 22f =--, 极小值为2(1)ln 23f =--. (Ⅱ)2'()2(2)x mx x x m f x =-=-①当0m =时,()'20fx x =≥,3()3x f x =只有一个零点0,符合题意;②当0m <时,()f x 在(,2)m -∞单调递增, 在(2,0)m 单调递减,在(0,)+∞单调递增,(0)ln(1)f m m =-+-,令()ln(1)g m m m =-+-,(0)m <,显然()g m 单调递减,有()(0)0g m g >=,即(0)0f >, 则()f x 只有一个零点,符合题意;③当01m <<时,()f x 在(,0)-∞单调递增, 在(0,2)m 单调递减,在(2,)m +∞单调递增,(0)ln(1)f m m =-+-,(01)m <<,由②构造的函数知, (0)ln(1)0f m m =-+-<,则()f x 只有一个零点,符合题意.综上所述,1m <时,函数()f x 有且只有一个零点. 【点睛】本题考查导数的应用,关键在于对含参数的函数单调性的判断,熟练使用分类讨论的思想以及学会构造函数,使问题化繁为简,属难题.21.定义:平面内两个分别以原点和两坐标轴为对称中心和对称轴的椭圆E 1,E 2,它们的长短半轴长分别为a 1,b 1和a 2,b 2,若满足a 2=a 1k ,b 2=b 1k (k ∈Z ,k ≥2),则称E 2为E 1的k 级相似椭圆,己知椭圆E 1:22214x y b +=1,E 2为E 1的2级相似椭圆,且焦点共轴,E 1与E 2的离心率之比为2. (Ⅰ)求E 2的方程;(Ⅱ)已知P 为E 2上任意一点,过点P 作E 1的两条切线,切点分别为A (x 1,y 1)、B (x 2,y 2).①证明:E 1在A (x 1,y 1)处的切线方程为11214x x y yb +=1; ②是否存在一定点到直线AB 的距离为定值,若存在,求出该定点和定值;若不存在,说明理由.【答案】(Ⅰ)222:1169x y E +=(Ⅱ)①见解析;②存在一定点()0,0C 到直线AB 的距离为定值1.【解析】(Ⅰ)根据相似椭圆的概念,可得12a =,24a =,221b b =,然后根据212247e e =,并结合离心率ce a=,简单计算,可得结果. (Ⅱ)①联立方程1122143143x x y yx y ⎧+=⎪⎪⎨⎪+=⎪⎩,可得关于x 的一元二次方程,然后使用∆,并根据221134120x y +-=,可得结果.②根据①的结论,可得在点B 的切线方程22143x x y y +=,根据10102020143143x x y y x x y y ⎧+=⎪⎪⎨⎪+=⎪⎩,可得直线AB 的方程,假设定点,使用点到线的距离公式,根据式子为定值,可得结果. 【详解】(Ⅰ)由题意知12a =,24a =,221b b =,则222211112144a b b e a --==,22222222221616a b b e a --==, 而()221124221144441647b e e b b -===-+,解得213b =,23b =, 故椭圆221:143x y E +=,椭圆222:1169x y E +=.(Ⅱ)①联立椭圆与直线方程,11221122143361240143x x y y x x x y x y ⎧+=⎪⎪⇒-+-=⎨⎪+=⎪⎩, 点A 在椭圆221:143x y E +=上,有221134120x y +-=, 所以()()2222111136121241234120x y x y ∆=--=+-=,即直线与椭圆相切.所以过点A 的切线方程为11143x x y y +=. ②由①知,过点B 的切线方程为22143x x y y +=, 设()00,P x y ,则22001169x y +=,即2200916144x y +=, 两条切线都经过点P ,则满足方程组10102020143143x x y y x x y y ⎧+=⎪⎪⎨⎪+=⎪⎩. 那么点A 和点B 都在直线00143x y x y +=上, 则直线AB 的方程为00143x y x y +=,即003412x x y y += 假设存在一定点(),C C C x y 到直线AB 的距离为定值,即00341212C C x x y y d ⋅+⋅-==为定值, 则0C C x y ==,1d =,故存在一定点()0,0C 到直线AB 的距离为定值1.【点睛】本题考查椭圆的综合应用,考验分析能力以及计算能力,属难题.22.在直角坐标系xOy 中,以坐标原点为极点,x 轴的非负半轴为极轴建立极坐标系;曲线C 1的普通方程为(x -1)2 +y 2=1,曲线C 2的参数方程为.x y θθ⎧=⎪⎨=⎪⎩(θ为参数).(Ⅰ)求曲线C 1和C 2的极坐标方程:(Ⅱ)设射线θ=6π(ρ>0)分别与曲线C 1和C 2相交于A ,B 两点,求|AB |的值. 【答案】(Ⅰ)2cos 0ρθ-=,22222cos 3sin 60ρθρθ+-=;(Ⅱ)||AB = 【解析】(Ⅰ)根据222,cos ,sin x y x y ρρθρθ=+==,可得曲线C 1的极坐标方程,然后先计算曲线C 2的普通方程,最后根据极坐标与直角坐标的转化公式,可得结果. (Ⅱ)将射线θ=6π分别与曲线C 1和C 2极坐标方程联立,可得A ,B 的极坐标,然后简单计算,可得结果.【详解】(Ⅰ)()22221120x y x y x -+=⇒+-=由222,cos ,sin x y x y ρρθρθ=+== 所以曲线1C 的极坐标方程为2cos 0ρθ-=,曲线2C 的普通方程为232360x y +-=则曲线2C 的极坐标方程为22222cos 3sin 60ρθρθ+-=(Ⅱ)令(0)6πθρ=>,则1,6A πρ⎛⎫ ⎪⎝⎭,2,6B πρ⎛⎫ ⎪⎝⎭, 则2222222cos 3sin 6066ππρρ+-=,即22924ρ=,所以2||3OB ρ==,1||2cos 6OA πρ===,故||||||3AB OA OB =-=-. 【点睛】本题考查极坐标方程和参数方程与直角坐标方程的转化,以及极坐标方程中ρ的几何意义,属基础题.23.已知a >0,b >0,a +b =2.(Ⅰ)求111a b ++的最小值; (Ⅱ)证明:2.a b b a ab+≥ 【答案】(Ⅰ)最小值为43;(Ⅱ)见解析 【解析】(1)根据题意构造平均值不等式,结合均值不等式可得结果; (2)利用分析法证明,结合常用不等式和均值不等式即可证明.【详解】(Ⅰ)11111[(1)]131a b a b a b ⎛⎫+=+++ ⎪++⎝⎭则1111421313b a a b a b +⎡⎤+=++≥⎢⎥++⎣⎦ 当且仅当21a b a b +=⎧⎨=+⎩,即32a =,12b =时, 所以111a b ++的最小值为43. (Ⅱ)要证明:2a b b a ab +≥, 只需证:20a b b a ab+-≥, 即证明:2220a b ab+-≥, 由0,0a b >>,也即证明:222a b +≥.因为2a b +≤,所以当且仅当a b =1≥, 即222a b +≥,当1a b ==时等号成立. 所以2.a b b a ab+≥ 【点睛】本题考查均值不等式,分析法证明不等式,审清题意,仔细计算,属中档题.。
2020年江西省高考数学(文科)模拟试卷(1) 含详细答案解析
17.( 12 分)已知数列 { an} 的前 n 项和为 Sn,满足 Sn= 2an﹣ 2.
( 1)求数列 { an} 的通项公式;
( 2)设 bn=( 2n﹣ 1) an,求数列 { bn} 的前 n 项和 Tn.
18.( 12 分)每当《我心永恒》这首感人唯美的歌曲回荡在我们耳边时,便会想起电影《泰
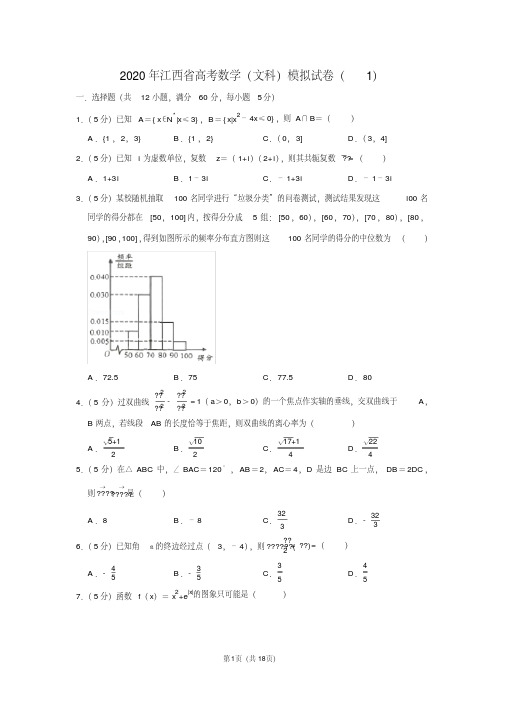
90),[90 ,100] ,得到如图所示的频率分布直方图则这 100 名同学的得分的中位数为 ( )
A .72.5
B .75
C. 77.5
D. 80
??2 ??2
4.( 5 分)过双曲线 ??2 - ??2 = 1( a> 0, b> 0)的一个焦点作实轴的垂线,交双曲线于
A,
B 两点,若线段 AB 的长度恰等于焦距,则双曲线的离心率为(
16 4
PF1F2 的面积为(
)
A .8
B .4√2
C. 4
二.填空题(共 4 小题,满分 20 分,每小题 5 分)
D. 2 √2
13.( 5 分)函数 f( x)=( x+2019 )?lnx 在 x= 1 处的切线方程为
.
14.( 5 分)已知数列 { an} 满足 a1+2a2+3a3+… +nan= 2n,则 an=
2.( 5 分)已知 i 为虚数单位,复数 z=( 1+i )( 2+ i),则其共轭复数 ??= ( )
A .1+3 i
B .1﹣ 3i
C.﹣ 1+3i
D.﹣ 1﹣ 3i
3.( 5 分)某校随机抽取 100 名同学进行“垃圾分类”的问卷测试,测试结果发现这
l00 名
数学文科答案

江西省重点中学盟校2020届高三第一次联考数学文科试卷参考答案与试题解析选择题填空题解答题17、【解析】(Ⅰ)设等差数列{}n a 的公差为d ,7348a a d -==,即2d =,…………………………………………………………… 2分3113a a ∴-=+,1562a a =+-,…………………………………………………………………… 3分 31a -是11a +,52a -的等比中项,()()()2315112a a a ∴-=+⋅-,即()()()2111+3=16a a a ++,解得13a =.…………………………………………………………………………………5分∴数列{}n a 的通项公式为21n a n =+.……………………………………………………6分(Ⅱ)由(Ⅰ)得()()111111212322123n n n b a a n n n n +⎛⎫===- ⎪++++⎝⎭.……………………………… 7分1212n n T b b b ∴=++⋅⋅⋅+=11111135572123n n ⎛⎫-+-+⋅⋅⋅+- ⎪++⎝⎭()1112323323nn n ⎛⎫=-= ⎪++⎝⎭,…………………………………………………………10分 由()232315n n <+,得6n <.…………………………………………………………… 11分∴使得215n T <成立的最大正整数n 的值为5.………………………………………… 12分 18、【解析】(I) 2×2列联表如下:K 2=()250310271037301320⨯⨯-⨯⨯⨯⨯≈9.98>6.635 (5)分所以有99%的把握认为“使用微信交流”的态度与人的年龄有关.…………………6分(列联表填对得两分)(II) 设年龄在[55,65)中不赞成“使用微信交流”的人为A ,B ,C ,赞成“使用微信交流”的人为a ,b ,则从5人中随机选取2人有AB ,AC ,Aa ,Ab ,BC ,Ba ,Bb ,Ca ,Cb ,ab ,共10种结果,其中2人中至少有1人不赞成“使用微信交流”的有AB ,AC ,Aa ,Ab ,BC ,Ba ,Bb 、Ca 、Cb ,共9种结果,………………………………………………………………………10分所以2人中至少有1人不赞成“使用微信交流”的概率为P =910. ………………12分(未列举只得2分)19、【解析】(Ⅰ)在图2中,四边形ABCD 是矩形, AB CD ∴,又AE CD ⊥,AE AB ∴⊥………………………………………………………………1分 又,AD AB AEAD A ⊥=,AB ∴⊥平面EAD .…………………………………………………………………………2分 ED ⊂平面EHD ,AB ED ∴⊥,…………………………………………………………………………………3分又,AE ED AE AB A ⊥=,ED ∴⊥平面EAB .…………………………………… 4分又ED ⊂平面EHD∴平面EHD ⊥平面EAB .……………………………………………………………6分(Ⅱ)由(I )可知,AB ⊥平面EAD ,AB ⊂平面ABCD ,∴平面EAD ⊥平面ABCD .……………………7分2EA ED ==,∴点E 到平面ABCD 的距离为.……………………………………………………………………………………………8分如图,设,AC HD 交于点,连接,则三棱锥E ACD -与三棱锥E AHD -公共部分即三棱锥E AOD -.…………………………………………………………………………………9分H 为BC 的中点,12142323AODS AD AB∆∴=⨯⨯=⨯=,………………………………………10分1183339E AOD AODV S-∆∴=⨯=⨯=.…………………………………………12分20、【解析】(I)12AF F∆bc=2分又2cea==,222a b c=+,解得:24a=,21b=…………………………………4分∴椭圆C的方程为:2214xy+=…………………………………………………………5分(II)假设y轴上存在点()0,M t,ABM∆是以M为直角顶点的等腰直角三角形设()11,A x y,()22,B x y,线段AB的中点为()00,N x y由2214xyy x m⎧+=⎪⎨⎪=+⎩,消去y可得:2258440x mx m++-=()()2226420441650m m m∆=--=->,解得:25m<1285mx x∴+=-,212445mx x-=……………………………………………………6分12425x x mx+∴==-,005my x m=+=4,55m mN⎛⎫∴-⎪⎝⎭……………………7分依题意有AM BM⊥,MN l⊥由MN l ⊥可得:5114015m t m -⨯=-⎛⎫--⨯ ⎪⎝⎭,可得:35m t =-……………………8分 由AM BM ⊥可得:12121y t y tx x --⋅=- 11y x m =+,22y x m =+代入上式化简可得:()()()2121220x x m t x x m t +-++-=………………………10分则:()222244880555m m m -⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭,解得:1m =±…………………………11分当1m =时,点30,5M ⎛⎫- ⎪⎝⎭满足题意;当1m =-时,点30,5M ⎛⎫ ⎪⎝⎭满足题意故y 轴上存在点30,5M ⎛⎫± ⎪⎝⎭,使得ABM ∆是以M 为直角顶点的等腰直角三角形.……12分21、【解析】(I )()()2ln x a x g x x x -=+,()()ln '12x x g x x a a +--+=,由题意()'120g a =-=,所以2a =,…………………………………………………2分 所以()()()'12ln 1g x x x =-+,令()'0g x =,得1x =3分当0,x e ⎛∈ ⎝⎭时,()'0g x >,当x e ⎛⎫∈ ⎪ ⎪⎝⎭时,()'0g x <,当()1,x ∈+∞时,()'0g x >, 所以函数()g x的单调递增区间是0,e ⎛ ⎝⎭和()1,+∞;……………………………………5分(II )依题意,12ln 0m x x x e--+<, 即12ln 0x m x x e+-->在()0,∞+上恒成立, 令()12ln x m x x p x e=+--, 则()22211'1m x mx x x xp x --=--=.……………………………………………………6分 对于21y x mx =--,2m 40∆=+>,故其必有两个零点,且两个零点的积为1-, 则两个零点一正一负,设其中一个零点为()00x ∈+∞,,则20010x mx --=,即001m x x =-, 且()p x 在()00,x 上单调递减,在()0,x +∞上单调递增,故()00p x >,即00000112ln 0x x x x x e⎛⎫+---> ⎪⎝⎭,……………………………………8分 令()112ln q x x x x x x e⎛⎫=+--- ⎪⎝⎭, 则()222111'11ln 1q x x x x x ⎛⎫⎛⎫=--+-- ⎪ ⎪⎝⎭⎝⎭211ln x x ⎛⎫=-+ ⎪⎝⎭, 当()0,1x ∈时,()'0q x >,当()1,x ∈+∞时,()'0q x <, 则()q x 在()0,1上单调递增,在()1,+∞上单调递减,又()10q q e e ⎛⎫== ⎪⎝⎭,故01,x e e ⎛⎫∈ ⎪⎝⎭,……………………………………………………10分显然函数001m x x =-在1e e ⎛⎫⎪⎝⎭,上是关于0x 的单调递增函数,则11,m e e ee ⎛⎫∈-- ⎪⎝⎭, 故实数m 的取值范围为11,e e e e ⎛⎫-- ⎪⎝⎭.……………………………………………………12分选做题22、【解析】(I)由题知4A π⎫⎪⎭,4B π⎛⎫⎪⎝⎭, 故点B 的直角坐标为()2,2,由l OA ⊥知直线l 的倾斜角为34π, 故直线l 的直角坐标方程为4x y +=,………………………………………………………3分所以其极坐标方程为cos sin 4ρθρθ+=即sin 4πρθ⎛⎫+= ⎪⎝⎭……………………5分 (II )由题知可设()1,P ρθ,()2,Q ρθ,其中30,4πθ⎛⎫∈ ⎪⎝⎭, 则PQ 中点的极坐标为12,2ρρθ+⎛⎫⎪⎝⎭,由P 在曲线C 上得12sin ρθ=,由Q 在直线l上得2sin 4ρπθ=⎛⎫+ ⎪⎝⎭,故PQ中点的极坐标为sin ,sin 4θθπθ⎛⎫⎪ ⎪+⎛⎫ ⎪+ ⎪ ⎪⎝⎭⎝⎭, 所以PQ中点轨迹的极坐标方程为3sin 04sin 4πρθθπθ⎛⎫=+<< ⎪⎛⎫⎝⎭+ ⎪⎝⎭.……………10分 23、【解析】(I )因为()2f x a ≥对x R ∀∈恒成立,则()2min f x a ≥,由绝对值三角不等式可得()2min 22f x x a x a a =--=≥,即2a ≤,解得22a -≤≤.故实数a 的取值范围是[]22-,;……………………………………………………………5分 (II )由题意2m =,故424x y z ++=,………………………………………………6分 由柯西不等式知,()()()()()22222222421424216x y y z x y y z x y z ⎡⎤++++-++-+=++=⎡⎤⎣⎦⎣⎦≥,所以()2221621x y y z +++≥,当且仅当421x y y z+==-时等号成立 从而,最小值为1621,当且仅当87x =,821y =-,421z =时等号成立.………………10分附:什么样的考试心态最好大部分学生都不敢掉以轻心,因此会出现很多过度焦虑。
2020年高考第一次模拟考试数学(文科)试卷(含答案)

2020年高考第一次模拟考试数学(文科)试卷一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|-1≤x ≤5},B={x|x 2-2x >3},则A ∩B=A.{x|3<x ≤5}B.{x|-l ≤x ≤5} C .{x|x<-l 或x>3} D .R2.已知复数z 满足i(3+z )=1+i ,则z 的虚部为A .-iB .iC .-1D .13.已知函数⎩⎨⎧>≤-=1,ln ,1,)1()(3x x x x x f 若f(a))>f(b),则下列不等关系正确的是 A .111122+<+b a B .33b a > C .ab a <2 D .)1ln()1ln(22+>+b a 4.国家统计局服务业调查中心和中国物流与采购联合会发布的2018年10月份至2019年9月份共12个月的中国制造业采购经理指数( PMl)如下图所示,则下列结论中错误的是A .12个月的PMI 值不低于50%的频率为31 B .12个月的PMI 值的平均值低于50% C .12个月的PMI 值的众数为49. 4% D .12个月的PMI 值的中位数为50.3% 5.已知函数)42sin()(π-=x x f 的图象向左平移ϕ)0(>ϕ个单位后得到函数)42sin()(π+=x x g 的图象,则ϕ 的最小值为 A .4π B .83π C .2π D .85π 6.已知数列{a n }满足a n+1-a n =2,且a 1,a 3,a 4成等比数列,若{a n }的前n 项和为S n ,则S n 的最小值为A. - 10 B .- 14 C .-18 D .-207.已知32)2019cos(-=+a π,则=-)22sin(a π A .97 B .95 C .-95 D .-97 8.已知双曲线C: 2222by a x -=l(a>0,b>0)的右焦点为F ,过右顶点A 且与x 轴垂直的直线交双曲线的一条渐近线于M 点,MF 的中点恰好在双曲线C 上则C 的离心率为 A .5-1 B .2 C .3 D .59.执行如图所示的程序框图,若输出的结果为11,则图中的判断条件可以为A .S> -1?B .S<0?C .S<-l?D .S >0?10.过抛物线E:x 2 =2py(p>0)的焦点F 作两条相互垂直的弦AB ,CD ,没P 为抛物线上的一动点,Q(1,2).若41||1||1=+CD AB ,则|PF|+|PQ|的最小值是 A .1 B .2 C .3 D .411.已知函数f(x)=x 3 -ax -1,以下结论正确的个数为①当a=0时,函数f(x)的图象的对称中心为(0,一1);②当a ≥3时,函数f(x)在(-1,1)上为单调递减函数;③若函数f(x)在(-1,1)上不单凋,则0<a<3;④当n =12时f(x)在[-4,5]上的最大值为15.A .1B .2C .3D .412.已知四棱锥E-ABCD ,底面ABCD 是边长为1的正方形,ED=1,平面ECD 上平面ABCD ,当点C 到平面ABE 的距离最大时,该四棱锥的体积为A. 62 B .31 C .32 D.1 二、填空题:本题共4小题.每小题5分.共20分.13.已知向量a =(l ,1),|b |=3,(2a +b )•a =2,则|a -b |=14.为激发学生团结协作、敢于拼搏、不言放弃的精神,某校高三5个班进行班级间的拔河比赛.每两班之间只比赛l 场,目前(一)班已赛了4场,(二)班已赛了3场,(三)班已赛了2场,(四)班已赛了1场.则目前(五)班已经参加比赛的场次为____. 15.将底面直径为4,高为3的圆锥形石块打磨成一个圆柱,则该圆柱的侧面积的最大值为16.如图,已知圆内接四边形ABCD ,其中AB =6,BC =3,CD =4,AD =5,则=+BA sin 2sin 2 .三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.第17 - 21题为必考题,每个试题考生都必须作答,第22,23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(12分)已知数列{a n }的各项都为正数,a 1 =2,且.1211+=++n n n n a a a a。
江西省南昌市2020届高三第一次模拟测试文科数学试题(含答案)

3
2
32
6
所以 BC
2
sin A
2
2
3
;
BA 3 sin C 3 3
………5 分
(Ⅱ) 1 BC BD sin 2 2 1 BA BD sin ,
2
2
所以 4 2 sin cos 2 2 2 sin cos
2
,
2
所以 , ABC 3 3 ,
4
4
………8 分 ………10 分
所以 AC2 16 8 2 4 2 2 ( 2 ) 40 ,所以边 AC 2 10 . 2
f (0) m ln(1 m) ,( 0 m 1),由②构造的函数知, f (0) m ln(1 m) 0 ,
则 f (x) 只有一个零点,符合题意.
综上所述, m 1时,函数 f (x) 有且只有一个零点.
………12 分
21.【解析】(Ⅰ)由题意知 a1 2 , a2 4 , b2 b12 ,
增, f (0) m ln(1 m) ,令 g(m) m ln(1 m) ,( m 0 ),
显然 g(m) 单调递减,有 g(m) g(0) 0 ,即 f (0) 0 ,
则 f (x) 只有一个零点,符合题意;
………9 分
③当 0 m 1 时, f (x) 在 (, 0) 单调递增,在 (0, 2m) 单调递减,在 (2m, ) 单调递增,
NCS20200607 项目第一次模拟测试卷
文科数学参考答案及评分标准
一、选择题:本大题共 12 个小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,只有一 项是符合题目要求的.
题号1
2
3
4
5
6
