24.2.1比例线段 学案
24.2（2）比例线段（黄金分割）
标题:24.2比例线段（2）关键词:比例中项、黄金分割描述:教学目标1.会运用同高(或等高)的两个三角形的面积之比等于对应底边的比,进行三角形的面积比与线段比的转化.2.在比例线段性质的证明与运用过程中,体会方程思想的作用.3.会找出一条线段的黄金分割点，找出一个图形中的黄金分割点.4.经历黄金分割点的探索过程，从中体会转化、分类讨论的思想方法.教学重点及难点黄金分割的意义.熟练并灵活运用黄金分割的意义解题.学科:初中九年级>数学第一学期>24.2（2）语种:汉语媒体格式:教学设计.doc课件.ppt学习者:学生资源类型:文本类、课件类素材教育类型:初中教育>初中九年级作者:方忠平单位:上海市风华初级中学地址:共和新路2800号（200072）Email:********************24.2比例线段（2）上海市风华初级中学方忠平41教学内容分析本课主要是两个部分.第一部分是线段的比例中项问题；第二部分是黄金分割及黄金数的有关知识.教学目标1. 会运用同高(或等高)的两个三角形的面积之比等于对应底边的比,进行三角形的面积比与线段比的转化.2. 在比例线段性质的证明与运用过程中,体会方程思想的作用.3. 会找出一条线段的黄金分割点，找出一个图形中的黄金分割点.4.经历黄金分割点的探索过程，从中体会转化、分类讨论的思想方法.教学重点及难点重点：黄金分割的意义.难点：熟练并灵活运用黄金分割的意义解题．教学用具准备投影仪、笔记本，预习本教学流程设计教学过程一、 情景引入1．观察（1） 请同学们欣赏一段芭蕾舞表演， 对学生视觉上形成美的冲击.师:“芭蕾舞在跳法上和其他舞种有什么区别吗？” 生:“要掂起脚尖.”师:“你们想知道这是为什么吗？”让学生有了强烈的求知欲.（2） 展示四个国家的国旗.中华人民共和国朝鲜新西兰新加坡2．思考师：请问这四面国旗中有共同图案吗？若有，请指出来.师：为什么都会选择五角星这个图案呢？除了政治因素外，还有一个非常重要的原因就是：五角星是一个非常完美的图案. 古希腊数学家毕达哥拉斯有一句名言：“凡是美的东西，都具有共同的特征，这就是部分与部分以及部分与整体之间的协调一致.”下面就让我们从数学的角度来探究五角星中部分与部分以及部分与整体之间存在着怎样的一种关系.[说明] 通过创设情境“四个国家的国旗中都有五角星这个图案”，就会使同学们认识到五角星这个图案不一般，也就会非常想知道五角星中部分与部分以及部分与整体之间到底蕴涵着怎样的一种关系.有了探究的欲望，就会很乐意完成下面的做一做. 3．讨论度量点C 到点A 、B 的距离，计算和的值，你发现了什么？AB AC ACBC [说明」（通过学生亲自动手操作、计算，最终发现了＝，即部AB AC ACBC 分与部分之比等于部分与整体之比，符合毕达哥拉斯的审美观点，很自然地就引出了黄金分割的概念.）二、学习新课1．概念辨析例题1如图，线段AB 的长度是，点P 为线段AB 上的一点，l ，求线段AP 的长.ABAPAP PB如果点P 把线段AB 分割成AP 和PB （AP>PB ）两段，其中AP 是AB 和PB 的比例中项，那么称这种分割为黄金分割，点P 称为线段AB温组形，组部每作教育下简合的黄金分割点AP 与AB 的比值为，近似值为0.618，这个比值215 称做黄金分割数（简称黄金数）.师：下面就让我们来解决刚才的问题，若由黄金分割点来看，理想身材的黄金分割点是肚脐，即一个人的上半身的长度与下半身的长度的比值或下半身的长度与整个身高的比值越接近0.618，就会越给別人有一种美的感觉.但是很可惜，一般人的这个比值大约只有0.58到0.60左右（腿长的人会有较高的比值），由此可见，芭蕾舞演员掂起脚尖跳舞是为了提高这个比值，增加美感.现实生活中这样的例子也很多，比如：女性穿高跟鞋，会让人体看起来更美些.黄金分割是古希腊数学家毕达哥拉斯发现的，古希腊人把它广泛应用于艺术创作当中，其中最经典的作品就是雕像——维纳斯女神，她的上半身和下半身的比率正是0.618.[说明]当学生了解了黄金分割的概念之后，再来解决芭蕾舞演员跳舞要掂起脚尖的问题，并欣赏雕像-----维纳斯女神，能使学生感受到黄金分割的美学价值.2．例题分析问题一（1） 线段AB 有没有除点P 以外的黄金分割点呢？（2） 点D 应满足怎样的条件？（3） 在五角星中点D 是线段AB 的黄金分割点吗？（4） 你还发现了什么？[说明]（这四个问题是有层次性的，问题（1）的结论是显然的，但学生得到的方法却是多样的，有的是凭直觉，有的是利用轴对称得到的，有的是采用旋转方法得到的；问题（2）进一步强化了黄金分割的概念；有了问题1的铺垫，问题（3）、（4）的结论很容易得出，这时学生就真正体会到了五角星确实是一个完美的图形，进一步感受到了黄金分割的美.）问题二师：下面我们再来了解黄金分割在现实生活中的应用.请同学们观察两幅照片，哪一更具有美感呢？师：你们知道这是为什么吗？因为绝对的对称会给人单调、静止、缺乏活力的感觉，为了打破这种感觉，我们在构图的时候，就需要灵活地运用黄金分割来构图，把画面的上下左右用黄金分割来做出4条线，人们发现4条线交汇的4个点是人们的视觉最敏感的地方，被反复证明的是当被摄主体处于或发布在这4个点附近最容易得到“眼球”，在摄影理论里把这4个点称为“趣味中心”.[说明]学生选择图（2）完全是一种直觉，并不明白其中的原因，当把上述道理讲给学生听时，他们对黄金分割的美学价值有更深的认识.问题三师：下面再来看看黄金分割在建筑上的应用.（展示巴黎埃斐尔铁塔、上海东方明珠电视塔、古埃及金字塔三幅图片，讲述其中蕴涵的黄金分割比例，体会黄金分割在建筑上的应用价值和人文价值.）问题四师：同学们已经了解到线段的黄金分割是完美的分割，事实上现实生活中还有另外一种有趣的黄金分割现象.请同学们在下面十个矩形（请若干个同学来找出他认为最合乎美的矩形，最后大部分同学将目标锁定在第①、⑤、⑧和⑩这四个矩形上，此时告诉他们这四个矩形分别是5×8，8×13，13×21，21×34的矩形，请他们用计算器算出这四个矩形的宽与长的比值（结果保留3个有效数字），结果分别是：0.625，0.615，0.619，0.618，这时同学们惊奇地发现这四个矩形的宽与长的比值均接近于黄金比，从而引出黄金矩形的概念.[说明]黄金矩形的概念并不是直接告诉学生的，而是通过亲身经历这么一个活动过程，自己感悟到合乎美的矩形和黄金分割的内在联系.）矩形的宽与长的比为黄金比，这样的矩形称之为黄金矩形.师：古希腊人已经发现黄金矩形是最合乎美的矩形，他们将建筑物的门、窗的轮廓都设计成黄金矩形的形状，其中最著名的就是巴特农神庙.如果把巴特农神庙的轮廓抽象为矩形ABCD ，以矩形ABCD 的宽为边在其内部作正方形AEFD ，那么我们可以惊奇的发现，，点E 是AB 的黄金分割点吗？矩形ABCD 的宽与长的比是BCABBE BC =黄金比吗？[说明]这里涉及到比例变形的一些技巧，要给学生时间进行充分的交流.最终发现巴特农神庙的轮廓为黄金矩形，展示了黄金分割的文化价值.师：黄金矩形之所以称为黄金矩形，并不仅仅因为它的宽与长的比等于黄金比，更重要的是：由上述方法作图后得到的新的矩形BCFE 也为黄金矩形（原因留给同学们课后思考）.巴特农神庙之所以神奇，并不仅仅因为它的的轮廓恰好为黄金矩形，它有更深层次的美.[说明]动画演示巴特农神庙在构造上不断符合黄金矩形的神奇现象. 通过动画演示巴特农神庙在构造上不断符合黄金矩形的神奇现象，同学们已经被巴特农神庙中所蕴涵的建筑艺术所折服，使学生再一次感受到了黄金分割和黄金矩形的美学价值.3．问题拓展例题2已知：如图，四边形ABCD 的对角线AC 、BD 交于点O ，求证：.AOD BOC S S ∆∆=OACOOB DO =证略尝试：（1）作顶角为的等腰三角形ABC;036（2）分别量出底边BC 与腰AB 的长度;（3）作的平分线，交AC 于点D ，量出的底边CD 的长度.B ∠BCD ∆最后，分别求出与的底边与腰的长度的比值（精确ABC ∆BCD ∆到0.001）问：比值是多少？所以我们把顶角为的三角形称为黄金三角形.它具有如下的o 36性质：（1）;618.0≈ABBC（2）设BD 是的底角的平分线，则也是黄金三角形，ABC ∆BCD ∆且点D 是线段AC 的黄金分割点;（3）如再作的平分线，交BD 于点E ，则也是黄金三C ∠CDE ∆角形，如此继续下去，可得到一串黄金三角形.巩固练习已知点C 是线段AB 的黄金分割点AC ＝，且AC ＞BC ，求555-线段AB 与BC 的长.课堂小结1、今天我们共同研究了什么数学知识？2、和以往的数学知识相比，今天的内容有什么不同？作业布置书后练习1、2、3，练习册24.2（2）教学设计说明本节课的研究对象是“黄金分割”，我采用从“美学”——“数学”的逻辑顺序去阐述这个课题，能够极大的提高学生探究的兴趣.并且引用了四个生活中的例子，使学生在不断享受“美”的过程中掌握知识，体验数学的社会功能.。
(课件)24.2相似图形的性质(成比例线段)
a 各等于多少？ ab
、
习题和24.2
3．判断下列各组线段是否是成比例线段： （1） 2厘米，3厘米，4厘米，1厘米； （2） 1．5厘米，2．5厘米，4．5厘米，6．5厘米； （3） 1．1厘米，2．2厘米，3．3厘米，4．4厘米； （4） 1厘米，2厘米，2厘米，4厘米．
∴ ad＝bc， 在等式两边同加上ac， ∴ ad＋ac＝bc＋ac， ∴ ac－ad＝ac－bc， ∴ a（c－d）＝（a－b）c， 两边同除以（a－b）（c－d）， a c ∴ ab cd
．
a b ， 2．已知： 线段a、b、c满足关系式 b c 且b＝4，那么ac＝______．
之间有关系_______________
图 24.2.1
像这样，对于四条线段a、b、c、d，如果 其中两条线段的长度的比等于另外两条线段的 a c 比， 如 b d （或a∶b＝c∶d），那么，
这四条线段叫做成比例线段，简称比例 线段．此时也称这四条线段成比例．
例1判断下列线段a、b、c、d是否是成比例线段：
a c ab cd ； 例2 证明：（1）如果 ，那么 b d b d
a c 证明（1）∵ b d
在等式两边同加上1， a c ∴ 1 1 b d
∴
ab cd b ． d
（2）
a c （2） ∵ b d
a c a c 如果 ，那么 a b c d b d
（1）a＝4，b＝6，c＝5，d＝10； 5 1 a 4 2 c 解 （1） ∵ b 6 3 d 10 2
a c ， ∴ bቤተ መጻሕፍቲ ባይዱd
，
，
∴ 线段a、b、c、d不是成比例线段．
沪教版(上海)初中数学九年级第一学期 24.2 比例线段-黄金分割 课件
比例的等比性质：
如果
a
,b
c d
k
(b,
d
0)
那么
ac a c _b___d___b____d_.
k
a k b a kb
c k d c kd
a c kb kd k bc bd
例1 在梯形ABCD中，对角线AC与BD相交于点
O，SAOD
SBOC ，求证：
DO OB
CO OA
想一想：将条件 SAOD SBOC 换成DC//AB，其它条 件不变，能证明原来的结论正确吗？
AC AD
1.如图，在△ ABC中，点D、E分别在AB、AC
上，且 AD AE
DB EC
.已知S △ ADE=1，S △ DBC=12，
求S △ ABC.
H
3.已知四条线段长分别为1厘米， 2 厘米，2厘米，
x厘米，它们是成比例线段，则x=
厘米.
例2 如图，线段AB的长度为l，点P是线段AB上一 点， PB AP (线段AP是PB、AB的比例中项）,
我们做过调查，如果市场上有的电视频主要 有两种，一种是宽:长为3∶4的，另一种是 9∶16的.这两个比值都很接近0.618，也就 是因为黄金矩形是最美的.
画家们发现，按 0.618∶1来设计腿长与 身高的比例，画出的人 体身材最优美，
现今的女性，腰身以下 的长度平均只占身高的 0.58，因此古希腊维纳 斯女塑像及太阳神阿波 罗的形象都通过故意延 长双腿，使之与身高的 比值为0.618，
B P1
∵点P1称为AB的 黄金分割点 （点P1靠近B）
P1B AP1 5 1 0.618 (黄金数) AP1 AB 2
∵点P2称为AB的 黄金分割点 （点P2靠近B）
242(1)比例线段
24.2比例线段一、教学目标：1.理解两条线段的比、比例线段的概念.2.掌握比例线段的基本性质.3.理解比例的合比性质、等比性质.4.培养学生学习数学、应用数学的能力.二、教学重、难点：重点：理解比例线段的概念.掌握比例线段的基本性质.难点：比例的合比性质、等比性质的理解.三、课前预习1.比例的基本性质：如果那么,dc b a = ； 2.比例的合比性质：=+=bb a dc b a ，那么如果 ；=-b b a 。
比例的等比性质：如果=++==db c a ,那么k d c b a= = 3.下列各组线段成比例的是（ ）。
A. 1cm ，3cm ，2cm ，4cmB. 1cm ，20cm ，5cm ，25cmC. 4cm cm 2cm 6,3，cmD. 4cm ，8cm ，6cm ，12cm四、新授新课探索一（1）思考 四个数a,b,c,d,若21,k dc k b a ==，请问在什么情况下，就说这四个数成比例？k1=k2时,就说这四个数成比例.如果两个数的比值与另两个数的比值相等,就说这四个数成比例.通常我们把a,b,c,d 四个实数成比例表示成a:b=c:d,或dc b a =。
其中b,c 称做内项,a,d 称做外项.新课探索一（2）两条线段的长度的比叫做两条线段的比.求两条线段的比时,对这两条线段一定要用同一长度单位来度量.两条线段的比值总是正数.在四条线段中,如果其中两条线段的比与另两条线段的比相等,那么这四条线段叫做成比例线段,简称比例线段(proportional segments).根据DE 是△ABC 的中位线的条件,你能找出成比例线段吗?线段DE,BC,AD,AB 是比例线段.新课探索一（3）如果a,b,c,d 是比例线段,即dc b a =（或d c b a ::=），那么线段d a ,是比例外项，线段b 、c 是比例内项，线段d 是a,b,c 的第四比例项。
比例线段有以下基本性质： 如果d c b a=，那么bc ad =寻找一下上述变化规律.新课探索二（1）比例线段除了具有上述性质以外,还有其他性质吗?思考 如果线段d c b a ,,,满足d c b a =，那么dd c b b a d d c b b a -=-+=+,是否成立？ 新课探索二（2）比例的合比性质：新课探索二（3）请运用上述设比值为k 的思想方法来说明:比例的等比性质:等比性质可以推广到任意有限多个相等的比的情形.例如:注意 在实数范围内,式中的分母不能为零,如b+d ≠0,b1+b2+b3≠0.新课探索三五、课内练习六、本课小结比例线段1.两条线段的长度的比叫做两条线段的比.2.在四条线段中,如果其中两条线段的比与另两条线段的比相等,那么这四条线段叫做成比例线段,简称比例线段(proportional segments).如果a,b,c,d 是比例线段,即dc b a = (或a:b=c:d), 那么线段a,d 是比例外项, 线段b,c 是比例内项, 线段d 是a,b,c 的第四比例项.3.比例线段的性质:(1)比例线段的基本性质: 如果dc b a =,那么ad=bc. (可写出有关a,b,c,d 成立的8个比例式.)（2）比例的合比性质：(3) 比例的等比性质:。
24.2(2)比例线段(教案)
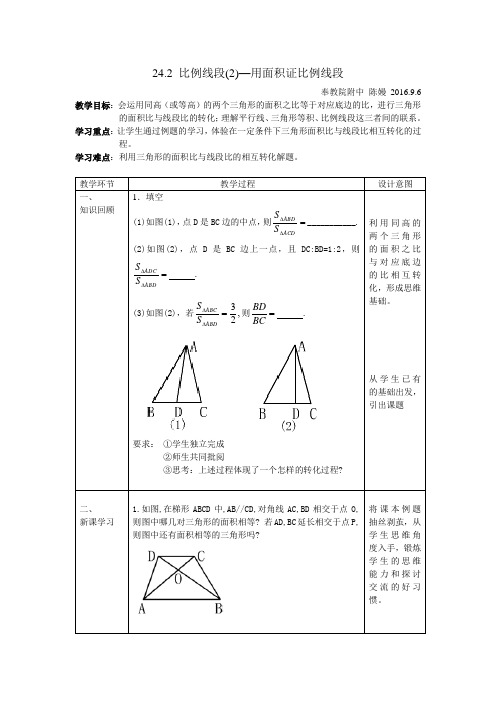
24.2 比例线段(2)—用面积证比例线段奉教院附中 陈嫚 2016.9.6 教学目标：会运用同高（或等高）的两个三角形的面积之比等于对应底边的比，进行三角形的面积比与线段比的转化；理解平行线、三角形等积、比例线段这三者间的联系。
学习重点：让学生通过例题的学习，体验在一定条件下三角形面积比与线段比相互转化的过程。
学习难点：利用三角形的面积比与线段比的相互转化解题。
教学环节 教学过程设计意图一、 知识回顾1．填空(1)如图(1)，点D 是BC 边的中点，则=∆∆ACDABDS S ___________. (2)如图(2)，点D 是BC 边上一点，且DC:BD=1:2，则=∆∆ABDADCS S . (3)如图(2)，若,23=∆∆ABD ABC S S 则BDBC= .要求： ①学生独立完成②师生共同批阅③思考：上述过程体现了一个怎样的转化过程?利用同高的两个三角形的面积之比与对应底边的比相互转化，形成思维基础。
从学生已有的基础出发，引出课题二、 新课学习1.如图,在梯形ABCD 中,AB//CD,对角线AC,BD 相交于点O,则图中哪几对三角形的面积相等? 若AD,BC 延长相交于点P,则图中还有面积相等的三角形吗?将课本例题抽丝剥茧，从学生思维角度入手，锻炼学生的思维能力和探讨交流的好习惯。
思考:你能利用上述面积之比与线段之比可转化的思想方法,证明OACOOB DO =吗？要求：①老师巡视②同学之间可以小组讨论解决问题③师生共同解题，板演变式：已知：在四边形ABCD 中,对角线AC,BD 相交于点O ，且OACO OBDO =求证：AB//CD 、AOD BOC S S ∆∆=要求：学生自主探究，学生板演，写出证明过程．通过变式的训练让学生对新知的相互转化有更深的理解。
三、 新知检测1. 已知:如图,四边形ABCD 的对角线AC 与BD 相交于点O.求证:.AOB COBAOD CODS S S S ∆∆∆∆=2.已知,AD,BE 是△ABC 的两条高.求证：BC BEAC AD=.3.如图,在△ABC 中,AD 平分∠BAC,请利用线段之比可转化为面积之比的思想方法,求证:ACABDC BD =.检测同学们对“同高的两个三角形的面积之比与对应底边的比的相互转化”的掌握程度。
近年学年九年级数学上册24.2比例线段(1)教案沪教版五四制(2021学年)
201７学年九年级数学上册２４．2 比例线段（1）教案沪教版五四制编辑整理：尊敬的读者朋友们:这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方,但是任然希望(２017学年九年级数学上册２4．2 比例线段(1)教案沪教版五四制）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步,以下为2017学年九年级数学上册 24.2 比例线段（1）教案沪教版五四制的全部内容。
比例线段屋架跨度的一半OP长为5米，高度以上就是本文的全部内容，可以编辑修改。
高尔基说过：“书是人类进步的阶梯。
”我希望各位朋友能借助这个阶梯不断进步。
物质生活极大丰富,科学技术飞速发展，这一切逐渐改变了人们的学习和休闲的方式。
很多人已经不再如饥似渴地追逐一篇文档了,但只要你依然有着这样一份小小的坚持,你就会不断成长进步，当纷繁复杂的世界牵引着我们疲于向外追逐的时候，阅读一文或者做一道题却让我们静下心来,回归自我。
用学习来激活我们的想象力和思维,建立我们的信仰，从而保有我们纯粹的精神世界,抵御外部世界的袭扰。
The abovｅ iｓtｈｅ wｈｏle conｔent of this article，Ｇｏrky ｓaｉd: "thｅｂook ｉs thｅladｄｅr of human prｏgress.＂ I hope you ｃａn m ａke progresｓwｉｔh ｔｈe hｅlp ｏf this lａｄdｅr. Ｍａｔerｉal lif ｅｉs extｒemely rich， sｃｉenｃｅ and tｅchnologｙ are ｄeｖｅｌoping rａpidly, alｌ of ｗｈich gradualｌy change tｈｅｗａy of peoｐｌe's ｓtudy aｎd ｌｅｉsuｒe. Mａnｙｐeople are no lｏngeｒ eａｇer ｔｏ puｒsue ａ doｃumｅnt, but as ｌoｎg as yoｕ still ｈave sucｈ a smaｌl persi ｓteｎｃｅ, you will contｉｎue tｏgｒｏw and pｒogｒｅss． Wheｎ the co ｍplex worｌd leadｓ us to cｈaｓe ｏut, rｅading ａn article oｒｄoｉｎg a proｂleｍmaｋes us ｃalｍ doｗn ａnｄ reｔurn tｏouｒｓelｖes. With leaｒning, ｗe can actiｖaｔe oｕr iｍａginａtion ａnｄ thinking，estａbliｓｈｏur bｅｌｉｅf, keep our pure spｉrituaｌwｏrld and r ｅsｉsｔ the atｔａck of tｈe ｅxteｒnａl world．。
上海教育版数学九上24.2《比例线段》word教案
24.2（1）比例线段教学内容分析本课主要由两部分组成.第一部分是有关线段比例的基本概念和性质及相关的计算.第二部分是比例的拓展性质. 教学目标设计1.知道两条线段比的意义.2.理解比例线段及其有关概念.3.知道比例线段的性质.4. 掌握合比和等比性质,能结合具体图形进行简单的比例线段变形. 教学重点及难点重点:比例线段的概念及它的初步应用 难点:合比、等比性质的运用. 教学用具准备投影仪、笔记本，预习本. 教学流程设计教学过程设计一、 情景引入1．观察图形的相似与线段的比及比例有密切的关联.同学们学习了两条线段比的有关知识，这节课我们来学习和研究比例线段的有关问题.（板书课题） 2．思考在学习新知识之前，我们先回想一下两条线段比的定义及求法，请同学们求下面两条线段的比.引例：如图：AB =50，BC =25，''20A B =, ''10B C =.求 '''',AB A B BC B C.DABC[说明]两个数相除又叫做两数的比，记作ab或:a b ，其中a 叫比的前项，b 叫比的后项.解：∵50225AB BC ==, ''''20210A B B C ==,∴ C B B A BC AB ''''=.二、学习新课1．概念辨析在同一长度单位下，两条线段长度的比就是两条线段的比在四条线段中，如果其中两条线段的比等于另外两条线段的比，那么这四条线段叫做成比例线段，简称比例线段.四条线段a 、b 、c 、d 中，如果a 与b 的比等于c 与d 的比，即a b =cd，那么这四条线段a 、b 、c 、d 叫做成比例线段，简称比例线段.线段d 是a 、b 、c 的第四比例项. 提问：比例的基本性质是什么——两个外项的积等于两个内项的积.（1）请同学们想一想，由::a b c d =能否得到ad bc =？为什么？ 反过来，若a d=bc ，那么能否得到a ：b=c ：d 呢B 'A ''（2）由a ：b=b ：c 可得b 2= a c由b 2= a c 可得a ：b=b ：c ，线段 b 叫a 、c 的比例中项. （3）由此可以看出：利用比例的基本性质，可以实现比例式与等积式的互化. [说明]（1）定义告诉我们判定四条线段成比例线段的方法： （其中的一个比例式）⇒=dcba a 、b 、c 、d 四条线段成比例； （2）定义告诉我们若已知四条线段成比例，则一定有比例式， a 、b 、c 、d 四条线段成比例dc b a =⇒（3）因为两条线段的比是它们的长度的比，实质上就是两个数的比.由于成比例的数具有比例的基本性质，所以成比例的四条线段也具有比例的基本性质. 2．例题分析例题1 已知a 、b 、c 、d 是四条线段，它们的长度如下，试判断它们是不是成比例线段？⑴a =1mm , b=0.8cm , c=0.02cm , d=4cm;⑵711=a cm , b=0.4cm , c=40cm , cm d 213=. [说明] 解题小结：①统一单位；②从大到小（从小到大）排列； ③通过求比例或求积判断.⑴方法二、利用比例的基本性质 ∵dc=4×0.02=0.08, a b=0.1×0.8=0.08, ∴a b=dc,∴a 、b 、c 、d 四条线段成比例. 第⑵小题让学生练习. 补充练习：（1）已知线段a ＝30mm ，b ＝2cm ，c ＝45cm ，d ＝12mm ，试判断a 、b 、c 、d 是否成比例线段.（2）已知a 、b 、c 、d 是比例线段，其中a ＝6cm ，b ＝8cm ，c ＝24cm,则线段d 的长度是多长？学生练习：判断下列四条线段是否成比例⑴a=2, b=5 , c=15 , d=32;⑵a=2 , b=3, c=2 , d=3;⑶a=4, b=6 , c=5, d=10;⑷a=12, b=8, c=15, d=10. 3．问题拓展合比性质：引导学生运用类似的方法推导出比例的等比性质:如果a cb d=,那么a c a ckb d b d+===+等比性质可以推广到任意有限多个相等的比的情况如果,那么 .证明：设；则 ,∴ .等比性质的证明思路及思想非常重要，它是解决数学中连比问题的通法，希望同学们认真体会，务必掌握.三、巩固练习例题2（1）已知： ，求证： .证明：方法一：∵ ，∴方法二：∵，∴即11811,8a ab b=∴=（2）（拓展）已知：()0a cb d b d=±≠ ，求证： . 证明：a c b d =，a b c d∴= a c b dc d ++∴=（1 同理a cb dc d--=（2） 由（1）÷（2）得：a cb da cb d++=--. 例题3 已知：EC AE DB AD = 求证：（1）ECACDB AB =； （2）AEACAD AB =四、课堂小结1.今天我们研究了什么内容，又哪些收获呢？2.这些内容和过去的知识有没有联系，有怎样的联系呢？3.你有没有不明白的地方呢？如果要你自学你能够胜任吗五、作业布置基础练习：书后练习1、2、3，4练习册24.2（1）拓展练习（1）求 ①②③（2）求下列各式中的x . ①② ③ ④（3）把cd ab 21=写成比例式，下列写法不正确的是 A 、b d ca 2=B 、b d c a =2C 、b d c a =2D 、bc d a =2 七、教学设计说明学生在六年级时已经学过比例的基本性质，本课首先利用类比的方法使学生得到了线段的有关比和比例的基本性质.在此过程中特别强调线段的比实际也是和数字有关的，帮助学生能够过渡好.通过简单练习、巩固.然后再向大家介绍了比例的其他性质，作为拓展内容只需学生们了解即可，课后供大家研究.本堂课既做到面向全体学生，又做到了分层递进，作业也是从这个方面安排的.。
沪教版九年级(上)数学一课一练及单元测试卷和参考答案
第16题图
三、解答题
17.若 与 是相似形，点A与点 ，点B与点 ，点C与点 分别是对应顶点， ， ，AB=2, =5,BC=3, =6求 的度数与边AC, 的长
18如图所示ቤተ መጻሕፍቲ ባይዱ相似四边形中，求未知边x，y的长度和角 的大小
（A） 8 (B) 6 (C) 10 (D) 4
3．如图，已知梯形ABCD中，AB//CD，如果S△ODC: S△OBC=1:2,S△ODC：S△OBA（）
（A）1:2（B）1:3（C）1:4（D）1:6
第3题图第4题图第5题图
4.如图，已知AB⊥BD，ED⊥BD，垂足分别为B、D，AE与BD相交于点C，则下列各式错误的是（）
（A）1:7（B）1:6 (C). 1:5 (D). 1:3
第4题图第5题图第6题图
5.如图，在△ABC中，AD是角平分线，DE//AC，已知AB=12，AC=6,则DE的长（）
（A）3（B）4（C）5（D）6
6.在ABC中，AB//EF∥CD，AB=16，CD=48，则EF的长.为（）
（A）8（B）10 (C). 12 (D). 14
21、在梯形ABCD中，AD∥BC,点E在BD的延长线上，且CE∥AB，AC与BD相交于点O，求证：OB2=OD•OE。
数学九年级上第二十四章相似三角形
24.3 三角形一边的平行线 第二课时（1）
一、选择题
1、在△ABC中，DE//BC，DF//AC， ,则 等于 （ ）
(A) (B) (C) (D)
24.6 实数与向量相乘 第一课时（1）57
24.7向量的线性运算 第一课时（1）62
沪教版数学九年级上册24.2《比例线段》教学设计
沪教版数学九年级上册24.2《比例线段》教学设计一. 教材分析《比例线段》是沪教版数学九年级上册第24章第2节的内容。
本节内容是在学生已经掌握了线段的基本知识，以及比例的基本概念的基础上进行教学的。
本节课主要让学生了解比例线段的定义，会求解比例线段，并能够运用比例线段解决实际问题。
教材通过例题和练习题的形式，帮助学生理解和掌握比例线段的知识。
二. 学情分析九年级的学生已经具备了一定的逻辑思维能力和数学基础，对于线段和比例的概念已经有了一定的了解。
但是，对于比例线段的运用和解决实际问题可能还存在一定的困难。
因此，在教学过程中，需要注重学生的实际操作和实践，通过具体的例题和练习题，让学生理解和掌握比例线段的知识。
三. 教学目标1.知识与技能：理解比例线段的定义，掌握求解比例线段的方法，能够运用比例线段解决实际问题。
2.过程与方法：通过观察、操作、思考、交流等过程，培养学生的逻辑思维能力和解决问题的能力。
3.情感态度与价值观：激发学生对数学的兴趣，培养学生的团队合作意识和积极的学习态度。
四. 教学重难点1.重点：比例线段的定义和求解方法。
2.难点：运用比例线段解决实际问题。
五. 教学方法1.情境教学法：通过具体的例题和练习题，让学生在实际情境中理解和掌握比例线段的知识。
2.合作学习法：通过小组讨论和合作，培养学生的团队合作意识和解决问题的能力。
3.引导发现法：教师引导学生观察和思考，发现比例线段的规律和方法。
六. 教学准备1.教学PPT：制作相关的教学PPT，展示例题和练习题。
2.练习题：准备一些相关的练习题，用于巩固和拓展学生的知识。
3.教学工具：准备尺子、直尺等教学工具，方便学生实际操作。
七. 教学过程1.导入（5分钟）教师通过提问方式引导学生回顾线段和比例的知识，为新课的学习做好铺垫。
2.呈现（10分钟）教师通过PPT展示比例线段的定义和例题，让学生观察和思考，引导学生发现比例线段的规律和方法。
沪教版数学九年级上册24.2《比例线段》教学设计
沪教版数学九年级上册24.2《比例线段》教学设计一. 教材分析《比例线段》是沪教版数学九年级上册第24章的一部分，主要介绍了比例线段的概念、性质和应用。
本节内容是在学生已经掌握了相似三角形的性质和坐标与图形的性质的基础上进行学习的，对于学生来说，比例线段是一个比较抽象的概念，需要通过具体实例和实践活动来理解和掌握。
教材通过丰富的例题和练习题，帮助学生逐步理解和运用比例线段的知识，为后续学习相似三角形和解析几何打下基础。
二. 学情分析九年级的学生已经具备了一定的数学基础，对于相似三角形的性质和坐标与图形的性质有一定的了解。
但是，比例线段作为一个新的概念，对学生来说还是相对抽象的，需要通过具体实例和实践活动来理解和掌握。
此外，学生的学习兴趣和动机也是影响教学效果的重要因素，因此，在教学过程中，需要通过设计有趣的教学活动和实例，激发学生的学习兴趣和动机。
三. 教学目标1.知识与技能：使学生理解比例线段的概念，掌握比例线段的性质，能够运用比例线段的知识解决实际问题。
2.过程与方法：通过观察、操作、交流等活动，培养学生的观察能力、动手能力和表达能力。
3.情感态度与价值观：激发学生对数学的兴趣和好奇心，培养学生的合作意识和创新精神。
四. 教学重难点1.重点：比例线段的概念和性质。
2.难点：比例线段的运用和实际问题的解决。
五. 教学方法1.启发式教学：通过设计有趣的问题和实例，激发学生的思考和探索兴趣，引导学生主动学习和参与。
2.实践活动：通过观察、操作、交流等活动，让学生在实践中学习和体验，提高学生的动手能力和观察能力。
3.合作学习：鼓励学生之间进行合作和交流，共同解决问题，培养学生的合作意识和团队精神。
六. 教学准备1.教学PPT：制作相关的教学PPT，包括教材内容、实例、练习题等。
2.教学素材：准备一些相关的图片和实例，用于引导学生观察和操作。
3.练习题：准备一些练习题，用于巩固和检验学生的学习效果。
七. 教学过程1.导入（5分钟）通过一个实际问题引入比例线段的概念，例如：“在一条直线上，有两点A和B，点A到直线的距离是6cm，点B到直线的距离是8cm，请问点A和点B之间的距离是多少？”让学生思考和讨论，引出比例线段的概念。
浙教版初中数学九年级上册4.1《比例线段(2)》导学案
浙教版初中数学重点知识精选掌握知识点，多做练习题，基础知识很重要！浙教版初中数学和你一起共同进步学业有成！4.1 比例线段（2）导学案学习目标：1. 了解两条线段的比和比例线段的概念；2. 能根据条件写出比例线段；3. 会运用比例线段解决简单的实际问题；学习重难点：重点：比例线段的概念，在简单的基本图形中能找到比例线段。
难点：例1要求根据具体的问题发现等量关系，找出比例式，有一定的隐蔽性。
导学过程：一．复习旧知：1. 判断下列四个数是否成比例，如果成比例请写出比例式。
2. 根据下列条件，求x 与y 的比。
2322(1)(2)325x y x y y -==3. 比例的基本性质是 二．新知学习1.两条线段的长度的比，叫做这两条线段的比。
1111AB AC A B AC ====已知线段请你计算AB 与A 1B 1，AC 与A 1C 1的比。
2.一般地，四条线段a,b,c,d 中，如果a 与b 的比等于c 与d 的比，即= ，那a b c d么这四条线段a 、b 、c 、d 叫做成比例线段，简称比例线段.请你说说上面四条线段成比例吗？说明理由。
3.练一练：(1)已知线段a=10cm ，b=6cm ，c=2cm ，d=3cm.问：这四条线段是否成比例？为什么?(2)P120课内练习2；P 120 A 组 第1题三．应用新知1.已知,这四条线段成比例吗？请说明理由。
1111AB AC A B AC ⨯=⨯2. 如图，在Rt △ABC 中，CD 是斜边AB 上的高.请找出一组比例线段，并说明理由.3.练一练：P120 第4题和第5题4. 如图，是我国台湾省的几个城市的位置图，问基隆市在高雄市的哪一个方向？到高雄市的实际距离是多少km ？四．课后提高：1. 相同时刻的物高与影长成比例。
如果一电视塔在地面上影长为180m ，同一时刻高为2m 的竹竿的影长为3m ，那么电视塔的高是多少？鹂鹂Cń2. 如图，已知,求 32AD AE DB EC ==,,AB EC AB DB AE AD五．学习反思相信自己，就能走向成功的第一步教师不光要传授知识，还要告诉学生学会生活。
比例线段(第一课时) 教学设计-1
比例线段（第一课时）教学设计-1 1. 教学目标•理解比例线段的概念，并能准确计算比例线段的长度。
•学会应用比例线段解决实际问题。
•培养学生观察、分析和解决问题的能力。
2. 教学内容2.1 比例线段的定义•定义比例线段的概念。
•讲解比例线段的计算方法。
2.2 应用题•利用比例线段解决实际问题。
3. 教学重点•比例线段的定义和计算方法。
4. 教学步骤4.1 引入新知识•通过提问和举例的方式引入比例线段的概念。
•与学生互动探讨比例线段的特点和计算方法。
4.2 讲解和示范•讲解比例线段的定义和计算方法。
•用白板或投影仪展示示例题，演示比例线段的计算过程。
4.3 练习和巩固•让学生通过练习题独立计算比例线段的长度。
•检查学生的答案，解答他们可能出现的困惑和疑问。
4.4 应用题的讲解和解答•将一些实际问题转化为比例线段的计算问题。
•示范解答应用题，引导学生理解如何用比例线段解决实际问题。
5. 教学扩展•鼓励学生寻找更多比例线段的实际应用。
•引导学生思考其他与比例线段相关的概念和定理。
6. 教学评估•在课堂练习和应用题解答中评估学生掌握比例线段的程度。
•观察学生在课堂互动中的参与情况和提问能力。
7. 教学反思本节课采用了多种教学方法，如提问、演示和练习等，以增强学生对比例线段概念的理解和运用能力。
在教学中，学生在实际问题转化为比例线段的计算问题上存在一定的困惑，需要进一步加强练习和讲解。
对于学生的巩固练习，可以设计更多的练习题目，使学生能够熟练运用比例线段的计算方法。
同时，还可以结合实际生活中的例子，帮助学生理解比例线段的应用场景。
此外，教师还应引导学生思考比例线段的相关定理和概念，扩展学生的数学思维和应用能力。
通过教学反思，可以调整教学策略，进一步提高教学效果。
比例线段教案(热门8篇)
比例线段教案(热门8篇）（经典版）编制人：__________________审核人：__________________审批人：__________________编制单位：__________________编制时间：____年____月____日序言下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。
文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!并且，本店铺为大家提供各种类型的经典范文，如计划总结、合同协议、管理制度、演讲致辞、心得体会、条据书信、好词好句、教学资料、作文大全、其他范文等等，想了解不同范文格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, our store provides various types of classic sample essays for everyone, such as plan summaries, contract agreements, management systems, speeches, insights, evidence letters, good words and sentences, teaching materials, complete essays, and other sample essays. If you want to learn about different sample formats and writing methods, please pay attention!比例线段教案(热门8篇）比例线段教案（1）教学内容：教科书第16页上的线段比例尺，练习五的第49题。
比例线段教案8篇
比例线段教案8篇比例线段教案8篇作为一位优秀的人民教师，就不得不需要编写教案，教案是教学蓝图，可以有效提高教学效率。
那么应当如何写教案呢？下面是小编精心整理的比例线段教案，欢迎阅读，希望大家能够喜欢。
比例线段教案1知识结构重难点分析本节的重点是线段的比和比例线段的概念以及比例的性质.以前的平面几何主要研究线段的位置关系和相等关系,从本章开始研究线段及相关图形的比例关系――相似三角形,这些内容的研究都离不开线段的比和比例性质的应用.本节的难点是比例性质及应用,虽然小学时已经接触过比例性质的一些知识,但由于内容比较简单,而且间隔时间较长,学生印象并不深刻,而本节涉及到的比例基本性质变式较多,合分比性质以及等比性质学生又是初次接触,内容不但多,而且轻易混淆,作题不知应用哪条性质,不知如何应用是常有的.教法建议1.生活中比例的例子比比皆是,在新课引入时最好从生活实例引入,可使学生感觉轻松自然,轻易产生爱好,增加学生学习的主动性2.小学时曾学过数的比及相关概念,学习时也可以复习引入,从数的比过渡到线段的比,渗透类比思想3.这一节概念比较多,也比较轻易混淆,教学中可设计不同层次的题组来进行巩固,非凡是要举一些反例,同时要注重对相近概念的比较4.黄金分割的内容要求学生理解,主要体现数学美,可由学生从生活中寻找实例,激发学生的爱好和参与感5.比例性质由于变式多,理解和应用上轻易出现错误,教学时可利用等式性质和分式性质来处理教学设计示例1(第1课时)一、教学目标1.理解线段的比的概念.2.通过与小学知识到比较,初步培养学生“类比”的数学思想.3.通过线段的比的有关计算,培养学习的计算能力.4.通过“引言”及“例1”的教学,激发学生学习爱好,对学生进行热爱爱国主义教育.二、教学设计先学后做,启发引导三、重点及难点1.教学重点两条线段比的概念.2.教学难点正确理解两条线段的比及应用.四、课时安排1课时五、教具学具预备股影仪、胶片、常用画图工具六、教学步骤复习提问找学生回答小学学过的比、比的前项和后项的概念.(两个数相除又叫做两数的比,记作或a:b,其中a叫比的前项,b叫比的后项)讲解新课把学生分成三组,分别以米、厘米、毫米作为长度单位,量一下几何教材的长与宽(令长为a,宽为b).再求出长与宽的比.然后找三名同学把结果写在黑板上.如:等.可以看出,在同一长度单位下,两条线段长度的比就是两条线段的比.一般地:若a、b的长度分别是、n(单位相同),那么就说这两条线段的比是 ,或写成 ,和数的比一样,a叫比的前项,b叫比的后项.关于两条线段比的概念,教学中要揭示它的实质,即表示a是b的倍,这是学生已有的知识,较易理解,也轻易使学生注重到求比时,长度单位要一致.另外,可组织学生举例实际生活中两条线段的比的问题,充分调动学生联系实际和积极思维的能力,对活跃课堂气氛也很有利,但教师需注重尺度.就刚才三组学生做过的练习及问题回答,在教师启发和点拨下,让学生讨论或试述两条线段的比应注重的问题,归纳出:(l)两条线段的比就是它们的长度的比.(2)比与所选线段的长度单位无关,求比时,两条线段的长度单位要一致.(3)两条线段的比值总是正数.(并不都是正数)(4)除了a=b之外, . 与互为倒数.例1 见教材P202.讲解完例1后:(l)提问学生AB是的多少倍, 是AB的多少倍,以加深学生对线段比的逾义的理解.(2)给出:比例尺= ,就例1的图上,若图距是8c的两地,实际距离是多少?另外,还可鼓励学生课后根据地图上的比例尺,测量并计算出你所在省会与首都北京的直线距离,从而丰富了知识,激发了学习爱好.例2 见教材P202.讲解完例2后:(l)可改变线段AB的长度,或给出AC、BC的长度,再求这些比,使学生熟悉这种三角形中边的比与长度无关.(2)常识1:有一锐角是30°的直角三角形中,三边(从小到大)的比为 .常识2:等腰直角三角形三边(从小到大)的比为1:1: .学生把握了这些常识可有两点好处:①知道例2中“ ”以及习题5.l第2题(1)中“边长为4”.(2)中的“对角线AC=a”这些条件实际上都是多余的.②这些题目若改成“填空题”,可避免一些不必要的计算.从而提高做题速度.这样不仅培养了能力,而且在考试中也受益匪浅.因此,今后如碰到和此常识有关的知识要反复渗透,反复给学生强调,让它扎根于学生的下意识中。
数学北师大版九年级上册教学设计.1成比例线段(二)教学设计
4.1成比例线段（二）一、教学目标（一）知识目标：了解线比例线段的基本性质；理解并掌握比例的基本性质及其简单应用；发展学生从数学的角度提出问题、分析问题和解决问题的能力。
（二）能力目标：经历运用线段的比解决问题的过程，在观察、计算、讨论、想象等活动中获取知识。
（三）情感与价值观目标：通过本节课的教学，培养学生的数学应用意识，体会数学与现实生活的密切联系。
二、学情分析学生的知识技能基础：这节课是“成比例线段”的第二课时，学生已经通过第一节课的学习，观察了大量的图片，列举了许多现实生活中的情境，认识了线段的比的知识，知道了选用同一单位长度量线段的长度，从而求出两条线段的比。
也学会了运用比例线段的基本性质解决实际问题，并通过图片创设的问题情境，重现了现实生活中的比例模型，初步掌握了解决有关比的问题的方法。
在这个基础上，进一步来学习成比例线段的有关性质，学生不会感到陌生，反而容易接受本节课的继续学习。
学生活动经验基础：上一节课，学生已经收集了一些相似图形的图片，如大小不同的两张中国地图、国旗，同底相片等。
已经感受了数学知识源于生活，用于生活。
各小组展示并讨论过线段比的事例，具有了一定的合作交流的基础和能力。
三、教学重难点教学重点：让学生理解并掌握比例的基本性质及其简单应用。
教学难点：运用比例的基本性质解决有关问题。
四、教学过程第一环节：温故知新活动内容：复习：(1)成比例线段定义（2）比例的基本性质（3）若 3m = 2n ，你可以得到n m 的值吗？mn 呢？ 活动目的：学生思考回顾上节课的内容，更好的进入本节课的学习。
第二环节：探究新知活动内容：1. 如图，HG AD FG CD EF BC HE AB ,,,的值相等吗？HG FG EF HE AD CD BC AB ++++++ 的值又是多少？在求解过程中，你有什么发现？2.已知，a ，b ，c ，d ，e ，f 六个数。
3.已知a,b,c,d …m,n 这些数(0),a c m b d n b d n ===++≠ 如果 .a c m a b d n b+++=+++ 那么还成立吗？小组讨论 第三环节：等比性质活动目的：每一个知识点的学习，都需要在一定的知识背景中去认识和练习才能得到巩固应用，从引例的结论中，引出 “等比性质”的学习。
比例线段 优质课教案
比例线段【教学目标】1．了解线段的比和成比例线段的概念，知道两条线段的比与所采用的度量单位无关。
2．理解并掌握比例的基本性质，了解比例中项的概念。
3．了解黄金分割，能利用比例的基本性质解决一些简单的问题。
【教学重难点】1．比例性质及有关计算。
2．黄金分割。
【教学过程】一、比例线段1．比：选用同一长度单位量得两条线段a 、b 的长度分别是m 、n ，那么就说这两条线段的比是::a b m n =（或a mb n=）。
2．比的前项，比的后项：两条线段的比:a b 中，a 叫做比的前项，b 叫做比的后项。
说明：求两条线段的比时，对这两条线段要用同一单位长度。
3．比例：两个比相等的式子叫做比例，如a cb d=。
4．比例外项：在比例a cb d =（或::a bcd =）中a 、d 叫做比例外项。
5．比例内项：在比例a cb d=（或::a b c d =）中b 、c 叫做比例内项。
6．比例线段：在四条线段中，如果其中两条线段的比等于另外两条线段的比，那么，这四条线段叫做成比例线段，简称比例线段。
7．比例的基本性质：如果::a b c d =那么ad bc =逆命题也成立，即如果ad bc =，那么::a b c d =。
8．比例的基本性质推论：如果::a b b d =那么2b ad =，逆定理是如果2b ad =那么::a b b d =。
说明：两个论是比积相等的式子叫做等积式。
比例的基本性质以及推例式与等积式互化的理论依据。
9．合比性质：如果a cb d =，那么a bcd b d ±±=。
10．等比性质：如果a c m b d n ===，（0b d m +++≠），那么a c m ab d n b+++=+++。
说明：应用等比性质解题时常采用设已知条件为k ，这种方法思路单一，方法简单不易出错。
11．如果点P 把线段AB 分割成AP 和PB （AP ＞PB ）两段，其中AP 是AB 和PB 的比例中项，那么称这种分割为黄金分割，点P 为线段AB 的黄金分割点。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
24.2.1《成比例线段》教学案
一、课时学习目标：
1、了解比例线段的概念。
知道与“线段的比”的区别与联系。
2、了解比例的基本性质，会进行简单的变形。
二、课前复习导学：
1、什么是相似图形？
2、问：这两张图形有什么联系？
它们是 图形，它们 的形状 ， 不相同，是相似形。
为什么有些图形是相似的，而有的图形看起来相像又不会相似呢？相似的两个图形有什么主要特征呢？为了探究相似图形的特征，本节课先学习线段的成比例。
三、课堂学习研讨
1、由上面的格点图可知，B A AB ''＝_________，C B BC '
'＝________，
这样
B A AB '
'与
C B BC '
'之间有关系_______________．
2、概括：像这样，对于四条线段a 、b 、c 、d ，如果其中两条线段的长度的比等于另外两条线段的比，如
d
c b a =（或a ∶b ＝c ∶
d ），那么，这四条线段叫做成比例线段，
简称比例线段．此时也称这四条线段成比例．
3、问题1判断下列线段a 、b 、c 、d 是否是成比例线段： （1）a ＝4，b ＝6，c ＝5，d ＝10； （2）a ＝2，b ＝5，c ＝152，d ＝35． 解：（1）∵
=b
a ＝ ，
=d
c ＝ ，
∴b a
d
c ∴线段a,b,c,
d 成比例线段。
（2）∵=b a
＝ ，
=d
c ＝ ，
∴
b
a
d
c ∴线段a,b,c,
d 成比例线段。
图24.2.1
4、练习：判断下列线段是否是成比例线段： （1）a ＝2cm ，b ＝4cm ，c ＝3m ，d ＝6m ； （2）a ＝0．8，b ＝3，c ＝1，d ＝2．4．
5、新结论：
对于成比例线段我们有下面的结论： 如果
d
c b a =，那么a
d ＝bc ． 如果ad ＝bc （a 、b 、c 、d 都不等于0），那么
d
c b
a =
．
以上结论称为比例的基本性质．
6、思考：请试着证明这两个结论。
这两个命题间有什么关系？
7、练习：（1）、如果
c
b b a =，那么b 叫做a 、
c 的比例中项，也可以写成2b = 。
（2）、已知：线段a 、b 、c 满足关系式c b
b a =
，且b ＝4，那么ac ＝______． 8、问题2 证明：（1）如果
d c b a =，那么
d d
c b b
a +=+； （2） 如果
d
c b a =，那么
d
c c
b
a a -=
-．
证明（1）
（2）
四、课堂达标练习 1、已知
2
3=b a ，那么
b
b a += 、
b
a a -= 。
2、在比例尺为1：8000的校地图上，矩形运动场的图上尺寸是cm cm 21⨯，矩形运动场的实际尺寸是多少？ 。
3、 在比例尺不同的城市两张地图中，量得A 、B 、C 三地的图上距离，第一张地图中量
AB=3.6cm ，AC=3cm ，在第二张地图上量得AB=6cm ，那么第二张地图中量得AC 为多少？
五、小结与作业：
P 51习题24.2第2，3题。
教学反思：。