余数问题(教师版)
《与余数有关的问题》(教学设计)

《与余数有关的问题》(教学设计)教学设计:一、教学目标1. 理解余数的概念。
2. 学会利用余数解决整除和求模问题。
3. 学会分析和解决余数有关的问题。
4. 通过练习,巩固和提高学生解决余数问题的能力。
二、教学重点1. 余数的概念和解题方法。
2. 整除和求模问题的解决方法。
3. 与余数有关的问题的解决方法。
三、教学难点1. 在解决问题时理解余数的应用。
2. 培养学生思维逻辑能力,分析问题的方法。
四、教学方法1. 经验教学法2. 演示教学法3. 互动探究法五、教学过程1. 导入环节(5分钟)老师可以在黑板上写上一个式子:“10÷4=2....2”。
然后问学生这个式子有什么意义和用途,引发学生余数的问题和疑惑。
2. 分组讨论(10分钟)教师将学生分成小组,要求学生在小组内讨论和比较什么情况下会产生余数,如何确定该余数,并说明产生此余数会如何影响整个式子。
3. 知识讲解(15分钟)教师在黑板上讲解余数及其应用,引导学生了解余数的概念和不同情况下的求余方法,并列举一些例子进行解释。
4. 练习(20分钟)教师在黑板上出示一些练习题,并给出解题步骤和解答。
然后,要求学生在课本上完成一些练习题,以检验学情和学生掌握余数的能力。
5. 总结(10分钟)老师简单总结余数的概念、应用和解题方法,并鼓励学生在生活和学习中多加尝试与余数有关的问题。
六、教学资源1. 黑板、彩笔2. 教师出示的练习题3. 学生课本七、教学评价1. 学生理解余数及其应用的能力是否提升。
2. 学生解决余数问题的能力是否提高。
3. 课堂练习、作业能否完成。
4. 学生在处理余数问题时的思维逻辑是否清晰、正确。
八、教学实验1. 解决整除问题的方法:(1)判断-如果除数被被除数整除,则结果为整数;否则有余数。
(2)整数除法-进行除法运算得到的结果为整数,而余数为0。
例如:判断100是否被4整除。
由于100÷4=25,且27×4=108,因此100不被4整除,余数为0。
有余数的除法(教师)
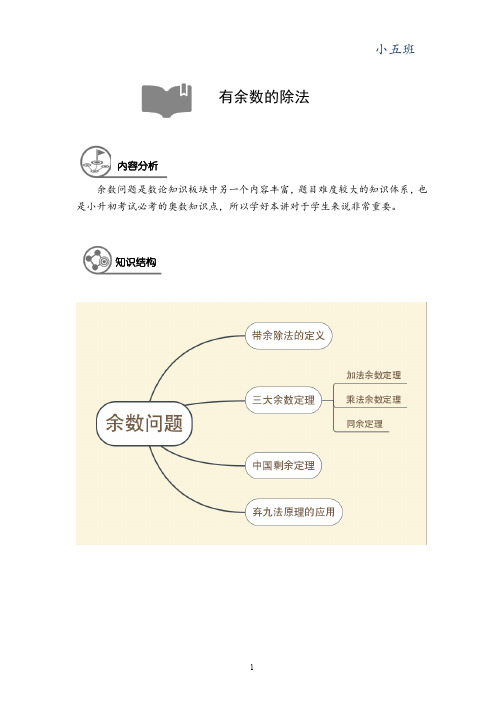
余数问题是数论知识板块中另一个内容丰富,题目难度较大的知识体系,也是小升初考试必考的奥数知识点,所以学好本讲对于学生来说非常重要。
有余数的除法内容分析知识结构1.272除以23的商为 ,余数为 。
【难度】★ 【答案】11,19【解析】解:272=23×11+192.已知某数被5除后的小数部分为0.4,则5除这个数的余数为 。
【难度】★ 【答案】2【解析】解:0.4×5=23. 7104×519的积被11除,得商为 ,余数为 。
【难度】★★ 【答案】335179 , 7 【解析】解:7104×519=(11×645+9)(11×47+2)=11×11×645×47+11×645×2+9×11×47+9×2 =11×11×645×47+11×645×2+9×11×47+11×1+7 =11×335179+7一般地,如果a 是整数,b 是整数(b ≠0),若有r b ⋅⋅⋅⋅⋅⋅=÷q a ,也就是r bq a += 其中q 是商,r 是余数,0≤r <b ;我们称上面的除法算式为一个带余除法算式。
这里: (1)当0r =时:我们称a 可以被b 整除,q 称为a 除以b 的商或完全商 (2)当0r ≠时:我们称a 不可以被b 整除,q 称为a 除以b 的商或不完全商知识精讲模块一:带余除法的定义与性质课前热身即 被除数=除数×商+余数, 或 被除数-余数=除数×商一个完美的带余除法讲解模型:如图,这是一堆书,共有a 本,这个a 就可以理解为被除数,现在要求按照b 本一捆打包,那么b 就是除数的角色,经过打包后共打包了c 捆,那么这个c 就是商,最后还剩余d 本,这个d 就是余数。
人教版二年级下册数学第六单元《有余数的除法)》作业设计教师版

人教版二年级下册数学第六单元《有余数的除法》作业设计
教师版
一、作业目的
本次作业旨在帮助学生进一步掌握有余数的除法概念,培养其整除和余数的计算能力。
二、作业内容
1.计算以下各题:
–23 ÷ 5
–35 ÷ 6
–48 ÷ 7
–57 ÷ 8
–68 ÷ 9
2.选择题:
1.25 ÷ 5 = ()余() A. 4 5 B. 6 0 C. 5 0 D. 6 1
2.38 ÷ 6 = ()余() A. 6 2 B. 5 8 C. 6 4 D. 5 6
三、完成时间
本次作业需在学习《有余数的除法》后一周内完成,收作业时需注意学生的计算过程和答案准确性。
四、作业要求
1.作业需以整洁的笔迹完成,不得有涂改。
2.答案需用算式或文字清晰表示,方便后续批改。
3.学生如有不懂之处,可在作业本上标明,以便老师及时解答。
五、评分标准
1.算术题:每题2分,计算准确得满分;
2.选择题:每题1分,正确选项得满分;
3.作业整洁度:5分;
4.提出问题:老师根据问题难易程度酌情给分。
六、注意事项
1.作业完成后请家长签字确认;
2.完成作业的学生可以获得相应的加分奖励。
以上是本次作业设计的内容,希望能帮助学生更好地掌握有余数的除法知识,提高他们的数学计算能力。
祝大家学习进步!。
余数问题教案2(教师版)

课题:余数问题班级姓名还是有两个机会有个年轻人,届逢兵役年龄,抽签的结果,正好抽中下下签,最艰苦的兵种--海军陆战队。
年轻人为此镇日忧心重重,几乎已到了茶不思、饭不想的地步。
年轻人深具智慧的祖父,见到自己的孙子这付模样,便寻思要好好开导他。
老祖父:“孩子啊,没什么好担心的。
当了海军陆战队,到部队中,还有两个机会,一个是内勤职务,另一个是外勤职务。
如果你分发到内勤单位,也就什么好担心的了!”年轻人问道:“那,若是被分发到外勤单位呢?”老祖父:“那还有两个机会,一个是留在本岛,另一个是分发外岛。
如果你分发在本岛,也不用担心呀!”年轻人又问:“那,若是分发到外岛呢?”老祖父:“那还是有两个机会,一个是后方,另一个是分发到最前线。
如果你留在外岛的后方单位,也是很轻松的!”年轻人再问:“那,若是分发到最前线呢?”老祖父:“那还是有两个机会,一个是站站卫兵,平安退伍;另一个是会遇上意外事故。
如果你能平安退伍,又有什么好怕的!”年轻人问:“那么,若是遇上意外事故呢?”老祖父:“那还是有两个机会,一个是受轻伤,可能送回本岛;另一个是受了重伤,可能不治。
如果你受了轻伤,送回本岛,也不用担心呀!”年轻人最恐惧的部分来了,他颤声问:“那……若是遇上后者呢?”老祖父大笑:“若是遇上那种情况,你人都死了,还有什么好担心的?倒是我要担心,那种白发人送黑发人的痛苦场面,可不是好玩的喔!”人生拥有的,是不断的抉择,端看您是用什么态度,去看待这些有赖您决定的无数机会。
能够综观每件事情、每个问题的正反两面,您将发现,内心最深沉的恐惧,也在所有状况明朗了解之后,将会自行化为乌有。
感悟:【运河通道1】a是自然数,除数b是自然数(a>b),商也是自然数时,出现的余数是小于除数的自然数的除法,叫做带余除法。
并且余数小于除数。
当余数不为零时,商叫做不完全商。
【运河通道2】余数有如下一些重要性质(a,b,c均为自然数):(1)余数小于除数。
(2)被除数=除数×商+余数;除数=(被除数-余数)÷商;商=(被除数-余数)÷除数。
593 余数问题(讲师版)

于 4,即两个余数的和 3+1. 当余数的和比除数大时,所求的余数等于余数之和再除以 c 的余数。 例如:23,19 除以 5 的余数分别是 3 和 4,所以 23+19=42 除以 5 的余数等
三.弃九法原理 在公元前 9 世纪,有个印度数学家名叫花拉子米,写有一本《花拉子米算
术》,他们在计算时通常是在一个铺有沙子的土板上进行,由于害怕以前的计算 结果丢失而经常检验加法运算是否正确,他们的检验方式是这样进行的:
例如:检验算式1234 1898 18922 678967 178902 889923 1234 除以 9 的余数为 1 1898 除以 9 的余数为 8 18922 除以 9 的余数为 4 678967 除以 9 的余数为 7 178902 除以 9 的余数为 0 这些余数的和除以 9 的余数为 2 而等式右边和除以 9 的余数为 3,那么上面这个算式一定是错的。 上述检验方法恰好用到的就是我们前面所讲的余数的加法定理,即如果这 个等式是正确的,那么左边几个加数除以 9 的余数的和再除以 9 的余数一定与 等式右边和除以 9 的余数相同。 而我们在求一个自然数除以 9 所得的余数时,常常不用去列除法竖式进行 计算,只要计算这个自然数的各个位数字之和除以 9 的余数就可以了,在算的 时候往往就是一个 9 一个 9 的找并且划去,所以这种方法被称作“弃九法”。 所以我们总结出弃九发原理:任何一个整数模 9 同余于它的各数位上数字 之和。 以后我们求一个整数被 9 除的余数,只要先计算这个整数各数位上数字之 和,再求这个和被 9 除的余数即可。 利用十进制的这个特性,不仅可以检验几个数相加,对于检验相乘、相除 和乘方的结果对不对同样适用
5-6-1_余数问题.题库教师版.doc(可编辑修改word版)

余数问题是数论知识板块中另一个内容丰富,题目难度较大的知识体系,也是各大杯赛小升初考试必考的奥数知识点,所以学好本讲对于学生来说非常重要。
许多孩子都接触过余数的有关问题,并有不少孩子说“遇到余数的问题就基本晕菜了!”余数问题主要包括了带余除法的定义,三大余数定理(加法余数定理,乘法余数定理,和同余定理),及中国剩余定理和有关弃九法原理的应用。
知识点拨一、带余除法的定义及性质一般地,如果 a 是整数,b 是整数(b≠0),若有a÷b=q……r,也就是 a=b×q+r,0≤r<b;我们称上面的除法算式为一个带余除法算式。
这里:(1)当r = 0 时:我们称 a 可以被 b 整除,q 称为a 除以b 的商或完全商(2)当r ≠ 0 时:我们称 a 不可以被 b 整除,q 称为a 除以b 的商或不完全商一个完美的带余除法讲解模型:如图这是一堆书,共有 a 本,这个 a 就可以理解为被除数,现在要求按照 b 本一捆打包,那么 b 就是除数的角色,经过打包后共打包了 c 捆,那么这个 c 就是商,最后还剩余 d 本,这个 d 就是余数。
这个图能够让学生清晰的明白带余除法算式中 4 个量的关系。
并且可以看出余数一定要比除数小。
二、三大余数定理:1.余数的加法定理a 与b 的和除以c 的余数,等于 a,b 分别除以 c 的余数之和,或这个和除以 c 的余数。
例如:23,16 除以5 的余数分别是 3 和1,所以 23+16=39 除以5 的余数等于 4,即两个余数的和 3+1.当余数的和比除数大时,所求的余数等于余数之和再除以 c 的余数。
例如:23,19 除以5 的余数分别是 3 和4,所以 23+19=42 除以5 的余数等于 3+4=7 除以 5 的余数,即2.2.余数的乘法定理a 与b 的乘积除以c 的余数,等于 a,b 分别除以 c 的余数的积,或者这个积除以 c 所得的余数。
5-6 余数问题教学目标例如:23,16 除以5 的余数分别是 3 和1,所以23×16除以5 的余数等于3×1=3。
5-5-2 带余除法(二).教师版

【答案】10
【例 3】 一个两位数除以 13 的商是 6,除以 11 所得的余数是 6,求这个两位数. 【考点】带余除法的估算问题 【难度】3 星 【题型】解答 【解析】因为一个两位数除以 13 的商是 6,所以这个两位数一定大于13 6 78 ,并且小于13 (6 1) 91;
是 31743 除以 823 可以看成余 469 也可以看成不足(823-469=)354,于是改动某位数字使得得到的新 数比原来大 354 或 354+823n 也是满足题意的改动.有 n=1 时,354+823:1177,n=2 时,354+823×2=2000, 所以当千位增加 2,即改为 3 时,有修改后的五位数 33743 为 823 的倍数. 【答案】33743
77777 41 □ 0 ,……,所以 77777 是 41 的倍数,而1996 5 3991 ,所以 777 77 可以分成
1996个7
399 段 77777 和 1 个 7 组成,那么它除以 41 的余数为 7.
【答案】7
【例 8】 已知 a 200820082008 ,问: a 除以 13 所得的余数是多少?
【例 2】 有 48 本书分给两组小朋友,已知第二组比第一组多 5 人.如果把书全部分给第一组,那么每人 4 本,有剩余;每人 5 本,书不够.如果把书全分给第二组,那么每人 3 本,有剩余;每人 4 本, 书不够.问:第二组有多少人?
【考点】带余除法的估算问题 【难度】3 星 【题型】解答 【关键词】小学数学夏令营 【解析】由 48 4 12 , 48 5 9.6 知,一组是 10 或 11 人.同理可知 48 3 16 , 48 4 12 知,二组是 13、
第5讲.有趣的余数问题.教师版

.在二年级的时候,我们就学习过一些周期问题的基本知识.但是由于本讲知识应用的广泛性,所以本讲又进行了拓展与延伸.本讲主要学习利用余数解答周期问题的方法, 知识点: 1.利用余数解决图形中的周期问题;2.利用余数解决生活中的周期问题; 3.利用余数解决年月日中的周期问题.周期现象:事物在运动变化的过程中,某些特征有规律循环出现. 周期:我们把连续两次出现所经过的时间叫周期.解答周期问题的关键是找规律,找出周期.确定周期后,用总量除以周期,如果正好有整数个周期,结尾就为周期里的最后一个; 闰 年:年份能被4整除;如果年份能被100整除,则年份必须能被400整除;一年有366天; 平 年:年份不能被4整除或能被4整除但不能被100整除;一年有365天. 一. 图形中的周期问题【分析】我们把开始的座次图当作第1幅图,第一次操作后的图当作第2幅图,……第十次操作的的图就是第11幅图,在这11幅图中,4幅图为一个周期,则11÷4=2……3,则知第11幅图(即第十次操作后的图)同第二次操作后的图.【基础班学案1】观察图中黑、白两色三角形的变化规律.请问:前200个图形中有多少个白色三角形?【分析】通过观察,发现()为一个周期,则200÷3=66(个)……2(个),说明共有66个周期,还余下一个黑色三角形一个白色三角形,白色三角形共有:66×2+1=133(个).例1经典精讲第五讲 有趣的余数问题【提高班学案1】如图所示,16幅图按规律排成一排.其中前三幅已经画出,请按规律画出第16幅图的样子.【分析】从前三幅图可知,每个对应位置上的小笑脸都是在按顺时针方向转动,且4组为一个周期,由16÷4=4(周),知第16幅对应的是第四幅图,即.【尖子班学案1】有同样大小的红、白、黑珠共90个,按先3个红的、2个白的、l个黑的排列着,如图:(1)黑珠共有几个?(2)第68个珠是什么颜色的?【分析】图形排列的顺序是,周期是3216÷=,一个周期内++=个,(1)那么90615有一个黑珠,所以黑珠一共有15个;(2)686112÷=,所以第68个是红色.例2【分析】由图知数数情况如下:大拇指、食指、中指、无名指、小指、无名指、中指、食指、大拇指、食指、……,可见每数8个数就重复对应一次手指的排序,则由200825÷=(次)知当数到200时正好数到食指.[巩固] 观察图中图形的规律,第200个图形应该是下面A、B、C、D四个图形中的哪一个?【分析】由颜色的规律知,周期数为3,由图的形状知:周期数为5,则由2003=662÷(个)知第200个图形的颜色是黑色.又由200540÷=组)知第200个图形的形状是☆.所以综合这两种情况知答案是A .[巩固] 如图所示,表格中每行的文字都是循环出现的:第一行是“黎曼假设”4个汉字不断重复,第二行是“庞加莱猜想”5个汉字不断重复,第三行则是“哥德巴赫猜想”6个汉字不断重复.第200列从上向下依次是哪3个汉字?【分析】第200列从一到下的3个汉字,即是每行中第200个汉字的组成,由200÷4=50(个),知第一行第200个汉字是“设”.由200÷5=40(个),知第二行第200个汉字是“想”,由200÷6=33(个)……2(个),知第三行第200个汉字是“德”.则第200列从上到下依次是“设、想、德”.二.生活中的周期问题:【分析】观察知“红,黄,蓝,绿”四种颜色为一个周期,那么46÷4=11……2,则知第46名同学手里拿的彩旗同周期里的第2个相同,为黄色.【分析】经过对已知条件的分析,我们发现,三种树6棵一组,每组按同样的顺序重复出现.这样,我们只需计算出100棵树中包含了几个6棵,然后把余数对照果树的排列顺序便可确定第100棵树是什么树了. 因为:1006164÷=,说明经过16次重复后还余4棵树.这4棵树的排列顺序应是:苹果树,梨树,梨树,桃树.所以,第100棵种的是桃树.并且这100棵树中有: 苹果树:116117⨯+=(棵) 梨树:216234⨯+=(棵) 桃树:316149⨯+=(棵)[巩固] 如果时钟现在表示的时间是18点整,那么分针旋转1990圈之后是几点钟?例4例3【分析】分针转一圈表示1小时,转24圈是一天,那么周期是24,1990248222÷=圈,那么过了82天,还多余了22圈,在过22小时后是18222416+-=点.【基础班学案2】广场挂了一排彩灯,共1997盏.彩灯排列的规则是:从头起每八盏为一组顺序排列.每组的八盏灯依次为三盏红灯,二盏黄灯,三盏绿灯.那么,最后一盏灯的颜色是.【分析】彩灯的排列规则是八盏灯为一组,每组按同样的方式重复出现.由于1997÷8=249……5,说明经过249次重复后还余5盏灯.这5盏灯应是:红,红,红,黄,黄.因此,第1997盏灯,即最后一盏灯应是黄色的.【提高班学案2】某商店门口挂了一串彩色气球,它们按“3红2黄2蓝”的顺序排列,那么第36个气球是什么颜色.第55个气球是什么颜色?【分析】气球是按“3红2黄2蓝”的顺序排列,周期是3227÷=个,第++=个,那么36751 36个是红色气球,55776÷=个,第55个是蓝色气球.【尖子班学案2】“亮灯工程”后,全市一到晚上,五光十色,非常漂亮,商业大厦楼上的彩灯按“3红2绿2黄1紫”排列,那么第43盏灯是什么颜色?第100盏灯是什么颜色?【分析】彩灯按“3红2绿2黄1紫”一组排列,周期是32218÷=盏,所+++=盏,那么43853以第43盏是红色;1008124÷=盏,第100盏是绿色.【基本班学案3】公园里的花坛种菊花,园林工人按1棵白、5棵黄、2棵红排列.那么,第30棵种什么颜色的花?第72棵该种什么颜色的花?【分析】菊花按1棵白、5棵黄、2棵红的顺序排列,周期是1528÷=棵,++=棵,那么30836第30棵种黄色,7289÷=,第72棵种红色.【提高班学案3】节日的校园内挂起了一盏盏小电灯,小明看出每两个白灯之间有红、黄、绿各一盏彩灯也就是说,从第一盏白灯起,每一盏白灯后面紧接着有3盏彩灯.那么第73盏灯是_____灯.【分析】从第一盏白灯开始,每隔三盏彩灯就又出现一盏白灯、不难看出周期是白灯、红灯、黄灯、绿灯,周期是4盏,那么734181÷=,第73盏是白灯.【尖子班学案3】为庆祝国庆节,学校插了很多彩旗.彩旗是按4面黄旗、3面红旗、2面绿旗、1面蓝旗的顺序排列的.第109面旗应是什么颜色?已插了几面黄旗、几面红旗、几面绿旗、几面蓝旗?【分析】彩旗按4面黄旗、3面红旗、2面绿旗、1面蓝旗的顺序排列,周期是432110+++=面,那么10910109÷=面,第109面是绿旗.一个周期内有4面黄旗,所以黄旗一共有⨯+=面,一个周期内有⨯+=面,一个周期内有3面红旗,所以红旗一共有103333104444绿旗2面,所以绿旗一共有102222⨯+=面,一个周期内有1面蓝旗,所以蓝旗有10面.三.报数游戏【分析】根据题意可知报出的数如下:1,7,9,3,1,7,9,3,……可见这些数是有规律的,且4个数为一个周期,周期里的数是1,7,9,3. 那么,100÷4=25,则知第100个同学报的是周期里的最后一个数3.四.星期中的周期问题【分析】(1)包括今天共有60161+=(天),且周期为7天,即(星期六,星期日,星期一,星期二,星期三,星期四,星期五),则61785÷=(天),所以再过60天是星期三. (2)从6月1日到8月1日共有:3031162++=(天),周期为7天,即:星期日,星期一,星期二,星期三,星期四、星期五、星期六.则:62786÷=(天),所以2008年8月1日是星期五.(3)因为2008年是闰年,所以从2008年2月8日到2009年2月8日共有3661367+=(天)周期是:星期五,星期六,星期日,星期一,星期二,星期三,星期四.则3677523÷=(天),所以答案是星期日.[巩固]三名学生,每天早晨轮流为李奶奶取牛奶,甲第一次取奶是星期一,那么,他第100次取奶是星期_______. 【分析】21天内,每人取奶7次,甲第8次取奶又是星期一,即每取7次奶为一个周期1007142÷=,所以甲第100次取奶是星期二.[巩固]阿奇和其他5个小朋友围成一圈,圆圈中央摆放着55个乒乓球,从阿奇开始,小朋友们沿逆时针方向依次拿球,每人每次拿3个,直到把乒乓球全部拿完为止(最后剩下的球不足3个就全拿).阿 奇总共拿到了几个球? 【分析】想知道阿奇共拿到了几个球,就必须知道阿奇取了几次,由题意知:55÷3=18(次)……1(个),(18+1)÷6=3(周)……1(次),所以阿奇共取了4次,而其中有1次只取了1个,则阿奇共取了:33110⨯+=(个).【基本班学案4】华罗庚金杯”少年数学邀请赛每隔一年举行一次1988年是第二届.2000年是第几届?【分析】“每隔一年举行一次”的意思是每2年举行一次.1988年到2000年还有2000-1988=12年,因此还要举行1226÷=届.1988年是第二届,所以22年是2+6=8届例6例5【提高班学案4】某月的最后一个星期五是这个月的25号,这个月的第一天是星期几?【分析】这个月的25号是周五,7321-=号也是星期五,l号即第一天是星期2.⨯=天,所以25214【尖子班学案4】某年的10月里有5个星期六,4个星期日.问:这年的10月1日是星期几?【分析】10月有31天,因为有5个星期六,只有4个星期日.所以10月31日是星期六,因为31473=⨯+,所以,3日也是星期六,l日是星期四.[巩固]今天是2008年3月16日星期日,阿奇研究日历时,发现再过1天是2008年3月17日星期一,再过2天则是2008年3月18日星期二……请问:(1)再过多少天才是2008年儿童节呢?(2)2008年的儿童节是星期几?【分析】(1)从2008年3月16日到2008年6月1日(包括6月1日)共有天数是:153031177+++=(天).(2)从2008年3月16日到2008年6月1日(包括这两天)共有天数是:163031178+++=(天),且这78天中的前7天对应的星期是:(星期日、星期一、星期二、星期三、星期四、星期五、星期六).由787111÷=(天)知这年的儿童节是星期日.【超常挑战】紧接着1989后面写一串数字,写下的每一个数字都是它前面两个数字的乘积的个位数.例如,8972⨯=,在9后面写2,9218⨯=,在2后面写8……得到一串数字:19892868…,问这串数字从1开始,往右数,第l999个数字是几?这1999个数字的和是多少?【分析】⑴根据题意,写出这列数的前面部分数字:19892868842868842……“286884”这6个数字重复出现,周期是6.⑵第1999个数字是:因为(19994)63323-÷=⋅⋅⋅,所以,第l999个数字是6.⑶这1999个数字的和是:+++++++++⨯+++271195216(1989)(286884)332(286)==++11995家庭作业1.找出下面图形的排列规律,根据规律算出第29个图形是什么?【分析】(1)周期是“∆∆”五个一周期,那么29554÷=,所以第29只是“”.(2)周期是“∆”四个一周期,那么29471÷=,所以第29个是““.2.图中的五角星处应填几?第四行的☆填______第五行的☆填_______,_______.【分析】第四行的☆填3927⨯=第五行的☆填32781⨯=⨯=,327813.有一组图形从左往右排列○○△☆☆○○△☆☆……那么第50个是什么图形?这50个中圆有多少个?【分析】图形排列的顺序是“○○△☆☆”,周期是5,那么50510÷=,第50个是“☆”,一个周期里有2个○,50个图形中有21020⨯=个.4. 有红、白和黑球共1993只,按红5只、白4只、黑3只、红5只……的顺序排列,如下图所示,最后一只球是什么颜色?【分析】周期是红球5只、白球4只、黑球3只,是54312÷=只,所以最++=只,1993121661后一只是红色.5.二(1)班有六位同学在进行报数游戏,他们围成一圈.小娟报“l”,小华报“2”,小丽报“3”,小捷报“4”,小强报“5”,小勇报“6”.每个人报的数总比前一个人多1.问“72”是谁报的?“190”是谁报的?【分析】报数是按照小娟,小华,小丽,小捷,小强,小勇的顺序,周期是6个人,那么72612÷=组,“72”是小勇报的,1906314÷=,所以190是小捷报的.6. 一月份有三十一天,如果某年的1月1日星期一,这年的2月22日是星期几?【分析】星期的周期是周一、周二、周三、周四、周五、周六、周天,l月l日到2月22日共312253+=天,53774÷=天,所以2月22日是星期四.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、带余除法的定义及性质一般地,如果a是整数,b是整数(b≠0),若有a÷b=q……r,也就是a =b×q+r,0≤r<b;我们称上面的除法算式为一个带余除法算式。
这里:(1)当0r=时:我们称a可以被b整除,q称为a除以b的商或完全商(2)当0r≠时:我们称a不可以被b整除,q称为a除以b的商或不完全商一个完美的带余除法讲解模型:这是一堆书,共有a本,这个a就可以理解为被除数,现在要求按照b 本一捆打包,那么b就是除数的角色,经过打包后共打包了c捆,那么这个c就是商,最后还剩余d本,这个d就是余数。
二、三大余数定理:1.余数的加法定理a与b的和除以c的余数,等于a,b分别除以c的余数之和,或这个和除以c 的余数。
例如:23,16除以5的余数分别是3和1,所以23+16=39除以5的余数等于4,即两个余数的和3+1.当余数的和比除数大时,所求的余数等于余数之和再除以c的余数。
例如:23,19除以5的余数分别是3和4,所以23+19=42除以5的余数等于3+4=7除以5的余数,即2。
知识精讲余数问题2.余数的乘法定理 a 与b 的乘积除以c 的余数,等于a ,b 分别除以c 的余数的积,或者这个积除以c 所得的余数。
例如:23,16除以5的余数分别是3和1,所以23×16除以5的余数等于3×1=3。
当余数的和比除数大时,所求的余数等于余数之积再除以c 的余数。
例如:23,19除以5的余数分别是3和4,所以23×19除以5的余数等于3×4除以5的余数,即2.3.同余定理若两个整数a 、b 被自然数m 除有相同的余数,那么称a 、b 对于模m 同余,用式子表示为:a ≡b ( mod m ),左边的式子叫做同余式。
同余式读作:a 同余于b ,模m 。
由同余的性质,我们可以得到一个非常重要的推论:若两个数a ,b 除以同一个数m 得到的余数相同,则a ,b 的差一定能被m 整除。
用式子表示为:如果有a ≡b ( mod m ),那么一定有a -b =mk ,k 是整数,即m |(a -b )【例1】用某自然数a 去除1992,得到商是46,余数是r ,求a 和r .【解析】 因为1992是a 的46倍还多r ,得到19924643......14÷=,得1992464314=⨯+,所以43a =,14r =.【例2】 甲、乙两数的和是1088,甲数除以乙数商11余32,求甲、乙两数.【解析】 (法1)因为 甲=乙1132⨯+,所以 甲+乙=乙1132⨯++乙=乙12321088⨯+=;【解析】 则乙(108832)1288 =-÷=,甲1088=-乙1000=.【解析】 (法2)将余数先去掉变成整除性问题,利用倍数关系来做:从1088中减掉32以后,1056就应当是乙数的(111)+倍,所以得到乙数10561288=÷=,甲数1088881000=-=.经典例题【例3】一个两位数除310,余数是37,求这样的两位数。
【解析】 本题为余数问题的基础题型,需要学生明白一个重要知识点,就是把余数问题---即“不整除问题”转化为整除问题。
方法为用被除数减去余数,即得到一个除数的倍数;或者是用被除数加上一个“除数与余数的差”,也可以得到一个除数的倍数。
本题中310-37=273,说明273是所求余数的倍数,而273=3×7×13,所求的两 位数约数还要满足比37大,符合条件的有39,91.【例4】有两个自然数相除,商是17,余数是13,已知被除数、除数、商与余数之和为2113,则被除数是多少?【解析】 被除数+除数+商+余数=被除数+除数+17+13=2113,所以被除数+除数=2083,由于被除数是除数的17倍还多13,则由“和倍问题”可得:除数=(2083-13)÷(17+1)=115,所以被除数=2083-115=1968。
【例5】有48本书分给两组小朋友,已知第二组比第一组多5人.如果把书全部分给第一组,那么每人4本,有剩余;每人5本,书不够.如果把书全分给第二组,那么每人3本,有剩余;每人4本,书不够.问:第二组有多少人?【解析】 由48412÷=,4859.6÷=知,一组是10或11人.同理可知48316÷=,48412÷=知,二组是13、14或15人,因为二组比一组多5人,所以二组只能是15人,一组10人.【例6】一个两位数除以13的商是6,除以11所得的余数是6,求这个两位数.【解析】 因为一个两位数除以13的商是6,所以这个两位数一定大于13678⨯=,并且小于13(61)91⨯+=;又因为这个两位数除以11余6,而78除以11余1,这个两位数为78583+=.【例7】有一个大于1的整数,除45,59,101所得的余数相同,求这个数.【解析】 这个题没有告诉我们,这三个数除以这个数的余数分别是多少,但是由于所得的余数相同,根据同余定理,我们可以得到:这个数一定能整除这三个数中的任意两数的差,也就是说它是任意两数差的公约数.1014556-=,594514-=,(56,14)14=,14的约数有1,2,7,14,所以这个数可能为2,7,14。
【例8】 20032与22003的和除以7的余数是________.【解析】 找规律.用7除2,22,32,42,52,62,…的余数分别是2,4,1,2,4,1,2,4,1,…,2的个数是3的倍数时,用7除的余数为1;2的个数是3的倍数多1时,用7除的余数为2;2的个数是3的倍数多2时,用7除的余数为4.因为20033667222⨯+=,所以20032除以7余4.又两个数的积除以7的余数,与两个数分别除以7所得余数的积相同.而2003除以7余1,所以22003除以7余1.故20032与22003的和除以7的余数是415+=.【例9】求2461135604711⨯⨯÷的余数. 【解析】 因为246111223...8÷=,1351112...3÷=,604711549...8÷=,根据同余定理(三), 2461135604711⨯⨯÷的余数等于83811⨯⨯÷的余数,而838192⨯⨯=, 1921117...5÷=,所以2461135604711⨯⨯÷的余数为5.【例10】 求19973的最后两位数.【解析】 即考虑19973除以100的余数.由于100425=⨯,由于3327=除以25余2,所以93除以25余8,103除以25余24,那么203除以25余1;又因为23除以4余1,则203除以4余1;即2031-能被4 和25整除,而4与25互质,所以2031-能被100整除,即203除以100余1,由于1997209917=⨯+,所以19973除以100的余数即等于173除以100的余数,而63729=除以100余29,53243=除以100余43,176253(3)3=⨯,所以173除以100的余数等于292943⨯⨯除以100的余数,而29294336163⨯⨯=除以100余63,所以19973除以100余63,即19973的最后两位数为63.【例11】2008222008+除以7的余数是多少?【解析】 328=除以7的余数为1,200836691=⨯+,所以200836691366922(2)2⨯==⨯+,其除以7的余数为:669122⨯=;2008除以7的余数为6,则22008除以7的余数等于26除以7的余数,为1;所以2008222008+除以7的余数为:213+=.【作业1】5122除以一个两位数得到的余数是66,求这个两位数。
【答案】79【作业2】明明在一次计算除法时,把被除数171错写成117,结果商少3而余数恰恰相同,这题中的除数是多少?【答案】18【作业3】两数相除,商4余8,被除数、除数、商数、余数四数之和等于415,则被除数是_______.【解析】 因为被除数减去8后是除数的4倍,所以根据和倍问题可知,除数为4154884179---÷+=()(),所以,被除数为7948324⨯+=。
【作业4】1013除以一个两位数,余数是12.求出符合条件的所有的两位数.【解析】 1013121001-=,100171113=⨯⨯,那么符合条件的所有的两位数有11,13,77,91,因为“余数小于除数”,所以舍去11,答案只有13,77,91。
【作业5】求478296351⨯⨯除以17的余数.【解析】 先求出乘积再求余数,计算量较大.可先分别计算出各因数除以17的余数,再求余数之积除以17的余数.478,296,351除以17的余数分别为2,7和11,(2711)179......1⨯⨯÷=.【作业6】一个大于1的数去除290,235,200时,得余数分别为a ,2a +,5a +,则这个自然数是多少?【解析】 根据题意可知,这个自然数去除290,233,195时,得到相同的余数(都为a ). 既然余数相同,我们可以利用余数定理,可知其中任意两数的差除以这个数肯定余0.那么这个自然数是29023357-=的约数,又是23319538-=的约数,因此就是57和38的公约数,因为57和38的公约数只有19和1,而这个数大于1,所以这个自然数是19.【作业7】有48本书分给两组小朋友,已知第二组比第一组多5人.如果把书全部分给第一组,那么每人4本,有剩余;每人5本,书不够.如果把书全分给第二组,那么每人3本,有剩余;每人4本,书不够.问:第二组有多少人?【解析】 由48412÷=,4859.6÷=知,一组是10或11人.同理可知48316÷=,48412÷=知,二组是13、14或15人,因为二组比一组多5人,所以二组只能是15人,一组10人.【作业8】某个大于1的自然数分别除442,297,210,得到相同的余数,则该自然数为 。
【分析】首先要清楚一个事实:两个数被同一个数除余数相同,则这两个数相减(大减小)能被这个数整除。
知道了这个事实后我们就很容易做这个题了。
因为该自然数能整除442297145-=,也能整除442210232-=,同样能整除29721087-=。
所以可知这个自然数必定是145,232,87的公约数。
而这三个数大于1的公约数只有29。
所以可知这个自然数为29。
【作业9】两位自然数ab 与ba 除以7都余1,并且a b >,求ab ba ⨯.【解析】 ab ba -能被7整除,即(10)10)9a b b a a b +-+=⨯-(()能被7整除.所以只能有7a b -=,那么ab 可能为92和81,验算可得当92ab =时,29 ba =满足题目要求,92292668ab ba ⨯=⨯=【作业10】学校新买来118个乒乓球,67个乒乓球拍和33个乒乓球网,如果将这三种物品平分给每个班级,那么这三种物品剩下的数量相同.请问学校共有多少个班?【解析】 所求班级数是除以118,67,33余数相同的数.那么可知该数应该为1186751-=和673334-=的公约数,所求答案为17.。
