量子物理基础习题解
第六部分量子物理基础习题

第六部分 量子物理基础 习题:1.从普朗克公式推导斯特藩玻尔兹曼定律。
(提示:15143π=-⎰∞dx e xx)解:λλπλλλd e hc d T M T M T k hc⎰⎰∞-∞-==52000112),()(令x Tk hc =λ,则dx kTxhc d 2-=λ,所以442545034234025252015212)(11)(2112)(TTch kdxexTc h k dxkTxhc e hckTx hc d e hc T M xxT k hcσπππλλπλ=⋅⋅=-=--=-=⎰⎰⎰∞∞∞-证毕。
2.实验测得太阳辐射波谱中峰值波长nm m 490=λ,试估算太阳的表面温度。
解:由维恩位移定律b T m =λ得到K bT m3931091.51049010897.2⨯⨯⨯==--=λ3.波长为450nm 的单色光射到纯钠的表面上(钠的逸出功A =2.29eV ),求: (1)这种光的光子能量和动量; (2)光电子逸出钠表面时的动能。
解:(1) 2.76eV J 1042.4104501031063.6199834==--⨯⨯⨯⨯⨯===-λhchv Es m /kg 1047.1104501063.6hp 27934⋅⨯⨯⨯---===λ(2)由爱因斯坦光电效应方程,得光电子的初动能为eV A hv E k 47.029.276.2=-=-=4.铝的逸出功是4.2eV ,现用波长nm 200=λ的紫外光照射铝表面。
试求: (1)发射的光电子的最大动能; (2)截止电压; (3)铝的红限频率。
解:(1)由光电效应方程得光电子的最大动能为J 102.3106.12.4102001031063.619199834----=⨯⨯⨯-⨯⨯⨯⨯=-=-=A hcA hv E k λ(2)截止电压V 0.2106.1102.319190=--⨯⨯==eE V k(3)红限频率Hz 1001.11063.6106.12.41534190⨯=⨯⨯⨯==--hA v5.在一次康普顿散射中,传递给电子的最大能量为MeV E 045.0=∆,试求入射光子的波长。
chapter1 量子力学基础知识习题解答

= 9.403×10-11m
(3) λ = h = h p 2meV
=
6.626 ×10−34 J ⋅ s
2× 9.109 ×10−31kg ×1.602×10−19 C × 300V
= 7.08×10−11m
4
乐山师范学院 化学与生命科学学院
【1.5】用透射电子显微镜摄取某化合物的选区电子衍射图,加速电压为 200kV,计算电子 加速后运动时的波长。
图 1.2 金属的 Ek ~ ν 图
3
乐山师范学院 化学与生命科学学院
h = Ek = ∆Ek ν −ν 0 ∆ν
即 Planck 常数等于 Ek − v 图的斜率。选取两合适点,将 Ek 和 v 值带入上式,即可求出 h 。
例如:
h
=
(2.7 −1.05) ×10−19 J (8.50 − 6.00) ×1014 s−1
乐山师范学院 化学与生命科学学院
01.量子力学基础知识
本章主要知识点
一、微观粒子的运动特征
1.
波粒二象性: E
= hν , p =
h λ
2. 测不准原理: ∆x∆px ≥ h, ∆y∆py ≥ h, ∆z∆pz ≥ h, ∆t, ∆E ≥ h
3. 能量量子化
二、量子力学基本假设
1. 假设 1:对于一个量子力学体系,可以用坐标和时间变量的函数ψ (x, y, z,t) 来
相反的两个电子。或者说:对于多电子体系,波函数对于交换任意两个电子是反
对称的。
三、箱中粒子的 Schrödinger 方程及其解
1. 一维无限势阱的 Schrödinger 方程:
− 2 d2ψ 2m dx2
= Eψ
其解为:ψ n (x) =
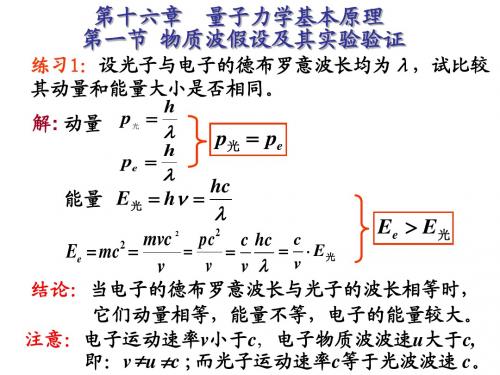
大学物理 第16章量子力学基本原理-例题及练习题
∴ n = 2,6,10...... 时概率密度最大
nhπ 6 × 10 = =1时 (3) n=1时: E = =1 2mL L
2 2 2 2 2 −38
A 例题3 例题3 设粒子沿 x 方向运动,其波函数为 ψ ( x ) = 方向运动, 1 + ix
( n = 1,2,3,...)
E n=4
p2 E = 2m p= nπh nh 2 mE = = a 2a
n=3 n=2 n=1
h 2a λ= = p n
二者是一致的。 二者是一致的。
( n = 1, 2, 3,...)
o a
x
例题2 粒子质量为m, 在宽度为L的一维无限 的一维无限深势 例题2 P516例1:粒子质量为m, 在宽度为 的一维无限深势 中运动,试求( 粒子在0 阱中运动,试求(1)粒子在0≤x≤L/4区间出现的概率。并 ≤ / 区间出现的概率。 求粒子处于n=1 状态的概率。 在哪些量子态上, 求粒子处于 1和n=∞状态的概率。(2)在哪些量子态上, 状态的概率 (2)在哪些量子态上 L/4处的概率密度最大?(3)求n=1时粒子的能量 补充 。 /4处的概率密度最大 (3)求 =1时粒子的能量(补充 处的概率密度最大? =1时粒子的能量 补充)。 2 nπ x 由题得: 解:(1) 由题得: 概率密度 |ψ | = sin
2 2 2 2 0
2
2
2
2
0
0
k
0
2
2
2 k
0
k
k
k
0
h ∴λ = = p
hc 2E m c + E
2 k 0
基本习题和答案解析量子力学

WORD格式整理量子力学习题(一)单项选择题 1. 能量为100ev 的自由电子的De Broglie 波长是 0 0 0 0 A. 1.2 A. B. 1.5 A. C. 2.1 A. D. 2.5 A. 2. 能量为0.1ev 的自由中子的De Broglie 波长是 0 0 0 0 A.1.3 A. B. 0.9 A. C. 0.5 A. D. 1.8 A. 3. 能量为0.1ev ,质量为1g 的质点的De Broglie 波长是 0A.1.4 A.B.1.9 0C.1.17 10J 2 A.D. 2.04.温度T=1k 时, 具有动能 010J 2 A. 0 A. =—k B T ( k B 2 为Boltzeman 常数)的氦原子的DeBroglie 波长是 0 A.8 A. B. 5.6 5.用 Bohr-Sommerfeld 0 A. 0 A. D. 12.6 0A. A. E n 二 n ,.B.C. 10 的量子化条件得到的一维谐振子的能量为(n 二0,1,2,…) E n = (n :);. 2 C. E n =(n 1) ? ■ .D. E n =2n •. 6.在0k 附近,钠的价电子的能量为3ev ,其 0 0A.5.2 A.B. 7.1 A.C. 8.4 De Broglie 波长是 0 A. 7. 钾的脱出功是2ev ,当波长为 最大能量为 A. 0.25 10J 8J. B. 1.25 C. 0.25 1046 J.D. 1.25 0A. D. 9.4 03500 A 的紫外线照射到钾金属表面时,光电子的 10」8J. 10J 6J. 8. 当氢原子放出一个具有频率--的光子,反冲时由于它把能量传递给原子而产生 的频率改变为 h A. . B. 2 . C.2七 2心 9. C ompton 效应证实了A.电子具有波动性.B.C.光具有粒子性.D. -2 '2走.D. PC .光具有波动性• 电子具有粒子性. 10. D avisson 和Germer 的实验证实了 A.电子具有波动性.B.光具有波动性. C.光具有粒子性.D. 电子具有粒子性. U (x )斗0,0:X7中运动,设粒子的状态由 [°°,x E0,X11.粒子在一维无限深势阱 J(x)二Csin 描写,其归一化常数C 为aA ^r 1. B. . C. .a• a■ a12.设t(x)—(x),在x-x ,dx 范围内找到粒子的几率为 22.D.13.设粒子的波函数为2A.屮(x, y, z) dxdydz.'■ (x, y,z),在x—x • dx范围内找到粒子的几率为2B.屮(x, y,z) dx.2 2C.( '- (x, y, z) dydz)dx .D. . dx dy dz'- (x, yz)14.设:Mx)和:2(x)分别表示粒子的两个可能运动状态,则它们线性迭加的态c「i(x)dd)的几率分布为2 2A.|汕1 +对2 .2 2 *B. |G屮l| +C2屮2 +C1C2屮1屮2.2 2 *C.k 屮1 +C2 屮2 +2GC2屮1屮2.2 2 * * * *D.- c^;2 +。
量子物理基础习题解

量⼦物理基础习题解量⼦物理基础17.1 夜间地⾯降温主要是由于地⾯的热辐射。
如果晴天夜⾥地⾯温度为-5°C ,按⿊体辐射计算,每平⽅⽶地⾯失去热量的速率多⼤?解:每平⽅⽶地⾯失去热量的速率即地⾯的辐射出射度2484W /m2922681067.5=??==-TM σ17.2 在地球表⾯,太阳光的强度是1.0?103W/m 2。
地球轨道半径以1.5?108km 计,太阳半径以7.0?108 m 计,并视太阳为⿊体,试估算太阳表⾯的温度。
解:42244TR I R M SE σππ==K103.51067.5)107.6(100.1)105.1(348283211422==S E R I R T 17.3宇宙⼤爆炸遗留在宇宙空间的均匀背景辐射相当于3K ⿊体辐射.求:(1)此辐射的单⾊辐射强度在什么波长下有极⼤值?(2)地球表⾯接收此辐射的功率是多少?[解答](1)根据公式λm T = b ,可得辐射的极值波长为λm = b/T = 2.897×10-3/3 = 9.66×10-4(m).(2)地球的半径约为R = 6.371×106m ,表⾯积为 S = 4πR 2.根据公式:⿊体表⾯在单位时间,单位⾯积上辐射的能量为 M = σT 4,因此地球表⾯接收此辐射的功率是 P = MS = 5.67×10-8×34×4π(6.371×106)2= 2.34×109(W).17.4 铝的逸出功是eV 2.4,今有波长nm 200=λ的光照射铝表⾯,求:(1)光电⼦的最⼤动能;(2)截⽌电压;(3)铝的红限波长。
解:(1) A chA h E k -=-=λνeV 0.22.4106.1102001031063.6199834=-=---(2)V 0.21/0.2/===e E U k c (3)Ahc c==0νλnm6.12.41031063.6719834=?==---17.5 康普顿散射中⼊射X 射线的波长是λ = 0.70×10-10m ,散射的X 射线与⼊射的X 射线垂直.求:(1)反冲电⼦的动能E K ;(2)散射X 射线的波长;(3)反冲电⼦的运动⽅向与⼊射X 射线间的夹⾓θ.[解答](1)(2)根据康普顿散射公式得波长变化为21222sin2 2.42610sin24πλΛ-?==??= 2.426×10-12(m),散射线的波长为λ` = λ + Δλ = 0.72426×10-10(m).反冲电⼦的动能为`k hchcE λλ=810106.63103106.63103100.7100.7242610----=-= 9.52×10-17(J).(3)由于/`tan /`hc hc λλθλλ==,0.70.96650.72426==,所以夹⾓为θ = 44°1`.17.6 求波长分别为71100.7-?=λm 的红光和波长1021025.0-?=λm 的X 射线光⼦的能量、动量和质量。
量子物理基础习题

17-1 在加热黑体过程中,其单色辐出度的峰值波长是由μm 69.0变化到μm 50.0,求总辐出度改变为原来的多少倍?解:由 4)(T T M B σ=,b T m =λ 得 63.3)5.069.0()()()(442112===m m B B T M T M λλ17-2解:(1)m 10898.21010898.21073--⨯=⨯==T b m λ (2)J 1086.610898.21031063.61610834---⨯=⨯⨯⨯⨯===λνch h E 17-3解:(1)4)(T T M B σ=,K 17001067.5001.0/6.473)(484=⨯==-σT M T B(2)m 1070.1170010898.263--⨯=⨯==T b m λ (3)162)()()(441212===T T T M T M B B ,2612W/m 10578.7001.06.47316)(16)(⨯=⨯==T M T M B B17-4 钾的光电效应红限波长为μm 62.00=λ。
求:(1)钾的逸出功;(2)在波长nm 330=λ的紫外光照射下,钾的截止电压。
解:(1)eV 2J 1021.31062.01031063.61968340=⨯=⨯⨯⨯⨯===---λνch h A (2)A h mv eU a -==ν221 V 76.11060.11021.3103301031063.619199834=⨯⨯-⨯⨯⨯⨯=-=-=----eA ch eA h U a λν17-5 铝的逸出功为eV 2.4。
今用波长为nm 200的紫外光照射到铝表面上,发射的光电子的最大初动能为多少?截止电压为多大?铝的红限波长是多大?解:(1)eV 2J 1023.3106.12.4102001031063.621191998342≈⨯=⨯⨯-⨯⨯⨯⨯=-=-=----A c h A h mv λν (2)221mv eU a =,V 2eV2==eU a (3)Hz 10014.11063.6106.12.41534190⨯=⨯⨯⨯==--h A νnm 296m 1096.210014.1103715800=⨯=⨯⨯==-νλc17-6 在光电效应实验中,对某金属,当入射光频率为Hz 102.215⨯时,截止电压为V 6.6,入射光频率为Hz 106.415⨯时,截止电压为V 5.16。
量子物理习习题解答

精心整理量子物理习题解答习题17—1用频率为1ν的单色光照射某一金属时,测得光电子的最大初动能为E k 1;用频率为2ν的单色光照射另一种金属时,测得光电子的最大初动能为E k 2。
那么[ ](A)1ν一定大于2ν。
(B)1ν一定小于2ν。
(C)1ν一定等于2ν。
(D)1ν可能大于也可能小于2ν。
解:根据光电效应方程,光电子的最大初动能为由此式可以看出,E k 不仅与入射光的频率ν有关,而且与金属的逸出功A 有关,因此我们无法判习题 所以L (A)。
习题所以习题(A)1/4。
(B)1/8。
(C)1/16。
(D)1/32。
解:根据玻尔的理论,氢原子中电子的动能、角动量和轨道半径分别为mP E k 22= ; n P r L n == ;12r n r n = 所以电子的动能与量子数n 2成反比,因此,题给的两种情况下电子的动能之比12/42=1/16,所以我们选择答案(C)。
习题17—5在康普顿效应实验中,若散射光波长是入射光波长的1.2倍,则散射光光子能量ε与反冲电子动能E k 之比k E ε为[ ](A)2。
(B)3。
(C)4。
(D)5。
解:由康普顿效应的能量守恒公式可得所以,应该选择答案(D)。
习题17—6设氢原子的动能等于温度为T 的热平衡状态时的平均动能,氢原子的质量为m ,那么此氢原子的德布罗意波长为[ ](A)mkT h 3=λ。
(B)mkT h 5=λ。
(C)h mkT 3=λ。
(D)h mkT 5=λ。
把此式代入德布罗意公式有所以因此,应该选择答案(D)。
习题17—10氩(Z =18)原子基态的电子组态是:[ ] (A)1S 22S 83P 8(B)1S 22S 22P 63d 8 (C)1S 22S 22P 63S 23P 6(D)1S 22S 22P 63S 23P 43d 2解:对(A)示组态,既违反泡利不相容原理,也违反能量最小原理,是一个不可能的组态;对(B)示组态和(D)示组态均违反能量最小原理,也都是不可能组态。
量子力学习题课

1.已知粒子在无限深势阱中运动,其波函数为
( x) 2 / a sin(x / a)
求发现粒子的概率为最大的位置.
(0 ≤x ≤a)
理学院
黄玉
第一章 波粒二象性 发现粒子的概率
量子物理学基础
( x) 2 / a sin 2 (x / a )
概率最大的位置对应
d d 2 ( x) (2 / a sin 2 (x / a)) 0 dx dx
m=1,赖曼系
m=2,巴耳末系(可见光)
m=3,帕邢系 (1)定态假设 玻尔理论
En Em (2)跃迁假设: h
(3)角动量量子化假设
L n
n 1,2,3
理论计算
理学院 黄玉
4 o n 2 2 2 10 rn n r ( n 1 , 2 , 3 , ) r 0 . 529 10 m 1 1 2 me
理学院 黄玉
第一章 波粒二象性
量子物理学基础
20.设康普顿效应中入射X射线(伦琴射线)的波长 =0.700 Å,散射的X射线与入射的X射线垂直,求: (1) 反冲电子的动能EK. (2) 反冲电子运动的动量及动量方向与入射的X射线之间的 夹角.
理学院
黄玉
量子物理学基础 第一章 波粒二象性 解:令、p 和 p 、 分别为入射与散射光子的动量
理学院
黄玉
第一章 波粒二象性
量子物理学基础
(1) 定态假设:原子处于一系列不连续稳定态。电子只 能在一定轨道上作圆周运动,且不辐射 能量。 (2) 角动量量子化假设:电子绕核作圆周运动的轨道只 能取决于
PL n
n 1,2,3
(3)跃迁假设:原子从一稳定态过度到另一稳定态吸收 或发出单色电磁辐射。即由光子假说和 能量守恒定律有 En Em h
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
量子物理基础17.1 夜间地面降温主要是由于地面的热辐射。
如果晴天夜里地面温度为-5°C ,按黑体辐射计算,每平方米地面失去热量的速率多大? 解:每平方米地面失去热量的速率即地面的辐射出射度2484W /m2922681067.5=⨯⨯==-TM σ17.2 在地球表面,太阳光的强度是1.0⨯103W/m 2。
地球轨道半径以1.5⨯108km 计,太阳半径以7.0⨯108 m 计,并视太阳为黑体,试估算太阳表面的温度。
解:42244TR I R M SE σππ==K103.51067.5)107.6(100.1)105.1(348283211422⨯=⨯⨯⨯⨯⨯⨯==-σS E R I R T 17.3宇宙大爆炸遗留在宇宙空间的均匀背景辐射相当于3K 黑体辐射.求: (1)此辐射的单色辐射强度在什么波长下有极大值?(2)地球表面接收此辐射的功率是多少?[解答](1)根据公式λm T = b ,可得辐射的极值波长为λm = b/T = 2.897×10-3/3 = 9.66×10-4(m). (2)地球的半径约为R = 6.371×106m , 表面积为 S = 4πR 2.根据公式:黑体表面在单位时间,单位面积上辐射的能量为 M = σT 4,因此地球表面接收此辐射的功率是 P = MS = 5.67×10-8×34×4π(6.371×106)2= 2.34×109(W).17.4 铝的逸出功是eV 2.4,今有波长nm 200=λ的光照射铝表面,求:(1)光电子的最大动能; (2)截止电压;(3)铝的红限波长。
解:(1) A chA h E k -=-=λνeV 0.22.4106.1102001031063.6199834=-⨯⨯⨯⨯⨯⨯=---(2)V 0.21/0.2/===e E U k c (3)Ahc c==0νλnm296m1096.2106.12.41031063.6719834=⨯=⨯⨯⨯⨯⨯=---17.5 康普顿散射中入射X 射线的波长是λ = 0.70×10-10m ,散射的X 射线与入射的X 射线垂直.求:(1)反冲电子的动能E K ;(2)散射X 射线的波长;(3)反冲电子的运动方向与入射X 射线间的夹角θ.[解答](1)(2)根据康普顿散射公式得波长变化为21222sin2 2.42610sin24ϕπλΛ-∆==⨯⨯= 2.426×10-12(m),散射线的波长为λ` = λ + Δλ = 0.72426×10-10(m). 反冲电子的动能为`k hchcE λλ=-34834810106.63103106.63103100.7100.7242610----⨯⨯⨯⨯⨯⨯=-⨯⨯= 9.52×10-17(J).(3)由于/`tan /`hc hc λλθλλ==,0.70.96650.72426==,所以夹角为θ = 44°1`.17.6 求波长分别为71100.7-⨯=λm 的红光和波长1021025.0-⨯=λm 的X 射线光子的能量、动量和质量。
解:光子能量为E = h ν = hc/λ,动量为 p = h/λ;由E = hc/λ = mc 2,得其质量为m = h/cλ.对于红光来说,能量为 J,1084.2100.71031063.61978341---⨯=⨯⨯⨯⨯=E动量为 ,s m kg 1047.9100.71063.61287341----⋅⋅⨯=⨯⨯=p质量为 .kg 1016.3100.71031063.63678341---⨯=⨯⨯⨯⨯=m对于X 射线来说,能量为J,1096.71025.01031063.615108342---⨯=⨯⨯⨯⨯=E动量为 ,s m kg 1065.21025.01063.612310342----⋅⋅⨯=⨯⨯=p质量为 .kg 1084.81025.01031063.632108342---⨯=⨯⨯⨯⨯=m17.7 处于第四激发态上的大量氢原子,最多可发射几个线系,共几条谱线?那一条波长最长.[解答]第四激发态的氢原子处于第5个能级,最多可发射四个线系.(1)能级5到4,1条谱线;(2)能级5和4到3,2条谱线;(3)能级5、4和3到2,3条谱线;(3)能级5、4、3和2到1,4条谱线. 共10条谱线.从能级5跃迁到4发射的光谱频率最小,波长最长.17.8 设氢原子中的电子从2=n 的轨道上电离出去,需多少能量? 解:氢原子能级公式为,1822204nhmeE n ⋅-=ε当n =1时,基态能级的能量为eV,6.131018.281822041-=⨯-≈-=-J hmeE ε因此 eV 6.132nE n -=.当电子从n 能级跃迁到m 能级时放出(正)或吸收(负)光子的能量为12211()n m E E E E nm∆=-=-.电离时,m 趋于无穷大.当电子从n = 2的能级电离时要吸收能量221113.6()2E ∆=--∞= -3.4(eV),因此需要3.4eV 的能量.17.9 略17.10 质量为m 的卫星,在半径为r 的轨道上环绕地球运动,线速度为v .(1)假定玻尔氢原子理论中关于轨道角动量的条件对于地球卫星同样成立.证明地球卫星的轨道半径与量子数的平方成正比,即r = Kn 2,(式中K 是比例常数);(2)应用(1)的结果求卫星轨道和下一个“容许”轨道间的距离,由此进一步说明在宏观问题中轨道半径实验上可认为是连续变化的(利用以下数据作估算:普朗克常数h = 6.63×10-34J·s ,地球质量M = 6×1024kg ,地球半径R = 6.4×103km ,万有引力常数G = 6.7×10-11N·m 2·kg -2.[解答](1)卫星绕地球运动的向心力是万有引力22M m m v G rr=;根据玻尔理论,角动量为mvr = nh /2π.将前式乘以mr 3得2222()()4nh GM m r mvr π==,所以 222224h nr K n G M mπ==,即:卫星的轨道半径与量子数的平方成正比.(2)假设卫星质量m = 100kg ,比例系数为2224hK G M mπ=342211242(6.6310)4 6.710610(100)π--⨯=⨯⨯⨯⨯⨯= 2.77×10-87.可见:比例系数很小.当r = R 时,地球表面的量子数为460 4.810n ==⨯.可见:地球表面处的量子数很大.地面以上的量子数设为n `,(n` = 1,2,3,…),则总量子数可表示为两个量子数之和:n =n 0 + n`.轨道间的距离为 Δr = K [(n 0 + n` + 1)2 - (n 0 + n`)2]= K [2(n 0 + n`) + 1].由于n 0>>1,所以Δr = 2Kn 0 + 2Kn`. 设n` = kn 0,即:取地面以上的量子数为地球表面量子数的倍数,有n = (k + 1)n 0,则r = Kn 02(k + 1)2,Δr = 2Kn 0(k + 1) = 2.66×10-40(k + 1). 这说明:当地面以上的量子数按k + 1成倍地增加时,半径将按k + 1的平方的规律增加,而轨道之间的距离只按k + 1的一次方的规律增加;由于Δr 的系数很小,所以轨道间距是非常非常小的,因此可认为轨道半径是连续变化的.17.11 电子和光子各具有波长2.0×10-10m ,它们的动量和总能量各是多少?[解答]它们的动量都为34106.6310210h p λ--⨯==⨯= 3.315×10-24(kg·m·s -1).根据公式E 2= p 2c 2 + m 02c 4,电子的总能量为E ==3×108×[(3.315×10-24)2+ (9.1×10-31×3×108)2]1/2=8.19×10-14(J). 光子的静止质量为零,总能量为 E = cp = 3×108×3.315×10-24 = 9.945×10-16(J).17.12 室温下的中子称为热中子K T 300=,试计算热中子的平均德布罗意波长。
解:中子热运动的平均速度的大小为nm kTπ8=v中子的质量m n = 1.673×10-27kg ,可得平均速度为 ,s m 102.50914-⋅⨯=v平均动量为.sm kg 104.2127--⋅⋅⨯==v n m P平均德布罗意波长为nm 158.0m 1058.110=⨯==-ph λ.17.13 假定对粒子动量的测定可以精确到千分之一,试确定下述粒子位置的不确定量。
(1)该粒子质量为3100.5-⨯kg ,以2m·s -1的速度运动;(2)该粒子是速度为8108.1⨯m·s -1的电子. 解:粒子的动量为 p = m v ,动量的不确定量为 Δp = p /1000,根据动量和位置的不确定关系Δp ·Δx ≧ћ/2,位置的不确定量为Δx = ћ/2Δp .m1028.5210514.341063.6100041000230334---⨯=⨯⨯⨯⨯⨯⨯==∆≥∆ph px πm1022.3108.1101.914.341063.610004100021083134---⨯=⨯⨯⨯⨯⨯⨯⨯==∆≥∆ph px π17.14 一束动量为P 的电子通过宽度为a 的狭缝发生单缝衍射,设缝与屏之间的距离为R ,试求屏上所观察到的单缝衍射中央明纹宽度。
解:根据动量和位置的不确定关系2/ ≥∆∆x p x ,其中位置不确定量为Δx = a ,动量的不确定量为Δp x = p sin θ.设电子衍射图样的中央明纹宽度为d ,则Rd 2tan sin =≈θθ, 可得,22 ≥Rpda .paR d ≥17.15 电视机显象管中电子的加速电压为9kV ,电子枪枪口直径取0.5mm ,枪口离荧光屏距离为0.30m ,求荧光屏上一个电子形成的亮斑直径。
这样大小的亮斑影响电视图像的清晰度吗?解:取mm 50.0=∆y ,则由不确定关系得yp y ∆=∆2而E m p e x 2=荧光屏上亮斑直径为Em y l yp l l p p d e xxy 22∆=∆=∆=nm2.1m 102.1106.1109101.92105.030.01005.1919331334=⨯=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=-----此亮斑的大小不会影响当前电视图像的清晰度。
