第7章二元系相图
合集下载
第7-2章二元系相图
（已知400℃时相的成分变为wCd=57%）。
18
19
20
答：（1） 549℃：包晶转变，（Cu）+L
547℃：包晶转变，+L
544℃：共晶转变，L+ 397℃：包晶转变，+L
314℃：共晶转变，L+（Cd）
21
（2）1点：开始发生匀晶转变，L（Cu） 2点：一部分液相发生包晶反应，（Cu）+L 2-3点：剩余液相继续发生匀晶反应，L 3点：剩余液相与一部分相发生包晶反应，+L 3点以下：剩余中析出部分相，
表达式：
L1+L2 →
5
4、具有熔晶转变的 相图 由一个固相恒温 分解为一个液相 和另一个固相的 转变。 表达式：
→+L
6
5、具有固态转 变的二元相图 （1）具有固溶 体多晶型转变 的相图
7
（2）具有共析转变 的相图 一个固相在恒温 下转变为另外两 个固相的转变。 表达式： →+
14
15
7.3.7 根据相图推测合金的性能
1、根据相图判断合金的使用性能
16
2、根据相图判断 合金的工艺性能
17
例1、Cu-Cd二元相图如图所示。
（1）写出图中三相平衡转变的名称及反应式；
（2）分析wCu=50%合金的平衡结晶过程； （ 3 ）写出 400℃时 wCu=50% 合金的平衡相并计算其质量 分数； （ 4 ）写出 400℃时 wCu=50% 合金的组织组成物并计算其 质量分数；
22
（3）400℃时合金中的平衡相为+，其质量分数分别为：
w w
57 50 100 % 66.7% 57 46.5 1 w 1 66.7% 33.3%
课件：第七章 二元相图及其合金的凝固
(7.7)式称为杠杆法则，在α和β两相共存时，可用杠杆法则求出两
相的相对量，α相的相对量为 x2 x ，β相的相对量为 x x1 ，
两相的相对量随体系的成分x而变x2。 x1
x2 x1
7.2.4 从自由能—成分曲线推测相图
根据公切线原理可求出体系在某一温度下平衡相的成分。图7．7表 示由T1，T2，T3，T4及T5温度下液相(L)和固相(S)的自由能一成分 曲线求得A，B两组元完全互溶的相图。
• 当Ω ＞0，A—B对的能量高于A-A和B-B对的平均能量，意味着 A—B对结合不稳定，A，B组元倾向于分别聚集起来，形成偏聚状 态，此时ΔHm ＞0。
7.2.2 多相平衡的公切线原理
两相平衡时的成分由两相自由能—成分曲线的公切线所确定，如图7．4 所示。
由图可知：
对于二元系在特定温度下可出现三相平衡，如7.5所示：
对上式用二阶泰勒级数展开，可得
由此表明， 在拐点迹线以内的溶混间隙区，任意小的成分起伏Δx都能使体系自 由能下降，从而使母相不稳定，进行无热力 学能垒的调幅分解，由上坡扩散使 成分起伏增大，从而直接导致新相的形成，即发生调幅分解。
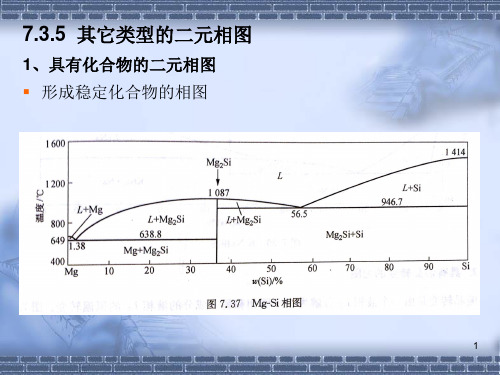
7.3.5 其他类型的二元相图
1. 具有化合物的二元相图
a．形成稳定化合物的相图 没有溶解度的化合物在相图中是一条垂线，可把它看作为一 个
7.1 相图的表示和测定方法
• 二元相图中的成分在国家标准有两种表示方法：质量分数（ω） 和摩尔分数（x），两者换算如下：
式中，ωA，ωB分别为A，B组元的质量分数；ArA，ArB分别为组元A，B的 相对原子质量；xA，xB分别为组元A，B的摩尔分数，并且ωA+ωB=1（或 100％），xA+xB=1（或100％）。
814材料科学基础-第七章 二元相图知识点讲解
共晶线：水平线CED叫做共晶线。
共晶反应：在共晶线对应的温度下，E点成分的合金同时结晶出C点成分的 α固溶体个D点成分的β，形成这两个相的机械混合物：
LE C D
共晶体：共晶反应的产物，即两相的机械混合物 共晶温度：发生共晶反应的温度。即共晶线CED对应的温度 共晶点：代表共晶温度和共晶成分的点，也就是共晶图中的E点。
过烧：当钢加热到接近熔化温度，并在此温度长时间停留，，不仅奥氏体 晶粒长大，同时由于氧化性气体渗入到晶界，使晶间物质Fe、C、S发生氧 化，形成易熔共晶体氧化物。这种现象称为过烧。
非平衡凝固总结
非平衡凝固对合金的影响：
（1）组织影响：晶内偏析、枝晶偏析（冷却速度越大，凝固相间距越大，那么枝晶偏析越 严重）
两相的相对量随体系的成分x变化而变化。
知识点5 自由能-成分曲线推测相图
根据公切线原理，可以求出某一温度下平衡相的成分。因此，可以根据二 元系的不同温度下的自由能-成分曲线画出二元系相图。
二元相图的几何规律
（1）相图中所有的线条都代表发生相转变的温度和平衡相的成分，所以相界线是相平衡的 体现，平衡相成分必须沿着相界线随着温度而变化；
的化学势相等。
dGa B A B A
dx
AB
dG B A B A
dx
AB
1.多相平衡公切线法则：多相 平衡必能作出公切线，切点对 应着各相平衡时的成分； 2.两相平衡时，混合物的自由 能位于切点之间的直线上。
知识点4 杠杆法则
（1）当二元系的成分x≤x1时，α固溶体的摩尔 吉布斯自由能低于β固溶体，故α相为稳定相， 即体系处于单相α状态； （2）当x≥x2时，β相的摩尔吉布斯自由能低于α 相，则体系处于单相β状态； （3）当x1＜x＜x2时，公切线上表示混合物的摩 尔吉布斯自由能低于α相或者β相的摩尔吉布斯 自由能，故α和β两相混合时，体系能量最低。
共晶反应：在共晶线对应的温度下，E点成分的合金同时结晶出C点成分的 α固溶体个D点成分的β，形成这两个相的机械混合物：
LE C D
共晶体：共晶反应的产物，即两相的机械混合物 共晶温度：发生共晶反应的温度。即共晶线CED对应的温度 共晶点：代表共晶温度和共晶成分的点，也就是共晶图中的E点。
过烧：当钢加热到接近熔化温度，并在此温度长时间停留，，不仅奥氏体 晶粒长大，同时由于氧化性气体渗入到晶界，使晶间物质Fe、C、S发生氧 化，形成易熔共晶体氧化物。这种现象称为过烧。
非平衡凝固总结
非平衡凝固对合金的影响：
（1）组织影响：晶内偏析、枝晶偏析（冷却速度越大，凝固相间距越大，那么枝晶偏析越 严重）
两相的相对量随体系的成分x变化而变化。
知识点5 自由能-成分曲线推测相图
根据公切线原理，可以求出某一温度下平衡相的成分。因此，可以根据二 元系的不同温度下的自由能-成分曲线画出二元系相图。
二元相图的几何规律
（1）相图中所有的线条都代表发生相转变的温度和平衡相的成分，所以相界线是相平衡的 体现，平衡相成分必须沿着相界线随着温度而变化；
的化学势相等。
dGa B A B A
dx
AB
dG B A B A
dx
AB
1.多相平衡公切线法则：多相 平衡必能作出公切线，切点对 应着各相平衡时的成分； 2.两相平衡时，混合物的自由 能位于切点之间的直线上。
知识点4 杠杆法则
（1）当二元系的成分x≤x1时，α固溶体的摩尔 吉布斯自由能低于β固溶体，故α相为稳定相， 即体系处于单相α状态； （2）当x≥x2时，β相的摩尔吉布斯自由能低于α 相，则体系处于单相β状态； （3）当x1＜x＜x2时，公切线上表示混合物的摩 尔吉布斯自由能低于α相或者β相的摩尔吉布斯 自由能，故α和β两相混合时，体系能量最低。
上海交通大学 材料科学基础第七章 二元相图及其合金的凝固
2013-8-19
相图测定方法
二元相图是根据各种成分材料的临界点绘制的，临界点 表示物质结构状态发生本质变化的相变点。 • 动态法
– 热分析法 – 膨胀法 – 电阻法
• 静态法
– 金相法 – X射线结构分析
精确测定相图需多种方法配合使用
2013-8-19
下面介绍用热分析法测量临界点来绘制二元相图的过程。
(4)相界线走向规则：当两相区与单相区的分界线与三相等温线相交 ，则分界线的延长线应进入另一两相区内，而不会进入单相区内。
2013-8-19
7.3 二元相图分析
7.3.1 匀晶相图和固溶体凝固-匀晶相图 1. 匀晶相图
两组元无限互溶的条件： • 晶体结构相同 • 原子尺寸相近，尺寸差<15% • 相同的原子价 • 相似的电负性（化学亲和力）
7.2.4 从自由能—成分曲线推测相图 根据公切线原理可求出体系在某一温度下平衡相的成分。图7．7表 示由T1，T2，T3，T4及T5温度下液相(L)和固相(S)的自由能一成分 曲线求得A，B两组元完全互溶的相图。
2013-8-19
图7．8表示了由5 个不同温度下L，α 和β 相的自由能一成分曲线求 得A，B两组元形成共晶系的相图。
组元B(x1)
组元B(x2)
混 合 物
α相 (n1摩尔，Gm1)
＋
β相 (n2摩尔，Gm2)
2013-8-19
混合物中B组元的摩尔分数(x):
n1 x1 n2 x2 x n1 n2
n1Gm1 n2Gm 2 Gm n1 n2
n1 x2 x n2 x x1
n1 Gm 2 Gm n2 Gm Gm1
x1 x x2
x2 x1 ( x2 x) ( x x1 )
相图测定方法
二元相图是根据各种成分材料的临界点绘制的，临界点 表示物质结构状态发生本质变化的相变点。 • 动态法
– 热分析法 – 膨胀法 – 电阻法
• 静态法
– 金相法 – X射线结构分析
精确测定相图需多种方法配合使用
2013-8-19
下面介绍用热分析法测量临界点来绘制二元相图的过程。
(4)相界线走向规则：当两相区与单相区的分界线与三相等温线相交 ，则分界线的延长线应进入另一两相区内，而不会进入单相区内。
2013-8-19
7.3 二元相图分析
7.3.1 匀晶相图和固溶体凝固-匀晶相图 1. 匀晶相图
两组元无限互溶的条件： • 晶体结构相同 • 原子尺寸相近，尺寸差<15% • 相同的原子价 • 相似的电负性（化学亲和力）
7.2.4 从自由能—成分曲线推测相图 根据公切线原理可求出体系在某一温度下平衡相的成分。图7．7表 示由T1，T2，T3，T4及T5温度下液相(L)和固相(S)的自由能一成分 曲线求得A，B两组元完全互溶的相图。
2013-8-19
图7．8表示了由5 个不同温度下L，α 和β 相的自由能一成分曲线求 得A，B两组元形成共晶系的相图。
组元B(x1)
组元B(x2)
混 合 物
α相 (n1摩尔，Gm1)
＋
β相 (n2摩尔，Gm2)
2013-8-19
混合物中B组元的摩尔分数(x):
n1 x1 n2 x2 x n1 n2
n1Gm1 n2Gm 2 Gm n1 n2
n1 x2 x n2 x x1
n1 Gm 2 Gm n2 Gm Gm1
x1 x x2
x2 x1 ( x2 x) ( x x1 )
7.3 二元相图分析(1)
第七章 二元系相图及其合金凝固
7.3.2 共晶相图及合金凝固
组成共晶相图（the eutectic phase diagram）的两组元的相互作用的特 点是:液态下两组元能无限互溶，固态下只能部分互溶(形成有限固溶体或化 合物)，甚至有时完全不溶，并具有共晶转变(the eutectic reaction)。 共晶转变是在一定条件下(温度、成分不变)，由均匀液体中同时结晶出两 种不同固相的转变。即：L→α+β 具有共晶转变的相图称为共晶相图。 所得到两固相的混合物称为共晶组织(eutectic structure)，其特点是两 相交替细弥混合，其形态与合金的特性及冷却速度有关，通常呈片层状。
过共晶合金的平衡结晶的显微组织
第七章 二元系相图及其合金凝固
共晶系合金的平衡凝固小结
• 共晶系合金的平衡凝固分为两类：固溶体合金和共晶型合金。前者的结 晶的组织为初生固溶体和次生组织；后者的结晶的组织为初生固溶体、共晶 体和次生组织。在室温时合金是由α和β两个基本相构成。 • 组织组成物是在结晶过程中形成的，有清晰轮廓的独立组成部分，如上 述组织中α、αⅡ、β、βⅡ、(α +β)都是组织组成物。相组成物是指组 成显微组织的基本相，它有确定的成分及结构但没有形态上的概念，上述各 类合金在室温的相组成物都是α相和β相。 • 不同成分范围的合金，室温的相组成除固溶体区外其余都是α+β，而 组织组成不相同 。图中6个组织区分别为： Ⅰ区：α单相组织； Ⅱ区： α+βⅡ ；Ⅲ区：α+βⅡ+(α+β) 共 ；Ⅳ区：(α+β) 共 ；Ⅴ区：β+αⅡ+ (α+β)共；Ⅵ区：β+αⅡ
第七章 二元系相图及其合金凝固
二元相图分析
ω (aM ) =
×100% =
×100% = 45.4%
亚共晶合金
最终室温组织为a 最终室温组织为 初+(a+ β)+ βⅡ
过共晶合金
成分位于E,N两点之间的合金。其平衡凝固过程及 两点之间的合金。 成分位于 两点之间的合金 平衡组织与亚共晶合金相似，只是初相为β固溶体 平衡组织与亚共晶合金相似，只是初相为 固溶体 而不是a固溶体 而不是 固溶体
在大多数情况下，由包晶反应所形成的β相倾向于依附初生相α 在大多数情况下，由包晶反应所形成的β相倾向于依附初生相α的表面形 以降低形核功，并消耗液相和α相而生长。 相被新生的β 核，以降低形核功，并消耗液相和α相而生长。当α相被新生的β相包围 以后， 相就不能直接与液相L接触。 Pt-Ag合金相图可知 液相中的Ag 合金相图可知， 以后，α相就不能直接与液相L接触。由Pt-Ag合金相图可知，液相中的Ag 含量较β相高， 相的Ag含量又比α相高，因此，液相中Ag Ag含量又比 Ag原子不断通 含量较β相高，而β相的Ag含量又比α相高，因此，液相中Ag原子不断通 相向α相扩散， 相的Pt原子以反方向通过β相向液相扩散， Pt原子以反方向通过 过β一 过程示于右图中。这样， 相同时向液相和α相方向生长， 过程示于右图中。这样，β相同时向液相和α相方向生长，直至把液相和 相全部吞食为止。由于β 包围初生相α α相全部吞食为止。由于β相是在 包围初生相α，并使之与液相隔开的 形式下生长的，故称之为包晶反应。 形式下生长的，故称之为包晶反应。
Cu-Ni相图及 相图及NiO-MgO相图 相图及 相图
固溶体的平衡凝固
平衡凝固是指凝固过程中的每个阶段都能达到平衡，即 在相变过程中有充分的时间进行组元间的扩散，以达到 平衡相的成分．现以w(Ni)为30%的Cu-Ni合金为例来描 述平衡凝固过程． 合金需略低于t 合金需略低于 温度
第7章二元相图2PPT课件
1）相图分析 两点：纯组元的熔点 两条曲线：液相线、固相线 三个区域：液相区、固相区
液、固两相并存区
Cu-Ni相图
23
2）匀晶相图 的其它类型
图7.5 具有极小点与极大点的相图 （a）具有极小点 (b) 具有极大点
极值点合金自由度：f＝c－p＋1＝1－2＋1＝0，恒温转变
1）相界线是相平衡的体现，平衡相成分 沿相界线随温度而变； 2）二元相图中，相邻相区的相数差为1 （点接触除外）－－相区接触法则； 3）二元相图中的三相平衡必为一条水平 线，表示恒温反应； 4）当两相区与单相区的分界线与三相等 温线相交，则分界线的延长线进入另一 两相区内，而不会进入单相区； 5）如果两个恒温转变中有两个是相同的 相，那么在这两条水平线之间一定是由 这两个相组成的两相区。
9
10
关于相图的几个概念
液相线：由凝固开始温度连接起来 的相界线 固相线：由凝固结束温度连接起来 的相界线 相 区：由相界线划分出来的区域
液相区、固相区、液固两相共存区
11
§7. 2 相图热力学的基本要点
一、固溶体的自由能－成分曲线 二、多相平衡的公切线原理 三、混合物的自由能和杠杆法则 四、从自由能－成分曲线推测相图 五、二元相图的几何规律
３）当 ｘ１<ｘ<ｘ２时,α＋β体系能量最低。
16
三、混合物的自由能和杠杆法则
2.杠杆法则
Gm1
Gm Gm2
x1
x x2
两相的相对含量： α相
β相
17
杠杆法则—适用于两相平衡
W ASW BR
连结线tie line
MSMLR
w
x2 x x2 x1
18
四、从自由能－成分曲线推测相图
液、固两相并存区
Cu-Ni相图
23
2）匀晶相图 的其它类型
图7.5 具有极小点与极大点的相图 （a）具有极小点 (b) 具有极大点
极值点合金自由度：f＝c－p＋1＝1－2＋1＝0，恒温转变
1）相界线是相平衡的体现，平衡相成分 沿相界线随温度而变； 2）二元相图中，相邻相区的相数差为1 （点接触除外）－－相区接触法则； 3）二元相图中的三相平衡必为一条水平 线，表示恒温反应； 4）当两相区与单相区的分界线与三相等 温线相交，则分界线的延长线进入另一 两相区内，而不会进入单相区； 5）如果两个恒温转变中有两个是相同的 相，那么在这两条水平线之间一定是由 这两个相组成的两相区。
9
10
关于相图的几个概念
液相线：由凝固开始温度连接起来 的相界线 固相线：由凝固结束温度连接起来 的相界线 相 区：由相界线划分出来的区域
液相区、固相区、液固两相共存区
11
§7. 2 相图热力学的基本要点
一、固溶体的自由能－成分曲线 二、多相平衡的公切线原理 三、混合物的自由能和杠杆法则 四、从自由能－成分曲线推测相图 五、二元相图的几何规律
３）当 ｘ１<ｘ<ｘ２时,α＋β体系能量最低。
16
三、混合物的自由能和杠杆法则
2.杠杆法则
Gm1
Gm Gm2
x1
x x2
两相的相对含量： α相
β相
17
杠杆法则—适用于两相平衡
W ASW BR
连结线tie line
MSMLR
w
x2 x x2 x1
18
四、从自由能－成分曲线推测相图
第七章_二元相图习题 - 副本
1. 常见二元合金相图的基本类型
1
4. 杠杆定律在Fe－C相图中的应用
2
1
K’ 1. 分别计算在共析温度下和室温时珠光体中相的相对重量百分比。 共析温度下：Qa= SK / PK = [(6.69-0.77)/(6.69-0.0218)]*100% = 88.8 % QFe3C = 100 % - 88.8% = 11.2 % 室温下：Qa= S’K’ / QK’ = [(6.69-0.77)/(6.69-0.0008)]*100% = 88.5 % QFe3C = 100 % - 88.5% = 11.5 %
3
2
K’
2. 计算45钢(含碳量为0.45％)在室温下相和组织组成物的相对重量百分比。 相组成：Qa= 2K’ / QK’ = [(6.69-0.45)/(6.69-0.0008)]*100% = 93.3 % QFe3C = 100 % - 93.3% = 6.7 % 组织组成：Qa= 2S’ / QS’ = [(0.77-0.45)/(0.77-0.0008)]*100% = 41.6 % QP = 100 % - 41.6% = 58.4 %
4.0％的过共析钢在室温下组织组成物的相对重量百分比，以及 在过共析钢区域范围内能够析出的Fe3CII的最大百分比。 组织组成：QFe3CII= 3S’ / S’K’ = [(1-0.77)/(6.69-0.77)]*100% = 3.9 % QP = 100 % - 3.9 % = 96.1 % Fe3CII最大百分比：QFe3CII= E’S’ / S’K’ = [(2.11-0.77)/(6.690.77)]*100% = 22.6 %
= 13.4 %
QP = 100 % - QLe’ - QFe3CII = 46 %
1
4. 杠杆定律在Fe－C相图中的应用
2
1
K’ 1. 分别计算在共析温度下和室温时珠光体中相的相对重量百分比。 共析温度下：Qa= SK / PK = [(6.69-0.77)/(6.69-0.0218)]*100% = 88.8 % QFe3C = 100 % - 88.8% = 11.2 % 室温下：Qa= S’K’ / QK’ = [(6.69-0.77)/(6.69-0.0008)]*100% = 88.5 % QFe3C = 100 % - 88.5% = 11.5 %
3
2
K’
2. 计算45钢(含碳量为0.45％)在室温下相和组织组成物的相对重量百分比。 相组成：Qa= 2K’ / QK’ = [(6.69-0.45)/(6.69-0.0008)]*100% = 93.3 % QFe3C = 100 % - 93.3% = 6.7 % 组织组成：Qa= 2S’ / QS’ = [(0.77-0.45)/(0.77-0.0008)]*100% = 41.6 % QP = 100 % - 41.6% = 58.4 %
4.0％的过共析钢在室温下组织组成物的相对重量百分比，以及 在过共析钢区域范围内能够析出的Fe3CII的最大百分比。 组织组成：QFe3CII= 3S’ / S’K’ = [(1-0.77)/(6.69-0.77)]*100% = 3.9 % QP = 100 % - 3.9 % = 96.1 % Fe3CII最大百分比：QFe3CII= E’S’ / S’K’ = [(2.11-0.77)/(6.690.77)]*100% = 22.6 %
= 13.4 %
QP = 100 % - QLe’ - QFe3CII = 46 %
胡赓祥《材料科学基础》第3版章节题库(二元系相图和合金的凝固与制备原理)【圣才出品】
2．为什么拉伸能提高结晶高分子的结晶度？ 答：由ΔG＝ΔH－TΔS 可知，自由能ΔG 必须小于零，结晶过程才能自发进行。物质从 非晶态到晶态，其中分子的排列是从无序到有序的过程，熵总是减小的，即ΔS＜0，此时－ TΔS＞0，而ΔH＜0（放热）。要使ΔG＜0，必须|ΔH|＞T|ΔS|。若某些高分子从非晶相到晶 相，|ΔS|很大，而结晶的热效应ΔH 很小，要使|ΔH|＞T|ΔS|只有两种途径：降低 T 或降低| ΔS|。但过分降低温度则分子流动困难，可能变成玻璃态而不结晶。若降低|ΔS|，可采用在 结晶前对高分子进行拉伸，使高分子链在非晶相中已经具有一定的有序性，这样，结晶时相 应的|ΔS|变小，使结晶能够进行。所以对结晶高分子，拉伸有利于提高结晶度。例如：天然 橡胶在常温下结晶需要几十年，而拉伸时只要几秒钟就能结晶。
3．简述高分子合金化的方法和优点。
2 / 31
圣才电子书 十万种考研考证电子书、题库视频学习平台
答：高分子合金是由两种以上组元聚合的复合体。 高分子合金的制备方法可以分为物理方法和化学方法。物理共混法包括干粉共混、熔融 共混及乳凝共混等方法，最常用的是熔融共混。化学共混法主要有共聚-共混法和互穿聚合 物网络法。 高分子通过合金化，可克服单组元高分子（均聚物）的某些性能的弱点，例如：聚丙烯 （PP）低温容易脆裂，但通过与顺丁胶（BR）共混合可明显提高聚丙烯的韧性；还可拓宽 高分子的用途。
4．指出下列相图中的错误（如图 7-1 所示），并加以改正。
答：如图 7-2 所示。
图 7-1
3 / 31
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 7-2 （1）任何温度下所作的连接线两端必须分别相交于液相线和固相线，不能相交于单一 液相线或单一固相线。 （2）A 组元的凝固温度恒定，所以液、固相线在 A 成分处相交于一点。 （3）在两元系的三相平衡反应中，三相的成分是唯一的。 （4）在两元系只能出现三相平衡反应。 5．根据图 7-3 分析，为什么含碳量小于 0.8%时随着含碳量增加临界冷却速度降低？ 而含碳量大于 1.0%时随着含碳量增加临界冷却速度升高？
材料科学基础-第7章2合金相图
8
8
Figure Solidification, precipitation, and microstructure of a Pb-10% Sn alloy. Some dispersion strengthening occurs as the β solid precipitates.
9
9
Example SOLUTION
Phases in the Lead–Tin (Pb-Sn) Phase Diagram
Determine (a) the solubility of tin in solid lead at 100oC, (b) the maximum solubility of lead in solid tin, (c) the amount of β that forms if a Pb-10% Sn alloy is cooled to 0oC, (d) the masses of tin contained in the α and β phases, and (e) mass of lead contained in the α and β phases. Assume that the total mass of the Pb-10% Sn alloy is 100 grams.
6
6
Figure Solidification, precipitation, and microstructure of a Pb10% Sn alloy. Some dispersion strengthening occurs as the β solid precipitates.
7
7
Example
22
22
第七章 二元系相图
2ቤተ መጻሕፍቲ ባይዱ 固溶体的平衡凝固－B
固溶体的凝固与纯金属的凝固相比有两个 显著特点： ⑴.固溶体合金凝固时结晶出来的固相成分 与原液相成分不同。上述结晶出的晶体与母相 化学成分不同的结晶称为异分结晶 ( 又称选择 结晶 ) ；纯金属凝固结晶时结晶出的晶体与母 相化学成分完全一样称为同分结晶 ⑵.固溶体凝固需要一定的温度范围，在此 温度范围内，只能结晶出一定数量的固相。
由一系列自由能曲线求得两组元 组成匀晶系的相图
由一系列自由能曲线求得两组元组成共晶系的相图
7.2.5 二元相图的几何规律
二元相图应遵循如下规律: (1) 相图中所有的线条都代表发生相转变的温度和平衡 相的成分，所以相界线是相平衡的体现，平衡相的成分必 须沿着相界线随温度而变化。 (2) 两个单相区之间必定有一个由该两相组成的两相区 分开，而不能以一条线接界(即两个单相区只能交于一点而 不能交于一条线)。两个两相区必须以单相区或三相水平线 分开。即 : 在二元相图中，相邻相区的相数差为 1 ，这个规 则为相区接触法则。 (3) 二元相图中的三相平衡必为一条水平线，表示恒温 反应。在这条水平线上存在3个表示平衡相的成分点，其中 两点在水平线两端，另一点在端点之间，水平线的上下方 分别与3个两相区相接。 (4) 当两相区与单相区的分界线与三相等温线相交则分 界线的延长线应进入另一两相区内，而不会进入单相区。
第七章 二元系相图 及其合金凝固
本章要求
1. 几种基本相图： 匀晶相图（Cu-Ni合金相图）、 共 晶相图（Pb-Sn合金相图）、包晶相图（Pt-Ag合金相 图）。 2. 相律，杠杆定律及其应用。 3. 二元合金相图中的几种平衡反应： 共晶反应、共析 反应、包晶反应、包析反应 、偏晶反应、熔晶反应、 合晶反应。 4. 二元合金相图中合金的结晶转变过程及转变组织。 5. 熟练掌握Fe-Fe3C相图。熟悉Fe-C合金中各相与组织 的结构。会几种典型Fe-C合金的冷却过程分析 。熟练 杠杆定律在Fe-C合金的应用。
第7-3章二元系相图
38
当w(c)>1%时，渗碳体形成连续网状分布于晶界，则合金
的塑性和韧性显著下降，脆性增加，致使抗拉强度也随
之降低。
在白口铸铁中，由于含有大量的渗碳体，故脆性很大，
强度很低。
39
例1、同样形状和大小的两块铁碳合金，其中一块是低碳钢， 一块是白口铸铁。试问用什么简便方法可迅速将它们区分 开来？ 答：由于两种合金的含碳量不同，使它们具有不同的特性。 最显著的是硬度不同，低碳钢含碳量低，硬度低，韧性好； 白口铸铁含碳量高，硬度高，脆性大。若从这方面考虑， 可以有多种方法，如
7
8
9
10
②ω c=0.77%的合金（共析钢）：结晶过程
共析钢室温时的平衡组织为珠光体。
室温时珠光体中铁素体和渗碳体的相对量可由杠杆法则求得：
珠光体的层片间距随冷却速度增大而减小，珠光体层片越细， 其强度越高，塑性和韧性也越好。 片状珠光体呈片层状两相的机械混合物，经球化退火后渗碳 体可呈球状分布在铁素体基体上，称为粒状珠光体。 粒状珠光体的强度比片状珠光体低，但塑性和韧性比其好。
4.3 0.0008 w(Fe 3C ) 100 % 64.2% 6.69 0.0008 4.3 2.11 w(Fe3C 共晶 ) 100 % 47.8% 6.69 2.11
26
2.11 0.77 6.69 - 4.3 w(Fe 3C ) 100 % 11.8% 6.69 0.77 6.69 - 2.11
27
28
⑥ω c=3.0%的合金（亚共晶白口铸铁）：结晶过程
29
亚共晶白口铸铁室温时的平衡组织为室温莱氏体+珠光体+ 二次渗碳体。其相对量为：
当w(c)>1%时，渗碳体形成连续网状分布于晶界，则合金
的塑性和韧性显著下降，脆性增加，致使抗拉强度也随
之降低。
在白口铸铁中，由于含有大量的渗碳体，故脆性很大，
强度很低。
39
例1、同样形状和大小的两块铁碳合金，其中一块是低碳钢， 一块是白口铸铁。试问用什么简便方法可迅速将它们区分 开来？ 答：由于两种合金的含碳量不同，使它们具有不同的特性。 最显著的是硬度不同，低碳钢含碳量低，硬度低，韧性好； 白口铸铁含碳量高，硬度高，脆性大。若从这方面考虑， 可以有多种方法，如
7
8
9
10
②ω c=0.77%的合金（共析钢）：结晶过程
共析钢室温时的平衡组织为珠光体。
室温时珠光体中铁素体和渗碳体的相对量可由杠杆法则求得：
珠光体的层片间距随冷却速度增大而减小，珠光体层片越细， 其强度越高，塑性和韧性也越好。 片状珠光体呈片层状两相的机械混合物，经球化退火后渗碳 体可呈球状分布在铁素体基体上，称为粒状珠光体。 粒状珠光体的强度比片状珠光体低，但塑性和韧性比其好。
4.3 0.0008 w(Fe 3C ) 100 % 64.2% 6.69 0.0008 4.3 2.11 w(Fe3C 共晶 ) 100 % 47.8% 6.69 2.11
26
2.11 0.77 6.69 - 4.3 w(Fe 3C ) 100 % 11.8% 6.69 0.77 6.69 - 2.11
27
28
⑥ω c=3.0%的合金（亚共晶白口铸铁）：结晶过程
29
亚共晶白口铸铁室温时的平衡组织为室温莱氏体+珠光体+ 二次渗碳体。其相对量为：
材料科学基础第七章1.1
2、相图的类型和结构
(1)二组元在液态无限溶解，在固态无限固溶，并形成连 续固溶体的匀晶相图。 (2)二组元在液态无限溶解，在固态有限固溶，并有共晶 反应的共晶相图。 (3)二组元在液态无限溶解，在固态有限固溶，有包晶反 应的包晶相图。 (4)二组元在液态无限溶解，在固态形成化合物的相图。 (5)二组元在液态无限溶解，在固态有共析或包析转变的 相图。 (6)二组元在液态有限溶解，并有偏晶或合晶反应的相图。 (7)其他相图。
5、二元相图的几何规律
(1) 相图中所有的线条都代表发生相转变 的温度和平衡相的成分，所以相界线是相平 衡的体现，平衡相的成分必须沿着相界线随 温度而变化。 (2) 两个单相区之间必定有一个由该两相 组成的两相区分开，而不能以一条线接界(即 两个单相区只能交于一点而不能交于一条线)。 两个两相区必须以单相区或三相水平线分开。 即:在二元相图中，相邻相区的相数差为1， 这个规则为相区接触法则。
具有匀晶转变的二元合金系主要有：Cu-Ni，FeCr，Ag-Au，W-Mo，Nb-Ti，Cr-Mo，Cd-Mg， Pt-Rh等。 属于二元匀晶相图的二元陶瓷有NiO－CoO、CoO －MgO、NiO－MgO等.
一、平衡凝固 平衡凝固（equilibrium solidification） 是指凝固过程是在无限缓慢地冷却，原 子(组元)扩散能够充分进行以达到相平 衡的成分。这种凝固方式所得到的组织 称为平衡组织。
两个单相区只能交于一点而不能交于一条线
5、二元相图的几何规律
(3) 二元相图中的三相平衡必为一条水平线， 表示恒温反应。在这条水平线上存在3个表示 平衡相的成分点，其中两点在水平线两端， 另一点在端点之间，水平线的上下方分别与3 个两相区相接。 (4) 当两相区与单相区的分界线与三相等温 线相交则分界线的延长线应进入另一两相区 内，而不会进入单相区。
二元系相图
CP w 100% CD
PD wL 100% CD
室温平衡组织 w 3 F 100% w G 3 100% 相对量 GF GF
对于包晶点成分合金，即将发生包晶反应时，
CP w 100% CD
wL CP w PD
发生包晶反应时， β相的成分在P点，液相L
（1）形成稳定化合物的相图
Mg-Si相图
（1）形成稳定化合物的相图
Cd-Sb相图
（2）形成不稳定化合物的相图
K-Na相图
5.具有固态相变的相图 （1）具有共析转变 的相图 Cu-Sn相图
（2）具有固溶体 多晶型转变 的相图 Fe-Ti相图
四、二元相图的几何规律 1.两个单相区只能有一个点接触；
三、二元系相图的类型
1.匀晶相图（Isomorphous system) 由液相结晶出单相固溶体的过程称为匀晶转变。 当两个组元化学性质相近，晶体结构相同，晶格 常数相差不大时，它们不仅可以在液态或熔融态完全 互溶，而且在固态也完全互溶，形成成分连续可变的 固溶体，称为无限固溶体或连续固溶体，它们形成的 相图即为匀晶相图。
w w d w man ce jg 100% cd fg
③亚共晶合金
合金Ⅲ w(Sn）＝50％
2
从一个固溶体中析出另一个固相——脱溶。次 生的 固溶体以 表示（ ）。
室温下 相组成物 ,
组织组成物 ( )
（共晶型）
反应式 Lα+β
相图特征
共析转变
偏晶转变 熔晶转变 包晶转变
γα+β
L1L2+α δγ+L L+βα γ+βα L1+L2α
材料科学基础 第7章 其他类型的二元相图
其他类型的二元相图
1. 具有化合物的二元相图 2. 具有偏晶转变的相图 3. 具有合晶转变的相图 4. 具有熔晶转变的相图 5. 具有固态转变的二元相图
1. 具有化合物的二元相图
在某些二元系中，可形成一个或多个化合 物，化合物一般处于相图的中间位置，又称 为中间相（intermediate phase）。根据两 组元间形成化合物的稳定性，可分为：
复杂二元相图的分析方法
分析复杂二元相图的步骤和方法如下：
(1) 首先看相图中是否存在化合物，如有稳定化合物，则以这 些稳定化合物为界(把化合物视为组元)，把相图分成几个区域 (基本相图)进行分析。(2)Biblioteka 根据相区接触法则，认清各相区的组成相。
组成二元相图的基本单元有单相区、两相区和三相水平线。这 些单元根据相区接触法则组合在一起。
(4) 应用相图分析典型合金的组晶过程和组织变化规 律。
单相区；相成分、质量与原合金相同。
双相区；在不同温度下两相成分沿相界线变化，各相 的相对量可由杠杆法则求得。
三相共存(平衡)时，三个相的成分固定不变，可用杠 杆法则求出恒温转变前、后相组成的相对量。
二元相图恒温转变类型
恒温转变类型
反应式
转变特征：是在一定温度下从一 个液相中同时分解出一个固相和 另一成分的液相的过程，且固相 的相对量总是偏多。 即：
L1→A+L2
3.具有合晶转变的相图
合晶转变（syntectic reaction）相图(图7.41)特点：二元 组在液态下有限溶解，存在不熔合线，不熔合线以下的两液相 L1和L2。
Mg-Si合金, 就能形成稳定化合物Mg2Si。Mg-Si合金相图 属于含有稳定化合物的相图。
在分析将整个Mg-Si相图可分为Mg-Mg2Si和Mg2Si-Si两个相图来进行分析
1. 具有化合物的二元相图 2. 具有偏晶转变的相图 3. 具有合晶转变的相图 4. 具有熔晶转变的相图 5. 具有固态转变的二元相图
1. 具有化合物的二元相图
在某些二元系中，可形成一个或多个化合 物，化合物一般处于相图的中间位置，又称 为中间相（intermediate phase）。根据两 组元间形成化合物的稳定性，可分为：
复杂二元相图的分析方法
分析复杂二元相图的步骤和方法如下：
(1) 首先看相图中是否存在化合物，如有稳定化合物，则以这 些稳定化合物为界(把化合物视为组元)，把相图分成几个区域 (基本相图)进行分析。(2)Biblioteka 根据相区接触法则，认清各相区的组成相。
组成二元相图的基本单元有单相区、两相区和三相水平线。这 些单元根据相区接触法则组合在一起。
(4) 应用相图分析典型合金的组晶过程和组织变化规 律。
单相区；相成分、质量与原合金相同。
双相区；在不同温度下两相成分沿相界线变化，各相 的相对量可由杠杆法则求得。
三相共存(平衡)时，三个相的成分固定不变，可用杠 杆法则求出恒温转变前、后相组成的相对量。
二元相图恒温转变类型
恒温转变类型
反应式
转变特征：是在一定温度下从一 个液相中同时分解出一个固相和 另一成分的液相的过程，且固相 的相对量总是偏多。 即：
L1→A+L2
3.具有合晶转变的相图
合晶转变（syntectic reaction）相图(图7.41)特点：二元 组在液态下有限溶解，存在不熔合线，不熔合线以下的两液相 L1和L2。
Mg-Si合金, 就能形成稳定化合物Mg2Si。Mg-Si合金相图 属于含有稳定化合物的相图。
在分析将整个Mg-Si相图可分为Mg-Mg2Si和Mg2Si-Si两个相图来进行分析
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
四、二元相图的几何规律
� (3)
二元相图中的三相平衡必为一条水平 线，表示恒温反应。在这条水平线上存在 3个 线，表示恒温反应。在这条水平线上存在3 表示平衡相的成分点，其中两点在水平线两 端，另一点在端点之间，水平线的上下方分 3个两相区相接。 别与 别与3 (4) 当两相区与单相区的分界线与三相等 � 温线相交则分界线的延长线应进入另一两相 区内，而不会进入单相区。
7.3.1匀晶相图
2.固溶体的平衡凝固 T2温度 温度降至 温度降至T •凝固出的固相成分沿 α2 ，与之 固相线变至 固相线变至α 平衡的液相成分则沿液 相线变至 L2 相线变至L
7.3.1匀晶相图
2.固溶体的平衡凝固
T2温度 温度降至 温度降至T 两相的含量为
;
a 2o L2 % = 100% L2a 2
四、二元相图的几何规律
: 二元相图应遵循如下规律 二元相图应遵循如下规律: (1) 相图中所有的线条都代表发生相转变的温度 � 和平衡相的成分，所以相界线是相平衡的体现， 平 衡相的成分必须沿着相界线随温度而变化。 � (2) 两个单相区之间必定有一个由该两相组成的 (即两个单相区只 两相区分开，而不能以一条线接界 两相区分开，而不能以一条线接界( )。两个两相区必须以 能交于一点而不能交于一条线 能交于一点而不能交于一条线) :在二元相图中，相邻 单相区或三相水平线分开。即 单相区或三相水平线分开。即: 1，这个规则为相区接触法则。 相区的相数差为 相区的相数差为1
31.5 35
42.5
C0 - CL R 35 - 31.5 Wa % = = = = 32% R + S Ca - CL 42.5 - 31.5
7.3.1匀晶相图
依赖原子互相扩散达到成分均匀，凝固速度比纯金属慢
结晶中的原子扩散
1.匀晶过程动画
7.3.1匀晶相图
固溶体凝固与纯金属凝固的比较
凝固得到的固相成分与液相不一致 固相成分 不 ，先凝固的与后凝固的 ，先凝固的与后凝固的固相成分 固相成分不 一致的现象
�
课堂作业
判断左边相图的正 3. 3.判断左边相图的正 误，说明为什么是错 的，并改正。 4. 二元相图中的三相平 4.二元相图中的三相平 衡反应为什么是在恒 温下进行的。 二元合金正常凝固和 5. 5.二元合金正常凝固和 平衡凝固是否相同？ 说明两者之间的相同 和不同之处。
7.3二元相图分析
7.3.1匀晶相图 7.3.2共晶相图 7.3.3包晶相图 7.3.5具有其他类型的二元相图
7.3.1匀晶相图
3.固溶体的非平衡凝固
•
每一温度下固相平均成分点连接起 来，得到固相平均成分线，在固相 线的下方
固相线与冷却速度无关，位置固定 固相平均成分线随冷速的改变而移动
• •
冷速愈大，偏离固相线愈远 冷却极慢（平衡凝固）与固相 线重合
7.3.1匀晶相图
3.固溶体的非平衡凝固
依赖原子互相扩散达到成分均匀，凝固速度比纯金属慢
80% Bi ， x2：含 20%Cd Cd，
重量百分数和原子百分数
AA x A wA = 100% AA x A + AB xB
AB xB wB = 100% AA x A + AB xB
WB AB xB = 100% WA AA + WB AB
WA和WB表示A和B组元的质量分数 AA和AB表示A和B组元的摩尔量 XA和XB表示A和B组元的摩尔分数
如：0%Cu、20%Cu、40%Cu、60%Cu、80%Cu、100%Cu 六组合金。
Cu20% Cu60%Cu80% Cu Ni Cu40%
1600
1500
1400
1400 1300
L
（L+ α）
T
1200
1200 1100
1000
1000 900
α
0 20 40 60 80 100
800
t
800
第7章二元系相图及其合金的凝固
二元相图
合金
�
两种以上 的金属和非金属熔合（或烧结）在一起而具 两种以上的金属和非金属熔合（或烧结）在一起而具 有金属特性 的物质 金属特性的物质 (四元以上 ) 分二元合金、三元合金，多元合金 分二元合金、三元合金，多元合金( 四元以上)
�
合金相图
�
用图的形式表明一个合金系的成份、温度和相态之间 的关系
在微观体积内 高于或低于平 均成分的现象
7.3.1匀晶相图
固溶体平衡凝固的三个过程
（1）液体内的扩散过程 （2）固相的继续长大 （3）固相内的扩散过程
7.3.1匀晶相图
3.固溶体的非平衡凝固
：冷速快，固相不能均匀化 不平衡原因 不平衡原因：冷速快，固相不能均匀化
7.3.1匀晶相图
3.固溶体的非平衡凝固
Ag-Cu 共晶相图及合金的凝固 Ag-Cu共晶相图及合金的凝固
7.3.2共晶相图
1.共晶相图
E 点：共晶点 共晶点E ，纯组元熔点 ，最大溶解度 点
Ag-Cu共晶相图及合金的凝固
液相线 共晶线
和BE 线 AE AE和 BE线
固相线
和BD AC AC和
三相平衡 LE→αC＋βD，亦为固相线，自由度 CED, CED,三相平衡 三相平衡L 为零，温度和相成分都恒定不变 和DG ：α和β固溶体的溶解度随温度的降低而减少 CF CF和 DG：
合金品种
金属材料合金品种非常多
�
种元素配制合金，任取三种元素组成的 80 80种元素配制合金，任取三种元素组成的 三元合金系有 80 ×79 ×78/3 ×2=82160 种 三元合金系有80 80× 79× 78/3× 2=82160种 各组元的相对含 每一合金系中还可以改变 每一合金系中还可以改变各组元的相对含 形成许多合金品种 量， 量，形成许多合金品种
Cu-Ni合金相图的建立
WCu(%)
二、热分析法测绘Cu-Ni二元相图
测定合金的冷却（或加热）曲线 1. 选取代表性合金，测 1.选取代表性合金，测 绘其冷却曲线，获得 相变临界点
2. 将同类临界点成分 -温 2.将同类临界点成分 将同类临界点成分度图上连接
Cu-Ni二元相图形成动画
二、热分析法测绘Cu-Ni二元相图
线的合金，凝固时 CD CD线的合金，凝固时 有共晶反应 亚共晶合金
C、E之间的 成分在 成分在C 合金属于亚共晶合金
Ag-Cu共晶相图及合金的凝固
课堂练习
1、根据二元相图相区接触规则， � A 两个单相区之间必定有一个三相区隔开 � B 两个两相区必须以单相区或三相水平线隔开 � C 三相水平线和四个两相区相邻 � 2、根据相律，二元系三相平衡时自由度为0.即表明 三相反应是在恒温下进行,三个平衡相的成分也是相 同的，不可改变。 � A 正确 � B 错误
L2o a 2% = 100% L2a 2
7.3.1匀晶相图
2.固溶体的平衡凝固 再降温，凝固过程 继续进行
;
T4 温度降至 温度降至T
•
遇到固相线，凝固 完毕 α4 ，相 固相成分为 固相成分为α 当于原合金成分，为 α固溶体晶粒 均匀的 均匀的α
•
7.3.1匀晶相图
例（如图）
;
Ca - C0 S WL % = = R + S Ca - CL 42.5 - 35 = = 68% 42.5 - 31.5
液相线 液相区 T,°C
1500 1400 1300 1200 1100 1000
L
1455 L+ α
纯镍 熔点
纯铜 熔点
1083
α
100
固相线 Ni
Cu 固相区 20 40 60 Ni% 80
液固两相区
三、杠杆定律
在二元合金相图的两相区内，温度一定时，两相的重量比是一定的。 C0，总重量为 1, 在T 合金成分为 合金成分为C ，总重量为1, 温度时，由液相和固相组成，液 CL,重量为 WL，固相成 相的成分为 相的成分为C 重量为W Cα,重量为 Wα。 份为 份为C 重量为W
�
) 合金成分为50%B，凝固到某温度 时液相含有40%B，固体含有80%B，此 时液体和固体各占多少分数？
�(d
2.指出下列相图中的错误，并加以改正。
7.3.2共晶相图
1.共晶相图
α和β，具有共晶 两组元在固态部分溶解，形成有限固溶体 两组元在固态部分溶解，形成有限固溶体α 转变 Ag-Cu、Pb-Sn、Al-Si、AlSn、Cd-Sn、Au-Pt…… Al-Sn
后凝固的晶体外层部分枝与枝之间（黑色）含铜量高
7.3.1匀晶相图
3.固溶体的非平衡凝固
通过扩散退火或均匀化退火消除晶内偏析
(a) Ni-Cu的组织经均匀化退火后的晶粒组织 的组织经均匀化退火后的晶粒组织(a) 及穿过晶粒的电子探针扫描图象 (b)
1. 固溶体合金的相图如图所示，试根据相图确定： (a) 成分为40%B的合金首 先凝固出来的固体成分； � (b) 若首先凝固出来的固体 成分含60%B，合金的成分 为多少？ � (c) 成分为70%B的合金最 后凝固的液体成分；
固溶度线
7.3.2共晶相图
1.共晶相图
单相区 两相区
3个，自由度ƒ=2 ， =2， 3个，ƒ=1
如T0温度 α和β相的 温度α k和h 成分分别为 成分分别为k 三相区 一条水平线
2 共晶系合金的平衡凝固和组织
D点右边的合金属 C点左边和 点左边和D 于固溶体合金
�
固3.1匀晶相图
1.匀晶相图 液态 和固态 下均 无限互溶 时所构成的相图称二元匀晶相图。 两组元在 两组元在液态 液态和 固态下均 下均无限互溶 无限互溶时所构成的相图称二元匀晶相图。 以Cu-Ni 合金为例进行分析。 Cu-Ni合金为例进行分析。 L