沿程阻力损失系数表
沿程阻力系数表
在模型图中可以找到沿管道的阻力系数，即λ、re和K/D的关系曲线，这是液压系统中常用的。
K是管内壁的绝对粗糙度。
管道沿线水头损失计算：H=λ（L/D）[v^2/（2G）]对于管内层流：λ=64/re（雷诺数re=VD/ν）圆管粗糙过渡区：1/√（λ）=-2*LG[K/（3.7d）+2.51/re√（λ）]对于管的湍流粗糙区：1/√（λ）=-2*LG[K/（3.7d）]也可用作λ=0.11（K/D）^0.25还有许多经验公式：例如，钢管和铸铁管的Shevlev公式为：过渡粗糙区（V<1.2m/s）：λ=（0.0179/D^0.3）*（1+0.867/V）^0.3；阻力平方面积（V>=1.2m/s）：λ=0.21/D^0.3摩擦阻力：流体流经一定直径的直管时，由于流体的内摩擦而产生阻力。
电阻与距离的长度成正比。
简介在计算管道沿程阻力损失（直管阻力）的公式中，λ-摩擦系数与雷诺数Re和壁面粗糙度ε有关，可以通过实验测量或计算。
层流如何确定一个通道的阻力系数对于层流，可以从理论上严格推断。
在工程中，湍流的确定有两种方法：一种是基于湍流半经验理论结合实验结果，另一种是直接根据实验结果综合阻力系数的经验公式。
前者具有更一般的含义。
沿途阻力系数变化规律3-8计算沿途水头损失的经验公式3-3--8沿途水头损失的经验公式3-9局部水头损失3-9局部水头损失3-7沿程阻力系数的变化规律可从本章各节中了解。
对于层流，沿程阻力系数的规律是已知的。
到目前为止，还没有一个沿程阻力系数的理论公式。
为了探索沿程阻力系数的变化规律，尼古拉斯进行了一系列实验研究，揭示了沿途水头损失的规律。
下面介绍这一重要的实验研究成果。
1尼古拉斯试验条件。
管道的人工粗糙表面：在管壁上粘上相同尺寸的均匀砂粒。
注：此粗糙表面与天然粗糙表面完全不同。
相对粗糙度：Δ/r0相对平滑度：r0/ΔΔ=dr0沿途阻力系数试验装置。
管路沿程压力损失计算
������
0.013064026 0.000284966 0.019251026
1 1
0.855601136 0.147383647
*绿色区域是可以手动输入的区域，其他区域受保护，保护密码123 吸油管－－1m/s；压力油管－－5m/s；回油管－－3m/s。λ =(64/2000),液压油密度选取 900kg/m³ 管道主要损失分为沿程损失和局部损失。 Δ h=Σ λ L/d*（v²/2g）+Σ ξ v²/2g。其中的λ 和ξ 都是系数，这个是需要在手册上查询的。 L-------管路长度。 d-------管道内径。 v-------有效断面上的平均流速，一般 v=Q/s，其中Q是流量，S是管道的内截面积
管路沿程压力损失计算
q(l/min) 260 内径d（mm） 管道容量 压力损失MPa(未计 V(L) 算局部压力损失) 32 5.38836109 48.25214862 0.78392975 流速v(m/s)
局部压力损失计算
q(l/min) 260 60 30 50 70 800 850 400 内径d（mm） 32 40 10 19 10 20 32 22 流速v(m/s) 5.38805806 0.79577473 6.36619783 2.93914951 14.8544616 42.4413189 17.6148052 17.5377351 局部阻力系 数ζ 1 1 1 局部压力பைடு நூலகம்失Mpa
管路长度 （m） 60
备注
Δ������_������=ζ 备注
2000),液压油密度选取
是需要在手册上查询的。
管路沿程阻力计算
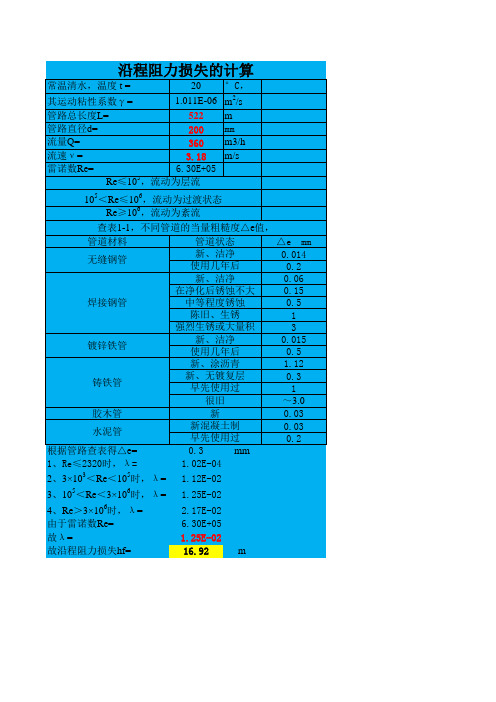
1.25E-02 2.17E-02 6.30E+05 1.25E-02 16.92
m
沿程阻力损失的计算
常温清水，温度 t = 其运动粘性系数γ = 管路总长度L= 管路直径d= 流量Q= 流速ν = 雷诺数Re= 20 1.011E-0E+05 °C， m2/s m mm m3/h m/s
Re≤105，流动为层流 105＜Re≤106，流动为过渡状态 Re≥106，流动为紊流 查表1-1，不同管道的当量粗糙度△e值， 管道状态 管道材料 △e mm 新、洁净 0.014 无缝钢管 使用几年后 0.2 新、洁净 0.06 在净化后锈蚀不大 0.15 焊接钢管 中等程度锈蚀 0.5 陈旧、生锈 1 强烈生锈或大量积垢 3 新、洁净 0.015 镀锌铁管 使用几年后 0.5 新、涂沥青 1.12 新、无镀复层 0.3 铸铁管 早先使用过 1 ～3.0 很旧 新 0.03 胶木管 新混凝土制 0.03 水泥管 早先使用过 0.2 根据管路查表得△e= 0.3 mm 1、Re≤2320时，λ = 1.02E-04 3 5 2、3× 10 ＜Re＜10 时，λ = 1.12E-02 3、105＜Re＜3× 106时，λ = 4、Re＞3× 10 时，λ = 由于雷诺数Re= 故λ = 故沿程阻力损失hf=
管道阻力计算表格
紊流
7 工业管道当量糙粒高度（K）
mm
0.15
查的
8
工业管道相对粗糙度
/
0.001
9 查莫迪图沿程阻力系数（λ）
0.020
查的
10பைடு நூலகம்
紊流下限
m/s 0.035053333 和流速比较
11
紊流上限
m/s 1.418066667 和流速比较
12
管内流水的流速大于紊流上限值：λ=0.11*（K/d)0.25
13
管内流水的流速上下限值之间：λ=0.11*（K/d+68/Re)0.25
14
管内流水的流速小于下限值：λ=0.3164/Re0.25
15
沿程阻力系数（λ）
/
0.020
大于上限值
16
沿程阻力系数（λ）
/
0.020
上限值之间
17
沿程阻力系数（λ）
/
0.01208
小于下限值
18
沿程阻力损失（m）H=λ×L/d×υ2/2g
序号 1 2 3 4 5
名称 管内水的流速（υ）
管道直径(d） 运动粘度（ν） 动力粘度（η）
密度（ρ）
单位 m/s mm 10-6m2/s 10-6pa·s kg/m³
数值 1.5 150 0.478 469.9 983.2
备注
50℃水查的 50℃水查的 50℃水查的
6
雷诺数（Re）
/
470711
25 当量直径de=4R。当量直径应用到沿程阻力计算和雷诺数计算的公式中。
26
沿程阻力：H=λ×L/de×υ2/2g
27
雷诺数：Re=υde/ν
注：1、铝管和铜管当量粗糙度K≤0.01；2、玻璃管当量粗糙度K≤0.01；3、普通钢 管当量粗糙度K=0.02~0.1；4、镀锌钢管当量粗糙度K=0.15；5、生锈钢管当量粗糙 度K=0.5~1.0；6、铸铁管当量粗糙度K=0.25；7、塑料管当量粗糙度K=0.05；8、具 有轻度腐蚀的无缝钢管K=0.2~0.3；9、具有腐蚀的无缝钢管K=0.5以上；
管道阻力计算表格
2.25 0.15 Re=υdρ/η Re=υd/ν
19.6 圆面积公式：πr2 圆周长公式：πd
19
沿程阻力损失（Pa）P=λ×L/d×ρυ2/2
20
管道长度（L)
m
100
N/kg
21
重力系数（g）
（m/s2)
9.8
地球表面附近
22
沿程阻力损失（m）
m
1.4970
23
非圆管道内沿程损失：水力半径：R=A/χ[A:过流断面面积；χ：过流断面接 触即润湿固体壁面部分的周长]
24 圆管水力半径：R=d/4[d:管道直径]；矩形管水力半径：R=ab/2（a+b）；
25 当量直径de=4R。当量直径应用到沿程阻力计算和雷诺数计算的公式中。
26
沿程阻力：H=λ×L/de×υ2/2g
27
雷诺数：Re=υde/ν
注：1、铝管和铜管当量粗糙度K≤0.01；2、玻璃管当量粗糙度K≤0.01；3、普通钢 管当量粗糙度K=0.02~0.1；4、镀锌钢管当量粗糙度K=0.15；5、生锈钢管当量粗糙 度K=0.5~1.0；6、铸铁管当量粗糙度K=0.25；7、塑料管当量粗糙度K=0.05；8、具 有轻度腐蚀的无缝钢管K=0.2~0.3；9、具有腐蚀的无缝钢管K=0.5以上；
紊流
7 工业管道当量糙粒高度（K）
mm
0.15
查的
8
工业管道相对粗糙度
/
0.001
9 查莫迪图沿程阻力系数（λ）
0.020
查的
10
紊流下限Biblioteka m/s 0.035053333 和流速比较
11
紊流上限
m/s 1.418066667 和流速比较
管道水力损失计算
140~150
当量粗糙度 △（mm）
-
-
-
-
0.010~0.030
3. 管道（渠）局部水力损失宜按下式计算：
hj =
v2 2g
式中 ς
--- 管道（渠）局部水力损失系数
工程在可研阶段，根据管线的敷设情况，管道局部水头损失可按沿程水头损
失的 5%~10%计算。
配水管网水力平差计算，一般不考虑局部水头损失。
2. 管道（渠）沿程水力损失，可分别看下列公式计算：
（1）塑料管：
1）管道（渠）沿程水力损失计算：
式中
hy
λ
l
dj
v
g
hy
=
l dj
v2 2g
--- 管道（渠）沿程水力损失（m）
--- 沿程阻力系数
--- 管段长度（m）
--- 管道计算内径（m）
--- 管道断面水流平均流速（m/s）
--- 重力加速度（m/s2），取 g=9.81
2）沿程阻力系数计算：
=
0.304 Re0.239
Re = v dj
式中 λ Re l dj v µ
--- 沿程阻力系数 --- 雷诺数 --- 管段长度（m） --- 管道计算内径（m） --- 管道断面水流平均流速（m/s） --- 水中的运动粘滞度（m3/s）
水中的运动粘滞度在不同温度时可按下表选取。
水在不同温度是的 µ 值（×10-6）
水温（℃） 0
5
10 15 20 25 30 40
µ（m3/s） 1.78 1.52 1.31 1.14 1.00 0.89 0.80 0.66
（2）混凝土管（渠）及采用水泥砂浆内衬的金属管道：
阻力损失计算表给水手册版
管径DN 流速
流量（m3/min） 距离(m)
单位阻力损 局部损失系
失
数
沿程损失
1000 6.366198
5
50 0.033409257
2 1.670462845
800 5.96831
3
10 0.039271843
2 0.392718426
700 5.196896
2
10 0.035704454
2 0.357044537
沿程损失m
水力摩阻 系数
总水头损 失
局部损失
单位局部 损失
6.08792212 0.0391123 6.148801 0.062261 0.062261
1.43319033 0.0181131 1.461854 0.102862 0.051431
1.28962347 0.0165705 1.328312 0.186783 0.062261
沿程损失m
水力摩阻 系数
总水头损 失
局部损失
单位局部 损失
34.3305736 0.3433057 34.57962 0.249044 0.249044
10.4765482 0.1047655 10.76228 0.285728 0.142864
7.84268174 0.0784268 8.262944 0.420262 0.140087
管径DN 流速m/s 流量t/h
40 1.105243 65 1.004528 80 1.105243 100 1.414711 150 0.94314 200 0.884194 300 0.78595
管道阻部损失m 局部损失
5
100 0.060879221
沿程损失的简单分析
管道流动沿程损失的数值模拟及实验一、 背景流体在管道中流动时， 存在一定的能量损失，为克服摩擦阻力而损耗的能量称为沿程损失。
沿程损失与管道长度、管径、粗糙度及流体的流速都存在一定的关系。
二、原理如图所示，当流体从1点流至2点时，其流体的总能量（动能、压能和势能）将降低。
根据伯努利方程：2212112222l j V V p gz p gz E E ρρρρ++=++++（1.1）式中，111,,V p z 分别为1点处的流速、压强和高度；222,,V p z 分别为2点处的流速、压强和高度；ρ为流体的密度；g 为重力加速度；,l j E E 分别为沿程和局部能量损失。
沿程能量损失是指流体在直径不变的管道中流动，流动未发生急变时的能量损失。
用量纲分析的方法，沿程能量损失可用下面公式来计算：(Re)21),,,,(E 2λρμρd lV V d l f l ==，其中，l ，d 分别为管道的长度和直径；λ为沿程阻力系数，是雷诺数Re （Re Vd ν=，ν为流体的运动粘性系数）的函数。
三、 数值模拟用FLUENT 软件进行数值模拟，计算沿程阻力系数的方案：12（1）几何模型：建立三维管道模型，设置管径d=50mm ， l=20d=1m 如下图（1）：1 d 2图（1）（2）网格划分与计算：划分网格时，由于在边界上参量变化较大，边界层上网格应加密，设置相关系统参数后进行计算。
总体网格划分：边界层加密：·分析，直径d=0.5，根据边界 层与雷诺数和管道尺寸的关系2/1Re ~)(-d v d d δ，得出，边界层的厚度为0.01左右，如图 所示加密边界层。
lV（3）结果分析：对截面1、2进行分析，根据伯努利方程： 2212112222l j V V p gz p gz E E ρρρρ++=++++，由于从截面1到截面2没有截面突扩，没有高度差，管道尺寸也没有发生改变，则管道的局部损失0=j E ，两截面高度差021=-=∆z z z ，两截面处的速度V V V ==21，故沿程损失21p p E l -=，得沿程阻力系数221)(2lVdp p ρλ-=。
重大流体力学实验5(沿程水头损失)
1）关闭压差计连通管上的止水夹，全开流量调节阀，15秒时间测算流量、测读电测仪读数、测量水体的温度。
2）逐步关小循环水泵上的旁通阀，使电测仪读数第一次递增150cm，第二次关闭，分别记录相应数据。
五、实验过程原始记录(数据、图表、计算等)
沿程水头损失与沿程阻力系数计算表
序号
体积V/
时间t/s
371.14
27.4
0.00850
30000
103
7
1816
7.2
252.2
664.79
27.9
0.00840
55000
283
8
1534
4.8
319.6
842.46
28.5
0.00829
71000
407
六、实验结果及分析
流量Q/( /s)
流速v/(cm/s)
水温T/
黏度 /(c /s)
雷诺数Re
压差计读数
沿程水头损失 /cm
沿程阻力系数
Re<2000 =64/Re
1
460
180
2.56
6.75
24.8
0.009
520
23.6
23.3
0.3
0.12
2
808
180
4.49
11.84
25.9
0.00898
916
23.7
23.1
4、分析沿程阻力系数与雷诺数 的关系。
二、实验原理
两过流断面之间的总水头损失等于沿程损失，等于两断面的测压管水头差。 ，有压圆管流的沿程水头损失计算公式变为：
在层流运动中，沿程阻力系数为：
系统阻力表
沿程阻力损失计算公式 式中：L—风管长度，m。
py R0L
局部阻力损失计算公式
式中：ξ —局部阻力系数
p j
u2 2
(Pa)
天圆地方：0.17 21-23 26.80 2.01 13.33 196.8 90。弯头(2 个)：0.44 0.71 71.27 5.52 4
软连接：0.10 软连接：0.10
90。弯头 17-20 26.80 2.01 13．33 196.8 (2 个)：0.44 0.85 85.33 5.52 4
管段 标号
1-3
流量 (m3/s)
26.80
表 4-2 烟气净化系统阻力计算表
截面 流速 动压
积 (m2)程压力损失部分
局部阻力系数
局部阻 局部阻 单位摩 长度
力系数 力损失 擦阻力 总和 (pa) (pa/m) (m)
沿程阻 总阻力 力损失 (pa)
(pa)
天圆地方：0.17
2.01 13.33 196.8 90。弯头(2 个)：0.44 0.71 71.27 5.52 4 22.08 93.35
软连接：0.10
软连接：0.10
4-7 26.80 2.01 13．33 196.8
90。弯头
0.85 85.33 5.52 4 22.08 107.41
(2 个)：0.44
天圆地方：0.31 8-10 20.96 1.54 13.62 217.0 90。弯头（3 个） 0.66 66.26 7.74 18.3 141.64 207.90
11-12 41.92 3.14 13.35 209.6 三通：1.3 7
1.3 130.90 3.52 2
矩形风管道的沿程阻力及损失.ppt
R' （4DL2 ）2
mD
2
R''
1
（ L ）2
ab
m 4 ab
2
2(a b)
矩形风管道的沿程阻力及损失
2、矩形风管的沿程损失
注意：利用当量直径求矩形风管的沿程损失，要注意其对应 关系。 1）当采用流速当量直径时，必须采用矩形风管内的空气流速去查比摩阻； 2）当流量当量直径时，必须用矩形风管中的空气流量去查比摩阻。
矩形风管道的沿程阻力及损失
1、沿程损失 Pm
式中 ——摩擦阻力系数；
1 4Rs
v 2
2
l
v ——风道内空气的平均流速，m/s；
——空气的密度，kg/m3；
Rs
F P
l ——风道的长度，m；
ቤተ መጻሕፍቲ ባይዱ
Rs——风道的水力半径，m； F ——管道中充满流体部分的横断面积，m2；
P ——湿周，在通风系统中即为风管周长，m。
当流速与比摩阻均相同时，水力半径必相等，则有
Rs Rs
D 4
ab （2 a
b）
Dv
D
2ab ab
矩形风管道的沿程阻力及损失
2、矩形风管的沿程损失
② 流量当量直径（DL）
圆形风管流量
L D2v
4
v'
4L
D 2
矩形风管流量
L abv
v'' L ab
令
则
Rm Rm''
DL
D
1.2655
a3b3 ab
比摩阻：单位长度的摩擦阻力。
Rm
1 4Rs
v2
2
矩形风管道的沿程阻力及损失
铸铁管沿程阻力系数表
铸铁管沿程阻力系数表
摘要：
1.铸铁管的概述
2.铸铁管沿程阻力系数表的含义
3.铸铁管沿程阻力系数表的应用
4.铸铁管沿程阻力系数表的优点
5.铸铁管沿程阻力系数表的局限性
正文：
铸铁管是一种广泛应用于给排水、燃气输送等领域的管道材料。
由于其具有较高的抗压强度、抗腐蚀性和耐磨性，铸铁管在工程中有着广泛的应用。
铸铁管沿程阻力系数表是为了方便工程师在设计铸铁管道时，能够快速查找铸铁管在各种流速下的沿程阻力系数而制定的表格。
铸铁管沿程阻力系数表列出了不同管径、不同流速和不同介质条件下的沿程阻力系数。
这些数据可以帮助工程师在设计管道时，精确计算流体在管道中的摩擦阻力，从而优化管道设计，降低能耗，提高输送效率。
铸铁管沿程阻力系数表的优点主要体现在以下几点：
1.提高设计效率：通过查阅沿程阻力系数表，工程师可以快速获取所需的技术参数，节省了大量计算时间。
2.精确度高：沿程阻力系数表的数据经过科学计算和实验验证，具有较高的精确度。
3.适用范围广：铸铁管沿程阻力系数表覆盖了各种常见的管径、流速和介
质条件，可以满足多种工程需求。
然而，铸铁管沿程阻力系数表也存在一定的局限性：
1.对于特殊工况，如高温、高压或腐蚀性介质等，沿程阻力系数表可能无法提供合适的数据。
2.实际工程中，管道布置和流体性质可能会发生变化，这时需要对沿程阻力系数表的数据进行修正。
总之，铸铁管沿程阻力系数表为工程师提供了一种快速、准确地获取铸铁管道沿程阻力系数的方法，极大地提高了设计效率。