沿程摩擦阻力系数计算
沿程阻力系数表
在模型图中可以找到沿管道的阻力系数，即λ、re和K/D的关系曲线，这是液压系统中常用的。
K是管内壁的绝对粗糙度。
管道沿线水头损失计算：H=λ（L/D）[v^2/（2G）]对于管内层流：λ=64/re（雷诺数re=VD/ν）圆管粗糙过渡区：1/√（λ）=-2*LG[K/（3.7d）+2.51/re√（λ）]对于管的湍流粗糙区：1/√（λ）=-2*LG[K/（3.7d）]也可用作λ=0.11（K/D）^0.25还有许多经验公式：例如，钢管和铸铁管的Shevlev公式为：过渡粗糙区（V<1.2m/s）：λ=（0.0179/D^0.3）*（1+0.867/V）^0.3；阻力平方面积（V>=1.2m/s）：λ=0.21/D^0.3摩擦阻力：流体流经一定直径的直管时，由于流体的内摩擦而产生阻力。
电阻与距离的长度成正比。
简介在计算管道沿程阻力损失（直管阻力）的公式中，λ-摩擦系数与雷诺数Re和壁面粗糙度ε有关，可以通过实验测量或计算。
层流如何确定一个通道的阻力系数对于层流，可以从理论上严格推断。
在工程中，湍流的确定有两种方法：一种是基于湍流半经验理论结合实验结果，另一种是直接根据实验结果综合阻力系数的经验公式。
前者具有更一般的含义。
沿途阻力系数变化规律3-8计算沿途水头损失的经验公式3-3--8沿途水头损失的经验公式3-9局部水头损失3-9局部水头损失3-7沿程阻力系数的变化规律可从本章各节中了解。
对于层流，沿程阻力系数的规律是已知的。
到目前为止，还没有一个沿程阻力系数的理论公式。
为了探索沿程阻力系数的变化规律，尼古拉斯进行了一系列实验研究，揭示了沿途水头损失的规律。
下面介绍这一重要的实验研究成果。
1尼古拉斯试验条件。
管道的人工粗糙表面：在管壁上粘上相同尺寸的均匀砂粒。
注：此粗糙表面与天然粗糙表面完全不同。
相对粗糙度：Δ/r0相对平滑度：r0/ΔΔ=dr0沿途阻力系数试验装置。
矿井局部通风机选型计算参考(详细)
矿井局部通风机选型计算（详细计算方法介绍）仅供从事煤矿行业技术人员参考使用，并结合各自矿井相关参数，进行计算。
局部通风机选型一、风量计算1.按瓦斯涌出量计算：根据进风立井揭4#煤实测瓦斯涌出量为0.4 m3/min 进行计算，其公式如下：Q 掘=100×QCH4×K=100×0.4×2= 80m3/min其中：Q-掘进工作面需风量，k-掘进工作面的通风系数，取2，QCH4-掘进工作面的瓦斯绝对涌出量，m3/min 。
2． 按炸药量计算需风量：min /2661.14104847.266.030/8.7t 8.733223222m P L KAS Q =⨯⨯⨯=•=炸式中 Q 炸 ——按爆破炸药量计算的工作需风量，m3/min;t ——通风时间，取t=30min ;A —— 一次爆破最大炸药量，kg;S ——巷道断面，m 2;L---掘进巷道通风长度；P ——局部通风机吸入风量和掘进工作面风筒出口风量比，取P=1.1；k---井筒淋水修正系数,取0.6；3． 按最多工作人数计算Q 掘=4×N=4×50=200m 3/min式中 Q 掘—掘进工作面实际需要的风量，m 3/min ；N —掘进工作面同时工作的最多人数，取交接班时50人；4—每人供给的最小风量，m 3/min 。
4． 按最低风速进行计算：Q 掘=60VminSmax=60×0.3×33=594m3/min式中 Q 掘—掘进工作面实际需要的风量，m3/min ；Vmin —最低风速，按煤巷掘进工作面进行计算取0.25m/s ；Smax —巷道最大断面，考虑到进风大巷联络巷配风量，断面计算取22+（22/2）=33m 2。
根据计算取以上1、2、3、4式中最大值进行计算，即：594m 3/min 。
二、 局扇选型计算1.通风阻力计算：由于该通风系统为非负压通风，通风阻力为巷道通风阻力与风筒通风阻力之和。
管道摩擦阻力计算
长距离输水管道水力计算公式的选用1． 常用的水力计算公式:供水工程中的管道水力计算一般均按照均匀流计算,目前工程设计中普遍采用的管道水力计算公式有：达西（DARCY ）公式:gd v l h f 22**=λ（1）谢才（chezy ）公式:i R C v **= （2）海澄－威廉（HAZEN-WILIAMS ）公式：87.4852.1852.167.10dC lQ h h f ***= （3) 式中h f --———-—————-沿程损失,mλ―――沿程阻力系数 l ――管段长度,md —--——管道计算内径，m g--——重力加速度,m/s 2 C ——--谢才系数 i ——--水力坡降;R ―――水力半径，mQ ―――管道流量m/s 2 v ————流速 m/sC n -—--海澄――威廉系数其中大西公式，谢才公式对于管道和明渠的水力计算都适用。
海澄－威廉公式影响参数较小,作为一个传统公式，在国内外被广泛用于管网系统计算。
三种水力计算公式中 ，与管道内壁粗糙程度相关的系数均是影响计算结果的重要参数。
2． 规范中水力计算公式的规定3． 查阅室外给水设计规范及其他各管道设计规范，针对不同的设计条件，推荐采用的水力计算公式也有所差异，见表1：表1 各规范推荐采用的水力计算公式4． 公式的适用范围： 3．1达西公式达西公式是基于圆管层流运动推导出来的均匀流沿程损失普遍计算公式，该式适用于任何截面形状的光滑或粗糙管内的层流和紊流.公式中沿程阻力系数λ值的确定是水头损失计算的关键，一般采用经验公式计算得出。
舍维列夫公式，布拉修斯公式及柯列勃洛克（C 。
F.COLEBROOK ）公式均是针对工业管道条件计算λ值的著名经验公式。
舍维列夫公式的导出条件是水温10℃，运动粘度1。
3*10—6 m 2/s,适用于旧钢管和旧铸铁管，紊流过渡区及粗糙度区.该公式在国内运用教广. 柯列勃洛可公式)Re 51.27.3lg(21λλ+∆*-=d (Δ为当量粗糙度，Re 为雷诺数）是根据大量工业管道试验资料提出的工业管道过渡区λ值计算公式，该式实际上是泥古拉兹光滑区公式和粗糙区公式的结合，适用范围为4000<Re 〈108.大量的试验结果表明柯列勃洛克公式与实际商用圆管的阻力试验结果吻合良好，不仅包含了光滑管区和完全粗糙管区,而且覆盖了整个过渡粗糙区，该公式在国外得到及为广泛的应用。
风管沿程阻力计算公式
风管沿程阻力计算公式
风管阻力是指风管内风流的摩擦阻力和弯曲阻力，计算风管沿程
阻力需要结合多个因素，如风管形状、风速、管道长度、管道内壁粗
糙度等。
一般来说，风管沿程阻力的计算公式包括：Darcy–Weisbach公式、Colebrook公式、Fanning公式等。
其中，Darcy–Weisbach公式比较
常用，其公式为：hf = f * (L/D) * (V^2/2g)。
其中，hf表示风管沿程阻力，f表示风管内的摩擦系数，L表示风管长度，D表示风管内直径，V表示风速，g表示重力加速度。
在实际应用中，为了更精确地计算风管沿程阻力，需要进行多次
实验和数据处理。
一般来说，可以利用CFD（计算流体动力学）软件进行模拟计算；也可以通过测试仪器测量风管内流体的速度、温度、压
力等参数，来计算阻力。
此外，在设计风管系统时，还需要充分考虑
风管的材料、管道的连接方式、管道附属设备等因素，以保证系统的
安全、稳定运行。
总之，风管沿程阻力计算是设计和优化风管系统的重要环节，应
该进行充分的实验和计算，并结合系统的实际情况，进行合理的改进
和调整，以确保系统的运行效率和稳定性。
管路沿程阻力计算
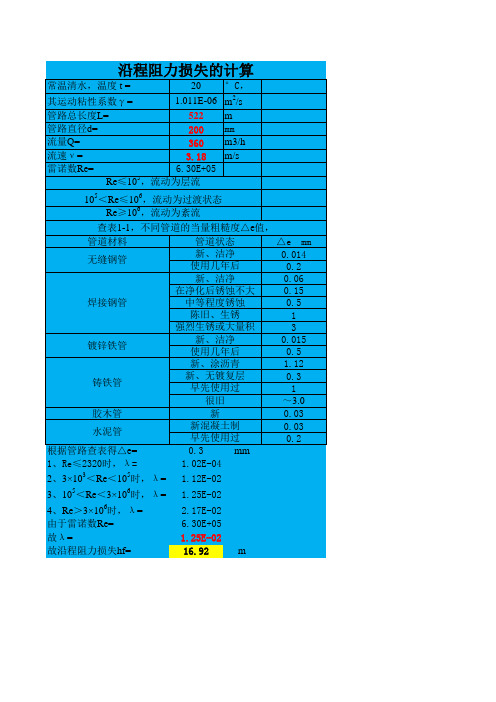
1.25E-02 2.17E-02 6.30E+05 1.25E-02 16.92
m
沿程阻力损失的计算
常温清水，温度 t = 其运动粘性系数γ = 管路总长度L= 管路直径d= 流量Q= 流速ν = 雷诺数Re= 20 1.011E-0E+05 °C， m2/s m mm m3/h m/s
Re≤105，流动为层流 105＜Re≤106，流动为过渡状态 Re≥106，流动为紊流 查表1-1，不同管道的当量粗糙度△e值， 管道状态 管道材料 △e mm 新、洁净 0.014 无缝钢管 使用几年后 0.2 新、洁净 0.06 在净化后锈蚀不大 0.15 焊接钢管 中等程度锈蚀 0.5 陈旧、生锈 1 强烈生锈或大量积垢 3 新、洁净 0.015 镀锌铁管 使用几年后 0.5 新、涂沥青 1.12 新、无镀复层 0.3 铸铁管 早先使用过 1 ～3.0 很旧 新 0.03 胶木管 新混凝土制 0.03 水泥管 早先使用过 0.2 根据管路查表得△e= 0.3 mm 1、Re≤2320时，λ = 1.02E-04 3 5 2、3× 10 ＜Re＜10 时，λ = 1.12E-02 3、105＜Re＜3× 106时，λ = 4、Re＞3× 10 时，λ = 由于雷诺数Re= 故λ = 故沿程阻力损失hf=
圆管稳流过渡区的沿程阻力系数
圆管稳流过渡区的沿程阻力系数一、引言圆管稳流过渡区的沿程阻力系数是指在圆管内，当流动从一种状态转变为另一种状态时，由于流动的不连续性所引起的局部阻力损失。
这种不连续性主要是由于管道几何形状的变化或者流速的变化所引起的。
本文将介绍圆管稳流过渡区的沿程阻力系数。
二、理论分析1. 流动状态转变在管道内，当流速发生改变或者管道截面积发生改变时，都会导致流动状态发生改变。
对于稳定的非压缩性流体来说，在圆管中，当雷诺数Re>2300时，就会从层流转变为湍流。
而在湍流状态下，能量将被输送到较小尺度上，并且会产生很多涡旋和涡核。
2. 沿程阻力系数计算沿程阻力系数是指在圆管中，由于局部阻力损失所引起的总体阻力损失与无局部阻力损失时所需能量之比。
其计算公式为：ΔP = fρLV²/2D其中ΔP为压降；f为沿程阻力系数；ρ为流体密度；L为管道长度；V 为平均流速；D为管道直径。
可以看出，沿程阻力系数f与管道的几何形状、流量、雷诺数等因素有关。
对于圆管而言，在层流状态下，沿程阻力系数f可表示为：f = 64/Re在湍流状态下，沿程阻力系数f可表示为：1/√f = -2.0log(ε/D/3.7 + 2.51/Re√f)其中ε为相对粗糙度。
三、实验验证1. 实验装置本文采用的实验装置如下图所示：2. 实验步骤（1）将水泵启动，并将水导向进入圆管中。
（2）调整水泵出口阀门，使得水流量稳定在一定范围内。
（3）测量不同位置的压力差，并记录数据。
（4）根据实验数据计算出沿程阻力系数。
3. 实验结果及分析本文进行了多次实验，并得到了如下的实验结果：可以看出，在湍流状态下，随着雷诺数的增加，沿程阻力系数也会增加。
而在层流状态下，沿程阻力系数与雷诺数成反比关系。
相对粗糙度ε也会影响沿程阻力系数的大小。
四、结论本文介绍了圆管稳流过渡区的沿程阻力系数的理论分析和实验验证。
实验结果表明，在湍流状态下，沿程阻力系数随着雷诺数的增加而增加。
风管阻力计算
通风管道阻力计算对于空调通风专业来说，我们最终的目的是让整个系统达到或接近设计及业主的要求。
对于整套空调系统而言主要应该把握几个关键的参数：风量、温度、湿度、洁净度等。
可见无论空调是否对新风做处理，我们送到房间的风量是一定要达到要求。
否则别的就更不用考虑了。
管道内风量主要是由风管内阻力影响的。
风管内空气流动的阻力有两种，一种是由于空气本身的粘滞性及其与管壁间的摩擦而产生的沿程能量损失，称为摩擦阻力或沿程阻力；另一种是空气流经风管中的管件及设备时，由于流速的大小和方向变化以及产生涡流造成比较集中的能量损失，称为局部阻力。
下边为标准工况且没有扰动的情况下的计算，如实际不是标准工况且有扰动需要进行修正。
一：摩擦阻力(沿程阻力)计算摩擦阻力(沿程阻力)计算一：（公式推导法）根据流体力学原理，无论矩形还是圆形风管空气在横断面形状不变的管道内流动时的摩擦阻力(沿程阻力) 按下式计算：ΔPm=λν2ρL/2D以上各式中：ΔPm———摩擦阻力(沿程阻力)，Pa。
λ————摩擦阻力系数【λ根据流体不同情况而改变不具有规律性，不可用纯公式计算，只能靠实验得到许多不同状态的半经验公式：其中最常用的公式为：，《K-管壁的当量绝对粗糙度，mm （见表1-1）；D-风管当量直径，mm(见一下介绍) ；Re雷诺数判断流体流动状态的准则数,（见表1-1）；其实λ一般由莫台图所得，见图】莫台曲线图表1-1 一般通风管道中K、Re、λ的经验取值ν————风管内空气的平均流速，m/s; 【其中ν=Q/F；Q为管内风量m3/S，F为管道断面积M2 ；其中矩形风管F=a×b;圆形风管F=πD2 /4，一般设计也直接选风速见表1-2】表1-2 一般通风系统中常用空气流速（m/s）ρ————空气的密度，Kg/m3;【在压力B0=101.3kPa、温度t0=20℃、一般情况下取ρ=1.205Kg/m3; 见表1-3】L ———风管长度，m 【横断面形状不变的管道长度】D———风管的当量直径，m; 【矩形风管流速当量直径：；流量当量直径：；圆形风管D为风管直径】摩擦阻力(沿程阻力)计算二：（比摩阻法）由以上计算看出计算V和D较容易而计算λ难度很大，所以我们选择查表更合适快捷。
紊流过渡区的沿程阻力系数
紊流过渡区的沿程阻力系数紊流过渡区是指在河流或管道中，当流速增大到一定程度时，流体的运动状态从层流转变为紊流的过程。
在紊流过渡区，由于涡旋的形成和湍流的发展，会产生较大的阻力。
沿程阻力系数是描述紊流过渡区中阻力大小的一个参数。
一、紊流过渡区的定义和特点1. 紊流过渡区定义：当河流或管道中的液体运动状态由层流转变为紊流时，称之为紊流过渡区。
在这个区域内，液体分子之间的相互作用变得复杂，并且出现了湍动和涡旋。
2. 特点：- 流速增大：在紊流过渡区内，由于湍动和涡旋的形成，使得整个系统内部能量损失增加，从而导致总阻力增大。
- 液体混合：在紊流过渡区内，不同层次的液体会发生混合，使得整个系统内部物质交换更加充分。
- 阻力波动：由于湍动和涡旋的存在，在紊流过渡区内阻力会产生周期性波动。
二、沿程阻力系数的定义和计算方法沿程阻力系数是用来描述紊流过渡区中阻力大小的一个参数。
它表示单位长度内的阻力与流体动能之比，通常用符号λ表示。
沿程阻力系数的计算方法有多种，其中一种常用的方法是利用Prandtl-Kármán公式：λ = (τw / (ρ * V^2)) * L其中，λ为沿程阻力系数，τw为壁面摩擦应力，ρ为液体密度，V为平均流速，L为参考长度。
三、影响紊流过渡区沿程阻力系数的因素1. 流速：流速是影响紊流过渡区沿程阻力系数的主要因素。
当流速增大时，紊流过渡区扩展并向上游延伸，导致沿程阻力系数增加。
2. 管道或河道形状：管道或河道的形状对紊流过渡区和沿程阻力系数有很大影响。
较粗短、光滑且直径变化小的管道或河道会减小紊流过渡区，并降低沿程阻力系数。
3. 粗糙度：管壁或水底的粗糙度也会影响紊流过渡区和沿程阻力系数。
较粗糙的壁面或水底会增加摩擦阻力，导致沿程阻力系数增大。
4. 流体性质：流体的黏度和密度也会对紊流过渡区和沿程阻力系数产生影响。
黏度较大的流体会增加摩擦阻力，导致沿程阻力系数增大。
5. 液面坡度：液面坡度对紊流过渡区和沿程阻力系数也有一定影响。
矿井局部通风机选型计算示例
矿井局部通风机选型计算示例一、风量计算1、按瓦斯涌出量计算：根据进风立井揭4#煤实测瓦斯涌出量为0.4m3/min进行计算，其公式如下：Q掘=100×QCH4×K=100×0.4×2=80m3/min其中：Q-掘进工作面需风量，k-掘进工作面的通风系数，取2，QCH4-掘进工作面的瓦斯绝对涌出量，m3/min。
2、按炸药量计算需风量：式中Q炸——按爆破炸药量计算的工作需风量，m3/min；t——通风时间，取t=30min；A——一次爆破最大炸药量，kg；S——巷道断面，m2；L---掘进巷道通风长度；P——局部通风机吸入风量和掘进工作面风筒出口风量比，取P=1.1；k---井筒淋水修正系数,取0.6；3、按最多工作人数计算Q掘=4×N=4×50=200m3/min式中Q掘—掘进工作面实际需要的风量，m3/min；N—掘进工作面同时工作的最多人数，取交接班时50人；4—每人供给的最小风量，m3/min。
4、按最低风速进行计算：Q 掘=60VminSmax=60×0.3×33=594m 3/min式中Q 掘—掘进工作面实际需要的风量，m 3/min ；Vmin —最低风速，按煤巷掘进工作面进行计算取0.25m/s ；Smax —巷道最大断面，考虑到进风大巷联络巷配风量，断面计算取22+（22/2）=33m 2。
根据计算取以上1、2、3、4式中最大值进行计算，即：594m 3/min 。
二、局扇选型计算1.通风阻力计算：由于该通风系统为非负压通风，通风阻力为巷道通风阻力与风筒通风阻力之和。
1.1巷道通风阻力计算：R 巷道=R 井筒+R 进风大巷+R 集中胶带上山R 井筒=（α×L ×P/S 3）×K=（0.003×310×22/26.93）×1.2=0.0013R 井筒－风筒的阻力，N ×s 2÷m 8；α－摩擦阻力系数0.003L －巷道长度310mP －巷道周长22mS －巷道的净断面38.5-8.9=26.9m 2K －风压系数，包括局部阻力等因素，取1.2。
层流沿程水头损失公式
层流沿程水头损失公式其中：- h_f为沿程水头损失。
- λ为沿程阻力系数，对于层流，λ = (64)/(Re)，这里Re为雷诺数，Re=(vd)/(ν)（v为断面平均流速，d为管径，ν为运动黏滞系数）。
- l为管长。
- d为管道直径。
- v为管内平均流速。
- g为重力加速度。
在学习这个公式时，以下几点很关键：一、公式各参数的物理意义。
1. 沿程阻力系数λ- 在层流状态下，λ与雷诺数Re成反比。
雷诺数是一个无量纲数，它反映了水流的流态是层流还是紊流。
当水流为层流时，通过理论分析可以得出λ=(64)/(Re)。
这表明层流的沿程阻力系数只与雷诺数有关，而雷诺数又取决于流速、管径和流体的运动黏滞系数。
2. 管长l和管径d- 管长l表示流体在管道中流动的距离。
沿程水头损失与管长成正比，这意味着在其他条件相同的情况下，管道越长，沿程水头损失越大。
- 管径d对沿程水头损失有着重要影响。
从公式中可以看出，沿程水头损失与管径成反比。
管径越小，水流受到的摩擦阻力相对越大，沿程水头损失也就越大。
3. 流速v和重力加速度g- 流速v的大小直接影响着沿程水头损失。
流速越大，水流的动能越大，与管壁以及流层之间的摩擦作用也越强，从而导致沿程水头损失增大。
- 重力加速度g是一个常量，在地球上不同地点略有差异，但在一般工程计算中取9.8m/s^2或近似值10m/s^2。
它在公式中的存在是由于水头损失概念与能量概念相关，在能量方程的推导过程中涉及到重力势能的转化等因素。
二、公式的应用示例。
1. 已知条件求解沿程水头损失。
- 例如，已知某圆管中水流为层流，管长l = 10m，管径d=0.1m，流速v = 0.1m/s，水的运动黏滞系数ν = 1×10^-6m^2/s。
- 首先计算雷诺数Re=(vd)/(ν)=(0.1×0.1)/(1×10^-6) = 10000。
- 然后计算沿程阻力系数λ=(64)/(Re)=(64)/(10000)=0.0064。
经常用到的给排水流体力学计算公式
经常用到的给排水流体力学计算公式：
1、h f=(λL/d)*(v2/2g)
h f ——流段的沿程水头损失（m液柱或气柱）
L——流段的长度（m）
d——管段的直径（m）
v——流体的流动速度（m/s）
λ——沿程阻力系数（或摩擦阻力系数），在层流运动中，该值可根据λ=64/Re求出。
给水工程经常采用钢管和铸铁管，由于管内壁容易锈蚀和积垢，所以管壁的粗糙度按旧钢管和铸铁管考虑，并为一个常数。
管内水流温度一般为10℃左右，运动粘度也可以为一个常数。
这样是的沿程阻力系数λ的经验计算公式比较简单，在紊流区内：
v＜1.2 m/s时，λ=(0.0179/d0.3)*(1+0.867/ v)0.3
v≥1.2 m/s时，λ=0.021/ d0.3
上式中，d为管道的内径（m），不是公称直径；v为流速（m/s）。
2、v=(1/n)R2/3i1/2
n——粗糙系数
R——过流断面的水利半径（m）
i——渠底或管底的坡度
常用材料的粗糙系数n值。
通风管道阻力的计算与公式
风管内空气流动的阻力有两种，一种是由于空气本身的粘滞性及其与管壁间的摩擦而产生的沿程能量损失，称为摩擦阻力或沿程阻力；另一种是空气流经风管中的管件及设备时，由于流速的大小和方向变化以及产生涡流造成比较集中的能量损失，称为局部阻力。
一、摩擦阻力根据流体力学原理，空气在横断面形状不变的管道内流动时的摩擦阻力按下式计算：ΔPm=λν2ρl/8Rs对于圆形风管，摩擦阻力计算公式可改写为：ΔPm=λν2ρl/2D圆形风管单位长度的摩擦阻力（比摩阻）为：Rs=λν2ρ/2D以上各式中λ————摩擦阻力系数ν————风管内空气的平均流速，m/s;ρ————空气的密度，Kg/m3;l ————风管长度，mRs————风管的水力半径，m;Rs=f/Pf————管道中充满流体部分的横断面积，m2；P————湿周，在通风、空调系统中既为风管的周长，m；D————圆形风管直径，m。
矩形风管的摩擦阻力计算我们日常用的风阻线图是根据圆形风管得出的，为利用该图进行矩形风管计算，需先把矩形风管断面尺寸折算成相当的圆形风管直径，即折算成当量直径。
再由此求得矩形风管的单位长度摩擦阻力。
当量直径有流速当量直径和流量当量直径两种；流速当量直径：Dv=2ab/(a+b)流量当量直径：DL=1.3（ab）0.625/(a+b)0.25在利用风阻线图计算是，应注意其对应关系：采用流速当量直径时，必须用矩形中的空气流速去查出阻力；采用流量当量直径时，必须用矩形风管中的空气流量去查出阻力。
二、局部阻力当空气流动断面变化的管件（如各种变径管、风管进出口、阀门）、流向变化的管件（弯头）流量变化的管件（如三通、四通、风管的侧面送、排风口）都会产生局部阻力。
局部阻力按下式计算：Z=ξν2ρ/2ξ————局部阻力系数。
局部阻力在通风、空调系统中占有较大的比例，在设计时应加以注意，为了减小局部阻力，通常采用以下措施：1. 弯头布置管道时，应尽量取直线，减少弯头。
水流状态与沿程阻力系数
1、按平均水温60℃计，密度ρ=983.28，运动粘度ν=0.478，管壁粗糙度k=0.2(室内钢管)、0.5(室外钢管)、0.05（塑料管）。 2、流速V=353.68G/(d2ρ)，雷诺数Re=1000Vd/ν，沿程阻力系数λ由流态及管壁状态和运动粘度决定，比摩阻R=500λρV2/d。 3、当Re≤2300，为层流λ=64/Re。当Re＞2300为紊流：Re＜20d/k（或V≤11ν/k）为紊流光滑区，λ=0.3164/Re0.25；当20d/k＜Re＜250d/k （或11ν/k＜V≤445ν/k）
管壁 运动粘度 流速V 粗糙 雷诺数 ν Re 度k m/s 20d/k 2 mm /s mm 钢管（流态主要考虑V和445ν /k的关系） 1409.8 DN40 41.00 983.28 0.30 0.2 0.478 25875 4100 1134.6 DN32 35.75 983.28 0.32 0.2 0.478 23882 3575 520.8 DN25 27.00 983.28 0.26 0.2 0.478 14515 2700 192.6 DN20 21.25 983.28 0.15 0.2 0.478 6820 2125 96.3 DN15 15.75 983.28 0.14 0.2 0.478 4601 1575 流量G kg/h 管材 规格 内径d mm 密度ρ 3 kg/m 塑管(地暖管为防气阻，V≥0.5，最小0.25） φ40× 1200.0 29.00 983.28 0.51 0.05 5.5 φ32× 800.0 23.20 983.28 0.53 0.05 4.4 φ25× 506.1 18.00 983.28 0.56 0.05 3.5 404.9 φ20×2 16.00 983.28 0.57 0.05 流态特征
风管沿程阻力计算方法
风管沿程阻力计算方法布质风管系统在沿管长方向上还有由于摩擦阻力和局部阻力造成的压力损失。
因为压力损失与风速成正比关系，当气流沿管长方向风速越来越小时，阻力损失也不断下降。
与此同时，风管个标准件以及出风口也存在局部阻力损失。
布质风管系统中以直管为主，系统中三通、弯头及变径很少，一般以沿程阻力损失为主，空气横断面形状不变的管道内流动时的沿程摩擦阻力按下式计算：——摩擦阻力系数；——风管内空气的平均流速，m/s；——空气的密度，kg/m3；——风管长度，m；——圆形风管直径（内径），m；摩擦阻力系数是一个不定值，它与空气在风管内的流动状态和风管管壁的粗糙度有关。
根据对纤维材料和布质风管系统的综合性研究得到摩擦阻力系数不大于0.024（铁皮风管大约0.019），由于布质风管风管延长度方向上都有送风孔，管内平均风速就是风管入口速度的1/2。
由此可见，布质风管风管的延程损失比传统铁皮风管要小的多。
部件局部压损计算当布质风管风管内气流通过弯头、变径、三通等等部件时，断面或流向发生了变化，同传统风管一样会产生相应的局部压力损失：Z：局部压力损失（pa）ξ：局部阻力系数（主要由试验测得，同传统风管中类似）ρ：空气密度（kg/m3）v：风速（m/s）为了减少布质风管系统的局部损失，我们通常进行一定的优化设计：1．综合多种因素选择管经，尽量降低管道内风速。
2．优化异形部件设计，避免流向改变过急、断面变化过快。
根据实际工程经验，我们总结出各种布质风管部件的局部阻力值（风速＝8m/s），如下表：弯头（曲率＝1）等径三通变径（渐缩角30度）静压箱10 pa 12 pa 3 pa 46 pa例如：某超市压损计算说明对于该超市，AHU 空调箱风量为36000CMH，选取编号AHU-14号空调箱系统，主管尺寸为2000*610mm，共有5支支管，支管管径为55 9mm。
选取最长不利环路25米主管+20.6米支管作为计算依据；1，沿程阻力损失计算：主管：25米，2000*610mm，当量直径，支管道：20.6米，559mm，，2，局部阻力损失计算：等径三通局部损失为12Pa，对于变径三通取20Pa.最长不利环路压损为20+8.5+6=34.5Pa.可见布质风管系统尤其是直管系统的沿程阻力损失非常小，一般不会超过静压复得的值，所以在粗算时基本可以忽略不计！。
气体沿程阻力计算公式
气体沿程阻力计算公式气体在管道中流动时，会受到阻力的影响。
这个阻力就叫做沿程阻力。
要计算气体的沿程阻力，咱们得先搞清楚一个重要的公式。
沿程阻力的计算公式是：$h_f = λ\frac{l}{d} \frac{v^2}{2g}$ 。
这里面的 $h_f$ 表示沿程阻力损失，λ 是沿程阻力系数，l 是管道长度，d 是管道内径，v 是气体流速，g 是重力加速度。
先来说说这个沿程阻力系数λ 。
它可不是个固定的值，得看气体在管道里的流动状态。
要是气体流动得很平稳，咱们叫它层流；要是乱哄哄的，那就是紊流。
层流的时候，λ 跟雷诺数 Re 有个简单的关系；紊流的时候，那就复杂啦，得参考各种图表和经验公式。
我记得有一次，在工厂里实习的时候，就碰到了跟气体沿程阻力有关的问题。
那是一个通风系统，负责给车间里输送新鲜空气。
可不知道为啥，总有几个区域的空气流通不太好。
师傅带着我们几个实习生去检查，发现原来是管道设计不太合理，导致气体沿程阻力过大。
我们拿着工具，一段一段地测量管道的长度、内径，还得估算气体的流速。
那过程可不轻松，得趴在地上，钻进狭小的空间，有时候还弄得一身灰。
好不容易把数据都收集齐了，就开始用沿程阻力计算公式来分析。
算出来才发现，有几段管道的沿程阻力损失远远超出了正常范围。
师傅就带着我们重新设计，调整管道的走向和直径，还更换了一些阻力比较小的管件。
经过一番努力，终于让通风系统正常工作了，车间里的空气也变得清新多啦。
再说说管道长度 l 。
这个比较好理解，管道越长，气体受到阻力的机会就越多，沿程阻力损失也就越大。
所以在设计管道系统的时候，要尽量缩短管道长度，走直线，少拐弯。
管道内径 d 也很关键。
内径越大，气体流动的空间就越宽敞，阻力就越小。
就好比是一条宽宽的马路和一条窄窄的小巷，车在宽马路上跑肯定更顺畅。
气体流速 v 呢，速度越快，阻力损失也会增加。
但也不是流速越小越好，流速太小了，可能满足不了实际的需求。
所以得找到一个合适的平衡点。
沿程摩擦阻力公式
沿程摩擦阻力公式沿程摩擦阻力公式在流体力学中可是个相当重要的概念呢！咱先来说说啥是沿程摩擦阻力。
想象一下，水在长长的水管里流动，或者空气在通风管道里穿梭，它们在流动的过程中会遇到管道内壁的阻碍，这种阻碍产生的力就叫沿程摩擦阻力。
沿程摩擦阻力公式就像是一把神奇的钥匙，能帮助我们算出这种阻力的大小。
常用的沿程摩擦阻力公式是达西 - 威斯巴赫公式：$h_f =\lambda \frac{l}{d} \frac{v^2}{2g}$ 。
这里面的 $h_f$ 表示沿程水头损失，$\lambda$ 是沿程阻力系数，$l$ 是管长，$d$ 是管径，$v$ 是平均流速，$g$ 是重力加速度。
那这个公式到底咋用呢？给您举个例子。
比如说，有一条 100 米长的水管，管径是 0.1 米，水在里面的平均流速是 2 米每秒，沿程阻力系数咱假设是 0.02，重力加速度取 9.8 米每二次方秒。
那咱们来算算沿程水头损失。
先把数值代入公式：$h_f = 0.02 \times \frac{100}{0.1} \times\frac{2^2}{2 \times 9.8}$ ，然后仔细算算，就能得出沿程水头损失的数值啦。
在实际生活中，这个公式用处可大了。
就像我之前遇到过一个事儿，小区的供水系统出了问题，水压老是不够。
维修师傅来了之后，就用这个沿程摩擦阻力公式来分析管道的情况。
他们测量了各种数据，管径啊、管长啊、水流速度啥的，然后通过公式计算，发现有一段管道因为使用时间太长，内壁变得粗糙，导致沿程阻力系数增大，从而影响了水压。
最后，他们更换了那段管道，小区的供水就恢复正常啦。
再比如说，在工业生产中，一些液体的输送管道设计也得依靠这个公式。
如果不考虑沿程摩擦阻力，可能会导致输送效率低下，甚至出现故障。
总之，沿程摩擦阻力公式虽然看起来有点复杂，但只要咱们理解了它的原理，掌握了使用方法，就能在很多实际问题中派上大用场，让我们更好地理解和优化各种流体流动的系统。
管道沿程阻力系数测定实验报告
管道沿程阻力系数测定实验报告
实验目的：测量管道沿程阻力系数，了解管道对流体流动产生的阻力。
实验原理：
在流体力学中，沿程阻力系数是用来描述管道内流体流动过程中的阻力大小的一个参数。
在管道内流动的过程中，由于流体与管道壁面之间的粘性，流体流动的阻力会导致流速的减小。
沿程阻力系数可以通过下面的公式来计算：
f = (ΔP × 2L)/(ρ ×
g × A × V^2)
其中，f为沿程阻力系数，ΔP为管道两侧压力差，L为管道长度，ρ为流体密度，g为重力加速度，A为管道横截面积，V 为流速。
实验步骤：
1. 将实验装置搭建起来，包括一段直管道、压力计、高度计和流量计等设备。
2. 在管道的一侧连接流量计，另一侧连接压力计。
3. 打开流速调节阀，调节流量计的流速。
4. 记录流量计的读数，即流速V。
5. 通过高度计测量管道两侧的压力差ΔP。
6. 测量管道的长度L和横截面积A。
7. 根据实验原理中的公式计算沿程阻力系数f。
实验结果与分析：
根据实验步骤中的测量数据，可计算得到沿程阻力系数。
通过多组实验数据的对比可以分析出管道内流体流动的阻力特性。
实验结果应该与理论值相符合，如果存在差异，可以进一步讨论可能的原因，如管道壁面的粗糙度等因素对流动阻力的影响。
结论：
本实验通过测量管道沿程阻力系数，了解了管道对流体流动产生的阻力大小。
实验结果与理论值的差异可以进一步讨论影响因素，为实际工程中的流体输送提供参考依据。
沿程压力损失计算公式及释义
沿程压力损失计算公式及释义
沿程压力损失指的是流体在管道中运动时，由于摩擦、弯头、阀门等因素导致的压力损失。
为了准确计算沿程压力损失，需要使用一些公式和参数来计算。
下面是沿程压力损失计算公式及释义：
1. 管道阻力系数公式：
K=ΔP/ρV^2/2
其中，K为管道阻力系数，ΔP为管道两端压力差，ρ为流体密度，V为流速。
2. 阻力系数公式：
f=K/D^4/L
其中，f为摩阻系数，K为管道阻力系数，D为管道内径，L为管道长度。
3. 摩阻系数公式：
f=16/Re
其中，f为摩阻系数，Re为雷诺数。
4. 管道直线段压力损失公式：
ΔP=LfρV^2/2D
其中，ΔP为管道直线段压力损失，L为管道长度，f为摩阻系数，ρ为流体密度，V为流速，D为管道内径。
5. 弯头压力损失公式：
ΔP=KρV^2/2
其中，ΔP为弯头压力损失，K为弯头阻力系数，ρ为流体密度，
V为流速。
以上是沿程压力损失计算公式及释义，希望能对大家进行相关计算提供一些帮助。
井巷摩擦风阻计算公式
井巷摩擦风阻计算公式说井巷摩擦风阻计算公式，咱得先聊聊井巷里的风流。
风流在井巷里流动，可不是一帆风顺的，得遇到不少阻力。
这阻力啊，有摩擦阻力，也有局部阻力。
今儿咱就说说这摩擦阻力，也叫沿程阻力，是怎么计算的。
你得先知道，风流在井巷里流动，得跟井巷壁面摩擦，还得跟流体层间摩擦，这摩擦一来二去的，能量就损失了，这就是摩擦阻力。
计算这摩擦阻力，咱得用个公式，叫达西公式，听着挺高大上的，其实挺简单。
公式是这样的：Hf=λ×L/d×ρν²/2pa。
这λ啊，是摩擦阻力系数，跟井巷壁的粗糙程度有关。
L是风道长度，d是圆形风管直径，非圆形的话就用当量直径。
ρ是空气密度，ν是断面平均风速。
这些参数啊，你得根据实际情况去测，或者查表得到。
说到这λ啊，我得插一嘴。
这λ值啊，一般矿井巷道的λ值仅取决于井巷壁的相对粗糙度，跟Re无关。
对于几何尺寸和支护已定型的井巷，相对粗糙度一定，则λ可视为定值。
所以啊，你得知道，这λ值可不是随便来的，得根据实际情况去测。
咱再接着说公式。
这公式啊，看着挺复杂，其实挺有规律。
你看，这Hf跟λ、L、d、ρ、ν都有关系。
λ大了，Hf就大；L长了，Hf也大；d小了，Hf还是大。
这ρ和ν啊，也是影响Hf的重要因素。
所以啊，要想减小摩擦阻力，你就得从这些参数上下功夫。
不过啊，这摩擦阻力可不是你想减小就能减小的。
你得根据实际情况，综合考虑各种因素，才能找到最合适的解决方案。
比如说，你得保证有足够大的井巷断面，断面扩大了，Rf值就能减少。
你还得选用周长较小的井巷，圆形断面的周长最小，拱形断面次之，矩形、梯形断面的周长较大。
说到这啊，我得提一句。
这井巷啊，可不是你想怎么挖就怎么挖的。
你得根据地质条件、开采方式、通风要求等因素综合考虑，才能设计出合理的井巷。
所以啊，这摩擦阻力的计算啊，也得根据实际情况来。
咱再回到公式上。
这公式啊，不仅能算摩擦阻力，还能算摩擦风阻。
你看，把公式里的λ、L、P、S归结为一个参数Rf，这Rf就是巷道的摩擦风阻。