沿程阻力系数的自定义函数及其应用
流体力学5-6沿程阻力
17
旧钢管及旧铸铁管
当v＜1.2m/s
0.0179 d 0.3
1
0.867 v
0.3
当v >1.2m/s
0.021
d 0.3
舍维列夫公式是在水温为10oC，运动粘滞系数 ν=1.3×10-6m2/s的条件下得出的，前式适用于紊流过渡区， d 以m计，v 以m/s计；后式适用于阻力平方区, d 以m计
1932年尼古拉兹根据实验结果提
出了此式，n 为指数随雷诺数Re而变
化。该指数公式完全是经验性的，但 因公式形式简单，被广泛应用
u um ax
y r0
n
8
三、λ的半经验公式
1、尼古拉兹光滑管公式
1 2 lg Re
2.51
2、尼古拉兹粗糙管公式
1 2 lg 3.7d
Re vd
d l
2g v2
hf
算出若干组Re和λ值，将其点绘 在双对数坐标纸上，就得到=f(Re, ks /d）曲线，即尼古拉兹曲线图
2
3
尼古拉兹实验曲线
I.ab线层流区， =f(Re) ，=64/Re， Re<2300 II. bc线范围窄， =f(Re) ， Re=2300~4000，层流向紊流
光滑区速度分布半经验公式
u 5.75lg yv 5.5
v
7
2．紊流粗糙区
u v
1
ln
y ks
c2
自然根对据数尼换古成常拉用兹对实数验，取便β=得0.4到、c2=8.48代入上式，并把
粗糙区速度分布半经验公式 u 5.75lg y 8.48
静压动压 沿程阻力系数
静压动压沿程阻力系数
静压动压是流体力学中的重要参数，用于描述流体在管道中流动时的压力变化情况。
沿程阻力系数是用来描述流体在管道中流动过程中受到的阻力大小的无量纲参数。
静压指的是在流体静止或低速流动时的压力，通常用P表示。
动压则是指在流体高速流动时由于运动而产生的附加压力，通常用ρv²/2表示，其中ρ表示流体的密度，v表示流体的流速。
沿程阻力系数是一个与管道尺寸、流体性质和流速等有关的无量纲参数，通常用λ表示。
它描述了单位长度的管道中流体受到的摩擦阻力与流体动压之间的关系。
沿程阻力系数越大，表示流体在管道中受到的阻力越大。
沿程阻力系数可以通过实验或经验公式进行计算。
常见的经验公式有Darcy-Weisbach公式和Chézy公式等。
Darcy-Weisbach公式表示为：
ΔP = λ(D/L)(ρv²/2)
其中ΔP表示单位长度的压力损失，D表示管道的直径，L表
示流体在该段管道中的长度。
Chézy公式表示为：
v = C(RhS)^(1/2)
其中C表示Chézy系数，Rh表示湿周半径，S表示流体在管
道中的平均水头斜率。
需要注意的是，沿程阻力系数与管道的摩擦阻力、雷诺数等参数密切相关，不同的流动情况下，沿程阻力系数的取值也会有所不同。
沿程阻力系数λ计算公式
沿程阻力系数λ计算公式
沿程阻力系数（Coefficient of Friction, λ）是用于描述物体在
沿一定路径或表面移动时所受到的阻力大小的一个参数。
计算沿程阻力系
数可以帮助我们理解和预测运动物体所受到的阻力大小，以及影响阻力的
因素。
1.牛顿第二定律应用：
沿程阻力力（F）可以由牛顿第二定律来计算，即F=m·a
其中m为物体的质量，a为物体的加速度。
通过实验或测量，可以测
得物体在给定路径上的加速度，然后利用该公式计算沿程阻力系数。
2.摩擦力计算：
当物体在平面上运动时，摩擦力是主要的沿程阻力。
摩擦力可以由Coulomb摩擦定律来计算。
摩擦力的大小可以用公式F=μ·N来表示
其中F为摩擦力，μ为摩擦系数，N为法向力。
摩擦系数μ一般是
通过实验测定得到的。
3.空气阻力计算：
当物体在流体（如空气）中运动时，主要存在的沿程阻力是空气阻力。
空气阻力可以用多种方法来估计。
一个常用的方法是根据物体在流体中的运动状态来近似计算空气阻力。
例如，当物体以较低速度在空气中运动时，空气阻力（F）可以用公
式F=0.5·C_d·ρ·A·V^2来计算
其中C_d为空气阻力系数，ρ为空气密度，A为物体在运动方向上的横截面积，V为物体的速度。
持续读取..。
流体力学湍流阻力系数
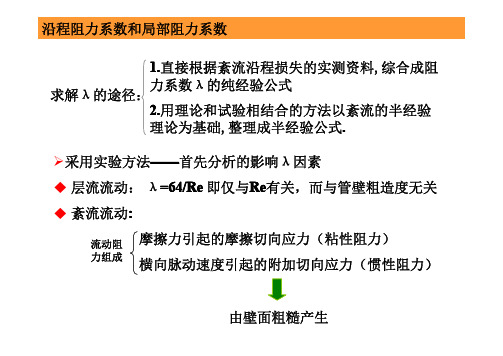
Re 1.E+05
粗糙区
1.E+06
1.E+07
1.E+08
过渡粗糟区
Δ /d
10.0
1.0
0.000001～ 0.05 0.05 0.04 0.03 0.02 0.015 0.01 0.008 0.004 0.002 0.001 0.0008 0.0006 0.0004 0.0002 0.0001 0.00005 0.00001 0.000005 0.000001
沿程阻力系数和局部阻力系数
1944，英国人Moody 对各种工业管道进行了试验 研究。试验用的管道非常广泛，有：玻璃管、混凝土 管、钢管、铜管、木管等，试验条件就是自然管道， 管道的壁面就是天然管壁，而非人工粗糙面。
沿程阻力系数和局部阻力系数
1.E+02 100.0
层流区
1.E+03
1.E+04
1
2
沿程阻力系数和局部阻力系数
1
2
突然扩大的管件中的流动
根据连续方程 有:
p
实验证实，p=p1
A1 v2 = v1 A2
A2 v1 = v2 A1
根据动量方程有 :
p1A1-p2A2+p(A2-A1)=ρqV(v2-v1)
p1-p2=ρv2(v2-v1)
对截面1-1、2-2列伯努里方程（取动能修正系数α=1）
沿程阻力系数和局部阻力系数 1.直接根据紊流沿程损失的实测资料,综合成阻 力系数λ的纯经验公式 求解λ的途径： 2.用理论和试验相结合的方法以紊流的半经验 理论为基础,整理成半经验公式. �采用实验方法——首先分析的影响λ因素 � 层流流动： λ=64/Re 即仅与Re有关，而与管壁粗造度无关 � 紊流流动:
流体力学第五章 管路中的沿程阻力-3
沿程阻力是造成沿程水头损失的原因，用达 西公式计算。这节课的目的是探讨公式中
l v2 hf d 2g
f (Re, ) d
一 尼古拉兹实验 1933年的实验，砂粒涂于管道内 壁，六种相对粗糙度不同的管路， 对不同Re做实验，以Re为横坐 标：
hf 2pd 2 l v lv 2 d 2g
d 68 0.25 ) Re
过渡区的上限和下限
d d 22.2( ) 7 Re 597( ) 8
1
8 9
5、粗糙管湍流区(阻力平方区)：
层流不起作用，湍流遍及整个管道。
d 2 lg( )
2
简化
0.11( )0.25
d
Hale Waihona Puke 理论和半经验公式较准确但复杂，经验公式准确性较差但计 算方便，有时可作理论公式的迭代初始值，迭代2,3次即可。
为纵坐标
将实验点标在双对数坐标纸上，即为尼古拉兹曲线。
从尼古拉兹曲线看出,沿程损失很复杂,不存在统一的曲线描述其特点,分为五段 1、层流区：Re小于2320， =64/Re
2、临介区：Re大于2320，小于4000。不稳定。 0.0025 Re
1 3
3、光滑管湍流区
0.3164 , h f v1.75 0.25 Re 0.221 105 Re 3 106，＝0.0032＋ 0.237 Re 4000 Re 105 ,
9
3判断阻力区域类型, 选择相应的公式计算阻力系数
4 根据达西公式计算沿程水头损失
例 消防水龙带直径为100mm,长为20m,要求流量为0.1 l/s, 求沿程水头损失。
沿程阻力系数
(3) 关闭排水阀，观察测压管的液柱高度是否齐平。若不
平，则需然后排除压差板上测压玻璃管中空气。
2、测录数据 (1) 调节出水阀门，使实验管中水流有稳定的流速，读取测 量断面的压差值。 (2) 流量 Q 用体积法测量。 (3) 依次增大流量，工作 6 次。 (4) 用温度计测记本次实验的水温。
五、实验数据计算和处理
二、实验装置
流体力学综合实验台
三、实验原理
流体在管道中流动时，由于流体的粘性作用产生摩擦 阻力，阻力表现为流体的能量损失。 当对 L 长度两断面列能量方程式时，可以求得 L 长度
上的沿程水头损失：
h f ( z1 p1 ) ( z2 p2 ) h1 h2 h
达西公式
测速实验记录表
d= 次序 1 2 3 4 5 h1 mm h2 L＝ mm t 水温＝ Q ℃ V
h
Re
6
流 体 的 运 动 粘 度 曲 线
水的动力粘度曲线
流体力学课程实习
xilei
注意事项
1. 不要开启储水箱的3个阀门；
2. 不要动与本次实验不相关的开关；
3. 注意脚下，避免绊倒，不要踩盖板； 4. 实验结束后，关掉水电； 5. 填写实验记录本。
第三讲
一、实验目的
沿程阻力系数测定
1. 掌握测定管道沿程阻力系数的方法。
2. 测定在等直圆管内沿程阻力系数与雷诺数Re的关系。L V2 hf 源自 d 2g沿程阻力系数
2 gdhf LV 2
2 gdh LV 2
式中：d — 实验管内径；
g — 重力加速度。
四、实验步骤
1、实验前的准备 (1) 熟悉实验装置的结构，并关闭恒定水箱上水总阀。 (2) 启动水泵，慢慢开启沿程实验管的进水阀至全开状态， 使排管充水，并关闭其他的进水阀、排水阀。
沿程阻力系数公式
沿程阻力系数公式好的，以下是为您生成的文章：咱们今天来聊聊沿程阻力系数公式这个听起来有点专业的东西。
先给大家讲讲我曾经的一段小经历。
有一次，我去参加一个工程实地考察，那是一个正在修建的大型输水管道项目。
我在现场看到工人们忙碌地操作着各种设备，管道一节一节地被铺设着。
就在这时，一位工程师拿着图纸，满脸愁容地跟旁边的同事讨论着什么。
我好奇地凑过去听，原来他们正在为计算管道中的沿程阻力系数而犯愁。
这就让我想到了咱们今天要说的沿程阻力系数公式。
沿程阻力系数在流体力学中可是个相当重要的概念。
它主要用于描述流体在管道或者渠道中流动时，由于摩擦和粘性作用而产生的能量损失。
常见的沿程阻力系数公式有很多，比如说达西-韦斯巴赫公式中的沿程阻力系数λ。
这个公式中的沿程阻力系数λ跟管道的粗糙度、雷诺数等因素都有关系。
咱们就拿常见的圆管流动来说吧。
管道的粗糙度越大，沿程阻力系数就越大，这就意味着能量损失也会越大。
就好像我们在一条平坦的马路上开车，马路很平整，开起来就顺畅，耗油也少；但要是这马路坑坑洼洼的，车开起来费劲，油耗也跟着上去了。
雷诺数也是影响沿程阻力系数的一个重要因素。
雷诺数反映了流体的流动状态，当雷诺数较小时，流体流动是层流状态，沿程阻力系数相对较大；当雷诺数较大时，流体流动变成了紊流状态，沿程阻力系数会相对较小。
再说说实际应用吧。
在水利工程中，比如设计灌溉渠道或者排水管道，准确计算沿程阻力系数能帮助工程师合理确定管道的尺寸和水泵的功率，确保水流能够顺利输送，还能节省能源和成本。
在日常生活中，沿程阻力系数公式也不是毫无用处哦。
比如我们家里的自来水管，如果管道老化生锈，内壁变得粗糙，水流通过时的阻力就会增大，可能会导致水压变小，水流变弱。
这时候，了解沿程阻力系数的知识，就能大概明白是怎么回事啦。
回到最开始我在工程现场看到的那一幕，后来经过工程师们的努力，他们准确计算出了沿程阻力系数，顺利解决了问题，工程得以顺利推进。
减压阀的沿程阻力计算公式
减压阀的沿程阻力计算公式在工程领域中，减压阀是一种常用的控制装置，用于控制流体的压力，确保系统能够正常运行。
在设计和使用减压阀时，了解其沿程阻力计算公式是非常重要的。
本文将介绍减压阀的沿程阻力计算公式及其应用。
减压阀的沿程阻力计算公式可以帮助工程师和技术人员准确地预测减压阀在系统中的性能，并进行合理的设计和选择。
在实际工程中，沿程阻力是指流体在管道中通过减压阀时所受到的阻力，它直接影响着流体的流速和压力，因此对系统的稳定性和效率具有重要影响。
减压阀的沿程阻力可以通过以下公式进行计算：ΔP = K ρ V^2 / 2。
其中，ΔP表示减压阀的沿程阻力，单位为帕斯卡（Pa）；K表示阻力系数，是一个与减压阀本身和管道特性相关的常数；ρ表示流体的密度，单位为千克/立方米（kg/m^3）；V表示流体的流速，单位为米/秒（m/s）。
在实际工程中，阻力系数K是一个非常重要的参数，它可以通过实验或者计算得到。
通常情况下，K的数值与减压阀的结构、流体的性质以及管道的特性有关。
对于不同类型的减压阀和不同工况下的流体，K的数值也会有所不同。
因此，在进行减压阀的沿程阻力计算时，需要根据实际情况合理地选择和确定K的数值。
在实际工程中，减压阀的沿程阻力计算常常涉及到流体的流速和压力的变化。
一般来说，流速越大，沿程阻力也会越大；而流速越小，沿程阻力也会越小。
因此，在进行减压阀的沿程阻力计算时，需要准确地测量和确定流体的流速，并结合实际情况进行合理的分析和计算。
减压阀的沿程阻力计算公式在工程实践中具有重要的应用价值。
通过合理地使用该公式，工程师和技术人员可以准确地预测减压阀在系统中的性能，为系统的设计和运行提供重要的参考依据。
同时，该公式还可以帮助工程师和技术人员进行减压阀的选择和优化，提高系统的稳定性和效率。
总之，减压阀的沿程阻力计算公式是工程领域中一个非常重要的工具，它可以帮助工程师和技术人员准确地预测减压阀在系统中的性能，并进行合理的设计和选择。
沿程阻力系数的自定义函数及其应用
尺 为雷诺数 ， ｅ ｅ ｄ为相对粗糙度
层 流 区
ⅡＲ ＜ ＝ ３０Ｔ ｅ 沿 程 阻力 系 数 Ａ＝ ４ Ｒ ｅ ２ ２ ｈｎ ６￣ ｅ 过 渡 区
ＩＲ ＞２２ ｎ ｅ ４ ０ ｈｎ沿程 阻力系数 Ａ ｆ ｅ ３ ０Ａ ｄＲ ＜ ０ ０Ｔ ｅ
个 区合并为一个区。即当 Ｒ ２ ． ８ ｄ ｅ 时 ， ｅ ６９ （／ ） 统一
使用公式 （ ） ５ 进行编程 。 另外 ， 验算 ｅ ｄ＝ ． ３０ ０ ／ ０ ０ 、．４和 ０ ０ ．５时 ， 发现对应
收稿 日期 ：０ ０—０ ２ ２１ ２— １ 作者 简 介 ： 徐 隽 （９ ６一 ） 女 ， 苏建 湖人 ， 师 １７ ， 江 技
２１ ０ ０年 ６月
Ｊｎ ２ ｌ ‘ ｕ ．０ Ｏ
沿 程 阻 力 系数 的 自定 义 函数 及 其 应 用
徐 隽 ， 淼 陈
（． １江西 中电电力工程有 限责任公司 ， 江西 南 昌 ３ ０ ３ ２ 江西 电力职业技术学 院， ３ ０９；． 江西 南昌 ３０ ３ ） ３０ ２
摘 要 ： 应用 Ｖ Ａ编写了沿程摩擦阻力系 Ｂ 数 的自定义函数。该函数不仅计算结果准确， 而且应用非常方便， 应用该
算公式进行计算。 为了便于使用 ， 本文应 用沿程摩 擦阻力 系数 Ａ的
１ 沿程摩擦 阻力系数 Ａ的计算公式
沿程摩擦阻力系数 Ａ的计算较复杂。根据雷诺数
ｍ 的取值范 围， 流动分 为若 干个 区域 ， 将 每个 区域有 相应的计算公式 。 表 １中列 出了各 区域 雷诺 数 的取值范围及相应 的计算公式。
一
雷诺数 ， 一相对粗糙度
管内沿程阻力系数测定
实验六 管内沿程阻力系数测定(一) 实验目的：通过实验掌握管内沿程阻力的测试方法。
(二) 基本原理：流体沿内径均匀的管道流动时，由于流体的粘性沿程水头损失f h 的大小与管长l 、管径d 、管壁粗糙度Δ、流体的平均流速V 密度ρ和粘度μ有关。
跟据相似原理分析，f h 可由以下关系式表示：g V d L d R f h e f 22∙⎪⎭⎫ ⎝⎛∆∙= (8—1) 令 ⎪⎭⎫ ⎝⎛∆∙=d R f e λ (8—2)则 gVdl h f 22∙=λ(8—3)沿程阻力系数λ是雷诺数和管壁对粗糙度Δ/的函数，它可以由理论推导及用实验的方法获得实验曲线或经验公式求得。
对于层流流动沿程阻力系数是用分析方法推导出来，并且以为实验所证实，而对于湍流流动, 沿程阻力系数的计算公式，则是人们在实验的基础上提出某些假设，经过分析和根据实验进行修正.而归纳出来的半径验公式，下面简单介绍一些常用公式：1． 层流区： e R <232∆eR 64=λ (8—4)2.湍流光滑管区:3798.262320⎪⎭⎫⎝⎛∆<<d R e (8—5)3.湍流粗糙管过渡区:85.0372416198.26⎪⎭⎫⎝⎛∆<<⎪⎭⎫ ⎝⎛∆d R d eeR d88.20096.0/=∆+=λ (8—6)式中/∆ 代表一种正比于圆壁平均凹凸的粗糙长度。
4.湍流粗糙平方阴力区:85.024160⎪⎭⎫⎝⎛∆>d R e222874.1-⎪⎭⎫ ⎝⎛∆+=d λ (8—7)在教学实验条件的限制下，只能就一种特定d∆的管道，在不同的e R 下做若干个实验点，把这些实验点联成一条()e R f =λ曲线，这条曲线的某一段可以用一个经验公式来表达。
本实验中流速V 可由流量计测得流量后经计算而得，沿程损失f h 可用差压计测得，水平安装的管道，沿程损失水头损失与管道两端压差关系为:gp p h f ρ21-=(8—8) 用所求得的流速V 和沿程损失f h 及管道直径d ，管道长度L 即可求得管道沿程阻力系数λ，同时也可求出νVdR e =,即可画出λ与e R 的关系曲线。
沿程阻力简便计算
沿程阻力简便计算沿程阻力是指物体在运动过程中由于与介质的相互作用而产生的阻碍其运动的力。
在运动中，物体需要克服沿程阻力才能继续前进。
了解沿程阻力的大小对于物体运动的预测和设计非常重要。
本文将介绍沿程阻力的计算方法，包括简便计算公式和实际测量方法。
1.沿程阻力简便计算：简便计算方法可以通过物体的一些特性进行近似计算。
以下是两种常用的简便计算方法：-阻力系数法：可以通过使用阻力系数乘以物体所受的一些力来计算沿程阻力。
具体公式如下：F=0.5*ρ*v^2*A*Cd其中，F是沿程阻力，ρ是介质（如空气或水）的密度，v是物体的速度，A是物体在垂直于其运动方向的截面积，Cd是阻力系数。
该公式适用于大多数常见的情况，但是需要知道物体的阻力系数和截面积等数据。
-简化的力学模型法：当物体在低速或中速运动时，可以使用一个简化的力学模型来计算沿程阻力。
该模型基于两种主要的阻力类型：粘性阻力和压力阻力。
粘性阻力：可以通过以下公式计算：Fv=0.5*ρ*v^2*Av其中，Fv是粘性阻力，Av是物体在垂直于其运动方向的有效面积。
压力阻力：可以通过以下公式计算：Fp=P*Ap其中，Fp是压力阻力，P是介质的压强，Ap是物体在垂直于其运动方向的截面积。
然后，可以将粘性阻力和压力阻力相加得到总的沿程阻力：F=Fv+Fp这种简化的计算方法适用于一些简单的情况，但是需要一些近似和假设。
2.实际测量方法：实际测量方法可以通过在实验室或现场对物体进行测试来获得沿程阻力的真实值。
以下是常见的两种实际测量方法：-滑移实验法：可以将物体放置在一个倾斜的平面上，并测量物体在不同坡度和速度下的滑移距离。
通过测量滑移距离和推力，可以计算沿程阻力。
需要注意的是，该方法适用于一些特定的形状和介质，而且可能需要进行多次实验以获得准确结果。
-动力学测试法：可以使用动力学测试仪器来测量物体在运动过程中所受的力。
这些仪器可以记录物体的速度、加速度和力的变化，并通过计算来推导沿程阻力。
沿程阻力系数表
沿程阻力系数表
阻力：
妨碍物体运动的作用力，称“阻力”。
在一段平直的铁路上行驶的火车，受到机车的牵引力，同时受到空气和铁轨对它的阻力。
牵引力和阻力的方向相反，牵引力使火车速度增大，而阻力使火车的速度减小。
如果牵引力和阻力彼此平衡，它们对火车的作用就互相抵消，火车就保持匀速直线运动。
物体在液体中运动时，运动物体受到流体的作用力，使其速度减小，这种作用力亦是阻力。
例如划船时船桨与水之间，水阻碍桨向后运动之力就是阻力。
又如，物体在空气中运动，因与空气摩擦而受到阻力。
阻力，又称后曳力、空气阻力或流体阻力，是物体在流体中相对运动所产生与运动方向相反的力。
阻力的方向和其所在流场的流速方向相反。
一般摩擦力不随速度变化而变化，但阻力会随速度而变化。
沿程阻力系数表：
沿程阻力（Frictional Drag）：流体流经一定管径的直管时，由于流体内摩擦力而产生的阻力，阻力的大小与路程长度成正比。
简介：
沿程阻力（直管阻力）损失的计算式中λ——摩擦系数，与雷诺数Re和管壁粗糙度ε有关，可实验测定，也可计算得出。
沿程阻力系数的确定方法：
对于层流流动，可以严格地从理论推导出来。
对于紊流流动，工程上通过以下两种途径确定：一种是以紊流的半经验理论为基础，结合实验结果，整理成阻力系数的半经验公式；
另一种是直接根据实验结果，综合成阻力系数的经验公式。
前者具有更为普遍的意义。
沿程损失阻力系数的FLUENT数值模拟(计算流体力学作业)
计算流体力学课程作业作业题目：沿程损失阻力系数的FLUENT数值模拟学生姓名：易鹏学生学号：专业年级：动力工程及工程热物理12级学院名称：机械与运载工程学院2012年5月2日沿程损失阻力系数的 FLUENT 数值模拟一、 引言沿程损失（pipeline friction loss ）是指管道内径不变的情况下，管内流体流过一段距离后的水头损失。
其中边界对水流的阻力是产生水头损失的外因，液体的粘滞性是产生水头损失的内因，也是根本原因。
沿程能量损失的计算公式是：2f l v h =λd 2g。
其中：l 为管长，λ为沿程损失系数，d 为管道内径，2v 2g 为单位重力流体的动压头（速度水头），v 为流体的运动粘度系数。
粘性流体在管道中流动时，呈现出两种流动状态，管道中的流速cr v v <(cr v 为层流向湍流转变的临界流速)为层流，此时整个流场呈一簇互相平行的流线。
则cr v v >时为湍流，流场中的流体质点作复杂的无规则的运动。
沿程损失与流动状态有关，故计算各种流体通道的沿程损失，必须首先判别流体的流动状态。
沿程损失能量损失的计算公式由带粘性的伯努利方程22112212f v p v p ++z =++z +h 2g ρg 2g ρg 推出，可知，12f P -P h =ρg其中：——单位质量流体的动能（速度水头）。
流体静止时为0。
——单位质量流体的势能（位置水头）。
——单位质量流体的压力能（压强水头）。
2v 2gzp ρg又由量纲分析的π定理，得出 2Δp L=λ1d ρV 2，计算出达西摩擦因子22Δpdλ=LρV， 则2fL V h =λD 2g ,由于Vd Re =ν，μν=ρ，则d λ=f(Re )。
关于沿程损失最著名的是尼古拉茨在1932～ 1933年问所做的实验(右图为实验装置图)。
其测得曲线如图1，从此得出了几个重要结论：1．层流区 Re ＜2320为层流区。
在该区域内，管壁的相对粗糙度对沿程损失系数没有影响。
沿程损失阻力系数的FLUENT数值模拟(计算流体力学作业)
计算流体力学课程作业作业题目：沿程损失阻力系数的FLUENT数值模拟学生姓名：易鹏学生学号：专业年级：动力工程及工程热物理12级学院名称：机械与运载工程学院2012年5月2日沿程损失阻力系数的 FLUENT 数值模拟一、 引言沿程损失（pipeline friction loss ）是指管道内径不变的情况下，管内流体流过一段距离后的水头损失。
其中边界对水流的阻力是产生水头损失的外因，液体的粘滞性是产生水头损失的内因，也是根本原因。
沿程能量损失的计算公式是：2f l v h =λd 2g。
其中：l 为管长，λ为沿程损失系数，d 为管道内径，2v 2g 为单位重力流体的动压头（速度水头），v 为流体的运动粘度系数。
粘性流体在管道中流动时，呈现出两种流动状态，管道中的流速cr v v <(cr v 为层流向湍流转变的临界流速)为层流，此时整个流场呈一簇互相平行的流线。
则cr v v >时为湍流，流场中的流体质点作复杂的无规则的运动。
沿程损失与流动状态有关，故计算各种流体通道的沿程损失，必须首先判别流体的流动状态。
沿程损失能量损失的计算公式由带粘性的伯努利方程22112212f v p v p ++z =++z +h 2g ρg 2g ρg 推出，可知，12f P -P h =ρg其中：——单位质量流体的动能（速度水头）。
流体静止时为0。
——单位质量流体的势能（位置水头）。
——单位质量流体的压力能（压强水头）。
2v 2gzp ρg又由量纲分析的π定理，得出 2Δp L=λ1d ρV 2，计算出达西摩擦因子22Δpd λ=LρV， 则2fL V h =λD 2g ,由于Vd Re =ν，μν=ρ，则d λ=f(Re )。
关于沿程损失最著名的是尼古拉茨在1932～ 1933年问所做的实验(右图为实验装置图)。
其测得曲线如图1，从此得出了几个重要结论：1．层流区 Re ＜2320为层流区。
在该区域内，管壁的相对粗糙度对沿程损失系数没有影响。
阻力平方区的紊流的沿程阻力系数
阻力平方区的紊流的沿程阻力系数在航空、航天和流体力学等领域，阻力是一项非常关键的参数。
它可以影响到各种飞行器的性能，包括速度、飞行距离和燃料消耗等。
因此，了解阻力的性质和计算方法是非常必要的。
阻力平方区的紊流的沿程阻力系数是其中一个重要的概念，本文将对此进行详细介绍。
首先，让我们回顾一下阻力的基本概念。
阻力是物体移动时产生的一种阻碍运动的力。
当物体移动时，它与周围的流体（如空气或水）发生摩擦，摩擦力就会产生阻碍物体继续移动的力。
这个力的大小取决于多种因素，如物体的形状、速度、流体密度和黏性等。
如果考虑到流体的黏性，那么阻力可以分为两种：层流阻力和紊流阻力。
层流阻力发生在流体的运动过程中，流线较为平滑，流速也较为匀称。
这种情况下阻力较小，可以采用流体力学中基于无黏性流体的Bernoulli方程来计算。
而紊流阻力则是在流体速度达到一定范围时出现的，此时流线变得复杂，速度和压力的分布也变得不规则。
这种情况下阻力往往较大，难以精确计算。
阻力平方区的紊流，是指流体速度较高时，其硬件表面上的压强和速度分布日益不规则，流线开始形成旋涡和湍流。
在这个区域内的紊流是以一种二次方程的形式出现的，这就是阻力平方区。
从数学上把它描述为近似二次方程，其与物体面交点附近的压力差与底层流体速度的平方成正比关系。
为了描述在阻力平方区内的阻力，并用于计算流体的性质，人们引入了沿程阻力系数的概念。
沿程阻力系数（C_d）指单位面积内产生的阻力力和动压力之比。
它是一个无单位的纯量，通常用实验和计算得出。
定义C _d作为沿程单位面积阻力系数采取的是一个广泛使用的灵敏无量纲阻力系数。
其计算公式为C_d = f (re, m)，其中re是雷诺数，m是横流马赫数，f是二者的函数。
在阻力平方区内，C_d的值通常很高，远高于其他区域。
它可以随着速度的增加而增加，因为当流速足够高时，流体将进入阻力平方区，从而增加阻力。
总之，在流体力学中，了解阻力平方区的紊流及其沿程阻力系数是非常重要的。
沿程阻力系数的自定义函数及其应用
沿程阻力系数的自定义函数及其应用
徐隽;陈淼
【期刊名称】《江西电力职业技术学院学报》
【年(卷),期】2010(023)002
【摘要】应用VBA编写了沿程摩擦阻力系数λ的自定义函数.该函数不仅计算结果准确,而且应用非常方便,应用该函数大大地方便了在Excel中进行管道水力计算.【总页数】3页(P42-44)
【作者】徐隽;陈淼
【作者单位】江西中电电力工程有限责任公司,江西,南昌,330039;江西电力职业技术学院,江西,南昌,330032
【正文语种】中文
【中图分类】TV131
【相关文献】
1.应用电子计算机计算粮油工业通风管道沿程阻力系数 [J], 胡维国;郭建生
2.粗糙度对幂律流体湍流沿程阻力系数的影响 [J], 康艳蓓;张浩;许岩
3.“黄河浑水沿程阻力系数研究与工程应用”项目通过评审验收 [J], 邢天明;刘敏香;
4.基于CFD的沿程阻力系数的计算 [J], 高志强;王慧;张晓艳;常岩娟;赵锴岑
5."双一流"建设中流体沿程阻力系数测定实验教学探索 [J], 杨嵩;林英;王辉;于萍;陈延礼;朱先勇
因版权原因，仅展示原文概要，查看原文内容请购买。
沿程阻力系数的自定义函数及其应用
kefluiddynamiclineresistancecoefficienselfdefinitionfunction上接第32生产的产品虽然该塔芯材料性能好另外马利公司在我国的技术推广力度不大这一技术还没有被众多的业主单位及设计单位所认可随着能源项目节能减排的力度不断加大以及电源工程项目的设计招投标的不断推进在节能以及投资方面都具有优势的马利塔技术将逐步得到广大业主单位及设计单位的青睐北京
关键词 :流体力学 ;沿程摩擦阻力系数 ;自定义函数 中图分类号 : TV131 文献标识码 : A 文章编号 : 1673 - 0097 (2010) 02 - 0042 - 03
0 引言
系数 λ的自定义函数 。有了该自定义函数 , 既可以十 分方便地确定沿程摩擦阻力系数 λ数值 , 也可以利用
舍维列夫公式计算沿程阻力系数
舍维列夫公式计算沿程阻力系数沿程阻力系数是一个在空气动力学中被广泛应用的概念。
它描述了在飞行器运动过程中所受到的阻力与速度的关系。
舍维列夫公式是计算沿程阻力系数的一种常用方法。
在本文中，我们将介绍舍维列夫公式的原理和应用，并通过一个具体的例子来展示其计算过程。
让我们来了解一下沿程阻力系数的定义。
沿程阻力系数（drag coefficient）是一个无量纲的物理量，用来描述飞行器在运动过程中所受到的阻力的大小。
它是阻力与空气密度、速度和参考面积的乘积之比。
具体而言，沿程阻力系数（Cd）可以表示为以下公式：Cd = D / (0.5 * ρ * V^2 * S)其中，D是飞行器所受到的阻力，ρ是空气密度，V是速度，S是参考面积。
舍维列夫公式是一种用来计算沿程阻力系数的经验公式。
它是根据实验数据和理论推导得到的，适用于不同形状和尺寸的飞行器。
舍维列夫公式可以表示为以下形式：Cd = Cd0 + K * CL^2其中，Cd0是零升力阻力系数，K是一个与飞行器外形和空气动力学特性相关的常数，CL是升力系数。
通过舍维列夫公式，我们可以计算出飞行器在不同速度和升力条件下的沿程阻力系数。
这对于飞行器的设计和性能分析非常重要。
现在让我们通过一个具体的例子来展示舍维列夫公式的计算过程。
假设我们有一架飞机，其零升力阻力系数（Cd0）为0.02，常数K 为0.05。
我们希望计算出在速度为100米/秒，升力系数（CL）为0.4时的沿程阻力系数。
根据舍维列夫公式，我们可以进行如下计算：Cd = 0.02 + 0.05 * 0.4^2= 0.02 + 0.05 * 0.16= 0.02 + 0.008= 0.028因此，在速度为100米/秒，升力系数为0.4的条件下，该飞机的沿程阻力系数为0.028。
通过舍维列夫公式的计算，我们可以了解到飞行器在不同运动条件下的阻力大小。
这对于飞行器的性能评估、设计和优化非常重要。
同时，舍维列夫公式也为我们提供了一种简化计算沿程阻力系数的方法。
流体力学湍流阻力系数
沿程阻力系数和局部阻力系数
尼古拉兹实验 试验条件 管道 人工粗糙面：将大小一致的均匀砂粒粘贴在管壁上 注意：这种粗糙面和天然粗糙面完全不同
相对粗糙度： ε /2r0
r0
ε
=d
沿程阻力系数和局部阻力系数
l
方法
hf
沿程阻力系数的试验装置
V Q= t
对于一系列相对粗糙度ε /d 、测量流速υ和水头 损失hf ，得到不同雷诺数Re=υd/ν与沿程阻力系数 λ=hf(d/l )(2g/υ2)的试验关系曲线。
Re — Δ — 雷诺数。 管壁绝对粗糙度。
沿程阻力系数与Re, Δ/d 有关，可通过实验方法来获得其经验关系。
沿程阻力系数和局部阻力系数
尼古拉兹(J.Nikuradse)实验
• 实验目的：为了确定λ=f(Re, ε/d)的变化规律。德国学者 (J.Nikuradse，1933-1934)首次进行了实验研究，具有重 大的理论意义。 • 实验方案：用人工制成的均匀颗粒粗糙圆管，考察6种不同 的相对粗糙度的圆管中测出不同流速υ 、管长l 间的水头 损失 hf 和水温，以推算Re=υd/ν 和沿程阻力系数λ。 • 实验结果： 发现5个有显著规律的区域，揭示了λ=f(Re, ε/d)的影响关系。1)层流区: λ=64/Re; 2)层-紊流过渡 区; 3)光滑管区; 4)光滑管向粗糙管过渡区; 5)粗糙管区
1 0 0 0λ
光滑区
可见，沿程阻力系数的变化规律 和尼古拉兹试验基本相同 差别在于：紊流过渡粗糙区曲线 形状不同（一个是沿程增加，另一个 是沿程降低） 由该图得到的沿程阻力系数和实 际情况较符合。
沿程阻力系数和局部阻力系数
2、局部阻力系数
流体经过阀门、弯管、突扩和突缩等管件
(完整版)莫迪图
莫迪图表示沿程阻力系数λ与△/d、Re之间的函数关系，查莫迪图首先确定流动的雷诺数Re，到莫迪图上查对应横坐标；查表“管道的管壁绝对粗糙度△”，除以管道直径d，如果是非圆管道，则除以当量直径de，计算△/d，这个值对应着莫迪图的右边纵坐标和莫迪图区域中央的曲线。
由横坐标的雷诺数Re，右边纵坐标△/d，对应确定莫迪图区域中央曲线上的一个点，这个点对应着莫迪图左边纵坐标的沿程阻力系数λ，再由λ计算管道内的沿程阻力。
莫迪图以及尼古拉兹图的区别尼古拉兹实验：人工粗糙管，5个阻力区的沿程阻力系数的计算公式及各公式的适用条件（详见课堂笔记），尼古拉兹图；莫迪图（用以查工业管道，与尼古拉兹图查人工粗糙管不同）插值法插值法又称“内插法”，是利用函数f (x)在某区间中插入若干点的函数值，作出适当的特定函数，在这些点上取已知值，在区间的其他点上用这特定函数的值作为函数f (x)的近似值，这种方法称为插值法。
如果这特定函数是多项式，就称它为插值多项式。
主要有lagrange插值、newton插值、hermite插值、分段多项式插值及样条插值法等。
目录1内容简介2主要类别Lagrange插值Newton插值Hermite插值分段多项式插值样条插值1 内容简介插值法是函数逼近的一种重要方法，是数值计算的基本课题。
该节只讨论具有唯一插值函数的多项式插值和分段多项式插值，对其中的多项式插值主要讨论n次多项式插值的方法，即给定n+1各点处的函数值后，怎样构造一个n次插值多项式项式。
介绍内容有：lagrange插值、newton插值、hermite插值、分段多项式插值及样条插值。
2 主要类别Lagrange插值Lagrange插值是n次多项式插值，其成功地用构造插值基函数的方法解决了求n次多项式插值函数问题。
★基本思想将待求的n次多项式插值函数pn(x）改写成另一种表示方式，再利用插值条件⑴确定其中的待定函数，从而求出插值多项式。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
收稿日期 : 2010 - 02 - 21 作者简介 :徐 隽 (1976 - ) ,女 ,江苏建湖人 ,技师.
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
表 1 沿程摩擦阻力系数的计算表
分 区
计算公式
公式编号
层流区 R eΦ 2320
λ = 64 /Re
(1)
过渡区 2320 < R e < 4000
λ = 010025R e1 /3
(2)
光滑管区
λ = 0. 3164 /R e0. 25 ( 4000Φ R e < 105 )
(3)
4000Φ R e < 26198 ( d /ε) 8 /7
在进行管内流动损失计算时 , 沿程摩擦阻力系数 λ的确定是必需的 。
沿程摩擦阻力系数 λ可以根据已知参数 - 雷诺数 R e和管道壁面相对粗糙度 ε/ d (其中 :ε为管壁的绝对
该函数在 Excel中做管道的水力计算 。
1 沿程摩擦阻力系数 λ的计算公式
沿程摩擦阻力系数 λ的计算较复杂 。根据雷诺数
图 2 根据假设的流速计算的结果
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
44
江西电力职业技术学院学报
第 22卷
图 3 经单变量求解后的结果
2006. [ 2 ]孙 丽 君. 工 程 流 体 力 学 [M ]. 北京 : 中 国 电 力 出 版 社 ,
2005. [ 3 ]韩小良 ,韩舒婷. ExcelVBA 应用开发 [M ]. 北京 :电子工
业出版社 , 2007. [ 4 ]山东工学院 ,东北电力学院. 工程流体力学 [M ]. 北京 :水
λ=1/
1.
74
+ 2 lg
d 2ε
2
(6)
2 沿程摩擦阻力系数 λ自定义函数编程
由于紊流粗糙管区的计算公式 ( 6)是紊流粗糙管 过渡区的计算公式 ( 5)的简化公式 , 因此 , 本文将该两 个区合并为一个区 。即当 R eΕ 26. 98 ( d /ε) 8 /7时 , 统一 使用公式 ( 5)进行编程 。
粗糙度 , d为管内径 ) 查莫迪图获得 ; 或者由相应的计 R e的取值范围 , 将流动分为若干个区域 , 每个区域有
算公式进行计算 。 为了便于使用 ,本文应用沿程摩擦阻力系数 λ的
相应的计算公式 。[1 - 2 ]表 1 中列出了各区域雷诺数 R e 的取值范围及相应的计算公式 。
计算公式 ,在 Excel中应用 VBA 编写了沿程摩擦阻力
If R e > = 4000 Then If ed = 0 Then 光’ 滑管时常不给出相对粗糙度 If R e > = 4000 And R e < 100000# Then 沿程阻 力系数 λ = 0. 3164 /R E^0. 25 If R e > = 100000# And R e < 3000000# Then 沿 程阻力系数 λ = 0. 0032 + 0. 221 /R e^ 0. 237 Else If R e < 26. 983 ed^( - 8 /7) Then If R e > = 4000 And R e < 100000# Then 沿程阻力 系数 λ = 0. 3164 /R e^0. 25 If R e > = 100000# And R e < 3000000# Then 沿程 阻力系数 λ = 010032 + 0. 221 /R E^0. 237 End If
由于管内流速未知 ,因此 , 无法计算雷诺数 , 也就 不能确定沿程阻力系数 λ。所以 , 要求解可以先假设 管内流速 V,然后进行迭代计算 。
在 Excel中 ,应用“单变量求解 ”功能可以非常容 易地解决迭代计算问题 。
先任意假设流速 V 的值 (图 2中假设流速 V = 2m / s) ,由此可计算出雷诺数 ,再利用沿程阻力系数 λ自定 义函数求出沿程阻力系数 λ, 进而计算出管道水头损 失 hf 和管内流量 Q。图 2所示为根据假设的速度计算 得到的初步结果 。在图 2 所得的初步结果的基础上 , 选中单元格 B5,应用“单变量求解 ”功能 , 在弹出的对 话框中 ,设定“目标值 ”为 6 (已知 hf = 6m ) ,“可变单元 格 ”为 B2,“确定 ”后即可得到图 3 的计算结果 。该结 果与文献 [ 4 ]的结果一致 。
关键词 :流体力学 ;沿程摩擦阻力系数 ;自定义函数 中图分类号 : TV131 文献标识码 : A 文章编号 : 1673 - 0097 (2010) 02 - 0042 - 03
0 引言
系数 λ的自定义函数 。有了该自定义函数 , 既可以十 分方便地确定沿程摩擦阻力系数 λ数值 , 也可以利用
A b s tra c t: This paper has p rogrammed the self - definition function of line resistance coefficientλ by the p rogramm ing language
- VBA. U sing the function, the accurate calculation result can be got, and using the function to calculate p ipeline resistance in Excel will greatly facilitate.
由于 Excel具有很强的计算功能 ,因此可以直接在 Excel中进行管道水力计算 。有了沿程阻力系数 λ自 定义函数 , 也大大方便了在 Excel中进行管道水力计 算。
例 : 15℃的水 (运动粘度 v = 1113 ×10 - 6 m2 / s) , 流 过直径 d = 300mm 的铆接钢管 (绝对粗糙度 ε= 3mm) 。 若在长度 l为 300m 的管道上水头损失 hf = 6m,试确定 流量 Q。[4 ]
“沿程阻力系数 λ( R e, ed) ”,在弹出的对话框中分别引 用 A1和 A2两个单元格 ,如图 1示 。 (也可以直接将已 知参数输入到对应的输入框中 ) 。“确定 ”后 , 在 A3 中 就会自动计算出相应的沿程阻力系数 λ = 0. 0294932。
图 1 沿程阻力系数 λ自定义函数输入框 R e—雷诺数 , Ed—相对粗糙度
λ = 0. 0032 + 0. 221R e - 0. 237 ( 105 Φ R e < 3 ×106 )
(4)
紊流粗糙管过渡区 26. 98 ( d /ε) 8 /7 Φ R e < 4160 ( d /2ε) 0. 85
1 λ
= 1.
74
-
2 lg
2ε d
+
18. 7 λ
1 Re
(5)
紊流粗糙管区 (阻力平方区 ) R eΕ 4160 ( d /2ε) 0. 85
另外 ,验算 ε/ d = 0103、0104 和 0105 时 , 发现对应
的 26198 ( d /ε) 8 /7分别为 148411、106813 和 82718。显 然 ,这三个数据均小于 2320, 处于层流区 。因此 , 在应 用公式 ( 5)时 , 应加上条件 R e > 4000。
有时 ,当流动处于层流区或光滑管区时 , 已知条件 只给出雷诺数 R e,而没有给出相对粗糙度 ε/ d, 这时取 相对粗糙度 ε/ d = 0, 并根据给出的雷诺数 R e判定流 动处于层流区还是光滑管区 。
4 结束语
如上所述 ,沿程阻力系数 λ自定义函数不仅使用 方便 ,而且计算准确 。
有些管道水力计算问题是要求确定管内流量 Q 或
确定管道直径 d。这类问题因流速未知 , 计算时需要 迭代 。如上例所示 ,用 Excel并借助本文的沿程阻力系 数 λ自定义函数来解决这类问题 ,是十分方便的 。
参考文献 : [ 1 ]夏泰淳. 工程流体力学 [M ]. 上海 :上海交通大学出版社 ,
b = 1 / b^ 2
If A bs ( b - a) > 0. 0001 Then a = b GoБайду номын сангаасo 1
End If 沿程阻力系数 λ = b End If
End Function 与莫迪图进行对比 ,该自定义函数的计算结果准确。
3 应用举例
在 Excel中 , 沿程阻力系数 λ自定义函数的用法 与 Excel的内嵌函数用法相同 。例如 ,要确定 R e = 105 , ε/ d = 01002时的沿程阻力系数 λ值 ,可以将雷诺数 R e 的值和相对粗糙度 ε/ d的值分别放在任意两个单元格 如 A1和 A2中 , 则可在单元格 A3 中插入自定义函数
Ke y wo rd s: fluid dynam ics; line resistance coefficient; self - definition function
[上接第 32页 ]
4 存在的问题
马利塔作为一种成熟的塔型 ,在国外有大量的工 程业绩 ,但在我国运用的案例非常少 。虽然近几年各 电力设计单位都做过很多研究比较 ,也推荐采用马利 塔方案 ,但是真正实施的项目很少 ,分析起来有以下几 个方面的原因 :首先 ,国内设计单位已经完全掌握了常 规塔的热力计算 、塔体的结构计算等 ,并已开发出成熟 的设计软件 ,而马利塔的热力计算 、结构计算等都要依 赖马利公司的技术 ,这造成了应用上的瓶颈 ;其次 ,常 规塔的塔芯材料如淋水填料 、喷头等在国内拥有众多 的供货商 ,而马利塔的塔芯材料则需要采用马利公司