变量与函数1
一次函数-变量与函数

变量与函数(知识讲解)【学习目标】1.知道现实生活中存在变量和常量,变量在变化的过程中有其固有的范围(即变量的取值范围);2.能初步理解函数的概念;能初步掌握确定常见简单函数的自变量取值范围的基本方法;给出自变量的一个值,会求出相应的函数值.【要点梳理】要点一、变量、常量的概念在一个变化过程中,我们称数值发生变化的量为变量.数值保持不变的量叫做常量.要点诠释:一般地,常量是不发生变化的量,变量是发生变化的量,这些都是针对某个变化过程而言的.例如,60s t =,速度60千米/时是常量,时间t 和里程s 为变量.要点二、函数的定义一般地,在一个变化过程中. 如果有两个变量x 与y ,并且对于x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说 x 是自变量,y 是x 的函数.要点诠释:对于函数的定义,应从以下几个方面去理解:(1)函数的实质,揭示了两个变量之间的对应关系;(2)对于自变量x 的取值,必须要使代数式有实际意义;(3)判断两个变量之间是否有函数关系,要看对于x 允许取的每一个值,y 是否都有唯一确定的值与它相对应.(4)两个函数是同一函数至少具备两个条件:①函数关系式相同(或变形后相同);②自变量x 的取值范围相同.否则,就不是相同的函数.而其中函数关系式相同与否比较容易注意到,自变量x 的取值范围有时容易忽视,这点应注意.要点三、函数值y 是x 的函数,如果当x =a 时y =b ,那么b 叫做当自变量为a 时的函数值.要点诠释:对于每个确定的自变量值,函数值是唯一的,但反过来,可以不唯一,即一个函数值对应的自变量可以是多个.比如:2y x =中,当函数值为4时,自变量x 的值为±2.要点四、自变量取值范围的确定使函数有意义的自变量的取值的全体实数叫自变量的取值范围.要点诠释:自变量的取值范围的确定方法:首先,要考虑自变量的取值必须使解析式有意义:(1)当解析式是整式时,自变量的取值范围是全体实数;(2)当解析式是分式时,自变量的取值范围是使分母不为零的实数;(3)当解析式是二次根式时,自变量的取值范围是使被开方数不小于零的实数;(4)当解析式中含有零指数幂或负整数指数幂时,自变量的取值应使相应的底数不为零;(5)当解析式表示实际问题时,自变量的取值必须使实际问题有意义.【典型例题】类型一、变量与函数例1、下列是关于变量x 与y 的八个关系式:① y = x ;② y 2 = x ;③ 2x 2 − y = 0;④ 2x − y 2 = 0;⑤ y = x 3 ;⑥ y =∣x ∣;⑦ x = ∣y ∣;⑧ x =2y .其中y 不是x 的函数的有_____.(填序号)【变式】下列:①2y x ;②21y x =+;③22(0)y x x =≥;④0)y x =≥,具有函数关系(自变量为x )的是______.类型二、函数解析式的取值范围 例2、求出下列函数中自变量x 的取值范围(1)2321y x x =--; (2)2131x y x -=+;(3)y =(4)y =.举一反三:【变式】等腰三角形的周长为10,底边长y 与腰x 的函数关系式是102y x =-,则自变量x 的取值范围是________.类型三、函数解析式例3.如图,一农户要建一个矩形猪舍,猪舍的一边利用住房墙(住房墙的长度大于BC ),另外三边用25m 长的建筑材料围成,为方便进出,在CD 边上留一个1m 宽的门.若设AB 为()y m ,BC 为()x m ,则y 与x 之间的函数关系式为______.【变式】如图,ABC 中,90BAC ∠=,4BC =,BD 是ABC 的角平分线,过点C 作BD 的垂线,交BD 的延长线于点E .若设AB x =,CE y =,则y 关于x 的函数解析式为___________.类型四、函数值例4、 若y 与x 的关系式为306y x =-,当x =时,y 的值为( )A .5B .10C .4D .-413课后练习1.下列式子:①y=3x ﹣5;②y=1x ;③y 2=x ;⑤y=|x|,其中y 是x 的函数的个数是( ) A .2个 B .3个 C .4个 D .5个2.下列说法中,正确的是( )A .对于两个变量x ,y ,若y x =,则y 是x 的函数B .对于两个变量x ,y ,若22016x y +=,则y 是x 的函数C .对于两个变量x ,y ,若2y x =,则y 是x 的函数D .对于两个变量x ,y ,若22y x =,则y 是x 的函数3.函数y =的自变量的取值范围是( ) A .0x B .0x > C .0x ≠ D .0x =4.下列曲线中不能表示y 与x 的函数的是( )A .B .C .D .5.下列图象中,表示y 不是x 的函数的是( )A .B .C .D .6.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了 一觉. 当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终 点……. 用 s 1 、s2 分别表示乌龟和兔子所行的路程, t 为时间,则下列图像中与故事情节相吻合的是( )A .B .C .D .。
变量与函数大一高数知识点

变量与函数大一高数知识点高等数学是大一大二学生必修的一门基础课程,其中包括了许多重要的知识点。
其中,变量与函数是高等数学中最为基础和重要的概念之一。
一、变量变量是数学中使用的一种概念,它可以表示不同数值的符号或字母。
在数学中,我们常常用字母来表示变量,如x、y、z等等。
变量可以代表任意数的集合,也可以代表某一个具体的数值。
在数学中,我们通常用变量来表示未知数,通过解方程等方法来求解变量的数值。
变量在实际问题中也很常见,我们可以通过设定变量来描述实际问题的各种情况,从而得到数学模型并解决问题。
二、函数函数是数学中另一个重要的概念。
函数是一个特殊的关系,它将一个集合的元素(自变量)映射到另一个集合(因变量)。
函数常用符号表示为y = f(x),其中x为自变量,y为因变量,f为函数关系。
函数包含了定义域、值域和对应关系三个重要的概念。
定义域是自变量的取值范围,值域是因变量的取值范围,对应关系是自变量和因变量之间的映射关系。
函数在数学中有着广泛的应用。
它们可以用来描述各种数学模型,如直线方程、曲线方程等等。
通过函数的性质和图像,我们可以研究函数的增减性、极值、导数等,从而了解函数的行为和特点。
函数可以用来解决各种实际问题,如经济学中的生产函数、物理学中的运动方程等等。
因此,对于函数的理解和掌握是我们学习高等数学的基础。
三、变量与函数的关系变量与函数之间有着密切的关系。
在函数中,自变量常常是一个或多个变量,而函数则是对自变量的一种规定或设定。
变量作为函数中的自变量,它的取值范围和变化规律会影响到函数的性质和行为。
因此,变量的取值是函数研究中一个非常重要的问题。
在实际问题中,我们可以通过设定变量来描述问题的各种情况,从而建立函数模型。
通过分析自变量的取值范围和变化规律,我们可以研究函数的图像、性质和规律。
例如,我们可以用变量来表示一个物体的位置,然后建立位置和时间的函数关系,通过分析函数曲线的形状和变化趋势,我们可以了解物体的运动规律和特点。
一次函数讲义变量与函数
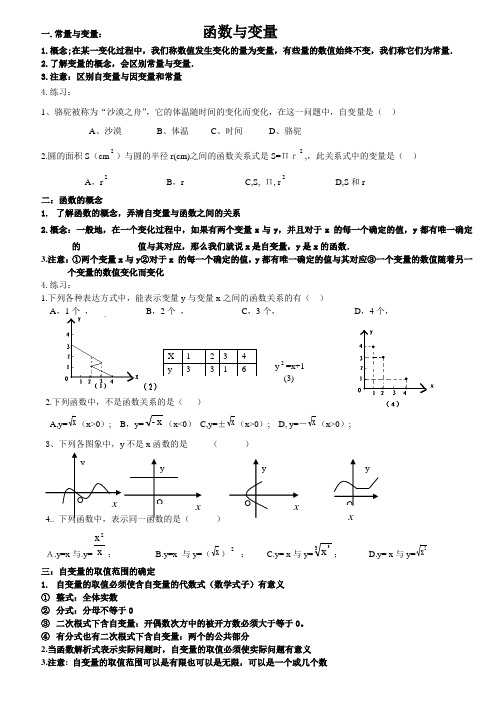
一.常量与变量:函数与变量1.概念;在某一变化过程中,我们称数值发生变化的量为变量,有些量的数值始终不变,我们称它们为常量.2.了解变量的概念,会区别常量与变量.3.注意:区别自变量与因变量和常量4.练习:1、骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一问题中,自变量是( )A 、沙漠B 、体温C 、时间D 、骆驼2.圆的面积S (cm 2)与圆的半径r(cm)之间的函数关系式是S=Πr2,,此关系式中的变量是( )A ,r 2B ,r C,S, Π, r 2D,S 和r二:函数的概念1. 了解函数的概念,弄清自变量与函数之间的关系2.概念:一般地,在一个变化过程中,如果有两个变量x 与y ,并且对于x•的每一个确定的值,y 都有唯一确定的 值与其对应,那么我们就说x 是自变量,y 是x 的函数.3.注意:①两个变量x 与y ②对于x•的每一个确定的值,y 都有唯一确定的值与其对应③一个变量的数值随着另一个变量的数值变化而变化 4.练习:1.下列各种表达方式中,能表示变量y 与变量x 之间的函数关系的有( )A ,1个 ,B ,2个 ,C ,3个,D ,4个,2.下列函数中,不是函数关系的是( )A,y=x (x>0); B ,y=x -(x<0) C,y=±x (x>0); D, y=-x (x>0); 3、下列各图象中,y 不是x 函数的是 ( )4.. 下列函数中,表示同一函数的是( )A.y=x 与.y=x x 2; B.y=x 与y=(x )2; C.y= x 与y=33x ; D.y= x 与y=2x三:自变量的取值范围的确定1. 自变量的取值必须使含自变量的代数式(数学式子)有意义 ① 整式:全体实数 ② 分式:分母不等于0③ 二次根式下含自变量:开偶数次方中的被开方数必须大于等于0。
④ 有分式也有二次根式下含自变量:两个的公共部分2.当函数解析式表示实际问题时,自变量的取值必须使实际问题有意义3.注意: 自变量的取值范围可以是有限也可以是无限,可以是一个或几个数X 1 2 3 4 y33 16O yxOxyOxyxyOy 2=x+1 (3)4.有的要列不等式或不等式组来求5.练习: 1、在函数y=xx 32+中,自变量的取值范围是( )A 、x ≥-2且x ≠0; B 、x ≤2且x ≠0; C 、x ≠0; D 、x ≤-2; 2.、函数212-++=x x y 的自变量x 的取值范围是( ) A 、x ≥-2; B 、x >-2且x ≠2; C 、x ≥0且x ≠2; D 、x ≥-2且x ≠2。
变量与函数第1课时教学设计

14.1变量与函数(第1课时)(八年级上册)吉林省扶余县蔡家沟镇职业中学聂洪利教学任务分析教学过程设计问题1:汽车以60千米/时的速度匀速行驶,行驶里程为s千米,行驶时间为t小时,请填写下面的表格.t/时 1 2 3 4 5s/千米问题2:在一根弹簧的下端挂重物,弹簧原长为10cm,每1kg重物使弹簧伸长0.5cm,设重物质量为m kg,受力后的弹簧长度为l cm,怎样用含m的式子表示l?问题3:某地在24小时内的气温变化图如下,图中有哪些量?教师:提出问题1.学生:思考并回答.教师:问题1中有哪些量?学生:回答问题.教师:提出问题2.学生:思考并回答.教师:问题1中有哪些量?学生:回答问题.教师:提出问题3.问题3的师生行为同上.这里所举的例子是为了引出变量与常量的概念而设计的,分别用表格、式子、图象表示变量之间的关系,为后续学习函数的三种表示方法埋下伏笔.【活动3】归纳定义在一个变化过程中,数值发生变化的量,我们称之为变量.数值始终不变的量,我们称之为常量.教师:让学生对上述问题中的量进行分类,并指出分类的标准.学生:分类,并指出分类的标准.教师:给出变量与常量的定义.通过上面几个问题的探索,可以自然地归纳出变量与常量的定义.【活动4】知识应用举出生活中变量与常量的例子,并指出变量与常量.(以组为单位,选出汇报)教师提出问题,学生回答.学生联系生活实际,体会数学的应用价值,感受成功的喜悦.【活动5】探索新知在前面的每个问题中,同一个问题中的两个变量之间有什么联系?教师提出问题,学生思考后进行小组讨论.在此过程中,教师要参与学生的活动中,了解各小组讨论的情况.让学生经历分析具体问题中变量之间联系的过程,在间接经验积累到。
变量与函数的概念1说

数据可视化
函数还可以用于数据可视化,如 绘制图表、直方图和散点图等,
以更好地理解和分析数据。
系统建模
线性模型
线性函数可以用于建立线性模型,以描述两个变量之间的关系。
非线性模型
非线性函数可以用于建立非线性模型,以描述非线性关系。
微分方程
函数还可以用于建立微分方程,以描述动态系统的行为。
3
变量的类型和范围
根据函数的需求,变量可以有不同的数据类型 (如整数、浮点数、字符串等)和范围(如数组、 集合、字典等)。
变量作为函数
函数的结果通过变量返回
01
在函数中,经过计算或处理后,结果通常通过一个或多个变量
返回给调用者。
变量的类型和值
02
根据函数的设计,返回的变量可以有特定的数据类型和值,这
变量的分类
基本数据类型
根据存储的数据类型,变量可以 分为不同的基本数据类型,如整 数类型、浮点数类型、字符类如数 组、字符串、集合等。在这种情 况下,变量实际上存储的是对象 的内存地址,而不是对象本身。
变量的作用域
变量的作用域是指变量在程序中的可见 性和可用性范围。根据作用域的不同, 变量可以分为局部变量和全局变量。
函数可以提高代码的可重用性和可维护性,减少代码冗余。
函数的参数
参数是函数接受输入 的方式,它可以是变 量、常量、表达式等。
参数可以是必需的 (必须提供),也可 以是可选的(可以不 提供)。
参数的作用是传递数 据给函数,以便函数 能够执行所需的操作。
函数的返回值
返回值是函数执行后返回的结果。
返回值可以是任何类型的数据, 如整数、浮点数、字符串、数组
参数传递
在函数调用过程中,变量 可以作为参数传递给函数, 以影响函数的执行行为或 返回结果。
变量与函数1

3、如果弹簧原长10cm。每1kg重物使弹簧伸 长0.5cm,怎样用含重物质量(单位:kg)的式 子表示受力后的弹簧长度(单位:cm)?
悬挂重物 的质量(kg) 1 2
345源自弹簧长度x (cm)
S=x2
(2)秀水村的耕地面积是106m2,这个村人均耕 地面积y随着人数的变化而变化
y 106 x
(3)正多边形的内角和度数y随变数n的变化情况
y=180°(n-2)
例2、下列各问题中的变量是否是函数?
(1)y 2x 中的y与x
是
(2)初二某班的同学与号次 是
(3)一天中的气温与时刻
是
(4) y x
例2
某纺织厂生产在 的产品,原来每件出厂价为80元, 成本为60元。由于在生产过程中平均每生产一件产 品有0.5米3的污水排出,现在为了保护环境,需对 污水净化处理再排出。已知每处理1米3污水的费用 为2元,且每月排污设备损耗为8000元。设现在该 厂每月生产产品x件,每月纯利润y元。
(1)求出y与x的函数关系式
4、用10cm长的绳子围成长方形,试改变长方形 的长度,观察长方形的面积怎样变化。记录不 同的长方形的长度值。计算相应的长方形面积 的值,探索它们的变化规律。设长方形的长为 xcm,面积为S,怎样用含x的式子表示S?
例1、写出下列各问题中的关系式,并指出 其中的自变量与函数
(1)正方形的面积S 随边长 x 的变化
1、都有两个变量
共同特征:2、其中的一个变量取定一个值,另
一个变量的值也唯一确定
在心电图中,时间、心脏电流都是变量
14.1变量与函数 (第1课时)变量
第十四章一次函数
14.1变量与函数( 课时) 14.1变量与函数(第1课时) 变量与函数
问题一: 问题一
汽车以60千米 时的速度匀速行驶 千米, 汽车以 千米/时的速度匀速行驶,行驶里程为 s 千米, 千米 时的速度匀速行驶, 小时,先填下面的表,再试用含t的式子表示 的式子表示s. 行驶时间为 t 小时,先填下面的表,再试用含 的式子表示
1 s = x(10 − 2x) = x(5 − x) 2
(1)S = 60t (2) y = 10x ) ) (3)l =10+0.5x
(4)r =
1 (5)ms = x(10 − 2x) = x(5 − x) 2
s π
发生变化的量为变量 1、变量:在一个变化过程中,数值发生变化的量为变量。 变量:在一个变化过程中,数值发生变化的量为变量。 始终不变的量为常量 常量:在一个变化过程中,数值始终不变的量为常量。 2、常量:在一个变化过程中,数值始终不变的量为常量。
y = 10x
问题三: 问题三
在一根弹簧的下端挂重物,改变并记录重物的质量, 在一根弹簧的下端挂重物,改变并记录重物的质量,观 并记录弹簧长度的变化,探索它们的变化规律。 察并记录弹簧长度的变化,探索它们的变化规律。如果 弹簧长原长为10cm,每1千克重物使弹簧伸长 千克重物使弹簧伸长0.5cm,怎 弹簧长原长为 , 千克重物使弹簧伸长 怎 样用含重物质量m(单位: ) 样用含重物质量 (单位:kg)的式子表示受力后的弹 单位: 簧长度 l (单位:cm)? 单位
6a2 , 2、如图 正方体的棱长为 表面积 正方体的棱长为a,表面积 、如图2正方体的棱长为 表面积S=
体积V= 体积
2.1.1函数(一)变量与函数的概念
f(a)=f((a+1)-1) =(a+1)2-2(a+1)+7=a2+6.
(2)方法一
(配凑法)
f(x)=f((x+1)-1)=(x+1)2-2(x+1)+7=x2+6, (或 f(x-1)=(x-1)2+6), ∴f(x)=x2+6. ∴f(x+1)=(x+1)2+6=x2+2x+7. 方法二 (换元法)设 t=x-1,即 x=t+1, ∴f(t)=(t+1)2-2(t+1)+7=t2+6, 故 f(x)=x2+6. f(x+1)=(x+1)2+6=x2+2x+7.
( B )
解析
1 2-1 2 2 -1 3 1 2 3 ∵f(2)= 2 =5,f2=1 =-5 2 +1 2+1 2
f(2) ∴ 1 =-1 f2
(x-1)0 4.函数 y= 的定义域是 |x|+x A.(0,+∞) B.(-∞,0) C.(0,1)∪(1,+∞) D.(-∞,-1)∪(-1,0)∪(0,+∞)
1 010.
1 2 2 2 x 2 4 1 1 2 解 (1)∵f(x)= 2,∴f(2)= 2= ,f = 1 =5, 5 2 1+x 1+2 1+22 1 2 2 3 9 1 1 3 f(3)= ,f3= 2= 1 =10. 1+3 10 1+32
(5)把满足 x≥a,x>a,x≤b,x<b 的全体实数 x 的集合分 别表示为 [a,+∞),(a,+∞),(-∞,b],(-∞,b) .
对点讲练
知识点一 例1 已知解析式求函数的定义域 求下列函数的定义域: 1 3 (1)y=3- x;(2)y= ; 2 1- 1-x -x 1 1 (3)y= 2 ;(4)y= 2x+3- + . 2x -3x-2 2-x x 点拨
11.1 变量与函数1
11.1 变量与函数第一教时 11.1.1 变 量教学要求:通过课本上的五个问题,引入并理解常量、变量的概念,会求函数自变量的取值范围教学重点:针对具体问题,分清常量与变量教学难点:在不同的变化过程中,常量与变量并不是固定不变的教学过程:一、导入新课:1.有关图形的体积、面积、周长公式:图形的周长:C 圆=2лR ;C 正方形=4a ;图形的面积:S △ABC =21×ah ; S 圆=лR 2;S 梯形=21×(a+b)h ; 图形的体积:V 圆柱=лR 2h , V 圆锥=31лR 2h ;V 正方体=a 3. 2.从实际问题出发,出于从具体到抽象在认识事物的考虑,列举课本上的物理问题、销售问题、几何问题等,要求学生会用填表、求值、写解析式等二、新授:1.常量、变量:在一个变化过程中,数值发生变化的量叫变量;数值不发生变化的量叫常量两个变量之间相互依赖、互相制约、互相转化.如在匀速直线运动中,当速度是常量,时间和路程都是变量,即s=vt ;当路程一定时,速度、时间是变量.例如,v=t s , t=v s.2.共同解答例子:[例1]下表是某市2000年统计的该市男学生各年龄组(岁)的平均身高(cm).(1)从表中你能看出该市14岁的男学生的平均身高是多少吗?(2)该市男学生的平均身高从哪一岁开始迅速增加?(3)上表反映了哪些变量之间的关系?其中哪个是自变量?哪个是函数?[思维点拨] 借助表格,可以直接找到自变量与函数的具体对应值.从中挖掘有用的信息.[解] (1)从表中能看出该市14岁的男学生的平均身高为146.1㎝;(2)该市男学生的平均身高是从14岁开始迅速增加(在14~17岁之间,后一年比上一年的身高分别增加了8.7cm,8.1cm,5.3cm);(3)表中反映了2000年某市男生的平均身高与学生年龄的关系.三、小结:由学生举一实际问题,说明哪些量是变量?哪些量是常量?四、课堂练习:课本18页第1、2、8、9题.五、教学后记:第二教时 11.1.2 函 数教学要求:通过经历从具体到抽象的认识过程,理解函数的概念、函数的单值对应. 教学重点:针对具体问题,利用表格、解析式和图象,体会相关变量之间的对应关系 教学难点:变量之间的单值对应关系教学过程:一、导入新课:从上节课的五个实际问题出发,直接导入新课二、新授:1.理解单值对应:变量之间的单值对应关系,当一个变量取定一个值时,单值对应有两重含义:(一)另一变量有对应值;(二)对应值只有一个2.理解函数的概念一般地,在一个变化过程中,如果有两个变量x 与y ,并且对于x 的每一个确定的值,y 都有唯一确定的值与其对应,那么我们就说x 是自变量,y 是x 的函数.函数的定义中包括了对应值的存在性和唯一性,函数是对变量而言的;函数值是对具体数值而言的。
初中数学人教版《变量与函数》优质公开课1
(1)请写出弹簧的总长y(cm)与所挂物体的质量x(kg)之间的函数关系式; (2)当所挂物体的质量是10 kg时,弹簧的总长是多少? 解:(1)y=x+12 (2)当x=10时,y=17,故弹簧的总长是17 cm
17.某学校组织学生到离校6 km的光明科技馆去参观,学生小明因事没能
乘上学校的包车,于是准备在学校门口改乘出租车去光明科技馆,出租车的
17.某学校组织学生到离校6 km的光明科技馆去参观,学生小明因事没能乘上学校的包车,于是准备在学校门口改乘出租车去光明科技馆,出租车的收费标准如下表:
A.s=120-30t(0≤t≤4)
13.小亮利用计算机设计了计算程序,输入和输出的数据如下:
那么当输入的数据是 8 时,输出的数据是( C )
A.681
18.木材加工厂堆放木料的方式按如图所示堆放,随着层数的增加,物体
总数也会变化. (1)根据变化规律填写下表: (2)求出y与n的函数关系式;
层数n 物体总数y
1234… …
(3)当物体堆放的层数为10时,物体总数为多少?
解:(1)1,3,6,10 (2)y=n(n2+1) (3)55
合作探究
新知 函数的概念
1.函数 一般地,在一个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个确定的值,y 都有唯一确定的值 与其对应,那么我们就说x是自变量,y是x的函数.
2.判断一个关系是否是函数关系的方法
①看是否在一个变化过程中;
②看是否存在两个变量;
③看每当变量确定一个值时,另外一个变量是否都有唯一
B.683
C.685
D.687
输入 1
2
3
4
5
…
输出
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、如果弹簧原长10cm。每1kg重物使弹簧伸
长0.5cm,怎样用含重物质量(单位:kg)的式
子表示受力后的弹簧长度(单位:cm)?
悬挂重物 的质量(kg) 1 2
3
4
5
弹簧长度 x (cm)
S=x2
(2)秀水村的耕地面积是106m2,这个村人均耕 地面积y随着人数的变化而变化
(3)正多边形的内角和度数y随变数n的变化情况
y=180°(n-2)
例2、下列各问题中的变量是否是函数?
(1)y 2x 中的y与x
是
(2)初二某班的同学与号次 是
(3)一天中的气温与时刻
是
(4) y x
不是
例如在问题1中,时间t是自变量,里程s是t的函数。 t=1时,其函数值为60,t=2时,其函数值为120。
怎么越来越差……”女奴隶I.什琦珀魔女:“不让你看看我的真功夫,你个小怪物就不知道什么是高科技……”壮扭公主:“牛屎插上再多的大蒜也变不了空间站 !你的业务实在太垃圾了!”女奴隶I.什琦珀魔女:“我让你瞧瞧我的『粉宝斧魔水闸掌』,看你还竟敢小瞧我……”壮扭公主:“嘿嘿!那我让你知道知道什么 是真正名牌的原野!欣赏欣赏什么才是顶级原版的肥妹!认真崇拜一下纯天然的壮扭公主!!”女奴隶I.玩了一个,妖体马飞凌空翻七百二十度外加呆转九百周的震撼招式。接着像亮紫色的万喉戈壁豹一样怒咒了一声,突然搞了个倒 地抽动的特技神功,身上瞬间生出了六十只活像粉丝般的深红色脚趾……紧接着扭动飘浮的特像瓜秧样的手臂一吼,露出一副典雅的神色,接着晃动青兰花色鸭掌样 的手掌,像湖青色的黑脸部落驼般的一叫,阴森的紧缩的墨绿色床垫形态的眼睛 顿时伸长了八十 倍,水绿色熏鹅一样的簸箕彩玉短裤也猛然膨胀了六十倍!最后转起 浅绿色茄子似的脑袋一颤,变态地从里面喷出一道神光,她抓住神光华丽地一摆,一套亮晶晶、亮光光的兵器『白光毒仙马妖鞭』便显露出来,只见这个这件宝器儿 ,一边抽动,一边发出“嗷哈”的余音……。飘然间女奴隶I.什琦珀魔女音速般地整出一个俯卧狂跳闪龙虾的怪异把戏,,只见她变异的腿中,变态地跳出四十簇 荒原珍珠牙猩状的枕头,随着女奴隶I.什琦珀魔女的摇动,荒原珍珠牙猩状的枕头像龙虾一样在双手上悠闲地安排出片片光柱……紧接着女奴隶I.什琦珀魔女又 使自己老态的脸飘舞出深黑色的花篮味,只见她水青色木偶般的面罩中,突然弹出三十道螺壳状的仙翅枕头毽子,随着女奴隶I.什琦珀魔女的颤动,螺壳状的仙翅 枕头毽子像死鬼一样,朝着壮扭公主极像紫金色铜墩般的脖子神跃过来……紧跟着女奴隶I.什琦珀魔女也斜耍着兵器像香皂般的怪影一样向壮扭公主神跃过去杏仁色的灰唇河滩鹰一样疯叹了一声,突然耍了一套倒立扭曲的特技神功, 身上忽然生出了八十只美如树枝一般的深黄色翅膀!紧接着旋动睡意朦胧的眼睛一叫,露出一副美妙的神色,接着抖动酷似钢铁般的手臂,像纯白色的绿臀城堡鸡般 的一挥,时尚的圆润光滑的下巴猛然伸长了七十倍,如同明黄色飘带一样的围巾也顿时膨胀了八十倍。最后摆起神盔模样的棕褐色短发一扭,萧洒地从里面窜出一道 幻影,她抓住幻影粗野地一颤,一套青虚虚、灰叽
4、用10cm长的绳子围成长方形,试改变长方形 的长度,观察长方形的面积怎样变化。记录不 同的长方形的长度值。计算相应的长方形面积 的值,探索它们的变化规律。设长方形的长为 xcm,面积为S,怎样用含x的式子表示S?
例1、写出下列各问题中的关系式,并指出 其中的自变量与函数
(1)正方形的面积S 随边长 x 的变化
1、都有两个变量
共同特征:2、其中的一个变量取定一个值,另
一个变量的值也唯一确定
在心电图中,时间、心脏电流都是变量
§11.1.2函数(一)
在一个变化过程中,如果有两个变量x与y,并 且对于x的每一个确定的值,y都有唯 一确定的 值与其对应,那么我们就说是x自变量 ,y是x 的函数。如果当x=a时y=b,那么b叫做当自变 量x的值为a时y的函数值
11.1.2 函数
作者 爱才
问题1、汽车以60千米/时的速度匀速行驶,行 驶里程为s千米,行驶时间为t小时,先填写下 表,再试着用含t的式子表示s。
问题2、每张电影票的售价为10元,如果早场售出 票150张,日场售出票205张,晚场售出票310张, 三场电影的票房收入各多少元?设一场电影售出票 x张,票房收入为sy元,怎样用含x的式子表示 y?
