六年级下册数学《比例的应用》专项典型考点试题(含答案)
六年级数学下册第四单元：比例的应用题专项练习一(解析版)人教版
六年级数学下册典型例题系列之第四单元：比例的应用题专项练习一（解析版）1．（2019·河北沧州·六年级期末）一堵墙,量得25层砖高1米50厘米,这堵墙有150层砖。
这堵墙高多少米？【解析】解：设这堵墙高x 米,1米50厘米 1.5=米1.525150x = 25 1.5150x =⨯1.515025x ⨯= 9x =答：这堵墙高9米。
2．（2021·河北保定·小升初真题）数学兴趣小组的同学测得一座塔的影长是22.5米,同时把一根1米长的标竿直立在地上,测得影长0.9米。
这座塔高多少米？（用比例解）【解析】解：设这座塔高x 米。
x ∶22.5＝1∶0.90.9x ＝22.50.9x ÷0.9＝22.5÷0.9x ＝25答：这座塔高25米。
3．（2021·河南·中牟县教育体育局教学研究室六年级期末）2020年我国正式进入5G 时代。
目前5G 正以更快的速度、更稳定的连接与更大的容量融入各行各业。
小明原来用4G 下载电影《流浪地球》需要8分钟,而他现在用5G 下载这部电影所用的时间与用4G 下载所用时间的比是1∶100。
那么他用5G 下载这部电影要用多少秒？（用比例解）【解析】解：设他用5G下载这部电影要用x秒。
8分钟＝480秒x∶480＝1∶100100x＝480x＝480÷100x＝4.8答：他用5G下载这部电影要用4.8秒。
4．（2021·广东肇庆·小升初真题）一批啤酒用载重8吨的汽车运,需要15辆,如果改用载重10吨的汽车运,需要多少辆？（用比例解）【解析】解：设如果改用载重10吨的汽车运,需要x辆。
10x＝8×1510x＝120解得x＝12答：需要12辆。
5．（2021·广东河源·小升初真题）用500g海水可以晒15g海盐,照这样计算,用10吨海水可以晒多少g海盐？（用比例的方法解答）【解析】10吨＝10000千克解：设10000千克海水可以晒x千克海盐。
六年级下册数学《比例的应用》专项典型考点试题(含答案)
六年级下册数学《比例的应用》专项典型考点试题一、单选题1.求未知数x．1.2∶x＝6 x＝( )A. 16B. 0.2C.D. 52.求未知数x．x∶12.8＝10∶8x＝( )A. 16B. 0.2C.D. 53.用一个放大10倍的放大镜来观察一个30度的角，则看到的角（）A. 大小不变B. 缩小了100倍C. 放大了100倍4.求未知数x．x∶＝x＝( )A. 16B. 0.2C.D. 5二、判断题5.判断对错．（）解比例时，未知内项x等于两个外项的积乘已知内项的倒数。
6.判断对错（）三、填空题7.X=________8.X=________9.解比例：3.6：5.4=15：x,则x=________10.解比例：x：51=30：17，则x=________11.X=________四、解答题12.解比例：（1）3.6:9=10：x（2）5.5:2.5=x：2013. 求未知数．（1）=5：（2）1 ：0.26=x：15（3）4 ：1 =2 ：（1﹣x）五、综合题14.求出下列x的值（1）7：2=28：x（2）=（3）：3=x：（4）：x= ：．六、应用题15.解比例。
① ② ③ ④参考答案一、单选题1.【答案】B2.【答案】A3.【答案】A4.【答案】C二、判断题5.【答案】正确6.【答案】正确三、填空题7.【答案】8.【答案】9.【答案】22.510.【答案】9011.【答案】4四、解答题12.【答案】（1）解：3.6:9=10：x 3.6x=9×10 x=90÷3.6 x=25 （2）解：5.5:2.5=x：20 2.5x=20×5.5 2.5x=110 x=44 13.【答案】（1）解：=5：，=5÷ ，=5× ，×8=17.5×8，x=140（2）解：1 ：0.26=x：15，0.26x=1 ×15，0.26x=16.25，x=62.5（3）解：4 ：1 =2 ：（1﹣x），4 ×（1﹣x）=1 ×2 ，1﹣x= × × ，1﹣x= ，x=五、综合题14.【答案】（1）解：7：2=28：x7x=2×287x=56x=8（2）解：=2x=1.2×52x=6x=3（3）解：：3=x：3x= ×x=（4）解：：x= ：x= ×x=x=六、应用题15.【答案】① ② 0.75③0.64 ④1050。
六年级数学下册试题-比例的应用人教版含答案
比例的应用【运用比例解决问题】(2019﹒天河区模拟）晴晴全家“五一”到中山公园游玩，拍了许多照片，她买了一本相册，如果每页放6张照片，刚好放16页，现在晴晴打算每页只放4张，25页够放下这些照片吗？（用比例解）【考点】比例的应用．用比例解决问题【分析】根据照片的数量是一定的，每页放相片的张数×放照片的页数＝照片的数量（一定），由此判断每页放相片的张数与放照片的页数成反比例，设出未知数，列出比例解答即可．【解答】解：设每页只放4张，可以放x 页，4x ＝6×16,x ＝6×164, x ＝24，因为25＞24,所以25页够放下这些照片，答：25页够放下这些照片．【点评】解答此题的关键是，根据题意，先判断哪两种相关联的量成何比例，即两个量的乘积一定则成反比例，两个量的比值一定则成正比例；再列出比例解答即可．例2 (2019春﹒法库县期末）淘气和笑笑收集的邮票张数的比是3：5．淘气收集了36张邮票，笑笑收集了多少张邮票？【用比例解】【考点】比例的应用．比例的应用【专题】比和比例应用题．【分析】已知淘气和笑笑收集的邮票张数的比是3：5．淘气收集了36张邮票，设笑笑收集了x 张邮票，据此列比例解答．【解答】解：设笑笑收集了x 张邮票，3：5＝36：x3x ＝5×36x ＝5×363x ＝60．答：笑笑收集了60张邮票．【点评】此题考查的目的是理解掌握比例的意义、比例的基本性质及应用．例3 一辆汽车从甲地开往乙地，每小时行70千米，5小时到达。
如果要4小时到达，每小时要行多少千米？（1）这道题里的路程是一定的，________和________成_______比例。
所以两次行驶的________和________的________________是相等的。
（2）如果设每小时需要行驶X 千米答：每小时需要行驶 千米。
(3)如果把例2中的第三个已知条件和问题互换一下：一辆汽车从甲地开往乙地，每小时行70千米，5小时到达。
精选练习六年级下册 正比例、反比例应用题专项训练 含答案解析
正比例、反比例应用题一、应用题1.小兰的身高1.5m，她的影长是2.4m。
如果同一时间同一地点测得一棵树的影子长4米，这棵树有多高？2.一间房子要用方砖铺地，用边长5分米的方砖需用2000块，如果改用边长是4分米的方砖，需用多少块？（用比例解）3.用同样的砖铺地，铺18平方米要用618块砖．如果铺地24平方米，要用多少块砖？（用比例知识来解）4.测量小组要测量一棵树的高度，先量得树的影子长12米，接着在树的附近直立了一根长2米的竹竿，量得竹竿的影子长1.2米．这棵树的高度是多少米？5.王师傅完成一批零件，计划每天加工240个，20天完成。
实际每天多加工60个，多少天完成任务?(用比例知识解答)6.青艺农场收割小麦．前6天收割了114公顷，剩下152公顷．（1）照前几天的工作效率，剩下的还要多少天才能完成?(用比例解)（2）前几天收割的比后几天收割的少百分之几?（3）每公顷平均收小麦7.5吨，这个农场用载重5吨的卡车运回全部小麦，需要运多少次?7.小华的身高是1.6米，他的影长是2.4米．如果在同一时间、同一地点测得一棵树的影长为6米，这棵树有多高？8.市政工程队铺一条路，原计划每天铺0.6千米，24天完成．实际每天铺0.8千米，实际用多少天完成?9.给学校教务处办公室铺地砖，原计划选用3分米的方砖，需要960块；后来实际选用了4分米的方砖铺地，实际用了多少块4分米的方砖？10.甲乙两地相距360千米，一辆汽车从甲地到乙地计划7小时行完全程，汽车时间234…．（小时）路程100150200…．（千米）4.5千米，20天完成，实际每天修6千米，实际几天可修完？（用比例解）12.一辆汽车3小时行了135千米，照这样计算，行驶315千米需要几小时？（用比例解）13.一辆汽车从甲地出发，每小时行45千米，4小时到达乙地．如果每小时行60千米，几小时可到达乙地？（用比例解）14.（2015•邹城市）一艘轮船从甲港开往乙港，去时顺水，每小时行24千米，15小时到达．返回时逆水，速度降低了25%，多少小时返回甲港？（用比例解）15.用边长是40厘米的方砖给教室铺地需500块，如果改用边长是50厘米的方砖铺地，可节省多少块？16.六年级甲、乙、丙三个班植树，任务分配是：甲班要植三个班总棵数的40%，乙、丙两班植树棵数的比是4：3．当甲班植了200棵树时，正好完成三个班植．求丙班植树多少棵？树总棵数的2717.一间房子要用方砖铺地，用边长是5分米的方砖需要400块，如果改用边长是4分米的方砖，需要多少块？（用比例解）18.育美小学的六年级同学参加军校的行军训练，3小时行了15千米．照这样计算，再行17.5千米就可到达目的地，到达目的地还要行几小时?(用比例解) 19.A、B两地相距360km，一辆汽车从甲地到乙地，原计划每小时行90km，实际这辆汽车是按照下表的速度行驶的．问这辆汽车能否在原计划时间内到达目的时间（h）234…10…路程（km）100150200…500…平方米的客厅要用87.5块，那么18平方米的卧室要用多少块？21.印刷厂用一批纸装订英语练习本．如果每本36页，能订4000本，如果每本32页，能订多少本？车厢种类车厢节数每节车厢可乘人数硬座7108硬卧1678软卧43423.一间房子要用方砖铺地，用面积是9平方分米的方砖，需用96块，如果改用边长是4分米的方砖，需用多少块？（用比例解）24.在春游活动中，我班共创建了8个活动小组，每组5人。
苏教版数学六年级下册专项～比例解决问题【含答案】
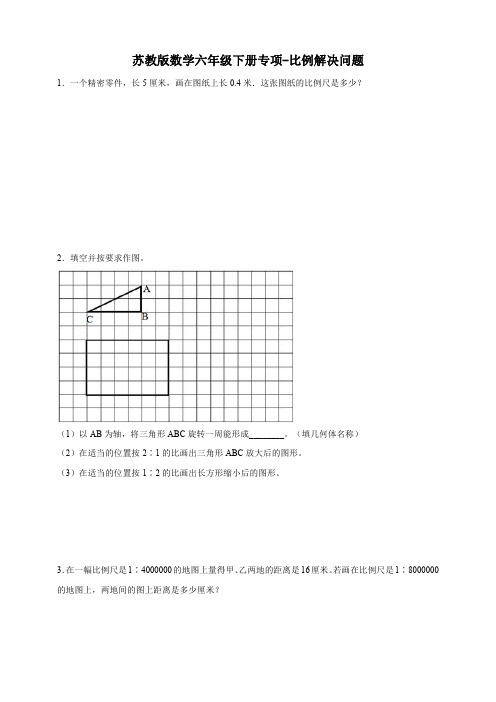
苏教版数学六年级下册专项-比例解决问题1．一个精密零件，长5厘米，画在图纸上长0.4米．这张图纸的比例尺是多少？2．填空并按要求作图。
（1）以AB为轴，将三角形ABC旋转一周能形成________。
（填几何体名称）（2）在适当的位置按2∶1的比画出三角形ABC放大后的图形。
（3）在适当的位置按1∶2的比画出长方形缩小后的图形。
3．在一幅比例尺是1∶4000000的地图上量得甲、乙两地的距离是16厘米。
若画在比例尺是1∶8000000的地图上，两地间的图上距离是多少厘米？4．画一画，填一填。
（1）按3∶1的比画出图形A放大后得到的图形B。
（2）按1∶2的比画出图形B缩小后得到的图形C。
我发现：放大或缩小前后的图形（）变了，但（）没有变，而且图形各部分长度是按一定的比变化的。
5．在一张比例尺是1∶150的建筑图纸上，量得一座大楼的长是6分米，这座大楼的实际长与宽的比是3∶1，这座大楼的实际宽是多少米？6．下图中小平行四边形按比放大后得到大平行四边形，求大平行四边形的高。
（单位：分米）12．根据图中提供的信息，完成下列问题。
（1）自来水厂要从水库取水，取水管道怎样铺最短，请在图中画出来。
（2）自来水厂到城区的送水管道经测算最短是2000米，请你测算：自来水厂到水库的取水管道最短需多少米？13．在一幅地图上，用5厘米长的线段表示实际距离100千米，这幅地图的比例尺是多少？如果甲市至乙市的铁路线路长150千米，那么这段铁路线路在这幅地图上的长度是多少厘米？14．江苏省云龙湖景区杏花坞广场是人们夏天避暑纳凉的佳处。
广场绿地面积与铺装面积的比是6∶5，其中铺装面积共5000平方米，绿地面积有多少平方米？15．甲乙两城相距150千米，在一幅地图上量得甲乙两城之间的距离是5厘米，同时在这幅地图上量得乙丙两城之间的距离是8厘米。
乙丙两城之间的实际距离是多少千米？20．下图中A点是游乐场所在的位置，B点是电影院所在的位置，两地实际距离相距2千米。
比例应用题(专项训练)数学六年级下册人教版
比例应用题（专项训练）20232024学年数学六年级下册人教版典例分析一．工程队修一段公路，原计划每天修4.8千米，18天修完。
实际提前2天修完，实际每天修多少千米？【答案】5.4千米【分析】根据题意可知：工作总量是一定的，工作效率和工作时间成反比例关系，设实际每天修x千米，据此列比例解答。
【详解】解：设实际每天修x千米。
（18－2）x＝4.8×1816x＝86.4x＝86.4÷16x＝5.4答：实际每天修5.4千米。
【点睛】明确工作总量一定，工作效率和工作时间成反比例关系，据此列出比例是解答本题的关键。
典例分析二．如图，学校大门在孔子雕像的正东方240米处。
1号教学楼在孔子雕像北偏东45°的200米处。
（1）分别计算出学校大门、1号教学楼到孔子雕像的图上距离。
（2）在图纸上画出学校大门和1号教学楼的位置。
【答案】（1）学校大门6厘米；1号教学楼5厘米（2）见详解【分析】（1）根据进率“1米＝100厘米”以及“图上距离＝实际距离×比例尺”，分别求出学校大门、1号教学楼到孔子雕像的图上距离。
（2）以图上的“上北下南，左西右东”为准，在孔子雕像的正东方画6厘米长的线段，即是学校大门；在孔子雕像的北偏东45°方向画5厘米长的线段，即是1号教学楼。
【详解】（1）240米＝24000厘米24000×14000＝6（厘米）200米＝20000厘米20000×14000＝5（厘米）答：学校大门到孔子雕像的图上距离是6厘米，1号教学楼到孔子雕像的图上距离是5厘米。
（2）如图：【点睛】本题考查比例尺的应用、根据比例尺画图以及根据方向、角度和距离确定物体的位置。
典例分析三．旗杆有多长？（1）操场上，同学们正在阳光下测量不同长度的竹竿、木棒、大树的长度及它们的影长，测量数据如表：实际长度（米）影长（米）实际长度与影长的比值跟踪训练1．在比例尺是1∶400000的地图上量得甲、乙两地的距离是6厘米。
人教版六年级下学期数学 比例的应用 完整版例题+答案解析
比例的应用★知识概要1、比例尺1)数字比例尺：图上距离与实际距离的比。
前项是图上距离，后项是实际距离。
前项和后项的单位相同。
只能表示距离的比。
2)线段比例尺可以直观看出图上一厘米代表的实际距离。
2、正比例和反比例的应用：在实际问题中，两个呈比例的量，可以用比例的知识来解决。
1）两个成正比的量：比值相等列出比例方程。
2）两个成反比的量：乘积相等列出方程。
★精讲精练例1、（1）、化简。
20kg:10g = ___2000___: ____1____6 m : 120 cm = ___5___:____1____5cm: 250km=____1____:____500000____（2）、将线段比例尺化为数字比例尺0 20 40 60km1：2000000演练1、（1）、化简。
20km:15cm = ___4000____: ____3____6 cm : 150 m = ___1____:____2500____5cm: 24km=____1____:____480000____（2）、将线段比例尺化为数字比例尺0 30 60 90km1：3000000例2、（1）填表（2）一幅地图的比例尺为1 : 20000000,小芳在地图上量得广州到上海的 某条线路全长为7.5厘米。
那么广州到上海的这条线路实际距离是多少千米？实际距离：7.5x200=1500(千米)演练2、比例尺 图上距离 实际距离1：2000000 5cm 100km 15:17.5cm 5mm 1:7500002cm 15km（2）一幅地图的比例尺为 1 : 5000000,小新在地图上量得北京到上海的铁 路长度是29厘米。
一辆高速动车从北京南站出发，经过5小时到达 上海，这辆高速动车的时速是多少？实际距离：29÷50000001=145000000（厘米）=1450(千米) 速度：1450÷5=290（千米/小时）1599m30cm1:3000000例3、（1）学校篮球场平面图的比例尺为1 : 250,工程师在平面图上量得篮球场的长为11.2厘米，宽为6厘米。
北师大版六年级下册数学第二单元 比例应用题专题训练(含答案)
北师大版六年级下册数学第二单元比例应用题专题训练1．明明妈妈有一张站在梅花树下的全身照，照片上量得妈妈高3cm，梅花树高8cm，妈妈实际身高1.62m。
你能算出这棵梅花树的实际高度是多少吗？2．一个长方形零件，画在比例尺是20∶1的图纸上，量得图上周长是36cm，它的长与宽的比是5∶4，这个零件的实际面积是多少？3．在比例尺为3∶1的设计图上，量得精密零件的长为105毫米，这种精密零件的实际长度是多少？4．学校举行四驱车模比赛。
小强的车模速度为480米/分，跑完全程用了5分钟。
小瑞的车模跑完全程比小强的多用了1分钟，他的车模速度是多少？5．在同一张地图上，量得甲乙两地的图上距离是40厘米，乙丙两地的距离是50厘米，已知甲乙两地的实际距离是8千米，乙丙两地的实际距离是多少千米？6．恒大12号楼的实际高度是35m，它的高度与模型高度之比是500：1，模型的高度是多少厘米？（用比例知识解答）7．汽车厂按1∶20的比例生产了一批汽车模型。
（1）一辆轿车的模型长25.6厘米，它的实际长度是多少厘米？（2）一辆公共汽车长12.3米，模型车的长度是多少米？8．在一张比例尺是1：15000000的地图上，量得甲地到乙地的距离是3cm。
则两地间的实际距离是多少千米？一列火车从甲地到乙地用了3小时，那么火车的平均速度是多少？9．在比例尺为1：5000的图纸上，画了一个边长4厘米的正方形花坛，花坛的实际面积是多少公顷？10．在一幅比例尺是1：2000000的地图上，量得甲、乙两个城市之间高速公路的距离是4cm。
在另一幅比例尺是1：4000000的地图上，这条公路的图上距离是多少？（用比例解）11．运输公司的一辆汽车从甲地往乙地运送物资，原计划每小时行75千米，4小时到达。
现在情况有所变化，需要3小时到达，每小时要行多少千米？（用比例解）12．工程队修一条水渠，每天工作6小时，12天可以完成。
如果工作效率不变，每天工作8小时，多少天可以完成任务？（用比例解）13．工程队修一条水渠，每天工作8小时，15天可以修完。
比例应用题含有答案
比例应用题含有答案比例应用题含有答案【试题】【题1】甲数比乙数少20%，那么乙数比甲数多百分之几？【题2】有一堆糖果，其中奶糖占45%，再放入16块水果糖后，奶糖就只占25%，这堆糖中有奶糖多少块？【题3】一个正方体的棱长增加原长的1/2，他的表面积比原表面积增加百分之几？【题4】商店有篮球和排球共45个，其中篮球占60%，当卖出一批篮球后，篮球占现在总数的25%，卖出的篮球是多少个？【题5】把一个正方形的一边减少20%，另一边增加2公尺，得到一个长方形，他与原来的正方形面积相等，那么正方形的.面积是多少平方公尺？【题6】已知甲校学生数是乙校学生数的40%，甲校女生数是甲校学生数的30%，乙校男生数是乙校学生数的42%，那么，两校女生数占两校学生总数的百分之几？【题7】把25公克盐放进100公克水里制成盐水，制成的这种盐水，含盐量是百分之几？【题8】某次会议，昨天参加会议的男代表比女代表多700人，今天男代表减少10%，女代表增加5%，今天共1995人出席会议，昨天参加会议的有多少人？【题9】有甲、乙两家商店，如甲店的利润增加20%，乙店的利润减少10%，那么，这两店的利润就相同，问原来甲店的利润是原来乙店的利润的百分之几？【题10】有浓度为3.2%的盐水500公克，为把他变成浓度是8%的盐水，需要使他蒸发掉多少公克的水？【参考答案】1．【解答】20%÷（1－20%）=25%。
2．【解答】16÷【（1－25%）÷25%―（1―45%）÷45%】=9（块）。
3．【解答】【（1＋1/2）×（1＋1/2）×6】÷（1×1×6）－1 = 125%。
4．【解答】45×60%－18×【25%÷（1－25%）】 = 6（个）。
5．【解答】【2×（1－20%）÷20%】2 = 64（平方公尺）。
人教版六年级下册数学第四单元比例应用题训练(含答案)
人教版六年级下册数学第四单元比例应用题训练1．在比例尺为1：15000000 的地图上，量得两地间的距离为18 cm。
甲、乙两列动车同时从两地相对开出，6 小时后相遇。
已知甲、乙两列动车的速度比为11：9，两车相遇时，甲车相驶了多少千米?2．在比例尺是20：1的图纸上，量得一个零件的长是2cm。
这个零件的实际长是多少毫米?3．在比例尺是的地图上，量得扬州到北京的距离为12cm。
如果一列火车以每小时160 km的速度于上午8时从扬州火车站开出，那么下午几时几分这列火车可到达北京？4．身高1.8m的李华在公园里观赏一尊雕像时，想知道雕像的高度。
他灵机一动，站到雕像旁边拍了一张合影，然后量得照片上的他高3 cm，雕像高8 cm。
雕像的实际高度是多少米？5．一幅地图，图上4 cm表示实际距离32km。
如果实际距离是144 km，图上距离是多少厘米？(用两种方法解答)6．淘淘早上8时从家出发，平均每小时骑行30 km，下午4：30到了目的地，中间休息3小时，如果将淘淘的骑行距离在比例尺1：300000的图上表示出来，图上距离应该是多少厘米？7．王大爷种了一块直角三角形的菜地，两条直角边共长10.8 m，它们的长度比是5：4。
将这块菜地用1：200的比例尺画在图上，这块菜地的图上面积是多少平方厘米？8．某工厂要加工1296个零件，前5天已经加工了240个。
照这样计算，余下的还需要多少天才能完成？(用解比例的方法解答)9．一杯糖水中放了20 g糖和400 g水。
（1）如果想用600g水调出一杯甜度相同的糖水，应放多少克糖？（2）如果想用600 g糖调出一杯甜度相同的糖水，应加多少克水？10．小刚在教学楼前测得自己的身高与影子的长度比为5：4，这时教学楼的影子长12米，教学楼的高度是多少米?11．在比例尺是1：1000 的地图上量得甲、乙两地相距4厘米。
如果画在比例尺是1：8000的地图上，应该画多长?12．学校给一间边长为6米的正方形教室铺地，需要地砖288块。
六年级数学下册《比例》重点知识点+专项练习题
老师在整理了小学六年级数学下册《比例》知识点及练习题，考试重点，同学们可以收藏一份！02专项训练一、填一填1、（ ）叫做比例。
2、在一个比例中，两个内项正好互为倒数，已知一个外项是2/5，则另一个外项是（ ）。
3、北京到天津的实际距离是120千米，在比例尺是的地图上，两地的图上距离是（ ）厘米。
4、如果2a=3b，那么a:b=（ ）:（ ）。
5、用12的因数中的任意四个数组成一个比例是（ ）。
6、 3：（ ）=6：10=（ ）：357、在总价、单价和数量三种量中，当（ ）一定时，（ ）与（ ）成正比例当（ ）一定时，（ ）与（ ）成正比例当（ ）一定时，（ ）与（ ）成反比例8、配置一种淡盐水，盐占盐水的，盐与水的比是（ ）。
二、判断对错1、如果甲数是乙数的1/5（甲、乙均不为0），甲与乙的比是1：5。
（ ）。
2、用同样的方砖铺地，铺地面积与方砖块数成反比例。
（ ）3、一项工程，甲独做要10小时，乙独做要8小时，甲、乙工作效率的之比是5：4 （ ）4、圆的面积与它的半径成正比例关系。
（ ）5、求比例中的未知项，叫做解比例。
（ ）6、一幅地图的比例尺是1：500000m。
（ ）三、选一选，将正确答案的序号填在括号里。
1、一个加数一定，和与另一个加数（ ）。
A、成正比例 B成反比例 C不成比例2、出粉率一定，面粉质量与小麦质量成（ ）A、成正比例 B成反比例 C不成比例3、在一副平面图上，用图上距离2cm表示实际距离200m,这幅图的比例尺是（ ）A、1：100B、 1：1000 C 1：100004、按1：5将长方形缩小，就是将长方形的面积缩小到原来的（ ）A、1/5B、1/10C、1/255、用3、4、16、12四个数组成比例，正确的是（ ）A、3：16=4：12B、3：4=12：16C、16：12=4：3四、算一算，解比例五、画一画，操作题。
学校要建一个长100m,宽60m的长方形操场用1：1000的比例尺画出操场的平面图。
最新人教版六年级下册数学比例的应用练习题以及答案
最新人教版六年级下册数学比例的应用练习题以及答案最新六年级下册数学比例的单元测试题一、填空题：1、比例尺是指地图上的距离与实际距离之间的比例关系。
比例尺=图上的距离:实际距离。
2、在比例尺是1：xxxxxxx的地图上，图上距离1厘米表示实际距离1千米。
也就是图上距离是实际距离的xxxxxxx倍。
3、一种微型零件的长5毫米，画在图纸上长20厘米，这幅图的比例尺是1:400.4、甲数的3等于乙数的75%，那么甲数与乙数的比是4:3.5．比的前项一定，比的后项和比值成反比例。
6、当a一定时，b和c成正比例，当c一定时，a和b成反比例。
7、一项工程，甲单独做要10天完成，乙单独做要8天完成，甲乙两人的工作效率之比是5:4.8、订《小学生语文报》的份数和总金额成正比例。
9、1:0.25的比值是4，如果后项乘以4，要使比值不变，前项应该变成4，如果前、后项都除以0.25，比值是16.10、甲、乙两数的比是5:8，甲数是25，乙数是40.二、判断(对的打“√”，错的打“×”)。
1．圆周率一定，直径与周长成正比例。
×2．比例尺是一个比。
√3．正方体的棱长与体积成正比例。
×4．如果5a＝7b，那么5:a＝7:b。
√5．一幅地图用1厘米表示80千米．这幅图的比例尺是1:xxxxxxx。
×三、选择1．甲、乙两个圆的半径的比是2:3，它们的面积比是C．4:92．比例尺是1:xxxxxxx表示图上1厘米相当于地面上实际距离C．5千米3、如果y＝7x，y和x成正比例（A．正比例）4、与4:0.3能组成比例的是B．0.8:65、长方形的周长一定，长与宽成反比例（C．反比例）四、实际应用：1、（1）比例尺=13厘米:780千米=1:.2）A、B两城的实际距离=5厘米×=300千米。
2、甲车的速度=2x，乙车的速度=3x，甲、乙两车的速度比是2:3，所以2x:3x=2:3，解得x=300，甲车的速度=2x=600千米/小时，乙车的速度=3x=900千米/小时。
六年级下册比例试卷【含答案】
六年级下册比例试卷【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪种比例关系可以用正比例表示？A. 路程与时间B. 速度与时间C. 路程与速度D. 成本与数量2. 如果 a:b = c:d，那么 a 与 c 的关系是？A. a = cB. a > cC. a < cD. 无法确定3. 下列哪个比例关系可以用反比例表示？A. 工作量与人数B. 工作效率与人数C. 工作量与工作效率D. 工作时间与工作效率4. 已知 x:y = 3:4，如果 x 增加 3，y 增加 4，那么新的比例关系是？A. x:y = 6:8B. x:y = 3:4C. x:y = 6:7D. x:y = 7:85. 下列哪个选项不是比例的基本性质？A. 两内项之积等于两外项之积B. 两外项之积等于两内项之积C. 两内项之和等于两外项之和D. 两外项之和等于两内项之和二、判断题（每题1分，共5分）1. 如果 a:b = c:d，那么 a + b = c + d。
（）2. 在比例中，两个外项的乘积等于两个内项的乘积。
（）3. 速度和时间成正比例关系。
（）4. 如果两个相关联的量的乘积一定，那么它们成反比例关系。
（）5. 比例中的项可以是任何数值。
（）三、填空题（每题1分，共5分）1. 如果 a:b = 2:3，那么 2a = __b。
2. 已知 x:y = 4:5，如果 x = 8，那么 y = __。
3. 如果 a:b = c:d，那么 a/c = __。
4. 在比例中，两个外项的乘积等于两个内项的乘积，这个性质叫做比例的 __ 性。
5. 如果两个相关联的量的乘积一定，那么它们成 __ 比例关系。
四、简答题（每题2分，共10分）1. 请简述比例的基本性质。
2. 请解释正比例和反比例的区别。
3. 请举例说明比例在实际生活中的应用。
4. 请解释比例尺的意义。
5. 请解释如何解比例方程。
五、应用题（每题2分，共10分）1. 甲、乙两人分别有 120 元和 150 元，如果甲给乙 30 元，那么他们的钱数比是多少？2. 一辆汽车行驶 240 千米用了 3 小时，求这辆汽车的速度。
人教版六年级下册数学第四单元比例应用题专题训练(带答案)
人教版六年级下册数学第四单元比例应用题专题训练1．把一个长方形养鱼池按1：200 的比例尺画在图纸上，长是4d m，宽是3dm。
这个养鱼池的实际占地面积是多少平方米?2．两个互相咬合的齿轮，大齿轮有60个齿，每分钟转80圈，小齿轮有20个齿，每分钟转多少圈？3．一架飞机所带的燃料最多可以飞行6小时，飞机去时顺风，每小时可以飞行1500 km，返回时逆风，每小时可以飞行1200 km。
这架飞机最多能飞行多少千米就需要返回？4．制一批零件，甲单独完成要8小时，已知甲、乙的工作效率比是4：3，则乙单独完成要多长时间？5．有种钢管长6 m，把它锯成50 cm的小段，要锯44分钟，照这样计算，如果把它锯成40 cm的小段，要锯多少分钟？6．王大爷种了一块直角三角形的菜地，两条直角边共长10.8 m，它们的长度比是5：4。
将这块菜地用1：200的比例尺画在图上，这块菜地的图上面积是多少平方厘米？7．在比例尺为1 ：9000000的航空图上，甲、乙两地相距30cm，有两架飞机同时从甲、乙两地起飞，分别以810km/h和690km/h的速度相向飞行，经过几小时两架飞机在空中相遇？8．在比例尺是1：2500000的地图上，量得A、B两地相距12厘米。
如果李叔叔和王叔叔开车同时从两地相对出发，李叔叔开车每小时行105千米，王叔叔开车每小时行95千米，几小时后两人能相遇？9．为了加快推进美丽乡村建设，某工程队铺一条乡村公路，原计划每天铺320m，15天铺完。
实际施工时，由于改进了铺路方法，前4天就铺了1600m。
照这样计算，该工程队可以比原计划提前几天完成铺路任务？(用比例解答)10．一间房子用方砖铺地，如果用边长4分米的正方形地砖一共需要360块；如果改用边长为6分米的正方形地砖来铺，一共需要多少块？11．爸爸暑假准备开车带小明去上海迪士尼玩，他在一幅比例尺是1：4000000的中国地图上量得台州到上海的距离大约是8.5cm，如果爸爸开车平均每小时行驶85km，多少小时能到达？12．一间房子要用方砖铺地，用边长3分米的方砖，需要96块；如果改用边长是2分米的方砖，需要多少块？（用比例知识解答）13．在一幅比例尺是1∶5000000 的地图上，量得A地和B 地相距6 厘米。
青岛版六年级数学下册第四单元《比例尺的认识及应用》专项精选试卷 附答案
青岛版六年级数学下册核心考点专项评价6. 比例尺的认识及应用一、填空。
(每空 2 分，共 14 分)1. 甲、乙两地的实际距离为 8 千米，画在比例尺为 1 ∶ 50000 的图纸上，应画 ( )厘米。
2. 三角形的底和高都是 2 厘米，如果按3 ∶ 1 的比放大，放大后的三角形和原三角形的面积之比是( )。
3. 在比例尺是 10 ∶ 1 的图纸上，量得某零件的长为 6 厘米，这个零件的实际长为( )厘米。
4. 把图形按 4 ∶ 1 的比放大，就是把图形的各边长放大到原来的( )倍；按1 ∶ 3 的比缩小，就是把原来图形的各边长缩小到原来的⎝ ⎛⎭⎪⎫。
5. 阳光小区计划挖一条排水渠，在比例尺是1100的设计图上，水渠长 80 厘米，宽 0.5 厘米，深 0.4 厘米。
按图施工，挖这条水渠需挖土( )立方米。
6. 把正方形的边长按 2 ∶ 1 的比放大，放大后正方形的周长是原来的( )倍。
二、判断。
(每小题 4 分，共 16 分)1. 图上距离一定比实际距离小。
( )2. 把一个长方形操场画在 1∶100 的图纸上，图上操场的面积缩小到原来的1100。
( ) 3. 一幅地图，图上距离 50 厘米表示实际距离 50 米，这幅地图的比例尺是 1 ∶ 10。
( )4. 比例尺是一把测量长度的尺子。
( ) 三、选择。
(每小题 4 分，共 20 分)1. 下面三幅地图的图幅大小相同，把比例尺按由大到小的顺序排列正确的是( )。
①北京市朝阳区地图②中国地图③河北省地图A. ①③②B. ②①③C. ③①②D. ②③①2. 当一幅地图的图幅大小不变时，若选用的比例尺越小，则( )。
A. 画在图上的实际范围变小B. 画在图上的实际范围不变C. 图上表达的内容越简略D. 图上表达的内容越详细3. 在一幅比例尺是 1 ∶ 1000000 的地图上，用( )厘米表示 60 千米。
A. 0.6B. 6C. 60D. 6004. 把一个图形按 5∶1 的比放大后，( )。
人教版六年级下册数学第四单元比例应用题训练(含简单答案)
人教版六年级下册数学第四单元比例应用题训练1．曲港高速公路（曲阳至黄骅港）是河北省“东出西联”出海通道，其定州段连通京昆和京港澳高速，填补安国、博野两地无高速公路的空白，项目建设里程约为92千米，在一幅1∶4000000的地图上，这条高速公路的长度是多少？2．一个骑兵俑模型身高是18厘米，模型高度与实际高度的比是1∶10。
这个骑兵俑的实际身高是多少？（用比例解）3．在的地图上量得甲乙两地的距离是4厘米，甲乙两地的实际距离是多少？把它画在1∶4000000的地图上应画多长？4．在一幅比例尺为1∶2000000的地图上，量得甲乙两地之间的公路长10厘米。
一辆汽车和一辆货车从两地同时出发相向而行，汽车以每小时55千米的速度行驶，2小时后在超过中点10千米的地方相遇。
货车每小时行多少千米？5．在比例尺1∶4000000的地图上，量得天津到北京的距离是3厘米。
一辆汽车以每小时60千米的速度从天津开往北京，几小时能到达？6．一种药水，药液与水的比是1∶180，如果配制905千克的药水，需要药液多少千克？（用比例解）7．学校把制作爱心贺卡的任务按5∶4分配给六年级和五年级。
六年级实际制作了108张贺卡，超过原分配任务的20%，原计划五年级制作多少张爱心贺卡？8．小红去银行换港币，当天人民币与港币的兑换比是1∶1.25，小红要兑换1000元港币，她需要给银行多少元人民币？（用比例解）9．某市修一条道路，计划每天修120米，8天可以修完。
但因为天气原因，12天才完成任务，实际每天修多少米？（用比例方法解）10．一列动车从A城开往B城前3小时行了540千米，照这样的速度，动车还要行驶4小时才能到达B城，A城和B城相距多远？（用比例的方法解答）11．小明和小英住在同一个小区、小明家上个月用电102度，电费是61.2元。
小英家上个月用电85度，小英家上个月的电费是多少元？（用比例知识解答）12．小东家的客厅是正方形的，用边长0.6m的方砖铺地，正好需要100块。
【六年级数学】比例的应用训练题(含答案)
比例的应用训练题(含答案)
33 比例的应用基础训练题
（45分钟 100分）
一、引导记忆题（67分）
1、填一填。
（24分）
（1）通常把比例尺写成前项是（）的比。
（2），这是（）比例尺，改写成数值比例尺是（）。
（3）已知比例的两个内项互为倒数，一个外项是，另一个外项是（）。
（4）在水和糖的质量比是41的糖水中，含糖04克，含水（）克。
（5）甲、乙两车的速度比是45，行完一段路程，乙车所用时间和甲车所用时间的比是（）。
（6）甲、乙两城之间的距离是360千米，在一幅地图上量得两城之间的距离是4厘米，这幅地图的比例尺是（）。
2、对号入座（将正确答案的序号填在括号里）。
（28分）
（1）在11000000的地图上量得甲、乙两地间的距离是3厘米，表示实际距离是（）。
A 300米
B 300千米
c 30千米 D 3米
（2）下面每组中的两个比可以组成比例的是（）。
A 1012和3542
B 2018和6020
c 和812
（3）一个长方形按31变化后，得到的图形与原图形比较，正确的说法是（）。
A 面积扩大9倍
B 面积缩小9倍。
六年级比例的试题及答案
六年级比例的试题及答案一、选择题（每题2分，共10分）1. 以下哪个选项是比例关系？A. 3:4B. 3:4=6:8C. 3:4=7:9D. 3:4=5:6答案：B2. 一个比例的两个外项分别是8和12，两个内项分别是x和15，那么x的值是多少？A. 10B. 12C. 15D. 20答案：A3. 甲数与乙数的比例为3:2，甲数是18，那么乙数是多少？A. 12B. 24C. 36D. 48答案：A4. 一个比例的两个内项分别是4和9，两个外项分别是x和6，那么x 的值是多少？A. 2B. 3C. 4D. 5答案：B5. 一个比例的两个外项分别是5和10，两个内项分别是x和20，那么x的值是多少？A. 4B. 5C. 10D. 20答案：A二、填空题（每题2分，共10分）1. 如果2:3=4:6，那么6:9=______:12。
答案：42. 甲数是乙数的2倍，甲数与乙数的比例是______:1。
答案：23. 一个比例的两个内项分别是8和16，两个外项分别是4和______。
答案：324. 甲数与乙数的比例为5:3，如果甲数是25，那么乙数是______。
答案：155. 一个比例的两个外项分别是7和14，两个内项分别是______和28。
答案：4三、解答题（每题5分，共20分）1. 已知一个比例的两个外项分别是12和18，两个内项分别是x和y，且x+y=30，求x和y的值。
答案：根据比例的性质，我们有12/18 = x/y，即2/3 = x/y。
又因为x+y=30，可以设x=2k，y=3k，那么2k+3k=30，解得k=6。
所以x=12，y=18。
2. 甲、乙、丙三个数的比例为2:3:5，如果甲数是20，求乙数和丙数的值。
答案：根据比例关系，乙数是甲数的3/2倍，即20*3/2=30。
丙数是甲数的5/2倍，即20*5/2=50。
3. 一个比例的两个内项分别是10和15，两个外项分别是x和20，求x的值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
六年级下册数学《比例的应用》专项典型考点试题
一、单选题
1.求未知数x．1.2∶x＝6 x＝( )
A. 16
B. 0.2
C.
D. 5
2.求未知数x．
x∶12.8＝10∶8
x＝( )
A. 16
B. 0.2
C.
D. 5
3.用一个放大10倍的放大镜来观察一个30度的角，则看到的角（）
A. 大小不变
B. 缩小了100倍
C. 放大了100倍
4.求未知数x．
x∶＝
x＝( )
A. 16
B. 0.2
C.
D. 5
二、判断题
5.判断对错．（）
解比例时，未知内项x等于两个外项的积乘已知内项的倒数。
6.判断对错（）
三、填空题
7.
X=________
8.
X=________
9.解比例：3.6：5.4=15：x,则x=________
10.解比例：x：51=30：17，则x=________
11.
X=________
四、解答题
12.解比例：
（1）3.6:9=10：x
（2）5.5:2.5=x：20
13. 求未知数．
（1）=5：
（2）1 ：0.26=x：15
（3）4 ：1 =2 ：（1﹣x）
五、综合题
14.求出下列x的值
（1）7：2=28：x
（2）=
（3）：3=x：
（4）：x= ：．
六、应用题
15.解比例。
① ② ③ ④
参考答案
一、单选题
1.【答案】B
2.【答案】A
3.【答案】A
4.【答案】C
二、判断题
5.【答案】正确
6.【答案】正确
三、填空题
7.【答案】
8.【答案】
9.【答案】22.5
10.【答案】90
11.【答案】4
四、解答题
12.【答案】（1）解：3.6:9=10：x 3.6x=9×10 x=90÷3.6 x=25 （2）解：5.5:2.5=x：20 2.5x=20×5.5 2.5x=110 x=44
13.【答案】（1）解：=5：，
=5÷ ，
=5× ，
=17.5，
×8=17.5×8，
x=140
（2）解：1 ：0.26=x：15，
0.26x=1 ×15，
0.26x=16.25，
x=62.5
（3）解：4 ：1 =2 ：（1﹣x），
4 ×（1﹣x）=1 ×2 ，
1﹣x= × × ，
1﹣x= ，
x=
五、综合题
14.【答案】（1）解：7：2=28：x 7x=2×28
7x=56
x=8
（2）解：=
2x=1.2×5
2x=6
x=3
（3）解：：3=x：
3x= ×
3x=
x=
（4）解：：x= ：
x= ×
x=
x=
六、应用题
15.【答案】① ② 0.75
③0.64 ④1050。