四年级_和差问题
四年级_和差问题

巩固2
两个连续奇数的和是36,这两个数分别是多少? 两个连续奇数的差是2,利用和差公式解答如下. 较小数: 较大数:
( - 2) 2 17 36
36 17 19
巩固3
一辆公交车里有30位乘客,到大桥站有17人下车,又上 来19人,现在车上和原来比,人多了还是少了,多(或少) 几个人?
和差问题
和差问题是已知大小两个数的和与这 两个数的差,求大小两个数各是多少 的应用题。
学习目标
• 会判断什么样的应用题属于和差问题.已 知两个数的和以及两个数的差,要分别求 这两个数就属和差问题,并掌握和差问题 的特性,为以后继续学习和倍、差倍问题 做准备. • 总结归纳出解决和差问题的方法,并解决 一些实际问题.
巩固1
有一种小虫,每隔2秒钟分裂一次.分裂后的2只新的小虫经过2秒钟后又会 分裂.如果最初瓶中只有1只小虫,那么2秒后变2只,再过2秒后就变4只 ……2分钟后,正好满满一瓶小虫.现在这个瓶内最初放入2只这样的小 虫.经过多长时间,正巧也是满满一瓶小虫? 如果刚开始瓶里有1只小虫,每隔2秒钟分裂一次,第一次就分裂成2个, 第二次就分裂成4个……这样2分钟就正好有了满满一瓶小虫.如果瓶 里开始就放有2只小虫,那么第一次就分裂成4个,和原来比少了1个分 裂成两个的2秒,直接已经有了2个.这样如果瓶里有2只小虫,就会原 来的时间少2秒,需要1分钟58秒就分裂成了满满一瓶小虫.
知识点拨:
• 为了解答这种应用题,首先要弄清两个数相差多 少的不同叙述方式.有些题目明确给了两个数的差, 而有些应用题把两个数的差“暗藏”起来,我们 管暗藏的差叫“暗差”。 • 知道两个数的和,以及它们的差,要求这两个数, 解决和差问题需要我们画线段图来分析,方法如 下: 方法一: (和+差)÷2=大数 和-大数=小数 方法二: (和-差)÷2=小数 和-小数=大数
四年级和差问题2

四年级和差问题
1、三四年级平均每个年级有学生218人,三年级学生人数比四年级学生少10
人。
三四年级各有学生多少人?
2、小红和小芳4分钟共跳绳688下,已知小红平均每分钟比小芳少跳4下。
小
红和小芳平均每分钟各跳多少下?
3、哥哥和弟弟共有邮票70张。
如果哥哥给弟弟4张邮票,则哥弟俩的邮票同样
多。
哥哥弟弟原来各有邮票多少张?
4、一个两层书架共放书72本,若从上层书架拿出9本书给下层书架,则两层书
架上的书同样多。
上下层书架各放书多少本?
5、姐姐和妹妹共有糖果40块,如果姐姐给妹妹7块糖果,则姐妹俩的糖果数一
样多。
姐姐和妹妹原来各有糖果多少块?
6、甲乙两个笼子共有兔子16只,若给甲笼再放入4只兔子,从乙笼取出2只兔
子,这时甲乙两个笼子中兔子的只数就同样多。
甲乙两个笼子原来各有多少只?
7、把一条100米长的绳子剪成三段,要求第二段绳子比第一段绳子长16米、第
三段绳子比第一段绳子短18米。
三段绳子各长多少米?
8、某工厂第一、第二、第三车间共有工人280人,第一车间的工人数比第二车
间的工人数多10人,第二车间的工人数比第三车间的工人数多15人。
三个车间各有工人多少人?
9、某工厂将857元奖金分给在劳动技能比赛中荣获前三名的优秀工人,第一名
优秀工人比第二名优秀工人多得250元,第二名优秀工人比第三名优秀工人多得125元。
三名优秀工人各分得多少元奖金?
10、小明期末考试语文、数学和英语的平均分数是95分,数学比语文多得6分,
英语比语文多得9分。
小明这三门功课各得了多少分?。
四年级-和差问题

画线段图
在一道减法算式里,被减数、减数、差三个数的和是256,减数比差大32,求差是多少?
画线段图找出“差”
甲乙两人共30元,甲收入了5元,乙丢了2元,乙比甲还多3元,求甲原来有多少钱?
甲乙丙三班共120人,甲班比乙班多5人,甲乙两班比丙班多10人,求甲乙丙各多少人?
隐含的“差”
甲乙丙三人共89本书,甲比乙多2本书,乙比丙多3本,求甲、乙、丙各多少本书?
转化出“和”或“差”
已知:A+B=15,B+C=13,C+A=18,求A、B、C。
观察:
A+15①由①式可知A和B的和,那A和B的差?
B+C=13②③-②=A-B=5可知A和B的差。
A+C=18③
隐含的“和”—方程更简单
和差问题
1.公式的由来:大数=(和+差)÷2; 小数=(和-差)÷2
2.判断是和差问题:题目中仅提到“和”或“差”,找出隐藏的“差”或“和”
3.学会大招“线段图”
甲乙两班共有88人,甲班比乙班多12人,求两班各有多少人?导出公式
乙:12乙:则小数公式:
甲:甲:则大数公式:
隐含的“差”
甲乙两个仓库共142袋大米,从甲运25袋到乙仓库,甲比乙还多8袋,求甲原来有多少袋?
今年小强7岁,爸爸35岁,当两人的年龄和是58岁时,两人年龄各多少岁?
甲乙两筐苹果分给5个人,每人刚好分4个。如果甲框拿出4个苹果给乙筐,甲比乙还多2个,求甲、乙原来各有多少个苹果?
在一道减法算式里,被减数、减数、差共256,减数比差大32,求差是多少
四年级和差问题奥数题

1. 小明和小红的分数和为180分,小明的分数比小红多20分。
小明得了多少分?A. 80分B. 90分C. 100分D. 110分2. 甲乙两个仓库的货物总量为300吨,甲仓库的货物比乙仓库多40吨。
甲仓库有多少吨货物?A. 150吨B. 160吨C. 170吨D. 180吨3. 两筐苹果共重80千克,从甲筐取出5千克苹果放入乙筐后,两筐苹果重量相等。
原来甲筐有多少千克苹果?A. 35千克B. 40千克C. 45千克D. 50千克4. 兄弟两人共有邮票70张,如果哥哥给弟弟4张后还比弟弟多2张。
哥哥原来有多少张邮票?A. 35张B. 37张C. 39张D. 41张5. 甲乙两人的年龄和为30岁,乙比甲年轻3岁。
甲的年龄是多少岁?A. 15岁B. 16岁C. 17岁D. 18岁6. 小红和小明共有图书80本,如果小红给小明5本后,还比小明多4本。
小红原来有多少本图书?A. 42本B. 45本C. 47本D. 50本7. 两堆石子共40颗,从第一堆中拿出5颗放入第二堆后,两堆石子数量相同。
第一堆原来有多少颗石子?A. 15颗B. 20颗C. 25颗D. 30颗8. 甲乙两数的和为100,甲数比乙数大20。
甲数是多少?A. 40B. 50C. 60D. 709. 姐姐和弟弟共有贺卡80张,如果姐姐给弟弟3张后,还比弟弟多4张。
姐姐原来有多少张贺卡?A. 39张B. 41张C. 43张D. 45张10. 两个水桶共盛水50升,如果把第一桶里的水倒出10升到第二桶里,两个水桶中的水就一样多。
第一桶原来有多少升水?A. 15升B. 25升C. 30升D. 35升。
四年级数学上册『和差问题』思维训练题
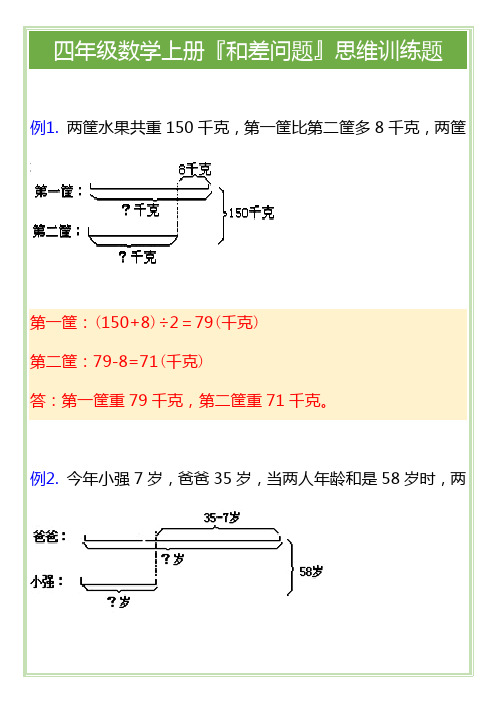
答:当父子两人的年龄和是58岁时,小强15岁,他爸爸43岁。
例3.小明期末考试时语文和数学的平均分数是94分,数学比语文多8分,问语文和数学各得了几分?
成绩之和:94×2=188(分)
数学:(188+8)÷2=196÷2=98(分)
语文:(188-8)÷2=180÷2=90(分)
例1. 两筐水果共重150千克,第一筐比第二筐多8千克,两筐水果各多少千克?
第一筐:(150+8)÷2=79(千克)
第二筐:79-8=71(千克)
答:第一筐重79千克,第二筐重71千克。
例2. 今年小强7岁,爸爸35岁,当两人年龄和是58岁时,两人年龄各多少岁?
爸爸的年龄:[58+(35-7)]÷2=43(岁)
答:小明期末考试语文得90分,数学得98分。
例4.甲乙两校共有学生864人,为了照顾学生就近入学,从甲校调入乙校32名同学,这样甲校学生还比乙校多48人,问甲、乙两校原来各有学生多少人?
乙校原有学生:(864-32×2-=488(人)
答:甲校原有学生488人,乙校原有学生376人。
四年级和差问题

和差问题1、两袋大米共重150千克,第二袋比第一袋多10千克,两袋大米各重多少千克?2、聪聪期末考试时语文和数学的平均分是98分,数学比语文多2分,问聪聪的语文和数学各得多少分?3、甲乙两车共有乘客160人,从甲站经乙站开往丙站,在乙站甲车增加17人,乙车减少23人,开往丙站时,两车原有乘客各多少人?4、今年小玲6岁,她父亲34岁,当两人年龄和是58岁时,两人年龄各自多少岁?5、甲、乙两生产组共有车床96台,如果甲组给乙组8台,则两组的台数相等,问两组车床各有多少台?6、甲、乙两个笼子里共有小鸡20只,甲笼里新放4只,乙笼里取出1只,这时乙笼还比甲笼多1只,求甲、乙两笼原来各有鸡多少只?7、甲、乙两个笼子里共有小鸡20只,甲笼里取出4只,乙笼里新放1只,这时乙笼还比甲笼多1只,求甲乙两笼原来各有鸡多少只?8、三只船运木板98块,第一只船比其余两船共运14块,第二船比第三船多运2块,三只船各运多少块木板?9、有A、B、C 三个数,它们的和是100,其中A比其余两数的和多10,B比C又多1,求三个数各是多少?10、一只三层的书架共放有108本书,上层比中层多11本,下层比中层少5本,上中下各有书多少本?11、某工厂第一,二,三车间共有工人280人,第一车间比第二车间多10人,第二车间比第三车间多15人,三个车间各有工人多少人?12、有A\B\C三个数,已知A+B=24,B+C=38,A+C=30,求A\B\C各是多少?13、甲、乙两箱水果共50千克,若从甲箱中取出6千克放到乙箱中,这时甲箱还比乙箱多2千克,问两箱原来各有多少千克?14、红光小学录取一年级新生104人,分成甲乙两个半,如果从甲班转2个学生到乙班去,两个班级的人数就一样多,问甲乙两个班原来各有学生多少人?15、甲、乙两箱水果共50千克,若从甲箱中取出6千克放到乙箱中,这时甲箱还比乙箱少2千克,问两箱原来各有多少千克?16、被减数,减数与差的和是170,其中减数比差多5,求减数是几?17、已知被减数,减数与差的和是180,其中减数比差少10,求减数是几?。
四年级和差问题
8部
第二车间
?部
第一车间
共96部
8部
?部
第一车间原有:(96+16)÷2=56(部) 第二车间原有:96-56=40(部)
答:第一车间原有车床56部,第二车间原有车床40部。
习题2、红星小学一年级学生共108人,分成甲、乙两个 班。如果从甲班转3个学生到乙班去,两班学生就一样多。 甲乙两班各有学生多少人?
例题5、四个人年龄之和是88岁,最小的是3岁,他与最
大的年龄之和比另外两个人年龄之和大8岁。最大的年龄
是多少岁?
解:线段图如下。
3岁
8岁
最小最大
?岁
另两个人
共88岁
?岁
最小最大之和:(88+8)÷2=48(岁) 最大的年龄: 48-3=45(岁)
答:最大的年龄是45岁。
习题5、小军一家四口年龄之和是129岁,小军7岁,妈妈 30岁,小军与爷爷年龄之和比他父母年龄之和大5岁。爷 爷和爸爸的年龄各是多少岁?
解:线段图如下。 18米
第一段
0米
第三段
?米
?米
第一段绳子长:102÷3=34(米)
第二段绳子长:34+16=50(米) 第三段绳子长:34-18=16(米) 答:第一段绳子长34米,第二段绳子长50米,第三段绳子长16米。
习题4、某工厂第一、二、三车间共有工人280人,第一
车间比第二车间多10人,第二车间比第三车间多15人。
三个车间各有工人多少人?
解:线段图如下。 18米
第一段
第二段
?米
16米
共100米
第三段
?米
?米
第一段绳子长:102÷3=34(米)
第二段绳子长:34+16=50(米) 第三段绳子长:34-18=16(米) 答:第一段绳子长34米,第二段绳子长50米,第三段绳子长16米。
四年级和差倍问题应用题及答案
四年级和差倍问题应用题及答案《和差问题》1.哥哥和妹妹共有水果糖 130 块,妹妹比哥哥多 48 块。
兄妹两人分别有多少块糖? 妹妹比哥哥多48块,如果哥哥增加48 块,两人共有130+48=178(块》.这时,两人的块数一样多。
178块的一半就是妹妹的块数。
妹妹:(130+48)÷2=89(块)哥哥:89-48= 41(块)2.小明和小亮语文成绩的总和是188分,小亮比小明少4分。
小明和小亮的语文成绩分别是多少分?小明的语文成绩:(188+4》÷2=96(分)小亮的语文成绩:96-4= 92(分)3.甲、乙两个修路队,4天修路 264米,又知甲队每天比乙队多修6米。
甲、乙两个修路队每天分别修多少米?甲、乙两队每天共修:264÷4=66(米)甲队每天修:(66+6)÷2=36(米)乙队每天修:36-6=30(米)《和倍问题》1.农场共养鸡、鸭1145只:其中鸡的数量是鸭的4倍。
鸡、鸭分别有多少只?如果把鸭的数量看成1份,鸡的数量就是4份。
合在一起,5份的数量是1145只,求出一份的数量也就求出了鸭的数量。
鸭的数量:1145÷(1+4)=229(只)鸡的数量:1145-229=916(只)2.王伯伯有两块地,共32公项,第一块地的面积比第二块地多2倍,这两块地分别有多少公顷?第一块地比第二块地多2倍,也就是说第一块地的面积是第二块地的3倍。
第二块地:32÷(1+3)=8(公顷)第一块地:8×3=24(公顷)3.小明和奶奶今年的岁数和是 96 岁,奶奶的岁数是小明的7倍,小明和奶奶今年分别为多少岁?小明:96÷(1+7)=12(岁)奶奶:12×7=84(岁)《差倍问题》1.花店里的玫瑰的总枝数是康乃馨的5倍:其中康乃馨比玫瑰少1200 枝。
玫瑰和康乃馨分别有多少枝?如果把康乃馨的枝数看作1份,玫瑰的枝数就是5份.玫瑰的枝数比康乃馨的枝数多4份,4份的总数是1200枝。
四年级数学思维训练题之和差、和倍与差倍问题
小学数学思维题——和差、和倍与差倍问题和差问题:大数=(和+差)÷2小数=(和-差)÷2例:长方形的长和宽之和为18厘米,长比宽多2厘米,求长方形的面积。
解:长=(18+2)÷2=10(厘米)宽=(18-2)÷2=8(厘米)长方形的面积=10×8=80(平方厘米)答:长方形的面积为80平方厘米。
和倍问题:总和÷(几倍+1)=较小的数总和-较小的数=较大的数较小的数×几倍=较大的数例:东西两个仓库共存粮480吨,东库存粮数是西库存粮数的1.4倍,求两库各存粮多少吨?解:西库存粮数=480÷(1.4+1)=200(吨)东库存粮数=480-200=280(吨)答:东库存粮280吨,西库存粮200吨。
差倍问题:两个数的差÷(几倍-1)=较小的数较小的数×几倍=较大的数例:爸爸比儿子大27岁,今年,爸爸的年龄是儿子年龄的4倍,求父子二人今年各是多少岁?解:儿子年龄=27÷(4-1)=9(岁)爸爸年龄=9×4=36(岁)答:父子二人今年的年龄分别是36岁和9岁。
小学数学思维题——和差、和倍与差倍问题和差问题:大数=(和+差)÷2小数=(和-差)÷2例:长方形的长和宽之和为18厘米,长比宽多2厘米,求长方形的面积。
解:长=(18+2)÷2=10(厘米)宽=(18-2)÷2=8(厘米)长方形的面积=10×8=80(平方厘米)答:长方形的面积为80平方厘米。
和倍问题:总和÷(几倍+1)=较小的数总和-较小的数=较大的数较小的数×几倍=较大的数例:东西两个仓库共存粮480吨,东库存粮数是西库存粮数的1.4倍,求两库各存粮多少吨?解:西库存粮数=480÷(1.4+1)=200(吨)东库存粮数=480-200=280(吨)答:东库存粮280吨,西库存粮200吨。
四年级和差问题
和差问题1. 学校有排球、足球共50个,排球比足球多4个,排球、足球各多少个?2. 甲乙两个工程队合挖一条长48千米的水渠,甲队比乙队多挖了6千米,求甲、乙工程队各挖了多少千米?3. 果园里有苹果树和梨树共1280棵,苹果树比梨树少150棵,果园里有苹果树和梨树各多少棵?4. 甲、乙两个仓库共运进货物1260吨,如果从甲仓库调出120吨货物到乙仓库,则两个仓库的货物一样多,求甲乙两仓库原来运进货物各多少吨?5. 姐姐和妹妹共同做了56朵纸花,姐姐给妹妹4朵后,两人的一样多。
问姐姐和妹妹各做了多少朵纸花?6. 甲、乙两筐苹果共64千克,从甲筐里取出4千克放到乙筐里去,结果甲筐的苹果和乙筐的苹果相等。
甲、乙两筐原有苹果各多少千克?7. 学校食堂共有三种蔬菜,其中黄瓜、番茄共重50千克,青菜、黄瓜共重70千克,青菜、番茄共重60千克。
这三种蔬菜各有多少千克?8. 阿派到场市场去买水果,他买的苹果个数是梨的3倍,苹果比梨多18个,阿派买苹果和梨各几个?9. 米德和欧拉参加学校组织的植树活动,两人一共种了12棵树,其中欧拉植树的棵数是米德的2倍,米德一共种了几棵树?10. 阿派在玩具店看中了两件汽车模型,如果两件都买,一共需要400元,已知这两件模型相差60元,这两件模型各要多少元钱?11. 纺织厂有职工480人,其中女职工数是男职工人数的3倍。
请问:男、女职工各有几人?12. 阿派和欧拉一共有23个草莓,阿派比欧拉多3个草莓,他们各有几个草莓?13. 两个加数之和为45,其中一个加数比另一个加数大15,问两个加数分别是多少?14.两筐水果共重128千克,第二筐比第一筐多4千克,两筐水果各重多少千克?15. 甲班和乙班共83人,乙班和丙班共86人,丙班和丁班共88人,甲班和丁班共多少人?16. 用一根长108厘米的铁丝围成一个平行四边形,使长边比短边长12厘米。
长边和短边各是多少厘米?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巩固1 巩固1
丁丁在期中考试时,语文、数学两科平均分是 分 丁丁在期中考试时,语文、数学两科平均分是91分,数学比 语文多2分 那么丁丁语文和数学各得了多少分? 语文多 分,那么丁丁语文和数学各得了多少分?
在这道题中, 在这道题中,我们已知丁丁数学成绩比 语文成绩多2分,也就是知道了数学成 语文成绩多 分 绩和语文成绩之差, 绩和语文成绩之差,如果找到数学成绩 和语文成绩之和, 和语文成绩之和,就转换成和差问题来 解答了. 解答了.又因为知道了语文和数学的平 均分是91分,那么两科成绩之和就是 91 × 2 = 182 分) 均分是 分 ( 方法一:数学: + 2) 2 = 92 (分)语文:92 − 2 = 90 (分) 182 ÷ (
巩固2 巩固2
果园共260棵桃树和梨树,其中桃树的棵数比梨树多20 棵桃树和梨树,其中桃树的棵数比梨树多 果园共 棵桃树和梨树 桃树和梨树各有多少棵? 棵.桃树和梨树各有多少棵?
方法一: 方法一: 桃树:( :(260+20)÷2=140(棵) 梨树:140-20=120(棵) 梨树: 桃树:( ) ( (
巩固1 巩固1
二年级一班和二班共有85人 一班比二班多3人 问一班、 二年级一班和二班共有 人,一班比二班多 人.问一班、 二班各有多少人? 二班各有多少人?
本题是和差问题的基本题型, 本题是和差问题的基本题型,已知 两个数的和与两个数的差, 两个数的和与两个数的差,然后求 大小两个数各是多少. 大小两个数各是多少.和差问题一 般可以借助线段图来进行分析. 般可以借助线段图来进行分析.
例3
长方形操场的长与宽相差80米 沿操场跑一周是 长方形操场的长与宽相差 米,沿操场跑一周是400米,求 米 这个操场的长与宽是多少米? 这个操场的长与宽是多少米?
长方形一周的长是指两条长和两条宽的和, 由条件可知一条长与一条宽的和为
400 ÷ 2 = 200 (米)
由此我们就知道了长和宽之和是200米,又知道长和宽之差是80米, 根据和差问题来解答: 方法一:长: 200 + 80) 2 = 140 (米) 宽:140 − 80 = 60 (米) ÷ ( 方法二:长: 200 − 80) 2 = 60 (米) 宽: 60 + 80 = 140 (米) ÷ (
巩固1 巩固1
分钟共打了240个字, 个字, 甲、乙两人同时以相同的速度打字,2分钟共打了 乙两人同时以相同的速度打字, 分钟共打了 个字 已知甲每分钟比乙多打10个字 问甲、 个字. 已知甲每分钟比乙多打 个字.问甲、乙两人每分钟各打多 少个? 少个?
首先要理解2分钟共打了 个字, 首先要理解 分钟共打了240个字,那么甲、 分钟共打了 个字 那么甲、 乙两人一分钟就打了240÷2=120(个)这 乙两人一分钟就打了 ÷ ( 样就转换成典型和差问题了. 样就转换成典型和差问题了.
方法一: 甲:(240÷2+10)=65 (个) 方法二: 乙:(240÷2-10)÷2=55 (个)
乙:65-10=55 (个)
甲:55+10=65(个)
在研究完这两道题目以后,我们来总结和差问题的解决方法. 在研究完这两道题目以后,我们来总结和差问题的解决方法.
解答和差问题的应用题,可以先画出线段图, 解答和差问题的应用题,可以先画出线段图,从线段图上找 到大数和小数,并找到解决方法. 到大数和小数,并找到解决方法. (两数的和-两数的差)÷2=较小的数 两数的和-两数的差 ÷ 较小的数 两数的和 较小的数+两数的差 较大的数 较小的数 两数的差=较大的数 两数的差 (两数的和 两数的差 ÷2=较大的数 两数的和+两数的差 两数的和 两数的差)÷ 较大的数 较大的数-两数的差=较小的数 较大的数-两数的差 较小的数
方法一: 一班人数: + 3)÷ 2 = 44 (人) ,二班人数: − 3 = 41 (人) (85 44 方法二: 二班人数:85 − 3)÷ 2 = 41 (人) ,一班人数:41 + 3 = 44 (人) (
巩固2 巩固2
两个连续奇数的和是36,这两个数分别是多少? 两个连续奇数的和是 ,这两个数分别是多少? 两个连续奇数的差是2,利用和差公式解答如下. 较小数: 较大数:
方法一:假设跳跳多 厘米 厘米, 方法一:假设跳跳多4厘米,那么就和点 点一样长,这时总长增长到了16+4=20 点一样长,这时总长增长到了 (厘米), 个点点的长是20厘米, 厘米),2个点点的长是 厘米, ), 个点点的长是 厘米 那么点点的长就是20÷ 那么点点的长就是 ÷2=10(厘米) (厘米) 跳跳就是10-4=6(厘米) 跳跳就是 (厘米) 列式:点点:(16+4)÷2=10(厘米) 列式:点点:( :( ) (厘米) 跳跳: 跳跳:10-4=6(厘米) (厘米)
解决和差问题的应用题, 解决和差问题的应用题,首先学会画线段图 是关键, 是关键,在这里借助两把尺子来进行比较分 比较直观和形象, 析,比较直观和形象,然后再从直观的实物 图过渡到抽象的线段图, 图过渡到抽象的线段图,这样比较容易理 此处是本节课的难点突破所在, 解.此处是本节课的难点突破所在,对于方 法的研究老师要引导学生来思考. 法的研究老师要引导学生来思考.
方法一: 方法一: 题目中知道了苹果比梨多2袋,如果能求出苹果和梨一共的袋数,就 题目中知道了苹果比梨多 袋 如果能求出苹果和梨一共的袋数, 可以用和差问题来解决了.而题目中只告诉我们苹果和梨共40千克, 可以用和差问题来解决了.而题目中只告诉我们苹果和梨共 千克, 千克 不过还告诉我们苹果和梨每袋都重5千克,那么就可以求出 不过还告诉我们苹果和梨每袋都重 千克, 千克 苹果和梨一共有 40 ÷ 5 = 8 袋) (
知识点拨: 知识点拨:
• 为了解答这种应用题,首先要弄清两个数相差多 为了解答这种应用题, 少的不同叙述方式.有些题目明确给了两个数的差 有些题目明确给了两个数的差, 少的不同叙述方式 有些题目明确给了两个数的差, 而有些应用题把两个数的差“暗藏”起来, 而有些应用题把两个数的差“暗藏”起来,我们 管暗藏的差叫“暗差” 管暗藏的差叫“暗差”。 • 知道两个数的和,以及它们的差,要求这两个数, 知道两个数的和,以及它们的差,要求这两个数, 解决和差问题需要我们画线段图来分析, 解决和差问题需要我们画线段图来分析,方法如 下: 方法一: 和 差 ÷ 大数 大数=小数 方法一: (和+差)÷2=大数 和-大数 小数 大数 方法二: 和 差 ÷ 小数 小数=大数 方法二: (和-差)÷2=小数 和-小数 大数 小数
方法二: 方法二: 假设点点少4厘米,那么就和跳跳一样长, 假设点点少 厘米,那么就和跳跳一样长,总 厘米 长就减少到了16-4=12(厘米) 长就减少到了 (厘米) 2个跳跳的长是 厘米 个跳跳的长是12厘米 个跳跳的长是 那么跳跳的长就是12÷ 那么跳跳的长就是 ÷2=6(厘米) (厘米) 点点就是6+4=10(厘米) 点点就是 (厘米) 列式:跳跳:(16-4)÷2=6厘米) 厘米) 列式:跳跳:( :( ) 厘米 点点: 点点: 6+4=10(厘米) (厘米)
方法二: 方法二: 梨树:( :(260-20)÷2=120(棵) 桃树:120+20=140(棵) 桃树: 梨树:( ) ( ( 答:桃树有140棵,梨树有 桃树有 棵 梨树有120棵. 棵
巩固3 巩固3
有一根钢管长12米 要锯成两段,使第一段比第二段短 有一根钢管长 米,要锯成两段,使第一段比第二段短2 每段各长多少米? 米.每段各长多少米? 第一段:( 第一段:(12-20)÷2=5 (米) :( ) 米 第二段: 第二段:12-5=7 (米) 米 答:第一段长5米,第二段长 米. 第一段长 米 第二段长7米
例2
文具王国的尺子点点和跳跳是一对好朋友, 文具王国的尺子点点和跳跳是一对好朋友,他们一会儿高兴地把自 己绑在一起,一会儿又闹起小别扭,竖起小脑袋比比谁长的高, 己绑在一起,一会儿又闹起小别扭,竖起小脑袋比比谁长的高,每 天他们总是有使不完的劲儿.同学们!你能根据下面的图, 天他们总是有使不完的劲儿.同学们!你能根据下面的图,算出点 点和跳跳各有多长吗? 点和跳跳各有多长吗?
÷ (36 - 2) 2 = 17
36 − 17 = 19
巩固3 巩固
一辆公交车里有30位乘客,到大桥站有 人下车 人下车, 一辆公交车里有 位乘客,到大桥站有17人下车,又上 位乘客 来19人,现在车上和原来比,人多了还是少了,多(或少) 人 现在车上和原来比,人多了还是少了, 或少) 几个人? 几个人?
例题精讲
例1
两筐水果共重150千克,第一筐比第二筐少10千克,两筐水 千克,第一筐比第二筐少 千克 千克, 两筐水果共重 千克 果各多少千克? 果各多少千克? 本题也是和差问题的基本题型, 本题也是和差问题的基本题型, 借助线段图来分析如下: 借助线段图来分析如下:
方法一: 把第二筐多的10千克减掉,看成两个第一筐的重量来计算. 列式: 第一筐:150 − 10) 2 = 70(千克) ÷ ( 第二筐: 70 + 10 = 80 (千克) 方法二: 把第一筐少的10千克补上,看成两个第二筐的重量来计算. 列式: 第二筐: 150 + 10) 2 = 80(千克) ÷ ( 第一筐: 80 − 10 = 70 (千克)
