工程力学竞赛复习题及答案
工程力学复习题及参考答案

课程考试复习题及参考答案工程力学一、填空题:1.受力后几何形状和尺寸均保持不变的物体称为。
2.构件抵抗的能力称为强度。
3.圆轴扭转时,横截面上各点的切应力与其到圆心的距离成比。
4.梁上作用着均布载荷,该段梁上的弯矩图为。
5.偏心压缩为的组合变形。
6.柔索的约束反力沿离开物体。
7.构件保持的能力称为稳定性。
8.力对轴之矩在情况下为零。
9.梁的中性层与横截面的交线称为。
10.图所示点的应力状态,其最大切应力是。
11.物体在外力作用下产生两种效应分别是。
12.外力解除后可消失的变形,称为。
13.力偶对任意点之矩都。
14.阶梯杆受力如图所示,设AB和BC段的横截面面积分别为2A和A,弹性模量为E,则杆中最大正应力为。
15.梁上作用集中力处,其剪力图在该位置有。
16.光滑接触面约束的约束力沿指向物体。
17.外力解除后不能消失的变形,称为。
18.平面任意力系平衡方程的三矩式,只有满足三个矩心的条件时,才能成为力系平衡的充要条件。
19.图所示,梁最大拉应力的位置在点处。
20.图所示点的应力状态,已知材料的许用正应力[σ],其第三强度理论的强度条件是。
21.物体相对于地球处于静止或匀速直线运动状态,称为。
22.在截面突变的位置存在集中现象。
23.梁上作用集中力偶位置处,其弯矩图在该位置有。
24.图所示点的应力状态,已知材料的许用正应力[σ],其第三强度理论的强度条件是。
25.临界应力的欧拉公式只适用于杆。
26.只受两个力作用而处于平衡状态的构件,称为。
27.作用力与反作用力的关系是。
28.平面任意力系向一点简化的结果的三种情形是。
29.阶梯杆受力如图所示,设AB和BC段的横截面面积分别为2A和A,弹性模量为E,则截面C的位移为。
30.若一段梁上作用着均布载荷,则这段梁上的剪力图为。
二、计算题:1.梁结构尺寸、受力如图所示,不计梁重,已知q=10kN/m,M=10kN·m,求A、B、C处的约束力。
2.铸铁T梁的载荷及横截面尺寸如图所示,C为截面形心。
工程力学复习题答案

工程力学复习题答案一、单项选择题1. 刚体在平面内运动时,其运动学描述不包括以下哪一项?A. 平移B. 旋转C. 振动D. 变形答案:D2. 材料力学中,下列哪一项不是应力的类型?A. 正应力B. 剪应力C. 拉应力D. 扭应力答案:C3. 在梁的弯曲问题中,以下哪一项不是梁的内力?A. 剪力B. 弯矩C. 扭矩D. 轴力答案:C二、多项选择题1. 以下哪些因素会影响材料的弹性模量?A. 材料类型B. 温度C. 材料的微观结构D. 材料的密度答案:A, B, C2. 根据胡克定律,以下哪些描述是正确的?A. 应力与应变成正比B. 比例系数称为弹性模量C. 应力与应变成反比D. 弹性模量是材料的固有属性答案:A, B, D三、填空题1. 在材料力学中,材料在外力作用下发生形变,当外力移除后,材料能够恢复原状的性质称为_______。
答案:弹性2. 当梁受到均布载荷时,其最大弯矩通常出现在梁的_______。
答案:中点3. 材料的屈服强度是指材料在受到外力作用时,从弹性变形过渡到塑性变形的临界应力值,通常用_______表示。
答案:σy四、简答题1. 简述材料力学中应力集中的概念及其对结构设计的影响。
答案:应力集中是指在构件的局部区域,由于几何形状、材料不连续性或其他原因,导致应力值远高于周围区域的现象。
这种现象可能导致结构的局部应力超过材料的强度极限,从而引发裂纹或断裂,对结构的安全性和可靠性造成影响。
因此,在结构设计中,应尽量避免应力集中的产生,或采取适当的措施来降低其影响。
2. 描述梁在弯曲时的正应力分布规律。
答案:梁在弯曲时,其横截面上的正应力分布规律是:在中性轴上,正应力为零;在中性轴上方,正应力为拉应力,且随着距离中性轴的增加而增大;在中性轴下方,正应力为压应力,且随着距离中性轴的增加而增大。
这种分布规律可以用弯曲应力公式σ=My/I来描述,其中M是弯矩,y是距离中性轴的距离,I是横截面的惯性矩。
工程力学竞赛复习题及答案

16. 画岀杆AB的受力图17. 画岀杆AB的受力图18. 画岀杆AB的受力图25. 画岀杆AB的受力图RR物系受力图26. 画岀图示物体系中杆AB轮C、整体的受力图7.图示圆柱A重力为G在中心上系有两绳AB和AC,绳子分别绕过光滑的滑轮B和C,并分别悬挂重力为G和G a的物体,设G> G。
试求平衡时的a角和水平面D对圆柱的约束力。
解(1) 取圆柱A画受力图如图所示。
AB AC绳子拉力大小分别等于G, G(2) 建直角坐标系,列平衡方程:X F x= 0,-G i+Gcos a= 0困柏柬龊力阳主动RZZZZZ.=^C0S2iB所受到的压力F NA,F NB。
有人认为F NA=GCOS a , F NB F G COS B,对不对,为什么?(1 )取翻罐笼画受力图如图所示。
(2)建直角坐标系,列平衡方程:X F x = 0, F NA sin a -F NB sin B= 0X F y = 0 , F NA COS a +F NB COS B -G= 0(3)求解未知量与讨论。
将已知条件G=3kN,a =30°,B =45°分别代入平衡方程,解得:F NA= 2.2kN F NA= 1.55kN有人认为F N/F G COS S F NB=G COS B是不正确的,只有在a =B =45°的情况下才正确。
X F y= 0 ,(3) 求解未知量。
F N+ Gsin a -G = 08.图示翻罐笼由滚轮A, B支承,已知翻罐笼连同煤车共重G=3kN, a =30°,B =45°,求滚轮A,9. 图示简易起重机用钢丝绳吊起重力G=2kN的重物,不计杆件自重、摩擦及滑轮大小,三处简化为铰链连接;求AB和AC所受的力。
(2)建直角坐标系如图,列平衡方程:X F x= 0, -F AB- Fsin45 °+Fcos60°= 0X F y= 0, -F AC- Fsin60 °- Fcos45°= 0(3)求解未知量。
工程力学竞赛复习题及参考答案

16.画出杆AB的受力图。
17. 画出杆AB的受力图。
18. 画出杆AB的受力图。
25. 画出杆AB的受力图。
物系受力图26.7. 和G2的解(1(2(38.F NA,F NB解(1(2∑F x=0,∑F y=0,(3F NA=有人认为NA NB9.图示简易起重机用钢丝绳吊起重力G=2kN的重物,不计杆件自重、摩擦及滑轮大小,A,B,C三处简化为铰链连接;求AB和AC所受的力。
解(1)取滑轮画受力图如图所示。
AB、AC杆均为二力杆。
(2)建直角坐标系如图,列平衡方程:∑F x=0,-F AB-Fsin45°+Fcos60°=0∑F y=0,-F AC-Fsin60°-Fcos45°=0(3)求解未知量。
将已知条件F=G=2kN代入平衡方程,解得:F AB=-0.414kN(压)F AC=-3.15kN(压)10. 图示简易起重机用钢丝绳吊起重力G=2kN的重物,不计杆件自重、摩擦及滑轮大小,A,B,C三处简化为铰链连接;求AB和AC所受的力。
解:(1)取滑轮画受力图如图所示。
AB、AC杆均为二力杆。
(2∑F x∑F y(324.解(1(2∑F x∑F y∑M B(327.解:求解顺序:先解CD部分再解ABC部分。
解CD部分(1)取梁CD画受力图如上左图所示。
(2)建直角坐标系,列平衡方程:∑F y=0,F C-q×a+F D=0∑M C(F)=0,-q×a×0.5a +F D×a=0(3)求解未知量。
将已知条件q=2kN/m,a=1m代入平衡方程。
解得:F C=1kN;F D=1kN(↑)解ABC部分(1)取梁ABC画受力图如上右图所示。
(2)建直角坐标系,列平衡方程:∑F y=0,-F/C+F A+F B-F=0∑M A(F)=0,-F/C×2a+F B×a-F×a-M=0(3)求解未知量。
力学竞赛试题及答案

力学竞赛试题及答案一、 四叶玫瑰线解:(1)对于四叶玫瑰曲线θρ2cos a =,在直角坐标系中可写成(图3-1)⎩⎨⎧==θρθρsin cos y x 将θρ2cos a =代入上式, 得 ⎩⎨⎧==θθθθsin 2cos cos 2cos a y a x (1) 利用三角函数的积化和差公式 )]cos()[cos(21cos cos βαβαβα-++=)]sin()[sin(21sin cos βαβαβα-++=可得 ⎪⎪⎩⎪⎪⎨⎧-=+=)sin 3(sin 2 )cos 3(cos 2θθθθa y a x (2)图3-1 图3-2(2)现设计一行星齿轮机构来画此曲线。
如图3-2所示的行星齿轮机构,小齿轮1O 在固定内齿轮O 内作纯滚动,其中内齿轮的半径为R ,小齿轮的半径为r ,画笔所在E 点离小齿轮圆心1O 的距离为e 。
随系杆1OO 的转动,其E 点的轨迹为⎩⎨⎧--=+-=ϕθϕθsin sin )( cos cos )( e r R y e r R x EE 利用小齿轮的纯滚动条件)(θϕθ+=r R ,有θϕrrR -=,代入上式可得⎪⎪⎩⎪⎪⎨⎧---=-+-=)sin(sin )( )cos(cos )( ϕθϕθr r R e r R y r r R e r R x E E 作变换,令βϑ3=,上式可改写为⎪⎪⎩⎪⎪⎨⎧---=-+-=)3sin(3sin )( )3cos(3cos )( ϕβϕβr r R e r R y r r R e r R x E E (3)对照式(2)和式(3)中的系数,有2ae =, 2a r R =-, 13=-r r R联解之,得a R 2=, a r 23=, 2ae = (4) 做一个如图3-2所示的行星齿轮绘图机构,取式(4)中的参数,即可画出θρ2cos a =的四叶玫瑰曲线。
二. 手指转笔在你思考问题时有用手指转笔的习惯吗?请你用下述刚体简化模型,进行分析计算: (1)本问题与力学中的什么内容有关系?(2)求出笔绕手指无滑动转一周中,手指作用于笔的正压力和摩擦力的大小; (3)给出笔与手指间的摩擦因数μ随AC 长度x 变化应满足的条件。
力学竞赛大学试题及答案

力学竞赛大学试题及答案一、选择题(每题5分,共20分)1. 一个物体在水平面上以恒定速度直线运动,其运动状态是:A. 静止B. 匀速直线运动C. 匀速圆周运动D. 变速直线运动答案:B2. 牛顿第二定律的数学表达式是:A. F = maB. F = mvC. F = m(v^2)D. F = m(v^2)/r答案:A3. 根据能量守恒定律,下列说法正确的是:A. 能量可以在不同形式之间转换B. 能量可以在不同物体之间转移C. 能量的总量可以增加D. 能量的总量可以减少答案:A4. 一个物体从静止开始做自由落体运动,其下落高度与时间的关系为:A. h = 1/2gt^2B. h = gtC. h = 2gtD. h = gt^2答案:A二、填空题(每题5分,共20分)1. 根据牛顿第三定律,作用力和反作用力大小________,方向________,作用在________的物体上。
答案:相等;相反;不同2. 一个物体的动能与其质量成正比,与其速度的平方成正比,其公式为:Ek = ________。
答案:1/2mv^23. 一个物体在斜面上下滑时,其受到的摩擦力大小与斜面的倾角成________关系。
答案:正比4. 根据胡克定律,弹簧的弹力与其形变成正比,其公式为:F =________。
答案:kx三、计算题(每题10分,共20分)1. 一辆汽车以20m/s的速度在水平公路上匀速行驶,求汽车受到的摩擦力大小,已知汽车质量为1500kg,摩擦系数为0.05。
答案:汽车受到的摩擦力大小为750N。
2. 一个质量为2kg的物体从10m高处自由落下,忽略空气阻力,求物体落地时的速度。
答案:物体落地时的速度为20m/s。
四、简答题(每题10分,共20分)1. 简述牛顿第一定律的内容及其物理意义。
答案:牛顿第一定律,也称为惯性定律,指出一切物体在没有受到外力作用时,总保持静止状态或匀速直线运动状态。
其物理意义是,物体具有惯性,即物体倾向于保持其当前的运动状态,除非有外力作用。
2021年国际工程力学竞赛试题

2021年国际工程力学竞赛试题第一部分:选择题(共30题,每题2分,共60分)1.以下哪个选项最准确地描述了力学?A.研究物体的运动和力的科学B.研究自然界中的能量转化过程的科学C.研究物体的形变和应力分布的科学D.研究热力学过程的科学2.下列哪个选项不是力学的主要分支?A.静力学B.动力学C.统计力学D.流体力学3.下列哪个物理量不是力学中常用的基本物理量?B.加速度C.力D.温度4.力是一个矢量量,它有大小和方向。
力的大小用什么单位来表示?A.米B.秒C.千克D.牛顿5.以下哪个物理量与力不是成正比关系?A.加速度B.质量C.位移6.以下哪个公式描述了牛顿第二定律?A. F = maB. F = mvC. a = mvD. a = F/m7.弹性力是指在一个物体上产生变形时所产生的力。
下列哪个公式可以用来计算弹性力?A. F = kxB. F = mvC. F = maD. F = µN8.在接触面上的压强等于单位面积上承受的力的大小。
下列哪个公式描述了压强?A. P = F/AB. P = F/dC. P = F/mD. P = F/v9.功是力对物体作用时所做的功。
下列哪个公式可以用来计算功?A. W = FvB. W = FdC. W = F/AD. W = mv10.若两个物体相互作用的力的大小相等方向相反,则它们产生的效果是?A.加速度为零B.加速度为正C.加速度为负D.加速度无法确定11.勾股定理是力学中常用的定理,它用来计算什么?A.初速度B.加速度C.位移D.力12.力矩是描述物体绕轴旋转的能力的物理量。
下列哪个公式可以用来计算力矩?A. M = F/dB. M = F/AC. M = FvD. M = F/f13.弹性势能是指物体由于变形而具有的能量。
下列哪个公式可以用来计算弹性势能?A. PE = 1/2mv²B. PE = mghC. PE = kx²D. PE = Fd14.动能是指物体由于运动而具有的能量。
力学竞赛综合练习含答案
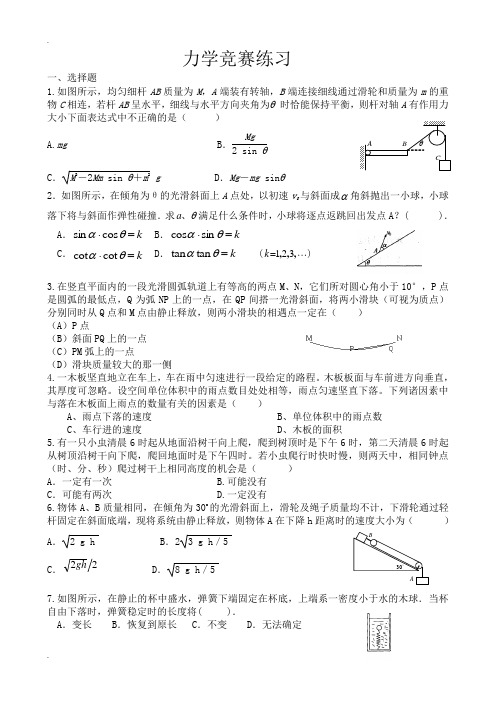
力学竞赛练习一、选择题1.如图所示,均匀细杆AB 质量为M ,A 端装有转轴,B 端连接细线通过滑轮和质量为m 的重物C 相连,若杆AB 呈水平,细线与水平方向夹角为θ 时恰能保持平衡,则杆对轴A 有作用力大小下面表达式中不正确的是( ) A.mgB .Mg 2 sin θC .M 2-2Mm sin θ+m 2 gD .Mg -mg sin θ2.如图所示,在倾角为θ的光滑斜面上A 点处,以初速v 0与斜面成α角斜抛出一小球,小球落下将与斜面作弹性碰撞.求a θ、满足什么条件时,小球将逐点返跳回出发点A ?( ). A .k =⋅θαcos sin B .k =⋅θαsin cosC .k =⋅θαcot cotD .k =θαtan tan (123=,,,k )3.在竖直平面内的一段光滑圆弧轨道上有等高的两点M 、N ,它们所对圆心角小于10°,P 点是圆弧的最低点,Q 为弧NP 上的一点,在QP 间搭一光滑斜面,将两小滑块(可视为质点)分别同时从Q 点和M 点由静止释放,则两小滑块的相遇点一定在( ) (A )P 点 (B )斜面PQ 上的一点(C )PM 弧上的一点 (D )滑块质量较大的那一侧4.一木板坚直地立在车上,车在雨中匀速进行一段给定的路程。
木板板面与车前进方向垂直,其厚度可忽略。
设空间单位体积中的雨点数目处处相等,雨点匀速坚直下落。
下列诸因素中与落在木板面上雨点的数量有关的因素是( )A 、雨点下落的速度B 、单位体积中的雨点数C 、车行进的速度D 、木板的面积5.有一只小虫清晨6时起从地面沿树干向上爬,爬到树顶时是下午6时,第二天清晨6时起从树顶沿树干向下爬,爬回地面时是下午四时。
若小虫爬行时快时慢,则两天中,相同钟点(时、分、秒)爬过树干上相同高度的机会是( ) A .一定有一次 B.可能没有 C .可能有两次 D.一定没有6.物体A 、B 质量相同,在倾角为30o 的光滑斜面上,滑轮及绳子质量均不计,下滑轮通过轻杆固定在斜面底端,现将系统由静止释放,则物体A 在下降h 距离时的速度大小为( ) A . 2 g h B .2 3 g h /5 C .22gh D .8 g h /57.如图所示,在静止的杯中盛水,弹簧下端固定在杯底,上端系一密度小于水的木球.当杯自由下落时,弹簧稳定时的长度将( ).A .变长B .恢复到原长C .不变D .无法确定A B θCBA30mM θ8.如图所示,M 、N 是两个共轴圆筒的横截面.外筒半径为R ,内筒半径比R 小得多,可以忽略不计.筒的两端是封闭的,两筒之间抽成真空.两筒以相同的角速度ω绕其中心轴线(图中垂直于纸面)匀速转动.设从M 筒内部可以通过窄缝S(与M 筒的轴线平行)不断地向外射出,两种不同速率v1和v2的微粒,从S 处射出时初速度方向都是沿筒的半径方向,微粒到达N 筒后就附着在N 筒上.如果R 、v1和v2都不变,而ω取某一合适的值,则( ) A .有可能使微粒落在N 筒上的位置都在a 处一条与S 缝平行的窄条上B .有可能使微粒落在N 筒上的位置都在某一处如b 处一条与S 缝平行的窄条上C .有可能使微粒落在N 筒上的位置分别在某两处如b 处和c 处与S 缝平行的窄条上D .只要时间足够长,N 筒上将到处落有微粒 量为二、填空题1.一均匀的不可伸长的绳子,其两端悬挂在A 、B 两点,B 点比A 点高h .在A 点,绳子张力为T A .绳子的质m ,绳长为L .则在B 点绳子的张力T B = .2.质量为m 的小球挂在长为L 、不可伸长的轻线上,静止于自然悬挂状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
16.画出杆AB的受力图。
17. 画出杆AB的受力图。
18. 画出杆AB的受力图。
25. 画出杆AB的受力图。
物系受力图26. 画出图示物体系中杆AB、轮C、整体的受力图。
7. 图示圆柱A重力为G,在中心上系有两绳AB和AC,绳子分别绕过光滑的滑轮B和C,并分别悬挂重力为G1和G2的物体,设G2>G1。
试求平衡时的α角和水平面D对圆柱的约束力。
解(1)取圆柱A画受力图如图所示。
AB、AC绳子拉力大小分别等于G1,G2。
(2)建直角坐标系,列平衡方程:∑F x=0,-G1+G2cosα=0∑F y=0,F N+G2sinα-G=0(3)求解未知量。
8.图示翻罐笼由滚轮A,B支承,已知翻罐笼连同煤车共重G=3kN,α=30°,β=45°,求滚轮A,B所受到的压力F NA,F NB。
有人认为F NA=Gcosα,F NB=Gcosβ,对不对,为什么?解(1)取翻罐笼画受力图如图所示。
(2)建直角坐标系,列平衡方程:∑F x=0,F NA sinα-F NB sinβ=0∑F y=0,F NA cosα+F NB cosβ-G=0(3)求解未知量与讨论。
将已知条件G=3kN,α=30°,β=45°分别代入平衡方程,解得:F NA=2.2kN F NA=1.55kN有人认为F NA=Gcosα,F NB=Gcosβ是不正确的,只有在α=β=45°的情况下才正确。
9.图示简易起重机用钢丝绳吊起重力G=2kN的重物,不计杆件自重、摩擦及滑轮大小,A,B,C三处简化为铰链连接;求AB和AC所受的力。
解(1)取滑轮画受力图如图所示。
AB、AC杆均为二力杆。
(2)建直角坐标系如图,列平衡方程:∑F x=0,-F AB-Fsin45°+Fcos60°=0∑F y=0,-F AC-Fsin60°-Fcos45°=0(3)求解未知量。
将已知条件F=G=2kN代入平衡方程,解得:F AB=-0.414kN(压)F AC=-3.15kN(压)10. 图示简易起重机用钢丝绳吊起重力G=2kN的重物,不计杆件自重、摩擦及滑轮大小,A,B,C三处简化为铰链连接;求AB和AC所受的力。
解:(1)取滑轮画受力图如图所示。
AB、AC杆均为二力杆。
(2)建直角坐标系如图,列平衡方程:∑F x=0,-F AB-F AC cos45°-Fsin30°=0∑F y=0, -F AC sin45°-Fcos30°-F=0(3)求解未知量。
将已知条件F=G=2kN代入平衡方程,解得:F AB=2.73kN(拉)F AC=-5.28kN(压)24. 试求图示梁的支座反力。
已知F=6kN,M=2kN·m,a=1m。
解(1)取梁AB画受力图如图所示。
(2)建直角坐标系,列平衡方程:∑F x=0,F A-F Bx=0∑F y=0,F By-F=0∑M B(F)=0,-F A×a+F×a+M=0(3)求解未知量。
将已知条件F=6kN,M=2kN·m,a=1m代入平衡方程,解得:F A=8kN(→);F Bx=8kN(←);F By=6kN(↑)。
27. 试求图示梁的支座反力。
已知F=6kN,q=2kN/m,M=2kN·m,a=1m。
解:求解顺序:先解CD部分再解ABC部分。
解CD部分(1)取梁CD画受力图如上左图所示。
(2)建直角坐标系,列平衡方程:∑F y=0,F C-q×a+F D=0∑M C(F)=0,-q×a×0.5a +F D×a=0(3)求解未知量。
将已知条件q=2kN/m,a=1m代入平衡方程。
解得:F C=1kN;F D=1kN(↑)解ABC部分(1)取梁ABC画受力图如上右图所示。
(2)建直角坐标系,列平衡方程:∑F y=0,-F/C+F A+F B-F=0∑M A(F)=0,-F/C×2a+F B×a-F×a-M=0(3)求解未知量。
将已知条件F=6kN,M=2kN·m,a=1m,F/C = F C=1kN代入平衡方程。
解得:F B=10kN(↑);F A=-3kN(↓)梁支座A,B,D的反力为:F A=-3kN(↓);F B=10kN(↑);F D=1kN(↑)。
32. 图示汽车起重机车体重力G1=26kN,吊臂重力G2=4.5kN,起重机旋转和固定部分重力G3=31kN。
设吊臂在起重机对称面内,试求汽车的最大起重量G。
解:(1)取汽车起重机画受力图如图所示。
当汽车起吊最大重量G时,处于临界平衡,F NA=0。
(2)建直角坐标系,列平衡方程:∑M B(F)=0,-G2×2.5m+G max×5.5m+G1×2m=0(3)求解未知量。
将已知条件G1=26kN,G2=4.5kN代入平衡方程,解得:G max=7.41kN33. 汽车地秤如图所示,BCE为整体台面,杠杆AOB可绕O轴转动,B,C,D三点均为光滑铰链连接,已知砝码重G1,尺寸l,a。
不计其他构件自重,试求汽车自重G2。
解:(1)分别取BCE和AOB画受力图如图所示。
(2)建直角坐标系,列平衡方程:对BCE列∑F y=0,F By-G2=0对AOB列∑M O(F)=0,-F/By×a+F×l=0(3)求解未知量。
将已知条件F By=F/By,F=G1代入平衡方程,解得:G2=l G1/a3. 拉杆或压杆如图所示。
试用截面法求各杆指定截面的轴力,并画出各杆的轴力图。
解:(1)计算A端支座反力。
由整体受力图建立平衡方程:∑F x=0,2kN-4kN+6kN-F A=0F A=4kN(←)(2)分段计算轴力杆件分为3段。
用截面法取图示研究对象画受力图如图,列平衡方程分别求得:F N1=-2kN(压);F N2=2kN(拉);F N3=-4kN(压)(3)画轴力图。
根据所求轴力画出轴力图如图所示。
4. 拉杆或压杆如图所示。
试用截面法求各杆指定截面的轴力,并画出各杆的轴力图。
解:(1)分段计算轴力杆件分为3段。
用截面法取图示研究对象画受力图如图,列平衡方程分别求得:F N1=-5kN(压); F N2=10kN(拉); F N3=-10kN (压)(2)画轴力图。
根据所求轴力画出轴力图如图所示。
7. 圆截面阶梯状杆件如图所示,受到F=150kN的轴向拉力作用。
已知中间部分的直径d1=30mm,两端部分直径为d2=50mm,整个杆件长度l=250mm,中间部分杆件长度l1=150mm,E=200GPa。
试求:1)各部分横截面上的正应力σ;2)整个杆件的总伸长量。
10. 某悬臂吊车如图所示。
最大起重荷载G=20kN,杆BC为Q235A圆钢,许用应力[σ]=120MPa。
试按图示位置设计BC杆的直径d。
1. 图示切料装置用刀刃把切料模中Ф12mm的料棒切断。
料棒的抗剪强度τb=320MPa。
试计算切断力。
2. 图示螺栓受拉力F作用。
已知材料的许用切应力[τ]和许用拉应力[σ]的关系为[τ]=0.6[σ]。
试求螺栓直径d与螺栓头高度h的合理比例。
3. 已知螺栓的许用切应力[τ]=100MPa,钢板的许用拉应力[σ]=160MPa。
试计算图示焊接板的许用荷载[F]。
6. 阶梯轴AB如图所示,AC段直径d1=40mm,CB段直径d2=70mm,外力偶矩M B=1500N·m,M A=600N·m,M C=900N·m,G=80GPa,[τ]=60MPa,[φ/]=2(º)/m。
试校核该轴的强度和刚度。
7. 图示圆轴AB所受的外力偶矩M e1=800N·m,M e2=1200N·m,M e3=400N·m,G=80GPa,l2=2l1=600mm [τ]=50MPa,[φ/]=0.25(º)/m。
试设计轴的直径。
8.直径d=25mm的圆钢杆,受轴向拉力F=60kN作用时,在标矩l=200mm的长度内伸长Δl=0.113mm;受外力偶矩M e=200N·m,的作用时,相距l=150mm 的两横截面上的相对转角为φ=0.55º。
试求钢材的E和G。
8. 试列出图示梁的剪力方程和弯矩方程,画剪力图和弯矩图,并求出F S和,max M max。
设q,F,l均为已知。
9.试列出图示梁的剪力方程和弯矩方程,画剪力图和弯矩图,并求出F S和,max M max。
设q,l均为已知。
10. 试列出图示梁的剪力方程和弯矩方程,画剪力图和弯矩图,并求出F S,max 和M max。
设q,l,F,M e均为已知。
11. 不列剪力方程和弯矩方程,画出图示各梁的剪力图和弯矩图,并求出F S,max 和M max。
解:(1)由静力平衡方程得:F A=F,M A= Fa,方向如图所示。
(2)利用M,F S,q之间的关系分段作剪力图和弯矩图。
(3)梁最大绝对值剪力在AB段内截面,大小为2F。
梁最大绝对值弯矩在C截面,大小为2Fa。
12. 不列剪力方程和弯矩方程,画出图示各梁的剪力图和弯矩图,并求出F S,max 和M max。
解:(1)由静力平衡方程得:F A=3q l/8(↑),F B=q l/8(↑)。
(2)利用M,F S,q之间的关系分段作剪力图和弯矩图。
(3)梁的最大绝对值剪力在A右截面,大小为3q l/8。
梁的最大弯矩绝对值在距A端3l/8处截面,大小为9q l2/128。
13. 不列剪力方程和弯矩方程,画出图示各梁的剪力图和弯矩图,并求出F S,max 和M max。
解:(1)由静力平衡方程得:F B=2qa,M B=qa2,方向如图所示。
(2)利用M,F S,q之间的关系分段作剪力图和弯矩图。
(3)梁的最大绝对值剪力在B左截面,大小为2qa。
梁的最大绝对值弯矩在距AC段内和B左截面,大小为qa2。
15. 不列剪力方程和弯矩方程,画出图示各梁的剪力图和弯矩图,并求出F S,max 和M max。
解:(1)由静力平衡方程得:F A=9qa/4(↑),F B= 3qa/4(↑)。
(2)利用M,F S,q之间的关系分段作剪力图和弯矩图。
(3)梁最大绝对值剪力在A右截面,大小为5qa/4。
梁最大弯矩绝对值在A截面,大小为qa2/2。
7. 空心管梁受载如图所示。
已知[σ]=150MPa,管外径D=60mm,在保证安全的条件下,求内经d的最大值。
8. 铸铁梁的荷载及横截面尺寸如图所示,已知I z=7.63×10-6m4,[σt]=30MPa,[σc]=60MPa,试校核此梁的强度。
