多恩布什宏观经济学第十版课后习题答案04
多恩布什宏观经济学第十版课后习题答案03

CHAPTER 3Solutions to the Problems in the TextbookConceptual Problems:1. The production function provides a quantitative link between inputs and output. Forexample, the Cobb-Douglas production function mentioned in the text is of the form: Y = F(N,K) = AN1-θKθ,where Y represents the level of output. (1 - θ) and θare weights equal to the shares of labor (N) and capital (K) in production, while A is often used as a measure for the level of technology. It can be easily shown that labor and capital each contribute to economic growth by an amount that is equal to their individual growth rates multiplied by their respective share in income.2. The Solow model predicts convergence, that is, countries with the same productionfunction, savings rate, and population growth will eventually reach the same level of income per capita. In other words, a poor country may eventually catch up to a richer one by saving at the same rate and making technological innovations. However, if these countries have different savings rates, they will reach different levels of income per capita, even though their long-term growth rates will be the same.3. A production function that omits the stock of natural resources cannot adequatelypredict the impact of a significant change in the existing stock of natural resources on the economic performance of a country. For example, the discovery of new oil reserves or an entirely new resource would have a significant effect on the level of output that could not be predicted by such a production function.4. Interpreting the Solow residual purely as technological progress would ignore, forexample, the impact that human capital has on the level of output. In other words, this residual not only captures the effect of technological progress but also the effect of changes in human capital (H) on the growth rate of output. To eliminate this problem we can explicitly include human capital in the production function, such that Y = F(K,N,H) = AN a K b H c with a + b + c = 1.Then the growth rate of output can be calculated as∆Y/Y = ∆A/A + a(∆N/N) + b(∆K/K) + c(∆H/H).5. The savings function sy = sf(k) assumes that a constant fraction of output is saved.The investment requirement, that is, the (n + d)k-line, represents the amount of investment needed to maintain a constant capital-labor ratio (k). A steady-stateequilibrium is reached when saving is equal to the investment requirement, that is, when sy = (n + d)k. At this point the capital-labor ratio k = K/N is not changing, so capital (K), labor (N), and output (Y) all must be growing at the same rate, that is, the rate of population growth n = (∆N/N).6. In the long run, the rate of population growth n = (∆N/N) determines the growth rateof the steady-state output per capita. In the short run, however, the savings rate, technological progress, and the rate of depreciation can all affect the growth rate.7. Labor productivity is defined as Y/N, that is, the ratio of output (Y) to labor input(N). A surge in labor productivity therefore occurs if output grows at a faster rate than labor input. In the U.S. we have experienced such a surge in labor productivity since the mid-1990s due to the enormous growth in GDP. This surge can be explained from the introduction of new technologies and more efficient use of existing technologies. Many claim that the increased investment in and use of computer technology has stimulated economic growth. Furthermore, increased global competition has forced many firms to cut costs by reorganizing production and eliminating some jobs. Thus, with large increases in output and a slower rate of job creation we should expect labor productivity to increase. (One should also note that a higher-skilled labor force also can contribute to an increase in labor productivity, since the same number of workers can produce more output if workers are more highly skilled.)Technical Problems:1.a. According to Equation (2), the growth of output is equal to the growth in labortimes the labor share plus the growth of capital times the capital share plus the rate of technical progress, that is,∆Y/Y = (1 - θ)(∆N/N) + θ(∆K/K) + ∆A/A, where1 - θis the share of labor (N) and θis the share of capital (K). Thus if we assumethat the rate of technological progress (∆A/A) is zero, then output grows at an annual rate of 3.6 percent, since∆Y/Y = (0.6)(2%) + (0.4)(6%) + 0% = 1.2% + 2.4% = + 3.6%,1.b. The so-called "Rule of 70" suggests that the length of time it takes for outputto double can be calculated by dividing 70 by the growth rate of output. Since 70/3.6 = 19.44, it will take just under 20 years for output to double at an annual growth rate of 3.6%,1.c. Now that ∆A/A = 2%, we can calculate economic growth as∆Y/Y = (0.6)(2%) + (0.4)(6%) + 2% = 1.2% + 2.4% + 2% = + 5.6%.Thus it will take 70/5.6 = 12.5 years for output to double at this new growth rateof 5.6%.2.a. According to Equation (2), the growth of output is equal to the growth in labortimes the labor share plus the growth of capital times the capital share plus the growth rate of total factor productivity (TFP), that is,∆Y/Y = (1 - θ)(∆N/N) + θ(∆K/K) + ∆A/A, where1 - θ is the share of labor (N) and θ is the share of capital (K). In this exampleθ = 0.3; therefore, if output grows at 3% and labor and capital grow at 1% each, then we can calculate the change in TFP in the following way3% = (0.3)(1%) + (0.7)(1%) + ∆A/A ==> ∆A/A = 3% - 1% = 2%,that is, the growth rate of total factor productivity is 2%.2.b. If both labor and the capital stock are fixed and output grows at 3%, then allthis growth has to be contributed to the growth in factor productivity, that is, ∆A/A = 3%.3.a. If the capital stock grows by ∆K/K = 10%, the effect on output would be an additionalgrowth rate of∆Y/Y = (.3)(10%) = 3%.3.b. If labor grows by ∆N/N = 10%, the effect on output would be an additional growthrate of∆Y/Y = (.7)(10%) = 7%.3.c. If output grows at ∆Y/Y = 7% due to an increase in labor by ∆N/N = 10%, and thisincrease in labor is entirely due to population growth, then per capita income would decrease and people’s welfare would decrease, since∆y/y = ∆Y/Y - ∆N/N = 7% - 10% = - 3%.3.d. If this increase in labor is due to an influx of women into the labor force, theoverall population does not increase and income per capita would increase by ∆y/y = 7%. Therefore people's welfare would increase.4. Figure 3-4 shows output per head as a function of the capital-labor ratio, that is,y = f(k). The savings function is sy = sf(k), and it intersects the straight (n + d)k-line, representing the investment requirement. At this intersection, the economy is in a steady-state equilibrium. Now let us assume that the economy is in a steady-state equilibrium before the earthquake hits, that is, the steady-state capital-labor ratio is currently k*. Assume further, for simplicity, that the earthquake does not affect people's savings behavior.If the earthquake destroys one quarter of the capital stock but less than one quarterof the labor force, then the capital-labor ratio falls from k*to k1 and per-capita output falls from y*to y1. Now saving is greater than the investment requirement, that is, sy1 > (d + n)k1, and the capital stock and the level of output per capita will grow until the steady state at k* is reached again.However, if the earthquake destroys one quarter of the capital stock but more than one quarter of the labor force, then the capital-labor ratio increases from k* to k2.Saving now will be less than the investment requirement and thus the capital-labor ratio and the level of output per capita will fall until the steady state at k*is reached again.If exactly one quarter of both the capital stock and the labor stock are destroyed, then the steady state is maintained, that is, the capital-labor ratio and the output per capita do not change.If the severity of the earthquake has an effect on peoples’savings behavior, then the savings function sy = sf(k) will move either up or down, depending on whether the savings rate (s) increases (if people save more, so more can be invested in an effort to rebuild) or decreases (if people save less, since they decide that life is too short not to live it up).yy = f(k)y2y* (n+d)ky1syk1 k* k2 k5.a. An increase in the population growth rate (n) affects the investment requirement,and the (n + d)k-line gets steeper. As the population grows, more saving must be used to equip new workers with the same amount of capital that the existing workers already have. Therefore output per capita (y) will decrease as will the new optimal capital-labor ratio, which is determined by the intersection of the sy-curve and the (n1+ d)k-line. Since per-capita output will fall, we will have a negative growth rate in the short run. However, the steady-state growth rate of output will increase in the long run, since it will be determined by the new and higher rate of population growth.y (n 1 + d)ky = f(k)y o (n o + d)ky1 syk1 k o k5.b. Starting from an initial steady-state equilibrium at a level of per-capita outputy*, the increase in the population growth rate (n) will cause the capital-labor ratio to decline from k* to k1. Output per capita will also decline, a process that will continue at a diminishing rate until a new steady-state level is reached at y1. The growth rate of output will gradually adjust to the new and higher level n1.yy*y1t o t1 tkk*k1t o t1 t6.a. Assume the production function is of the formY = F(K, N, Z) = AK a N b Z c ==>∆Y/Y = ∆A/A + a(∆K/K) + b(∆N/N) + c(∆Z/Z), with a + b + c = 1.Now assume that there is no technological progress, that is, ∆A/A = 0, and that capital and labor grow at the same rate, that is, ∆K/K = ∆N/N = n. If we also assume that all natural resources available are fixed, such that ∆Z/Z = 0, then the rate of output growth will be∆Y/Y = an + bn = (a + b)n.In other words, output will grow at a rate less than n since a + b < 1. Therefore output per worker will fall.6.b. If there is technological progress, that is, ∆A/A > 0, then output will grow fasterthan before, namely∆Y/Y = ∆A/A + (a + b)n.If ∆A/A > c, then output will grow at a rate larger than n, in which case output per worker will increase.6.c. If the supply of natural resources is fixed, then output can only grow at a ratethat is smaller than the rate of population growth and we should expect limits to growth as we run out of natural resources. However, if the rate of technological progress is sufficiently large, then output can grow at a rate faster than population, even if we have a fixed supply of natural resources.7.a. If the production function is of the formY = K1/2(AN)1/2,and A is normalized to 1, then we haveY = K1/2N1/2.In this case capital's and labor's shares of income are both 50%.7.b. This is a Cobb-Douglas production function.7.c. A steady-state equilibrium is reached when sy = (n + d)k.From Y = K1/2N1/2 ==> Y/N = K1/2N-1/2 ==> y = k1/2==>sk1/2= (n + d)k ==> k-1/2 = (n + d)/s = (0.07 + 0.03)/(.2) = 1/2 ==> k1/2= 2 = y ==> k = 4 .8.a. If technological progress occurs, then the level of output per capita for any givencapital-labor ratio increases. The function y = f(k) increases to y = g(k), and thus the savings function increases from sf(k) to sg(k).y g(k)y2 f(k)(n +d)ksg(k)y1sf(k)k1 k2k8.b. Since g(k) > f(k), it follows that sg(k) > sf(k) for each level of k.Therefore the intersection of the sg(k)-curve with the (n + d)k-line is ata higher level of k. The new steady-state equilibrium will now be at a higherlevel of saving and output per capita, and at a higher capital-labor ratio.8.c. After the technological progress occurs, the level of saving and investmentwill increase until a new and higher optimal capital-labor ratio is reached.The ratio of investment to capital will also increase in the transition period, since more has to be invested to reach the higher optimal capital-labor ratio.kk2k1t1 t2t9. The Cobb-Douglas production function is defined asY = F(N,K) = AN1-θKθ.The marginal product of labor can then be derived asMPN = (∆Y)/(∆N) = (1 - θ)AN-θKθ = (1 - θ)AN1-θKθ/N = = (1 - θ)(Y/N)==> labor's share of income = [MPN*(N)]/Y = (1 - θ)(Y/N)*[(N)/(Y)] =(1 - θ)欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习资料等等打造全网一站式需求。
(NEW)多恩布什《宏观经济学》(第10版)笔记和课后习题详解

答:总供给—总需求模型是把总需求与总供给结合在一起来分析国民收 入与价格水平的决定及其变动的国民收入决定模型。
在图1-4中,横轴代表国民收入( ),纵轴代表价格水平( ), 代 表原来的总需求曲线, 代表短期总供给曲线, 代表长期总供给曲 线。最初,经济在 点时实现了均衡,均衡的国民收入为 ,均衡的价 格水平为 。这时 点又在长期总供给曲线 上,所以, 代表充分就 业的国民收入水平。在短期内,政府通过扩张性的财政政策或货币政 策,增加了总需求,从而使总需求曲线从 向右上方平行地移动到了
(1)经济增长模型
主要解释:经济增长的源泉;各国经济增长率差异的原因;经济起飞的 原因;分析投入的积累和技术进步如何导致生活水平的提高。
(2)经济波动模型:总供给—总需求模型(如图1-1所示)
图1-1 总供给—总需求模型
总供给—总需求模型解释物价水平与产出的决定与波动。
总供给水平:现有资源和技术条件下,经济能够生产的产出量。
潜在产出水平附近接近于一条垂直的直线。
4 经济周期(business cycle)
答:经济周期又称经济波动或国民收入波动,指总体经济活动的扩张和 收缩交替反复出现的过程。现代经济学中关于经济周期的论述一般是指 经济增长率的上升和下降的交替过程,而不是经济总量的增加和减少。
一个完整的经济周期包括繁荣、衰退、萧条、复苏(也可以称为扩张、 持平、收缩、复苏)四个阶段。在繁荣阶段,经济活动全面扩张,不断 达到新的高峰。在衰退阶段,经济短时间内保持均衡后出现紧缩的趋 势。在萧条阶段,经济出现急剧的收缩和下降,很快从活动量的最高点 下降到最低点。在复苏阶段,经济从最低点恢复并逐渐上升到先前的活 动量高度,进入繁荣。衡量经济周期处于什么阶段,主要依据国民生产 总值、工业生产指数、就业和收入、价格指数、利息率等综合经济活动 指标的波动。
多恩布什《宏观经济学》课后习题详解(增长与政策)【圣才出品】
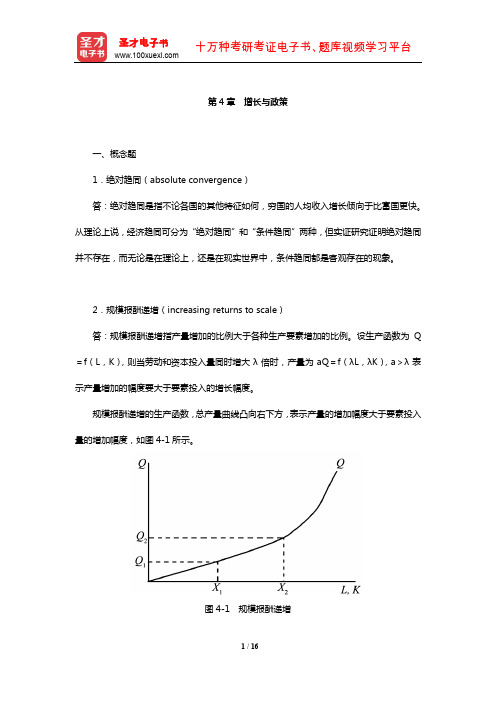
第4章增长与政策一、概念题1.绝对趋同(absolute convergence)答:绝对趋同是指不论各国的其他特征如何,穷国的人均收入增长倾向于比富国更快。
从理论上说,经济趋同可分为“绝对趋同”和“条件趋同”两种,但实证研究证明绝对趋同并不存在,而无论是在理论上,还是在现实世界中,条件趋同都是客观存在的现象。
2.规模报酬递增(increasing returns to scale)答:规模报酬递增指产量增加的比例大于各种生产要素增加的比例。
设生产函数为Q =f(L,K),则当劳动和资本投入量同时增大λ倍时,产量为aQ=f(λL,λK),a>λ表示产量增加的幅度要大于要素投入的增长幅度。
规模报酬递增的生产函数,总产量曲线凸向右下方,表示产量的增加幅度大于要素投入量的增加幅度,如图4-1所示。
图4-1 规模报酬递增图4-1中,横轴表示劳动L和资本投入量K,纵轴表示产量Q,曲线Q为总产量曲线。
当各种要素投入量由X1增加到X2时,引起产量由Q1增加到Q2,要素投入量增加了一倍,而产量的增加大于一倍。
产生规模报酬递增的主要原因是企业生产规模扩大所带来的生产效率的提高。
它可以表现为:生产规模扩大以后,企业能够利用更先进的技术和机器设备等生产要素,而较小规模的企业可能无法利用这样的技术和生产要素。
随着对较多的人力和机器的使用,企业内部的生产分工能够更加合理和专业化。
此外,人数较多的技术培训和具有一定规模的生产经营管理也可以节省成本。
3.稳定均衡(stable equilibrium)答:稳定均衡指如果经济体系的均衡状态遭到暂时破坏时,依靠其自身的力量最终还会恢复到原来所处的均衡状态的一种均衡。
其特点是一个经济体系的均衡状态,在制约它的各种外部条件发生变动时,会使该经济体系产生脱离均衡状态的运动,但是,经济体系内部又同时会自动地产生一种力量,这种力量使体系中的各种变量重新恢复到原来的均衡状态。
例如,当某一商品的供给曲线在均衡点的斜率大于需求曲线的斜率时,脱离均衡状态的波动幅度会自动逐渐缩小以至消失,并最终停留在原均衡点上,这就是阐述动态均衡的蛛网理论所描述的收敛型蛛网情况。
多恩布什《宏观经济学》(第10版)笔记和课后习题详解 第4章 增长与政策【圣才出品】

第4章增长与政策4.1复习笔记1.内生增长理论内生增长理论是指罗默、卢卡斯等经济学家提出的,用规模收益递增和内生技术进步来说明一个国家长期经济增长和各国增长率差异的一种经济增长理论。
该理论试图将增长率解释为社会决策的函数,特别是储蓄率的函数。
修改新古典增长模型中假定的生产函数的形状,在一定程度上就会出现容许自我持续的(即内生的)增长。
(1)基本假设①社会储蓄函数为S sY =,其中s 为储蓄率;②劳动增长率n 不变;③资本的边际产品不变;④存在外部经济且外部报酬相当大;⑤技术进步是内生要素,技术与总体经济中每个工人的资本水平成正比例,/A K N k αα==,并假定技术属于劳动增加型。
(2)基本方程在上述假定下,把生产函数写为()Y F K AN =,,该生产函数满足规模报酬不变。
对生产函数求全微分:()F F Y K N A A N K AN∂∂∆=⨯∆+⨯∆+⨯∆∂∂Y K F K K AN F AN N AN F AN A Y K N A∆⨯∂∂∆⨯∂∂∆⨯∂∂∆=⋅+⋅+⋅由于生产函数满足规模收益不变,要素及产品市场属于完全竞争市场,运用欧拉定理得:K F K θ⨯∂∂=,1AN F AN θ⨯∂∂=-即有:()()11Y K N Aθθθ∆∆∆∆=⨯+-⨯+-⨯人均产出增长率表达式:()1Y N K N A YN K N A θθ∆∆∆∆∆⎛⎫⎛⎫-=-⨯+⨯- ⎪ ⎪⎝⎭⎝⎭即有:()1y k A y k Aθθ∆∆∆=⨯+⨯-将技术增长公式A K N k A K N k∆∆∆∆=-=代入GDP 增长方程,得:()()11y k A k k k y k A k k kθθθθ∆∆∆∆∆∆=⨯+⨯-=+-=可以判断,y k是常数。
将生产函数除以K 可得出该常数:()()()1F K AN y F K K AN K F k Kαα===≡,,,资本积累方程为()k sy n d k k ∆=-+,联立上式可得,内生增长模型的人均产出增长率的基本公式为:()()y k sy g n d sa n d y k k∆∆===-+=-+。
多恩布什《宏观经济学》第10版课后习题详解(货币、利息与收入)【圣才出品】

5. IS 曲线( IS curve)
答: IS 曲线指将满足产品市场均衡条件的收入和利率的各种组合的点连结起来而形成
的曲线。它是反映产品市场均衡状态的一幅简单图像。它表示的是任一给定的利率水平上都
M P h h kbG
h 与 k 数值越小,b 与 G 数值越大,增加实际余额对均衡收入水平的扩张性效应也越大。 b 与 G 的数值大,对应着非常平直的 IS 曲线。
4.中央银行(central bank) 答:中央银行指在一国金融体系中居于主导地位,负责制定和执行国家的金融政策,调 节货币流通与信用活动,对国家负责,在对外金融活动中代表国家,并对国内整个金融体系 和金融活动实行管理与监督的金融中心机构。中央银行具有三大职能,即它是“发行的银行”、 “银行的银行”和“政府的银行”。
2 / 21
圣才电子书 十万种考研考证电子书、题库视频学习平台
(1)中央银行是发行的银行,这一职能指中央银行服务于社会和经济发展,供应货币、 调节货币量、管理货币流通的职能。
(2)中央银行是银行的银行,这一职能指中央银行服务于商业银行和整个金融机构体 系,履行维持金融稳定、促进金融业发展的职责。
6.货币市场的均衡曲线(money market equilibrium schedule)
3 / 21
圣才电子书 十万种考研考证电子书、题库视频学习平台
答:LM 曲线即货币市场的均衡曲线,它显示能使其实际余额需求等于供给的所有利率
与收入水平的组合。沿着 LM 曲线,货币市场处于均衡状态。要使货币市场处于均衡状态,
A bi
多恩布什《宏观经济学》第10版课后习题详解(国际调整与相互依存)【圣才出品】

多恩布什《宏观经济学》第10版课后习题详解第20章国际调整与相互依存一、概念题1.自动调节机制(automatic adjustment mechanisms)答:自动调节机制指自动起作用消除国际收支失衡问题的机制。
在纯粹的自由经济中有货币—价格机制、收入机制及利率机制等国际收支自动调节机制。
货币—价格机制,也称“价格—现金流动机制”,其描述的是国内货币供给存量与一般物价水平变动以及相对价格水平变动对国际收支的影响。
当一国处于逆差状态时,对外支付大于收入,货币外流,物价下降,本国汇率也下降,由此导致本国出口商品的价格绝对或相对下降,从而出口增加,进口减少,贸易收入得到改善。
收入机制的调节作用表现为:当国际收支逆差时,国民收入下降。
国民收入下降引起社会总需求下降,从而进口需求也下降,进而改善贸易收支。
利率机制的调节作用表现为:当国际收支发生逆差时,本国货币供给存量减少,利率因此上升,这意味着本国金融资产的收益上升,从而对本国金融资产的需求上升,对外国金融资产的需求相对下降。
这样,资金外流减少或内流增加,资本与金融项目收支得到改善。
当国际收支顺差时,上述的自动调节仍然起作用,只是方向相反而已。
2.内部和外部平衡(internal and external balance)答:内部平衡指国民经济处于无通货膨胀的充分就业状态。
内部均衡时国内产品市场、货币市场和劳动市场同时达到均衡,宏观经济处于充分就业水平上,并且没有通货膨胀的压力,经济稳定增长。
内部均衡目标包括经济增长、价格稳定和充分就业。
外部均衡指国际收支平衡,也即贸易品的供求处于均衡状态。
当国际收支平衡时,既无国际收支顺差,也无国际收支逆差。
在开放经济中,宏观经济的最终目标是实现内部均衡和外部均衡。
英国经济学家詹姆斯·米德开创性地提出了“两种目标、两种工具”的理论模式,即在开放经济条件下,一国经济如果希望同时达到对内均衡和对外均衡的目标,则必须同时运用支出增减政策和支出转换政策两种工具。
多恩布什《宏观经济学》第10版课后习题详解(货币政策与财政政策)【圣才出品】
多恩布什《宏观经济学》第10版课后习题详解第11章货币政策与财政政策一、概念题1.预期的货币政策(anticipatory monetary policy)答:预期的货币政策指为了对估计到的未来将会发生的问题(例如通货膨胀的压力)作出反应而采用的货币政策。
比如,在一个预先防范的货币政策的例子中,央行不是对总需求与通货膨胀压力的现有情况作出反应,而是对经济如果增长过快,会发生通货膨胀的这种担心作出反应。
该政策的基本问题是:确定货币政策时,应当往前看。
2.投资税减免(investment tax credit)答:投资税减免指国家以法律形式规定的在一定条件下允许纳税人以用于某些方面的投资抵免一定税款的政策措施。
实行这种政策,表明国家是鼓励税收减免的,即国家为支持投资而在税收方面作出优惠的减免税的规定。
这种政策对鼓励和吸引投资有一定成效。
我国在改革开放中也使用了这种政策。
3.政策组合(policy mix)答:政策组合指为了实现宏观经济目标而采取的财政政策、货币政策以及其他一些政策工具的组合。
扩张性的财政政策表现为IS曲线右移,在使收入增加的同时会带来利率的上升,而扩张性的货币政策表现为LM曲线右移,在使收入增加的同时会带来利率的下降。
因此,为实现收入和利率的不同组合,将两种政策搭配使用,即财政政策和货币政策的混合使用。
政府和中央银行可以根据具体情况和不同目标,选择不同的政策组合。
例如,当经济萧条但又不太严重时,用扩张性财政政策刺激总需求,又用紧缩性货币政策控制通货膨胀;当经济发生严重通货膨胀时,用紧缩货币来提高利率,降低总需求水平,又紧缩财政,以防止利率过分提高;当经济中出现通货膨胀又不太严重时,用紧缩财政压缩总需求,又用扩张性货币政策降低利率,以免财政政策紧缩而引起衰退;当经济严重萧条时,用扩张财政增加总需求,用扩张货币降低利率以克服“挤出效应”。
4.古典情况(classical case)答:古典情况即垂直的LM曲线,是货币需求对于实际利率十分敏感的情况。
多恩布什《宏观经济学》第10版课后习题详解(重大事件:萧条经济学、恶性通货膨胀和赤字)【圣才出品】
圣才电子书 十万种考研考证电子书、题库视频学习平台
6.可信的政策(credible policy) 答:可信的政策指人们相信政府将会遵循的政策。可信的政策有利于赢得公众的信心, 从而在最大程度上降低政策成本。政府政策的可信度不高,会降低公众对政府的信心,使得 政府无法引导公众预期,加大政策执行难度。因此,政府应该努力提高政策的可信性,合理 引导公众预期,降低政策成本。
4.信任奖励(credibility bonus) 答:信任奖励又称信誉红利,指在理性预期下政府政策的可信性所获得的报偿。政府在 降低通货膨胀的斗争中,由于公众相信政府的反通货膨胀政策会得到执行从而降低通货膨胀 预期,这样即使政策未执行也会使通货膨胀降低,从而避免经济的衰退,政府政策的可信性 便获得了报偿。 通货膨胀是由经济的基本方面(总需求与总供给的相对变动)所决定的。在恶性通货膨 胀中,货币的增长支配了所有的其他基本因素。但是,人们关于未来的预期也发挥了作用。 相信政策已经改变本身就会驱动预期的通货膨胀率下降,并且因此而引起短期的菲利普斯曲
2 / 38
圣才电子书 十万种考研考证电子书、题库视频学习平台
线向下移动。所以,在反通货膨胀的战斗中,一种可信任的政策会赢得社会对可信性的褒奖。 从美联储 1979 年 10 月改变其货币政策开始,在美国整个反通货膨胀时期,一直着重
强调政策的可信性。理性预期的一些支持者衰退。
新政的主要内容包括: (1)对工商业大量的贷款和津贴,刺激私人投资; (2)提高物价,减少农业生产,克服农产品过剩; (3)兴建公共工程,增加就业机会; (4)对失业者给予最低限度救济。 新政实施的结果使美国逐渐摆脱了危机,为千百万人提供了就业和生活的保障,使经济 不平衡状况有所改善。1935 年起所有经济指标都稳步上升,失业人数大幅度下降。新政大 多是应急措施,没有完整的理论依据,但体现了凯恩斯主义国家干预经济的思潮,反映了现 代私人垄断资本主义向国家垄断资本主义过渡这一总的趋向,对美国以后历届政府的政策影 响很大。
宏观经济学第十版第二章课后习题完美精简中文版
多恩布什宏观经济学第十版第二章课后习题答案完美中文精简版概念题1,他们作为政府雇员支取TR美元,但是不做任何工作,实际上就是加大了政府支出,GDP会增长。
2,a..厂商为经理买车应该看成投资,经理自己购买轿车则是消费。
b.雇佣配偶的行为是消费,计算GDP时会被计入;而无偿要求她担任此工作则是无形中忽略掉了消费环节,不计入GDP。
c.买美国轿车会使GDP增长,买德国车也会使GDP增加,但是会减少净出口。
3,GDP与GNP的区别在于:GNP是指一个国家(或地区)所有国民在一定时期内新生产的产品和服务价值的总和。
GNP是按国民原则核算的,只要是本国(或地区)居民,无论是否在本国境内(或地区内)居住,其生产和经营活动新创造的增加值都应该计算在内。
GDP是指一个国家(或地区)在一定时期内所有常住单位生产经营活动的全部最终成果。
GDP是按国土原则核算的生产经营的最终成果。
使用GDP计量产出更好,GDP的精确度高。
4,NDP是国内生产净值,NDP是从国内生产总值GDP中扣除资本折旧得到的。
如果用于计算产量,它比GDP更接近产品价值,但是折旧率是人来计算,所以会存在一定误差,在计算数值非常大时用GDP计算比较好。
5,GDP的增加不代表福利的增加,比如说GDP增加,同时人口也增长了,一平均,每个人的GDP没有变化。
我觉得最大的问题是人口问题,人口的增长和减少对人均GDP有影响。
6,CPI居民消费价格指数,是反映与居民生活有关的商品及劳务价格统计出来的物价变动指标,通常作为观察通货膨胀水平的重要指标。
PPI是衡量企业购买的一篮子物品和劳务的总费用。
从消费者的立场计算时我会选择用CPI计算。
7,GDP紧缩指数=(名义GDP/实际GDP) *100区别答不出。
8,物价是否翻了一倍,以及GDP紧缩指数有没有变化。
9,伤心。
以实际利率说明的,将要支付更少利息。
技术题12,b.收入增加意味着可支配收入增加,那么此时就能够购买更多的产品。
多恩布什宏观经济学第十版课后答案
宏观经济学第二章概念题1.如果政府雇用失业工人,他们曾领取TR美元的失业救济金,现在他们作为政府雇员支取TR美元,不做任何工作,GDP会发生什么情况?请解释。
答:国内生产总值指一个国家(地区)领土范围,本国(地区)居民和外国居民在一定时期内所生产和提供的最终使用的产品和劳务的价值。
用支出法计算的国内生产总值等于消费C、投资I、政府支出G和净出口NX之和。
从支出法核算角度看:C、I、NX保持不变,由于转移支付TR美元变成了政府对劳务的购买即政府支出增加,使得G增加了TR美元,GDP会由于G的增加而增加。
2.GDP和GNP有什么区别?用于计算收入/产量是否一个比另一个更好呢?为什么?答:(1)GNP和GDP的区别GNP指在一定时期内一国或地区的国民所拥有的生产要素所生产的全部最终产品(物品和劳务)的市场价值的总和。
它是本国国民生产的最终产品市场价值的总和,是一个国民概念,即无论劳动力和其他生产要素处于国内还是国外,只要本国国民生产的产品和劳务的价值都记入国民生产总值。
GDP指一定时期内一国或地区所拥有的生产要素所生产的全部最终产品(物品和劳务)的市场价值的总和。
它是一国范围内生产的最终产品,是一个地域概念。
两者的区别:在经济封闭的国家或地区,国民生产总值等于国内生产总值;在经济开放的国家或地区,国民生产总值等于国内生产总值加上国外净要素收入。
两者的关系可以表示为:GNP=GDP+[本国生产要素在其他国家获得的收入(投资利润、劳务收入)-外国生产要素从本国获得的收入]。
(2)使用GDP比使用GNP用于计量产出会更好一些,原因如下:1)从精确度角度看,GDP的精确度高;2)GDP衡量综合国力时,比GNP好;3)相对于GNP而言,GDP是对经济中就业潜力的一个较好的衡量指标。
由于美国经济中GDP和GNP的差异非常小,所以在分析美国经济时,使用这两种的任何一个指标,造成的差异都不会大。
但对于其他有些国家的经济来说明,这个差别是相当大的,因此,使用GDP作为衡量指标会更好。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
CHAPTER 4GROWTH AND POLICYSolutions to the Problems in the TextbookConceptual Problems:1. Endogenous or self-sustained growth supposedly can be achieved by policies that affect anation's savings rate and therefore the proportion of GDP that goes towards investment.The neoclassical growth model of Chapter 3 predicted that long-term growth can only be achieved through technological progress and that changes in the savings rate have only transitory effects. The endogenous growth model, however, predicts that countries with a higher savings rate can achieve higher long-term growth and that a nation's government can affect the long-term growth rate by implementing policies that affect the savings rate.2. A simple model with constant returns to scale to capital alone implies increasingreturns to scale to all factors taken together, which could cause a single large firm to dominate the economy. However, such a model ignores the possibility that external returns to capital exist, in addition to the internal (private) returns. In other words, more investment not only leads to a higher and more efficient capital stock but also to new ideas and new ways of doing things, which can then be copied by others. Therefore, a single firm does not necessarily reap all of the benefits of increased output.3.In the neoclassical growth model, an increase in the savings rate does not increase thelong-term growth rate of output. However, because of the short-run adjustment process, there is some transitional gain that will lead to a higher level of output per capita. In the endogenous growth model, however, the savings rate does affect the long-term growth rate of output.4.a. Chapter 4 suggests that the key to long-term economic growth is investment in humanand physical capital with particular emphasis on research and development.4.b. (i) Investment tax credits may potentially affect economic growth in the long run byachieving a higher rate of technological progress.(ii) R&D subsidies and grants lead to technological advances that will have private andsocial returns. They are very effective in stimulating long-term economic growth.(iii) According to the endogenous growth model, policies designed to increase thesavings rate will increase the long-term growth rate of output. However, empiricalevidence does not lend much support to that notion.(iv) Increased funding for primary education has large private and social returns andis therefore an excellent means to stimulate long-term growth, even though it may take along time until these policies have their full effect.5. The notion of absolute convergence states that economies with the same savings rate andrate of population growth will reach the same steady-state equilibrium if they have access to the same technology. The notion of conditional convergence states that economies that have access to the same technology and the same rate of population growth but different savings rates will reach steady-state equilibria at a different level of output but the same economic growth rate. There is empirical evidence to support the notion of conditional convergence across countries.6. Endogenous growth theory assumes that the steady-state growth rate of output isaffected by the rate at which the factors of production are accumulated. Therefore, an increase in the savings rate would increase the rate at which the capital stock is accumulated and this would increase the growth rate of output. While this notion may be important in explaining the growth rates of highly developed countries at the leading edge of technology, it cannot explain the differences in growth rates across poorer countries.For these countries, the notion of conditional convergence seems to hold.7. Investing in physical capital will lead to a higher capital stock and to a higher level ofoutput in the short run, but often to the detriment of long-term growth unless there are significant external returns to capital. Therefore, investing in human capital is a better strategy, since it has high returns and leads to an increase in long-term growth.8.a. A country that is able to choose its rate of population growth through population controlpolicies can shift the investment requirement down, thereby increasing the level of steady-state output. With a lower rate of population growth it is possible to achieve a higher level of income per capita with a lower level of investment spending. Therefore, implementing population control policies may be an effective way to escape the so-called poverty trap.8.b. In an endogenous growth model, a lower population growth rate (n) will increase anation's long-term growth rate (∆y/y). We can see this since, in the second optional section, the per-capita growth rate was derived, as follows:∆y/y = sa - (n + d).9. The Asian Tigers (Hong Kong, Singapore, South Korea, and Taiwan) experienced a highrate of economic growth between 1966 and 1990 by concentrating on improving the education of the population and increasing the savings rate, as suggested by the endogenous growth model. However, increases in the labor forces of these countries suggested by the neoclassical growth model, were also at work.10. The decline in living standards experienced by Eastern European countries in transitionfrom centrally planned economies to free market economies cannot easily be explained by neoclassical or endogenous growth theory. The decline in GDP in these countries was largely due to disorganized markets that lacked properly assigned property rights or liability rules and an insufficiently developed banking system. In addition, the need for large-scale replacement of outdated production technology caused further disruption.11. In is unclear whether countries can actually experience indefinite increases in theirgrowth potential. However, if technological advances occur continuously and if intelligent resource management is practiced, it is conceivable that economic growth will continue for a very, very long time.Technical Problems:1.a. A production function that displays both a diminishing and a constant marginal product ofcapital can be displayed by drawing a curved line (as in an exogenous growth model), followed by a upward-sloping line (as in an endogenous growth model). Such a graph is depicted below.1.b. The first equilibrium (Point A in the graph below) is a stable low-income steady-stateequilibrium. Any deviation from that point will cause the economy to eventually adjust again at the same steady-state income level (and capital-output ratio). The second equilibrium (Point B) is an unstable high-income steady-state equilibrium. Any deviation from that point will lead to either a lower income steady-state equilibrium (if the capital-labor ratio declines) or ongoing growth (if the capital-labor ratio increases).yy = f(k)y BsyB (n+ d)ky AAk A k B k1.c. A model like the one in this question can be used to explain how some countries can findthemselves in a situation with no growth and low income while others have ongoing growth and a high level of income. In the first case, a country may have invested in physical capital, leading to some short-term growth at the expense of long-term growth, whereas in the second case, a country may have invested heavily in human capital, reaping significant social returns.2.a. If population growth is endogenous, that is, if a country can influence the rate of population growth through government policies, then the investment requirement is no longer a straight line. Instead it is curved as depicted below.yy C y = f(k)y B[n(y) + d]]kC sf(k)y A BAk A k B k C k2.b. The first equilibrium (Point A) is a stable steady-state equilibrium. It is a situation of lowincome and high population growth, indicating that the country is in a poverty trap. The second equilibrium (Point B) is an unstable steady-state equilibrium. It is a situation of medium income and low population growth. The third equilibrium (Point C) is a stable steady-state equilibrium. It is a situation of high income and low population growth. None of these three equilibria have ongoing growth.2.c. To escape the poverty trap (Point A), a country has several possibilities: First, it cansomehow find the means to increase the capital-labor ratio above a level consistent with Point B (perhaps by borrowing funds or seeking direct foreign investment). Second, it can increase the savings rate such that the savings function no longer intersects the investment requirement curve at either Point A or Point B. Third, it can decrease the rate of population growth through specifically designed policies, such that the investment requirement shifts down and no longer intersects with the savings function at Point A or Point B.3.a. If we incorporate endogenous population growth into a two-sector model in Problem 2,then we get a curved line for the investment requirement line and a production function with first a diminishing and then a constant marginal product of capital as depicted below.(Note that the savings function has the same shape as the production function.)yy = f(k)y Dsf(k)D [n+d)]ky Cy By A CBAk A k B k C k D k3.b. There should be four intersections of the savings function and the investment requirement.The first equilibrium (at Point A) is a stable low-income steady-state equilibrium. Any deviation from that point will cause the economy to eventually adjust again at the same steady-state income level (and capital-output ratio). The second equilibrium (at Point B) is an unstable low-income equilibrium. Any deviation from that point will lead to either a lower income steady-state equilibrium at Point A (if the capital-labor ratio declines) or a higher income steady-state equilibrium at Point C (if the capital-labor ratio increases).Point D is again an unstable equilibrium but at a high level of income. Any deviation from that point will lead to either a lower income steady-state equilibrium at Point C (if the capital-labor ratio declines) or ongoing growth (if the capital-labor ratio increases). 3.c. This model is more inclusive than either of the two models discussed previously, andtherefore has greater explanatory power. But now the graphical analysis is far more complicated. It may not be worth the effort to introduce such complications.4.a. The production function is of the formY = K1/2(AN)1/2 = K1/2(4[K/N]N)1/2= K1/2(4K)1/2= 2K4.b. Since a = y/k = 2, it follows that the growth rate of output isg = sa - (n + d) = (0.1)2 - (0.02 + 0.03) = 0.15 = 15%.4.c. The term "a" in the equation above stands for the marginal product of capital. If weassume that the level of labor-augmenting technology (A) is proportional to the capital-labor ratio (k), we imply that the level of technology depends on the amount of capital per worker that we have, which may not be realistic.4.d. In this model, we have a constant marginal product of capital, and therefore we have anendogenous growth model.5.a. The production function is of the formY = K1/2N1/2==> Y/N = (K/N)1/2 ==> y = k1/2.From k = sy/(n + d) = sk1/2/(n +d) ==> k1/2 = s/(n + d)==> y* = s/(n + d) = (0.1)/(0.02 + 0.03) = 2==> k* = sy*/(n + d) = (0.1)(2)/(0.02 + 0.03) = 45.b. Steady-state consumption equals steady-state income minus steady-state investment, thatis,c* = f(k*) - (n + d)k* .The golden rule capital stock corresponds to the highest permanently sustainable level of consumption. Steady-state consumption is maximized when the marginal increase in capital produces just enough extra output to cover the increased investment requirement.From c = k1/2 - (n + d)k ==> (∆c/∆k) = (1/2)k-1/2 - (n + d) = 0==> k-1/2 = 2(n + d) = 2(.02 + .03) = .1==> k1/2 = 10 ==> k = 100Since k*= 4 < 100, we have less capital at the steady state than the golden rule suggests.5.c. From k = sy/(n + d) = sk1/2/(n + d) ==> s = k1/2(n + d) = 10(0.05) = .55.d. If we have more capital than the golden rule suggests, then we are saving too much andwe do not have the optimal amount of consumption.。
