专题_拉氏变换与Z变换
拉氏变换和z变换表
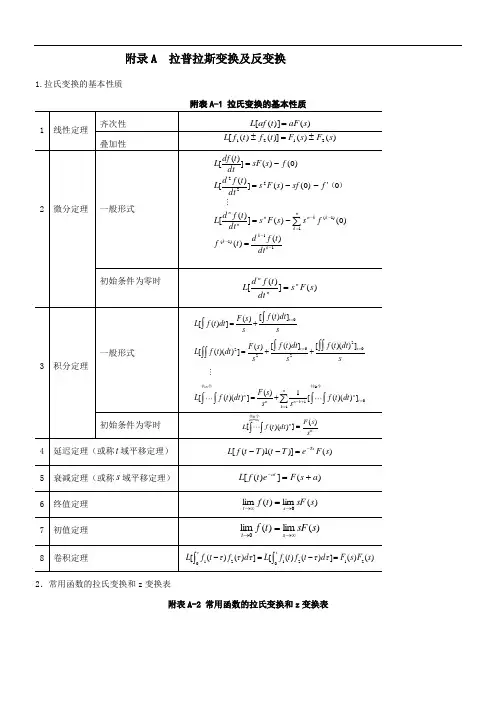
附录A 拉普拉斯变换及反变换1.拉氏变换的基本性质1()([n n k f t dt s s-+=+∑⎰个2．常用函数的拉氏变换和z变换表附表A-2 常用函数的拉氏变换和z变换表3． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。
设)(s F 是s 的有理真分式，即1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- （m n >） 式中，系数n n a a a a ,,...,,110-和011,,,,m m b b b b -都是实常数；n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
（1）0)(=s A 无重根：这时，F(s)可展开为n 个简单的部分分式之和的形式，即∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)( （F-1）式中，n s s s ,,,21 是特征方程A(s)＝0的根；i c 为待定常数，称为()F s 在i s 处的留数，可按下列两式计算：lim()()ii i s s c s s F s →=- （F-2）或iss i s A s B c ='=)()( （F-3）式中，)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质，从式（F-1）可求得原函数为[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(＝1in s ti i c e =∑ (F -4) （2）0)(=s A 有重根：设0)(=s A 有r 重根1s ，F(s)可写为())()()()(11n r rs s s s s s s B s F ---=+ =nn i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11111111)()()( 式中，1s 为F(s)的r 重根，1+r s ，…，n s 为F(s)的n r -个单根；其中，1+r c ，…，n c 仍按式(F-2)或式(F-3)计算，r c ，1-r c ，…，1c 则按下式计算：)()(lim 11s F s s c r s s r -=→11lim[()()]ir r s s dc s s F s ds-→=-)()(lim !11)()(1s F s s dsd j c r j j s s jr -=→- (F-5))()(lim )!1(11)1()1(11s F s s dsd r c r r r s s --=--→原函数)(t f 为 [])()(1s F Lt f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 111111111)()()( t s nr i i t s r r r r ie c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1( （F-6）。
拉氏变换和z变换表
附录A 拉普拉斯变换及反变换1.拉氏变换的基本性质1()([n n k f t dt s s-+=+∑⎰个2．常用函数的拉氏变换和z 变换表附表A-2 常用函数的拉氏变换和z 变换表3． 用查表法进行拉氏反变换用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。
设)(s F 是s 的有理真分式，即1110111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- （m n >） 式中，系数n n a a a a ,,...,,110-和011,,,,m m b b b b -都是实常数；n m ,是正整数。
按代数定理可将)(s F 展开为部分分式。
分以下两种情况讨论。
（1）0)(=s A 无重根：这时，F(s)可展开为n 个简单的部分分式之和的形式，即∑=-=-++-++-+-=ni ii n n i i s s c s s c s s c s s c s s c s F 12211)( （F-1）式中，n s s s ,,,21 是特征方程A(s)＝0的根；i c 为待定常数，称为()F s 在i s 处的留数，可按下列两式计算：lim()()ii i s s c s s F s →=- （F-2）或iss is A s B c ='=)()( （F-3）式中，)(s A '为)(s A 对s 的一阶导数。
根据拉氏变换的性质，从式（F-1）可求得原函数为[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 111)()(＝1in s ti i c e =∑ (F-4) （2）0)(=s A 有重根：设0)(=s A 有r 重根1s ，F(s)可写为())()()()(11n r rs s s s s s s B s F ---=+ =nn i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11111111)()()( 式中，1s 为F(s)的r 重根，1+r s ，…，n s 为F(s)的n r -个单根；其中，1+r c ，…，n c 仍按式(F-2)或式(F-3)计算，r c ，1-r c ，…，1c 则按下式计算：)()(lim 11s F s s c r s s r -=→11lim[()()]ir r s s dc s s F s ds-→=-)()(lim !11)()(1s F s s dsd j c r j j s s jr -=→- (F-5))()(lim )!1(11)1()1(11s F s s dsd r c r r r s s --=--→原函数)(t f 为 [])()(1s F Lt f -=⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 111111111)()()( t s nr i i t s r r r r ie c e c t c t r c t r c ∑+=---+⎥⎦⎤⎢⎣⎡+++-+-=1122111)!2()!1( （F-6）。
Z变换与F、L变换的关系
Ω= 0，S平面的实轴， ω= 0，Z平面正实轴；
Ω=Ω0(常数)，S:平行实轴的直线， ω= Ω0T,Z:始于
原点的射线；
Ω ( , ), S:宽 2的水平条带， ω ( , ) 整个z平面.
TT
T
j 3
jIm[Z]
Tபைடு நூலகம்
T
T
3
T
ω
0
Re[Z]
S平面到Z平面的映射是多值映射，不是单一映射。
总结：z 变 换 的 本 质 是 理 想 冲 激 抽 样 的 拉 普 拉 斯 变
二.Z变换和傅氏变换的关系
连续信号经理想取样后,其频谱产生周期延拓，
即
Xˆ a (
j)
1 T
k
Xa(
j
jk
2
T
)
我们知道,傅氏变换是拉氏变换在虚轴S=jΩ
的特例,因而映射到Z平面上为单位圆。因此,
X (z)ze jT X (e jT ) Xˆ a ( j)
这就是说,（取样）序列在单位圆上的Z变换,就等
σ 0, s jΩ
H jΩ H s s jΩ
4. z平面单位圆上的z变换即为序列的傅氏 变换（DTFT）
z 1, z ejω
X e jω X z zejω
四.序列的傅氏变换
1.正变换:
F[x(n)] x(e j ) X (z)ze j x(n)e jn , n
收敛条件为： x(n) n
即X (z) zesT X (esT ) Xˆ a (s)
2.Z变换与拉氏变换的关系( S、Z平面映射关系）
S平面用直角坐标表示为：s j
Z平面用极坐标表示为： z re j
又由于 z esT
拉氏变换与Z变换的基本公式及性质
拉氏变换与Z变换的基本公式及性质拉氏变换（Laplace Transform）是一种重要的信号分析工具，它将时域函数转换为复域函数，使得分析和处理复杂的差分方程、微分方程、线性时不变系统等问题变得更加简单。
拉氏变换的定义如下：对于一个定义在半轴t≥0上的实值函数f(t)，它的拉氏变换F(s)定义为：F(s) = L{f(t)} = ∫[0,∞] e^(-st) f(t) dt其中s是一个复变量，e^(-st)是一个复数系数。
拉氏变换的基本公式：1.映射常数L{1}=1/s2. $L{e^{at}}=\frac{1}{s-a}, Re(s)>a$3.时间平移L{f(t-a)u(t-a)} = e^(-as)F(s)4.频域平移L{e^(as)f(t)} = F(s-a)5.合并函数L{f(t)+g(t)}=F(s)+G(s)6.乘法L{f(t)g(t)}=F(s)*G(s)7.单位冲激函数L{δ(t-a)} = e^(-as)拉氏变换的性质：1.线性性质L{af(t) + bg(t)} = aF(s) + bG(s)2.积分性质L{∫[0,t]f(τ)dτ}=1/s*F(s)3.拉氏变换的导数性质L{f'(t)}=sF(s)-f(0)4.初始值定理f(0+) = lim(s->∞) sF(s)5.最终值定理lim(t->∞) f(t) = lim(s->0) sF(s)Z变换是一种由离散信号而来的变换，它将离散序列变换到复平面上。
Z变换的定义如下：对于一个离散序列x[n]，它的Z变换X(z)定义为：X(z)=Z{x[n]}=∑[-∞,∞]x[n]z^(-n)其中z是一个复变量。
Z变换的基本公式：1.映射常数Z{1}=12.单位序列Z{δ[n]}=13.线性性质Z{ax[n] + by[n]} = aX(z) + bY(z)4.平移Z{x[n-a]}=z^(-a)X(z)5.单位冲激响应函数Z{h[n]}=H(z)6.时域乘法Z{x[n]y[n]}=X(z)Y(z)Z变换的性质：1.线性性质Z{ax[n] + by[n]} = aX(z) + bY(z)2.移位性质Z{x[n-k]}=z^(-k)X(z)3.初始值定理x[0] = lim(z->∞) X(z)4.最终值定理lim(n->∞) x[n] = lim(z->1) (1-z^(-1))*X(z)5.时域卷积性质Z{x[n]*y[n]}=X(z)Y(z)6.时域乘法性质Z{x[n]y[n]}=X(z)Y(z)总结：拉氏变换和Z变换都是用于信号分析和处理的重要工具。
第七讲拉氏变换傅氏变换与Z变换
jω)决定。
故称H(ejω)
为线性时不变系统的频率响应。线性时不变系统的
频率响应是其单位脉冲响应的傅里叶变换。
线性时不变系统的频率响应 H(ejω) 是以 2π 为周期的连续周
期函数, 是复函数。它可以写成模和相位的形式
H (e ) | H (e ) | e
j
j
j arg[ H ( e j )]
1 2k Xa j T k T
单位圆上序列的Z变换为序列的傅里叶变换 数字频谱是其被采样的连续信号频谱周期延拓后再对采样 频率的归一化。
2.6 序列的傅氏变换 因单位圆上序列的Z变换为序列的傅里叶变换，用ejω代替z， 得到序列傅里叶变换的定义为
求系统的单位脉冲响应及系统性质。
1 | z | 2 2
解 收敛域包括单位圆但不包括∞点，因此系统是稳定的但
是非因果的。由系统函数的Z反变换可得
1 n h(n) u(n) 2 u(n 1) 2
由于存在2nu(-n-1)项， 因此系统是非因果的。
n
2.10.3 系统频率响应的意义
利用傅里叶变换性质得到
F［y(n)］=F［x(n) * h(n)］
即
Y(ejω)=X(ejω)H(ejω)
对于线性时不变系统，其输出序列的傅里叶变换等于输入序
列的傅里叶变换与系统频率响应的乘积。
|Y(ejω)|=|H(ejω)|·|X(ejω)| arg［Y(ejω)］=arg［H(ejω)］+arg［X(ejω)］
式中:
m
h(m)e
jn
H (e
j
)
y(n)=ejωnH(ejω)
上式表明，当线性时不变系统输入是频率为ω的复正弦序列
专题拉氏变换与Z变换
F ( z ) F * ( s )
s T k f ( kT ) z ln z k 0
F(z)与f*(t)或{f(kT)}构成变换对，它不是连续时间函数f(t)的Z变换。
专题1 拉氏变换与Z变换
2 Z变换及其性质 对于序列{f(kT)}（也就是采样信号），可以定义它的z变换为
j t e e 1 1 st 1 L [sin t ] sin te dt e dt ( ) 2 2 0 0 2 j 2 j s j s j s
st
j t
j t ee 1 1 1 s s t Lt [ c o s ] c o s t e d t e d t ( ) 2 2 0 0 2 2 s j s j s
at at st ( s a ) t
（3）单位脉冲函数 (t )
1 t 0 0 t 0
s t L [ () t] () t e d t 1 0
专题1 拉氏变换与Z变换
1 拉氏变换及其性质 1.2 简单函数的拉氏变换
cos t
专题1 拉氏变换与Z变换 1 拉氏变换及其性质
1.1 拉氏变换的基本概念 定义: 对于函数f(t)如果满足下列条件： （1）当t<0时，f(t)=0； 当t>0时，f(t)在每个有限区间上是分段连续的。
（2） ，其中σ是正实数，也就是说f(t) 0 是指数级； 那么定义f(t)的拉氏变换F(s)为
at L [ e f ( t )] F ( s a )
专题1 拉氏变换与Z变换
2 Z变换及其性质 2.1 Z变换的定义 采样信号的数学表达式为 f * ( t) f( t) ( t kT )
(完整版)§8.6 z变换与拉氏变换的关系
1
j
Xs
e sT z -1 nds
2pj - j
n0
此式的收敛条件是：|z|>|esT|，当符合这一条件时
e sT z -1 n
1
n0
1 - e sT z -1
X z 1 j X s
ds 1
例如：当X(s)有一单阶极点s1时
Re
s
zX z-
s e sT
ss1
z
s - s1 X z - e sT
s
k1z k1z
s s1
z - e s1T
z - z1
以上从拉氏逆变换式出发推证了拉氏变换式 与z变换式的关系式。 下面把信号按部分分式分解进行讨论 若连续时间信号xˆ(t)由N项指数信号相加组合而成
xˆ t xˆ 1 t xˆ 2 t xˆ n t
N
N
xˆ i t Ai e pitut
i1
i 1
N
容易求得，它的拉式变换为 L xˆ t
Ai
i1 s - pi
若序列X(nT)由N项指数序列相加组合而成
xnT x1nT x2 nT xN nT
X s
s2
ω0 ω02
显然X(s)的极点位于s1=j0, s2= -j0,其留数分别为
A1
-j 2
及A2
j 2
于是， X(s)可以展成部分分式
-j
j
X s 2 2
s - jω0 s jω0
可以得到sin(0nT)u(nT)的z变换为
对傅里叶变换、拉氏变换、z变换详细剖析
对傅里叶变换、拉氏变换、z变换详细剖析变换的实质是将一个信号分离为无穷多多正弦/复指数信号的加成，也就是说，把信号变成正弦信号相加的形式——既然是无穷多个信号相加，那对于非周期信号来说，每个信号的加权应该都是零——但有密度上的差别，你可以对比概率论中的概率密度来思考一下——落到每一个点的概率都是无限小，但这些无限小是有差别的。
所以，傅里叶变换之后，横坐标即为分离出的正弦信号的频率，纵坐标对应的是加权密度。
对于周期信号来说，因为确实可以提取出某些频率的正弦波成分，所以其加权不为零——在幅度谱上，表现为无限大——但这些无限大显然是有区别的，所以我们用冲激函数表示。
已经说过，傅里叶变换是把各种形式的信号用正弦信号表示，因此非正弦信号进行傅里叶变换，会得到与原信号频率不同的成分——都是原信号频率的整数倍。
这些高频信号是用来修饰频率与原信号相同的正弦信号，使之趋近于原信号的。
所以说，频谱上频率最低的一个峰（往往是幅度上最高的），就是原信号频率。
傅里叶变换把信号由时域转为频域，因此把不同频率的信号在时域上拼接起来进行傅里叶变换是没有意义的——实际情况下，我们隔一段时间采集一次信号进行变换，才能体现出信号在频域上随时间的变化。
我的语言可能比较晦涩，但我已尽我所能向你讲述我的一点理解——真心希望能对你有用。
我已经很久没在知道上回答过问题了，之所以回答这个问题，是因为我本人在学习傅里叶变换及拉普拉斯变换的过程中着实受益匪浅——它们几乎改变了我对世界的认识。
傅里叶变换值得你用心去理解——哪怕苦苦思索几个月也是值得的——我当初也想过：只要会算题就行。
但浙大校训“求是”时时刻刻鞭策着我追求对理论的理解——最终经过很痛苦的一番思索才恍然大悟。
建议你看一下我们信号与系统课程的教材：化学工业出版社的《信号与系统》，会有所帮助。
（另一种说法）对于周期函数f，傅立叶变换就是把这个函数分解成很多个正弦函数fn的和，每个fn的频率是f的n倍。
完整word版拉氏变换和z变换表
附录A拉普拉斯变换及反变换1.拉氏变换的基本性质419102 z 附表A-2常用函数的拉氏变换和z 变换表5 (t)外(t) =2 6(t -nT)n 兰1(t)Tz (z —1)22T z(z+1)拉氏变换E(s)时间函数e(t)Z 变换E(s)丄s 31 s +a(s+a)2 as(sb -a(s + a)(s +b)t n n-ate丄 -atte” -at1 -e-at_bte -ea m 0卑-(宀) T n! c a z-ezZaTz -eT -aTTze； ,2 (z —e )(1-eR)z (z-1)(z-eR)z z-aT —-bTZ-ez-e4213. 用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。
设F(s)是s 的有理真分式，即f , 、 ■ m . ,m-1匚(、_ B(s) b m S + b mj S F(s)— A# \ — n ,A(s) a n S +a^^s式中，系数ao®,…，a n 亠a n 和b o ,bjll,b m 」b m 都是实常数；m,n 是正整数。
按代数定理分以下两种情况讨论。
这时，F(s)可展开为n 个简单的部分分式之和的形式，即式中，S H S 2,…，S n 是特征方程 A(s) = 0的根；C i 为待定常数，称为 F(S)在S i 处的留数, 可按下列两式计算：C =lim(s-s)F(s)(F-3)+…+bis + b o n」+…+a 1s + a o(n Am )可将F(s)展开为部分分式。
(1) A(s)=O 无重根:C iC2F(s)—2+…+-2^+…—CL_S-sS-S n irn S-s(F-1)(F-2)s=s i式中，A'(s)为A(s)对s的一阶导数。
根据拉氏变换的性质，从式( F-1 )可求得原函数为10423(2) A(S)=O 有重根：设A(S)=O 有r 重根S 1 , F(s)可写为F (S )=r(s-s) (s- Sr G …(s - S )2(z —1)3「n C f (t) =L*(s)]= L 」匡— , =Z C i e st[i 丄 S — S j 」i 4F-4)C r(S-S i )r (S-SjH+…+ C i +CrHi+…+C i +…+ C n(S-S i ) S-S r 韦 S — S i s - S n式中，S i 为F(S)的r 重根， 式(F-2)或式(F-3)计算，C r , C r 」，…，C i 则按下式计算: S rHt , …，S n 为F(s)的n —r 个单根；其中，C r ，…，C n 仍按c 「= lim (s — S i )「F (s) T i dr c-=iS mj-[(s-s) F(s)] i d (D新(S -S i)r F(S)j=ys^id>(S —S i )r F(S)丿 (F-5)原函数f(t)为 f(t) =「〔F(s) C rC i Cr 「+— +■■- + Ci + C f [(s-s)r (s-s)r 」 (s-s) S-S"+■■■ S-S i+亠S-S nC rt 「4 + C「4 t 「"2■+■…L (r -i)!t+ C 2t +C fe Stn+ Z C i e Siti:±4t(F-6)B(s)。
第五章 拉普拉斯变换和Z变换_第一讲
Ai X ( s) = ∑ i =1 s + ai
m
Signals and Systems
All Rights Reserved by Stone, 2008
信号系统与信号处理
HangZhou Dianzi University, Lab of PRIS
杭州电子科技大学
5.11 拉普拉斯变换（双边拉氏变换）
−∞
+∞
−σ t
]e
− jωt
dt
所以可以看成是 x(t )e −σ t 的傅里叶变换，即使 x(t )不满 足傅里叶变换的条件，也可以调整 σ 的取值，使得 x(t )e −σ t 满足。 因此拉氏变换具有更加广泛的分析对象。
Signals and Systems
All Rights Reserved by Stone, 2008
那么其拉氏变换：
1 X ( s ) = ∫ e u (t )e dt = ∫ e e dt = −∞ 0 a + σ + jω 1 1 L − at = → ；a + σ > 0；记为：e u (t ) ←⎯ ； {s} > − a Re s+a s+a
− at − (σ + jω ) t − ( a +σ ) t − jωt +∞ +∞
Signals and Systems
All Rights Reserved by Stone, 2008
信号系统与信号处理
HangZhou Dianzi University, Lab of PRIS
杭州电子科技大学
5.11 拉普拉斯变换（双边拉氏变换）
概念：收敛域（ROC）
傅里叶变换、拉氏变换、z变换的含义
傅里叶变换、拉氏变换、z变换的含义1、什么是傅里叶变换？答：fourier变换是将连续的时间域信号转变到频率域；它可以说是laplace变换的特例，laplace变换是fourier变换的推广，存在条件比fourier变换要宽，是将连续的时间域信号变换到复频率域（整个复平面，而fourier变换此时可看成仅在jΩ轴）；z变换则是连续信号经过理想采样之后的离散信号的laplace变换，再令z=e^sT时的变换结果（T为采样周期），所对应的域为数字复频率域，此时数字频率ω=ΩT。
——参考郑君里的《信号与系统》。
傅里叶变换的实质是将一个信号分离为无穷多多正弦/复指数信号的加成，也就是说，把信号变成正弦信号相加的形式——既然是无穷多个信号相加，那对于非周期信号来说，每个信号的加权应该都是零——但有密度上的差别，你可以对比概率论中的概率密度来思考一下——落到每一个点的概率都是无限小，但这些无限小是有差别的。
所以，傅里叶变换之后，横坐标即为分离出的正弦信号的频率，纵坐标对应的是加权密度。
对于周期信号来说，因为确实可以提取出某些频率的正弦波成分，所以其加权不为零——在幅度谱上，表现为无限大——但这些无限大显然是有区别的，所以我们用冲激函数表示。
已经说过，傅里叶变换是把各种形式的信号用正弦信号表示，因此非正弦信号进行傅里叶变换，会得到与原信号频率不同的成分——都是原信号频率的整数倍。
这些高频信号是用来修饰频率与原信号相同的正弦信号，使之趋近于原信号的。
所以说，频谱上频率最低的一个峰（往往是幅度上最高的），就是原信号频率。
傅里叶变换把信号由时域转为频域，因此把不同频率的信号在时域上拼接起来进行傅里叶变换是没有意义的——实际情况下，我们隔一段时间采集一次信号进行变换，才能体现出信号在频域上随时间的变化。
我的语言可能比较晦涩，但我已尽我所能向你讲述我的一点理解——真心希望能对你有用。
我已经很久没在知道上回答过问题了，之所以回答这个问题，是因为我本人在学习傅里叶变换及拉普拉斯变换的过程中着实受益匪浅——它们几乎改变了我对世界的认识。
信号的拉普拉斯变换和z变换
⎰∞∞--=t e t f s F st b d )()(⎰∞--=0def d e )()(t t f s F st)(d e )(j 21)(j j deft s s F t f st επσσ⎥⎦⎤⎢⎣⎡=⎰∞+∞-第三章信号的拉普拉斯变换和z 变换一、拉普拉斯变换的定义1.双边拉普拉斯变换只有选择适当的σ值才能使积分收敛，信号f(t)的双边拉普拉斯变换存在。
※象函数相同，但收敛域不同。
双边拉氏变换必须标出收敛域。
2.单边拉氏变换3.常见函数的拉普拉斯变换及其⎰∞+∞-=j j d e )(j21)(σσπs s F t f st b Fb(s)称为f(t)的双边拉氏变换（或象函数），f(t)称为Fb(s)的双边拉氏逆变换（或原函数）。
从0-开始收敛域二、拉普拉斯变换性质线性性质尺度变换证明：[]⎰∞--=de)()(tatfatf L st，则令atτ=时移特性与尺度变换相结合复频移（s域平移）特性时域的微分特性（微分定理）若f(t)←→F(s),Re[s]>σ0,则f’(t)←→sF(s)–f(0-)证明：()()()())(deedessFfttsft ftt f ststst+-=⎥⎦⎤⎢⎣⎡--='--∞-∞---∞-⎰⎰推广：()()[])0()0()()0(d)(d22----'--='--=⎥⎦⎤⎢⎣⎡fsfsFsffsF sttfL∑-=----=⎥⎦⎤⎢⎣⎡1)(1)0()(d)(d nrrrnnnfssFsttfL若f1(t)←→F1(s)Re[s]>σ1,f2(t)←→F2(s)Re[s]>σ2则a1f1(t)+a2f2(t)←→a1F1(s)+a2F2(s)Re[s]>max(σ1,σ2)若f(t)←→F(s),Re[s]>σ0，且有实数a>0，则f(at)←→)(1asFa若f(t)<----->F(s),Re[s]>σ0,且有实常数t0>0,则f(t-t0)ε(t-t0)<----->e-st0F(s),Re[s]>σ0若f(t)←→F(s),Re[s]>σ0,且有复常数s a=σa+jΩa,则f(t)e s a t←→F(s-s a),Re[s]>σ0+σas-→2：?)(sin ←→t t t ε=三、拉普拉斯逆变换三种方法：（1）查表（2）利用性质（3）部分分式展开-----结合∴......,,321为不同的实数根，n p p p p nn p s K p s K p s K s F -++-+-= 2211)(ip s i i s F p s K =-=)()()(e ]1[1t p s L t p i i ε=--若象函数F(s)是s 的有理分式，可写为1110111.......)(a s a s a s b s b s b s b s F n n n m m m m ++++++++=----若m ≥n （假分式）,可用多项式除法将象函数F(s)分解为有理多项式P(s)与有理真分式之和。
拉氏变换傅氏变换与Z变换
响应h(n)来表示。对于一个给定的输入x(n)，其输出y(n)为
y(n)x(n)h(n) x(m )h(nm )
对等式两端取Z变换，得
m
Y(z)H (z)X(z)
则
H(z) Y(z) X (z)
H(z)定义为线性时不变系统的系统函数，它是单位脉冲响
应的Z变换，即
H(z)Z[h(n)] h(n)zn n
2.6 序列的傅氏变换
因单位圆上序列的Z变换为序列的傅里叶变换，用ejω代替z， 得到序列傅里叶变换的定义为
F[x(n)]X(ej) x(n)ejn n
序列的傅里叶反变换公式
x ( n ) F 1 [ X ( e j ) ] 2 1 j|z | 1X ( z ) z n 1 d 2 z 1 X ( e j ) e j n d
h(n)1nu(n)2nu(n1) 2
由于存在2nu(-n-1)项， 因此系统是非因果的。
2.10.3 系统频率响应的意义
对于稳定系统，如果输入序列是一个频率为ω的复正弦序列：
x(n)=ejωn -∞<n<∞
线性时不变系统的单位脉冲响应为h(n)，则其输出为
y(n)x(n)h(n) h(m)x(nm)
例 2-23 已知系统函数为
H(z)112 z12 3z(112z1)1121z1112z1
求系统的单位脉冲响应及系统性质。
2<|z|≤∞
解 系统函数H(z)有两个极点z1=0.5, z2=2。
从收敛域看，收敛域包括∞点，因此系统一定是因果系统。 但是单位圆不在收敛域内，因此可以判定系统是不稳定的。
线性时不变系统的频率响应H(ejω)是以2π为周期的连续周 期函数, 是复函数。它可以写成模和相位的形式
z变换与拉氏变换的比较分析论文
z 变换与拉氏变换比较分析1 z 变换与拉氏变换性质分析z 变换是将离散系统的数学模型——差分方程转化为简单的代数方程，使其求解过程得以简化。
对离散信号)(n x 进行z 变换时，只有当级数收敛，即满足∑∞-∞=-∞<n n z n x |)(|时，其z 变换∑∞-∞=-=n n z n x z X )()(才有意义。
对于任意给定的有界序列)(n x ，使z 变换定义式级数收敛的所有z 值的集合成为z 变换)(z X 的收敛域 。
在收敛域内，z 变换及它的导数是z 的连续函数，即z 变换函数是收敛域内每一点的解析函数。
对于单边变换，序列与变换式具有一一对应的关系，同时也具有惟一的收敛域。
而在双边变换时，不同的序列在不同的收敛条件下可能映射为同一变换式。
拉氏变换是将线性时不变系统的时域模型简便地进行变换，经求解再还原为时间函数。
对连续信号进行拉氏变换时引入了一个衰减因子t e σ-(σ为任意实数)使之与原函数)(t f 相乘，取时间∞→t 的极限，若当0σσ>时，该极限为零，则函数t e t f σ-)(在0σσ>的全部范围内收敛，其积分存在，可以进行拉氏变换。
对于有界的非周期信号的拉氏变换一定存在，对于周期信号只要稍加衰减就可收敛，由)(t f 的性质与σ值得相对关系决定其收敛坐标0σ。
与z 变换情况类似，单边变换序列对于惟一变换式及收敛域，双边变换不同序列不同收敛域可能映射为同一变换式。
2 z 变换与拉氏变换比较分析(一) z 平面与s 平面的映射关系z 变换中复变量z 与拉氏变换中复变量s 具有一下关系：sT e z = (1-1) 或 z Ts ln 1= 式中T 为序列的时间间隔，重复频率Tπω2= 。
将s 表示成坐标形式，z 表示成极坐标形式，即：ωσj s += (1-2) θj re z =将式(1-2)代入式(1-1) T j j e re)(ωσθ+= 于是得到: s e e r T ωπσσ2== (1-3) s T ωωπωθ2== 上式表明z s ~平面有以下映射关系：(1)s 平面上的虚轴),0(ωσj s ==映射到z 平面是单位圆，其右半平面映射到z 平面是单位圆的圆外，左半平面映射到z 平面是单位圆的园内。
专题拉氏变换与Z变换.ppt
证明： L( ( f (t, a))) f (kT , a)zk f (kT , a)zk F (z, a)
a
k 0 a
a k 0
a
例题见课本P21例2.6，自学。
Z反变换
专题1 拉氏变换与Z变换
3 Z反变换
Z反变换，即由象函数F（z）求序列f(kT)或者采样函数f*(t)的 变换。
f
()
lim(1
z 1
z1)F (z)
1
lim
z 1
1
0.2
z
1
1.25
专题1 拉氏变换与Z变换
2 Z变换及其性质
（8）偏微分定理
若 Z[ f (t,a)] F(z,a) ，其中a是一个独立变量或者常数，则有
L( ( f (t, a))) F(z, a)
a
a
z eaT
1 z eaT
（4）复数位移定理
若 Z[ f (t)] F(z) ，则 Z[eat f (t)] F (eaT z)
证明：Z[eat f (t)] eakT f (kT )zk f (kT )(e aT z)k F (e aT z)
k 0
证明： Z[f1 (t) f2 (t)] (f1 (t) f2 (t))z k k 0
f1 (t) z k f2 (t)z k F1 Biblioteka z) F2 (z)k 0
k 0
（2）延迟定理（滞后定理右移定理）
设 kT 0 时， y(kT) 0
z n ( f (0) f (T ) z1 f (2T )z 2 ) z n F (z)
拉氏变换及Z变换理论
故采样信号e*(t)的拉氏变换
E * ( s ) e * (t )e st dt [ e(nT ) (t nT )]e st dt
n 0
e(nT )[ (t nT )e st dt]
n 0
由广义脉冲函数的筛选性质
k 1 n 0
Z [e(t kT)] z k [ E ( z ) e(nT ) z n ]
复数位移定理
Z [e at e(t )] E ( ze aT )
终值定理
lim e(nT ) lim ( z 1) E ( z )
n z 1
卷积定理
E ( z ) e(0) e(T ) z 1 e(2T ) z 2 e(nT ) z n
部分分式法 F(s)=1/s(s+1)，分解得 F(s)=1/s-1/(s+1)
1/s的z变换为z/z-1，1/s+1的z变换为 z/z-e-T，得： F(z)=(z/z-1)-(z/z-e-T)。
x(nT ) * y (nT ) x(kT) y[( n k )T ]
g (nT ) x(nT ) * y(nT )
k 0
G( z ) X ( z ) * Y ( z )
Z反变换
e(nT ) Z 1[ E ( z )]
1、部分分式法 又称为查表法
2、幂级数法
又称综合除法 3、反演积分法
sT
E ( z ) E * (s) |
1 s ln z T
e(nT ) z n
n 0
记作 E( z) Z[e * (t )] Z (e(t )) 后一记号是为了书写方便。 Z变换仅是一种在采样拉氏变换中取z e sT 的变量置换。 通过这种置换，可将s的超越函数变换为z的幂级数 或z的有理分式。 Z变换方法 级数求和法
专题_拉氏变换与Z变换
F ( s) f (0) s s
1
1 拉氏变换及其性质
f 2 (0) f n (0) n 1 s s
n
② 若 f (0) f (0) 则 L[ f (t )( dt) n ] F (ns)
n个
Байду номын сангаас1
2
f
3
(0) f
(0) 0
s
（4）位移定理 L[ f (t a) 1(t a)] e as F ( s) （5）延时定理 lim f (t ) lim sF (s) （6）初值定理 t 0 s （7）终值定理 lim f (t ) lim sF (s) t s 0 （8）卷积定理 L[ f (t ) * g (t )] F (s) G(s)
k 0
2 Z变换及其性质
f 1 (t ) z
k 0
k
f 2 (t )z k F1 ( z ) F2 ( z )
k 0
（2）延迟定理（滞后定理右移定理）
设 kT 0 时， y(kT) 0 n 若 Z[ f (t )] F ( z) ，则 Z [ f (t nT )] z F ( z ) 即离散信号在时域内延迟采样周期T，则等价于它的z变换乘以z-1，所以 z-1可看成是滞后一个采样周期的滞后算子。 证明： 注意证明的前提条件 f (t ) 0 t0
1 ( s a ) t 1 dt e 0 sa sa
（3）单位脉冲函数 (t )
L[ (t )] (t ) e st dt 1
0
1 t 0 0 t 0
专题1 拉氏变换与Z变换
拉普拉斯变换与Z变换
tia
e − at
l
f (t ) = L−1 [ F ( s )] 。
例 1 求单位阶跃函数 u (t ) = 解 由拉氏变换的定义有：
C
0, t < 0 的拉氏变换。 1, t > 0
+∞
on
0 0
F(s)称为 f(t)的拉氏变换（或称为象函数） 。 若 F(s)是 f(t)的拉氏变换，则称 f(t)为 F(s)的拉氏反变换（或称为象原函数） ，记为：
定义：设函数 f(t)当 t≥0 时有定义，而且积分 某一域内收敛，则由此积分所描述的函数可写为
∫
+∞
0
f (t )e − st dt （s 是一个复参量）在 s 的
F ( s) = ∫
+∞
0
f (t )e − st dt
en
Z 变换 F(z) 1
其中 s = σ + jω 为复变量，σ为实部，ω为虚部。
2
ny
11 12
sinωt
cosωt
pa
13
e − at sin ωt
ω (s + a) 2 + ω 2 s+a (s + a) 2 + ω 2
om
14
e − at cos ωt
C
fid
2
ze −T sin ωT z 2 − 2 ze −T cos ωT + e −2 aT z 2 − ze − aT cos ωT ) z 2 − 2 ze −aT cos ωT + e − 2 aT
1 1 − e −Ts 1 s 1 s+a 1 s − (1 / T ) ln a 1 s2
专题_拉氏变换与Z变换18页PPT
•
29、在一切能够接受法律支配的人类 的状态 中，哪 里没有 法律， 那里就 没有自 由。— —洛克
•
30、风俗可以造就法律，也可以废除 法律。 ——塞·约翰逊
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂，怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
专题_拉氏变换与Z变换
•
26、我们像鹰一样，生来就是自由的 ，但是 为了生 存，我 们不得 不为自 己编织 一个笼 子，然 后把自 己关在 里面。 ——博 莱索
•
27、法律如果不讲道理，即使延续时 间再长 ，也还 是没有 制约力 的。创造出来的。 ——马 克罗维 乌斯
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
n 1
特别地，若初始条件 f (0) f (T ) f (2T ) f ((n 1)T ) 0
则
Z [ f (t nT )] z n F ( z )
k
证明： Z [ f (t nT )] f ((k n)T ) z
k 0
z
n
f ((k n)T ) z
z 1
1 F ( z) 例3 已知 1 1.2 z 1 0.2 z 2
，求终值 f () 1 1 z 1 1 解： 1 1 (1 z ) F ( z ) (1 z ) 1 2 1 0.2 z 1 1 1.2 z 1 0.2 z 2 1 1.2 z 0.2 z 极点为0.2，位于单位圆内，所以有
k 0
(k n)
令m=k+n，则
Z [ f (t nT )] z
n 1
n
mn
f (mT ) z
m
z ( f (mT ) z
n m 0
m
f (mT ) z m )
m 0
n 1
z n F ( z ) f (mT ) z n m
m 0
专题1 拉氏变换与Z变换 1 拉氏变换及其性质
1.3 拉氏变换的性质 （1）叠加性质 若 L[ f1 (t )] F1 (s) ， L[ f 2 (t )] F2 (s) 则 L[af1 (t ) bf 2 (t )] aF1 (s) bF2 (s) 证明：略 d L[ f (t )] sF ( s) f (0) （2）微分定理 dt 推论 dn ① L[ n f (t )] s n F (s) s n1 f (0) s n2 f (0) sf ( n2) (0) f ( n1) (0)
f (t )e t dt
F (s) L[ f (t )] f (t )e st dt 0 式中，s—复变量，且 Re(s)
；
f(t)—原函数； F(s)—象函数
专题1 拉氏变换与Z变换 1 拉氏变换及其性质
1.2 简单函数的拉氏变换 （1）单位阶跃函数1(t)
1 ( s a ) t 1 dt e 0 sa sa
（3）单位脉冲函数 (t )
L[ (t )] (t ) e st dt 1
0
1 t 0 0 t 0
专题1 拉氏变换与Z变换
1 拉氏变换及其性质 1.2 简单函数的拉氏变换 （4）正弦函数 sin t 和余弦函数 根据欧拉公式，有
f () lim(1 z 1 ) F ( z ) lim
z 1
1 1.25 z 1 1 0.2 z 1
专题1 拉氏变换与Z变换
2 Z变换及其性质
（8）偏微分定理
若
Z[ f (t , a)] F ( z, a)
，其中a是一个独立变量或者常数，则有
L(
( f (t , a))) F ( z, a) a a
1 2
f (kT) z k
k 0
2.2 几类典型函数的z变换 （1）单位阶跃函数1(t) 1 * (t ) (t k T) k 0 单位阶跃函数1(t)的采样函数 故有： 1 k 1 2
Z [1(t )] z
k 0
1 z z
cost
e j cos j sin e j cos j sin
则
e j e j e j e j sin , cos 2j 2
那么利用上面的指数函数的拉氏变换结果，得出正弦函数和余弦函数的拉氏变换。
L[sin t ] sin te dt
比较：
Z [ f (t nT )] f (( k n)T ) z k
延迟定理
0 0z
1
f (0) z n f (T ) z ( n1) f (2T ) z ( n 2)
k 0
z n ( f (0) f (T ) z 1 f (2T ) z 2 ) z n F ( z )
L[e at f (t )] F ( s a)
专题1 拉氏变换与Z变换
2 Z变换及其性质 2.1 Z变换的定义 采样信号的数学表达式为 f * (t ) f (t ) (t k T)
k 0
对采样信号两边进行拉氏变换，得
F * ( s ) L[ f * (t )] f (k T)
dt
②若 dn 则 L[ n
dt
f (0) f (0) f (0) f ( n2) (0) f ( n1) (0) 0
f (t )] s n F ( s)
专题1 拉氏变换与Z变换
L[ f (t )dt] （3）积分定理 1 式中， f (t ) f (t )dt 推论 F ( s) f 1 (0) n ① L[ f (t )(dt) ] s n s n
f (k T) z k
k 0
F(z)与f*(t)或{f(kT)}构成变换对，它不是连续时间函数f(t)的Z变换。
专题1 拉氏变换与Z变换
2 Z变换及其性质 对于序列{f(kT)}（也就是采样信号），可以定义它的z变换为
F ( z ) Z { f (kT)} f (0) f (T ) z f (2T ) z
k 0
1 1 e aT z 1
z z e aT
由此，有课本P18页表2.1，Z变换表
专题1 拉氏变换与Z变换
4） z变换的性质 （1）线性性质 若 Z[ f1 (t )] F1 ( z), Z[ f 2 (t )] F2 ( z) ，有 Z[f1 (t ) f 2 (t )] F1 ( z) F2 ( z) 其中αβ常数。 证明： Z [f1 (t ) f 2 (t )] (f1 (t ) f 2 (t )) z k
st 0
0
e jt e jt st 1 1 1 e dt ( ) 2 2j 2 j s j s j s 2
L[cos t ] cos te dt
st 0
0
e jt e jt st 1 1 1 s e dt ( ) 2 2 2 s j s j s 2
专题1 拉氏变换与Z变换
2 Z变换及其性质
例1 试求 e a ( t T ) 的z变换 解 根据实数位移定理，有
Z [e
a ( t T )
] z Z [e
1
at
z 1 ] z aT z e z e aT
1
（4）复数位移定理 若 Z [ f (t )] F ( z ) 证明：Z [e
专题1 拉氏变换与Z变换 1 拉氏变换及其性质
1.1 拉氏变换的基本概念 定义: 对于函数f(t)如果满足下列条件： （1）当t<0时，f(t)=0； 当t>0时，f(t)在每个有限区间上是分段连续的。
（2） 0 ，其中σ是正实数，也就是说f(t) 是指数级； 那么定义f(t)的拉氏变换F(s)为
k 0
k 0
f (k T) (t k T)e st dt
st
(t k T)e dt f (k T)e kTs
k 0
e kTs 是超越函数，不好计算，于是令 z eTs
则有
F ( z ) F * (s)
ln z s T
z
lim F ( z)
k
存在，则
lim
k 0
f (kT) lim F ( z)
（6）终值定理 若 Z[ f (kT)] F ( z) ，且 (1 z 1 ) F ( z) 在复平面的单位圆上或外没有极 点，那么
lim
k
f (kT) lim (1 z 1 ) F ( z)
专题1 拉氏变换与Z变换
2 Z变换及其性质
(3)超前定理（左移定理）
若 Z[ f (t )] F ( z) ，则 Z [ f (t nT )] z
n
( F ( z ) f (mT ) z
m 0
n 1
m
) z F ( z ) f (mT ) z n m
n m 0
at
，则
akT
Z [e at f (t )] F (e aT z )
k
f (t )] e
k 0
f (kT ) z
f (kT )(e aT z ) k F (e aT z )
k 0
例2 求 f (t ) te at Tz 解：
Z [t ]
n个
F ( s) f (0) s s
1
1 拉氏变换及其性质
f 2 (0) f n (0) n 1 s s
n
② 若 f (0) f (0) 则 L[ f (t )( dt) n ] F (ns)
n个
1
2
f
3
(0) f
(0) 0
s
（4）位移定理 L[ f (t a) 1(t a)] e as F ( s) （5）延时定理 lim f (t ) lim sF (s) （6）初值定理 t 0 s （7）终值定理 lim f (t ) lim sF (s) t s 0 （8）卷积定理 L[ f (t ) * g (t )] F (s) G(s)