《统计学》答案_第三版
统计学第三版答案
统计学第三版答案第1章统计和统计数据第2章 1.1 指出下⾯的变量类型。
第3章（1）年龄。
第4章（2）性别。
第5章（3）汽车产量。
第6章（4）员⼯对企业某项改⾰措施的态度（赞成、中⽴、反对）。
第7章（5）购买商品时的⽀付⽅式（现⾦、信⽤卡、⽀票）。
第8章详细答案：第9章（1）数值变量。
第10章（2）分类变量。
第11章（3）数值变量。
第12章（4）顺序变量。
第13章（5）分类变量。
第14章1.2 ⼀家研究机构从IT从业者中随机抽取1000⼈作为样本进⾏调查，其中60%回答他们的⽉收⼊在5000元以上，50%的⼈回答他第15章们的消费⽀付⽅式是⽤信⽤卡。
第16章（1）这⼀研究的总体是什么？样本是什么？样本量是多少？第17章（2）“⽉收⼊”是分类变量、顺序变量还是数值变量？第18章（3）“消费⽀付⽅式”是分类变量、顺序变量还是数值变量？第19章详细答案：第20章（1）总体是“所有IT从业者”，样本是“所抽取的1000名IT从业者”，样本量是1000。
第21章（2）数值变量。
第22章（3）分类变量。
第23章1.3 ⼀项调查表明，消费者每⽉在⽹上购物的平均花费是200元，他们选择在⽹上购物的主要原因是“价格便宜”。
第24章（1）这⼀研究的总体是什么？第25章（2）“消费者在⽹上购物的原因”是分类变量、顺序变量还是数值变量？第26章详细答案：第27章（1）总体是“所有的⽹上购物者”。
第28章（2）分类变量。
第29章1.4 某⼤学的商学院为了解毕业⽣的就业倾向，分别在会计专业抽取50⼈、市场营销专业抽取30、企业管理20⼈进⾏调查。
第30章（1）这种抽样⽅式是分层抽样、系统抽样还是整群抽样？第31章（2）样本量是多少？第32章详细答案：第33章（1）分层抽样。
第34章（2）100。
第2章⽤图表展⽰数据（3）帕累托图如下：（4）饼图如下：2.2 为确定灯泡的使⽤寿命（单位：⼩时），在⼀批灯泡中随机抽取100只进⾏测试，所得数据如下：710~720 13 13720~730 10 10730~740 3 3740~750 3 3合计100 100（2）直⽅图如下：从直⽅图可以看出，灯泡使⽤寿命的分布基本上是对称的。
统计学教材部分参考答案第三版
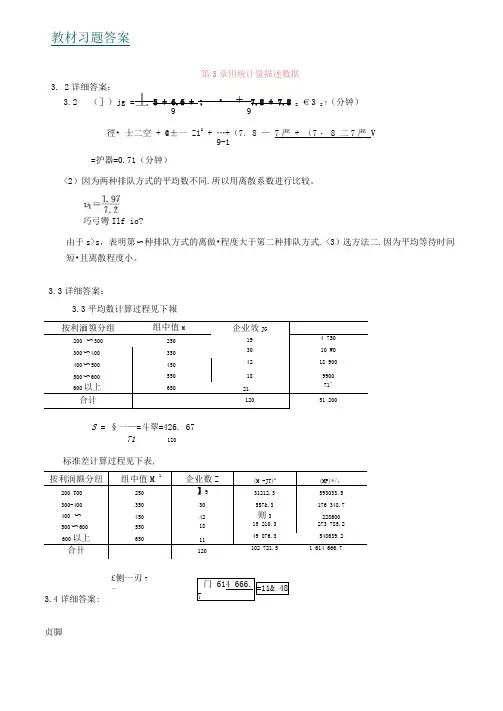
教材习题答案第3章用统计量描述数据3. 2详细答案： 3.2 （］）jg =丄5 + 6.6 + ；・ + 7.8 + 7.8 =€3= ?（分钟）9 9徑• 士二空 + @±一 Z12+ …+（7. 8 — 7严 + （7・ 8 二7严 V 9-1 =护器=0.71（分钟）<2）因为两种排队方式的平均数不同.所以用离散系数进行比较。
巧弓彎Ilf io?由于s>s ，表明第〜种排队方式的离做•程度大于笫二种排队方式. <3）选方法二.因为平均等待时间短•且离散程度小。
3.3详细答案：3.3平均数计算过程见下報 按利湎领分组组中值M企业效JG200 〜300 250 19 4 750 300〜400 350 30 10 WO 400〜500 450 42 18 900 500〜600 550 18 9900 600以上 65021 71" 合计12051 200S = §一—=斗翠=426. 6771 1Z03.4详细答案:贞脚按利润额分纽组中值M 1企业数Z(M -JT)1(MP)*/； 200 TOO 250 】931212.3 593033.5 300-400 350 30 5S7&.3176 348.7 400 〜 450 42 则3228600 500〜600 550 18 15 210.3 273 785.2 600以上65011 49 876.3 548639.2 合卄120102 721.51 614 666.7标准差计算过程见下表, £侧一刃7―门 614 666. 7=11& 48通过计算标准化值来判断，Z ^=1 , Z B = 0-5，说明在A 项测试中该应试者比平均分数高出1 个标准差，而在B 项测试中只高出平均分数0.5个标准差，由于A 项测试的标准化值高于B 项测试, 所以A 项测试比较理想。
3. 5详细答案：3种方法的主要描述统计量如下：(1) 从集中度、离散度和分布的形状三个角度的统计量来评价。
统计学课后答案(第3版)第8章方差分析习题答案
第八章 方差分析习题答案一、单选1.D ；2.B ；3.A ；4.C ；5.C ；6.C ；7.C ；8.A ；9.B ；10.A二、多选1.ACE ；2.ABD ；3.BE ；4.AD ；5.BCE6.ABCD ；7.ABCDE ；8.ABCE ；9.ACD ；10.ABD三、计算分析题1、运用EXCEL 进行单因素方差分析，有：方差分析：单因素方差分析SUMMARY组 观测数 求和 平均 方差列 1 5 1.21 0.242 2.45E-05列 2 5 1.38 0.276 0.00226列 3 5 1.31 0.262 1.35E-05方差分析差异源 SS df MS F P-value F crit 组间 0.00292 2 0.00146 1.906005 0.191058 3.885294 组内 0.009192 12 0.000766总计 0.012112 14由于P 值=1.906005＞05.0=α，不拒绝原假设，没有证据表明3个总体的均值之间有显著差异。
（或用F 值判断，有同样结论）2、运用EXCEL 进行单因素方差分析，有：方差分析：单因素方差分析SUMMARY组 观测数 求和 平均 方差列 1 5 222 44.4 28.3列 2 5 150 30 10列 3 5 213 42.6 15.8方差分析差异源 SS df MS F P-value F crit 组间 615.6 2 307.8 17.06839 0.00031 3.885294 组内 216.4 12 18.03333总计 832 14由于由于P 值=0.00031＜05.0=α，拒绝原假设，表明3个总体的均值之间有显著差异。
（或用F 值判断，有同样结论）进一步用LSD 方法见教材P2063、（1）按行依次为：420、2、1.478（第一行）；27、142.07（第二行）；4256（第三行）。
（2）由于P 值=0.245946＞05.0=α，不拒绝原假设，没有证据表明3种方法组装产品数量有显著差异。
《统计学》第三版习题答案
《统计学》第4章习题参考答案与答疑答案与答疑加入时间：2008-10-21 17:53:07点击：10494.1 (1)M o=10(台);Me=10(台);Mean=9.6(台)(2)Q L=5.5 ;Q U=12(3)s=4.2(台)(4)左偏分布4.2 (1)M o=19(岁);M o=23(岁);Me=23(岁)(2)Q L=19; Q U=26.5(3)Mean=24(岁);s=6.65(岁)(4)SK=1.08;KU=0.77(5)样本数据的均值为24岁,但标准差较大,说明网民年龄之间差异较大.从偏态和峰度系数来看,网民年龄呈现右偏尖峰分布.4.3 (1)略;(2)Mean=7(分钟); s=0.714(分钟)(3)由于均值不同,采用V进行比较:V1=0.274,V2=0.102(4)选择第二种(Mean小,V2<V1)分类变量4.4 (1)Mean=274.1(万元);(2)略;(3)s=21.174.5 Mean甲=19.41(元);Mean乙=18.29(元);由于单位成本较低的产品在乙企业中占的比重比较大,拉低了总平均成本.4.6 Mean=426.67(万元);s=116.48(万元);SK=0.203;KU=-0.6884.7(1)MEAN大体相同;(2)S大体相同;(3)较大样本的研究人员机会更多.4.8(1)Vmale=0.08;Vfemale=0.1(2)Mean male=132(磅);s male=11(磅);Mean female=110(磅);s female=11(磅);(3)68%.(4)95%4.9 Z A=1 Z B=0.5,A项更理想一些.(思路:标准分数)4.10 周一和周六(思路:标准分数)4.11 (1)离散系数,由于数据水平高低不同;(2)V adult=0.024 ;V child=0.0354.12 略4.13 略《统计学》第5章习题参考答案与答疑答案与答疑加入时间：2008-10-30 9:15:45点击：7765.1 (1)Ω=［0,100］(2)Ω=N(3)Ω=﹛10,11,12,13,14,....﹜5.2 P(A∩B)=0.305.3 P(B)=2/95.4 7/125.5 (1)P(AB)=0.56;(2)P(A∪B)=0.94;(3)P=0.385.6 P=0.725.7 P=2/35.8 P初中=5/11 ;P高中=28/555.9 P A=0.25 ;P B=0.115.10 P(x=0)=1/4;P(x=1)=1/2;P(x=2)=1/45.11(1)P(x=100)=0.001;P(x=10)=0.01;P(x=1)=0.2;P(x=0)=0.789;(2)E(X)=0.45.12 (1)θ=2;(2)E(X)=3/2;(3)D(X)=3/205.13 1/645.14 2/3e5.15 k=λ-1 或k=λ5.16 (1)0.7;(2)1/25.17 ≤3985.18 (1)0.93 (2)0.39。
统计学教材课后答案 第三版 袁卫 庞皓 曾五一 贾俊平主编
第四章、参数估计1．简述评价估计量好坏的标准答：评价估计量好坏的标准主要有：无偏性、有效性和相合性。
设总体参数θ的估计量有1ˆθ和2ˆθ，如果()1ˆE θθ=，称1ˆθ是无偏估计量；如果1ˆθ和2ˆθ是无偏估计量，且()1ˆD θ小于()2ˆD θ，则1ˆθ比2ˆθ更有效；如果当样本容量n →∞，1ˆθθ→，则1ˆθ是相合估计量。
2.说明区间估计的基本原理答：总体参数的区间估计是在一定的置信水平下，根据样本统计量的抽样分布计算出用样本统计量加减抽样误差表示的估计区间，使该区间包含总体参数的概率为置信水平。
置信水平反映估计的可信度，而区间的长度反映估计的精确度。
3．解释置信水平为95％的置信区间的含义答：总体参数是固定的，未知的，置信区间是一个随机区间。
置信水平为95％的置信区间的含义是指，在相同条件下多次抽样下，在所有构造的置信区间里大约有95％包含总体参数的真值。
4．简述样本容量与置信水平、总体方差、允许误差的关系答：以估计总体均值时样本容量的确定公式为例：()22/22z n E ασ= 样本容量与置信水平成正比、与总体方差成正比、与允许误差成反比。
练习题：●1.解：已知总体标准差σ=5，样本容量n =40，为大样本，样本均值x =25，（1）样本均值的抽样标准差σ5=0.7906 （2）已知置信水平1－α=95%，得 α/2Z =1.96，于是，允许误差是E =α/2Z 6×0.7906=1.5496。
●2.解：（1）已假定总体标准差为σ=15元，则样本均值的抽样标准误差为x σ15=2.1429（2）已知置信水平1－α=95%，得 α/2Z =1.96，于是，允许误差是E=α/2Z 6×2.1429=4.2000。
（3）已知样本均值为x =120元，置信水平1－α=95%，得 α/2Z =1.96，这时总体均值的置信区间为±α/2x Z 0±4.2=124.2115.8 可知，如果样本均值为120元，总体均值95%的置信区间为（115.8，124.2）元。
《统计学》答案_第三版
第2章统计数据的描述——练习题●2.解:（1）要求对销售收入的数据进行分组，全部数据中,最大的为152，最小的为87,知数据全距为152－87=65；为便于计算和分析，确定将数据分为6组，各组组距为10,组限以整10划分;为使数据的分布满足穷尽和互斥的要求,注意到，按上面的分组方式,最小值87可能落在最小组之下，最大值152可能落在最大组之上，将最小组和最大组设计成开口形式;按照“上限不在组内”的原则，用划记法统计各组内数据的个数-—企业数，也可以用Excel进行排序统计(见Excel练习题2.2)，将结果填入表内，得到频数分布表如下表中的左两列;将各组企业数除以企业总数40，得到各组频率,填入表中第三列；在向上的数轴中标出频数的分布，由下至上逐组计算企业数的向上累积及频率的向上累积，由上至下逐组计算企业数的向下累积及频率的向下累积。
整理得到频数分布表如下:●13.:因为女生的离散系数为V=＝＝0。
1男生体重的离散系数为V=＝＝0。
08对比可知女生的体重差异较大。
(2) 男生：=＝27。
27（磅)，s ==2。
27（磅）;女生:==22.73(磅），s ==2.27（磅）;（3）68%; （4）95%.14 解：（1）应采用离散系数,因为成年人和幼儿的身高处于不同的水平，采用标准差比较不合适.离散系数消除了不同组数据水平高低的影响，采用离散系数就较为合理。
(2)利用Excel进行计算,得成年组身高的平均数为172。
1，标准差为4。
202，从而得:成年组身高的离散系数：；又得幼儿组身高的平均数为71。
3,标准差为2。
497,从而得:幼儿组身高的离散系数：;由于幼儿组身高的离散系数大于成年组身高的离散系数,说明幼儿组身高的离散程度相对较大。
第四章参数估计（1）●1. 解：已知总体标准差σ=5，样本容量n=40，为大样本，样本均值=25, （1）样本均值的抽样标准差===0.7906（2）已知置信水平1－=95%，得=1。
统计学第三版课后答案
统计学第三版课后答案第一章1.什么是统计学？统计学是一门研究如何收集、分析和解释数据的学科。
它涉及到收集数据的方法、数据的描述和分析、以及通过数据来进行推断和预测。
2.数据可以分为哪两种类型？数据可以分为定量数据和定性数据。
定量数据是可以用数字表示的，例如身高、体重等；定性数据是描述性的，例如颜色、性别等。
3.描述性统计与推论统计有什么区别？描述性统计是对收集到的数据进行总结、整理和展示的过程，主要通过统计指标如平均数、中位数等来描述数据的特征。
推论统计则是通过对样本数据进行推断，从而对整个总体进行推断和预测。
4.什么是样本？样本是从总体中选取出来的一部分个体。
通过对样本进行统计分析，我们可以对整个总体进行推断和预测。
5.什么是抽样误差？抽样误差是指由于样本选择的随机性所导致的样本统计量与总体参数之间的差异。
第二章1.总体和样本的区别是什么？总体是指研究对象的全体个体，而样本是从总体中选取出来的一部分个体。
2.简单随机抽样和分层抽样的区别是什么？简单随机抽样是指每个个体被抽中的概率相等且相互独立的抽样方法，适用于总体中各个个体之间没有明显分层的情况。
而分层抽样是将总体分为若干层次，然后从每个层次中分别抽取样本，适用于总体中各个层次之间存在明显差异的情况。
3.什么是系统抽样？系统抽样是指根据某种规则，从总体中以一定间隔选取样本的抽样方法。
例如，每隔k个个体选取一个个体作为样本。
4.方便抽样和判断抽样的特点是什么？方便抽样是指通过方便快捷的方法选取样本，例如通过问卷调查、网络调研等。
方便抽样的特点是样本选择的随机性不足，很容易导致样本与总体之间存在偏差。
判断抽样则是基于研究者的判断来选取样本，因此也可能存在主观性和偏见。
5.什么是多阶段抽样？多阶段抽样是指将总体分为若干个阶段，先从每个阶段中按一定方法抽取较小的样本，然后再从这些小样本中抽取最终的样本。
第三章1.什么是频率？频率是指某个数值或范围在样本或总体中出现的次数。
统计学(第三版)课后习题答案
附录1：各章练习题答案2.1 （1）属于顺序数据。
（2）频数分布表如下：服务质量等级评价的频数分布服务质量等级家庭数（频率）频率%A1414B2121C3232D1818E1515合计100100（3）条形图（略）2.2 （1）频数分布表如下：（2）某管理局下属40个企分组表按销售收入分组（万元）企业数（个）频率（%）先进企业良好企业一般企业落后企业11119927.527.522.522.5合计40 100.0 2.3 频数分布表如下：某百货公司日商品销售额分组表按销售额分组（万元）频数（天）频率（%）25～30 30～35 35～40 40～45 45～5046159610.015.037.522.515.0合计40 100.0 直方图（略）。
2.4 （1）排序略。
（2）频数分布表如下：100只灯泡使用寿命非频数分布按使用寿命分组（小时）灯泡个数（只）频率（%）650~660 2 2660~670 5 5670~680 6 6680~690 14 14690~700 26 26700~710 18 18710~720 13 13720~730 10 10730~740 3 3740~750 3 3合计100 100直方图（略）。
2.5 （1）属于数值型数据。
（2）分组结果如下：分组天数（天）-25~-20 6-20~-15 8-15~-10 10-10~-5 13-5~0 120~5 45~10 7合计60（3）直方图（略）。
2.6 （1）直方图（略）。
（2）自学考试人员年龄的分布为右偏。
2.7 （1（2）A班考试成绩的分布比较集中，且平均分数较高；B班考试成绩的分布比A班分散，且平均成绩较A班低。
2.8 箱线图如下：（特征请读者自己分析）2.9 （1）x =274.1（万元）；Me=272.5 ；Q L =260.25；Q U =291.25。
（2）17.21=s （万元）。
2.10 （1）甲企业平均成本＝19.41（元），乙企业平均成本＝18.29（元）；原因：尽管两个企业的单位成本相同，但单位成本较低的产品在乙企业的产量中所占比重较大，因此拉低了总平均成本。
统计学原理第三版课后习题答案
1：各章练习题答案2.1 （1）属于顺序数据。
（2）频数分布表如下：服务质量等级评价的频数分布服务质量等级家庭数（频率）频率%A1414B2121C3232D1818E1515合计100100（3）条形图（略）2.2 （1）频数分布表如下：40个企业按产品销售收入分组表按销售收入分组（万元）企业数（个）频率（%）向上累积向下累积企业数频率企业数频率100以下100～110 110～120 120～130 130～140 140以上591274312.522.530.017.510.07.55142633374012.535.065.082.592.5100.04035261473100.087.565.035.017.57.5合计40 100.0 ————（2）某管理局下属40个企分组表按销售收入分组（万元）企业数（个）频率（%）先进企业良好企业一般企业落后企业11119927.527.522.522.5合计40 100.0 2.3 频数分布表如下：某百货公司日商品销售额分组表按销售额分组（万元）频数（天）频率（%）25～30 30～35 35～40 40～45 45～5046159610.015.037.522.515.0合计40 100.0 直方图（略）。
2.4 （1）排序略。
（2）频数分布表如下：100只灯泡使用寿命非频数分布按使用寿命分组（小时）灯泡个数（只）频率（%）650~660 2 2660~670 5 5670~680 6 6680~690 14 14690~700 26 26700~710 18 18710~720 13 13720~730 10 10730~740 3 3740~750 3 3合计100 100 直方图（略）。
（3）茎叶图如下：65 1 866 1 4 5 6 867 1 3 4 6 7 968 1 1 2 3 3 3 4 5 5 5 8 8 9 969 0 0 1 1 1 1 2 2 2 3 3 4 4 5 5 6 6 6 7 7 8 8 8 8 9 970 0 0 1 1 2 2 3 4 5 6 6 6 7 7 8 8 8 971 0 0 2 2 3 3 5 6 7 7 8 8 972 0 1 2 2 5 6 7 8 9 973 3 5 674 1 4 72.5 （1）属于数值型数据。
统计学高教第三版课后习题答案
第一章1.什么是统计学？怎样理解统计学与统计数据的关系？答：统计学是一门收集、整理、显示和分析统计数据的科学。
统计学与统计数据存在密切关系，统计学阐述的统计方法来源于对统计数据的研究，目的也在于对统计数据的研究，离开了统计数据，统计方法以致于统计学就失去了其存在意义。
2．简要说明统计数据的来源答：统计数据来源于两个方面：直接的数据：源于直接组织的调查、观察和科学实验，在社会经济管理领域，主要通过统计调查方式来获得，如普查和抽样调查。
间接的数据：从报纸、图书杂志、统计年鉴、网络等渠道获得。
3.简要说明抽样误差和非抽样误差答：统计调查误差可分为非抽样误差和抽样误差。
非抽样误差是由于调查过程中各环节工作失误造成的，从理论上看，这类误差是可以避免的。
抽样误差是利用样本推断总体时所产生的误差，它是不可避免的，但可以控制的。
4.答：（1）有两个总体：A品牌所有产品、B品牌所有产品（2）变量：口味（如可用10分制表示）（3）匹配样本：从两品牌产品中各抽取1000瓶，由1000名消费者分别打分，形成匹配样本。
（4）从匹配样本的观察值中推断两品牌口味的相对好坏。
第二章、统计数据的描述思考题1描述次数分配表的编制过程答：分二个步骤：（1）按照统计研究的目的，将数据按分组标志进行分组。
按品质标志进行分组时，可将其每个具体的表现作为一个组，或者几个表现合并成一个组，这取决于分组的粗细。
按数量标志进行分组，可分为单项式分组与组距式分组单项式分组将每个变量值作为一个组；组距式分组将变量的取值范围（区间）作为一个组。
统计分组应遵循“不重不漏”原则（2）将数据分配到各个组，统计各组的次数，编制次数分配表。
2．解释洛伦兹曲线及其用途答：洛伦兹曲线是20世纪初美国经济学家、统计学家洛伦兹根据意大利经济学家帕累托提出的收入分配公式绘制成的描述收入和财富分配性质的曲线。
洛伦兹曲线可以观察、分析国家和地区收入分配的平均程度。
3. 一组数据的分布特征可以从哪几个方面进行测度？答：数据分布特征一般可从集中趋势、离散程度、偏态和峰度几方面来测度。
统计学第三版答案(20200920015332)
第1章统计和统计数据第2章指出下面的变量类型第3章(1) 年龄。
第4章(2) 性别。
第5章(3) 汽车产量。
第6早(4) 员工对企业某项改革措施的态度（赞成、中立、反对）第7早(5) 购买商品时的支付方式（现金、信用卡、支票）。
第8章详细答案：第9章（1）数值变量。
第10章（2）分类变量。
第11章（3）数值变量。
第12章（4）顺序变量。
第13章（5）分类变量。
第14章一家研究机构从IT从业者中随机抽取1000人作为样本进行调查，其中60%回答他们的月收入在5000元以上，50%的人回答他第15章们的消费支付方式是用信用卡。
第16章（1）这一研究的总体是什么？样本是什么？样本量是多少？第17章（2）月收入”是分类变量、顺序变量还是数值变量？第18章（3）消费支付方式”是分类变量、顺序变量还是数值变量？第19章详细答案：第20章（1 ）总体是所有IT从业者”样本是所抽取的1000名IT从业者”样本量是1000。
/第21章（2）数值变量。
第22章（3）分类变量。
第23章一项调查表明，消费者每月在网上购物的平均花费是200元，他们选择在网上购物的主要原因是价格便宜第24章（1）这一研究的总体是什么？第25章（2）消费者在网上购物的原因”是分类变量、顺序变量还是数值变量？第26章详细答案：第27章（1）总体是所有的网上购物者” \第28章（2）分类变量。
第29章某大学的商学院为了解毕业生的就业倾向，分别在会计专业抽取50人、市场营销专业抽取30、企业管理20人进行调查。
第30章（1）这种抽样方式是分层抽样、系统抽样还是整群抽样？第31章（2）样本量是多少？第32章详细答案：第33章（1）分层抽样。
第34 章（2）100。
第2章用图表展示数据为评价家电行业售后服务的质量，随机抽取由100家庭构成的一个样本。
服务质量的等级分别表示为：A.好；B.较好；C•一般；D.较差；E.差。
调查结果如下：(1)用Excel制作一张频数分布表。
统计学课后习题答案(统计学 第三版
第1章1．什么是统计学?怎样理解统计学与统计数据的关系?2．试举出日常生活或工作中统计数据及其规律性的例子。
3．．一家大型油漆零售商收到了客户关于油漆罐分量不足的许多抱怨。
因此，他们开始检查供货商的集装箱，有问题的将其退回。
最近的一个集装箱装的是2 440加仑的油漆罐。
这家零售商抽查了50罐油漆，每一罐的质量精确到4位小数。
装满的油漆罐应为4.536 kg。
要求：(1)描述总体；(2)描述研究变量；(3)描述样本；(4)描述推断。
答：(1)总体：最近的一个集装箱内的全部油漆；(2)研究变量：装满的油漆罐的质量；(3)样本：最近的一个集装箱内的50罐油漆；(4)推断：50罐油漆的质量应为4.536×50＝226.8 kg。
4．“可乐战”是描述市场上“可口可乐”与“百事可乐”激烈竞争的一个流行术语。
这场战役因影视明星、运动员的参与以及消费者对品尝试验优先权的抱怨而颇具特色。
假定作为百事可乐营销战役的一部分，选择了1000名消费者进行匿名性质的品尝试验(即在品尝试验中，两个品牌不做外观标记)，请每一名被测试者说出A品牌或B品牌中哪个口味更好。
要求：(1)描述总体；(2)描述研究变量；(3)描述样本；(4)一描述推断。
答：(1)总体：市场上的“可口可乐”与“百事可乐”(2)研究变量：更好口味的品牌名称；(3)样本：1000名消费者品尝的两个品牌(4)推断：两个品牌中哪个口味更好。
第2章统计数据的描述——练习题(1) 指出上面的数据属于什么类型；(2)用Excel制作一张频数分布表；(3) 绘制一张条形图，反映评价等级的分布。
解：（1）由于表2.21中的数据为服务质量的等级，可以进行优劣等级比较，但不能计算差异大小，属于顺序数据。
（2）频数分布表如下：服务质量等级评价的频数分布服务质量等级家庭数（频数）频率%A1414B2121C 32 32D 18 18E 15 15 合计100100（3）条形图的制作：将上表(包含总标题，去掉合计栏)复制到Excel 表中，点击：图表向导→条形图→选择子图表类型→完成(见Excel 练习题2.1)。
高等教育出版社《统计学》第三版答案
第1章绪论1什么是统计学怎样理解统计学与统计数据的关系2试举出日常生活或工作中统计数据及其规律性的例子。
3一家大型油漆零售商收到了客户关于油漆罐分量不足的许多抱怨。
因此他们开始检查供货商的集装箱有问题的将其退回。
最近的一个集装箱装的是2 440加仑的油漆罐。
这家零售商抽查了50罐油漆每一罐的质量精确到4位小数。
装满的油漆罐应为4.536 kg。
要求1描述总体2描述研究变量3描述样本4描述推断。
答1总体最近的一个集装箱内的全部油漆2研究变量装满的油漆罐的质量3样本最近的一个集装箱内的50罐油漆4推断50罐油漆的质量应为4.536×50226.8 kg。
4“可乐战”是描述市场上“可口可乐”与“百事可乐”激烈竞争的一个流行术语。
这场战役因影视明星、运动员的参与以及消费者对品尝试验优先权的抱怨而颇具特色。
假定作为百事可乐营销战役的一部分选择了1000名消费者进行匿名性质的品尝试验即在品尝试验中两个品牌不做外观标记请每一名被测试者说出A品牌或B品牌中哪个口味更好。
要求1描述总体2描述研究变量3描述样本4一描述推断。
答1总体市场上的“可口可乐”与“百事可乐” 2研究变量更好口味的品牌名称3样本1000名消费者品尝的两个品牌4推断两个品牌中哪个口味更好。
第2章统计数据的描述——练习题●1. 解1由于表2.21中的数据为服务质量的等级可以进行优劣等级比较但不能计算差异大小属于顺序数据。
2频数分布表如下服务质量等级评价的频数分布服务质量等级家庭数频数频率 A 14 14 B 21 21 C 32 32 D 18 18 E 15 15 合计100 100 3条形图的制作将上表包含总标题去掉合计栏复制到Excel表中点击图表向导→条形图→选择子图表类型→完成见Excel练习题2.1。
即得到如下的条形图02040ABCDE服务质量等级评价的频数分布频率服务质量等级评价的频数分布家庭数频数●2. 解1要求对销售收入的数据进行分组全部数据中最大的为152最小的为87知数据全距为1528765 为便于计算和分析确定将数据分为6组各组组距为10组限以整10划分为使数据的分布满足穷尽和互斥的要求注意到按上面的分组方式最小值87可能落在最小组之下最大值152可能落在最大组之上将最小组和最大组设计成开口形式按照“上限不在组内”的原则用划记法统计各组内数据的个数——企业数也可以用Excel 进行排序统计见Excel练习题2.2将结果填入表内得到频数分布表如下表中的左两列将各组企业数除以企业总数40得到各组频率填入表中第三列在向上的数轴中标出频数的分布由下至上逐组计算企业数的向上累积及频率的向上累积由上至下逐组计算企业数的向下累积及频率的向下累积。
统计学教材部分参考答案(第三版)
统计学教材部分参考答案(第三版)教材习题答案第3章用统计量描述数据3.2详细答案：3.3 详细答案：3.4 详细答案：通过计算标准化值来判断，，，说明在Ａ项测试中该应试者比平均分数高出1个标准差，而在B项测试中只高出平均分数0.5个标准差，由于A 项测试的标准化值高于B项测试，所以A项测试比较理想。
3.5详细答案：3种方法的主要描述统计量如下：方法B 方法C方法A平均165.6 平均128.73 平均125.53高且离散程度较小。
第5章参数估计5.3详细答案：第6章假设检验6.3详细答案：，，，不拒绝，没有证据表明该企业生产的金属板不符合要求。
6.4 详细答案：，，，拒绝，该生产商的说法属实。
6.6详细答案：设，。
，＝1.36，，不拒绝，广告提高了平均潜在购买力得分。
第7章方差分析与实验设计第8章一元线性回归8.1详细答案：（1）散点图如下：产量与生产费用之间为正的线性相关关系。
（2）。
检验统计量，，拒绝原假设，相关系数显著。
8.4 详细答案：（1）方差分析表中所缺的数值如下：方差分析表变差来源 df SS MS F Significance F回归 1 1422708.6 1422708.6 354.277 2.17E-09残差 10 40158.07 4015.807 ——总计 11 1642866.67 ———（2）。
表明汽车销售量的变差中有86.60%是由于广告费用的变动引起的。
（3）。
（4）。
回归系数表示广告费用每变动一个单位，销售量平均变动1.420211个单位。
（5）Significance F＝2.17E-09第10章时间序列预测10.1 详细答案：（1）时间序列图如下：从时间序列图可以看出，国家财政用于农业的支出额大体上呈指数上升趋势。
（2）年平均增长率为：。
（3）。
10.2 下表是1981年—2000年我国油彩油菜籽单位面积产量数据（单位：kg / hm2）年份单位面积产量年份单位面积产量1981 1451 1991 12151982 1372 1992 12811983 1168 1993 13091984 1232 1994 12961985 1245 1995 14161986 1200 1996 13671987 1260 1997 14791988 1020 1998 12721989 1095 1999 14691990 1260 2000 1519（1）绘制时间序列图描述其形态。
统计学第三版课后答案
统计学第三版答案第一章1.什么是统计学？怎样理解统计学与统计数据的关系？答：统计学是一门收集、整理、显示和分析统计数据的科学。
统计学与统计数据存在密切关系，统计学阐述的统计方法来源于对统计数据的研究，目的也在于对统计数据的研究，离开了统计数据，统计方法以致于统计学就失去了其存在意义。
2．简要说明统计数据的来源答：统计数据来源于两个方面：直接的数据：源于直接组织的调查、观察和科学实验，在社会经济管理领域，主要通过统计调查方式来获得，如普查和抽样调查。
间接的数据：从报纸、图书杂志、统计年鉴、网络等渠道获得。
3.简要说明抽样误差和非抽样误差答：统计调查误差可分为非抽样误差和抽样误差。
非抽样误差是由于调查过程中各环节工作失误造成的，从理论上看，这类误差是可以避免的。
抽样误差是利用样本推断总体时所产生的误差，它是不可避免的，但可以控制的。
4.答：（1）有两个总体：A品牌所有产品、B品牌所有产品（2）变量：口味（如可用10分制表示）（3）匹配样本：从两品牌产品中各抽取1000瓶，由1000名消费者分别打分，形成匹配样本。
（4）从匹配样本的观察值中推断两品牌口味的相对好坏。
第二章、统计数据的描述思考题1描述次数分配表的编制过程答：分二个步骤：（1）按照统计研究的目的，将数据按分组标志进行分组。
按品质标志进行分组时，可将其每个具体的表现作为一个组，或者几个表现合并成一个组，这取决于分组的粗细。
按数量标志进行分组，可分为单项式分组与组距式分组单项式分组将每个变量值作为一个组；组距式分组将变量的取值范围（区间）作为一个组。
统计分组应遵循“不重不漏”原则（2）将数据分配到各个组，统计各组的次数，编制次数分配表。
2．解释洛伦兹曲线及其用途答：洛伦兹曲线是20世纪初美国经济学家、统计学家洛伦兹根据意大利经济学家帕累托提出的收入分配公式绘制成的描述收入和财富分配性质的曲线。
洛伦兹曲线可以观察、分析国家和地区收入分配的平均程度。
《统计学》高等教育出版社第三版课后习题答案
第一章1.什么是统计学？怎样理解统计学与统计数据的关系？答：统计学是一门收集、整理、显示和分析统计数据的科学。
统计学与统计数据存在密切关系，统计学阐述的统计方法来源于对统计数据的研究，目的也在于对统计数据的研究，离开了统计数据，统计方法以致于统计学就失去了其存在意义。
2．简要说明统计数据的来源答：统计数据来源于两个方面：直接的数据：源于直接组织的调查、观察和科学实验，在社会经济管理领域，主要通过统计调查方式来获得，如普查和抽样调查。
间接的数据：从报纸、图书杂志、统计年鉴、网络等渠道获得。
3.简要说明抽样误差和非抽样误差答：统计调查误差可分为非抽样误差和抽样误差。
非抽样误差是由于调查过程中各环节工作失误造成的，从理论上看，这类误差是可以避免的。
抽样误差是利用样本推断总体时所产生的误差，它是不可避免的，但可以控制的。
4.答：（1）有两个总体：A品牌所有产品、B品牌所有产品（2）变量：口味（如可用10分制表示）（3）匹配样本：从两品牌产品中各抽取1000瓶，由1000名消费者分别打分，形成匹配样本。
（4）从匹配样本的观察值中推断两品牌口味的相对好坏。
第二章、统计数据的描述思考题1描述次数分配表的编制过程答：分二个步骤：（1）按照统计研究的目的，将数据按分组标志进行分组。
按品质标志进行分组时，可将其每个具体的表现作为一个组，或者几个表现合并成一个组，这取决于分组的粗细。
按数量标志进行分组，可分为单项式分组与组距式分组单项式分组将每个变量值作为一个组；组距式分组将变量的取值范围（区间）作为一个组。
统计分组应遵循“不重不漏”原则（2）将数据分配到各个组，统计各组的次数，编制次数分配表。
2．解释洛伦兹曲线及其用途答：洛伦兹曲线是20世纪初美国经济学家、统计学家洛伦兹根据意大利经济学家帕累托提出的收入分配公式绘制成的描述收入和财富分配性质的曲线。
洛伦兹曲线可以观察、分析国家和地区收入分配的平均程度。
3. 一组数据的分布特征可以从哪几个方面进行测度？答：数据分布特征一般可从集中趋势、离散程度、偏态和峰度几方面来测度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第2章 统计数据的描述——练习题●2. 解：（1）要求对销售收入的数据进行分组，全部数据中，最大的为152，最小的为87，知数据全距为152－87=65；为便于计算和分析，确定将数据分为6组，各组组距为10，组限以整10划分； 为使数据的分布满足穷尽和互斥的要求，注意到，按上面的分组方式，最小值87可能落在最小组之下，最大值152可能落在最大组之上，将最小组和最大组设计成开口形式；按照“上限不在组内”的原则，用划记法统计各组内数据的个数——企业数，也可以用Excel 进行排序统计(见Excel 练习题2.2)，将结果填入表内，得到频数分布表如下表中的左两列；将各组企业数除以企业总数40，得到各组频率，填入表中第三列； 在向上的数轴中标出频数的分布，由下至上逐组计算企业数的向上累积及频率的向上累积，由上至下逐组计算企业数的向下累积及频率的向下累积。
整理得到频数分布表如下：●13.因为女生的离散系数为V=s x ＝550＝0.1 男生体重的离散系数为 V=s x ＝560＝0.08 对比可知女生的体重差异较大。
（2） 男生：x =602.2公斤公斤＝27.27（磅），s =2.25公斤公斤=2.27（磅）；女生：x =2.250公斤公斤=22.73（磅），s =2.25公斤公斤=2.27（磅）；（3）68%； （4）95%。
14 解：（1）应采用离散系数，因为成年人和幼儿的身高处于不同的水平，采用标准差比较不合适。
离散系数消除了不同组数据水平高低的影响，采用离散系数就较为合理。
（2）利用Excel 进行计算，得成年组身高的平均数为172.1，标准差为4.202，从而得：成年组身高的离散系数：024.01.1722.4==s v ； 又得幼儿组身高的平均数为71.3，标准差为2.497，从而得：幼儿组身高的离散系数： 2.4970.03571.3s v ==； 由于幼儿组身高的离散系数大于成年组身高的离散系数，说明幼儿组身高的离散程度相对较大。
第四章参数估计（1） ●1. 解：已知总体标准差σ=5，样本容量n =40，为大样本，样本均值x =25， （1）样本均值的抽样标准差x σσ5=0.7906（2）已知置信水平1－α=95%，得 α/2Z =1.96，于是，允许误差是E =α/2σZ 6×0.7906=1.5496。
●2. 解：（1）已假定总体标准差为σ=15元， 则样本均值的抽样标准误差为x σσ15=2.1429（2）已知置信水平1－α=95%，得 α/2Z =1.96，于是，允许误差是E =α/2σZ 6×2.1429=4.2000。
（3）已知样本均值为x =120元，置信水平1－α=95%，得 α/2Z =1.96， 这时总体均值的置信区间为±α/2σx Z 0±4.2=124.2115.8可知，如果样本均值为120元，总体均值95%的置信区间为（115.8，124.2）元。
●3. 解：⑴计算样本均值x ：将上表数据复制到Excel 表中，并整理成一列，点击最后数据下面空格，选择自动求平均值，回车，得到x =3.316667，⑵计算样本方差s ：删除Excel 表中的平均值，点击自动求值→其它函数→STDEV →选定计算数据列→确定→确定，得到s=1.6093也可以利用Excel 进行列表计算：选定整理成一列的第一行数据的邻列的单元格，输入“＝(a7-3.316667)^2”，回车，即得到各数据的离差平方，在最下行求总和，得到：∑2i（x -x ）=90.65再对总和除以n-1=35后，求平方根，即为样本方差的值。
⑶计算样本均值的抽样标准误差： 已知样本容量 n =36，为大样本， 得样本均值的抽样标准误差为 x σ1.6093=0.2682⑷分别按三个置信水平计算总体均值的置信区间：① 置信水平为90%时：由双侧正态分布的置信水平1－α=90%，通过2β－1=0.9换算为单侧正态分布的置信水平β=0.95，查单侧正态分布表得 α/2Z =1.64， 计算得此时总体均值的置信区间为±α/2sx Z 7±1.64×0.2682= 3.75652.8769可知，当置信水平为90%时，该校大学生平均上网时间的置信区间为（2.87，3.76）小时；② 置信水平为95%时：由双侧正态分布的置信水平1－α=95%，得 α/2Z =1.96，计算得此时总体均值的置信区间为±α/2sx Z 7±1.96×0.2682= 3.84232.7910可知，当置信水平为95%时，该校大学生平均上网时间的置信区间为（2.79，3.84）小时；③ 置信水平为99%时：若双侧正态分布的置信水平1－α=99%，通过2β－1=0.99换算为单侧正态分布的置信水平β=0.995，查单侧正态分布表得 α/2Z =2.58， 计算得此时总体均值的置信区间为±α/2sx Z 7±2.58×0.2682= 4.00872.6247●6. 解：已知样本容量n =200，为大样本，拥有该品牌电视机的家庭比率p =23%，拥有该品牌电视机的家庭比率的抽样标准误差为p σ⑴双侧置信水平为90%时，通过2β－1=0.90换算为单侧正态分布的置信水平β=0.95，查单侧正态分布表得 α/2Z =1.64，此时的置信区间为 p ±αZ %±1.64×2.98%=27.89%18.11%可知，当置信水平为90%时，拥有该品牌电视机的家庭总体比率的置信区间为（18.11%，27.89%）。
⑵双侧置信水平为95%时，得 α/2Z =1.96，此时的置信区间为 p ±αZ %±1.96×2.98%=28.8408%17.1592%可知，当置信水平为95%时，拥有该品牌电视机的家庭总体比率的置信区间为；（17.16%，28.84%）。
●7.解： 已知总体单位数N =500，重复抽样，样本容量n =50，为大样本，样本中，赞成的人数为n 1=32，得到赞成的比率为 p =n 1n =3250=64%（1）赞成比率的抽样标准误差为=6.788% 由双侧正态分布的置信水平1－α=95%，得 α/2Z =1.96，计算得此时总体户数中赞成该项改革的户数比率的置信区间为p ±αZ 64%±1.96×6.788%=77.304%50.696%可知，置信水平为95%时，总体中赞成该项改革的户数比率的置信区间为（50.70%,77.30%）。
（2）如预计赞成的比率能达到80%，即 p =80%，由得样本容量为 n =20.80.2(6.788%)⨯= 34.72 取整为35， 即可得，如果小区管理者预计赞成的比率能达到80%，应抽取35户进行调查。
●13. 解：已知总体比率π=2%=0.02，由置信水平1-α=95%，得置信度α/2Z =1.96，允许误差E ≤ 4%即由允许误差公式 E=/2Z ασ整理得到样本容量n 的计算公式：n=2()Eα/2P Z σ=2=2E 2α/2Z π(1-π)≥20.020.980.04⨯⨯21.96=47.0596 由于计算结果大于47，故为保证使“≥”成立，至少应取48个单位的样本。
●14. ？解：已知总体标准差x σ=120，由置信水平1-α=95%，得置信度α/2Z =1.96，允许误差E ≤ 20即由允许误差公式 E=/2Z x ασ整理得到样本容量n 的计算公式：n=2()Eα/2xZ σ≥2()20⨯1.96120=138.2976 由于计算结果大于47，故为保证使“≥”成立，至少应取139个顾客作为样本。
第6章 假设检验——练习题(全免)6.1 研究者想要寻找证据予以支持的假设是“新型弦线的平均抗拉强度相对于以前提高了”，所以原假设与备择假设应为：1035:0≤μH ，1035:1>μH 。
6.2 （1）第一类错误是该供应商提供的这批炸土豆片的平均重量的确大于等于60克，但检验结果却提供证据支持店方倾向于认为其重量少于60克；（2）第二类错误是该供应商提供的这批炸土豆片的平均重量其实少于60克，但检验结果却没有提供足够的证据支持店方发现这一点，从而拒收这批产品； （3）连锁店的顾客们自然看重第二类错误，而供应商更看重第一类错误。
第七章●4. 解：（1）利用EXCEL 制作数据散点图：将已知表格的后两列复制到Excel 中，选择该表格后，点击：图表向导→XY 散点图→确定，即得散点图如下：（2）根据散点图可以看出，随着航班正点率的提高，投诉率呈现出下降的趋势，说明航班整点率与投诉率两者之间，存在着一定的负相关关系。
[利用Excel 的统计函数“CORREL ”计算得到相关系数r = －0.88261，属于高度负相关]（3）求投诉率依赖航班正点率的估计的回归方程设投诉率为Y ，航班正点率为X建立回归方程 i i X Y 21ββ+= 解法一：应用Excel 函数计算：应用统计函数“SLOPE ”计算直线斜率为：2β=－0.07041应用统计函数“INTERCEPT ”计算直线与y 轴的截距为：1β= 6.017832解法二：应用Excel 列表计算：作出Excel 运算表格如下：得回归系数为： 222)n xy x y n x x -=-(∑∑∑∑∑β9523.215667.27.18949590.46⨯-⨯=⨯-2（667.2） = 81.5611158.3-= —0.0704144初始值 y x =-12ββ=y x nn-∑∑2β = 7.18667.20.070414499+⨯=6.01783 于是得回归方程为^6.01780.07i i Y X =-（4）参数的经济意义是：航班正点率每提高一个百分点，相应的投诉率（次/10万名乘客）下降0.07。
（5）航班按时到达的正点率为80%时，估计每10万名乘客投诉的次数可能为：4187.08007.00178.6ˆ=⨯-=iY （次/10万）第八章 时间序列分析——练习题●1. 解：设i 年的环比发展水平为x i ，则由已知得：x 2003＝30， （1）又知：320042005200620032004200516%x x x x x x ≥+（），2200720082006200715%x x x x ≥+（），求x 2008由上得32200820072008200320032007(16%)(15%)x x x x x x =≥++ 即为3220081.061.0530x ≥，从而2008年该厂汽车产量将达到 得 x 2008≥30× 31.06×21.05= 30×1.3131 = 39.393（万辆） 从而按假定计算，2008年该厂汽车产量将达到39.393万辆以上。