离散数学结构试题集5-7
离散考试题123456

一、证明题(10分)1) (P∧Q∧A→C)∧(A→P∨Q∨C)⇔ (A∧(P↔Q))→C。
P<->Q=(p->Q)合取(Q->p)证明: (P∧Q∧A→C)∧(A→P∨Q∨C)⇔(⌝P∨⌝Q∨⌝A∨C)∧(⌝A∨P∨Q∨C)⇔((⌝P∨⌝Q∨⌝A)∧(⌝A∨P∨Q))∨C反用分配律⇔⌝((P∧Q∧A)∨(A∧⌝P∧⌝Q))∨C⇔⌝( A∧((P∧Q)∨(⌝P∧⌝Q)))∨C再反用分配律⇔⌝( A∧(P↔Q))∨C⇔(A∧(P↔Q))→C2) ⌝(P↑Q)⇔⌝P↓⌝Q。
证明:⌝(P↑Q)⇔⌝(⌝(P∧Q))⇔⌝(⌝P∨⌝Q))⇔⌝P↓⌝Q。
二、分别用真值表法和公式法求(P→(Q∨R))∧(⌝P∨(Q↔R))的主析取范式与主合取范式,并写出其相应的成真赋值和成假赋值(15分)。
主析取范式与析取范式的区别:主析取范式里每个括号里都必须有全部的变元。
主析取范式可由析取范式经等值演算法算得。
证明:公式法:因为(P→(Q∨R))∧(⌝P∨(Q↔R))⇔(⌝P∨Q∨R)∧(⌝P∨(Q∧R)∨(⌝Q∧⌝R))⇔(⌝P∨Q∨R)∧(((⌝P∨Q)∧(⌝P∨R))∨(⌝Q∧⌝R))分配律⇔(⌝P∨Q∨R)∧(⌝P∨Q∨⌝Q)∧(⌝P∨Q∨⌝R)∧(⌝P∨R∨⌝Q)∧(⌝P ∨R∨⌝R)⇔(⌝P∨Q∨R)∧(⌝P∨Q∨⌝R)∧(⌝P∨⌝Q∨R)⇔4M使(非P析取Q析取R)为0所赋真值,即100,二进制M∧5M∧6为4⇔0m∨1m∨2m∨3m∨7m所以,公式(P→(Q∨R))∧(⌝P∨(Q↔R))为可满足式,其相应的成真赋值为000、001、010、011、111:成假赋值为:100、101、110。
真值表法:P Q R Q↔R P→(Q∨R)⌝P∨(Q↔R) (P→(Q∨R))∧(⌝P∨(Q↔R))0 0 0 0 0 1 0 1 00 1 11 0 0 1 0 1 1 1 0 1 1 1 1111111111111111111111由真值表可知,公式(P→(Q∨R))∧(⌝P∨(Q↔R))为可满足式,其相应的成真赋值为000、001、010、011、111:成假赋值为:100、101、110。
离散数学考试题及详细参考答案

离散数学考试题(后附详细答案)一、命题符号化(共6小题,每小题3分,共计18分)1.用命题逻辑把下列命题符号化a)假如上午不下雨,我去看电影,否则就在家里读书或看报。
b)我今天进城,除非下雨。
c)仅当你走,我将留下。
2.用谓词逻辑把下列命题符号化a)有些实数不是有理数b)对于所有非零实数x,总存在y使得xy=1。
c) f 是从A到B的函数当且仅当对于每个a∈A存在唯一的b∈B,使得f(a)=b.二、简答题(共6道题,共32分)1.求命题公式(P→(Q→R)) (R→(Q→P))的主析取范式、主合取范式,并写出所有成真赋值。
(5分)2.设个体域为{1,2,3},求下列命题的真值(4分)a)x y(x+y=4)b)y x (x+y=4)3.求x(F(x)→G(x))→(xF(x)→xG(x))的前束范式。
(4分)4.判断下面命题的真假,并说明原因。
(每小题2分,共4分)a)(A B)-C=(A-B) (A-C)b)若f是从集合A到集合B的入射函数,则|A|≤|B|5.设A是有穷集,|A|=5,问(每小题2分,共4分)a)A上有多少种不同的等价关系?b)从A到A的不同双射函数有多少个?6.设有偏序集<A,≤>,其哈斯图如图1,求子集B={b,d,e}的最小元,最大元、极大元、极小元、上界集合、下界集合、上确界、下确界,(5分)f g图17.已知有限集S={a1,a2,…,a n},N为自然数集合,R为实数集合,求下列集合的基数S;P(S);N,N n;P(N);R,R×R,{o,1}N(写出即可)(6分)三、证明题(共3小题,共计40分)1.使用构造性证明,证明下面推理的有效性。
(每小题5分,共10分)a)A→(B∧C),(E→ F)→ C, B→(A∧ S) B→Eb)x(P(x)→ Q(x)), x(Q(x)∨R(x)),x R(x) x P(x)2.设R1是A上的等价关系,R2是B上的等价关系,A≠ 且B≠ ,关系R满足:<<x1,y1>,<x2,y2>>∈R,当且仅当< x1, x2>∈R1且<y1,y2>∈R2。
离散数学习题集(十五套)-答案
离散数学试题与答案试卷一一、填空 20% (每小题2分)1.设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且(N :自然数集,E + 正偶数) 则 =⋃B A 。
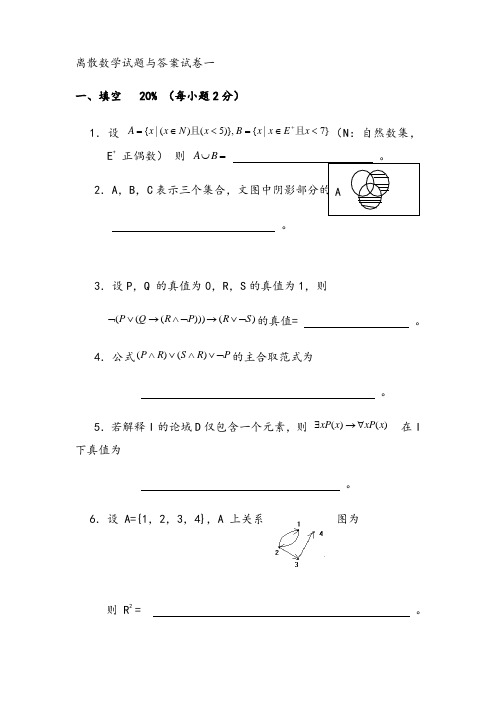
2.A ,B ,C 表示三个集合,文图中阴影部分的集合表达式为 。
3.设P ,Q 的真值为0,R ,S 的真值为1,则)()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 。
4.公式P R S R P ⌝∨∧∨∧)()(的主合取范式为。
5.若解释I 的论域D 仅包含一个元素,则 )()(x xP x xP ∀→∃ 在I 下真值为。
6.设A={1,2,3,4},A 上关系图为则 R 2 = 。
A B7.设A={a,b,c,d},其上偏序关系R的哈斯图为则 R= 。
8.图的补图为。
9.设A={a,b,c,d} ,A上二元运算如下:* a b cda bcda b cdb c dac d abd a bc那么代数系统<A,*>的幺元是,有逆元的元素为,它们的逆元分别为。
10.下图所示的偏序集中,是格的为。
二、选择 20% (每小题 2分)1、下列是真命题的有()A . }}{{}{a a ⊆;B .}}{,{}}{{ΦΦ∈Φ;C . }},{{ΦΦ∈Φ;D . }}{{}{Φ∈Φ。
2、下列集合中相等的有( )A .{4,3}Φ⋃;B .{Φ,3,4};C .{4,Φ,3,3};D . {3,4}。
3、设A={1,2,3},则A 上的二元关系有( )个。
A . 23 ;B . 32 ;C . 332⨯;D . 223⨯。
4、设R ,S 是集合A 上的关系,则下列说法正确的是( )A .若R ,S 是自反的, 则S R 是自反的;B .若R ,S 是反自反的, 则S R 是反自反的;C .若R ,S 是对称的, 则S R 是对称的;D .若R ,S 是传递的, 则S R 是传递的。
离散数学结构试题集5-7

第5章一.填空题1. 群中有唯一的()。
2. 如果群运算是可交换的,则群为()。
3. 设*是定义在集合A上的二元运算,如果对于A中任意的两个元素x,y,都有x*y∈A,则称二元运算*在A上是()。
4. 设*是定义在集合A上的二元运算,如果对于A中任意的两个元素x,y,都有x*y=y*x,则称二元运算*在A上是()。
5. 设★是定义在有理数集合Q上的二元运算,如果对于Q中任意的两个元素x,y,都有x★y=x+y-x*y,其中*表示普通乘法元算,则二元运算★在Q上是()。
(填写可交互/不可交换)6. 设*是定义在集合A上的二元运算,如果对于A中任意的元素x,y,z,都有(x*y)*z=x*(y*z),则称二元运算*在A上是()。
7. 设★是定义在非空集合A上的二元运算,如果对于A中任意的两个元素x,y,都有x*y=y,则二元运算★在A上是()。
(填写可结合/不可结合)8. 设*,★是定义在集合A上的两个二元运算,如果对于A中任意的元素x,y,z,都有(x*y)★z=(x★z)*(y★z),z★(x*y)=(z★x)*(z★y),则称二元运算★对于*在A上是()。
9. 设*,★是定义在集合A上的两个可交换的二元运算,如果对于A中任意的元素x,y,都有x*(x★y)=x, x★(x*y)=x,则称二元运算*对于★在A上满足()。
10. 设*是定义在集合A上的二元运算,如果对于A中任意的元素x,都有x*x=x,则称二元运算*是()。
11. 设*是定义在集合A上的二元运算,如果在A中存在元素el,对于A中任意的元素x,都有el*x=x,则称el为A中关于运算*的()。
12. 设*是定义在集合A上的二元运算,如果在A中存在元素ol,对于A中任意的元素x,都有ol*x=x,则称ol为A中关于运算*的()。
13. 设*是定义在集合A上的二元运算,如果在A中存在元素er,对于A中任意的元素x,都有x*erl =x,则称er为A中关于运算*的()。
(完整版)离散数学试题及答案,推荐文档

11 设 A,B,R 是三个集合,其中 R 是实数集,A = {x | -1≤x≤1, xR}, B = {x | 0≤x < 2, xR},则
A-B = __________________________ , B-A = __________________________ ,
A∩B = __________________________ , . 13. 设集合 A={2, 3, 4, 5, 6},R 是 A 上的整除,则 R 以集合形式(列举法)记为___________ _______________________________________________________. 14. 设一阶逻辑公式 G = xP(x)xQ(x),则 G 的前束范式是__________________________
二、选择题
1. C. 2. D. 3. B. 4. B.
5. D. 6. C. 7. C.
8. A. 9. D. 10. B. 11. B.
第 5 页 共 18 页
13. {(2, 2),(2, 4),(2, 6),(3, 3),(3, 6),(4, 4),(5, 5),(6, 6)}.
14. x(P(x)∨Q(x)). 15. 21.
16. (R(a)∧R(b))→(S(a)∨S(b)). 17. {(1, 3),(2, 2)}; {(1, 1),(1, 2),(1, 3)}.
8. 设命题公式 G=(P(QR)),则使公式 G 为真的解释有
__________________________,_____________________________,
__________________________.
离散数学习题集(十五套) - 答案

离散数学试题与答案试卷一一、填空 20% (每小题2分)1.设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且(N :自然数集,E + 正偶数) 则 =⋃B A 。
2.A ,B ,C 表示三个集合,文图中阴影部分的集合表达式为 。
3.设P ,Q 的真值为0,R ,S 的真值为1,则 )()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 。
4.公式P R S R P ⌝∨∧∨∧)()(的主合取范式为。
5.若解释I 的论域D 仅包含一个元素,则 )()(x xP x xP ∀→∃ 在I 下真值为。
6.设A={1,2,3,4},A 上关系图为则 R 2 = 。
7.设A={a ,b ,c ,d},其上偏序关系R 的哈斯图为则 R= 。
8.图的补图为 。
9.设A={a ,b ,c ,d} ,A 上二元运算如下:* a b c dA BCa b cda b c db c d ac d a bd a b c那么代数系统<A,*>的幺元是,有逆元的元素为,它们的逆元分别为。
10.下图所示的偏序集中,是格的为。
二、选择20% (每小题2分)1、下列是真命题的有()A.}}{{}{aa⊆;B.}}{,{}}{{ΦΦ∈Φ;C.}},{{ΦΦ∈Φ;D.}}{{}{Φ∈Φ。
2、下列集合中相等的有()A.{4,3}Φ⋃;B.{Φ,3,4};C.{4,Φ,3,3};D.{3,4}。
3、设A={1,2,3},则A上的二元关系有()个。
A.23 ;B.32 ;C.332⨯;D.223⨯。
4、设R,S是集合A上的关系,则下列说法正确的是()A.若R,S 是自反的,则SR 是自反的;B.若R,S 是反自反的,则SR 是反自反的;C.若R,S 是对称的,则SR 是对称的;D.若R,S 是传递的,则SR 是传递的。
5、设A={1,2,3,4},P(A)(A的幂集)上规定二元系如下|}||(|)(,|,{tsApt st sR=∧∈><=则P(A)/ R=()A.A ;B.P(A) ;C.{{{1}},{{1,2}},{{1,2,3}},{{1,2,3,4}}};D.{{Φ},{2},{2,3},{{2,3,4}},{A}}6、设A={Φ,{1},{1,3},{1,2,3}}则A上包含关系“⊆”的哈斯图为()7、下列函数是双射的为()A.f : I→E , f (x) = 2x ;B.f : N→N⨯N, f (n) = <n , n+1> ;C.f : R→I , f (x) = [x] ;D.f :I→N, f (x) = | x | 。
《离散数学》试题及答案

一、填空题1设集合A,B,其中A={1,2,3}, B= {1,2}, 则A - B={3} ; ρ(A) - ρ(B)={3},{1,3},{2,3},{1,2,3}} .2. 设有限集合A, |A| = n, 则|ρ(A×A)| = 22n.3.设集合A = {a, b}, B = {1, 2}, 则从A到B的所有映射是α1= {(a,1), (b,1)}, α2= {(a,2), (b,2)},α3= {(a,1), (b,2)}, α4= {(a,2), (b,1)}, 其中双射的是α3, α4 .4. 已知命题公式G=⌝(P→Q)∧R,则G的主析取范式是(P∧⌝Q∧R)5.设G是完全二叉树,G有7个点,其中4个叶点,则G的总度数为12,分枝点数为3.6设A、B为两个集合, A= {1,2,4}, B = {3,4}, 则从A⋂B={4} ; A⋃B={1,2,3,4};A-B={1,2} .7.设R是集合A上的等价关系,则R所具有的关系的三个特性是自反性, 对称性传递性.8. 设命题公式G=⌝(P→(Q∧R)),则使公式G为真的解释有(1, 0, 0), (1, 0, 1),(1, 1, 0)9. 设集合A={1,2,3,4}, A上的关系R1 = {(1,4),(2,3),(3,2)}, R2 = {(2,1),(3,2),(4,3)}, 则R1∙R2 ={(1,3),(2,2),(3,1)} , R2∙R1 = {(2,4),(3,3),(4,2)} _R12 ={(2,2),(3,3).10. 设有限集A, B,|A| = m, |B| = n, 则| |ρ(A⨯B)| = .11设A,B,R是三个集合,其中R是实数集,A = {x | -1≤x≤1, x∈R}, B = {x | 0≤x < 2, x∈R},则A-B = -1<=x<0 , B-A = {x | 1 < x < 2, x∈R} ,A∩B ={x | 0≤x≤1, x∈R} , .13.设集合A={2, 3, 4, 5, 6},R是A上的整除关系,则R以集合形式(列举法)记为{(2, 2),(2, 4),(2, 6),(3, 3),(3, 6),(4, 4),(5, 5),(6, 6)} .14. 设一阶逻辑公式G = ∀xP(x)→∃xQ(x),则G的前束范式是∃x(⌝P(x)∨Q(x)) .15.设G是具有8个顶点的树,则G中增加21 条边才能把G变成完全图。
离散数学习题集(十五套)---答案.docx
离散数学试题与答案试卷一一、填空20%(每小题 2 分)1.设A{ x | ( x N )且 ( x5)}, B{ x | x E 且 x7}( N:自然数集, E+正偶数)则 A B。
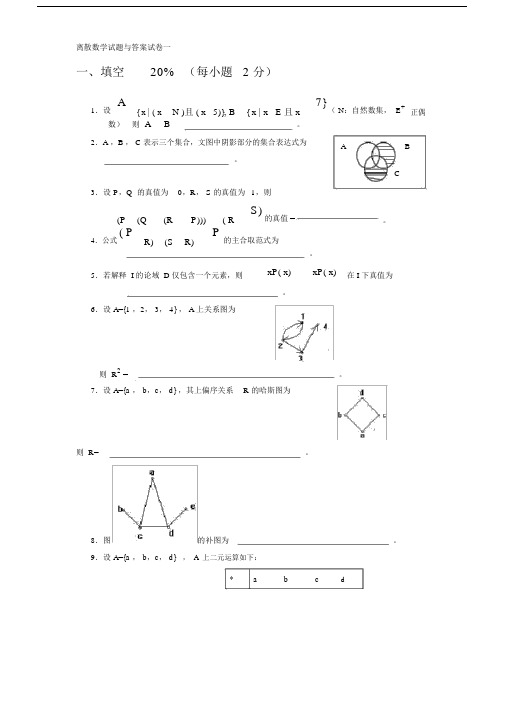
2.A ,B , C 表示三个集合,文图中阴影部分的集合表达式为A B。
C 3.设 P,Q 的真值为0,R, S 的真值为1,则(P(Q(R P)))( R S)的真值 =。
4.公式( PR)(S R)P的主合取范式为。
5.若解释 I 的论域 D 仅包含一个元素,则xP( x)xP( x)在 I 下真值为。
6.设 A={1 ,2, 3, 4} , A 上关系图为则 R2 =。
7.设 A={a , b,c, d} ,其上偏序关系R 的哈斯图为则 R=。
8.图的补图为。
9.设 A={a , b,c, d},A上二元运算如下:*a b c da abc db bcd ac cd a bd d a b c那么代数系统<A ,*> 的幺元是,有逆元的元素为,它们的逆元分别为。
10.下图所示的偏序集中,是格的为。
二、选择20%(每小题 2 分)1、下列是真命题的有()A .{ a}{{ a}};B .{{}}{ ,{ }};C.{{},} ;D.{ }{{}} 。
2、下列集合中相等的有()A . {4 , 3}; B. {,3, 4} ;C. {4 ,, 3,3} ;D . {3 , 4} 。
3、设 A={1 ,2, 3} ,则 A 上的二元关系有()个。
A . 23;B . 32;C. 23 3;D.32 2。
4、设 R,S 是集合 A 上的关系,则下列说法正确的是()A .若 R, S 是自反的,则RS 是自反的;B .若 R, S 是反自反的,则 R S 是反自反的;C.若 R, S 是对称的,则RS 是对称的;D .若 R, S 是传递的,则RS 是传递的。
5、设 A={1 ,2, 3, 4} , P( A )(A 的幂集)上规定二元系如下R{s,t| s,t p( A)(| s || t |}则 P(A ) / R=()A . A; B. P(A) ; C. {{{1}} , {{1 , 2}} , {{1 ,2, 3}} , {{1 , 2, 3, 4}}} ;D. {{} ,{2}, {2 ,3} , {{2 , 3, 4}} , {A}}6、设 A={, {1} , {1 , 3} , {1 , 2, 3}} 则 A上包含关系“”的哈斯图为()7、下列函数是双射的为()A . f : I E , f (x) = 2x;B. f : N N N, f (n) = <n , n+1> ;C. f : R I , f (x) = [x]; D . f :I N, f (x)= | x | 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章一.填空题1. 群中有唯一的()。
2. 如果群运算是可交换的,则群为()。
3. 设*是定义在集合A上的二元运算,如果对于A中任意的两个元素x,y,都有x*y∈A,则称二元运算*在A上是()。
4. 设*是定义在集合A上的二元运算,如果对于A中任意的两个元素x,y,都有x*y=y*x,则称二元运算*在A上是()。
5. 设★是定义在有理数集合Q上的二元运算,如果对于Q中任意的两个元素x,y,都有x★y=x+y-x*y,其中*表示普通乘法元算,则二元运算★在Q上是()。
(填写可交互/不可交换)6. 设*是定义在集合A上的二元运算,如果对于A中任意的元素x,y,z,都有(x*y)*z=x*(y*z),则称二元运算*在A上是()。
7. 设★是定义在非空集合A上的二元运算,如果对于A中任意的两个元素x,y,都有x*y=y,则二元运算★在A上是()。
(填写可结合/不可结合)8. 设*,★是定义在集合A上的两个二元运算,如果对于A中任意的元素x,y,z,都有(x*y)★z=(x★z)*(y★z),z★(x*y)=(z★x)*(z★y),则称二元运算★对于*在A上是()。
9. 设*,★是定义在集合A上的两个可交换的二元运算,如果对于A中任意的元素x,y,都有x*(x★y)=x, x★(x*y)=x,则称二元运算*对于★在A上满足()。
10. 设*是定义在集合A上的二元运算,如果对于A中任意的元素x,都有x*x=x,则称二元运算*是()。
11. 设*是定义在集合A上的二元运算,如果在A中存在元素el,对于A中任意的元素x,都有el*x=x,则称el为A中关于运算*的()。
12. 设*是定义在集合A上的二元运算,如果在A中存在元素ol,对于A中任意的元素x,都有ol*x=x,则称ol为A中关于运算*的()。
13. 设*是定义在集合A上的二元运算,如果在A中存在元素er,对于A中任意的元素x,都有x*erl =x,则称er为A中关于运算*的()。
14. 设*是定义在集合A上的二元运算,如果在A中存在元素or,对于A中任意的元素x,都有x*or=x,则称or为A中关于运算*的()。
15. 如果对于集合中的二元运算*,存在左零元和右零元,且左零元等于右零元,则零元是()。
16. 如果对于集合中的二元运算*,存在左么元和右么元,且左么元等于右么元,则么元是()。
17. 设*是定义在集合A上的二元运算,且e是A中关于运算*的么元,如果对于A中的元素x,存在A中的元素y,有y*x=e,则称y为x的()。
18. 对于实数域上的乘法元算,每个元素()逆元。
(填写一定有/不一定有)19. 对于实数域上的加法运算,()零元。
(填写存在/不存在)20. 对于整数域上的加法运算,()么元。
(填写存在/不存在)21. 对于非空集合S上二元运算*,是封闭且可结合的,那么<S,*>叫做()。
22. 正整数上的加法运算()半群。
(填写是/不是)23. 实数域上的除法运算()半群。
(填写是/不是)24. 整数域上的加法运算()群。
(填写是/不是)25. .如果群的运算满足交换率,则这个群叫()。
26. 循环群()生成元。
(填写必有/不一定有)27. 设f是由<A, ★>到<B,*>的一个同态,如果f( ),则称f为满同态的。
28. 设f是由<A, ★>到<B,*>的一个同态,如果f( ),则称f为同构的。
29. 设f是群<A, ★>到<B,*>的一个同态映射,如果e’是B中的么元,Ker(f)=( ),则称Ker(f)为同态映射f的核。
30. 设R是代数系统<A, ★>上的一个等价关系,如果当<a,b>,<c,d>∈R时,蕴含着<a★c,b★d>∈R,则称R为A上关于★的()。
二.选择题1. 下面那个性质不是群必有的?()A)运算的封闭性B)幺元C)零元D)运算的交换性2. 设集合A={1,2,…,10},下面定义的那个二元运算*关于A不封闭?()A)x*y=max(x,y) B)x*y=质数p的个数,使得x<=p<=yC)x*y=min(x,y) D)x*y=((x+y)mod 10)+13. <S,*>是一个半群,如果S是一个有限集,则必有()A)幺元B)零元C)等幂元D)不确定4. 下面那个代数系统表示的范围最大?()A)群B)半群C)阿贝尔群D)独异点5. 同构关系必然是一个()A)等价关系B)偏序关系C)同余关系D)同态关系6. 在自然数集N上,下列哪种运算是可结合的?()A) a*b=a-b B) a*b=max{a,b} C) a*b=a+2b D) a*b=|a-b|7. 同构关系必然是一个()A.等价关系 B.偏序关系 C.同余关系 D.相容关系8. 设<G,*>是群,a,b∈G,则下列结论不正确的是()A.(a*b)-1=b-1*a-1 B.a*x=b有唯一解C.a*x=a*y,则x=y D.a*b=b*a9. 下面那个运算不满足运算的封闭性?()A)自然数上的加法B)有理数上的乘法C)1到10之间的模11加法D)0到9之间的模10加法10. 下面那个不满足结合律?()A)自然数上的加法B)有理数上的乘法C)自然数上的max(a,b) D)自然数上的减法11. 对于代数系统<Nk,+k>,Nk ={0,1,…,k-1},+k是定义在Nk上的模k加法,下面说法不对的是:()A)有零元B)有么元C)每个元素都有逆元D)<Nk,+k>是半群12. 下面关于半群的说法正确的是()A)必有零元B)必有么元C)必然服从交换律D)必然服从结合律13. 若果<S,*>为半群,且S是有限集合,则以下说法正确的是()A)必有a∈S,且a*a=a B) 必有a∈S,且a*b=bC)必有零元D)必有零元14. 关于独异点,下列说法正确的是()A)必有零元B)必有等幂元C)必有么元D)必然满足交换律15. 以下说法不正确的是()A)群表示范围比半群小B)交换群表示范围比半群小C)阿贝尔群表示范围比群小D)广群表示的范围比半群小16. 下面关于群的说法不正确的是()A)必有零元B)必有么元C)每个必然有逆元D)必然服从结合律17. 下面那个是群?()A)自然数上的乘法B)实数域上的乘法C) 0到9之间的模10加法D) 0到9之间的模10乘法18. 下面关于群<G,*>的说法不正确的是()A)对于任a,b∈G,存在唯一的x∈G,使得a*x=bB)对于任a,b,c∈G,若有a*b=a*c,则必有b=cC)任a∈G,必有唯一的x∈G,使得a*x=e,e为么元D) 任a∈G,必有唯一的x∈G,使得a*x=x,x为零元19. 下面关于群的说法正确的是()A)没有等幂元B) 有1个等幂元C)有2个等幂元D)和群的阶数有关20. 设<G,*>为一个群,下面关于G的子群的说法正确的是()A)如果S是G的非空子集且*在S上是封闭的,则<S,*>就是<G,*>的子群B) 如果S是G的非空子集且含有么元,则<S,*>就是<G,*>的子群C) 如果S是G的非空子集,且对于任意S中的连个元素a,b都有a*b-1∈G,则<S,*>就是<G,*>的子群D) 如果S是G的非空子集,且<S,*>是半群,则<S,*>就是<G,*>的子群21. 下列说法那个是错误的。
()A)循环群必定是阿贝尔群B)循环群必定有等幂元C)阿贝尔群必定是循环群D)循环群必定是交换群22. 下列那个说法是正确的?()A)同态一定是同构的B)同构一定是同态的C)同态一定是同余的D)同态一定是等价的23. 如果f:R->R,对于任意的x∈R,f(x)=5x,则f是从<R,+>到<R,*>的一个()A)单一同态B)满同态C)双射同态D)同构24. 含有3个元素的群有()种情形。
A)1 B) 2 C) 3 D)025. .设G是非零乘法群,判断下列哪个f不是G到G的同态映射。
()A)f(x)=|x| B)f(x)=-x C)f(x)=x+1 D)f(x)=1/x26. 下面关于群的说法不正确的是:()A)有么元B)有零元C)每个元素都有逆元D)满足结合律27. .下面那个是群。
()A)整数域上的加法运算B)实数域上的乘法运算C)自然数域上的除法运算D)整数1到5之间的模6加法运算28. .如果<A,+,*>是一个环,下列关于环的说法错误的是()。
A)<A,+>是阿贝尔群B)<A-{θ},*>是阿贝尔群C)运算*对于+是可分配的D)运算+对于*是可分配的29. 关于独异点说法错误的是()。
A)必有左么元B)必有右零元C)必然满足结合律D)必是含么半群30. 关于阿贝尔群说法错误的是()。
A)必有左么元B)必有右零元C)必然满足交换律D)必是半群三.判断题1. 半群一定是独异点。
( )2. 代数系统中有可能有很多个左零元和右零元,它们有可能相等,也有可能不等。
( )3. 群中不可能有零元。
( )4. 群中的某些元素可能有多个不同的逆元。
()5. 群的运算一定符合交换律。
()6. 如果定义在集合A上的*运算既有左零元,又有右零元,那么必有唯一的零元。
()7. 循环群必有等幂元。
()8. 有等幂元的群一定是有限群。
()9. 阿贝尔群运算一定符合交换律。
()10. 有限群一定有么元。
()11. 含有零元的半群叫独异点。
()12. 在群中,出了么元外,可能还还有其他等幂元。
()13. 对一个群<G,*>,它的任意一个非空有限子集B, 如果*在B上封闭,则<B,*>一定也是群。
()14. .循环群一定是阿贝尔群。
()15. 同构的一定是同态的。
()16. 同态可以诱导一个唯一的等价关系。
()17. .f是代数系统<A,*>到代数系统<B, ★>的同态映射,如果<A,*>半群,则在f作用下,同态象<f(A), ★>也是半群。
()18. 循环群中必有零元。
()19. <R-{0},*>(*表示乘法)与<R,+>同构。
()20. 定义在自然数集合上的模k加法是一个群。
()四.计算题1. 验证二元运算在实数集上是否满足交换律和结合律?2. 对于实数集合R,在下面表格中填写“是”或“否”3.设G={[1],[2].[3],[4],[5],[6]},G上的二元运算如表所示。
