自动控制理论基础左为恒周林主编机械工业出版社习题解
自动控制理论_习题集(附含答案解析)
三、作图题
51.已知单位负反馈系统开环传递函数 ，
(1)绘制闭环根轨迹；
(2)确定使闭环系统阶跃响应无超调的K值范围。
(1)由开环传递函数绘根轨迹如下图。
分离点的坐标d可由方程：
解得d1=-0.586,d2=-3.414
(2)将s=d1、s=d2分别代入根轨迹方程G(s)= –1求K值：
则：
对C(s)/R(s)，前向通路有两条：
；没有与之不接触的回路：
；没有与之不接触的回路：
带入梅逊公式公式得：
对E(s)/R(s)，前向通路有两条：
；有一不接触的回路：
；没有与之不接触的回路：
带入梅逊公式公式得：
27.一个回路：
，
无互不接触的回路，则：
对C(s)/R(s)，前向通路有两条：
；没有与之不接触的回路：
A．图(a)B．图(b)
C．图(c)D．图(d)
22.当ω从−∞→+∞变化时惯性环节的极坐标图为一个（B）。
A．位于第一象限的半圆B．位于第四象限的半圆
C．整圆D．不规则曲线
23.下列串联校正环节中属于滞后校正的是（A）。
A． B．
C． D．
24.下列环节中属于PI校正的是（C）。
A． B．
C． D．K(1+Ts)
由 ，得K=11.656；
由 ，得K=0.34
闭环根位于实轴上时阶跃响应无超调,综合得K取值范围：
K>11.656,K<0.34
52.已知G(s)H(s)= ，绘制K从0到∞的闭环根轨迹，确定分离点坐标、渐近线方程，判断闭环系统稳定性。
53.某单位负反馈系统的开环传递函数为 ，试
自动控制理论基础(1)
比例环节： 成比例地反映控制系统的偏差信号 e(t)。偏差一旦产生，控制器立即产生 控制作用，以减少偏差。
不能消除稳态误差。 比例系数加大会引起系统的不稳定。
4.3 比例-积分-微分控制
积分环节： 用于消除静差，强弱取决于积分时
间常数。 越大积分作用越弱。积分作用太强会 使系统超调加大，甚至出现振荡。
4.2 开环与闭环控制
(4) 例—步进电机
方向 计 算 机 指令 脉冲 脉 冲 分 配 功 率 驱 动 步进 电机 工作台
4.2 开环与闭环控制
步进电机为执行元件。没有位置反馈。 每当向步进电机发出一个进给脉冲时，
步进电机的转子就在此脉冲所产生的同 步转矩下旋转一个固定的角度。
步进电机通过传动机构带动工作台移动。
4.3 比例-积分-微分控制
位置式PID控制算法是非递推形式的， 计算u(k)不仅需要本次及上次采样偏差 值e(k)和e(k-1)，还需要e(0)到e(k)的所有 值。当k很大时，要占用很多内存，计 算机运算量大。
4.3 比例-积分-微分控制
增量式PID控制算法
u(k ) K P e(k ) K I e( j ) K D e(k ) e(k 1) u0
u(k ) K P e(k ) K I e( j ) K D e(k ) e(k 1) u0
j 0
k
KP—比例系数；KI—积分系数， KI = KP * T / TI ； KD—微分系数， KD = KP * TD / T ；T—采样周期。 k — 采样序号，k=0，1，2，… u(k) —第k次采样时刻的计算机输出值； e(k)—第k次采样时刻输入的偏差值。
《自动控制理论》作业集参考答案(专本科函授)第一部分.
此为第一部分如合适，请再下第二部分1-6解 控制系统的任务是使摄像机自动跟踪光点显示器指示的方向。
当摄像机方向角与光点显示器指示的方向一致时，12θθ=，自整角机输出0=e ，交流放大器输出电压0=u ，电动机静止，摄像机保持原来的协调方向。
当光点显示器转过一个角度，12θθ≠时，自整角机输出与失谐角21θθθ-=∆成比例的电压信号（其大小、极性反映了失谐角的幅值和方向），经电位器后变成e ，经放大器放大后驱动伺服电动机旋转，并通过减速器带动摄像机跟踪光点显示器的指向，使偏差减小，直到摄像机与光点显示器指向重新达到一致时为止。
测速发电机测量电动机转速，进行速度反馈，用以改善系统性能。
系统中，摄像机是被控对象，摄像机的方向角2θ是被控量，给定量是光点显示器指示的方向角1θ。
系统方框图如图解1-6所示。
参 考 答 案第一章1-1解 （1）负反馈连接方式为：d a ↔，c b ↔； （2）系统方框图如图解1-1 所示。
1-3解 加热炉采用电加热方式运行，加热器所产生的热量与调压器电压c u 的平方成正比，c u 增高，炉温就上升，c u 的高低由调压器滑动触点的位置所控制，该触点由可逆转的直流电动机驱动。
炉子的实际温度用热电偶测量，输出电压f u 。
f u 作为系统的反馈电压与给定电压r u 进行比较，得出偏差电压e u ，经电压放大器、功率放大器放大成a u 后，作为控制电动机的电枢电压。
在正常情况下，炉温等于某个期望值T °C ，热电偶的输出电压f u 正好等于给定电压r u 。
此时，0=-=f r e u u u ，故01==a u u ，可逆电动机不转动，调压器的滑动触点停留在某个合适的位置上，使c u 保持一定的数值。
这时，炉子散失的热量正好等于从加热器吸取的热量，形成稳定的热平衡状态，温度保持恒定。
当炉膛温度T °C 由于某种原因突然下降(例如炉门打开造成的热量流失)，则出现以下的控制过程：控制的结果是使炉膛温度回升，直至T °C 的实际值等于期望值为止。
自动控制理论 机械工业出版社 课后习题答案 夏德岑_第三版 PDF可打印
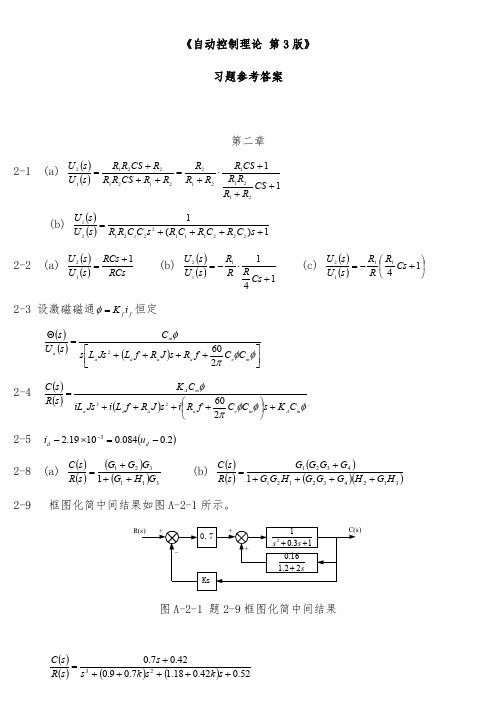
, t 0
比较上述两种情况， 可见有 z 1 零点时， 单位脉冲响应的振幅较无零点时小， 而且产生相移， 相移角为 arctg
1 2 n 。 1 n
2．单位阶跃响应 (a) 无零点时
ct 1
2 n t 1 2 t arctg 1 e sin n 1 2
G( s) 2a ss (2 a) s (2 2a)
2
根据条件（1） ，可得
Kv 1 2a 0.5 esr 2 2a
解得 a 1 ，于是由系统的开环传递函数为
G( s) 2 ss 3s 4
2
3-10
1M 2M
3t
s
p p
46.6%, t s 7.99s2%, ( n 2.12rad / s, 0.24) 16.3%, t s 8s2%, ( n 1rad / s, 0.5)
C m s 60 U a s s La Js 2 La f Ra J s Ra f C eC m 2
2-4
C s Rs
K A C m 60 iL a Js 3 iL a f Ra J s 2 i Ra f C eC m s K A C m 2
C 2 lim
s 0
d2 2(0.1s 2 s 10) 20(0.2s 1) 2 s lim 0 e s 0 ds 2 (0.1s 2 s 10) 3
(1)
s (t ) r (t ) R0 ，此时有 rs (t ) R0 , r r (t ) 0 ，于是稳态误差级数为 s esr t C0 rs (t ) 0 ， t 0
自动控制理论基础(4)
K 1 (s + 5) G (s) = s ( s + 2 )( s + 3 )
两条渐近线， 1 n-m=2,两条渐近线，其参数为 两条渐近线 π a = ± σa = 0 2 A ' ( s ) B ( s ) B ' ( s ) A( s ) = 0
2
jω
s + 10s + 25s + 15 = 0
第4章 习题解 章
4-1 开环零、极点如图 开环零、极点如图E4-1所示 试绘制出相应 所示,试绘制出相应 所示 的概略根轨迹图。 的概略根轨迹图。
j j j
0
0
0
（a） ）
（b） ）
（c） ）
1
j
j
j
0
0
0
（d） ）
（e） ） 图E4-1
（f） ）
2
4-2 单位反馈控制系统开环传递函数如下 试画 单位反馈控制系统开环传递函数如下,试画 出相应的闭环根轨迹图。 出相应的闭环根轨迹图。
3 2
-5
-3
-2
0
σ
用试探法求出会合点约为-0.9 用试探法求出会合点约为 时稳定。 3闭环特征方程如下，当K1>0时稳定。 闭环特征方程如下， 时稳定
s 3 + 5 s 2 + (6 + K 1 ) s + 5 K 1 = 0
4
K1 ( s + 20) ( 2) G ( s ) = s ( s + 10 + 10 j )( s + 10 10 j )
d1
5 2.17 ∵ β = sin = 38.3 5
1
∴ ζ = cos 38.3 = 0.824
自动控制理论课后习题详细解答答案(夏德钤翁贻方版)第五章
第五章5-1 已知单位反馈系统的开环传递函数，试绘制其开环频率特性的极坐标图(1)解：幅频特性：相频特性：列表取点并计算。
0.5 1.0 1.5 2.0 5.010.01.790.7070.370.2240.0390.0095-116.6-135-146.3-153.4-168.7-174.2系统的极坐标图如下：(2)解：幅频特性：相频特性：列表取点并计算。
00.20.50.8 1.0 2.0 5.010.910.630.4140.3170.1720.01950-15.6-71.6-96.7-108.4-139.4-162.96系统的极坐标图如下：(3)解：幅频特性：相频特性：列表取点并计算。
0.20.30.51254.55 2.74 1.270.3170.0540.0039-105.6-137.6-161-198.4-229.4-253系统的极坐标图如下：(4)解：幅频特性：相频特性：列表取点并计算。
0.20.250.30.50.60.8122.7513.87.86 2.520.530.650.317-195.6-220.6-227.6-251.6-261.6-276.7-288.4系统的极坐标图如下：5-2 试绘制上题中各系统的开环对数频率特性（伯德图）。
(1)解：系统为Ⅰ型，伯德图起始斜率为－20dB/dec，在处与=20=0相交。
环节的交接频率，斜率下降20dB/dec，变为-40dB/de c。
系统的伯德图如图所示:(2)解：伯德图起始为0dB线，的交接频率，斜率下降20dB/dec，变为－20dB/de c。
的交接频率，斜率下降20dB/dec，变为－40dB/de c。
系统的伯德图如图所示。
（3）解：系统为Ⅰ型，伯德图起始斜率为－20dB/dec，其延长线在=1处与=20=0相交。
的交接频率，斜率下降20dB/dec，变为－40dB/de c。
的交接频率，斜率下降20dB/dec，变为－60dB/de c。
自控原理习题解答
②R(s)和N(s)同时作用时系统的输出
∴ C(s) = CR (s) + CN (s)
=
G1G2 + G1G3 + G1G2G3H1
R(s) +
1+ G1G3 + G2H1 + G1G2 + G1G2G3H1
+ 1+ G2H1 + G1G2G4 + G1G3G4 + G1G2G3G4H1 N (s) 1+ G1G3 + G2H1 + G1G2 + G1G2G3H1
s(s + 1)
Kts
1.试分析速度反馈系数Kt对系统稳定性的影响。 2.试求KP、Kv、Ka并说明内反馈对稳态误差的影响。 解: 1.如果没有内反馈，系统的开环和闭环传递函数为
解：将系统开环传递函数与二阶系统典型开环传递函
数比较： 所以：
G(s) =
ωn2
s(s + 2ζωn )
ωn = 10K
2ζωn = 10 ζωn = 5
ζ= 5
10K
−πζ
σ = e 1−ζ 2 ×100%
tp
=π ωd
=
ωn
π 1−ζ 2
tS
(5%)
≈
3
ζωn
分别将K＝10 ，K＝20代入计算，结果如下：
10K1 = 10 1 + 10 K 2
解之得：K2＝0.9 K1＝10
Ø 3-4 单位反馈系统的开环传递函数为
G(s) = K = 10K s(0.1s + 1) s(s +10)
试分别求出K=10s–1和K=20s–1时，系统的阻尼比ζ 和
自动控制理论第一章引论86页PPT
控 制
A级，厌学型：不快乐、厌烦、心理上的强烈反感和抵触；
理 论
B级，被动型：消极、被动、麻木，在父母、老师的督促和
舆论的压力下取得进步；
C级，机械型：全身心投入、刻苦用功、头悬梁锥刺骨、按 部就班地朝着一流的方向努力；
D级，进取型：自信、主动、积极，把必须要做的事情做到 最好，持续性地保持一流的成绩；
俄国A.M.Lyapunov（李雅普诺夫，1892年）在《论运动稳 定性的一般问题》中建立了动力学系统的一般稳定性理论。 提出了李雅普诺夫第一法与第二法
H.Nyquist（乃魁斯特，1932年）提出乃氏判据，Bode(波特， 1927年）提出了对数频率特性的方法。
W.R.Evans（伊万斯，1948年)提出根轨迹法，此方法和规 则指的是当系统参数变化时特征方程式根变化的几何轨迹。 目前仍然是系统设计和稳定性分析的一种重要方法。
发表《论调节器》，研究调节器的微分方程，
线性化处理，系统稳定性取决于微分方程的
特征根是否都具有一对负的实部，针对二阶
和三阶系统讨论了使特征根具有负实部时，
特征多项式系数应满足的条件。
20
第一章 引 论
自
动（3） 系统稳定判据
控
制 理 由E.J.Routh（劳斯，1884年） 和 Hurwitz（霍尔维茨， 论 1895年）提出的劳斯-霍尔维茨稳定判据
29
第一章 引 论
自
动 控
第三节 自动控制和自动控制系统
制
理
论
一、自动控制的概念
1、手动控制 水箱水位的手动控制：
图1-1 水箱水位的人工 控制系统示意图
30
第一章 引 论
自
动 控
自动控制理论邹伯敏第3版课后答案总.doc
《自动控制理论 第2版》习题参考答案第二章2-1 (a)()()1121211212212122112+++⋅+=+++=CS R R R R CS R R R R R R CS R R R CS R R s U s U (b)()()1)(12221112212121++++=s C R C R C R s C C R R s U s U 2-2 (a)()()RCs RCs s U s U 112+= (b) ()()141112+⋅-=Cs R R R s U s U (c) ()()⎪⎭⎫⎝⎛+-=141112Cs R R R s U s U 2-3 设激磁磁通f f i K =φ恒定()()()⎥⎦⎤⎢⎣⎡++++=Θφφπφm e a a a a m a C C f R s J R f L Js L s C s U s 2602 2-4()()()φφφπφm A m e a a a a m A C K s C C f R i s J R f L i Js iL C K s R s C +⎪⎭⎫⎝⎛++++=260232-5 ()2.0084.01019.23-=⨯--d d u i2-8 (a)()()()()3113211G H G G G G s R s C +++= (b) ()()()()()31243212143211H G H G G G H G G G G G G s R s C +++++=2-9 框图化简中间结果如图A-2-1所示。
图A-2-1 题2-9框图化简中间结果()()()()52.042.018.17.09.042.07.023++++++=s k s k s s s R s C 2-10()()4232121123211G H G G H G G H G G G G s R s C ++-+=2-11 系统信号流程图如图A-2-2所示。
图A-2-2 题2-11系统信号流程图()()()()2154214212654212215421421321111H H G G G G G G G H G G G G G s R s C H H G G G G G G G G G G s R s C -++=-++=2-12 (a)()()()adgi abcdi agdef abcdef cdhs R s C +++-=11(b) ()()()1221211222112++++=s C R C R C R s C R C R R s R s C2-13 由选加原理,可得()()()()()()[]s D H G G s D G s D G s R G G G H G H s C 3121221221221111--+++=第三章3-1 分三种情况讨论 (a) 当1>ζ时()()()()()⎥⎥⎦⎤⎢⎢⎣⎡-+----+-=-+-=---=⎪⎭⎫ ⎝⎛-+-⎪⎭⎫ ⎝⎛---221221222211112121,122ζζζζωζωζωζζωζζωζζωζζt t n n nn n n e e t t c s s (b) 当10<<ζ时()()()⎪⎪⎭⎫⎝⎛-----+-=---+---=-+-=---=---22222222222121121sin 1121sin 1211cos 221,1ζζζωζωζωζωζωζζωζωζωζωζζωζζζωζωζωarctg t et t e t et t c j s j s n tnnn t nn tnnn n n n n(c) 当1=ζ时设系统为单位反馈系统,有()()()()()2222nn n r s s s s R s c s R s E ωζωζω+++=-= 系统对单位斜坡输入的稳态误差为 ()nn n n s sr s s s s s s im e ωζωζωζω22212220=+++⋅⋅=→ 3-2 (1) 0,0,50===a v p K K K (2) 0,,==∞=a v p K K K K(3) 10,,K K K K a v p =∞=∞= (4) 0,200,==∞=a v p K KK K 3-3 首先求系统的给定误差传递函数()101.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()()()0)101.0()12.0(20)101.0(2lim lim 1.0)101.0()12.0(10lim lim 0101.0)11.0(lim lim 322202202220012000=+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s e s s e s(1) 0)(R t r =，此时有0)()(,)(0===t r t r R t r s s s ，于是稳态误差级数为()0)(0==t r C t e s sr ，0≥t(2) t R R t r 10)(+=，此时有0)(,)(,)(110==+=t r R t r t R R t r s s s ，于是稳态误差级数为()1101.0)()(R t rC t r C t e s s sr =+= ，0≥t (3) 221021)(t R t R R t r ++=，此时有t R R t rt R t R R t r s s 212210)(,21)(+=++= ，2)(R t r s = ，于是稳态误差级数为 ())(1.0)(!2)()(21210t R R t r C t rC t r C t e s s s sr +=++= ，0≥t 3-4 首先求系统的给定误差传递函数()5001.0)11.0()(11)()(2+++=+==Φs s s s s G s R s E s e 误差系数可求得如下()⎪⎭⎫⎝⎛++-=-=-t e t t c s n t n nn n 21222,1ωωωωω()()()232220220222001200050098)5001.0()12.0(1000)5001.0(100lim lim 5001)5001.0()12.0(500lim lim 05001.0)11.0(lim lim =+++-++=Φ==+++=Φ==+++=Φ=→→→→→→s s s s s s ds d C s s s s ds d C s s s s s C s e s s es s e stt r t t rt t r s s s 5sin 25)(5cos 5)(5sin )(-===稳态误差级数为()[][][]tt tC t C C t e sr 5cos 1015sin 109.45cos 55sin 25224120 -⨯++⨯=-⨯+⎥⎦⎤⎢⎣⎡+⨯-=- 3-5 按技术条件（1）~（4）确定的二阶系统极点在s 平面上的区域如图A-3-1 (a) ~ (d)的阴影区域。
自动控制理论_(刘丁_著)_机械工业出版社_课后答案
习题31. 答案：t K >=0.32. 此温度计的时间常数T= t/4=15秒3. 答案： ()10.11s s φ=+4. 答案：b 变大系统阶跃响应的延迟时间、上升时间和调节时间都加长。
5.)1)(2(22++-=s s s X Y 6. 略7. 答案： (1)2600()70600G s s s =++,（2）24.5n w =，ζ=1.438. 答案： 1.24p t =,%9.5%σ= 1.58(5%)s t =∆=或 2.11(2%)s t =∆=9. 1）开环零点-2.5 开环极点-0.52）闭环零点-2.5 闭环极点-0.4500 ± 0.8930i 3）1=n ω ζ=0.45 4）38.1=r t 96.7=s t %6.22%=ο10. 答案：H K =0.9,0K =10 11. 答案：47,0.1K τ≈≈ 12. 答案：3 13. 答案：（1）不稳定，右半S 平面有2个根； （2）不稳定，右半S 平面有2个根； （3）不稳定，右半S 平面有1个根；14. 略15. 答案：系统的参数(),K ξ的稳定域为0020K ξξ><<，。
16. 答案：51499K << 17. 答案：（1）由()D s 表达式可见，当0β=时系统结构不稳定；当0β>时系统总是稳定的。
（2）由ξ=可见2%3.57s n t K ξσβξωβ⎧↑→↓⎪↑⇒⎨==↓⎪⎩（3） 1ss ss a a e e K K ββ==∴↑→↑。
18. 答案：a T 、M T 与K 均大于0且10zK T <<时闭环系统是稳定的。
19. 答案：121ssn K e K =-+20. 证明：是I 型系统；21.B K K v =KBe ss = 与K 成反比，与B 成正比 22.G=tf(80,[1 2 0]); GB=feedback(G,1); t=0:0.01:1; [y,t]=step(GB); e=1-y;m=length(t);subplot(2,1,1),plot(t,y,'k',t,ones(m,1),'k-.') %draw unit step response curve title('unit step response','FontSize',8)xlabel('Time(sec.)','Position',[5.5 -0.21],'FontSize',8) ylabel('Amplitude','FontSize',8) axis([0 6 0 2])subplot(2,1,2), plot(t,e,'k',t,zeros(m,1),'k-.') %draw error response curve title('error response','FontSize',8)xlabel('Time(sec.)','Position',[5.5 -1.21],'FontSize',8) ylabel('Amplitude','FontSize',8)012unit step responseTime(sec.)A m p l i t u d e-11error responseTime(sec.)A m p l i t u d e()()1()k B k G s s G s φ=+()()1()B k B s G s s φφ=-2()()Ks bG s s a k s+=+-0lim ()V s bK sG s a K →==-1ss v a k e K b-==23 clearnum=1;den=conv([0.5 1 0],[4 1]); rangek=[0.2,0.8,1.2]; t=linspace(1,60,300)'; for j=1:3s1=tf(num*rangek(j),den); sys=feedback(s1,1); y(:,j)=step(sys,t); endplot(t,y(:,1),'k',t,y(:,2),'r',t,y(:,3),'b')title('unit step response under different k','FontSize',8) xlabel('Time(sec.)','Position',[50 -1.8],'FontSize',8) ylabel('Amplitude','FontSize',8) axis([0 60 -1.5 3.5])gtext('k=0.2'),gtext('k=0.8'),gtext('k=1.2')Time(sec.)A m p l i t u d e求当k =0.8时系统的性能指标 clear num=1;den=conv([0.5 1 0],[4 1]); k=0.8;num=num*k; s1=tf(num,den); sys=feedback(s1,1); t=0:0.005:50; y=step(sys,t); r=1;while y(r)<1.0001 r=r+1; endrise_time=(r-1)*0.005 [ymax,tp]=max(y);peak_time=(tp-1)*0.005 max_overshoot=ymax-1 s=length(t);while y(s)>0.98 & y(s)<1.02s=s-1;endsettling_time=(s+1)*0.005运行结果：rise_time =4.5350peak_time =7.7950max_overshoot =0.5710settling_time =46.855024 num=[6.3223 18 12.811]den=[1 6 11.3223 18 12.811]step(num,den)25 num=1for kesi=0:0.2:1sys=tf(num,[1 2*kesi 1]);step(sys)hold onend习题41．(a) (b) (c)(d) (e) (f) 2．(1)(2)证明：s j σω=+代入1＋G(s)H(s)=0*()()0s s b k s a +++=*()(())(())0jw jw b k jw a σσσ++++++=*2()()0k a b σσσω+++-=*20k b a ++=消去*k 得：222()a a ab σω++=-所以根轨迹是以(-a,0) 3．答案：(1)（2）（3）（4）4．答案：（1）分离点： 3.854d =-渐近线 25,a a πσϕ=-=±，* 1.37K =，闭环系统稳定的*K 值的范围是*04K <<。
自动控制理论第一章习题答案.doc
第一章自动控制概论思考题1、什么是自动控制？他对人类活动有什么意义？所谓自动控制就是在没有人直接参与的情况下，通过控制装置使被控制对彖或生产过程自动地按照预定的规律运行，使Z达到预期的状态或性能要求。
自动控制是人类在认识世界和发明创新的过程屮发展起來的一门重要的科学技术。
依靠它，人类可以从笨重、重复性的劳动中解放出來，从事更富创造性的工作。
2、什么是反馈？什么是负反馈？通常，我们把输出量送回到输入端并与输入信号比较的过程称为反馈。
若反馈的信号是与输入信号相减而使偏差值越来越小，则称为负反馈。
3、开环控制系统是怎样实现控制作用的？请举例说明。
开环控制系统：如果系统的输出端和输入端Z间不存在反馈回路，输出量对系统的控制作用没有影响，这样的系统称为开环控制系统。
例：原始的数控机床进给系统就是开环控制系统。
指令输入到计算机控制系统Z中，带动步进电机运动，使工作台移动，产生位移输出。
在口常生活中，许多控制系统都可以理解成开环控制系统，如电风扇的转速是由档位决定的，不能根据环境温度自动调节；洗衣机定时系统是由功能和时间决定，不能根据所洗衣物清洁程度自动调节。
4、闭环控制系统是怎样实现控制作用的？请举例说明。
闭环控制系统：闭环控制（亦称为反馈控制，Feedback Control）是指能对输出量与输入量进行比较，并且将它们的偏差作为控制手段，以保持两者Z间预定关系的系统。
如：自动调温空调，当环境温度高于设定温度时，空调制冷系统自动开启，调定室温到设定值。
5、对自动控制系统的基本要求是什么？对控制系统的基本要求是：系统的稳定性、响应的快速性、响应的准确性。
6、试叙述电冰箱中温度控制系统的温度控制过程。
电冰箱温度控制系统由感温管，温度调节，执行动作等系统组成。
冰箱没工作时，感温管内气体遇热就膨涨，触点就将两原来断开的接触点靠在一起了。
冰箱在工作时，由于冰箱内制冷系统在给冰箱不段的输入冷气，就越来越冷，随着温度不短降低，感温管内的气体缩小，气垫就将断点段开，然而就将冰箱停止工作！7、试叙述骑自行车时的闭环控制过程。
自动控制原理习题集
图 1-9
晶体管稳压电路方框图
5
第二章 控制系统的数学模型
2-1a 试证明图 2-1(a)所示电气网络与图 2-1(b)所示的机械系统具有相同的传递函数。
（a）
图 2-1
（b）
解：对于图（a）所示的电气网络，其传递函数 U c ( s) / U i ( s) ，可以求得为
U c ( s) U r ( s)
图 1-2 冰箱制冷系统方框图
1-2a 图 1-3 为液位控制系统的示意图，试说明其工作原理并绘制系统的方框图。 说明 液位控制系统是一典型的过程 控制系统。控制的任务是：在各种扰动的 作用下尽可能保持液面高度在期望的位置 上。故它属于恒值调节系统。现以水位控 制系统为例分析如下。 解 分析图 1-3 可以看到：被控量为水位 高度 h（而不是水流量 Q2 或进水流量 Q1） ； 受控对象为水箱；使水位发生变化的主要 原因是用水流量 Q2，故它为系统的负载扰 图 1-3 液位控制系统示意图 动；而进水流量 Q1 是用以补偿用水流量的 改变，使水箱的水位保持在期望的位置上的 控制作用；控制进水流量的使由电动机驱动的阀门 V1，故电动机-减速器-阀门 V1 一起构成 系统的执行机构；而电动机的供电电压 ud 取决于电位器动触点与接零点之间的电位差，若
U c (s) z 2 R2 R2 R cs 1 1 1 1 U r ( s ) z1 R1 / R2 // R1 * R1 cs cs 1 R1 cs
图 2-2（b）示的有源网络传递函数 Uc(s)/Ur(s)可以求得为，
1 * R2 cs 1 1 // R2 R2 U c ( s) cs R /R cs 2 1 U r ( s) R1 R1 R2 cs 1
自动控制理论 (刘丁 著) 机械工业出版社 课后答案--习题四
习题41．(a) (b) (c)(d) (e) (f) 2．(1)(2)证明：s j σω=+代入1＋G(s)H(s)=0*()()0s s b k s a +++=*()(())(())0jw jw b k jw a σσσ++++++=*2()()0k a b σσσω+++-=*20k b a ++=消去*k 得：222()a a ab σω++=-所以根轨迹是以(-a,0)的圆。
3．答案：(1)（2）（3）（4）4．答案：（1）分离点： 3.854d =-渐近线25,a a πσϕ=-=±，* 1.37K =，闭环系统稳定的*K 值的范围是*04K <<。
（2）()()()()()()()()()()()()23220.4150.4150.4159261818185221s s s s s s s s s s s ss s s s φ-+-+-+===+++++++++-提示：()*111004D s K =-==1当s 时，由特征方程可得. 5．答案：*K 的范围（0，2）6．7．答案：负反馈：正反馈：8．答案：⋃∞系统无超调的k值范围(0,0.68][23.34,)9. （1）（2）根据K 值可计算出系统的闭环极点为-2和-5。
123102, 5.1s s K s s s -==⇒=-=-+10．11．答案：⑴实轴根轨迹：[]3,2--，[]1,0-；渐近线：1a σ=-，2a πϕ=±；分离点：0.53d =-。
题4－11图⑵主导极点：1,20.7 1.2s j =-± ()0.5ξ=23K = 53K *=。
12．答案：*716K <<渐近线31,,a a πσϕπ=-=±，与虚轴的交点1,2316;0,7K K ωω====， 分离点：1d =-，所以闭环系统稳定的开环增益范围是*716K <<。
13. (1)1189.5p οθ=,分离点3,3s s =-=(舍)(2)509τ≤<14．答案：与虚轴的交点*1;K ω== *K >1系统稳定；*K ξ↑→↑平稳性变好；当*K →∝时，0.707ξ→，()c t 振荡性减小，快速性得以改善。
自动控制理论第3版邹伯敏课件第04章
第二节 绘制根轨迹的基本规则 ➢根轨迹的起点和终点 ➢根轨迹的对称性和分支数 ➢实轴上的根轨迹段 ➢根轨迹的渐近线 ➢根轨迹在实轴上的分离点和会合点 ➢根轨迹与虚轴的交点 ➢根轨迹的出射角和入射角 ➢闭环极点的和与积、开环极点闭环极点
的关系
11
规则1. 根轨迹的起点和终点
起点：n条根轨迹起始于开环传递函数的n个极点。
d1 = 0.472
0
d 180 / k
如果方程的阶次高时，可用试探法确定分离点。
20
j
（5）虚轴的交点
D(s) 1 G(s)H (s) 1
K0
0
s(s 1)(s 5)
方法一： 令s=jω，则
s3 + 6s 2 + 5s + K0 = 0
60
-2
0
(jω)3 + 6(jω)2 + 5 (jω) + K0 = 0
方法一：在系统的闭环特征方程D(s) = 0中，令s = jω，D(jω) = 0的解即是交点坐标。
方法二：由劳斯稳定判据求出。
18
例4-2 设某负反馈系统的开环传递函数为
G(s)H(s)
K0
s(s 1)(s 5)
试绘制系统根轨迹。
解（1）起点： p1= 0、p2= 1、p3= 5。 终点：终于无穷远处
n
m
zx 180 (zx p j ) (zx zi )
j 1
i1,i x
=180 117 90 + 153 + 63.5 + 119 + 121 =149.5
j
-2
-1
j1
0
29
例4-5 设负反馈系统的开环传递函数为
自动控制理论第2版夏德钤 翁贻方第二章控制系统的数学模型
例2-1:图2-1为RC四端无源网络。试列写以U1(t)
为输入量，U2(t)为输出量的网络微分方程。
解：设回路电流i1、i2，根据克希霍夫定律，列
写方程组如下
R1
R2
U1 R1i1Uc1
(1)
1
Uc1
C1
(i1 i2)dt
(2)
Uc1R2i2Uc2
(3)
Uc2
1 C2
i2dt
n=1/T——无阻尼自然振荡频率。共轭复数极点为：
5．微分环节
式中
——比例系数,是随工作点A（x0，y0)不 同而不同的常数
具有两个以上输入量的非线性系统线性化处理方法与前述 方法相似。
求线性化微分方程的步骤 ① 按物理和化学定律，列出系统的原始方程式，确定平衡点处
各变量的数值。 ② 找出原始方程式中间变量与其它因素的关系，若为非线性函
数，在原平衡点邻域内，各阶导数存在并且是唯一的，则可 进行线性化处理。 ③ 将非线性特性展开为泰勒级数，忽略偏差量的高次项，留下 一次项，求出它的系数值。 ④ 消去中间变量，在原始方程式中，将各变量用平衡点的值用 偏差量来表示。
• 同一系统对不同的输入，可求得不同的传递函数，但其特征 多项式唯一。
• 在给定输入和初始条件下，解微分方程可以得到系统的输出 响应，包括两部分 系统响应=零输入响应+零状态响应 零输入响应——在输入为零时，系统对零初始状态的响应； 零状态响应——在零初始条件下，系统对输入的响应。
传递函数的几点性质
于是电动机可作为测速发电机使用。
•
第二节线性系统的输入—输出传递函数描述
一、传递函数 １．定义：线性定常系统的传递函数，定义为零
初始条件下，系统输出量的拉氏变换与输入量 的拉氏变换之比。零初使条件是指当t≤0时,系统 r(t)、c(t)以及它们的各阶导数均为零。 线性系统微分方程的一般形式为
自动控制理论(邹伯敏第三版)第05章
自动控制理论
第五章
频率响应
作者： 浙江大学
2015/12/11 第五章 频率响应
邹伯敏 教授
1
自动控制理论
第一节
一、频率特性的基本概念
频率特性
令
C (s) R(s)
G(s)
U (s) V (s)
A 已知 r (t ) A sint , R ( s ) 2 2 S
C (S )
U ( S ) A U (S ) A V (S ) S 2 2 (S P 1 )(S P 2 )(S P n ) ( S j )(S j )
n bj a a S j S j j 1 S p j
c(t ) ae jt a e jt b j e
1 T2 S 1 T2 j , Ga ( j ) 1 T1S 1 T1 j
Gb ( S )
这两个系统的幅频特性是相同的,即：
L( ) 20lg 1 (
1 T1
) 2 20lg 1 (
1 T2
)2
2015/12/11
第五章 频率响应
19
自动控制理论 相频特性却不同,分别为:
28
自动控制理论 根据不同的ζ值，作出的乃氏图如图5-24所示。
图5-24 0 式（5-43）的奈氏图
2015/12/11 第五章 频率响应 29
自动控制理论
2 2 2 2 2 j ( ) 2)G ( j ) 1 2 j 2 (1 2 ) 4 e 2 n n n n
第五章 频率响应
图5-14 由式（5-26）给出的对数幅 频曲线、渐近线和相频曲线
精品课程《自动控制理论》ppt课件第一章 引论
2021/7/23
36
经典控制理论的体系
时域分析方法： •根据系统的传递函数判定系统的稳定性； •根据系统的传递函数分析和计算系统的稳 态误差；
•根据系统的传递函数分析和计算系统的暂 态性能；
•用系统的根轨迹分析稳定性、稳态误差和 暂态性能
2021/7/23
37
经典控制理论的体系
频域分析方法
•根据系统的传递函数得到系统频率特性表 达式； •根据系统的开环频率特性定性和定量地分 析闭环系统的稳定性；
2021/7/23
42
问题解答?
2021/7/23
3
本课程构中起到承上启下作用 •构建和设计自动控制系统的理论与方 法 •后续课程——计算机控制系统、运动 控制系统、过程控制系统等
2021/7/23
4
本课程所需基础知识
•高等数学中的微分方程 •拉普拉斯变换 •电路理论中相关知识 •模拟电子技术中的运算放大器 •物理学相关知识
2021/7/23
40
本章重点
基本了解
•自动控制理论发展概况 •自动控制系统的分类 重点理解
•开环控制和闭环控制的特点 •闭环控制系统的工作原理 •本课程的研究对象是闭环的单变量线性定常 系统 •本课程学习经典控制理论
2021/7/23
41
本章重点
牢固掌握 •闭环控制系统的典型框图、组成环节与主 要变量 •闭环控制系统的作用以及存在的问题 •闭环控制系统需要分析的三个方面——稳 定性、稳态性能、暂态性能
2021/7/23
7
手动控制与自动控制的比较
手动控制靠人的观测与操作
2021/7/23
8
自动控制系统自动检测水位与控制阀门
2021/7/23
自动控制原理习题详解1
自动控制原理习题详解（上册）配合《自动控制原理》夏超英主编，科学出版社。
第一章 习题解答1-1什么是开环控制系统？什么是闭环控制系统？比较开环控制系统和闭环控制系统的不同，说明各自的优缺点。
答：在开环控制系统中，信号从控制器到执行机构再到被控对象单方向传递，输出量不对控制作用产生影响。
开环控制系统结构简单，成本低，但无法克服被控对象变化和扰动对输出的影响。
在闭环控制系统中，被控对象的输出反方向被引到控制系统的输入端，信号沿前向通路和反馈通路闭路传输，控制量不仅与参考输入有关，还与输出有关，即根据参考输入和系统输出之间的偏差进行控制。
闭环控制系统需要对输出量进行测量，存在稳定性设计问题，较开环控制系统复杂，但可以有效地克服被控对象变化和扰动对输出的影响。
1-2日常生活中反馈无处不在。
人的眼、耳、鼻和各种感觉、触觉器官都是起反馈作用的器官。
试以驾车行驶和伸手取物过程为例，说明人的眼、脑在其中所起的反馈和控制作用。
答：在驾车行驶和伸手取物过程的过程中，人眼和人脑的作用分别如同控制系统中的测量反馈装置和控制器。
在车辆在行驶过程中，司机需要观察道路和行人情况的变化，经大脑处理后，不断对驾驶动作进行调整，才能安全地到达目的地。
同样，人在取物的过程中，需要根据观察到的人手和所取物体间相对位置的变化，调整手的动作姿势，最终拿到物体。
可以想象蒙上双眼取物的困难程度，即使物体的方位已知。
1-3 水箱水位控制系统的原理图如图1-12所示，图中浮子杠杆机构的设计使得水位达到设定高度时，电位器中间抽头的电压输出为零。
描述图1-12所示水位调节系统的工作原理，指出系统中的被控对象、输出量、执行机构、测量装置、给定装置等。
进水阀门进水图1-12 水箱水位控制系统原理图答：当实际水位和设定水位不相等时，电位器滑动端的电压不为零，假设实际水位比设定水位低，则电位器滑动端的电压大于零，误差信号大于零（0e >），经功率放大器放大后驱动电动机M 旋转，使进水阀门开度加大，当进水量大于出水量时（12Q Q >），水位开始上升，误差信号逐渐减小，直至实际水位与设定水位相等时，误差信号等于零，电机停止转动，此时，因为阀门开度仍较大，进水量大于出水量，水位会继续上升，导致实际水位比设定水位高，误差信号小于零，使电机反方向旋转，减小进水阀开度。