第三章习题解答
第三章习题解答

第三章习题解答一、判断下列说法是否正确,凡对的在括号内打“√”,否则打“×”。
(1)现测得两个共射放大电路空载时的电压放大倍数均为-100,将它们连成两级放大电路,其电压放大倍数应为10000。
( )(2)阻容耦合多级放大电路各级的Q点相互独立,( )它只能放大交流信号。
( )(3)直接耦合多级放大电路各级的Q点相互影响,( )它只能放大直流信号。
( )(4)只有直接耦合放大电路中晶休管的参数才随温度而变化。
( )(5)互补输出级应采用共集或共漏接法。
( )二、现有基本放大电路:A.共射电路B.共集电路C.共基电路D.共源电路E.共漏电路根据要求选择合适电路组成两级放大电路。
(1)要求输入电阻为1kΩ至2kΩ,电压放大倍数大于3000,第一级应采用,第二级应采用。
(2)要求输入电阻大于10MΩ,电压放大倍数大于300,第一级应采用,第二级应采用。
(3)要求输入电阻为100kΩ~200kΩ,电压放大倍数数值大于100,第一级应采用,第二级应采用。
(4)要求电压放大倍数的数值大于10,输入电阻大于10MΩ,输出电阻小于100Ω,第一级应采用,第二级应采用。
(5)设信号源为内阻很大的电压源,要求将输入电流转换成输出电压,且,输出电阻R o<100,第一级应采用,第二级应采用。
三、选择合适答案填入空内。
(1)直接耦合放大电路存在零点漂移的原因是。
A.电阻阻值有误差B.晶体管参数的分散性C.晶体管参数受温度影响D.电源电压不稳定(2)集成放大电路采用直接耦合方式的原因是。
A.便于设计B.放大交流信号C.不易制作大容量电容(3)选用差分放大电路的原因是。
A.克服温漂B. 提高输入电阻C.稳定放入倍数(4)差分放大电路的差模信号是两个输入端信号的,共模信号是两个输入端信号的。
A.差B.和C.平均值(5)用恒流源取代长尾式差分放大电路中的发射极电阻R e,将使电路的。
A.差模放大倍数数值增大B.抑制共模信号能力增强C.差模输入电阻增大(6)互补输出级采用共集形式是为了使。
第三章 信道与信道容量 习题解答

,
,求
,
,
和
;
(2) 求该信道的信道容量及其达到信道容量时的输入概率分布。
解:
(1)先写出
:
根据公式
计算联合概率:
信宿端符号分布概率:
根据公式
计算:
3
求各熵: 信源熵:
比特/消息
信宿熵:
比特/消息
可疑度:
平均互信息量: 噪声熵: (2)二元对称离散信道的信道容量:
比特/消息 比特/消息
比特/秒
信源等概分布时(
解:设下标 1为原状况,下标 2为改变后状况。由
可得:
,
倍
如果功率节省一半则
倍 ,为 了 使 功 率 节 省 一 半 又 不 损 失 信 息 量 I,根 据
,可以: (1) 加大信道带宽 W,用带宽换取信噪比
,
,
7
缺点是对设备要求高。 (2) 加大传输时间 T,用传输时间换取信噪比,同理可得:
缺点是传输速度降低了。
噪声熵:
(5)平均互信息量:
2.有一个生产 A、B、C、D四种消息的信源其出现的概率相等,通过某一通信系统传输时,B和 C无误,A 以 1/4概率传为 A,以 1/4概率误传为 B、C、D,而 D以 1/2概率正确传输,以 1/2概率误传为 C,
(1)试求其可疑度?(2)收到的信号中哪一个最可靠?(3)散布度为多少? 解:(1)
,
将各数据代入: 解得:
如果
则
将各数据代入: 解得:
14.在理想系统中,若信道带宽与消息带宽的比为 10,当接收机输入端功率信噪比分别为 0.1和 10时,试
比较输出端功率信噪比的改善程度,并说明
与
之间是否存在阀值效应。
第三章存储系统(习题解答)

第三章存储系统(习题解答)————————————————————————————————作者:————————————————————————————————日期:第三章存储系统(习题参考答案)1.有一个具有20位地址和32位字长的存储器,问:(1)该存储器能存储多少个字节的信息?(2)如果存储器由512K×8位SRAM芯片组成,需要多少芯片?(3)需要多少位地址作芯片选择?解:(1)∵ 220= 1M,∴ 该存储器能存储的信息为:1M×32/8=4MB (2)(1024K/512K)×(32/8)= 8(片)(3)需要1位地址作为芯片选择。
(选择两个512K×32位的存储体)2. 已知某64位机主存采用半导体存储器,其地址码为26位,若使用256K×16位的DRAM芯片组成该机所允许的最大主存空间,并选用模块板结构形式,问:(1)每个模块板为1024K×64位,共需几个模块板?(2)每个模块板内共有多少DRAM芯片?(3)主存共需多少DRAM芯片? CPU如何选择各模块板?解:(1)最大主存空间为:226×64位,每个模块板容量为:1024K×64位=220×64位设:共需模块板数为m:则:m=(226×64位)/(220×64位)= 64 (块)(2). 设每个模块板内有DRAM芯片数为n:n=(/) ×(64/16)=16 (片)(3) 主存共需DRAM芯片为:m×n = 64×16=1024 (片)每个模块板有16片DRAM芯片,容量为1024K×64位,需20根地址线(A19~A0)完成模块板内存储单元寻址。
一共有64块模块板,采用6根高位地址线(A25~A20),通过6:64译码器译码,产生片选信号对各模块板进行选择。
3.用16K×8位的DRAM芯片组成64K×32位存储器,要求:(1) 画出该存储器的组成逻辑框图。
第3章习题答案

思考题:题3.1.1 组合逻辑电路在结构上不存在输出到输入的 ,因此 状态不影响 状态。
答:反馈回路、输出、输入。
题3.1.2 组合逻辑电路分析是根据给定的逻辑电路图,而确定 。
组合逻辑电路设计是根据给定组合电路的文字描述,设计最简单或者最合理的 。
答:逻辑功能、逻辑电路。
题3.2.1 一组合电路输入信号的变化顺序有以下三种情况,当 时,将可能出现竞争冒险。
(A )00→01→11→10 (B )00→01→10→11 (C )00→10→11→01 答:B题3.2.2 清除竞争冒险的常用方法有(1)电路输出端加 ;(2)输入加 ;(3)增加 。
答:电容,选通脉冲,冗余项。
题3.2.3 门电路的延时时间是产生组合逻辑电路竞争与冒险的唯一原因。
( ) 答:×题3.2.4 根据毛刺产生的方向,组合逻辑的冒险可分为 冒险和 冒险。
答:1型、0型。
题3.2.5 传统的判别方法可采用 和 法来判断组合电路是否存在冒险。
答:代数法、卡诺图。
题3.3.1 进程行为之间执行顺序为 ,进程行为内部执行顺序为 。
答:同时、依次。
题3.3.2 行为描述的基本单元是 ,结构描述的基本单元是 。
答:进程、调用元件语句。
题3.3.3 结构体中的每条VHDL 语句的执行顺序与排列顺序 。
答:无关题3.4.1串行加法器进位信号采用 传递,而并行加法器的进位信号采用 传递。
(A )超前,逐位 (B )逐位,超前 (C )逐位,逐位 (D )超前,超前 答:B题3.4.2 一个有使能端的译码器作数据分配器时,将数据输入端信号连接在 。
答:使能端题 3.4.3 优先编码器输入为70I I -(0I 优先级别最高),输出为2F 、1F 、0F (2F 为高位)。
当使能输入00,651====I I I S 时,输出012F F F 应为 。
答:110题3.4.4 用4位二进制比较器7485实现20位二进制数并行比较,需要 片。
第三章习题解答

第3章 力学基本定律与守恒律 习题及答案1.作用在质量为10 kg 的物体上的力为i t F)210(+=N ,式中t 的单位是s ,(1)求4s 后,这物体的动量和速度的变化.(2)为了使这力的冲量为200 N ·s ,该力应在这物体上作用多久,试就一原来静止的物体和一个具有初速度j 6-m ·s -1的物体,回答这两个问题.解: (1)若物体原来静止,则i t i t t F p t 1401s m kg 56d )210(d -⋅⋅=+==∆⎰⎰,沿x 轴正向,ip I imp v111111s m kg 56s m 6.5--⋅⋅=∆=⋅=∆=∆ 若物体原来具有6-1s m -⋅初速,则⎰⎰+-=+-=-=t tt F v m t m F v m p v m p 000000d )d (,于是⎰∆==-=∆t p t F p p p 0102d,同理, 12v v ∆=∆,12I I=这说明,只要力函数不变,作用时间相同,则不管物体有无初动量,也不管初动量有多大,那么物体获得的动量的增量(亦即冲量)就一定相同,这就是动量定理. (2)同上理,两种情况中的作用时间相同,即⎰+=+=tt t t t I 0210d )210(亦即 0200102=-+t t 解得s 10=t ,(s 20='t 舍去)2.一颗子弹由枪口射出时速率为10s m -⋅v ,当子弹在枪筒内被加速时,它所受的合力为 F =(bt a -)N(b a ,为常数),其中t 以秒为单位:(1)假设子弹运行到枪口处合力刚好为零,试计算子弹走完枪筒全长所需时间;(2)求子弹所受的冲量.(3)求子弹的质量. 解: (1)由题意,子弹到枪口时,有0)(=-=bt a F ,得ba t =(2)子弹所受的冲量⎰-=-=tbt at t bt a I 0221d )(将bat =代入,得 ba I 22=(3)由动量定理可求得子弹的质量202bv a v I m == 3.如图所示,一质量为m 的球,在质量为M 半径为R 的1/4圆弧形滑槽中从静止滑下。
第三章 习题解答-2.0
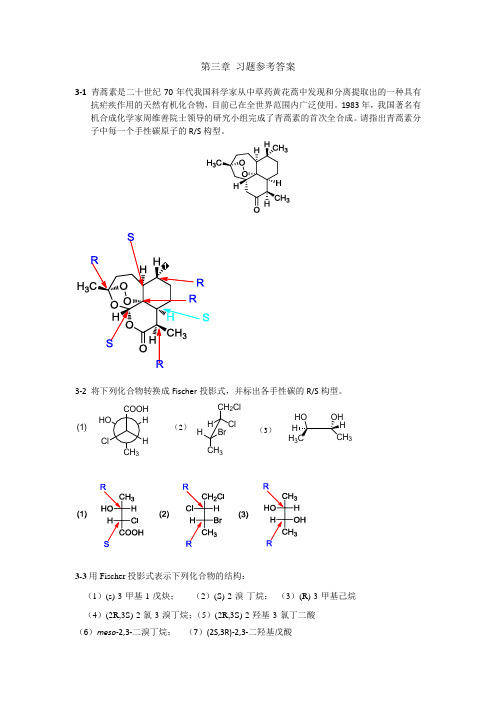
第三章 习题参考答案3-1 青蒿素是二十世纪70年代我国科学家从中草药黄花蒿中发现和分离提取出的一种具有抗疟疾作用的天然有机化合物,目前已在全世界范围内广泛使用。
1983年,我国著名有机合成化学家周维善院士领导的研究小组完成了青蒿素的首次全合成。
请指出青蒿素分子中每一个手性碳原子的R/S 构型。
3-2 将下列化合物转换成Fischer 投影式,并标出各手性碳的R/S 构型。
(2)(3)3BrHCH 3HClCH 2ClH 3H 3(1)3-3用Fischer 投影式表示下列化合物的结构:(1)(s)-3-甲基-1-戊炔; (2)(S)-2-溴-丁烷; (3)(R)-3-甲基己烷 (4)(2R,3S)-2-氯-3-溴丁烷;(5)(2R,3S)-2-羟基-3-氯丁二酸 (6)meso -2,3-二溴丁烷; (7)(2S,3R)-2,3-二羟基戊酸本题答案不唯一。
在画Fisher投影式时,习惯把含碳原子的基团放在竖键上,并把命名时编号最小的碳原子放在上端。
以下是较为符合习惯的Fisher投影式。
3-4下列化合物中哪些有手性?(1)、(3)、(5)、(7)、(9)无手性(2)、(4)、(6、)(8)、(10)有手性3-5长尾粉蚧壳虫信息素A是雌性长尾粉蚧壳虫(一种植物害虫)分泌的性激素,其外消旋体目前已被人工合成,并商业化用于农田害虫的控制和诱杀。
最近,化学家通过全合成途径确定了天然长尾粉蚧壳虫信息素的绝对构型(J. Org. Chem. 2013, 78, 6281−6284)。
通过全合成方法分别得到了A的2种立体异构体,发现其中的(S)-(+)-异构体具有吸引雄性长尾粉蚧壳虫的活性,而它的对映体(R)-( )-A则无此生物活性。
此结果表明雌性长尾粉蚧壳虫分泌的天然长尾粉蚧壳虫信息素为(S)-A。
商业化使用的外消旋体与纯的(S)-对映体生物活性相似,说明(R)-A对(S)-A的生物活性无抑制作用。
写出(R)-A和(S)-A的结构式。
第三章部分习题解答
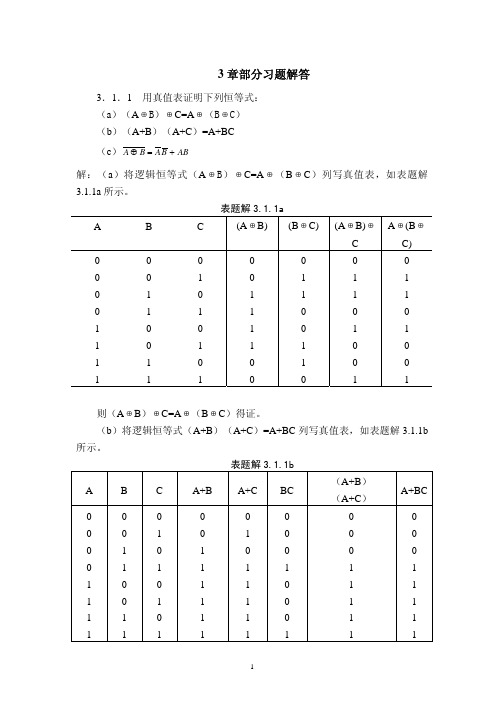
(b) ( A + B)(AB ) = AAB + BAB = AB
(c) ABC(B + C ) = ( A + B + C )(B + C ) = C + B( A + B ) = C + AB
(d) A + ABC + ABC + CB + CB = A(1 + BC + BC) + C(B + B ) = A + C
L3 = A3 ⊕ C
可分别用异或门、三态门设计逻辑电路,如图题解 3.4.4a、b 所示。
图题解 3.4.4
7
3.4.7 某雷达站有 3 部雷达 A、B、C,其中 A 和 B 功率消耗相等,C 的 功率是 A 的两倍。这些雷达由两台发电机 X 和 Y 供电,发电机 X 的最大输出功 率等于雷达 A 的功率消耗,发电机 Y 的最大输出功率是 X 的 3 倍。要求设计一 个逻辑电路,能够根据各雷达的启动和关闭信号,以最节约电能的方式启、停 发电机。
X = ABC + ABC + ABC + ABC = AB ⊕ C + B A ⊕ C
Y =AB+C 由逻辑表达式可设计出最节约电能的发电机启、停方式的逻辑电路,如图 题解 3.4.7b 所示。
表题解 3.4.7
A
B
C
X
Y
0
0
0
0
0
0
0
1
0
1
0
1
0
1
0
0
1
1
0
1
1
0
0
1
0
第三章 习题答案

第三章 消费者行为理论2. 假设某消费者的均衡如图3—1(即教材中第96页的图3—22)所示。
其中,横轴OX 1和纵轴OX 2分别表示商品1和商品2的数量,线段AB 为消费者的预算线,曲线图3—1 某消费者的均衡U 为消费者的无差异曲线,E 点为效用最大化的均衡点。
已知商品1的价格P 1=2元。
(1)求消费者的收入;(2)求商品2的价格P 2;(3)写出预算线方程;(4)求预算线的斜率;(5)求E 点的MRS 12的值。
解答:(1)图中的横截距表示消费者的收入全部购买商品1的数量为30单位,且已知P 1=2元,所以,消费者的收入M =2元×30=60元。
(2)图中的纵截距表示消费者的收入全部购买商品2的数量为20单位,且由(1)已知收入M =60元,所以,商品2的价格P 2=M 20=6020=3元。
(3)由于预算线方程的一般形式为 P 1X 1+P 2X 2=M 所以,由(1)、(2)可将预算线方程具体写为:2X 1+3X 2=60。
(4)将(3)中的预算线方程进一步整理为X 2=-23X 1+20。
很清楚,预算线的斜率为-23。
(5)在消费者效用最大化的均衡点E 上,有MRS 12=P 1P 2,即无差异曲线斜率的绝对值即MRS 等于预算线斜率的绝对值P 1P 2。
因此,MRS 12=P 1P 2=23。
5. 已知某消费者每年用于商品1和商品2的收入为540元,两商品的价格分别为P 1=20元和P 2=30元,该消费者的效用函数为U =3X 1X 22,该消费者每年购买这两种商品的数量应各是多少?每年从中获得的总效用是多少?解答:根据消费者的效用最大化的均衡条件MU 1MU 2=P 1P 2其中,由U =3X 1X 22可得 MU 1=d TU d X 1=3X 22; MU 2=d TU d X 2=6X 1X 2 于是,有 3X 226X 1X 2=2030 整理得 X 2=43X 1 (1) 将式(1)代入预算约束条件20X 1+30X 2=540,得20X 1+30·43X 1=540 解得 X 1=9 将X 1=9代入式(1)得 X 2=12因此,该消费者每年购买这两种商品的数量应该为X 1=9 ;X 2=12。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题三3.1一质量为M ,边长为L 的等边三角形薄板,求绕垂直于薄板平面并通过其顶点的转轴的转动惯量。
解:三角形的顶点与质心的距离为L 33,设所求转动惯量为0I ,垂直于薄板平面并通过其质心的转轴的转动惯量为1I ,利用平行轴定理,21031ML I I +=。
取直角坐标系原点位于转轴与边的交点,三角形的一个顶点位于L y x 33,0==处,等边三角形薄板的面密度为243LM ,则()()()⎰⎰⎰⎰⎰⎰+=+=+=sssdxdyyxLM dS LM yxdm yxI 22222222133443由于该积分区域是对y 轴对称的,y 积分区间从63-到33+,x 的积分区间从313-y 到331y-(单位均为L )。
将上述积分化为321I I I +=,其中,⎰⎰=sdxdy x LM I 222334 ,⎰⎰=sdxdy y LM I 223334⎰⎰---⋅=33131323363422334yy dx x dy LLM I (4L 是由于积分号内的单位L 被提出)⎰-⎪⎪⎭⎫⎝⎛-=33633233132334dy y ML()⎰--⋅⋅=3363323127132334dy yML 令y t 31-=⎰-⋅=23323324338dt t ML2241ML =⎰⎰---⋅=33131323363423334yy dx y dy LLM I⎰-⎪⎪⎭⎫ ⎝⎛-=3363223312334dy y y ML2241ML =所以:2232012531ML MLI I I =++=解2:在薄板平面内取直角坐标系,原点即为通过转轴的三角形顶点,另两个顶点分别位于⎪⎪⎭⎫ ⎝⎛23,21,⎪⎪⎭⎫ ⎝⎛-23,21则 ()()()⎰⎰⎰⎰⎰⎰+=+=+=sssdxdyyxLM dS LM yxdm yxI 2222222233443而由于该积分区域是对y 轴对称的,y 积分区间从0到23,x 的积分区间从33y -到33y +(单位均为L )。
将上述积分化为()⎰⎰-+⋅=3333222342334yy dx yxdy LLM⎰⋅=2334227320334dy y LLM2125ML =3.2一质量为M 、半径为R 的均匀球体,求对于通过球心转轴的转动惯量。
解:⎰⎰⎰⎰⎰⎰====RVVVdr r d d d drd r r dV r dm r I 04202222sin sin ρθθϕϕθθρρππ将343RM =ρ代入上式,即得252MR I =3.3一个轮子装在固定轴上,整个系统无摩擦地自由转动。
一条质量可忽略的带子缠绕在轴上,并以已知恒定的力F 拉之,以测定轮轴系统的转动惯量。
当带子松开的长度为L 时,系统转动的角速度为0ω,求系统的转动惯量I 。
解:外力做功为FL ,带子松开的长度为L 时,系统动能为221ωI ,所以22ωFLI =3.4质量为m 长为l 的均质杆,其B 端水平的放在桌上,A 端用手支住,问在突然撒手的瞬时,(1)绕B 点的力矩和角加速度各是多少? (2)杆的质心加速度是多少?解:(1)绕B 点的力矩τ由重力产生,设杆的线密度为ρ,lm =ρ,则绕B 点的力矩为m g l dx gx gxdm xdG lmmg210====⎰⎰⎰ρτ杆绕B 点的转动惯量为 22231ml dx x dm x I lm===⎰⎰ρ角加速度为lgI23==τβ(2)杆的质心加速度为 g l a 432==β3.6 飞轮的质量为60kg ,直径为0.50m ,转速为1000r/min ,现要求在5s 内使其制动,求制动力F 。
假定闸瓦与飞轮之间的摩擦系数μ=0.4,飞轮的质量全部分布在轮的外周上。
尺寸如图所示。
解:设在飞轮接触点上所需要的压力为F ', 由 dt dL =τ 本题中,摩擦力力矩不变为2d F 'μ ,角动量由2d mv变化到0,所以222d d m t d F ⋅='ωμ解得牛4.7852=='td m F μω牛2.31425.15.0='=F F3.7 如图所示,两物体1和2的质量分别为m 1与m 2,滑轮的转动惯量为J ,半径为r 。
⑴如物体2与桌面间的摩擦系数为μ,求系统的加速度a 及绳中的张力T 1与T 2(设绳子与滑轮间无相对滑动);⑵如物体2与桌面间为光滑接触,求系统的加速度a 及绳中的张力T 1与T 2。
解:⑴先做受力分析,物体1受到重力g m 1和绳的张力1T ,对于滑轮,受到张力1T 和2T ,对于物体2,在水平方向上受到摩擦力g m 2μ和张力2T ,分别列出方程 a m T g m 111=- (()a g m T -=11) a m g m T 222=-μ (()g a m T μ+=22)()ra JJ r T T ===-βτ21通过上面三个方程,可分别解出三个未知量()()Jr m m gr m m a ++-=221221μ ()()Jr m m Jg g r m m T ++++=22122111μ()()Jr m m Jgg r m m T ++++=22121221μμ ⑵ 在⑴的解答中,取0=μ即得()Jrm m grm a ++=22121()Jr m m Jgg r m m T +++=2212211()Jr m m gr m m T ++=22122123.8 电动机带动一个转动惯量为J=50k g ·m 2的系统作定轴转动。
在0.5s 内由静止开始最后达到120r/min 的转速。
假定在这一过程中转速是均匀增加的,求电动机对转动系统施 加的力矩。
解:由于转速是均匀增加的,所以角加速度β为 2/8min/605.0/2min /120s rad s s r rad r tππωβ=⨯⨯=∆∆=从而力矩为22310257.1850-⨯=⨯==skgm J πβτ3.9 求题3.6中制动力矩在制动过程中所作的功。
解:制动力矩在制动过程中所作的功等于系统动能的变化 J rm W 4221006.221⨯-=-=ω本题也可以先求出摩擦力做功的距离以及摩擦力的大小来求解。
3.10 一飞轮直径为0.30m ,质量为5.00kg ,边缘绕有绳子,现用恒力拉绳子的一端,使其由静止均匀的加速,经0.50s 转速达到10r/s 。
假定飞轮可看作实心圆柱体,求:⑴飞轮的角加速度及在这段时间内转过的转数; ⑵拉力及拉力所作的功;⑶从拉动后t=10s 时飞轮的角速度及轮边缘上一点的速度和加速度。
解:⑴ 飞轮的角加速度为2/7.1255.0/2/10s r a d sr r a d s r t=⨯=∆∆=πωβ 转过的圈数为 r s s r n 5.25.0/1021=⨯⨯=⑵ 飞轮的转动惯量为 221mr I =所以,拉力的大小为 牛1.477.12523.052121=⨯⨯⨯====ββτmr rI rF拉力做功为J d n F FS W 1113.014.35.21.47=⨯⨯⨯=⨯==π⑶从拉动后t=10s 时飞轮角速度为s r a d t /10257.1107.1253⨯=⨯='='βω 轮边缘上一点的速度为s m r v /18815.010257.13=⨯⨯='='ω 轮边缘上一点的加速度为2/8.1815.07.125s m r a =⨯==β3.11 弹簧、定滑轮和物体的连接如题3.11图所示,弹簧的劲度系数为2.0N m -1;定滑轮的转动惯量是0.5kg m 2,半径为0.30m ,问当6.0kg 质量的物体落下0.40m 时,它的速率为多大?假设开始时物体静止而弹簧无伸长。
解:当物体落下0.40m 时,物体减少的势能转化为弹簧的势能、物体的动能和滑轮的动能, 即 222222121rIv mvkh mgh ++=,将kg m 6=,2/8.9s kgm g =,m h 4.0=,25.0kgm I =,m r 3.0=代入,得 s m v /01.2=3.12 一均匀铅球从高为h ,与水平面夹角为α的固定斜面顶上由静止无滑动的滚下,求滚到底端时球心的速度。
试用下述几种方法求解:(1)转动定理,以球和斜面的接触点为瞬时转轴;(2)质心运动定理;(3)机械能守恒定律;(4)角动量定理。
3.13 质量为m 、半径为R 的自行车轮,假定质量均匀分布在轮缘上,可绕轴自由转动。
另一质量为m 0的子弹以速度v 0射入轮缘(如题2-31图所示方向)。
(1)开始时轮是静止的,在质点打入后的角速度为何值?(2)用m,m 0和θ表示系统(包括轮和质点)最后动能和初始动能之比。
3.14 在自由旋转的水平圆盘上,站一质量为m 的人。
圆盘的半径为R ,转动惯量为J ,角速度为ω。
如果这人由盘边走到盘心,求角速度的变化及此系统动能的变化。
解:系统的角动量在整个过程中保持不变,人在盘边时,角动量为 ()ωω2mR J I L +==人走到盘心时ωω'=''=J I L因此,()ωωJmR J 2+='人在盘边和在盘心时,系统动能分别为22212121ωωJ Rm W +=()222222121ωωJmR J J W +='=系统动能增加 24222122121ωωJR m R m W W W +=-=∆3.15 在半径为R 1,质量为m 的静止水平圆盘上,站一质量为m 的人。
圆盘可无摩擦地绕通过圆盘中心的竖直轴转动。
当这人开始沿着与圆盘同心,半径为R 2(< R 1)的圆周匀速地走动时,设他相对于圆盘的速度为v ,问圆盘将以多大的角速度旋转?解:整个体系的角动量保持为零,设人匀速地走动时圆盘的角速度为ω,则 ()0212122=--=+=ωωmR R R v m L L L 盘人解得 v RR R 2221222+-=ω3.16 如题3.16图示,转台绕中心竖直轴以角速度ω0作匀速转动。
转台对该轴的转动惯量J=5×10-5 kg·m 2。
现有砂粒以1g/s 的速度落到转台,并粘在台面形成一半径r=0.1m 的圆。
试求砂粒落到转台,使转台角速度变为021ω所花的时间。
解:要使转台角速度变为021ω,由于砂粒落下时不能改变体系角动量,所以必须要使体系的转动惯量加倍才行,即 J r m =2沙粒 将25105m kg J ⋅⨯=-和m r 1.0=代入得kg m 3105-⨯=沙粒所以 s sg kgt 5/11053=⨯=-3.17 一质子从远处射向一带电量为Z e 的重核,但没有瞄准,偏离了一个距离b (b 叫做散射参量),如习题3.17图所示。
