带通滤波器电路及参数的确定.
带通滤波器的设计和实现

带通滤波器的设计和实现随着科技的不断发展和应用场景的不断拓宽,信号处理在各个领域中扮演着重要的角色。
而滤波器作为信号处理的重要组成部分,其设计和实现对于信号处理的效果起到至关重要的作用。
本文将详细介绍带通滤波器的设计原理和实现方法。
一、带通滤波器的基本概念带通滤波器是一种对信号进行频率选择的滤波器,它能够将某一频率范围内的信号通过,而将其他频率范围内的信号抑制或削弱。
在信号处理中,常常需要对特定频率范围的信号进行提取或滤除,此时带通滤波器的应用便显得尤为重要。
二、带通滤波器的设计原理1. 滤波器的传输函数滤波器的传输函数是描述滤波器输入和输出之间关系的数学表达式。
带通滤波器的传输函数通常采用有理函数形式,例如巴特沃斯、切比雪夫等形式。
2. 频率响应带通滤波器的频率响应描述了滤波器对不同频率信号的处理效果。
通常采用幅度响应和相位响应两个参数来描述频率响应。
3. 滤波器的阶数滤波器的阶数表示滤波器的复杂程度,阶数越高,滤波器的频率选择性越强。
根据实际需求和应用场景,选择合适的滤波器阶数非常重要。
三、带通滤波器的实现方法1. 模拟滤波器的实现模拟滤波器是指基于传统电子电路的滤波器实现方法。
常见的模拟滤波器包括RC滤波器、RL滤波器、LC滤波器等。
模拟滤波器的设计需要考虑电路参数和元器件选择等因素,涉及到模拟电路设计的相关知识。
2. 数字滤波器的实现数字滤波器是指利用数字信号处理技术实现的滤波器。
常见的数字滤波器包括FIR滤波器、IIR滤波器等。
数字滤波器的实现采用离散系统的理论分析和数字信号处理算法的设计,需要掌握相关的数学知识和算法掌握。
四、带通滤波器的应用案例带通滤波器在实际应用中有着广泛的应用场景。
例如,在音频处理中,可以利用带通滤波器实现音乐频谱的提取和信号的降噪;在图像处理中,可以利用带通滤波器进行图像边缘检测和图像增强等处理;在通信系统中,带通滤波器可以用于信号调制和解调等关键环节。
五、总结本文对带通滤波器的设计原理和实现方法进行了详细介绍,并给出了相关的应用案例。
1到30赫兹的带通滤波器-概述说明以及解释

1到30赫兹的带通滤波器-概述说明以及解释1.引言1.1 概述在撰写本文中,我们将重点介绍1到30赫兹的带通滤波器。
带通滤波器是一种常见的电子滤波器,用于选择特定范围内的频率信号。
在本文中,我们将探讨其概念、工作原理和应用。
带通滤波器的基本原理是通过阻止或放行特定频率范围内的信号来实现滤波效果。
比如在1到30赫兹的频率范围内,滤波器可以过滤掉低于1赫兹和高于30赫兹的信号,只保留在这个范围内的信号。
这就使得滤波器非常适用于许多应用,如声音处理、通信系统和医学设备等。
带通滤波器通常由一个低通滤波器和一个高通滤波器级联而成。
低通滤波器可以将低于截止频率的信号通过,而高通滤波器可以将高于截止频率的信号通过。
当这两个滤波器结合在一起时,就形成了一个带通滤波器。
带通滤波器在各个领域都有广泛的应用。
在音频处理中,它可以用于消除噪音,提升音频质量。
在通信系统中,带通滤波器可以用来选择特定频段的信号,以便传输和接收。
在医学设备中,它可以用于识别和分析特定频率范围内的生物信号,如心电图和脑电图等。
综上所述,本文将详细介绍1到30赫兹的带通滤波器的概念、工作原理和应用。
通过阅读本文,读者将能够更好地理解带通滤波器的作用和重要性,并在相关领域中应用其知识。
接下来的章节将进一步探讨带通滤波器的细节和实际应用案例。
1.2文章结构1.2 文章结构本文将按照以下结构进行阐述:2.1 赫兹与频率的关系首先,我们将介绍赫兹与频率之间的关系。
赫兹是表示每秒周期性事件发生次数的单位,常用于描述声波、电磁波等波动现象的频率。
频率则是指每单位时间内所发生的周期性事件的次数,通常以赫兹为单位进行衡量。
我们将详细探讨赫兹与频率之间的转换关系,以便读者能够更好地理解本文涉及到的带通滤波器的工作原理。
2.2 带通滤波器的定义与原理在这一部分,我们将详细介绍带通滤波器的定义和原理。
带通滤波器是一种能够通过特定频率范围内的信号,而削弱或排除其他频率范围内的信号的设备。
带通滤波器设计 (2)

带通滤波器设计1. 引言在信号处理中,滤波器是一种重要的工具,用于去除或改变信号的特定频率成分。
带通滤波器是一种常用的滤波器,它可以传递一定范围内的频率成分,而抑制其他频率成分。
本文将介绍带通滤波器的基本原理和设计方法。
2. 带通滤波器的原理带通滤波器是一种频率选择性滤波器,它可以传递一定范围内的频率信号,而将其他频率信号抑制。
其基本原理是利用滤波器的频率响应特性,对输入信号进行滤波处理。
带通滤波器通常由一个低通滤波器和一个高通滤波器级联连接而成。
低通滤波器用于抑制高于截止频率的频率成分,而高通滤波器用于抑制低于截止频率的频率成分,从而实现带通滤波效果。
3. 带通滤波器的设计方法带通滤波器的设计通常包括以下几个步骤:在设计带通滤波器之前,需要确定滤波器的一些规格参数,包括中心频率、通带宽度、阻带宽度等。
这些参数决定了滤波器的性能和应用范围。
步骤二:选择滤波器的类型常见的带通滤波器类型包括巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器等。
根据具体的应用要求和设计指标,选择适合的滤波器类型。
步骤三:计算滤波器的阶数滤波器的阶数决定了滤波器的陡峭程度和相频特性。
根据设计要求和滤波器类型,计算滤波器的阶数。
步骤四:确定滤波器的传输函数根据滤波器的类型和阶数,使用滤波器设计方法计算滤波器的传输函数。
常用的设计方法包括频率折叠法、零极点法等。
根据滤波器的传输函数,采用模拟滤波器的设计方法,设计滤波器的电路结构和参数。
常用的设计方法包括电压法、电流法等。
步骤六:数字滤波器的设计对于数字信号处理系统,需要将模拟滤波器转换为数字滤波器。
常用的设计方法包括脉冲响应法、频率采样法等。
根据系统的采样率和滤波器的性能要求设计数字滤波器。
4. 带通滤波器的应用带通滤波器在信号处理领域有着广泛的应用。
例如,音频处理中常用带通滤波器对音频信号进行频率选择性处理,去除噪声和杂音。
图像处理中常用带通滤波器对图像进行频率域滤波,增强或抑制特定频率成分,实现图像增强、去噪等功能。
带通滤波器毕业设计

带通滤波器毕业设计带通滤波器毕业设计引言:在现代电子技术的发展中,滤波器是一种非常重要的电子元件。
它可以对信号进行处理,去除杂波和干扰,从而提高信号的质量。
而在电子工程师的毕业设计中,设计一个带通滤波器是一项常见的任务。
本文将介绍带通滤波器的原理、设计方法以及实际应用。
一、带通滤波器的原理带通滤波器是一种能够通过一定频率范围内的信号,而削弱其他频率信号的电子元件。
其原理是利用电容、电感和电阻等元件的组合,形成一个能够选择性地通过一定频率范围内信号的电路。
带通滤波器可以分为主动滤波器和被动滤波器两种类型。
主动滤波器采用了运算放大器等主动元件,能够提供放大和反馈功能,从而实现更精确的频率选择。
被动滤波器则只采用了电容、电感和电阻等被动元件,其频率响应相对较简单。
二、带通滤波器的设计方法1. 确定设计要求:在设计带通滤波器时,首先需要明确设计要求,包括通带范围、阻带范围、通带衰减和阻带衰减等参数。
这些参数将决定滤波器的性能和适用场景。
2. 选择滤波器类型:根据设计要求,选择适合的滤波器类型。
常见的带通滤波器类型有Butterworth滤波器、Chebyshev滤波器和Elliptic滤波器等。
它们在通带和阻带的衰减特性、相位响应等方面有所不同,因此需要根据具体需求进行选择。
3. 计算元件数值:根据选择的滤波器类型和设计要求,计算滤波器中各个元件的数值。
这包括电容、电感和电阻等元件的数值选择,以及元件的连接方式和拓扑结构。
4. 仿真和优化:通过电子设计自动化软件,进行滤波器的仿真和优化。
根据仿真结果,对滤波器的性能进行评估和调整,以达到设计要求。
5. 实际制作和测试:根据设计结果,制作实际的滤波器电路,并进行测试和验证。
测试结果将反馈给设计者,以便对设计进行进一步改进和优化。
三、带通滤波器的应用带通滤波器在电子领域有着广泛的应用。
以下是几个常见的应用场景:1. 语音信号处理:在通信系统中,带通滤波器可以用于去除语音信号中的噪声和杂音,提高通信质量。
带通滤波器的设计报告

带通滤波器的设计报告1.引言带通滤波器是一种电子电路,用于通过一定频率范围内的信号,而抑制超过该范围的信号。
在很多应用中,带通滤波器被用于选择或加强特定频率范围的信号,从而起到信号处理和频率分析的作用。
本报告将介绍带通滤波器的设计原理和步骤,并通过实际设计一个示例电路,进一步说明带通滤波器的应用和效果。
2.带通滤波器的基本原理带通滤波器通过将一个中心频率附近一定范围内的频率信号传递,而阻止低于和高于该频率范围的信号。
常见的带通滤波器包括:无源滤波器(如LC滤波器)、有源滤波器(如运算放大器滤波器)和数字滤波器(如数字信号处理器滤波器)等。
本报告将重点介绍一种常用的无源滤波器,即LC带通滤波器。
3.带通滤波器的设计步骤(1)确定中心频率和通带宽度:根据实际需求确定所需传递的频率范围,确定带通滤波器的中心频率和通带宽度。
例如,选择中心频率为10kHz,通带宽度为2kHz。
(2)计算所需的滤波器元件数值:根据所选中心频率和通带宽度的数值,结合滤波器设计公式,计算所需的电感(L)和电容(C)数值。
以LC带通滤波器为例,计算出所需电感和电容的数值。
(3)电路设计和模拟:根据计算结果,设计一个示例电路,并进行模拟分析和调试,以确认设计的有效性和滤波器的性能。
(4)电路实现和测试:根据设计的电路图,选择合适的元件进行实现,并进行测试,以验证实际效果和满足设计要求。
4.示例电路设计在本示例中,选择中心频率为10kHz,通带宽度为2kHz的带通滤波器。
根据计算结果,选择电感1mH和电容39nF。
示例电路图如下:```_______L_______Vin --- R1 --- C1_____L___________C_____R2_______L_______GND---R3---C2_____L_____GND```5.模拟分析和调试通过使用电路模拟软件,对示例电路进行分析和调试。
根据实际测试要求,选择合适的信号源输入和测量设备,并对电路的频率响应和增益进行分析和调整,以确保实际满足设计要求。
二阶有源带通滤波器设计及参数计算

之阳早格格创做滤波器是一种只传输指定频段旗号,压造其余频段旗号的电路.滤波器分为无源滤波器与有源滤波器二种:①无源滤波器:由电感L、电容C及电阻R等无源元件组成②有源滤波器:普遍由集成运搁与RC搜集形成,它具备体积小、本能宁静等便宜,共时,由于集成运搁的删益战输进阻抗皆很下,输出阻抗很矮,故有源滤波器还兼有搁大与慢冲效率. 利用有源滤波器不妨超过有用频次的旗号,衰减无用频次的旗号,压造搞扰战噪声,以达到普及疑噪比或者选频的手段,果而有源滤波器被广大应用于通疑、丈量及统造技能中的小旗号处理.从功能去上有源滤波器分为:矮通滤波器(LPF)、下通滤波器(HPF)、戴通滤波器(BPF)、戴阻滤波器(BEF)、齐通滤波器(APF).其中前四种滤波器间互有通联,LPF与HPF间互为对于奇闭系.当LPF的通戴截行频次下于HPF的通戴截行频次时,将LPF与HPF相串联,便形成了BPF,而LPF与HPF并联,便形成BEF.正在真用电子电路中,还大概共时采与几种分歧型式的滤波电路.滤波电路的主要本能指标有通戴电压搁大倍数AVP、通戴截行频次fP及阻僧系数Q等.戴通滤波器(BPF)(a)电路图(b)幅频个性图1 压控电压源二阶戴通滤波器处事本理:那种滤波器的效率是只允许正在某一个通频戴范畴内的旗号通过,而比通频戴下限频次矮战比上限频次下的旗号均加以衰减或者压造.典型的戴通滤波器不妨从二阶矮通滤波器中将其中一级改成下通而成.如图1(a)所示. 电路本能参数通戴删益核心频次通戴宽度采用性此电路的便宜是改变Rf战R4的比率便可改变频宽而没有效率核心频次.例.央供安排一个有源二阶戴通滤波器,指标央供为:通戴核心频次通戴核心频次处的电压搁大倍数:戴宽:安排步调:1)采用图2电路.2)该电路的传输函数:本量果数:通戴的核心角频次:通戴核心角频次处的电压搁大倍数:与,则:图2 无限删益多路背反馈有源二阶戴通滤波器电路。
带通滤波器分析
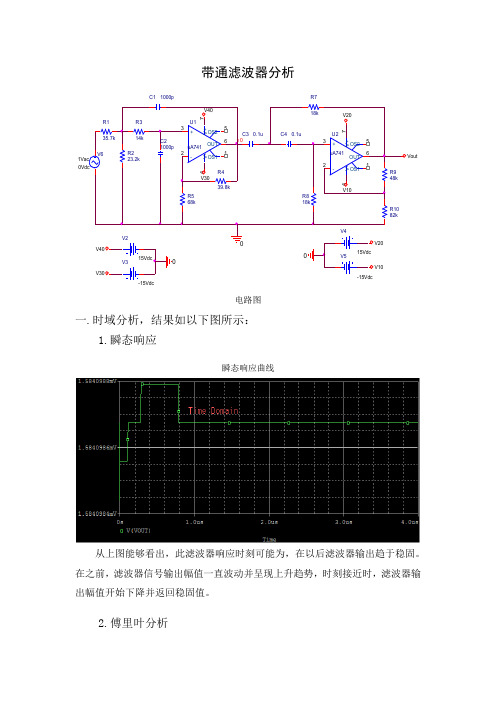
带通滤波器分析U2uA7413274615+-V+V-OUTOS1OS2V10R223.2kU1uA7413274615+-V+V-OUTOS1OS2V20R818kV215VdcR718kR439.8kV20R568kC40.1uVoutV415VdcV10R314k v0V30V40R948k V61Vac0VdcV5-15VdcC30.1uR135.7kC21000pR1082k V40V30C11000pV3电路图一.时域分析,结果如以下图所示:1.瞬态响应瞬态响应曲线从上图能够看出,此滤波器响应时刻可能为,在以后滤波器输出趋于稳固。
在之前,滤波器信号输出幅值一直波动并呈现上升趋势,时刻接近时,滤波器输出幅值开始下降并返回稳固值。
2.傅里叶分析参数设置如以下图,计算直流分量和从基波一直到九次谐波。
傅里叶分析结果如下:FOURIER COMPONENTS OF TRANSIENT RESPONSE V(VOUT)DC COMPONENT =HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZED NO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG)1 +01 +00 +01 +002 +02 +00 +01 +013 +02 +00 +01 +024 +02 +00 +01 +025 +02 +00 +01 +026 +02 +00 +01 +027 +02 +00 +01 +028 +02 +00 +01 +029 +02 +00 +01 +02TOTAL HARMONIC DISTORTION = +02 PERCENT由以上数据能够得出瞬态响应各次谐波的分量。
二.频域分析幅频特性相频特性由上图能够得出结论,此电路为带通滤波器,通带频率范围可能为100-10kHz。
由于鼓励信号的幅值为1,因此频率响应的幅值即为电压放大倍数,从图中能够看出,滤波器最大电压放大倍数为1,因此信号通过滤波器时,能够以原先的幅值正常的通过。
有源带通滤波器设计

有源带通滤波器设计
一、有源带通滤波器的基本原理
有源带通滤波器的核心是带通滤波器电路。
带通滤波器电路通常由一
个放大器、一个带通滤波器和一个反馈电路组成。
其中,放大器的作用是
增大输入信号的幅度,带通滤波器的作用是选择特定频率范围内的信号,
反馈电路的作用是将放大的信号重新引入放大器,从而实现对特定频率范
围内信号的放大。
二、有源带通滤波器的设计步骤
1.确定设计的频率范围:根据应用需求确定要选择和放大的频率范围。
2.选择放大器:根据信号的幅度要求选择适合的放大器。
常见的放大
器有运放放大器和晶体管放大器等。
3.设计带通滤波器:根据所选频率范围设计带通滤波器。
带通滤波器
可以采用主动滤波器或者被动滤波器。
主动滤波器采用放大器进行放大,
能够提高滤波器的增益和选择性。
4.设计反馈电路:设计反馈电路将放大的信号重新引入放大器,从而
实现对特定频率范围内信号的放大。
反馈电路的设计要考虑放大器的放大
倍数、输入和输出阻抗等因素。
5.验证设计:通过仿真或实际电路验证设计的性能和参数。
6.优化设计:根据测试结果,优化电路设计,提高性能和可靠性。
三、有源带通滤波器的应用
1.音频放大器:有源带通滤波器可以选择特定频率范围内的音频信号并放大,用于音频放大器的设计。
2.语音处理:有源带通滤波器可以用于语音的去噪、降噪和增强等处理。
3.通信系统:有源带通滤波器可以筛选特定频率范围内的信号,提高通信系统的性能。
4.仪器测量:有源带通滤波器可以用于仪器测量中,选择特定频率范围内的信号并放大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
范道中学七年级数学导学提纲课题:幂的乘方
出卷人:施培新审核人:陈益锋
2012-2-22 姓名
_____
课前参与
(一)预习内容:课本P43—44
(二)知识整理:
1.探索:
(1)(2)是幂2的_____次方,其意义是_____个2的连乘积,
可写成:(2)=2×2=2= 2=2。
(2)(a)是幂a的_____次方,其意义是____个a的连乘积,
可写成:(a)=()×()×()= a= a=
a;
由此得:(a)是幂a的______次方,其意义是______个a的连乘积,
可写成:(a)=()=a=a。
2.归纳:幂的乘方的法则:__________________________________________;
即写成公式:
(a)=a(m、n为正整数)。
3.尝试练习:
(1)(10)= (5)(-5)=
(2)(10)= (6)(-5)=
(3)(b)= (7 [(n-m)]
5
(4)(b)= (8 a·(a)2+ a·(a)3
4.推广:[(a m )n ]p =____________ (m 、n 、p 为正整数。
5.幂的乘方法则的逆用为___________________________。
(三)思考:
通过预习,你认为本节内容主要研究了什么?你还有什么问题需和大家一起探讨?你有没有新的发现和大家一起分享!
课中参与
例题1、计算:(1)(55)3 (2)(53)5
(3)(3x 5 (4)(35 x
例题2、计算:(1)[(a -b )] (2)[(x -y )]
例题3、计算:(1)-(y 4)3 (2)[(-y )4]3 (3)(-y 4)3
例题4、计算:(1)(a )·a (2)(b )·(b )
(3)a ·(a )-a ·(a )2
拓展:1、(1)[(2)] (2)[(-3)]
2、已知3=2,3y =3,求(1)33x ,3
2y 的值。
(2)求3的值.
3、已知:3=a ,3=b ,用含a 、b 的代数式表示3。
课后参与 课题:幂的乘方 姓名_____
一、填空:
(1)(7)5=_________; (2)[(-22]3=_________;
(3) (a )
=________; (4)(-a 5)3=_________;
(5)[(a -2)]=________; (6)[(x -y )]=______;
(7)(-m 3)2 ·(-m 4)3=_______;(8)(b 2m )3 ·(b m+1)2=____;
(9)3. 若(a 3)n =(a n )m
(m ,n 都是正整数),则m =_________
二、选择:
1、下列计算中,正确的个数有------------------------( )
a m a 2=a 2m ; (a 3)2=a 5; (-x 2)3=x 6; (-a 3)2 ·a 4= a 10. A .1个 B .2个 C .3个 D .4个
2、下列计算:①(a )= a ;②(a ) = a ;
③(a )= a ;④a ·a = a ;⑤a ·a =2 a ;⑥a +a =2 a
其中错误的有--------------------------------( )
A .2个 B.3个 C.4个 D.5个
3、计算(4×2n )2的正确结果是------------------------( )
A .4×22n B. 4
2n+4 C.22n D.22n+4 4、计算(-3)
2n+1+3×(-3)2n 结果正确是--------( ) A .32n+1 B. -32n+1 C.0 D.1
5、如果(9)=3,则n 的值是( )
A.4
B.2
C.3
D.无法确定
三、计算:
(1)、(83)4 (2)、-(y 7)2 (3)、(a )
(4)、(x 2n )3 (5)、[(-n )] (6)、(x 2)3 ·(x 2)2
(7)、(a·a 2)3 (8)、[(a-b 2x ]
(9)、[(a-b)3
]
2
·(b-a)
5
(10)、(x
n+1
)
2
-x
2
·(x
2
)
n
1.
(10)
(11)、(-x)+ 所示是一个多路负反馈二阶有源带通滤波器,它使用单个通用运算放大器(通用运放)接成单电源供电模式,易于实现。
它的上限截止频率和下限截止频率可以非常近,具有非常很强的频率选择性。
令C1=C2=C,Req是R1和
四、解答题
1、已知:2m·4 m·8,带宽BW,中心频率F,电容值C m的值。
另外关于PWM的低通滤波可以参考《德州仪器高性能单片机和模拟期间》。
