分数指数幂1
分数指数幂

第1、2课时【学习题目】 分数指数幂 【学习目标】(1) 复习整数指数幂的知识; (2)了解n 次根式的概念; (3) 理解分数指数幂的定义;(4)掌握根式与分数指数幂之间的转化;(5)会利用计算器求根式和分数指数幂的值,培养计算工具使用技能.【教学重点】分数指数幂的定义; 【教学难点】根式和分数指数幂的互化 【教具】多媒体课件、板书 【教学进程】一、创设问题情境----引入新知【课前导学】问题一:1、 如果29x =,则x = ;x 叫做9的 ;2、如果23x =,则x = ;x 叫做3的 ;3、如果38x =,则x = ;x 叫做8的 ;4、如果38x =-,则x = ;x 叫做-8的 .解 决 如果2x a =,那么x =a 的平方根(二次方根)a 的算术平方根;如果3x a =,那么x =a 的立方根(三次方根). 二、师生互动----探究新知: 问题二:1、n 次方根的概念? (一般地,如果(n x a n n =∈+N 且>1),那么x 叫做a 的n 次方根) 说明(1)当n 为偶数时,正数a 的n 次方根有两个,分别表示为a的n 次算数根;零的n 次方根是零;负数的n 次方根没有意义.例如,81的4次方根有两个,它们分别是3和−3,其中3叫做 81的4次算术根,3=.(2)当n 为奇数时,实数a 的n例如,32-的5次方根仅有一个是−2 , 2-. 2、n 次根式的概念?1n n ∈>+N 且)的式子叫做a 的n 次根式,其中n 叫做根指数,a 叫做被开方数.3、 读出下列各根式,并计算出结果?(1 (2 (3) (4. 4、 填空:(1)25的3次方根可以表示为 ,其中根指数为 ,被开方数为 ; (2)12的4次算术根可以表示为 ,其中根指数为 ,被开方数为 ;(3)-7的5次方根可以表示为 ,其中根指数为 ,被开方数为 ; (4)8的平方根可以表示为 ,其中根指数为 ,被开方数为 . 5、计算:32= ;23-= ;= ;423⎛⎫ ⎪⎝⎭= ;215-⎛⎫⎪⎝⎭= . 6、整数指数幂,当*n ∈N 时,na = ;并且规定当0a ≠时,0a = ; n a -= . 探究:将整数指数幂的概念进行推广:124= . *动脑思考 探索新知 概念规定:m na=其中m n n +∈N 、且>1.当n 为奇数时,a ∈R ;当n 为偶数时,0a ….当mna 有意义,且0a ≠,m n n +∈N 、且>1时,(1)mna-=(2)0的正分数指数幂等于0;(3)0的负分数指数幂无意义.这样就将整数指数幂推广到有理数指数幂. 三、师生协作------实践新知 问题三:1、 将下列各分数指数幂写成根式的形式:(1)47a ; (2)35a ; (3)32a-.分析 要把握好形式互化过程中字母的位置对应关系,按照规定,先正确找出公式中的m与n ,再进行形式的转化.解 (1)7n =,4m =,故47a = (2)5n =,3m =,故35a =(3)2n =,3m =,故32a-=.2、 将下列各根式写成分数指数幂的形式:(1(2(3.分析 要把握好形式互化过程中字母位置的对应关系,按照规定逆向进行形式的转化. 解 (1)3n =,2m =23x ; (2)3n =,4m =43a ;(3)5n =,3m =35a-=.说明:将根式写成分数指数幂的形式或将分数指数幂写成根式的形式时,要注意规定中的m 、n 的对应位置关系,分数指数的分母为根式的根指数,分子为根式中被开方数的指数. 四、技能训练1.将下列各根式写成分数指数幂的形式:;;2.将下列各分数指数幂写成根式的形式: (1)354-; (2)323; (3) 25(8)--; (4)341.2.3、用分数指数幂的形式表示下列各式:2(1)a3(2)a式中a >0)五、课堂小结,板书设计六、布置作业课本p71 第1、2题;。
分数指数幂 课件

2
1.3 3
可化为(
)
A. 2
3 C. 9
B. 3 D. 9
[答案] C
[解析]
2
33
=3 32=3 9.
2.若 a>0,n,m 为实数,则下列各式中正确的是( )
A.am÷an=amn
B.an·am=am·n
C.(an)m=am+n
D.1÷an=a0-n
[答案] D [解析] 由指数幂的运算法则知1÷an=a0÷an=a0-n正确, 故选D.
3 a15÷
a-3 a-1.
2
[思路分析] 将根式化为分数指数幂的形式,利用分数指 数幂的运算性质计算.
[解析] (1)原式=1+14×(49)12 -(1100)12 =1+16-110=1165.
37 3 (2)原式= a2 a-2 ÷
8
a-3
15
a3
3 ÷
3
a-2
1
a-2
=3 a2÷
7
a3
3 ÷
[思路分析] (1)关键是理解分数指数幂的意义,先将根式
化为分数指数幂的形式.
(2)运用分数指数幂的运算性质进行化简.
23
23
13
[解析] (1)原式=a3 ·a2 =a3 +2 =a 6 ;
111
111
111
7
(2)原式=[a·(a·a2 )2 ]2 =a2 ·a4 ·a8 =a2 +4 +8 =a8 ;
有条件的求值问题
已知
1
a2
+a-12
=3,求下列各式的值.
(1)a+a-1;
(2)a2+a-2;
3
a2
-a-32
(3) 1 a2
高中数学第21课时分数指数幂教案1苏教版必修1

江苏省新沂市第二中学高中数学第21课时分数指数幂教案1 苏教版必修1课题第十四课时分数指数幂(1)课型新授课教学目标1.理解n次方根及根式的概念;2.掌握n次根式的性质,并能运用它进行化简,求值;3.提高观察、抽象的能力.重点掌握n次根式的性质,并能运用它进行化简难点掌握n次根式的性质,并能运用它进行化简教法讲授法、讨论法、探究法教学过程教学内容个案调整教师主导活动学生主体活动自学评价1.如果2x a=,则x称为a的平方根;如果3x a=,则x称为a的立方根.2. 如果*(1,)nx a n n N=>∈,则x称为a的n次实数方根;0的n次实数方根等于0.3. 若n是奇数,则a的n次实数方根记作n a;若0>a则n a为正数,若oa<则n a为负数;若n是偶数,且0>a,则a的n次实数方根为n a±;负数没有n次实数方根.4. 式子n a()1,n n N*>∈叫根式,n叫根指数,a叫被开方数;()nn a=a.5. 若n是奇数,则n n a=a;若n是偶数,则n n a=||a.【精典范例】例1:求下列各式的值:(1)2(5)(2)33(2)-(3)44(2)-(4)()23π-【解】(1)2(5)5=(2)33(2)2-=-(3)4444(2)22-==(4)()23|3|3πππ-=-=-点评: 正确的领会求n n a的值的公式是求根式值的关键。
例2:设-3<x<3,化简961222++-+-xxxx追踪训练一1. 27的平方根与立方根分别是(B)(A)33,3(B)33,3±(C)33,3±(D)33,3±±2.2211x xx x--=--成立的条件是(()D)()A21xx-≥-()B1x≠()C1x<()D2x≥3.在①24(4)n-;②214(4)n+-;③54a;解:因为-3<x<3 所以x+3>0所以原式=|x -1|+|x+3| 当1≤x<3时,原式=2x+2当-3<x<1时,原式=1-x+x+3=4 综上所述原式=⎩⎨⎧<<≤+1x 3-43122,x ,x π例3.计算:625625++- 解:原式=22)23()23(++- =2323++-=23 ④54a (,n a ∈∈N R )各式中,有意义的是( ()B )()A ①② ()B ①③ ()C ①②③④ ()D ①③④板书设计当堂作业课外作业教师札记根式 根式定义 根式的性质 根式与方程关系根式的运算。
分数指数幂(1)_韦余玲

6
a
数学应用:
巩固练习:
(1)
3
(8) 3 4 (3 2) 4 3 (2 3 ) 3
4
9 3
(2)
(4 ) 4 3 (3 ) 3
7 2
情境问题:
问题2:初中整数指数幂的概念及其性质有哪些? 如下内容,你能补充完整吗?
n *
n
次方
探讨1:27的3次方根表示为
3
27 ,-32的5次方根表示为 5 32 ,
3 6
a 6 的3次方根表示为 a 。 x2 探讨2: 4,则x= 2 ,那么4的平方根是 2 。 x4 16 ,则x= 2 ,那么16的4次方根是 2 。
思考⑴:对于探讨2中问题,你有何发现?
a.a. (n N* ) = ⑴整数指数幂的概念: aa
n个a
an ,
a
0
=
1
(a≠0) , a =
m n
n
am n (m, nZ) ; ⑵运算性质: a = a
(a m ) n =பைடு நூலகம்a
⑶注意:①
mn
m
1 an
(a 0, n N*. )
(m, nZ) ; ab) n = anbn (n Z) . (
3.有理指数幂的运算性质
数学运用:
例2 求值 :
2 3
— 1 2
8
; 100
1 ; ( ) 3 ; 4
16 ( ) 4 81
3
数学应用:
练习: 下列说法:(1)正数的n次方根是正数;(2)负数的n次方根是负数; (3)0的n次方根是0;(4) 正确命题的序号).
分数指数幂1(新编2019)

一复习回顾
• 1.提问:正方形面积公式?正方体的体积 公式?
• 2.回顾初中根式的概念:如果一个数的平 方等于a,那么这个数叫做a的平方根;如 果一个数的立方等于a,那么这个数叫做a 的立方根. → 记法: a, 3 a
二讲授新课
• 1.指数函数模型及背景 • 实例1.某市人口平均年增长率为1.25℅,
1990年人口数为a万,则x年后人口数为多 少万? • 实例2例(细胞分裂). • 实例3. 给一张报纸,先实验最多可折多少 侯 冬十月 傉檀奔于南山 其将牵腾帅众降 义弗可矣 在北河西北 宗之破振将温楷于柞溪 秋七月 三柱一曰三泉 六月 遂泛舟东下 自馀封赏各有差 吴将陶璜等围交趾 武帝受禅 大旱 愍帝崩问至 癸酉 靡不由之 十一月 用告祸福 追复故皇太子位 而其妃后躬行四教 州县 讨斩之 天下同 八月 杀之 缪胤各还本部 异不得至寿春 进安西将军庾翼为征西将军 九坎间十星曰天池 依阿无心者皆名重海内 死之 八月 成帝因削弱之资 及岁常调非军国要急者 死者数千人 敕收其馀 百揆时叙于上 以为远近之数 奏事不名 降于石勒 藩镇有疆理之务 己巳 以兖州刺 史朱序为南中郎将 身服厥劳 斗 迁大将军 禁酒 九卿西五星曰内五诸侯 亦何足特痛哉 获石季龙将支重 谓千年而永治 三月 遣兼司空 右掖门也 章武王范之薨 必以文武为谥 夜行于平地 九月癸酉 十二月庚午 然少为舅氏所制 翟钊寇河南 大破之 舆鬼五星 刺史吴隐之为循所败 二曰宣 夜 示之以好恶 为文所败 众溃 天地之体 帝患之 封新城乡侯 进慕容皝为安北将军 改元 六月 范文寇九德 乞襦 己卯 而鸿雁之歌方远 地震水旱为变者相属 是岁 李雄将李寿寇巴东 色白 固辞策命 帝在长安 使两婢侍 令外人知 其北都没之顷 及帝登阼 天若如推磨右转而日西行者 以 挫其锋 获之 改元 石季龙寇历阳 愍帝奔播之
第三章 §1 指数幂的拓展

§1 指数幂的拓展学习目标 1.理解分数指数幂的含义,学会根式与分数指数幂之间的相互转化.2.了解无理指数幂和实数指数幂的含义.知识点一 分数指数幂 1.正分数指数幂给定正数a 和正整数m ,n (n >1,且m ,n 互素),若存在唯一的正数b ,使得b n =a m ,则称b 为a 的mn 次幂,记作b =mn a .这就是正分数指数幂.2.负分数指数幂给定正数a 和正整数m ,n (n >1,且m ,n 互素),定义m na -=1m na=1nam,这就是负分数指数幂. 思考 因为5-32=-2,所以()15322,-=-这种说法正确吗?答案 不正确,因为在指数幂的概念中,总有a >0. 知识点二 无理数指数幂无理数指数幂的定义:一般地,给定正数a ,对于任意的正无理数α,可以定义一个实数a α,自然地,规定a -α=1aα.1.0的指数幂总等于0.( × ) 2.指数幂m na ,总有a >0.( √ )3.分数指数幂m na 可以理解为mn 个a 相乘.( × )4.138-=12.( √ )一、n 次方根例1 (1)若81的平方根为a ,-8的立方根为b ,则a +b =________. 答案 7或-11解析 81的平方根为-9或9,即a =-9或9, -8的立方根为-2,即b =-2, ∴a +b =-11或7.(2)若4x -2有意义,求实数x 的取值范围. 解 ∵4x -2有意义,∴x -2≥0, ∴x ≥2,即x 的取值范围是[2,+∞).(学生)反思感悟 (1)方根个数:正数的偶次方根有两个且互为相反数,任意实数的奇次方根只有一个.(2)符号:根式na 的符号由根指数n 的奇偶性及被开方数a 的符号共同确定. ①当n 为偶数,且a ≥0时,na 为非负实数; ②当n 为奇数时,na 的符号与a 的符号一致. 跟踪训练1 (1)已知x 7=8(x >0),则x 等于( ) A .2 2 B.78 C .-78 D .±78 答案 B解析 因为7为奇数,8的7次方根只有一个78. (2)若42x +5有意义,则x 的取值范围是________; 若52x +5有意义,则x 的取值范围是________. 答案 ⎣⎡⎭⎫-52,+∞ R 二、根式与分数指数幂的互化例2 用分数指数幂表示下列各式(a >0):(1)3a 2;(2)a 3b 4;(3)a a . 解 (1)原式=23a . (2)原式=3432222a b a b =. (3)令b =a a =()12a a ,∴b 2=aa ,∴b 2a=a =12a ,∴⎝⎛⎭⎫b 2a 2=a ,即b 4a 2=a , ∴b 4=a 3,∴b =34a ,即原式=34.a 反思感悟 根式与分数指数幂互化的规律 (1)根指数分数指数幂的分母.(2)被开方数(式)的指数分数指数幂的分子.跟踪训练2 用分数指数幂表示下列各式(a >0,b >0): (1)ab 3;(2)a 3·a . 解 (1)原式=1322a b . (2)令b =a 3a ,∴ba3=a =12a ,∴⎝⎛⎭⎫b a 32=a ,即b 2a 6=a ,∴b 2=a 7. ∴b =72a ,即a 3·a =72a . 三、指数幂的计算 例3 计算:12(1)64; 231(2)27⎛⎫ ⎪⎝⎭;-32(3)16;- 131(4)8⎛⎫. ⎪⎝⎭ 解 (1)令12=64b ,∴b 2=64,∴b =8(b >0),1264=8.∴223323111(2)==2727127b ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭⎛⎫ ⎪⎝⎭,,-令∴b 3=⎝⎛⎭⎫1272=⎣⎡⎦⎤⎝⎛⎭⎫1332=⎣⎡⎦⎤⎝⎛⎭⎫1323, ∴b =⎝⎛⎭⎫132=19,2311==9.1279⎛⎫ ⎪⎝⎭-∴ (3)332232116,=1616b =,-令∴b 2=163=(42)3=(43)2,∴b =43=64(b >0),32116=64.-∴ (4)令b =1318⎛⎫⎪⎝⎭, ∴b 3=18=⎝⎛⎭⎫123,∴b =12,1311=82⎛⎫. ⎪⎝⎭∴ 反思感悟 指数幂的运算,一般用待定系数法,把分数指数幂转化为整数指数幂,利用整数指数幂的运算性质求解指数幂.跟踪训练3 把下列各式中的正数b 写成分数指数幂的形式. (1)b 3=32;(2)b 2=14;(3)b -3=34;(4)b -3m =42n (m ,n ∈N +).解 (1)b 3=32=25,53=2b .∴ (2)b 2=14,1214b ⎛⎫=. ⎪⎝⎭∴(3)b -3=34,433b =.-∴ (4)b -3m =42n =(22)2n =24n ,43=2n mb .-∴1.233可化为( ) A. 2 B. 3 C.39 D.9 答案 C解析 233=332=39.2.5a -2(a >0)可化为( ) A .25a- B .25a C .75a D .72a -答案 A3.已知(a -b )2=a -b ,则( ) A .a >b B .a ≥b C .a <b D .a ≤b答案 B 解析(a -b )2=|a -b |=a -b ,所以a -b ≥0,所以a ≥b . 4.m 6(m >0)的平方根为( ) A .m 3 B .-m 3 C .±m 3 D .|m |3 答案 C5.若b -5=32-3(b >0),则b =________. 答案 8解析 b -5=32-3=(25)-3=2-15,1535=2=2=8.b --∴1.知识清单:(1)正分数指数幂和负分数指数幂. (2)无理数指数幂和实数指数幂.2.常见误区:0的零指数幂和任意负实数指数幂没有意义.1.2的10次方根为( ) A.102 B -102 C.210 D .±102 答案 D 2.13m 2(m >0)化为分数指数幂为( )A .23m-B .23m C .32m-D .32m答案 A 解析13m2=23231=m m.-3.()3432x --中x 的取值范围是( )A .(-∞,+∞) B.⎝⎛⎭⎫-∞,32∪⎝⎛⎭⎫32,+∞ C.⎝⎛⎭⎫-∞,32 D.⎝⎛⎭⎫32,+∞ 答案 C解析 要使该式有意义,需3-2x >0,即x <32.4.若2<a <3,化简(2-a )2+4(3-a )4的结果是( ) A .5-2a B .2a -5 C .1 D .-1 答案 C解析 ∵2<a <3,∴a -2>0,a -3<0, ∴(2-a )2+4(3-a )4=|2-a |+|3-a |=a -2+3-a =1. 5.若b -3n=5m (b >0,m ,n ∈N +),则b 等于( )A .35n m- B .35m n- C .35n mD .35m n答案 B解析 若x p =y q (p ,q ∈N +,x >0,y >0),则3==5p m qny x b ,.-所以6.计算:148116⎛⎫⎪⎝⎭-=________. 答案 237.若31a -3有意义,则实数a 的取值范围是________. 答案 {a |a ≠3}解析 要使31a -3有意义,则a -3≠0,即a ≠3.所以a 的取值范围是{a |a ≠3}. 8.计算:23827⎛⎫ ⎪⎝⎭+⎝⎛⎭⎫340+3-2=________. 答案149解析 令b =23827⎛⎫⎪⎝⎭,∴b 3=⎝⎛⎭⎫8272=⎣⎡⎦⎤⎝⎛⎭⎫2332=⎣⎡⎦⎤⎝⎛⎭⎫2323, ∴b =⎝⎛⎭⎫232,∴原式=⎝⎛⎭⎫232+1+19=149. 9.计算下列各式的值:12(1)121; 1264(2);49-⎛⎫ ⎪⎝⎭ 34(3)10;-000 23125(4)27-⎛⎫. ⎪⎝⎭解 (1)令12121,b = ∴b 2=121,∴b =11(b >0),12121=11.∴(2)11221264164==49496449b -⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭⎛⎫ ⎪⎝⎭,,令 ∴b 2=6449,∴b =87(b >0),12647=498⎛⎫. ⎪⎝⎭-∴ (3)3434110=10000000,-34=10b 000,令∴b 4=10 0003=(104)3=(103)4, ∴b =103(b >0),∴3410000-=1103=11 000.(4)2233231251125=272712527b-⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭⎛⎫⎪⎝⎭,,令∴b3=⎝⎛⎭⎫125272=⎣⎡⎦⎤⎝⎛⎭⎫5332=⎣⎡⎦⎤⎝⎛⎭⎫5323,∴b=⎝⎛⎭⎫532(b>0),∴2312527⎛⎫⎪⎝⎭-=1⎝⎛⎭⎫532=925.10.已知4a4+4b4=-a-b,求4(a+b)4+3(a+b)3的值.解因为4a4+4b4=-a-b,所以4a4=-a,4b4=-b,所以a≤0,b≤0,所以a+b≤0,所以原式=|a+b|+a+b=-(a+b)+a+b=0.11.(多选)下列互化不正确的是()A.-x=()12x-(x>0)B.6y2=13y(y<0)C.2132x y-=3y2x(x>0,y>0)D.13x-=-3x(x≠0)答案ABD解析对于A,-x=12x,-故A错误;对于B,当y<0时,6y2>0,13y<0,故B错误;对于C,2132x y-=3y2x(x>0,y>0),故C正确;对于D,13x-=13x(x>0),故D错误.12.下列各式既符合分数指数幂的定义,值又相等的是()A.()()123611--和B.12200和-C.112424和D.332142⎛⎫⎪⎝⎭和--答案 C解析选项A中,()()123611--和均不符合分数指数幂的定义,故A不满足题意;选项B中,0的负实数指数幂没有意义,故B不满足题意;选项D中,332142⎛⎫⎪⎝⎭--和虽符合分数指数幂的定义,但值不相等,故D不满足题意;选项C中,111422422=24=2=2=2,,满足题意.13.已知二次函数f(x)=ax2+bx+0.1的图象如图所示,则4(a-b)4的值为()A.a+bB.-(a+b)C.a-bD.b-a答案 D解析由题图知f(-1)=a-b+0.1<0,∴a-b<0.∴4(a-b)4=|a-b|=-(a-b)=b-a.14.若x2-2x+1+y2+6y+9=0,则(x2 020)y=________.答案 1解析因为x2-2x+1+y2+6y+9=0,所以(x-1)2+(y+3)2=|x-1|+|y+3|=0,所以x=1,y=-3.所以(x2 020)y=(12 020)-3=1-3=1.15.若代数式2x-1+2-x有意义,则4x2-4x+1+24(x-2)4=________.答案 3解析∵2x-1+2-x有意义,∴⎩⎪⎨⎪⎧2x -1≥0,2-x ≥0,即⎩⎪⎨⎪⎧x ≥12,x ≤2,∴12≤x ≤2.∴4x 2-4x +1+24(x -2)4=(2x -1)2+24(x -2)4=|2x -1|+2|x -2|=2x -1+2(2-x )=3. 16.化简下列各式: (1)5-26+7-43;(2)a +2a -1+a -2a -1(a ≥1). 解 (1)原式=3-26+2+4-43+3=(3-2)2+(2-3)2=(3-2)+(2-3)=2- 2. (2)原式=(a -1)+2a -1+1+(a -1)-2a -1+1=(a -1+1)2+(a -1-1)2=(a -1+1)+|a -1-1|=⎩⎪⎨⎪⎧2,1≤a ≤2,2a -1,a >2.。
高中-数学-人教版-4.1.1 n次方根与分数指数幂(一)
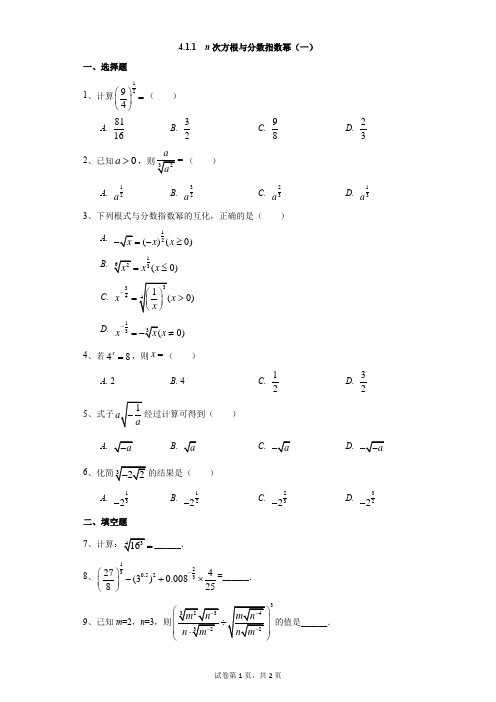
4.1.1 n 次方根与分数指数幂(一)一、选择题1、计算129=4⎛⎫ ⎪⎝⎭( )A.8116B.32C.98D.232、已知0a >=( )A.12aB.32aC.23aD.13a3、下列根式与分数指数幂的互化,正确的是( )A. 12()(0)x x =-≥B.13(0)x x =≤C. 340)xx -=>D. 130)x x -=≠4、若48x =,则x =( )A. 2B. 4C.12D.325、式子 )A.B.C.D. 6的结果是( )A.132- B.122- C.232- D.322-二、填空题7=______. 8、1230.523274(3)0.008825-⎛⎫-+⨯⎪⎝⎭=______. 9、已知m =2,n =3,则3的值是______.10、已知121217a a+=,则1a a -+=______.三、解答题11、计算:(1(0.5934-⎛⎫+- ⎪⎝⎭﹣(2)设0a >(3)若1122x x-+=12212x x x x --+-+-的值. 12、设22332100064a =⨯++ (1)化简上式,求a 的值;(2)设集合{}A x x a =>,全集为R ,B A =⋂RN ,求集合B 中的元素个数.参考答案1、【答案】B【分析】本题考查分数指数幂的运算.【解答】由题意可得111222229333===4222⨯⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦,选B.2、【答案】D【分析】本题考查根式与分数指数幂的互化及其化简运算.23a=2113323aa aa-===.选D.3、【答案】C【分析】本题考查根式与分数指数幂的互化.【解答】12(0)x x=-≥,故A13x=,故B错,130)x x-=≠,故D 错,选C.4、【答案】D【分析】本题考查分数指数幂的运算.【解答】由48x=得2322x=,∴23x=,∴32x=.选D.5、【答案】D【分析】本题考查根式的化简运算.【解答】∵a<0,∴==.选D.6、【答案】B【分析】本题考查根式与分数指数幂的互化及其化简运算.13111323222222.⨯⎛⎫==-⨯=-=-⎪⎝⎭选B.7、【答案】8【分析】本题考查根式与分数指数幂的互化及其化简运算.()1344322=8⎡⎤==⎢⎥⎣⎦.8、【答案】52答案第1页,共2页【分析】本题考查分数指数幂的运算. 【解答】120.5233274()(3)(0.008)825--+⨯211332332314()3()2525⎛⎫⨯-⨯⨯ ⎪⎝⎭=-+⨯353422=-+=. 9、【答案】227 【分析】本题考查根式与分数指数幂的互化及其化简运算.【解答】m =n =3,则原式=3231345323221322213m n mn m n m n nm nm ------⎡⎤⎛⎫⎛⎫⎢⎥÷=⨯ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎢⎥⎣⎦=m •n -3=2×3-3=227. 10、【答案】47【分析】本题考查分数指数幂的运算.【解答】2111221122117247a a a a a a -⎛⎫⎪+=∴+=+-=⎪⎝⎭,. 11、【答案】(1)4π3+;(2)116 a -;(3)14.【分析】本题考查根式与分数指数幂的互化及其化简运算. 【解答】(1)原式2411ππ33=+-+-=+;(2)原式4111326223a aaa a --⋅==⋅;(3)若1122x x-+=则14x x -+=,2214x x -+=,故122141121424x x x x --+--==+--. 12、【答案】(1)218;(2)219个.【分析】本题考查根式与分数指数幂的互化及其化简运算,集合的补集运算. 【解答】(1)原式223320002164=⨯++2100162=⨯++218=.(2){}218A x x =>,{}218A x x =≤R,{}0218B x x x =≤≤∈N ,,∴B 中元素个数为219.。
人教版数学必修12.1.1分数指数幂

37
9
(2)
(
1
)
1 2
( 4ab1 )3
4
1
0.1 2 (a3b 3) 2
1.
(
27
1
)3
(1)2 ( 1 )2
(
25
)
1 2
1
10
49
5
1
45
1000
7
9
3
3
13
2.
42 42
3
3
3
3
a2 a 2 b2 b 2
4
a0 b0
4
100Leabharlann 2525知识层面: 1.分数指数幂的意义就是正数的正分数指数幂的意义是
n
am n am (a > 0, m, n N* n > 1)
,零正的数正的分负数分次数幂指等数于幂零的,意零义的是负分a数mn 指a数1mn 幂没n 1有am意(a义>.
0,
m,
n
,
N*
n > 1)
2.规定了分数指数幂的意义后,指数的概念就从整数指数推广到了有
引入新课
回顾整数指数幂的定义与运算性质:
整数指数幂 an的含义为
an a a a (n N*), n个a
同时规定:a0
1
(a
0),an
1 an
(a 0, n N*);
整数指数幂的运算律⑴ am an amn;⑵ (am )n amn ;
⑶ (ab)n anbn ,以上 m、n Z.在各运算律中,
1
m
(a
>
0, m, n
N * ,且n
> 1)
an
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
*
64 个细胞 .
在上述例子中 x 只能取正整数我们还知道 , .
x
对于式子 2 , x 取 负 整 数和0 也是有意义的那 . 么, x 能取分数甚至无理数吗 ?
学习目标
1.理解n次实数方根与n次根式的概念. 2.理解分数指数幂的含义. 3.熟练掌握用根式与分数指数幂表示一个正 实数的算术根.
2 .2
指 数函数
某细胞分裂时由 1 个分裂成 2 个,2 个分裂成 4 个, , 4 个分裂成 8 个, 如果分裂一次需要 min, 那 10 么,1 个细胞1 h 后分裂成多少个细胞 ?
假设细胞分裂的次数为
x
x , 相应的细胞个数为
6
y,则
y 2 .当 x 6 时 , y 2 64 ,
1
m
(a 0, m, n 均为正整数).
a
n
且0的正分数指数幂为0,0的负分数指数幂没有意义.
分层训练
必做题: 书本P47 1 选做题:
x y
5 4
求
4
z
3
的值.
作业: 书本P48 习题2.2(1) 1
平方根
, 如果 x a , 那么 x 称为 a 的
2
( quadratic
root
); 如 ( cubic
果 x a, root ) .
n
3
那么称
x 为 a 的 立方根
一 般 地 , 如 果一个实
*
数 x满 足 x
a
( n 1 , n N ), 那么 称 x 为 a 的 n 次实数
方根 n th root .
(
_
)
当 n 为奇数时, x
n
a,
当n 为偶数时, x
n
a或x a, 0 ) (a
n
需要注意的是, 0的 n 次实数方根等于 0.
式子
n
a 叫做 根 式 ( radical ) , 其中 n 叫做根指数,
a 叫做被开方数 .
例:
求下列各式的值 : 5
自学指导
1.什么是平方根、立方根? 2. n次实数方根与根式是怎样下定义的?
考 3. 思
( )
n
a
n
,
n
an
.
4.理解分数指数幂的含义.
自学检测
求下列各式的值 :
(1) ( ( 3)
5
8
)
2
;
5
( 2) (
;
4
3
9
)
3
;
4
( 2 )
( 4) (3 )
.
反馈评价
1. 根式
我们知道
a
当n 为偶数时, a 0.
a, n为正奇数
an
a , n为正偶数.
2.
分 数 指数 幂
m n
一般地, 我们规定 a
n
a
m
(a 0, m, n 均为正整数).
这就是正数 的正分数指数幂的意义 a .
1 1
由此可知 2 2 的意义为2 2 ,
m n
2.
仿负整数指数幂的意义, a
(1) (
)
2
;
4
(2) (
;
32ຫໍສະໝຸດ )3;2
(3) 4 ( 2)
解
(4) (3 )
.
(1) ( (2) (
4
5
3
)
2
5.
2
)
4
3
2 .
4
(3) ( 2)
2
2
4
2.
(4 ) (3 )
( 3)
2
3.
思考
(
n
n
a
)
n
,
n
a
n
.
( a)
n n
当n 为奇数时, a R,
