2020高考数学预测试卷及答案

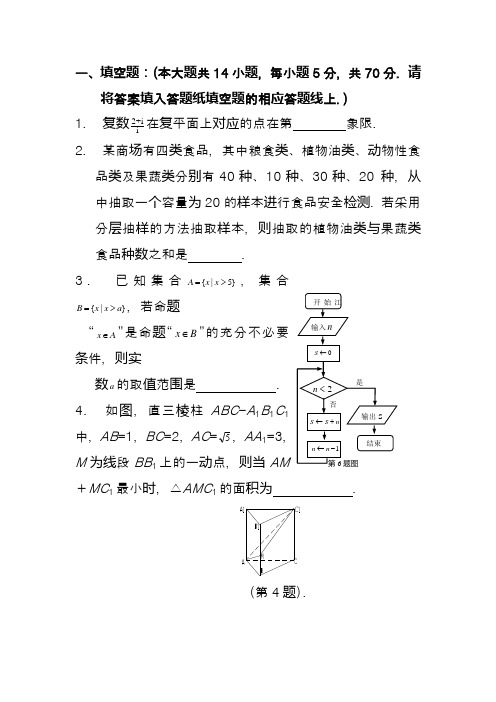
一、填空题：本大题共14小题，每小题5分，共计70分．请把答案填写在答卷纸的相应位置上．．．．．．．．．． 1．若复数z 满足(3)4i z i -=（i是虚数单位），则z = ▲ ．2．已知集合A ={x |6x +a >0}，若1∉A ，则实数a 的取值范围是 ▲ ．3．命题p ：函数y =tanx 在R 上单调递增，命题q ：△ABC 中，∠A >∠B 是sinA >sinB 的充要条件，则p ∨q 是 ▲ 命题．（填“真”“假”）4．某地区为了解中学生的日平均睡眠时间（单位：h ）， 随机选择了n 位中学生进行调查，根据所得数据 画出样本的频率分布直方图如图所示，且从左到 右的第1个、第4个、第2个、第3个小长方形 的面积依次构成公差为0.1的等差数列， 又第一小组的频数是10，则=n ▲ ．注 意 事 项考生在答题前请认真阅读本注意事项及各题答题要求 1．本试卷共4页，包含填空题（第1题——第14题）、解答题（第15题——第20题）．本卷满分160分，考试时间为120分钟．考试结束后，请将答题卡交回．2．答题前，请您务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请在答题卡上按照顺序在对应的答题区域内作答，在其他位置作答一律无效．作答必须用0．5毫米黑色墨水的签字笔．请注意字体工整，笔迹清楚．4． 如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗．5． 请保持答题卡卡面清洁，不要折叠、破损．一律不准使用胶带纸、修正液、可擦洗的圆珠笔．5．把一颗骰子投掷2次，观察出现的点数，记第一次出现的点数为a ，第二次出现的点数为b ，则方程组3,2 2.ax by x y +=⎧⎨+=⎩只有一个解的概率为 ▲ ．6．如果2(tan )sin 5sin cos f x x x x =-g ， 那么(5)f = ▲ ．7.已知双曲线1922=-my x 的一个焦点在圆05422=--+x y x 上，则双曲线的渐近线方程 为 ▲ ．8．程序框图如下，若恰好经过．．．．6．次．循环输出结果，则a = ▲ ．9．将函数y ＝sin （2x ＋56π）的图象向左平移至少 ▲ 个单位，可得一个偶函数的图象．10. 已知直线l ⊥平面α，直线m ⊂平面β，给出下列命题： ① 若//αβ，则l m ⊥； ②若αβ⊥，则//l m ； ③ 若//l m ，则αβ⊥； ④若l m ⊥，则//αβ. 其中正确命题的序号是 ▲ ．1 1 1 1 1 1 …Y结束开始0,1T i ←←(1)i T T a a a Z ←+>∈且输出T 200T >N1i i ←+11．某资料室在计算机使用中，产生如右表所示的编码，该编码以一定的规则排列，且从左至右以及从上到下都是无限的．此表中，主对角线上数列1，2，5，10，17，…的一个通项公式na =▲ ．12. 在ABC ∆中，A （1，1），B （4，5），C （—1，1）， 则与角A 的平分线共线且方向相同的单位向量 为 ▲ ．13. 已知函数f (x )满足f (1)=41，f (x )+ f (y )=4f (2y x +)g f (2y x -)(x ,y ∈R )，则f (—2011)=▲ ． 14. 已知二次函数2(),f x x x k k Z=-+∈，若函数2)()(-=x f x g 在31,2⎛⎫- ⎪⎝⎭上有两个不同的零点，则)(2)]([2x f x f +的最小值为▲ ．1 2 3 4 5 6 … 1 3 5 7 9 11 … 1 4 7 10 13 16 … 1 5 9 13 17 21 … 1 6 11 16 21 26 …… … … … … … …二、解答题：本大题共6小题，共计90分．请把答案写在答题卡相应的位置上．解答时应写出文字说明，证明过程或演算步骤．15．(本题满分14分)已知∆ABC 的面积S 满足443S ≤≤，且AB AC ⋅u u r u u u r=—8．（Ⅰ）求角A 的取值范围； （Ⅱ）若函数22cos 2sin 33sin cos 4444()x xx xf x -+⋅=，求()f A 的最大值．16．(本题满分14分)如图，把长、宽分别为4、3的长方形ABCD 沿对角线AC 折成直二面角．（Ⅰ）求顶点B 和D 之间的距离；（Ⅱ）现发现BC 边上距点C 的31处有一缺口E ，请过点E作一截面，将原三棱锥分割成一个三棱锥和一个棱台两部分，为使截去部分体积最小，如何作法？请证明你的结论．ABCDE .AC BE . D17．(本题满分15分)如图，已知：椭圆M 的中心为O ，长轴的两个端点为A 、B ，右焦点为F ，AF=5BF ．若椭圆M 经过点C ，C 在AB 上的射影为F ，且△ABC 的面积为5． （Ⅰ）求椭圆M 的方程；（Ⅱ）已知圆O ：22+x y =1，直线:l mx ny +=1，试证明：当点P (m ，n )在椭圆M 上运动时，直线l 与圆O 恒相交；并求直线l 被圆O 截得的弦长的取值范围．18．(本题满分15分)各项均为正数的等比数列}{n a ，a 1=1，2a 4a =16，单调增数列}{n b 的前n 项和为n S ，43a b =，且2632n n n S b b =++（*N n ∈）． （Ⅰ）求数列}{n a 、}{n b 的通项公式；xO F A F B Cy（Ⅱ）令nn nb c a =（*N n ∈），求使得1n c >的所有n 的值，并说明理由．(Ⅲ) 证明}{n a 中任意三项不可能构成等差数列．19．(本题满分16分)由一个小区历年市场行情调查得知，某一种蔬菜在一年12个月内每月销售量()P t （单位：吨）与上市时间t （单位：月）的关系大致如图（1）所示的折线ABCDE 表示，销售价格()Q t （单位：元／千克）与上市时间t （单位：月）的大致关系如图（2）所示的抛物线段GHR 表示（H 为顶点）． （Ⅰ）请分别写出()P t ,()Q t 关于t 的函数关系式，并求出在这一年内3到6月份的销售额最大的月份？ （Ⅱ）图（1）中由四条线段所在直线．．．．围成的平面区域为M ，动点(,)P x y 在M 内（包括边界），求5z x y =-的最大值； (Ⅲ) 由（Ⅱ），将动点(,)P x y 所满足的条件及所求的最大值由加法运算类比到乘法运算（如1233x y ≤-≤类比为2313x y≤≤），试列出(,)P x y 所满足的条件，并求出相应的最大值．（图1）（图2）20．(本题满分16分)如果实数x ，y ，t 满足|x —t |≤|y —t |，则称x 比y 接近t ．（Ⅰ）设a 为实数，若a |a | 比a 更接近1，求a 的取值范围；（Ⅱ）f (x )=ln 11+-x x ，证明：2()nk f k =∑比222(1)n n n n --+更接近0（k∈Z ）．数学附加题(满分40分，考试时间30分钟)21．【选做题】在A ，B ，C ，D 四小题中只能选做2题，每小题10分，共计20分．解答应写出文字说明、证明过程或演算步骤．A ．选修4—1 几何证明选讲 已知ABC ∆中，AC AB =,D 是ABC ∆外接圆劣弧AC 上的点（不与点C A ,重合），延长BD 至E . 求证：AD 的延长线平分CDE ∠.B ．选修4—2 矩阵与变换 已知矩阵⎥⎦⎤⎢⎣⎡=41b a A ，若矩阵A 属于特征值1的一个特征向量为α1＝⎥⎦⎤⎢⎣⎡-13，属于特征值5的一个特征向量为α2=⎥⎦⎤⎢⎣⎡11．求矩阵A ，并写出A 的逆矩阵．C ．选修4—4 参数方程与极坐标 已知圆C的参数方程为()为参数θθθ⎩⎨⎧+=+=sin 23,cos 21y x ，若P 是圆C 与x 轴正半轴的交点，以原点O 为极点,x 轴的正半轴为极轴建立极坐标系，设过点P 的圆C 的切线为l ，求直线l 的极坐标方程．D ．选修4—5 不等式证明选讲设c b a ,,均为正数，证明：c b a ac c b b a ++≥++222.【必做题】第22题、第23题，每题10分，共计20分．解答应写出文字说明、证明过程或演算步骤．22.已知一口袋中共有4只白球和2只红球（1）从口袋中一次任取4只球，取到一只白球得1分，取到一只红球得2分，设得分为随机变量X，求X的分布列与数学期望；（2）从口袋中每次取一球，取后放回，直到连续出现两次白球就停止取球，求6次取球后恰好被停止的概率．23.在平面直角坐标系xoy中，已知焦点为F的抛物线y2=上x4有两个动点A、B，且满足FB=, 过A、B两点分别作AFλ抛物线的切线，设两切线的交点为Ｍ．（1）求：→--OA→--⋅OB的值；（2）证明：ABFM⋅为定值．参考答案一、填空题 1. —1+3i 2. (,6]-∞- 3. 真 4. 100 5.11126. 07.x y 322±= 8. 2 9.3π 10.①③ 11. (n —1)2+1 12. )552,55(-13. 1414.2881 二、解答题15. （Ⅰ）∵AB AC ⋅u u u r u u u r =—8，∴||||cos AB AC AB AC A ⋅⋅⋅=u u r u u u r u u r u u u r=—8，∴ ||||AB AC ⋅u u r u u u r=8cos A- ① ∵|1|||sin 2BA AC S A ⋅=⋅uu r u u r ②将①代入②得4tan S A =-，由443S ≤≤，得3tan 1A -≤≤-，又(0,)A π∈，∴23,34A ππ⎡⎤∈⎢⎥⎣⎦.（Ⅱ）22()cos 2sin 33sincos 4444A A A Af A =-+⋅ =133(1cos )(1cos )sin22222A A A +--+ =3331sincos 22222A A +-=3113(sin cos )22222A A +- =13(sin cos cos sin )26262A A ππ+-=13sin()262A π+-，当262A ππ+=，即A =32π时，sin()26A π+ 取得最大值， 同时，()f A 取得最大值52．16. （Ⅰ）ACD OD ACD BO AC ACD ABC ABC BO 面面面面面面面⊂⊥⇒⎪⎪⎭⎪⎪⎬⎫=⋂⊂⊥∆ACD ABC O 垂足为AC,⊥BO 中作ABC 在BO OD ⎫⇒⊥⎬⎭ 由已知BO=512,OD=5193在Rt △BOD 中, BD=5337.（Ⅱ）方案(一)过E 作EF//AC 交AB 于F,EG//CD,交BD于G,EEG EF ACD 面EG//同理 ////=⋂⇒⎪⎭⎪⎬⎫⊂⊄ACD EF ACD AC ACD EF ACEF 面面面,⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫平面EFG//平面ABCDE.ACD原三棱锥被分成三棱锥B-EFG 和三棱台EFG-CAD 两部分,此时278)32(3==--ACD B EFG B V V . 方案(二)过E 作EP//BD 交CD 于P,EQ//AB,交AC于Q,同(一)可证平面EPQ//平面ABD,原三棱锥被分割成三棱锥C-EPQ 和三棱台EPQ-BDA 两部分,此时271)31(3==--BDAC EPQ C V V , 为使截去部分体积最小,故选用方案(二).17. （Ⅰ）由题意设椭圆方程为22221x y a b+=，半焦距为c ，由AF=5BF ，且AF=a+c,BF=a —c ，∴a+c=5（a-c ），得2a=3c .（1）由题意CF ⊥AB ，设 点C 坐标（c ，y ），C 在M上，代入得22222222()(1)c a c y b a a -=-=∴22a c y a-=． 由△ABC的面积为5，得221252a c a a-⋅⋅=，22a c -=5.（2） 解（1）（2）得a =3， c =2. ∴222b a c =-=9—4=5．∴所求椭圆M的方程为：22195x y +=．(Ⅱ) 圆O 到直线:l mx ny +=1距离d =221m n+，由点P (m,n )在椭圆M上，则22195m n +=，显然22m n +>2295m n +，∴22m n +>1，22m n +>1, ∴d =221m n+<1，而圆O 的半径为1，直线l 与圆O 恒相交． 弦长t =221d-=22211m n -+,由22195m n +=得225(1)9m n =-，∴22219445m n m =++, t =2291445m -+,||m a≤Q ，∴209m ≤≤，24544581m ≤+≤，∴2498154459m ≤-≤+ ，弦长t 的取值范围是[4542,53]．18．（Ⅰ）∵2a 4a =244116a q q ==，2q =4，∵0n a >，∴q =2， ∴12-=n n a∴b 3=4a ＝8. ∵263n n n S b b =++2 ① 当n ≥2时，211163n n n S b b ---=++2 ②①-②得2211633n n n n n b b b b b --=-+-即111()()3()n n n n n n b b b b b b ---+-=+ ∵0>nb ∴1n n b b --=3，∴}{n b 是公差为3的等差数列．当n ＝1时，211163b b b =++2，解得1b =1或1b =2，当1b =1时，32n b n =-，此时3b =7，与83=b 矛盾；当31=b 时31n b n =-，此时此时3b =8=4a ，∴31n b n =-．（Ⅱ）∵31n b n =-，∴n n nb c a =＝1312n n --，∴1c =2>1，2c =52＞1，3c =2>1,4118c =>1，578c =<1，下面证明当n ≥5时，1n c < 事实上，当n ≥5时，11323122n n n n n n c c +-+--=-＝432nn -＜0 即1n n c c +<，∵578c =<1 ∴当n ≥5时，1<n C ，故满足条件1>n C 的所有n 的值为1，2，3，4．(Ⅲ)假设}{n a 中存在三项p ,q ,r (p <q <r ,p ,q ,R ∈N *)使a p ,a q , a r 构成等差数列，∴ 2a q =a p +a r ，即2g 2q —1=2p —1+2r —1．∴2q —p +1=1+2r —p ． 因左边为偶数，右边为奇数，矛盾．∴假设不成立，故不存在任意三项能构成等差数列．19.解(Ⅰ)503,136,()1169,7912t t t t P t t t t t -+≤≤⎧⎪-<≤⎪=⎨-+<≤⎪⎪-<≤⎩ 21()(4)6(012)16Q t t t =--+≤≤．21()()(1)[(4)6]16P t Q t t t ⋅=---+ （36)t <≤'23(()())[(3)33]16P t Q t t ⋅=---0>在(3,6]t ∈恒成立，所以函数在]6,3(上递增当t =6时，max [()()]P t Q t g =34.5． ∴6月份销售额最大为34500元 ． (Ⅱ) ⎩⎨⎧≤-≤≤+≤71115y x y x ，z =x —5y ．令x —5y=A (x +y )+B(x —y )，则⎩⎨⎧=-=⇒⎩⎨⎧-=-=+3251B A B A B A ， ∴z =x —5y=—2(x +y )+3(x —y )．由10)(222-≤+-≤-y x ,21)(33≤-≤y x ，∴1911z -≤≤,则(z )max =11 ．(Ⅲ)类比到乘法有已知⎪⎩⎪⎨⎧≤≤≤≤71115y x xy ,求5y xz =的最大值．由5y x =(xy )A ·(yx )B⎩⎨⎧=-=⇒⎩⎨⎧-=-=+3251B A B A B A ．∴251)(12112≤≤-xy ,343)(13≤≤xy ∴253431211≤≤z ，则(z )max = 25343 ． 20. (Ⅰ)|a |a |—1|≤|a —1| （1）当0<a <1时, |a 2—1|≤|a —1|1-a 2≤1—a ，得a ≥1或a ≤0(舍去)（2）当a ≥1时，a 2—1≤a —1, 得a = 1；（3）当 a ≤0时， a 2+1≤1—a ，—1≤a ≤0 ．综上， a 的取值范围是{a |—1≤a ≤0或a =1} (Ⅱ) ∵+=∑=31ln )(2nk k f 42ln +53ln +…+11ln +-n n =)1(2ln+n n ， ∴2|()0|nk f k =--∑22|0|2(1)n n n n ---+=)1(22)1(2ln2+-+-+-n n n n n n ．令n （n +1）=t ，2≥n Θ∴t ∈),6[+∞，且t ∈Z ，则F （t ）=tt t222ln --- =tt t 22ln 2ln --+-．=-⋅--=x x xx xx F 2)2(12221)('x x x x 42224--=04)2(22<--xx x∴F （x ）在),2[+∞单调递减 ∴F （t ）≤f （6）<F(2)=—ln 1—0=0 ．∴0222ln ≤---t t t ,即)1(22)1(2ln 2+-+-+-n n n n n n ≤0．∴2()nk f k =∑比222(1)n n n n --+更接近0．附加题参考答案及评分标准A ．选修4—1 几何证明选讲 解（Ⅰ）设F 为AD 延长线上一点 ∵D CB A ,,,四点共圆， ∴CDF ABC ∠=∠3分 又ACAB = ∴ACBABC ∠=∠,5分 且ACB ADB ∠=∠, ∴CDFADB ∠=∠,7分对顶角ADB EDF ∠=∠, 故CDF EDF ∠=∠, 即AD的延长线平分CDE∠.10分B ．选修4—2 矩阵与变换 解：由矩阵A 属于特征值1的一个特征向量为α1＝⎥⎦⎤⎢⎣⎡-13可得，⎥⎦⎤⎢⎣⎡41b a⎥⎦⎤⎢⎣⎡-13＝⎥⎦⎤⎢⎣⎡-13， 即33=-b a ；3分由矩阵A 属于特征值5的一个特征向量为α2＝⎣⎢⎢⎡⎦⎥⎥⎤11，可得⎥⎦⎤⎢⎣⎡41b a ⎥⎦⎤⎢⎣⎡11＝5⎥⎦⎤⎢⎣⎡11，即5=+b a ，6分 解得⎩⎨⎧==32b a 即A ＝⎥⎦⎤⎢⎣⎡4312，7分 A 的逆矩阵是⎥⎥⎥⎦⎤-⎢⎢⎢⎣⎡-52535154 10分C ．选修4—4 参数方程与极坐标 解由题设知,圆心()()0.2, 3,1P C2分∠CPO=60°,故过P 点的切线的倾斜角为30° 4分设()θρ,M 是过P 点的圆C 的切线上的任一点， 则在△PMO 中，∠MOP=θ 00150, 30=∠-=∠OPM OMP θ由正弦定理得()θρ-=∴∠=∠0030sin 2sin150, sin sin OMP OP OPM OM8分()()()130sin 160cos 00=-=+∴θρθρ或，即为所求切线的极坐标方程. 10分D ．选修4—5 不等式证明选讲 证明：)()()(222222a ac c c b b b a c b a a c c b b a +++++=+++++3分c b a 222++≥ 9分即得c b a ac c b b a ++≥++222.10分另证利用柯西不等式.232221232221332211b b b a a a b a b a b a ++++≤++取a b c b b b ac a cb a ba a ======321321,,,,,代入即证.22.解：（1）X 的可能取值为4、5、6.P(X=4)= 1514644=C C P(X=5)= 158461234=C C C P(X=6)=156462224=C C C ∴X的分布列为P 456X 151158 156 ∴316156615851514)(=⨯+⨯+⨯=X E5分(2)设 “6次取球后恰好被停止”为事件A则72944323231]32)31(323132)31[()(2233=⨯⨯⨯⨯+⨯⨯+=C A P∴6次取球后恰好被停止的概率为7294410分23.解：设)4,(),4,(222211x x B x x AΘ焦点F （0,1）∴)14,(),41,(222211-=--=x x FB x x AFΘ FB AF λ=∴⎪⎩⎪⎨⎧-=-=-)14(41222121x x x x λλ 消λ得0)41()14(212221=-+-x x x x 化简整理得0)14)((2121=+-x x x x21x x ≠Θ421-=∴x x144222121=⋅=∴x x y y∴32121-=+=⋅y y x x OB OA （定值）（2）抛物线方程为241x y =x y 21='∴∴过抛物线A 、B 两点的切线方程分别为4)(212111x x x x y +-=和4)(212222x x x x y +-=即421211x x x y -=和421222x x x y -=联立解出两切线交点M 的坐标为⎪⎭⎫⎝⎛-+1,221x x ⎪⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-+=⋅∴4,2.221221221x x x x x x AB FM =02221222122=---x x x x （定值）。